Introduction

Fluorescence lifetime imaging microscopy (FLIM) has emerged as a powerful technique for biomedical imaging and sensing1,2,3,4,5. By resolving the excited state lifetime of endogenous and exogenous fluorophores, FLIM provides quantitative readouts of biochemical microenvironments related to metabolism, bonding, ion concentration, and more4,5,6. This functional imaging modality holds great promise for unraveling disease pathogenesis, guiding interventions, and monitoring treatments. However, widespread adoption of FLIM faces substantial barriers that have hindered clinical translation and utility. Conventional FLIM relies on time-correlated single photon counting (TCSPC) to construct fluorescence decay profiles with picosecond resolution7,8,9. While highly informative, TCSPC-FLIM acquires data sequentially pixel-by-pixel, imposing a trade-off between imaging speed, resolution, and field of view (FOV). Typical frame rates of minutes per megapixel restrict continuous observation of dynamic processes. Furthermore, prolonged exposure (repeated raster scanning involved in TCSPC) may increase photobleaching, phototoxicity, and susceptibility to sample perturbation and motion artifacts, especially for photon-inefficient two-photon FLIM. TCSPC also requires high peak power to achieve sufficient photon counts, precluding non-invasive imaging of live tissues. This codependence between measurement duration and fidelity has persisted as a fundamental limitation in FLIM.

Recent advances in FLIM have aimed to address these weaknesses through parallel detection schemes and gating methodologies. Wide-field time-gated FLIM10,11 provides 2D imaging at video rate but lacks depth sectioning. Light-sheet FLIM12,13 achieves fast optical sectioning yet requires sample transparency. Frequency-domain FLIM14,15 boasts image speed and superb sensitivity without temporal resolution and full decay information. While promising, these emerging techniques still face challenges in balancing field-of-view, resolution, depth sectioning, and acquisition speed. Notably, all FLIM modalities fundamentally suffer from trade-offs between measurement time and information content. Short measurement times yield sparse photon data, producing noisy fluorescence decay profiles that corrupt precision and accuracy of lifetime determination. Longer acquisition times enhance photon counts and decay statistics at the cost of observation latency. Modern FLIM systems sacrifice imaging speed to maintain fidelity. Circumventing this codependence could transform FLIM capabilities.

Recent years have witnessed remarkable advances in deep learning for imaging applications. In microscopy, deep learning has enabled denoising16,17, extended depth of field18, and super-resolution19,20. However, deep learning remains relatively unexplored in FLIM thus far. Modern deep learning strategies for FLIM analysis have predominantly focused on enhancing one-dimensional (1D) lifetime curves21,22,23 or two-dimensional (2D) mean lifetime maps24,25,26. While showing promising improvements, 1D and 2D analysis cannot fully leverage the rich spatial-temporal relationships within time-resolved FLIM data. Capturing correlations across the 3D data volume could enhance photon enrichment and denoising. The reported methods operated on already fitted lifetime data, which precluded recovering hidden information prior to fitting. Moreover, most networks have been evaluated on only single cell types or microscopic modes, with limited assessment in complex imaging environments. Rigorous validation across diverse imaging modes is imperative.

Here, we demonstrate SparseFLIM, an intelligent paradigm to reconstruct high-fidelity FLIM data from sparse photon measurements using coupled bidirectional propagation network. SparseFLIM enables significantly increasing photons and recovering hidden spatial-lifetime information in FLIM data. Quantitative analysis shows over tenfold photon enrichment, dramatically improving signal-to-noise ratio (SNR), lifetime accuracy, and correlation compared to the original sparse data. SparseFLIM also enables fast imaging by reconstructing spatially and temporally undersampled FLIM. The model generalizes well across experimental modalities including multispectral FLIM and in vivo endoscopic FLIM. By learning hidden information, semantic relationships, and avoiding noise overfitting, SparseFLIM circumvents conventional trade-offs to expand the utility of FLIM across biomedicine.

Results

SparseFLIM via bidirectional information flow learning

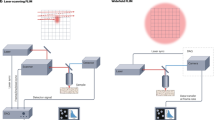
FLIM measurements were performed using a synchronized system comprising a femtosecond laser (~100 fs, 80 MHz, Chameleon Discovery, Coherent), galvanometric scanner (LSKGG4, Thorlabs), and high-speed time-resolved detectors (HPM-100-40, Becker & Hickl GmbH). The femtosecond excitation beam was relayed, magnified, and corrected by scan lenses (SL50-2P2, Thorlabs) and tube lenses (TTL200MP, Thorlabs) to match the back aperture of a 20× objective (MRD70200, 0.75 NA, Nikon), as shown in Fig. 1a. Emitted fluorescence was collected by the objective and separated from excitation using a long-pass dichroic (DMLP650R, Thorlabs). The second long-pass dichroic (DMLP490R, Thorlabs) split fluorescence from SHG signals. Fluorescence was then detected by the time-resolved detector connected to TCSPC electronics (SPC-150 and DCC-100, Becker & Hickl GmbH), which was synchronized with the laser signal to facilitate precise calibration of time delays. The data acquisition (DAQ) system generated frame pulses, line pulses, and pixel pulses based on the XY scanning signals using three counters, which were subsequently directed to the TCSPC electronics. The synchronization of time signals with scan signals resulted in the creation of a lifetime image as seen in Fig. 1b, providing information about the photon number distribution across spatial and temporal dimensions, \(n(x,y,t)\). We employed multi-field scanning to acquire big amounts of data for deep learning. For a 512 × 512 image with sufficient photon counts (around 1000 photons per pixel), the acquisition time is nearly 150 s without exogenous fluorescent labeling. For the same image size, but with sparse photon counts (around 100 photons per pixel), the acquisition time is nearly 10 sec (Fig. 1c). The SparseFLIM method is designed to process this sparse photon data and reconstruct it to match the quality of the sufficient photon data, which traditionally demands a much longer acquisition time. This suggests that SparseFLIM can achieve a remarkable 15-fold improvement in imaging speed while enhancing image quality and preserving critical information content.

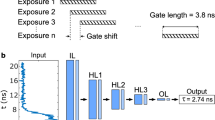
Fig. 1: General principle and validation of SparseFLIM.
figure 1

a FLIM setup and data acquisition. b Photon distribution in the \({{{\boldsymbol{x}}}}\)-\({{{\boldsymbol{y}}}}\) plane. c Comparison of photon counts between sparse and sufficient acquisition modes. d 2D mean lifetime (\({{{{\boldsymbol{\tau }}}}}_{{{{\boldsymbol{m}}}}}\)) images (left) and 3D lifetime stacks (right). e Network architecture of SparseFLIM. \({{{{\boldsymbol{t}}}}}_{{{{\boldsymbol{i}}}}}\) indicates the ith-frame time. \({{{{\boldsymbol{F}}}}}_{{{{\boldsymbol{f}}}}}\), forward propagation branch; \({{{{\boldsymbol{F}}}}}_{{{{\boldsymbol{b}}}}}\), backward propagation branch. \({{{\boldsymbol{A}}}}\), aggregation blocks. \({{{{\boldsymbol{F}}}}}_{{{{\boldsymbol{f}}}}}\) and \({{{{\boldsymbol{F}}}}}_{{{{\boldsymbol{b}}}}}\) are coupled indicated by the cyan arrow line. f Information refilling module. FE feature extractor; Conv convolution operations; Res residual blocks. g Comparison of the sparse photon input, network output, and sufficient photon reference. h Autofluorescence decay of the location indicated by the cross in g for the sparse photon acquisition. i Data restored from the sparse photon recording using our network, which is consistent with the autofluorescence decay of the sufficient photon recording. The bottom panels correspond to the fitting residuals. Also, see Supplementary Movie 1. Scale bar, 100 μm.

Full size image

Instead of reconstructing 1D time curves21,22,23 or 2D mean lifetime (\({\tau }_{m}\)) images that were fitted with a selected fitting algorithm24,25,26, our approach involved the reconstruction of the underlying \(x\)-\(y\)-\(t\) data. We decomposed the raw data into 3D stacks, each consisting of \({N}_{t}\) frames with an interval of 48.9 ps and a time span of ~5 ns. This temporal range was sufficient to reconstruct the autofluorescence lifetime accurately6,27,28, reducing non-semantic information learning repetitions and graphics memory requirements (“Methods”). Data of sparse photons and data of sufficient photons are sent to the network in pairs for training.

The basic principle of SparseFLIM is illustrated in Fig. 1e. This network was adapted from a video super-resolution framework29 and primarily consists of two branches: the forward branch (\({F}_{f}\)) and the backward branch (\({F}_{b}\)), which facilitate bidirectional information flow. The forward branch processes frames sequentially from the start to the end of the sequence. Each frame's features are computed from the current frame and the previous frames' propagated features. This allows accumulating information from preceding frames. Conversely, the backward branch processes frame recursively from the end to the start of the sequence. This allows incorporating future frame context. By leveraging correlations in both forward and reverse directions, the bidirectional propagation enables effectively accumulating long-term spatiotemporal information to maximize context available for reconstruction.

The coupled propagations exchange information between the forward and backward propagation branches. Specifically, the backward-propagated features are provided as additional inputs to the forward propagation branch, allowing the forward branch to exploit relevant features from future frames. Similarly, the forwards-propagated features are fused into the backward branch, providing it access to contextual guidance from preceding frames. This interconnection enables each branch to integrate useful features from the entire FLIM sequence, rather than just unidirectional segments. The feature exchange facilitates more holistic sequence modeling for high-fidelity photon enrichment and lifetime recovery.

The forward and backward propagation blocks concatenate into the aggregation block. The concatenation in the network consolidates complementary information from the bidirectional propagation branches via and produces high-fidelity FLIM reconstructions by capitalizing on the enriched features from both directions.

Additionally, the network incorporates a feature extractor from video restoration with enhanced deformable convolutional networks (EDVR)30. This approach can extract spatial and temporal features from the keyframes and their neighboring frames (Fig. 1f). The features extracted by EDVR include feature maps of different levels, which possess varying resolutions and distinct feature information. In the pyramid structure of cascading and deformable convolutions, the higher levels contain more structural information, but their positional information may undergo slight changes due to the blurring effect caused by repeated convolution and pooling operations. Conversely, the lower levels harbor richer details such as edge textures with more precise positional information. Therefore, performing deformable convolution based on different feature maps can generate more complex transformations, enabling the model to learn how to extract features from reference frames within complex spatiotemporal patterns. This mechanism is particularly beneficial for detailed regions where photon numbers are scarce. We also used temporal and spatial attention30 to fuse complementary features from the infrequent key frame extraction. This module aids the network in disregarding irrelevant feature information while emphasizing pertinent feature data for the reconstruction process.

An example reconstruction of a sparse photon lifetime image was presented in Fig. 1g. The cumulative intensity (\(I\)) image depicts the tissue structure clearly despite the limited photons. However, the mean fluorescence lifetime (\({\tau }_{m}\)) map31, derived from a bi-component fitting (Methods), exhibits a significant deviation from the \({\tau }_{m}\) map obtained with sufficient photons. After applying the network restoration, the \({\tau }_{m}\) map closely resembles the sufficient photon \({\tau }_{m}\), with underlying photon enrichment. Thus, the resulting composite image (\({I\times \tau }_{m}\)) parallels with that of sufficient photons (Fig. 1g). Specifically, we find that fluorescence decay curve of sparse photons (Fig. 1h) displays lower confidence compared to the results following network reconstruction (Fig. 1i). A low value for chi-square (\({\chi }^{2}\)) value means there is little difference between what was observed and what would be expected. The distribution of fluorescent photons in the sparse input data appears irregular, with the fitted \({\tau }_{m}\) at 0.6 ns (Fig. 1h). This leads to a 40% difference between the \({\tau }_{m}\) of network reconstruction and the reference \({\tau }_{m}\) for the sufficient photon data (1 ns in Fig. 1i). In the sparse input, the lack of photons and excessive noise prevents resolving the correct lifetime. However, during training on the photon-rich data, the network learns the lifetime features of different lifetime populations/components. When reconstructing from the sparse input, it can leverage this learned knowledge to “unmix” the disordered lifetime distribution and recover the underlying bifurcated ~1 ns components seen in the reference.

Moreover, the residual error of the SparseFLIM result is largely lower than that of the sparse input and even smaller than that of the sufficient photons as observed in the bottom panel of Fig. 1h, i. This smoothness arises because the network cannot effectively learn or reconstruct independent noise components with a zero mean present in the input data. As a result, when reconstructing from the sparse input during inference, the network can recover the high-SNR fluorescence decay patterns while inherently filtering out the random noise components that were present in the original sparse input. This noise suppression capability of the network leads to smoother and cleaner fluorescence decay traces in the SparseFLIM reconstruction compared to the high SNR reference, which may still contain some residual noise.

We conducted a comparative analysis of the reconstruction effects achieved by different models as presented in Supplementary Figs. 1–3. The fluorescence decay sequence obtained using the 3D UNet model32 appears to be less restorative and more similar to the input data. On the other hand, the self-supervised method16,33 shows promise in reducing noise; however, it struggles to enrich the number of photons. This limitation arises because neighboring frames, which serve as learning targets, are photon-sparse. The \({\tau }_{m}\) maps and composite maps reconstructed by the 3D residual channel attention networks (3D RCAN)20 are closer to the results achieved with a sufficient number of photons, yet there still exists a noticeable gap in accuracy compared to our method concerning the sufficient photon images. Our approach leverages the correlation between time frames, considering feature consistency and information flow. Despite small discrepancies in \({\tau }_{m}\) values between SparseFLIM results and Photon-rich reference in Supplementary Figs. 2 and S3, achieving perfect consistency is challenging due to noise in raw input data, errors in fitting procedures used to create the Photon-rich reference images, and fundamental limitations of sparse photon inputs and fluorescence emission. The network aims to balance noise reduction, feature preservation, and adherence to learned patterns from the training data.

Quantitative analysis of image enhancement and photon enrichment

We show a comparison of large-field input sparse photon image (Fig. 2a), network-enriched photon image (Fig. 2b), and photon-rich image (Fig. 2c) of human skin pathology. A notable disparity exhibited between the the raw input and the reference images. Although in zoom-in views with fewer photons (Fig. 2d), it is possible to resolve details like sweat glands, blood vessels, and dermis structure (upper panels). However, the \({\tau }_{m}\) map (bottom panels) in these regions lacks differentiation, hovering around 0.7–0.8 ns, which is significantly improved by the network restoration (Fig. 2e). Notably, red blood cells (RBCs) with a lifetime of ~0.4 ns recovered by the network exhibit substantial differences from the dermis (>1.4 ns). The lifetime value of these tissue structures aligns well with the results obtained with sufficient photons (Fig. 2f).

Fig. 2: Network enhance label-free FLIM data of human skin tissue.
figure 2

a Raw input image (\({{{{\boldsymbol{I}}}}{{{\boldsymbol{\times }}}}{{{\boldsymbol{\tau }}}}}_{{{{\boldsymbol{m}}}}}\)) with sparse photons (normalized). b Network-enriched photon image by SparseFLIM. c Reference photon-rich image. d–f corresponds to magnified view of the boxed regions in (a–c), showing gland (left), RBCs (middle), and dermis (right). Black arrowheads indicate RBC. The \({{{{\boldsymbol{\tau }}}}}_{{{{\boldsymbol{m}}}}}\) maps presented in the bottom panel offer an original look at the fluorescence lifetime characteristics in these regions. g Tukey box-and-whisker plot illustrating 3D SNR and 3D SSIM changes before and after SparseFLIM reconstruction (n = 45 x-y-t stacks). h Violin plot showing the Pearson correlations of fluorescence decay traces before and after network inference. n = 500,000. Photon-rich traces were used as the reference for correlation calculation. Histogram distribution of bi-component mean lifetime in sparse raw input (i), network-enriched photon (j), and photon-rich (k) data, with the standard deviation (SD). Black arrow indicates the photon enrichment. n = 7,772,430. l–n correspond to close-up RBC images of normalized input, network enrichment, and photon-rich reference. The \({{{\boldsymbol{x}}}}\)-\({{{\boldsymbol{t}}}}\) and \({{{\boldsymbol{y}}}}\)-\({{{\boldsymbol{t}}}}\) views of the RBCs visualizing fluorescence decay within a 5 ns window, with cumulative decay trace plotted in the bottom right, which corresponds to the lifetime components within the white box region in the \({{{\boldsymbol{y}}}}\)-\({{{\boldsymbol{t}}}}\) view. Two-tailed Wilcoxon matched-pairs signed rank tests were applied between the input and output in g and h. Spatial scale bars, 100 μm in (a) and 50 μm in (d, n). Temporal scale bar, 100 ps in (n).

Full size image

Following network enhancement, the 3D SNR demonstrates a significant improvement over the original shot-limit stacks, with an average increase of 16.6 dB (~12 dB over ~−4.6 dB), and the 3D SSIM also exhibits a substantial enhancement, with an average increase of 137% (from ~0.35 to ~0.84). The Pearson correlation comparison, the network reconstruction results, and the sparse inputs also exhibit a substantial enhancement, with an average increase of 24-fold (~0.63 over ~0.02). The low correlation likely arises because, for most pixels, the noise in the sparse data is so severe that the fitted lifetimes become essentially random, decorrelating from the true lifetimes. Only a small subset may by chance produce lifetimes that weakly correlate. With insufficient photons (<100/pixel), the raw decay curves in the sparse data are extremely distorted by noise, decorrelating from the true underlying decays.

Notably, our model achieves the most substantial SNR improvement compared to other models16,20,32,33,34,35 as shown in Supplementary Fig. 4a. Although the 3D RCAN model shows a competitive improvement, its lifetime correlation remains lower than that of our model as observed in Supplementary Fig. 4b. The superior performance of SparseFLIM benefits from its unique strengths in capturing spatiotemporal correlations, leveraging feature extraction and fusion, and learning temporal dynamics. The bidirectional approach allows the model to effectively capture and leverage long-term spatiotemporal correlations and dependencies within the FLIM data, both from past and future frames. In contrast, approaches like 3D UNet and 3D RCAN primarily rely on non-propagating reconstruction, which may limit their ability to capture and utilize the rich spatiotemporal relationships present in the FLIM data. The feature fusion mechanism allows SparseFLIM to capture and utilize more comprehensive information from the input data, leading to improved reconstruction of missing details and suppression of artifacts. Other approaches may not explicitly incorporate such a feature extraction and fusion mechanism, potentially limiting their ability to recover fine-grained spatial and temporal information.

Instead of determining lifetime values or decay components through biexponential fitting, we leveraged a fit-free phasor technique to directly transform time-resolved FLIM data into a graphical distribution, providing intuitive readouts of protein-bound and free fluorophore fractions (Supplementary Note 1 and Supplementary Fig. 5). Phasor plots were generated from the Fourier transforms of the raw sparse FLIM input, deep learning reconstructed output, and sufficient photon reference data. The phasor distributions and their ability to resolve cell types based on component makeup were compared using this fit-free technique without any biased or non-linear fitting procedures. The phasor patterns following deep learning reconstruction closely aligned with the phasor transforms of the sufficient photon acquisition, highlighting the network’s capability to enhance correlation and accuracy in an assumption-free manner.

In addition to SNR and lifetime correlation enhancement, the lifetime distribution of before and after the network reconstruction and the reference were quantitatively characterized in Fig. 2i–k. The network-enabled a tenfold improvement of photon count at all lifetime intervals on average across over 7 million fluorescence decay traces. The photon distribution generally reaches around 1000 at the network output compared to the ~100 of the input. However, the <1 ns lifetime components were likely restored with more photon counts than the 3–4 ns components. Shorter lifetimes mean faster fluorescence decay with sparser photons in fluorescence tail and more easily distorted when undersampled compared to longer lifetimes. The lack of photons might cause the fitting to erroneously biased towards artificially longer lifetimes. The network is able to correct for this artifact and recover the true, prevalent shorter ~1 ns components seen in the photon-rich data.

While the photon number histograms in Fig. 2j and Fig. 2k exhibit a high degree of overall similarity, there are subtle discrepancies between these two distributions. This may arise due to imperfect network reconstruction and errors in fitting methods. Nevertheless, these subtle differences have less potential impact on the reliability and accuracy of the inference results of SparseFLIM because the overall lifetime trends and shapes are closely aligned.

Visually, we presented \({x}\)-\(t\) and \(y\)-\(t\) orthogonal views of the spatiotemporal distribution of photons (Fig. 2l–n). The input images were normalized, otherwise invisible, exhibit more noise and speckled photon decay, particularly in the latter half (>2 ns) of the time range (Fig. 2l). In contrast, the results obtained through the SparseFLIM network (Fig. 2m) are notably distinct, and the clearer photon decay patterns agree well with the patterns obtained with sufficient photons (Fig. 2n). Importantly, since independent noise cannot be learned as its expected average is zero, the network reconstruction results were even less noisy than the data with >1000 photons, avoiding the generation of significant artifacts. This demonstrates the effectiveness of the SparseFLIM model in improving data quality and relationships.

Overall, despite originally inconsistent and uncorrelated decay patterns, SparseFLIM reconstruction establishes strong consistency between sparse photon inputs and sufficient references in addition to photon enrichment. This verifies precise recovery of underlying fluorescence properties and lifetime characteristics from sparse measurements.

Spatial sparsity enhancement

To achieve faster FLIM, a practical approach is to reduce the pixel count in the capturing images. For example, capturing 128 × 128 pixels is 16× faster (>100× faster if considering photon sparsity) than 512 × 512 pixels, irrespective of angle step response of galvanometer and loss of spatial structure information. To address this downgrading, we employed a spatial upsampling (SU) module, realized by sub-pixel convolution (pixel shuffle)36 following the feature aggregation within the network of SparseFLIM, as illustrated in Fig. 3a and described in detail in Methods. This approach is applicable to both photon sparsity and spatial sparsity. We proceeded to reconstruct images at 2×, 3×, and 4× pixel magnifications of fluorescent beads and presented frames at specific time points for comparison (Fig. 3b). In the input sparse data, the fluorescent beads remain vague due to the limited photons and low spatial resolution. However, after network reconstruction, the beads become clearly distinguishable with enriched photons and suppressed noise. The zoom-in views (Fig. 3c) reveal the changes in the contours of the beads. The outlines of the beads in the input data are irregular, particularly for longer decay times (\(t\) = 976 ps) and fewer pixels (128 × 128), resulting in more blurred and distorted shapes. These distortions and the loss of photons are effectively reconstructed by the SU SparseFLIM method, resulting in outcomes consistent with the photon-rich reference.

Fig. 3: Spatial and photon sparsity enhancement by SparseFLIM.
figure 3

a Network architecture of SU SparseFLIM. \({{{{\boldsymbol{U}}}}}_{{{{\boldsymbol{s}}}}}\), spatial upsampling module. CP collected pixels; UnCP uncollected pixels. b Input images of fluorescent beads and the corresponding network reconstruction results. Yellow dashed circles indicate invisible beads that are clearly resolved by the network. c Close-up images showing a pair of beads. The solid line in the images refers to the line of the shown cross-section. d Comparison of the input and output images of a skin tissue. The photon-rich image is presented as reference. e Tukey box-and-whisker plot illustrating 3D SNR changes in skin data between bicubic upsampling of the input and SU SparseFLIM result (n = 46 \({{{\boldsymbol{x}}}}\)-\({{{\bf{y}}}}\)-\({{{\boldsymbol{t}}}}\) stacks). f FSC measure on bicubic upsampling of the input and SU SparseFLIM result. Two-tailed Wilcoxon matched-pairs signed rank tests were applied between the input and output in (e). Scale bars, 20 μm in (b, c), 100 μm in (d).

Full size image

Furthermore, we presented the results of reconstructing images with both photon and spatial sparsity using human skin tissue slices (Fig. 3d). The reconstructed images at 2×, 3×, and 4×, including intensity and lifetime, closely match those of the 512 × 512 images with an adequate photon count. To assess the quality of the reconstructions, we employed 3D SNR as a quantifying measure (Fig. 3e). In the case of the 2×, 3×, and 4× bicubic upsampled images of the original data, the mean SNR registers at a mere −3.1 dB, −2.9 dB, and −2.2 dB, respectively. However, following the reconstruction process, these values increase substantially to 11.4 dB, 10.2 dB, and 9.8 dB. We also computed the Fourier shell correlation (FSC)37 between the 3D input/output images and photon-rich images (Fig. 3f). At lower spatial frequencies, the FSC values of the results approach 1. As the frequency increases, the SparseFLIM FSC values consistently exhibits a stronger correlation with high-SNR images compared to the input data. This improved correlation underscores the high reliability of network reconstruction. It is important to note that all improvements in quantitative metrics are calculated based on reference sufficient photon data. In essence, these metrics not only signify the enhancement in image quality but also underscore the exceptionally high similarity between the reconstructed data and the reference data.

Temporal sparsity enhancement

We assessed the feasibility of recovering time sparsity by removing multiple time frames (equivalent to reducing the 100 time channels). To address the information loss, we employed a temporal upsampling (TU) module, realized by increasing the output channels of the network (Fig. 4a, see details in Methods). In the absence of 2×, 3×, and 4× frame counts, the TU SparseFLIM effectively compensated for these missing frames (Fig. 4b), enriching photons to meet the requirements for lifetime fitting. The orthogonal views of an RBC revealed that previously invisible spatial and temporal details were clearly recovered by the network (Fig. 4c). These results were consistent with the photon-rich reference but with reduced noise. Notably, the SNR of the network inference significantly improved by 36.7 dB when compared to the shot-limit input. The reconstructed images of time sparsity at 2×, 3×, and 4×, including intensity and lifetime, closely matched those of images with sufficient photons (Fig. 4d). Different biological structures, e.g., pore networks, RBCs, and dermis were well resolved in lifetime at the three pixel multiplication rates using TU SparseFLIM compared to the input lifetime maps, which exhibit no lifetime difference between different structures and significant biases concerning the reference. The reconstructions led to remarkable improvements in lifetime correlation for the original 2×, 3×, and 4× frame-reduced images, with enhancements of 15 times, 24 times, and 12 times, respectively. These improvements align closely with the photon-rich references (Fig. 4e). To illustrate, the autofluorescence decay patterns resulting from the inference displayed a remarkable consistency with the photon-rich decays, in stark contrast to the scattered patterns observed in the input data (Fig. 4f).

Fig. 4: Temporal and photon sparsity enhancement by SparseFLIM.
figure 4

a Network architecture of TU SparseFLIM. \({{{{\boldsymbol{U}}}}}_{{{{\boldsymbol{t}}}}}\), temporal upsampling module. Dark boxes represent the collected frames, while white boxes represent the uncollected frames. b Images of RBCs and dermis, with the temporally padded frames reconstructed by the network outlined in green. c Orthogonal views of an RBC. The white dashed lines and arrows in the \({{{\boldsymbol{y}}}}\)-\({{{\boldsymbol{t}}}}\) views indicate selected \({{{\boldsymbol{x}}}}\)-\({{{\boldsymbol{y}}}}\) frames displayed at the ends. The column graph at the bottom right illustrates the SNR improvement, with mean ± SD. d Comparison of the input and output images of skin tissue, with the photon-rich image serving as the reference. e Violin plot demonstrates changes in lifetime correlation in skin data between the input (bicubic temporal upsampling) and TU SparseFLIM reconstruction. n = 500,197-lifetime traces. f Fluorescence decay of the location indicated by the cross in (d). Two-tailed Wilcoxon matched-pairs signed rank tests were applied between the input and output in (e). Scale bars, 150 μm in (b), 100 μm in (d).

Full size image

Model generalization

We assessed the adaptability of our SparseFLIM model by applying it to three other distinct imaging modes. One such mode is single-photon FLIM of liver metastasis. The distorted lifetime maps obtained from sparse photon acquisitions, which suffer from limited photon counts and noise, were effectively restored by the pre-trained SparseFLIM model to match the high-quality FLIM images acquired with sufficient photon counts (Supplementary Fig. 6a, c). We compared the fluorescence decay for the sparse photon, the network-enriched output, and the sufficient photon reference data (Supplementary Fig. 6b, d). The limited photon counts and noise introduced irregularities and distortions in the sparse photon data, causing it to deviate from the expected trend. However, after the network reconstruction, the decay curve of the sparse photon data became highly consistent with that of the sufficient photon reference, accurately capturing the fluorescence decay dynamics. This highlights ability of the network to recover the true fluorescence decay characteristics from single-photon excitation sparse and noisy data, effectively mitigating the detrimental effects of limited photon counts and noise.

We also assessed multispectral FLIM (Supplementary Fig. 7a), an advanced imaging technique that combines spectral and lifetime information for characterizing the tumor microenvironment38,39,40. This method is prone to deviations in lifetime fitting due to low collect efficiency, particularly when imaging spectral regions away from the fluorescence emission peak. In Fig. 1h, the “sparse” condition refers to using a short photon accumulation time during fast acquisition. In contrast, Supplementary Fig. 7a shows a different scenario of spectral sparsity, where the 441–466 nm and 466–491 nm channels had intrinsically low photon levels compared to the more intense 541–566 nm channel at 920 nm excitation, due to the spectral properties of the sample. To address this, we leveraged our pre-trained model to reconstruct data from photon-inefficient spectral segments and compared it with a spectral segment characterized by high photon counts. The results demonstrated remarkable consistency, with the lifetime map exhibiting greater accuracy than the original data (Supplementary Fig. 7b). The reconstruction process also effectively restored the parametric second harmonic generation (SHG) process, represented by a lifetime of zero, without any deviations. Notably, the fluorescence decay curve of sparse photons exhibits lower confidence compared to the results obtained after network reconstruction (Supplementary Fig. 7c). The SNR of the network-enhanced data shows a significant improvement over the original subpar, below shot-limit stacks, with an average increase of 21 dB. Additionally, the lifetime trace correlation analysis comparing the network reconstruction results with the sparse input data also demonstrates a high enhancement.

We finally tested the effectiveness of our SparseFLIM model for in vivo endoscopic FLIM41,42. This two-photon fluorescence lifetime microendoscopy based on fiber-bundle43 may encounter several challenges. Fiber dispersion and photon loss often lead to a reduced nonlinear excitation efficiency. The limited numerical aperture (NA) of an individual fiber core (0.35–0.39) and Grin lens (e.g., 0.5) could lead to a low fluorescence collection efficiency. Moreover, differences in the optical path of the multicore fiber can introduce variations in lifetime measurements. To address these issues, we used a pre-trained model to reconstruct low-SNR endoscopy imaging results. The outcome was a significant reduction in lifetime noise, along with the recovery of both intensity and lifetime information. The reconstructed images of the small intestine, liver, and tumor displayed clear details, with the lifetime information well recovered. These results demonstrate the noise reduction, photon enrichment, information recovery capabilities, and overall robustness of our model.

Discussion

This work demonstrates SparseFLIM, a deep-learning approach for reconstructing high-quality fluorescence lifetime images from sparse photon data. The method leverages bidirectional propagation and coupled reconstruction to effectively enrich photon counts and recover spatial-temporal information lost due to low fluence acquisitions. Notably, SparseFLIM might not literally generate or insert new photons into the data. Instead, it leveraged the spatial and temporal correlations learned from the forward and backward data to predict the underlying true fluorescence decay curve and photon distribution that would be observed with sufficient photon counts. More specifically, during the training process, the network learned a mapping between the sparse, noisy input data and the corresponding high photon count reference data. It captured the relationships between the sparse spatial-temporal patterns and the underlying fluorescence decays they represent. At inference time, when given a new sparse FLIM input, the network used this learned mapping to reconstruct and predict the full, enriched spatial-temporal distribution and decay curve that aligned with the high photon count data distribution.

SparseFLIM enables dramatic improvements in photon counts, SNR, and lifetime correlation for sparse FLIM data, reconstructing images comparable to sufficient photon acquisition. Quantitative analysis across millions of fluorescence traces showed over 10× photon enrichment on average. The resulting lifetime maps and decay patterns closely matched photon-rich references. The model also effectively addressed spatial and temporal sparsity through upsampling modules. Sparsely sampled FLIM could be reconstructed to full resolution, clearly resolving subcellular features. Similarly, temporally downsampled data was restored via frame synthesis. This could accelerate FLIM by reducing pixel counts and time channels. Moreover, SparseFLIM exhibited strong generalization across experimental modalities. The network reconstructed multispectral FLIM data, accurately recovering lifetimes even for low-efficiency spectral bands. It also enhanced in vivo endoscopic FLIM impaired by fiber dispersion and low NA. By learning semantic relationships, this approach avoids fitting random noise that still exists in higher fluence data, which demonstrates a denoising capability beyond merely enriching photons.

Despite these advances, several limitations still need to be addressed. First, although the current results suggest a degree of transferability of the pre-trained weights for datasets sharing core characteristics, the generalization performance across broader datasets remains to be fully validated. In cases involving significantly different optical setups (e.g., confocal microscopy), parameters (e.g., much fewer time bins), and sample types (e.g., fluorescent proteins in cells), it may be necessary to retrain the network for accurate reconstruction of lifetime decays. Second, the network restores the temporal and spatial distribution of fluorescence independently of single or double exponential fitting methods. While the bi-component nature of the spontaneous fluorescence of FAD has been extensively discussed in prior research6,27,28, practical applications should tailor the choice of model based on the specific fluorescence distribution characteristics of the sample. Third, while photon counts improved substantially, further optimization of the network architecture may enable more extreme enrichment. For example, hybrid networks leveraging physiological constraints and deep learning could improve accuracy. Expanding network capacity with deeper architecture or gleaning insight from fluorescence decay models could aid reconstruction. Optimizing training strategy, loss functions, and regularization may produce superior solutions. Fourth, extension to 3D FLIM and computation time/memory optimization would enhance practical utility. Further analysis of internal feature representations could provide insight into relationships captured by the network. Such knowledge may guide the development of analytical models to accelerate fitting.

In summary, we established a deep learning approach to achieve high-fidelity fluorescence lifetime imaging using sparse photon data. SparseFLIM generalized well across experimental modalities including multispectral FLIM and in vivo endoscopic FLIM with the pre-trained weights. The technique exhibits photon enrichment and denoising capabilities, producing cleaner reconstructions than the raw data. Together this work establishes deep learning as a promising strategy to enhance fluorescence lifetime imaging. By recovering hidden information, SparseFLIM may provide new biological insight from low-light imaging. Studying light-sensitive processes like circadian rhythms, neural activity, and cell signaling could benefit. Our approach could facilitate longitudinal FLIM studies by reducing photodamage. Enhanced imaging of endogenous fluorophores minimizes the need for exogenous labels. While this work focuses on FLIM, the core technique of learning from sparse data may generalize. SparseFLIM enables potential applications like rapid 3D FLIM, large-area sensing, and light-sensitive imaging. More broadly, this approach represents a paradigm for extracting latent information from sparse measurements that may generalize beyond FLIM. Future work should focus on advancing the network, assessing more varied experimental scenarios, and clinical translation.

Methods

Sample preparation

The procedures and protocols conducted in this study received approval from the Medical Ethics Committee, Shenzhen University Medical School (PN-202300128). Physicians and surgeons were responsible for patient recruitment and obtaining informed consent. All ethical regulations relevant to human research participants were followed. Utilizing de-identified residual tissue specimens that were previously archived, we conducted our experiments. Tissue samples, obtained through surgery, were promptly snap-frozen in liquid nitrogen and subsequently preserved at –80 °C until they were sectioned into 5 μm-thick slices for both unstained and stained applications. The frozen tissue sections were directly covered with coverslips, imaged using our microscope, and subsequently stored at –80 °C. The adjacent sections underwent standard H&E staining procedures. Pathological analysis was carried out by two dermatologists with expertize in skin cancer on the histological sections.

Network architecture

The network employs a recurrent neural network architecture with two key components: (1) Forward and backward propagation branches to leverage temporal correlations and accumulate long-term spatiotemporal information from both past and future frames, and (2) Coupled propagation blocks that exchange information between the forward and backward branches, enabling each branch to incorporate context from the entire sequence. This coupled bidirectional propagation mechanism, along with the recurrent nature of the architecture, allows the model to effectively capture and preserve long-term temporal dependencies at each pixel location. Thereby, the extremely sparse photons (approaching zero) at the tail end of fluorescence lifetime decay can be precisely reconstructed, relying on the photon distribution pattern learned by the network at high photon time points. Additional elements of the network include aggregation blocks to concatenate the complementary bidirectional information, and high-level feature fusion to reconstruct missing details and reduce artifacts by refining the propagation and aggregation processes.

Propagation branches

Bidirectional propagation is a core technique in the network that enables temporally aggregating information across the entire FLIM sequence. It involves separate forward and backward branches that process frames in opposite directions. The forward branch propagates frame features sequentially from the start to the end of the sequence. Each frame’s features are computed by fusing information from the current frame and the features propagated forward from the prior frame. This allows accumulating contextual guidance from preceding frames. Conversely, the backward branch propagates frame features recursively from the end to the start of the sequence. Each frame’s features are computed by fusing information from the current frame and the features propagated backward from the next frame. This maximizes the spatiotemporal information available to each frame for reconstruction, surpassing unidirectional or localized propagation schemes.

The bidirectional mechanism provides several advantages. First, it prevents early frames from suffering due to lack of future context, and later frames from deteriorating without past guidance, issues that plague unidirectional propagation. Second, it reduces cumulative alignment errors by allowing error correction from both directions. Occluded regions can be recovered by fusing information from before and after the occlusion. Third, it eases gradient flow during backpropagation for more effective optimization. Finally, bidirectional propagation facilitates modeling long-range dependencies essential for FLIM reconstruction. By aggregating information across hundreds of frames, the branches can capture subtle spatial-lifetime patterns critical for photon enrichment.

Coupled propagation

The network employs coupled propagation between the bidirectional branches to maximize information exchange. The backward branch features are provided as additional inputs to the forward propagation to better handle occlusion. Specifically, the coupled propagation fuses the backward-propagated features into the forward branch processing. This allows the forward branch to leverage features from future frames during alignment and aggregation. For example, during occlusion, the backward-propagated features contain contextual guidance from after the occlusion not available in preceding frames. Fusing this helps the forward branch reconstruct those regions.

Similarly, the backward-propagated features are useful for reconstructing boundaries and detail regions by providing future frame context. This facilitates handling noise and information loss. The expressions for bidirectional and coupled propagations are:

$${h}\, _{i}^{f}=\, {F}_{f}({x}_{i},{x}_{i-1},{h}_{i}^{b},{h}\, _{i-1}^{f})\\ {h}_{i}^{b}=\, {F}_{b}({x}_{i},{x}_{i+1},{h}_{i+1}^{b})$$
(1)

where \({x}_{i}\) is the input ith frame at the time \({t}_{i}\). \({F}_{f}\) and \({F}_{b}\) are the forward and backward propagation branches, respectively. \({h}\, _{i}^{f}\) and \({h}_{i}^{b}\) representing the output feature maps with two exits. \({h}\, _{i}^{f}\), \({h}_{i}^{b}=0\) for the first frame. One is the forward hidden state and backward hidden state as the next reference frame respectively, and the other is directly output to aggregation and upsampling for reconstruction.

Coupled propagation establishes interconnectivity between the bidirectional branches. By leveraging correlations in both forward and reverse directions, the full span of the FLIM sequence is covered. This mechanism maximizes temporal context available during alignment and propagation, improving occlusion, boundary, and detail handling without substantially increasing model complexity or computational load. Before these output features (\({h}\, _{i}^{f}\) and \({h}_{i}^{b}\)) were concatenated, we refilled the loss information due to undersampling.

Information-refill

The network incorporates an information-refill mechanism to reduce reconstruction errors during bidirectional propagation. It leverages additional feature extraction on select keyframes to refill missing information. Specifically, a separate feature extractor module processes the keyframes and their temporal neighbors to extract high-level and low-level representations. These complementary features are fused into the propagation branches to fill in information potentially lost due to inadequate photon collection.

For example, sparse photon and boundary regions often suffer from noise. By extracting contextual features from the keyframes before and after such events, the lost information can be refilled. Concretely, if the current reference frame is in the key frame set, the input to the module consists of the key frame and its two adjacent supporting frames. The feature extraction module is realized with a relatively lightweight EDVR30, so the result of feature extraction is actually the fusion result of EDVR taking these three frames as input and finally output these three frames:

$${e}_{i}=\, E({x}_{i-1},{x}_{i},{x}_{i+1})\\ {\hat{h}}_{i}^{\{b,f\}}=\, \left\{\begin{array}{c}C\left({e}_{i},{h}_{i}^{\{b,f\}}\right), \quad i\,\in \,{I}_{key}\\ {h}_{i}^{\{b,f\}},\hfill \quad\quad\quad i\,\notin {I}_{key}\hfill\end{array}\right.$$
(2)

where \(E\) is the feature extractor. \(C\) is the convolution. \({I}_{{key}}\) represents the keyframe number. \(\hat{h}\) is the result after information-refill. Briefly, the feature extractor \(E\) uses strided convolution filters to downsample the input frames and generate multi-scale pyramid representations, transforming the raw input frames into a set of feature maps that are suitable for subsequent fusion operations. For feature extraction of keyframes, the significance of the information contained within intra-frame regions varies. Support key frames may exhibit artifacts such as blur, noise, or loss of signal photons. To address this issue, we also included the temporal and spatial attention mechanism to disregard irrelevant feature information while focusing on pertinent data for accurate reconstruction, which was detailed in EDVR30. Briefly, the temporal attention map is computed between the extracted features \({e}_{i}\) of a neighboring frame and the aligned features \({e}_{i}^{{\prime} }\) of the reference frame:

$$h({e}_{i}^{\prime},{e}_{i})={{{\rm{sigmoid}}}}(\theta {({e}_{i})}^{T}\varphi ({e}_{i}^{\prime}))$$
(3)

where \(\theta\) and \(\varphi\) are embedding functions implemented by simple convolution filters. In this context, the key and value are the embedded features \(\varphi ({e}_{i}^{{\prime} })\) of the reference frame, while the query is the embedded features \(\theta ({e}_{i})\) of a neighboring frame. The temporal attention map \(h\) serves as the weight for the value, indicating how informative each neighboring frame’s features are for reconstructing the reference frame.

After temporal attention is applied and features are fused, spatial attention masks are computed from the fused features using a pyramid design to increase the attention receptive field. These spatial attention masks are then used to modulate the fused features through element-wise multiplication and addition. For spatial attention, the query, key, and value are all derived from the fused features that have already gone through temporal attention.

Next, transfer the result of information-refill to the feature reconstruction:

$${h}_{i}^{\{b, \, f\}}={R}_{b,j}({x}_{i},{\hat{h}}_{i}^{\{b, \, f\}})$$
(4)

where \({R}_{b,f}\) is the feature reconstruction module with eight residual blocks for backward and forward and branches. The information-refill can provide useful guidance to correct faulty lifetime decay reconstruction and enrich feature learning.

Aggregation and output

Aggregation in the network refers to consolidating useful information from the forward and backward propagation branches to generate the final FLIM reconstructions. Specifically, the output features from both branches are fused using concatenation:

$${A}_{i}={{{\rm{concat}}}}({x}_{i},{h} \, _{i}^{f},{h}_{i}^{b})$$
(5)

This simple aggregation joins the enriched bidirectional features to create an integrated representation encoding spatiotemporal relationships identified across the entire FLIM sequence. The aggregation unlocks the synergistic potential of the bidirectional branches.

The final modules include Leaky ReLU activation function and 2D convolutions. Leaky ReLU improves the training dynamics of neural networks by allowing gradients to flow more freely, reducing the risk of dead network neurons, and potentially enhancing the model’s ability to learn complex representations. Additionally, a dedicated upsampling module with transposed convolutions, pixel shuffling, and Leaky ReLU transforms the aggregated low-resolution features into full-resolution FLIM reconstructions.

The output frame \({y}_{i}\) is obtained by

$${y}_{i}= \left\{\begin{array}{cc}{F}_{f}({A}_{i}) & {{{\rm{for}}}}\,{{{\rm{SparseFLIM}}}}\\ {U}_{s}[{F}_{f}({A}_{i})] & \quad \,{{{\rm{for}}}}\,{{{\rm{SU}}}}\,{{{\rm{SparseFLIM}}}}\\ {U}_{t}[{F}_{f}({A}_{i})] & \quad \, {{{\rm{for}}}}\,{{{\rm{TU}}}}\,{{{\rm{SparseFLIM}}}}\end{array}\right.$$
(6)

where \({U}_{s}\) denotes the upsampling module, which comprises convolutional layers for extracting features and a pixel shuffle layer for upsampling:

$${U}_{s}=Leaky\,ReLU(PixelShuffle(conv({F}_{f}({A}_{i}))))$$
(7)

The convolutional layer extracts features from the input, which is the result of the fusion of the feature maps. PixelShuffle performs the actual spatial upsampling by rearranging the feature channels into a higher-resolution output image. It effectively increases the spatial resolution by a spatial upsampling factor (e.g., 2×, 3×, or 4×). These ultimately yield a high-resolution image as output.

\({U}_{t}\) represents a channel upsampling module that expands output channels of the last convolutional layer to more temporal channel bins and allocate adjacent ones:

$${U}_{t}=Leaky\,ReLU(conv({F}_{f}({A}_{i}),{s}_{t}))$$
(8)

where \({s}_{t}\) is the number of output channels of the convolutional layer, which match the desired temporal scale factor (e.g., 2×, 3×, or 4×). Then, these adjacent output channels are allocated to the collected frames and the missing frames that need to be reconstructed. For instance, the four output channels of the convolutional layer (\({s}_{t}=4\)), \({C}_{1}\), \({C}_{2}\), \({C}_{3}\), and \({C}_{4}\) can be allocated to \(I(x,y,{t}_{1})\), \(I(x,y,{t}_{2})\), \(I(x,y,{t}_{3})\), and \(I(x,y,{t}_{4})\), respectively. By expanding the output channels and assigning them appropriately, the TU module enables the network to reconstruct and synthesize the missing time frames, effectively recovering the temporal information lost due to temporal sparsity or downsampling during acquisition.

Unlike traditional interpolation techniques that rely on mathematical assumptions or predefined rules, our approach leverages expansion of the output channels of the network to reconstruct the temporal sparsity in FLIM data. Through the bidirectional propagation architecture and the recurrent nature of the network, the network can accurately recover missing temporal information by leveraging the knowledge gained from the high-SNR reference data during training. Traditional interpolation methods, on the other hand, may not capture these complex temporal patterns, potentially leading to inaccuracies or artifacts in the recovered temporal information. The coupled bidirectional propagation mechanism and the feature extraction and fusion components helps mitigate potential distortions or artifacts that may arise from interpolation techniques.

In summary, by integrating the bidirectional and coupled propagations, high-level feature fusion, and aggregation mechanisms into a tailored 3D architecture, the network outperforms conventional methods for reconstructing high-quality FLIM from sparse photon data and expands the potential of deep learning for enhanced fluorescence lifetime imaging.

Training options

The training process of the network is conducted in an end-to-end manner, utilizing paired datasets that include both sparse and sufficient photon FLIM data. The images have dimensions of 512 (\({N}_{x}\)) × 512 (\({N}_{y}\)) × 100 (\({N}_{t}\)). To address memory constraints, we segmented the images into sub-stacks with dimensions of 128 (\({N}_{x}\)) × 128 (\({N}_{y}\)) × 100 (\({N}_{t}\)) and maintained a batch size of one during the training phase. Data augmentation was performed using random flips and rotations. In total, we carried out 100,000 training iterations. The feature correction in each branch involved eight residual blocks, each with 64 channels. Comparative analysis of various keyframe selections, as well as the original BasicVSR (with flow-based feature-wise alignment)29 and BasicVSR + + (with grid propagation)44 was given in Supplementary Table 1. Reference keyframes were selected from the [8, 10, 12, 16]th frames with the highest attained SNR compared to other keyframe selections (Supplementary Table 1). The network can effectively leverage the high SNR, contrast, and low noise levels in these frames for feature extraction and training.

For the reconstruction module, we opted for the adaptive moment estimation (Adam)45 optimizer for the generator, with \({{{{\rm{\beta }}}}}_{1}=0.9\), \({{{{\rm{\beta }}}}}_{1}=0.99\). The training loss function is defined as the Charbonnier loss:

$$1 =\frac{1}{N} {\sum}_{i=0}^{N}\rho ({y}_{i}-{z}_{i})$$
(9)

where \(\rho \left(x\right)=\sqrt{{x}^{2}+{\epsilon }^{2}}\), \(\epsilon =1\times {10}^{-8}\). \({z}_{i}\) is the high-SNR reference. \(N\) is the number of sequences in a batch.

During the prediction phase, there is no need to crop the input images, which are of the full size, measuring 512 (\(x\)) × 512 (\(y\)) × 100 (\(t\)). It is essential to note that there was no data overlap between training and testing. In other words, the test images presented in this article were generated by the deep network in a blind manner, ensuring the reliability and objectivity of the results.

Benchmarks

We conducted comparative evaluations between our network architecture and several other representative techniques for sparse data reconstruction including 3D-UNet32,34, Self-supervised learning16,33, and 3D-RCAN20,35. 3D UNet represents a standard deep learning approach for volumetric image-to-image translation tasks. We implemented a 3D version of the popular UNet architecture using convolutional and transpose convolutional layers optimized for our photon-limited FLIM reconstruction application. Self-supervised learning provides a way to train deep networks without labeled data by using intrinsic structures within the data itself as supervisory signals. We adapted a recent noise2noise self-supervised learning technique to train a model for reconstructing sparse FLIM inputs using only the sparsity degraded data itself without sufficient photon references. 3D RCAN demonstrates good performance for various volumetric image restoration tasks. We customized this network containing stacked 3D residual channel attention blocks to translate our sparse FLIM data into photon-enriched outputs.

Through quantitative metrics and qualitative visualizations, we demonstrated that our proposed architecture achieves superior performance compared to these alternative techniques for reconstructing high-fidelity FLIM from sparse photon data. This is because our network leverages strengths of bidirectional propagation, interconnected reconstruction, and high-level feature fusion tailored for sparse FLIM inputs. In contrast, the other methods are not specialized for handling fluence-limited fluorescence decays. Our experiments highlight the advantages of SparseFLIM unique design components and training strategy for this application.

Data processing

The raw data captured and processed by the SPCImage (Becker & Hickl GmbH) were produced in 8-bit TIFF files using a custom MATLAB script to reduce storage requirements and speed up data read, write, and transfer21. We utilized an approximately 5 ns temporal range, corresponding to 100-time channels, for autofluorescence lifetime estimation. This range was chosen because the typical lifetimes observed for endogenous fluorophores present in the biological tissue samples under study, such as NADH and FAD, generally exhibit fluorescence lifetimes within a few nanoseconds (typically <5 ns)6,27,28. Nevertheless, comparative analysis revealed little differences in fluorescence lifetime estimates between 5 ns and 10 ns time windows (Supplementary Fig. 8). Our choice of a 5 ns window represents a careful compromise between capturing sufficient decay information and minimizing the influence of noise in the low-photon tail region. In sparse photon conditions, the tail end of the decay curve often suffers from increased noise due to low photon counts. We aim to capture the most informative portion of the decay curve while reducing the impact of noise-induced artifacts. By constraining the temporal range to the relevant timescale for the fluorescence decays of interest, the network circumvented the need to learn redundant or irrelevant information beyond that range. This approach enhances the learning efficiency and mitigates overfitting to noise or artifacts outside the region of interest despite impact for longer lifetime reconstructions. Additionally, the chosen temporal offset (i.e., the delay before the fluorescence begins to decay after excitation) of approximately 0.5 ns allows for preserving the fluorescent rising edge while ensuring a sufficient subsequent time range to capture the effective fluorescence decay. Moving forward, we will explore adaptive windowing techniques to potentially extend the analyzable decay range without compromising the robustness of our approach in low-photon conditions. These refinements will help to broaden the applicability of SparseFLIM while maintaining its advantages in processing speed and photon efficiency.

The invisible input images with a relatively low contrast were regulated by adjusting the dynamic ranges (brightness/contrast) in ImageJ to better display the indiscernible morphological features4. We use the conventional Levenberg–Marquardt algorithm (LMA) fitting routine, based on a minimization of the sum of the squared differences between the data points and the points of the model function, and works well for high photon count fitting. However, LMA is not very suitable for sparsely sampled data, which were thereby fitted using the Maximum Likelihood Estimation (MLE), based on calculating the probability that the values of the model function correctly represent the data points of the decay function.

Performance metrics

The quality metrics, including correlation and 3D SNR were calculated between the input or output lifetime trace \({I}_{t}\) and the photon-rich reference trace, \({I}_{t}^{{\prime} }\). Pearson correlation coefficient \(\rho\) is formulated as

$$\rho =\frac{{\sum}_{t}({I}_{t}-{\bar{I}}_{t})({I}_{t}^{\prime}-{\bar{I}}_{t}^{\prime})}{({N}_{t}-1){\sigma }_{t}{\sigma }_{t}^{{\hbox{'}}}}$$
(10)

where \({\bar{I}}_{t}\) are \({\sigma }_{t}\) are the mean and SD of \({I}_{t}\), respectively. \({\bar{I}}_{t}^{{\prime} }\) and \({\sigma }_{t}^{{\prime} }\) are the mean and SD of \({I}_{t}^{{\prime} }\), respectively. \({N}_{t}\) is the time channel number.

SNR is obtained by computing the ratio of summed squared magnitude of the input or output \(x\)-\(y\)-\(t\) stacks, \({I}_{{SIG}}\) to that of the noise:

$${{{\rm{SNR}}}}=20{\log }_{10}\frac{{{{\rm{RSS}}}}({I}_{SIG})}{{{{\rm{RSS}}}}({I}_{SIG}-{I}_{PR})}$$
(11)

where \({I}_{{PR}}\) is the photon-rich reference. RSS is the root-sum-of-squares:

$${{{\rm{RSS}}}}=\sqrt{{\sum}_{x,y,t}{|I|}^{2}}$$
(12)

FSC (normalized cross-correlation dependent on spatial frequency) measurements37 were calculated according to

$${{{\rm{FSC}}}}({r}_{j})=\frac{{\sum}_{r\in {r}_{j}}{F}_{1}(r)\cdot {F}_{2}{(r)}^{\ast }}{\sqrt{{\sum}_{r\in {r}_{j}}{F}_{1}^{2}(r)\cdot {\sum}_{r\in {r}_{j}}{F}_{2}^{2}(r)}}$$
(13)

where \({F}_{1}\) and \({F}_{2}\) are the 3D Fourier transforms of the two \(x\)-\(y\)-\(t\) stacks and \({r}_{j}\) is the jth frequency bin. Correlations were computed on the Fourier shells, and were restricted that are fully contained within the image. The value of FSC(\({r}_{j}\)) for each spatial frequency \({r}_{j}\) ranges from +1 to −1. When these values are close to 1, it signifies that the consistency of the two reconstructed structures is good, indicating a high level of reliability in the obtained structures.

Statistics and reproducibility

The sample sizes, as well as the statistical analyses encompassing mean, SD, and significant differences, were outlined in both figure legends and the accompanying text for each experiment. Within the Tukey box and whisker plots, the boxes denoted the upper and lower quartiles, with the line inside the box indicating the median. The lower whisker extended to the first data point greater than the lower quartile minus 1.5 times the interquartile range, while the upper whisker extended to the last data point less than the upper quartile plus 1.5 times the interquartile range. In the violin plots, three black lines denoted quartile positions, with the solid line representing the median. Additionally, p values indicating statistical differences were positioned above the data, and representative frames were thoughtfully presented in the figures, bearing similar conclusions to other frames.