A large-scale benchmark for network inference from single-cell perturbation data

Abstract

Mapping biological mechanisms in cellular systems is a fundamental step in early-stage drug discovery that serves to generate hypotheses on what disease-relevant molecular targets may effectively be modulated by pharmacological interventions. With the advent of high-throughput methods for measuring single-cell gene expression under genetic perturbations, we now have effective means for generating evidence for causal gene-gene interactions at scale. However, evaluating the performance of network inference methods in real-world environments is challenging due to the lack of ground-truth knowledge. Moreover, traditional evaluations conducted on synthetic datasets do not reflect the performance in real-world systems. We thus introduce CausalBench, a benchmark suite revolutionizing network inference evaluation with real-world, large-scale single-cell perturbation data. CausalBench, distinct from existing benchmarks, offers biologically-motivated metrics and distribution-based interventional measures, providing a more realistic evaluation of network inference methods. An initial systematic evaluation of state-of-the-art causal inference methods using our CausalBench suite highlights how poor scalability of existing methods limits performance. Moreover, methods that use interventional information do not outperform those that only use observational data, contrary to what is observed on synthetic benchmarks. CausalBench subsequently enables the development of numerous promising methods through a community challenge, thus demonstrating its potential as a transformative tool in the field of computational biology, bridging the gap between theoretical innovation and practical application in drug discovery and disease understanding. Thus, CausalBench opens new avenues for method developers in causal network inference research, and provides to practitioners a principled and reliable way to track progress in network methods for real-world interventional data.

Introduction

Causal inference is central to a number of disciplines including science, engineering, medicine and the social sciences. Causal inference methods are routinely applied to high-impact applications such as interpreting results from clinical trials¹, studying the links between human behavior and economic activity², optimizing complex engineering systems, and identifying optimal policy choices to enhance public health³. In the rapidly evolving field of computational biology, accurately mapping biological networks is crucial for understanding complex cellular mechanisms and advancing drug discovery. However, evaluating these methods in real-world environments poses a significant challenge due to the time, cost, and ethical considerations associated with large-scale interventions under both interventional and control conditions. Consequently, most algorithmic developments in the field have traditionally relied on synthetic datasets for evaluating causal inference approaches. Nevertheless, previous work⁴ has shown that such evaluations do not provide sufficient information on whether these methods generalize to real-world systems.

In biology, a domain characterized by enormous complexity of the systems studied, establishing causality frequently involves experimentation in controlled in-vitro lab conditions using appropriate technologies to observe response to intervention, such as for example high-content microscopy⁵ and multivariate omics measurements⁶. High-throughput single-cell methods for observing whole transcriptomics measurements in individual cells under genetic perturbations^7,8,9 has recently emerged as a promising technology that could theoretically support performing causal inference in cellular systems at the scale of thousands of perturbations per experiment, and therefore holds enormous promise in potentially enabling researchers to uncover the intricate wiring diagrams of cellular biology^10,11,12,13.

However, effectively utilizing such datasets remains challenging, as establishing a causal ground truth for evaluating and comparing graphical network inference methods is difficult^14,15,16. Furthermore, there is a need for systematic and well-validated benchmarks to objectively compare methods that aim to advance the causal interpretation of real-world interventional datasets while moving beyond reductionist (semi-)synthetic experiments.

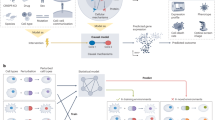
To facilitate the advancement of machine learning methods in this challenging domain, we introduce CausalBench—the largest openly available benchmark suite for evaluating network inference methods on real-world interventional data (Fig. 1). CausalBench contains meaningful biologically-motivated performance metrics, a curated set of two large-scale perturbational single-cell RNA sequencing experiments with over 200,000 interventional datapoints (each of which is openly available), and integrates numerous baseline implementations of state-of-the-art methods for causal network inference. An initial study leveraging a first iteration of CausalBench highlighted how poor scalability and inadequate utilization of the interventional data limited performance. We envision CausalBench can help accelerate progress on large-scale real-world causal graph inference, and that the methods developed against CausalBench could eventually lead to new therapeutics and a deeper understanding of human health by enabling the reconstruction of the functional gene-gene interactome. This vision was already partially fulfilled, as the utilization of CausalBench in a machine learning challenge lead to the development of promising methods¹⁷. The challenge lead to the discovery of state-of-the-art methods, as well as to further developments of CausalBench. The challenge methods perform significantly better than prior methods across all our metrics, and constitute a major step towards alleviating the limitations that were identified with CausalBench, such as scalability and utilization of the interventional information. CausalBench thus opens new research avenues and provides the necessary architecture to test future methodological developments, and demonstrate the importance of rigorous and thoughtful benchmarking as a tool to spur scientific advancement. Here, we recapitulate the state-of-the-art methods at the time of publication and conduct a thorough evaluation using CausalBench, offering a set of tools for practitioners to analyze large-scale perturbation datasets, as well as highlighting remaining method development opportunities.

Fig. 1: An overview of causal gene–gene network inference in mixed observational and perturbational single-cell data.

The causal generative process in its unperturbed form is observed in the observational data (left; 10,000+ datapoints in CausalBench) while data under genetic interventions (e.g. CRISPR knockouts) are observed in the interventional data (right; 200,000+ datapoints in CausalBench). Either observational or interventional plus observational data that were sampled from the true causal generative process (bottom distributions) can be used by network inference algorithms (bottom right) to infer a reconstructed causal graph (top right) that should as closely as possible recapitulate the original underlying functional gene-gene interactions.

The source code of the benchmark is openly available at https://github.com/causalbench/causalbench under Apache 2.0 license.

Results

We here present the comprehensive findings of our benchmarking analysis using CausalBench, and provide a complete image of the state-of-the-art at the time of publication. This includes an evaluation of various network inference methods applied to large-scale single-cell perturbation data, including methods developed as part of the CausalBench challenge¹⁷. Our analysis is designed to test the efficacy of these methods in real-world scenarios, comparing their performance across multiple metrics. We focus on highlighting key insights into the scalability, precision, and robustness of the tested methods, thereby offering a nuanced understanding of their applicability and limitations in the context of causal inference from complex biological data.

CausalBench We implemented a complete benchmarking suite called CausalBench. CausalBench builds on two recent large-scale perturbation datasets from ref. ¹⁸. The two datasets correspond to two cell lines, namely RPE1 and K562, which contain thousands of measurements of the expression of genes of individual cells under both control (observational data) and perturbed state (interventional data). Perturbations correspond to knocking down the expression of specific genes using the CRISPRi technology¹⁹. In CausalBench, unlike standard benchmarks with known or simulated graphs, the true causal graph is unknown due to the complex biological processes involved. We respond to this by developing synergistic cell-specific metrics with the aim of measuring the accuracy of the output network in representing the underlying complex biological processes. We employ two evaluation types: a biology-driven approximation of ground truth and a quantitative statistical evaluation. By leveraging comparisons between control and treated cells, our statistical metrics rely on the gold standard procedure for empirically estimating causal effects, making them inherently causal. For the statistical evaluation, we compute the mean Wasserstein distance and the false omission rate (FOR) of each model. The mean Wasserstein distance measures to what extent the predicted interactions correspond to strong causal effects. The FOR measures at what rate existing causal interaction are omitted by a model output. Details about both metrics can be found in “Evaluation”. As for precision and recall, the mean Wasserstein distance and the FOR complement each other as there is an inherent trade-off between maximizing the mean Wasserstein and minimizing the FOR.

We implement a representative set of existing state-of-the-art methods as recognized by the scientific community for the task of causal discovery from single-cell observational and mixed perturbational data. For the observational setting, we implement PC (named after the inventors, Peter and Clark; a constraint-based method)²⁰, Greedy Equivalence Search (GES; a score-based method)²¹, and NOTEARS variants NOTEARS (Linear), NOTEARS (Linear, L1), NOTEARS (MLP) and NOTEARS (MLP, L1)^22,23, Sortnregress²⁴ (a marginal variance-based method), and GRNBoost, GRNBoost + TF and SCENIC²⁵ (tree-based GRN inference methods at different step of the SCENIC pipeline). In the interventional setting, we include Greedy Interventional Equivalence Search (GIES, a score-based method and extension to GES)²⁶, the Differentiable Causal Discovery from Interventional Data (DCDI) variants DCDI-G and DCDI-DSF (continuous optimization-based methods)²⁷, and DCDI-FG²⁸. GES and GIES greedily add and remove edges until a score on the graph is maximized. NOTEARS, DCDI-FG, and DCDI enforce acyclicity via a continuously differentiable constraint, making them suitable for deep learning. We also include the best methods discovered in the context of the CausalBench challenge¹⁷, namely Mean Difference (top 1k and top 5k)²⁹, Guanlab (top 1k and top 5k)³⁰, Catran³¹, Betterboost³², and SparseRC^33,34. All the challenge methods are interventional, as utilization of the interventional information was a key requirement of the CausalBench challenge.

Network inference

We here summarize the experimental results of our baselines in both observational and interventional settings, on the statistical evaluations and the biologically-motivated evaluations. All results are obtained by training on the full dataset five times with different random seeds.

Trade-off between precision and recall

We highlight the trade-off between recall and precision. Indeed, we expect methods to optimize for these two goals, as we want to obtain a high precision while maximizing the percentage of discovered interactions. On both the biological and statistical evaluation, we observe this trade-off. Methods perform in general similarly on both evaluation types, validating the quality of our proposed metrics. Two methods stand-out: Mean Difference, Guanlab. Both methods perform highly on both evaluation, with Mean Difference performing slightly better on the statistical evaluation and Guanlab perfrom slightly better on the biological evaluation. Their performance is similar on both datasets. GRNBoost is the only method with a high recall on the biological evaluation, and low FOR on K562, but this comes with low precision. However, GRNBoost + TF and SCENIC have much lower FOR, as restricting the predictions to transcription factors-regulon interactions misses a lot of interactions of different types. Many of the other baselines have similar recall and varying precision (NOTEARS, PC, GES, GIES, Sortnregress, DCDIG, DCDI-MLP, DCDFG-MLP, Catran), suggesting those methods extract very little information from the data. Betterboost and SparseRC perform well on the statistical evaluation but not on the biological evaluation, supporting the importance of evaluation models from both angles. Results are summarized in Fig. 2 to highlight the trade-off. In Table 1, we compute the F1 score for the biological evaluation. In Table 2, we rank the methods in terms of the mean Wasserstein-FOR trade-off on the statistical evaluation.

Fig. 2: Precision-Recall trade-off.

Performance comparison in terms of Precision (in %; y-axis) and Recall (in %; x-axis) in correctly identifying edges substantiated by biological interaction databases (left panels); and our own statistical evaluation using interventional information in terms of Wasserstein distance and FOR (right panels). Performance is compared across 10 different methods using observational data (green markers), and 11 different methods using interventional data (pink markers) in K562 (top panels) and RPE1 (bottom panels) cell lines. For each method, we show the mean and standard deviation from five independent runs as markers with black borders, as well as individual results. Complete and detailed results can be found in “Additional results”.

Table 1 Ranking of models based on Mean F1 Score on the biological evaluation for K562 and RPE1

Table 2 Model ranking

Leveraging interventional information

In a previous version of the benchmark, we observed that contrary to what would be theoretically expected, existing interventional methods did not outperform observational methods, even though they are trained on more informative data. For example, on both datasets, GIES does not outperform its observational counterpart GES. Also, simple non-causal methods such as GRNBoost and Sortnregress perform well. GRNBoost performance is mainly driven by its capacity to recall most causal interactions, at the expense of its precision. The CausalBench challenge thus focused on encouraging the development of methods that leverage the interventional data. Mean Difference, Guanlab and SparseRC all show much higher utilization of the interventional information. This important improvement translates into much higher performance on both biological and statistical metrics. On both datasets, those methods exhibit mean Wasserstein scores that were unobserved with prior methods, for equivalent or lower FORs. To summarize the performance of the baselines, we propose a simple and unbiased way to compute a ranked scoreboard that takes into account the Wasserstein score and FOR. For interventional methods, we also train them on only 25% of the perturbations, to assess their performance in a setting where only part of the genes are perturbed. The detailed ranking can be found in Table 2. In both settings, the challenge methods top the ranking, even in the setting of low interventional data, which demonstrates the importance of leveraging the interventional information to recover the gene–gene interactions.

Characteristics of an optimal method for this task

For actual applicability to this real-world setting, the optimal method should exhibit properties that go beyond the best relative performance on the metrics presented previously. First, to uncover interactions among all encoding genes, the optimal graph inference method should computationally scale to graphs with a large number of nodes (in the thousands). Furthermore, the method performance should increase as more datapoints and more targeted genes are given as input. This ensures that a method is future-proof as we expect larger datasets that target almost all possible genes to become ubiquitous in the near future. The scale of the datasets used here allows us to test for these scaling properties in our benchmark by making the creation of settings with varying fractions of data or of number of interventions easy and principled. The result of this evaluation is summarized in Table 3.

Table 3 Model characteristics

Optimal methods should scale to the full graph

Unfortunately, many tested methods, with the exception of NOTEARS, GRNBoost (+ TF), SCENIC, DCDFG, Sortnregress and the challenge methods, do not computationally scale to graphs of the size typically encountered in transcriptome-wide GRN inference. Nonetheless, to enable a meaningful comparison, we partitioned the variables into smaller subsets where necessary and ran the methods on each subset independently, with the final output network being the union of the subnetworks. The proposed approach breaks the no-latent-confounder assumption that some methods may make, and it also does not fully leverage the information potentially available within the data. Methods that do scale to the full graph in a single optimization loop should therefore perform better. This assumption is supported by the better performance of the challenge methods, which all scale to the full graph. This highlights the necessity for a network inference method of scalability in terms of number of variables to be applicable to GRN inference.

Performance as a function of sample size

We additionally studied the effect of sample size on the performance of the evaluated state-of-the-art models. We randomly subset the data at different fractions and report the mean Wasserstein distance as shown in the figures of “Additional results”. In the observational setting, the sample size does not seem to have a significant effect on performance for most methods, indeed having a slightly negative effect for some methods. In the interventional setting, a positive impact is observable for a larger sample size, especially for the methods that rely on deep networks and gradient-based learning such as DCDI and SparseRC, whereas GIES seems to suffer in a large sample setting. For the challenge methods, all exhibit a positive trend in terms of a number of samples, but almost all of them plateau at around 50% of samples. Only SparseRC on RPE1 shows a trend that has not plateaued yet. This suggests two things: on one hand, the current state-of-the-art methods as identified by CausalBench may not need large number of datapoints, which reduces the number of cells per experiment needed. On the other hand, it opens an avenue for new methods that better leverage the information carried by each additional observed cell.

Performance by the fraction of perturbations

Beyond the size of the training set, we also studied the partial interventional setting—where only a subset of the possible genes to perturb are experimentally targeted. We adopt the fraction of randomly targeted genes from 5% (low ratio of interventions) to 100% (fully interventional). We randomly subset the genes at different fractions, using three different random seeds for each method, and report the mean Wasserstein distance as a measure of quantitative evaluation. We would expect a larger fraction of intervened genes to lead to higher performance, as this should facilitate the identification of the true causal graph. This evaluation serves two purposes. First, it is a diagnostic to assess whether a method is actually leveraging the interventional information. Second, it may inform on the amount of gene perturbation needed for a method to learn a gene network. Only Mean Difference, Guanlab, Betterboost and SparseRC exhibit large improvements in performance given more perturbation data. The other methods exhibit low or even negative utilization of the perturbation data. On the method development side, there are still avenues for improving the rate of convergence in terms of fraction of intervened genes, which would translate into a lower number of necessary gene perturbation and thus lead to cost reductions. We also envision that methods which can select the set of genes to target could converge even faster. In particular, the CausalBench challenge encouraged participants to improve on this metric. The winning methods all performed much higher compared to previous methods, and this improvement translated to all the other metrics of CausalBench, demonstrating the central importance of intervention scaling.

Robust performance across cell type

Another important characteristic of an optimal method for this task is the robustness of the performance across biological contexts or cell types. The data distribution and expression patterns can greatly differ across cell types and measurement technologies. As such, the performance of a particular method may not translate when applied to a new dataset not included in our benchmark. However, given that CausalBench contains data from two cell types, we can already assess the method’s robustness, albeit in a limited way. When comparing the results between the two cell lines, we can observe that the performance of the evaluated methods is in general consistent across the two cell types. For example, Mean Difference and Guanlab perform highly on both of them. Nevertheless, evaluating more datasets would be necessary to confidently conclude that the methods are robust. We envision that as more large-scale perturbational dataset become publicly available, their inclusion into CausalBench will make the evaluation more thorough.

Qualitative difference in recalling part of the Translation Initiation and Ribosome Biogenesis Complex

As an example, we focus on a part of the Translation Initiation and Ribosome Biogenesis Complex to illustrate how the two best methods Mean Difference and Guanlab qualitatively differ and how the differences in precision and recall as measured by the mean Wasserstein and FOR score are reflected in their output quality. In Fig. 3, we recapitulate the predicted interaction of Mean Difference (top 5k) and Guanlab (top 1K) on RPE1 for the genes EIF3B, RUVBL1, RPS13, RPL7, RPL23, TSR1. RPS13, RPL7 and RPL23 are ribosomal proteins. EIF3B is a core component of the translation initiation machinery and interacts directly with ribosomal proteins to facilitate the assembly and function of the translation initiation complex. TSR1 is involved in the maturation of ribosomal 40S subunits, and its interaction with ribosomal proteins is essential for ribosome assembly. RUVBL1 is known for its roles in DNA repair, transcription regulation, and as a part of ATP-dependent chromatin remodeling complexes. As can be observed, Guanlab (top 1k) predicts only interactions that are highly likely, but omits critical ones between EIF3B and the ribosomal proteins. Those interactions are recovered by Mean Difference (top 5k). However, the predicted interactions with RUVBL1 are more uncertain and may be expected to be indirect rather than direct, i.e., the effect may be mediated by other genes. This exemplifies how the difference in precision and recall are reflected qualitatively. This difference is predicted by our metrics, with Guanlab having a higher mean Wasserstein but lower FOR, suggesting it predicts mainly high-confidence interactions but may omit important ones.

Fig. 3: Interactions between the genes EIF3B, RUVBL1, RPS13, RPL7, RPL23, TSR1 as predicted by Mean Difference (top 5k) and Guanlab (top 1K) on RPE1.

Green interactions are predicted by both methods, blue by Mean Difference (top 5k) and red by Guanlab (top 1k). Mean Difference (top 5k), which has a lower FOR, recalls more interactions in this complex. However, it also predicts interactions with RUVBL1 that are more uncertain, and that are more likely indirect rather than direct. Guanlab (top 1k), which has a higher mean Wasserstein, recovers fewer interactions, but all of its predicted interactions among ribosomal proteins and TSR1, which are essential for ribosomal assembly and function, are highly likely. However, it omits the interactions with EIF3B, a key component of the translation initiation factor complex.

Discussion

Openly available benchmarks for network inference models for large-scale single-cell data can accelerate the development of new and effective approaches for uncovering gene regulatory relationships. However, some limitations to this approach remain: firstly, the biological networks used for evaluation do not fully capture ground-truth GRNs, and the reported connection are often biased towards better-studied systems and pathways³⁵. True ground-truth validation would require prospective and exhaustive interventional wet-lab experiments. However, at present, experiments at the scale necessary to exhaustively map gene-gene interactions across the genome are cost prohibitive for all possible edges. Moreover, the reported interactions in the reference databases used to construct the biological ground truth may be highly context dependent. To remedy this, we filter out interactions that are not validated by differential expression in the benchmark datasets. This filtering ensures that the biological evaluation is cell-specific. However, we can observe that this filtering greatly reduces the size of the true positive set, highlighting the difficulty of validating gene networks against prior knowledge. This is why in our study we greatly focus on developing a sound statistical evaluation, as we consider this approach to be less biased and fully context specific.

Beyond limitations in data sources used, there are limitations with some of the assumptions in the utilized state-of-the-art models. For instance, feedback loops between genes are a well-known phenomenon in gene regulation^36,37 that unfortunately cannot be represented by existing causal network inference methods at present that enforce acyclicity, which is the case for e.g. SparseRC and DCDI. While many causal discovery methods assume causal sufficiency, which posits that all common causes of any pair of variables are observed, it is important to note that this assumption may not hold true in the datasets included in CausalBench, as not all gene are observed. Lastly, the assumption of linearity of interaction may not hold for gene-gene interactions. We acknowledge these limitations and encourage ongoing research to address them. We can hypothesize that those limitations are strong obstacles for causality methods, as the challenge methods, such as Mean Difference and Guanlab, which do not enforce acyclicity and are also by design less sensitive to lack of causal sufficiency, perform much better. This is indeed an important takeaway message of our benchmarking that direct the community towards models that inherently allow feedback loops as they also empirically outperfom those that impose acyclicity.

Single-cell data presents idiosyncratic challenges that may break the common assumptions of many existing methods. Apart from the high dimensionality in terms of the number of variables and large sample size, the distribution of the gene expression presents a challenge as it is highly tailed at 0 for some genes³⁸, with those zeros being both biological as well as technical (dropout effect³⁹). Single-cell data often has much higher technical noise and variability than bulk RNA-seq, due to factors like amplification noise, low mRNA capture efficiency, and sequencing depth⁴⁰. In addition, different cells sampled from the same batch may not be truly independent as the cells may have interacted and influenced their states. Lastly, cells in scRNAseq experiments are measured at a fixed point in time and may therefore have been sampled at various points in their developmental trajectory or cell cycle⁴¹—making sampling time a potential confounding factor in any analysis of scRNAseq data.

For practitioners, our analysis with CausalBench suggests that Mean Difference and Guanlab are tools that should be part of any computational biologist toolbox when analyzing perturbation datasets. Both methods perform highly on both metrics and on both datasets, as well as in low-intervention settings. At the time of publication, we can thus confidently recommend those two methods as default choices. Between the two, there exist slight differences, such as Guanlab performing better on the biological evaluation and Mean Difference performing better on the statistical one. Nevertheless, we consider those differences to be too small to give a preference to one over the other, and we would thus recommend to run both methods when analyzing a dataset, given that they anyway exhibit low compute times (see Tables 9 and 10).

In our study, we observed that some methods do not return edge confidence, especially from the causality literature, which is why we focused on evaluating point estimates as there is not always a theoretically sound way to obtain uncertainty estimates. This approach encourages methods to return the Pareto optimal trade-off, providing a balance between precision and recall. However, for practitioners interested in edge confidence, bootstrapping^42,43 or stability selection⁴⁴ can be employed to calculate these values. It’s important to note that the two best-performing methods in our benchmark, Mean Difference, and Guanlab, are based on ranking the edges. This ranking inherently provides a measure of confidence in the predicted interactions, with higher-ranked edges being more confident. Therefore, even in the absence of explicit edge confidence values, these methods offer a form of confidence measure through their ranking system.

For method development, even though Mean Difference and Guanlab have already pushed the bar quite high, we consider that there still exist many exciting avenues for further improvements, with CausalBench serving as the ideal testing ground. For example, only SparseRC fulfills sample scaling. As such, a new method that borrows ideas from SparceRC and combines them with Mean Difference or Guanlab may perform even better. Also, there is a gap in performance between the low-intervention setting and the high-intervention setting. Partially closing that gap may have tremendous practical implications, as it would allow to dramatically reduce the number of necessary experiments to map cell-specific gene-gene interactomes.

To conclude, our work introduces CausalBench—a pioneering and comprehensive open benchmark specifically designed for the evaluation of causal discovery algorithms in the context of real-world interventional data, leveraging two expansive CRISPR-based interventional scRNA-seq datasets. CausalBench innovates by offering a suite of biologically meaningful performance metrics, enabling a nuanced and quantitative comparison of graphs generated by various causal inference methods. This comparison is bolstered by statistical evaluations, meticulously validated against established biological knowledge bases in a cell-specific manner.

CausalBench is meticulously crafted to optimize the evaluation process of causal discovery methods on real-world interventional data. Standardizing the non-model-related aspects of this process, it empowers researchers to concentrate their efforts on the refinement and advancement of causal network discovery methodologies. Built upon one of the largest open real-world interventional datasets, with over 200,000 data points¹⁸, CausalBench offers the computational biology and causal machine learning community an unparalleled platform for the development and assessment of network inference methods.

Our initial findings underscored the myriad challenges that contemporary models faced in this demanding domain, including issues with scalability and suboptimal use of interventional data. To address these challenges, a machine learning challenge was spearheaded, galvanizing the community to tackle this vital task in computational biology, with CausalBench serving as a foundational tool¹⁷. The winning methods from this challenge have significantly advanced the state-of-the-art, enhancing scalability and data utilization remarkably. This swift progress underscores the critical role of a well-constructed benchmark in catalyzing and accelerating scientific advancements.

We also aim for CausalBench to remain at the forefront of benchmarking bioinformatics methods tailored to perturbational biological datasets. The modularity of its implementation makes it straightforward to add new large-scale perturbational datasets as they become publicly available. The biological evaluation can also be readily updated as new or significantly expanded databases become available. New data dimensions can also be explored, either included by the methods themselves through the integration of prior knowledge (e.g. ATAC-seq data), or new data modalities given as input (e.g. time-series data). Such extensions may come from us as well as from community contributions directly to the public GitHub repository of CausalBench, as we are deeply committed to the long-term utility of our tool.

Beyond the scope of the challenge, CausalBench has already been employed in other studies^45,46, despite its recent introduction, attesting to its practical utility and the relevance of its datasets. We anticipate that CausalBench will continue to be a catalyst for methodological innovations, thereby making a profound and lasting impact in the realm of data-driven drug discovery.

Methods

Problem formulation

We introduce the framework of Structural Causal Models (SCMs) to serve as a causal language for describing methods, assumptions, and limitations and to motivate the quantitative metrics. The data’s perturbational nature requires this formal statistical language beyond associations and correlations. We use the causal view as was introduced by ref. ⁴⁷.

Structural Causal Models (SCMs)

Formally, an SCM ${\mathbb{M}}$ consists of a 4-tuple $\left({\mathbb{U}},{\mathbb{X}},{{{\mathcal{F}}}},P({{{\bf{u}}}})\right)$, where ${\mathbb{U}}$ is a set of unobserved (latent) variables and ${\mathbb{X}}$ is the set of observed (measured) variables⁴⁸. ${{{\mathcal{F}}}}$ is a set of functions such that for each ${X}_{i}\in {\mathbb{X}}$, X_i ← f_i(Pa_i, U_i), ${U}_{i}\in {\mathbb{U}}$ and $P{a}_{i}\in {\mathbb{X}}\setminus {X}_{i}$. The SCM induces a distribution over the observed variables P(x). The variable-parent relationships can be represented in a directed graph, where each X_i is a node in the graph, and there is a directed edge between all Pa_i to X_i. The task of causal discovery can then be described as learning this graph over the variables. In the most general sense, an intervention on a variable X_i can be thought as uniformly replacing its structural assignment with a new function ${X}_{i}\leftarrow \tilde{f}({X}_{{\widetilde{Pa}}_{i}},{\tilde{U}}_{i})$. In this work, we consider the gene perturbation as being atomic or stochastic intervention and denote an intervention on X_i as σ(X_i). We can then describe the interventional distribution, denoted ${P}^{\sigma ({X}_{i})}({{{\bf{x}}}})$, as the distribution entailed by the modified SCM. For consistency, we denote the observational distribution as both ${P}^{{{\emptyset}}}({{{\bf{x}}}})$ and P(x). This SCM framework is used throughout the paper.

Problem setting

We consider the setting where we are given a dataset of vector samples x ∈ R^d, where x_i represents the measured expression of gene i in a given cell. The goal of a graph inference method is to learn a causal graph ${{{\mathcal{G}}}}$, where each node is a single gene. The causal graph ${{{\mathcal{G}}}}$ induces a distribution over observed sample P(x), such that:

$$P({{{\bf{x}}}})=\prod p({x}_{i}| P{a}_{i})$$

(1)

The datasets contain data sampled from ${P}^{{{\emptyset}}}({{{\bf{x}}}})$, as well as ${P}^{\sigma ({X}_{i})}({{{\bf{x}}}})$ for various i. The observational setting only uses samples from ${P}^{{{\emptyset}}}({{{\bf{x}}}})$, the interventional setting includes observational and interventional data, while the partial interventional setting is a mix of the two, where only a subset of the genes are observed under perturbation.

Related work

Background

Given an observational data distribution, several different causal networks or directed acyclic graphs (DAGs) could be shown to have generated the data. The causal networks that could equally represent the generative process of an observational data distribution are collectively referred to as the Markov equivalence class (MEC) of that DAG⁴⁹. Interventional data offer an important tool for limiting the size of the MEC to improve the identifiability of the true underlying causal DAG⁵⁰. In the case of gene expression data, modern gene-editing tools such as CRISPR offer a powerful mechanism for performing interventional experiments at scale by altering the expression of specific genes and observing the resulting interventional distribution across the entire transcriptome^7,8,9. The ability to leverage such interventional experiment data at scale could significantly improve our ability to uncover underlying causal functional relationships between genes and thereby strengthen our quantitative understanding of biology. Establishing causal links between genes can help implicate genes in biological processes causally involved in disease states and thereby open up new opportunities for therapeutic development^51,52.

Network inference in mixed observational and interventional data

Learning network structure from both observational and interventional data presents significant potential in reducing the search space over all possible causal graphs. Traditionally, this network inference problem has been solved using discrete methods such as permutation-based approaches^26,53. Recently, several new models have been proposed that can differentiably learn causal structure⁵⁴. However, most of these models focus on observational datasets alone.⁵⁵ presented the first differentiable causal learning approach using both observational and interventional data.²⁸ improved the scalability of differentiable causal network discovery for large, high-dimensional datasets by using factor graphs to restrict the search space, and ref. ⁵⁶ introduced an active learning strategy for selecting interventions to optimize differentiable graph inference.

Gene regulatory network inference

The problem of GRN inference has been studied extensively in the bioinformatics literature in the case of observational datasets. Early work modeled this problem using a Bayesian network trained on bulk gene expression data⁵⁷. Subsequent papers approached this as a feature ranking problem where machine learning methods such as linear regression⁵⁸ or random forests^25,59 are used to predict the expression of any one gene using the expression of all other genes. However ref. ⁶⁰, showed that most GRN inference methods for observational data perform quite poorly when applied to single-cell datasets due to the large size and noisiness of the data. In the case of constructing networks using interventional data, there is relatively much less work given the recent development of this experimental technology.⁷ were the first to apply network inference methods to single-cell interventional datasets using linear regression. In recent years, several methods have also been developed to infer gene regulatory networks by integrating single-cell RNA sequencing and single-cell ATAC sequencing (scATAC-seq) data. Notably, SCENIC+⁶¹ is designed to construct enhancer-driven GRNs using combined or separate scRNA-seq and scATAC-seq data. Other methods have also been proposed, such as STREAM⁶², GLUE⁶³, DIRECT-NET⁶⁴, Pando⁶⁵, and scMEGA⁶⁶. These approaches leverage the complementary information provided by gene expression and chromatin accessibility to enhance the accuracy of GRN inference.

Benchmarks for causal discovery methods

To benchmark causal discovery methods, the main approach followed consists of evaluating purely synthetic data. The true underlying graph is usually drawn from a distribution of graphs, following procedures described in refs. ⁶⁷ (Erdös-Rényi graphs) and ⁶⁸ (scale-free graphs). Given a drawn graph, a dataset is then created under an additive noise model assumption, following some functional relationship such as linear or nonlinear functions of random Fourier features. The additive noise can follow various distributions, such as Gaussian or uniform. The predicted graph is then evaluated using structural metrics that compare the prediction to the true graph. Popular metrics include precision, recall, F1, structural hamming distance (SHD), and structural intervention distance (SID)⁶⁹. While this type of evaluation is valuable as a first validation of a new method in a controlled setting, it is limited in its capacity to predict the transportability of a method to a real-world setting. Indeed, the generated synthetic data tend to match the assumption of the proposed method, and the complexity of their distribution is reduced and uninformedly far from the distribution of real-world empirical data. To remedy this, synthetic data generators that mimic real-world data have been proposed, such as ref. ⁷⁰ for the GRN domain. Nevertheless, even these advanced synthetic datasets have their limitations. Specifically, they might not capture aspects or mechanisms of the biological system that we are currently unaware of, a concept we term “unknown-unknowns”. Such omissions underscore the inherent challenges in mimicking the full complexity of actual biological datasets. They also still offer a large set of degrees of freedom in the choice of hyperparameters ("researcher degrees of freedom" phenomenon⁷¹). Furthermore, the distribution over the true underlying graph still needs to be chosen, and how far those generated graphs are from a realistic causal graph is also unknown. As such ref. ⁴, thoroughly argues that the evaluation of causal methods should incorporate evaluative mechanisms that examine empirical interventional metrics as opposed to purely structural ones, and that such evaluations are best performed using real empirical data.

Benchmarks for gene regulatory network inference

Past work has looked at benchmarking of different GRN inference approaches using single-cell gene expression data⁶⁰. However, this work only considers observational data and looks at small datasets of ~5000 datapoints (cells). Moreover, it does not benchmark most state-of-the-art causal inference methods. The DREAM5 challenge⁷² provided a landmark benchmark by evaluating GRN inference approaches on both observational microarray data and experimental perturbation data from in vivo gene knockout and knockdown studies, particularly for organisms like E. coli and S. aureus. While DREAM5 significantly advanced the field by incorporating experimental perturbations, it remained limited to bulk data and did not address the high-resolution insights enabled by large-scale, single-cell perturbational datasets. Our work, CausalBench, extends this approach by benchmarking GRN inference on expansive single-cell perturbational data, with biologically relevant metrics that offer deeper insights into causal gene regulatory mechanisms at the single-cell level.

Benchmarking setup

Datasets for causal network inference

Effective GRN inference relies on gene expression datasets of sufficiently large size to infer underlying transcriptional relationships between genes. The size of the MECs inferred by these methods can hypothetically be reduced by using interventional data⁵⁰. For our analysis, we make use of gene expression data measured at the resolution of individual cells following a wide range of genetic perturbations. Each perturbation corresponds to the knock down of a specific gene using CRISPRi gene-editing technology¹⁹. This is the largest and best quality dataset of its kind that is publicly available⁷³, and includes two different biological contexts (cell lines RPE-1 and K562). The dataset is provided in a standardized format that does not require specialized libraries. We have also preprocessed the data so that the expression counts are normalized across batches and perturbations that appear to not have knocked down their target successfully are removed (Preprocessing). The goal was to ensure that this benchmark is readily accessible to a broad machine-learning audience while requiring no prior domain knowledge of biology beyond what is in this paper. A summary of the resulting two datasets can be found in Table 4. We hold out 20% of the data for evaluation, stratified by intervention target.

Table 4 Datasets characteristics

Network inference model input and output

The benchmarked methods are given either observational data only or both observational and interventional data—depending on the setting—consisting of the expression of each gene in each cell. For interventional data, the target gene in each cell is also given as input. We do not enforce that the methods need to learn a graph on all the variables, and further preprocessing and variables selection are permitted. The only expected output is a list of gene pairs that represent directed edges. No properties of the output network, such as acyclicity, are enforced either.

Preprocessing

We incorporated a two-level quality control mechanism for processing our data, considering the perturbations and individual cells separately.

In the perturbation-level control, we identified “strong” perturbations based on three criteria adopted from ref. ¹⁸: (1) inducing at least 50 differentially expressed genes with a significance of p < 0.05 according to the Anderson-Darling test after Benjamini-Hochberg correction; (2) being represented in a minimum of 25 cells passing our quality filters; and (3) achieving an on-target knockdown of at least 30%, if measured.

In the individual cell-level control, we checked the effectiveness of each perturbation by contrasting the expression level of the perturbed gene (X) post-perturbation against its baseline level. We established a threshold for expression level at the 10th percentile of gene X in the unperturbed control distribution. We excluded any cell where gene X was perturbed but its expression exceeded this threshold. However, if a perturbed gene’s expression was not measured in the dataset, we did not perform this filtering.

Lastly, we filter out genes that have less than 100 perturbed cells, such that the held-out datasets are big enough to have statistical power. See Fig. 4 for a visual representation of our filtering process.

Fig. 4: Cell and gene filtering.

Flowchart illustrating data filtering steps.

Baseline models

PC²⁰

PC is one of the most widely used methods in causal inference from observational data that assumes there are no confounders and calculates conditional independence to give asymptotically correct results. It outputs the equivalence class of graphs that conform with the results of the conditional independence tests.

Greedy Equivalence Search (GES)²¹

GES implements a two-phase procedure (Forward and Backward phases that add and remove edges from the graph) to calculate a score to choose within an equivalence class. While GES leverages only observational data, its extension, Greedy Interventional Equivalence Search (GIES), enhances GES by adding a turning phase to allow for the inclusion of interventional data.

NOTEARS^22,23

NOTEARS formulates the DAG inference problem as a continuous optimization over real-valued matrices that avoids the combinatorial search over acyclic graphs. This is achieved by constructing a smooth function with computable derivatives over the adjacent matrices that vanishes only when the associated graph is acyclic. Various versions of NOTEARS refer to which function approximator is employed (either an MLP or Linear) or which regularity term is added to the loss function (e.g. L1 for the sparsity constraint.)

Differentiable Causal Discovery from Interventional Data (DCDI)²⁷

DCDI leverages various types of interventions (perfect, imperfect, unknown), and uses a neural network model to capture conditional densities. DCDI encodes the DAG using a binary adjacency matrix. The intervention matrix is also modeled as a binary mask that determines which nodes are the target of intervention. A likelihood-based differentiable objective function is formed by using this parameterization, and subsequently maximized by gradient-based methods to infer the underlying DAG. DCDI-G assumes Gaussian conditional distributions while DCDI-DSF lifts this assumption by using normalizing flows to capture flexible distributions.

GRNBoost (+ TF), SCENIC²⁵

GRNBoost is a GRN-specific Gradient Boosting tree method, where for every gene, candidate parent gene are ranked based on their predictive power toward the expression profile of the downstream gene. As such, it acts as a feature selection method toward learning the graph. GRNBoost was identified as one of the best-performing GRN method in previous observational data-based benchmarks⁶⁰. GRNBoost is a step of the SCENIC pipeline. We thus also evaluate GRNBoost + TF, which consists of restricting the putative parents to a list of known transcription factors. SCENIC additionally leverages known motif to reduce the number of false positives.

Guanlab³⁰

This approach utilizes LightGBM, a supervised learning model, to identify gene pairs with causal relationships by transforming the task into a supervised learning problem. It constructs a dataset using observational and interventional data, computing the absolute correlations between gene expressions to determine positive samples indicative of causality. Features for the model are derived from normalized expression data of the gene pairs, and the LightGBM model is trained and evaluated on this constructed dataset. The top gene pairs (in this study the top 1000 or top 5000), ranked by the model’s scores, are selected to highlight significant causal relationships.

Mean Difference²⁹

This approach, referred to as Mean Difference estimation, quantifies the causal relationship between gene pairs X → Y by calculating the absolute difference in mean expression levels of gene Y between observational data and X-perturbed interventional data. By comparing these mean expression levels, it directly measures the impact of interventions on X in altering Y’s expression. Gene pairs are then ranked based on the magnitude of these differences, with the top k pairs—where k is predefined by the user—selected for analysis. In this study, we use k = 1000 and k = 5000.

SparseRC^33,34

SparseRC is based on the “few-root-causes" assumption, positing that gene activation can be modeled as a sparse linear system within a directed acyclic graph (DAG) framework. It employs a linear structural equation model (SEM) to describe gene-gene interactions. The approach assumes that only a few root causes (initial input values) drive the observed gene expressions. SparseRC involves solving an optimization problem that minimizes the difference between observed and estimated gene expressions, subject to a constraint that maintains the network’s acyclicity.

Catran³¹

Catran is a transformer-based method for learning causal relationships between genes, using vector embeddings to represent gene influences without explicitly learning a complex adjacency matrix. It simplifies the model and reduces parameters by randomly shuffling gene expression data for training, focusing on reconstructing perturbed data to refine gene embeddings. Additionally, Catran calculates interventional loss using perturbation information, estimating the significance of gene interactions to improve prediction accuracy and model interpretability.

Betterboost³²

Betterboost improves upon GRNBoost by integrating perturbation data from Perturb-seq experiments into gene regulatory network inference, using both predictive capacity and causal relationships between genes. GRNBoost assigns scores to gene interactions based on predictiveness, but BetterBoost introduces a ranking score that considers the causal impact of gene perturbations through statistical testing. It then combines the two scores into one to rank gene interactions.

Benchmark usage

CausalBench has been designed to be easy to setup and use. Adding or testing a new method is also straightfoward. A more comprehensive guide can be found in the README of the Github repository (https://github.com/causalbench/causalbench) as well as the starter repository of the CausalBench challenge (https://github.com/causalbench/causalbench-starter/).

Compute resources

All methods were given the same computational resources, which consisted of 20 CPU’s with 32GB of memory each. We additionally assign a GPU for the DCDI, DCDFG, CATRAN and SparseRC methods. The hyperparameters of each method, such as partition sizes, are chosen such that the running time remains below 30 hours. Partition sizes for each model can be found in section 4.6.

Evaluation

Biological evaluation

To implement the biologically-motivated evaluation, we extract network data from two widely used open biological databases: CORUM⁷⁴ and STRING^{75,76,77,78,79,80,81,82,83,84,85,86}. CORUM is a repository of experimentally characterized protein complexes from mammalian organisms. The complexes are extracted from individual experimental publications, and exclude results from high-throughput experiments. We extract the human protein complexes from the CORUM repository and aggregate them to form a network of genes. STRING is a repository of known and predicted protein-protein interactions. STRING contains both physical (direct) interactions and indirect (functional) interactions that we use to create two evaluation networks from STRING: Protein-protein interactions (network) and protein-protein interactions (physical). Protein-protein interactions (physical) contain only physical interactions, whereas protein-protein interactions (network) contains all types of know and predicted interactions. STRING, and in particular string-network, can contain less reliable links, as the content of the database is pulled from a variety of evidence, such as high-throughput lab experiments, (conserved) co-expression, and text-mining of the literature. Using these databases of domain knowledge, we can construct putatively true undirected subnetworks to evaluate the output networks in the understanding that the discovered edges that are not present in those databases are not necessarily false positives. To ensure that the constructed network for the biological evaluation is cell-specific, we additionally filter out interactions that are not present in the data. To do so, we perform a two-sided Mann-Whitney U rank test^87,88 between datapoints from control and perturbed datapoints corresponding to the tested interaction. If the test is not rejected at level 5%, we consider the interaction as a false positive and filter it out of the biological evaluation. We can then compute metrics such as precision and recall against those constructed networks. For the K562 cell line, we employed data from the Chip-Atlas⁸⁹ and ENCODE⁹⁰ databases to build a ChiPSeq network, restricting the links to those relevant to or recorded in the K562 cell line. However, the RPE1 cell line has not been as comprehensively characterized in existing research. To address this, we utilized networks derived in a similar manner, but from a more extensively studied epithelial cell line, HepG2, given that RPE1 is also an epithelial cell line. However, we can observe that the precision of the ChiPSeq network is surprisingly low, indicating a high number of false positives (see Table 5). This observation is in line with many existing analyses of the high number of false positives of ChiP-seq data^91,92. We nevertheless include it such as to build a comprehensive ground truth.

Table 5 Precision of each database in terms of percentage of links that are validated by differential expression in the datasets

Statistical evaluation

In contrast to the biologically-motivated evaluation, the statistical evaluation in CausalBench is data-driven, cell-specific, and does not rely on prior knowledge. This evaluation method is uniquely designed for single-cell perturbational data and provides a way to approximate ground-truth gene regulatory interactions, supplementing information found in biological databases. The evaluation uses the interventional data from perturbational scRNA-seq experiments to assess predicted edges in the output networks. Here, we thus closely follow the postulate of⁴ that causal methods should be evaluated on empirical data using interventional metrics that correlate with the strength of the underlying relationships.

The main assumption for this evaluation is that if the predicted edge from A to B is a true edge denoting a functional interaction between the two genes, then perturbing gene A should have a statistically significant effect on the distribution ${P}^{\sigma ({X}_{A})}({{{{\bf{x}}}}}_{B})$ of values that gene B takes in the transcription profile, compared to its observational distribution ${P}^{{{\emptyset}}}({{{{\bf{x}}}}}_{B})$ (i.e compared to control samples where no gene was perturbed). Conversely, we can test for the predicted absence of gene interactions. We call a gene interaction A to B negative if there is no path in the predicted graph from A to B. If no interaction exists in the true graph, then there should be no statistically significant change in the distribution of B when intervening on A. We thus aim to estimate the false omission rate (FOR) of the predicted graph. The FOR is defined as:

$$\,{{\mbox{FOR}}} = \frac{{{\mbox{False}}}\, {{\mbox{Negatives}}}} {{{\mbox{False}}} \, {{\mbox{Negatives}}}+{\mbox{True}} \, {\mbox{Negatives}}}$$

Algorithm 1

Estimation of False Omission Rate (FOR)

Input: Predicted graph, ${P}^{\sigma ({X}_{A})}({{{{\bf{x}}}}}_{B})$, ${P}^{{{\emptyset}}}({{{{\bf{x}}}}}_{B})$ for all A, B, number of samples N for estimation

Output: FOR

Initialize counter for false negatives, FalseNegativesCount  = 0

Sample N gene pairs (A, B) such that no directed path exists between them in the predicted graph

for each sampled gene pair (A, B) do

 Perform the two-sided Mann-Whitney U rank test between ${P}^{\sigma ({X}_{A})}({{{{\bf{x}}}}}_{B})$ and ${P}^{{{\emptyset}}}({{{{\bf{x}}}}}_{B})$

 if p-value < 0.05 then

  Increment FalseNegativesCount by 1

 end if

end for’

FOR $=\frac{{FalseNegativesCount}}{N}$

return FOR

To test the predicted interactions, we propose using the mean Wasserstein distance. For each edge from A to B, we compute a Wasserstein distance⁹³ between the two empirical distributions of ${P}^{\sigma ({X}_{A})}({{{{\bf{x}}}}}_{B})$ and ${P}^{{{\emptyset}}}({{{{\bf{x}}}}}_{B})$. We then return the mean Wasserstein distance of all inferred edges. We call this metric the mean Wasserstein. A higher mean Wasserstein distance should indicate a stronger interventional effect of intervening on the parent. Although the quantitative statistical approach cannot differentiate between causal effects from direct edges or causal paths in the graph, we expect direct relationships to have stronger causal effects⁹⁴. Despite this limitation, the quantitative evaluation offers a data-driven, cell-specific, and prior-free metric. It also correlates with the strength of the causal effects, and thus evaluates methods in their ability to recall the strongest perturbational effects, which is a downstream task of high interest. Moreover, it presents an approach for estimating ground-truth gene regulatory interactions that is uniquely made possible through the size and interventional nature of single-cell perturbational datasets. Then, we evaluate the predicted negative interactions of the output. To do so, we sample random pairs of genes such that there is no path in the predicted graph between the two. We then perform a two-sided Mann-Whitney U rank test^87,88 between datapoints from ${P}^{\sigma ({X}_{A})}({{{{\bf{x}}}}}_{B})$ and ${P}^{{{\emptyset}}}({{{{\bf{x}}}}}_{B})$ for all sampled negative pairs using the SciPy package⁹⁵ to test the null hyptothesis that the two distributions are equal. A rejected test, with a p-value threshold of 5%, indicates a false negative. The trade-off between maximizing the mean Wasserstein and minimizing the FOR exhibits the ranking nature of this applied task, as opposed to predicting against a fixed binary ground-truth. Contrary to structural metrics, errors in prediction are weighted given their causal importance⁴. To our knowledge, we are also the first to propose evaluation of the negative predictions.

$${W}_{1}(P,Q)={\inf }_{\gamma \in \Gamma (P,Q)}{\int}_{X\times X}\parallel x-y\parallel d\gamma (x,y)$$

(2)

$$\, {{\mbox{MeanWasserstein}}}\,=\frac{1}{| {G}_{p}| } {\sum}_{(A,B)\in {G}_{p}}{W}_{1}({P}^{\sigma ({X}_{A})}({{{{\bf{x}}}}}_{B}),{P}^{{{\emptyset}}}({{{{\bf{x}}}}}_{B}))$$

(3)

Lemma 1

(FOR for Complete Predicted Graph). Let G_p be the predicted graph and G_t be the true graph. If every causal interaction present in G_t is also present in G_p, then the False Omission Rate (FOR) is equal to the p-value threshold asymptotically. Specifically:

$$\,{\mbox{FOR}}\,=\alpha$$

(4)

where α is the p-value threshold (in this context, α = 0.05).

Proof

Assume that every causal interaction in G_t is also present in G_p. This ensures that any absent interaction in G_p corresponds to a true negative interaction. When evaluating the absence of these interactions using the Mann-Whitney U rank test, the test essentially checks the null hypothesis that these interactions are truly absent. Consequently, the probability of incorrectly rejecting the null hypothesis (deeming an interaction falsely present) would be equivalent to the set significance level, which is the p-value threshold α. Thus, the FOR, which measures the rate of these false negative identifications among all true negatives, will be exactly α. □

Analysis of the proposed quantitative evaluations

We here perform an analysis of the proposed metrics to validate their meaningfulness and to study their properties. We follow a procedure similar to ref. ⁴. We create a synthetic dataset using an additive noise model with random Fourier features, reusing code from ref. ⁹⁶. The training set consists of 500 datapoints and the test set consists of 1500 observational datapoints and 30 interventional datapoints per variable, which makes the test set comparable to the test sets in CausalBench. We then train the Notears (MLP, L1) model with various strengths of sparsity regularization (l ∈ {0.025, 0.05, 0.1, 0.2, 0.5, 0.75, 1.0}), repeated five times per value of l. The results are presented in Fig. 5. As can be observed, our proposed statistical metrics highlight the trade-off between recovering and omitting causal relationships, where a stronger regularization value leads to a smaller graph recalling the strongest causal relationship, but omitting many others. At the other end of the spectrum, we can see that at a value of l = 0.05 all causal relationships are recalled as the FOR is 5%, which is equal to the p-value threshold. Lastly, we can observe that the mean Wasserstein is well correlated with a structural metric such as SHD (absolute Spearmann correlation of 0.857), but that it gives a better ordering of the models that is weighted in terms of strength of the predicted causal relationship (Spearmann correlation of 1.0 between the value of l and both FOR and mean Wasserstein). As such, our proposed statistical metrics are well-suited for applied tasks and offer a meaningful tool for model comparison and selection in practice.

Fig. 5: Plots showing the characteristics of the proposed statistical evaluations, here validated on synthetic data.

A NOTEARS (MLP, L1) model is run with different regularization values. Each setting is run five times, with the mean and standard deviation score plotted across the five runs for each setting.

Additional results

We here recapitulate more detailed and extensive results of our analysis of state-of-the-art method using Causalbench. Figure 6 shows the same plot as in the main text but with single run as individual points. Tables 6 and 7 show the precision and recall scores for the biological evaluation for each database. Figure 7 shows the effect of varying the dataset or intervention set size for each method.

Fig. 6: Precision-Recall trade-off.

Performance comparison in terms of Precision (in %; y-axis) and Recall (in %; x-axis) in correctly identifying edges substantiated by biological interaction databases (left panels); and our own statistical evaluation using interventional information in terms of Wasserstein distance and FOR (right panels). Performance is compared across 10 different methods using observational data (green markers), and 11 different methods using interventional data (pink markers) in K562 (top panels) and RPE1 (bottom panels) cell lines. For each method, we show the score of five independent runs.

Table 6 Biological evaluation results on K562

Table 7 Biological evaluation results on RPE1

Fig. 7: Statistical evaluation of scaling characteristics.

Performance comparison in terms of Mean Wasserstein Distance (unitless; y-axis) of 10 methods for causal graph inference on observational data (top row; (see legend top right) and 11 methods on interventional scRNAseq data (top row; see legend top right) when varying the fraction of the full dataset size available for inference (in %; x-axis), and 11 methods on interventional data (bottom row; see legend bottom right) when varying the fraction of the full intervention set used (in %, x-axis). Markers indicate the values observed when running the respective algorithms with one of three random seeds, and colored lines indicate the median value observed across all tested random seeds for a method.

Partition sizes

We here recapitulate the partition sizes used to be able to run each method in Table 8.

Table 8 Partition sizes

Run time

We here present the average run time for each method in Table 9 for the K562 cell line and in Table 10 for the RPE1 cell line

Table 9 Run time K562

Table 10 Run time RPE1

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Statistics and reproducibility

All perturbation datasets used in this study are publicly available, and each cell line is considered an independent replicate. To ensure sufficient coverage of perturbations, we required a minimum of 100 cells per perturbed gene; details are described in the text. Randomization was performed by stratifying 20% of the data for the test set, and random seeds were used throughout to ensure reproducibility (including partition and subset selection). All statistical analyses—including Mann-Whitney U rank tests (at a significance level of 5%)—were used solely for evaluating the inferred gene-gene interactions, rather than for new hypothesis discovery, so no multiple-testing correction was applied.