Introduction

Capillary rise has long been considered a fundamental wetting phenomenon. Yet, the impact of surface roughness is poorly understood, even though all real surfaces have some degree of roughness. Occurrences of rough capillary rise are widespread and diverse, including water manipulation strategies in nature1,2,3,4,5,6, weathering and deterioration in geology and our built environment7,8,9,10,11,12,13, and fluid storage in fractured materials14,15,16.

Rough capillary rise sees the coupling of two wetting phenomena: capillary rise between the walls, and hemiwicking within the surface roughness. Individually, capillary rise and hemiwicking are well understood. The long-established Jurin’s law describes equilibrium capillary rise between smooth solid surfaces. This has been interpreted and refined by numerous luminaries such as Young and Laplace17,18, Gibbs19, and more recently de Gennes20,21. Regarding wetting of rough surfaces, the condition required for hemiwicking is also well established22,23,24,25. However, the maturity of these fields has regularly led to oversimplifications on the interplay between hemiwicking and capillary rise. This is evidenced throughout the literature on rough capillary rise dynamics, spanning an extraordinary range of fields such as porosity26,27, earth science28, biophysics29, textiles30,31 and engineering7 to name but a few. Thus, there is a lack of fundamental understanding of rough capillary rise, leading to erroneous predictions of the rise heights.

Here, we provide a detailed analysis and explanation of equilibrium rough capillary rise. Principally, we take a rigorous energy minimisation approach to develop the Dual-Rise model, which is analytic and valid for general roughness. We demonstrate quantitative accuracy when compared to both experiments and simulations. In order to achieve the coupling between the two modes of liquid rise, we show that it is essential to capture the interaction between two length scales: the scale of the roughness, and the scale of the capillary wall separation.

In previous works, a key assumption has been that hemiwicking and capillary rise are independent phenomena26,29,30,31,32. However, this approximation breaks down at narrow surface separations. This has several consequences. Firstly, the critical angle for hemiwicking is often considered a thermodynamic criterion dependant on the property of the surface roughness and the liquid wettability23,24,25. In contrast, here we show that it also depends on the surface separation, and hemiwicking can be suppressed even for perfectly wetting liquids. Secondly, across this transition, the rise heights change abruptly, so that capillary rise depends strongly on the presence or absence of hemiwicking. This regime is particularly important to model accurately, as this is where the largest rise heights occur, and is typical in many of the rough rise occurrences and applications listed previously1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16.

When predicting the capillary rise height, previous works typically assume that it is sufficient to treat the roughness in an effective manner by using the Cassie-Baxter33 and Wenzel34 models, used canonically across wetting physics. These approximations are attractive, as the roughness details are reduced to an effective contact angle which can then enter Jurin’s Law, and so are widely used9,28,29,32,35,36,37. However, a key issue with both models is that they provide no information on their ranges of validity. We also find a further issue with the Wenzel model: this approximation strongly underestimates capillary rise when the predicted Wenzel angle is 0°, which occurs for even modest roughness and substrate wettability. Unfortunately, the Wenzel model is being widely used in this invalid regime, from fundamental rise predictions to the storage of liquid contaminants22,28,29,36,37.

We also show that capturing the coupling between hemiwicking and capillary rise, and their two characteristic length scales, is vital for predicting the liquid volumes raised. Any variant of the Cassie-Baxter and Wenzel models is inaccurate, as they both ignore the hemiwicking contribution. Meanwhile, treating the surfaces as essentially smooth, used for example in9,35, underestimates the total volume, which can be substantial on real surfaces.

Overall, this detailed understanding of equilibrium rough capillary rise will aid investigations in rise dynamics29,32,38, and will be essential for the functionalisation of rough capillary rise currently being attempted. Innovations include controlling fluid localisation in 3D cellular fluidics39,40, determining the extent and volume of liquid required for vascular cementitious repair41, and designing novel carbon capture technologies based on liquid infused surfaces42.

Results

Defining equilibrium

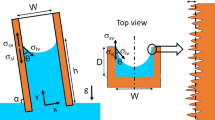
Here, we explore equilibrium rough capillary rise between parallel micropillared surfaces. A typical liquid rise morphology from simulations is shown in Fig. 1a, featuring both liquid rise between the plates, and hemiwicking within the surface texture.

Fig. 1: Defining the equilibrium rise heights in rough capillary rise.
figure 1

a Archetypal simulated rise heights in a rough parallel plate setup, exhibiting capillary rise between the surfaces, a meniscus, and hemiwicking within the roughness. b Definition of the model geometric parameters. Shown are the rise heights of the: capillary rise C, meniscus M, hemiwicking H, centre of mass of hemiwicking liquid HCOM, and total liquid height T. Also shown are the length scales of the: average roughness depth δ, average distance between hemiwicking columns d, and average total plate separation D. The area above the meniscus in the capillary region is denoted aM. Precise descriptions of all parameters are given in the text. c Plot of all metastable, pinned states observed for the simulated system SQ1 (detailed in methods, Table 4), featuring square posts with water as the rising liquid, d/δ = 5.43, and contact angle θ = 58∘. The vertical scale shows the reduced energy variation (ΔG) when raising liquid from the reservoir to each unique pinned state, normalised against the energy of hemiwicking a single pitch length in the absence of gravity (ΔG1). The normalised rise heights in the capillary region and hemiwicking region are indicated on the horizontal axis and colour scale respectively. The magnified inset highlights the density of metastable states around the global minimum energy state (the equilibrium state), indicated by ‘*’.

Full size image

In Fig. 1b, we distinguish two regions of liquid rise: the capillary region, which is separated into the capillary rise C and the meniscus M, and the hemiwicking region of height H. The total rise height T is the sum: T = C + M + H. Capillary rise is measured from the level of the reservoir (z = 0) at zero hydrostatic pressure, to the bottom of the meniscus. The meniscus height M is measured as the difference between the maximum and minimum heights of the liquid-gas interface between the two plates. The hemiwicking height H must be treated carefully. To illustrate the challenge, Fig. 1a shows how, at low contact angles, the hemiwicking region may exhibit an extended tail to large heights. The morphology of this tail is highly dependent on the specific roughness geometry27,43. However, as the energy minimisation will show in the proceeding section, a description of hemiwicking that is valid for general roughness can be obtained by using the centre of mass, HCOM, of the hemiwicking liquid, such that we define H = 2HCOM. This has the further advantage of always remaining a finite value. A direct benefit of this is that it resolves the issue of infinite rise height predictions in sharp grooves44.

Perpendicular to the plates, there are two length scales we focus on throughout. The first, δ, is defined as the average cross-sectional depth of liquid in the hemiwicking region. Here, we approximate δ as a constant, and equal to the average roughness depth. The relationship between δ and the rough texture geometries used throughout is shown in Table 1. The second length scale is d, associated with the plate separation. d is the average distance separating two hemiwicked plates. The two length scales are related by the average perpendicular distance between the two rough surfaces, D, where D = d + 2δ.

Table 1 The roughness parameters for a pillared texture, where the shape parameter α = 1 for square pillars, and α = π/4 for cylindrical pillars.
Full size table

To describe rough textures generally, three parameters are defined: the roughness r, the area fraction ϕ, and the wetted fraction f. As an example, these parameters are expressed in Table 1 for the square and cylindrical pillars used throughout, where P is the pitch length, wp is the pillar width for square pillars or pillar diameter for cylindrical pillars, and hp is pillar height. r is defined as the ratio between the total surface area of the texture to the projected area. ϕ is defined in the hemiwicked region as the ratio between the projected area of dry solid to the projected total solid area. f is defined in the hemiwicked region as the ratio of the wetted solid surface area to the total solid surface area. On flat-topped, smooth-topped, non-overhanging structures, as used here, f can be simplified to f = 1 − ϕ/r.

A complication in finding the equilibrium morphology via simulations and experiments is the presence of pinning. Pinning leads to a large range of metastable states. To illustrate this, in Fig. 1c we examine all pinned states for a texture we study in detail throughout: SQ1, a square array of square pillars, with water as the rising liquid (see Methods, Table 4 for a full description of all systems and abbreviations). For a single value of the plate separation δ/d = 5.43 and contact angle θ = 58°, 73 metastable states are observed. Each state is distinguished via its rise height in the capillary region, C + M (shown on the horizontal axis), and the hemiwicking height H (shown on the colour scale), normalised relative to the simulated pitch length P. The vertical scale shows the reduced energy change, which is the energy change of forming a given fluid configuration from an initially gas-filled system, ΔG, compared to the energy change of hemiwicking over a single pitch length from an initially gas-filled system ΔG1. For this system, we see three important states. Firstly, the lowest-height metastable state occurs when the meniscus pins on the 2nd pillar up from the reservoir with no hemiwicking. This state would be observed if an initially dry texture was contacted with the reservoir, and the liquid allowed to rise quasi-statically without any perturbations. Secondly, at the opposite extreme in rise heights, the meniscus pins on the 12th pillar, with hemiwicking observed for another 12 pillars above this. This state would be observed if the system was initially submerged in water, and the liquid allowed to reach a static state by draining. Both of these states are strongly dependent on how the roughness geometry controls the shape of the pinned three-phase contact line45. However, our principal interest here is the third important state, the equilibrium state, which occurs at intermediate rise heights (denoted * in Fig. 1c and the magnification panel). In this state, capillary forces and weight balance, so that pinning forces are minimal. It is not trivial to access the equilibrium state. In simulations, we must locate this state by finding the lowest energy configuration of all metastable states. In experiments, we do not have access to the energy directly, but instead perturb the system (tap the plates) to overcome the pinning barriers. This procedure is able to approximate the equilibrium state, with an estimated uncertainty of ± 1 pitch length.

Modelling equilibrium

The dual-rise model

We now develop the Dual-Rise model, to predict the equilibrium rough capillary rise. Taking an energy minimisation approach, we begin by constructing the energy change ΔG upon raising liquid from a reservoir to a configuration like that illustrated in Fig. 1a, and described in Fig. 1b,

$${{\Delta }}G={{\Delta }}{A}_{{{{{{{{\rm{sg}}}}}}}}}{\gamma }_{{{{{{{{\rm{sg}}}}}}}}}+{{\Delta }}{A}_{{{{{{{{\rm{sl}}}}}}}}}{\gamma }_{{{{{{{{\rm{sl}}}}}}}}}+{{\Delta }}{A}_{{{{{{{{\rm{lg}}}}}}}}}{\gamma }_{{{{{{{{\rm{lg}}}}}}}}}+{{\Delta }}{E}_{{{{{{{{\rm{g}}}}}}}}}.$$
(1)

ΔAsg, ΔAsl, and ΔAlg are the changes in the solid-gas, solid-liquid, and liquid-gas interfacial areas between the initial and final states respectively. ΔEg is the change in gravitational potential energy associated with the difference in liquid centre of mass height between the two states. γsg, γsl, and γlg are the solid-gas, solid-liquid, and liquid-gas surface tensions respectively.

Each term in Eq. (1) is defined separately for the capillary and hemiwicked regions in Table 2. For this work, we consider long range surface interactions to be negligible compared to the interfacial energy and gravitational potential energy scales.

Table 2 The free energy change contributions to ΔG arising from the capillary and hemiwicked regions.
Full size table

In order to produce an analytic and tractable model, we model the meniscus using the standard circular arc approximation. This is accurate for plate separations up to the order of the capillary length46. The curve has arclength lM, and segment area aM, shown as the green-shaded region in Fig. 1b. The centre of mass of this segment is located a distance zM below C + M. We will show that the only meniscus property affecting the equilibrium rise heights is aM. aM, lM, and zM are illustrated in Supplementary Note 1 (Supplementary Fig. S1), with their standard analytic expressions given in Supplementary Eqs. (S1–S3) respectively.

After substituting the terms in Table 2 into Eq. (1), we minimise ΔG with respect to both C and H, under the constraint that C, H, M, T > 0. An interesting consequence of this procedure is that two classes of solutions emerge. These two solutions are distinguished by either H = 0, or H > 0. Thus, from our minimisation scheme, the conditions for observing hemiwicking above the meniscus are defined. This important feature of the Dual-Rise model contrasts with the Cassie-Baxter and Wenzel effective-angle models, in which the hemiwicking state has to be known a priori.

Overall, the defining equations of the Dual-Rise model are:

$$C=\left\{\begin{array}{ll}\frac{2{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}}{D}r\cos \theta -M+\frac{{a}_{M}}{D}\quad &{{{{{{{\rm{if}}}}}}}}\,H=0,\\ \frac{2{\lambda }_{c}^{2}}{d}\cos {\theta }^{* }-M+\frac{{a}_{{{{{{{{\rm{M}}}}}}}}}}{d}\quad &{{{{{{{\rm{otherwise,}}}}}}}}\end{array}\right.$$
(2)
$$H=\frac{{\lambda }_{c}^{2}}{\delta }\left(r\cos \theta -\cos {\theta }^{* }-\frac{2\delta }{d}\cos {\theta }^{* }\right)-\frac{{a}_{{{{{{{{\rm{M}}}}}}}}}}{d},$$
(3)

and

$$T=\left\{\begin{array}{ll}\frac{2{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}}{D}r\cos \theta +\frac{{a}_{M}}{D}\quad &{{{{{{{\rm{if}}}}}}}}\,H=0,\\ \frac{{\lambda }_{c}^{2}}{\delta }\left(r\cos \theta -\cos {\theta }^{* }\right)\quad &{{{{{{{\rm{otherwise,}}}}}}}}\end{array}\right.$$
(4)

where, by the circular arc approximation,

$$M=\frac{d\left(1-\sin {\theta }_{{{{{{{{\rm{M}}}}}}}}}\right)}{2\cos {\theta }_{{{{{{{{\rm{M}}}}}}}}}}.$$
(5)

λc is the capillary length, \({\lambda }_{{{{{{{{\rm{c}}}}}}}}}=\sqrt{{\gamma }_{{{{{{{{\rm{lg}}}}}}}}}/(\rho g)}\) where ρ is the liquid density and g is the acceleration due to gravity. θ is the contact angle of liquid on a smooth solid substrate, and θ* is the Cassie-Baxter effective contact angle for liquid on a liquid-filled rough substrate33,

$$\cos {\theta }^{* }=r(1-f)\cos \theta +1-\phi ,$$
(6)

For the meniscus contact angle, θM, this must be defined for when hemiwicking is present and absent. A simple approximation is to use

$${\theta }_{{{{{{{{\rm{M}}}}}}}}}=\left\{\begin{array}{ll}{\theta }^{* }\quad &{{{{{{{\rm{if}}}}}}}}\,\theta \le {\theta }_{{{{{{{{\rm{c}}}}}}}}},\\ {\theta }_{{{{{{{{\rm{W}}}}}}}}}\quad &{{{{{{{\rm{if}}}}}}}}\,\theta \ge {\theta }_{{{{{{{{\rm{c}}}}}}}}},\end{array}\right.$$
(7)

where θc22,23 is the critical angle for hemiwicking,

$$\cos {\theta }_{{{{{{{{\rm{c}}}}}}}}}=(1-\phi )/(fr),$$
(8)

and θW is the Wenzel effective contact angle for wetting on a rough surface34,

$$\cos {\theta }_{{{{{{{{\rm{W}}}}}}}}}=r\cos \theta .$$
(9)

We note that an improved approximation for θM could be achieved by replacing θc in the two case conditions in Eq. (7) with the contact angle at which H = 0 in Eq. (3). However, this does not produce a closed set of equations for the rise heights, and we will show throughout that M in Eq. (7) is already sufficiently accurate. Further justification of our treatment of θM is shown in Supplementary Fig. S2.

It will prove most instructive to discuss the physical significance of each of these equations with reference to simulation and experimental data in the following section.

Dual-Rise dependence on separation

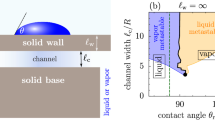
We begin by examining in detail the different modes of liquid rise in system SQ1, with water as the rising liquid and θ = 58°, as the plate separation d is varied. In Fig. 2a, three characteristic regimes of liquid rise are identified. The quantitative variation of the rise heights with plate separation is shown in Fig. 2b.

Fig. 2: The variation of the rough capillary rise heights with plate separation, compared between experiments, simulation, and theory.
figure 2

a Examples of the three regimes of rough capillary rise on system SQ1, a square-pillared system with water as the rising liquid (capillary length λc = 2.7 mm) and contact angle θ = 58°. Full images are simulation results, with insets showing magnifications of equivalent experimental systems on the region of interest. Scale bars = 1 mm. b Plot of the variation in the rise heights with plate separation d (normalised relative to the roughness depth δ) for system SQ1, where δ = 326 μm, separated into the three regimes. The capillary rise C, meniscus M, hemiwicking H, and total liquid height T, are labelled. Experimental data are shown as filled circles, with horizontal error bars indicating measured separation uncertainty, ±50 μm, and vertical error bars the ±1 post pinning uncertainty, ±709 μm. Simulation data are shown as empty triangles with vertical error bars indicating the ±1 post pinning uncertainty. Data at the extreme right indicate the rise heights on a single plate, equivalent to infinite plate separation. The Dual-Rise predictions are shown as lines. c Example images of the three regimes of rough capillary rise on system CY1, a cylindrically-pillared system with dodecane as the rising liquid (capillary length λc = 1.8 mm), and contact angle θ = 0°. Scale bars = 1 mm. d Plot of the variation in the rise heights with plate separation for system CY1, where δ = 325 μm. The shaded region indicates where the separation uncertainty (horizontal error bars) in the experimental data becomes large. The vertical ± 1 post pinning uncertainty is ±458 μm.

Full size image

At the largest plate separations, labelled regime 1 in Fig. 2a, b, the two rough surfaces are essentially non-interacting. This means that capillary rise is negligible, and the hemiwicking and meniscus heights are equivalent to those observed on a single, rough plate. Rise data for the single plate is shown at the extreme right of Fig. 2b. For the meniscus, the small rise height M measured in experiments (2.1 ± 0.7) mm, and simulations (2.8 ± 0.7) mm, is consistent with the analytical prediction of 2.6 mm from \(M={\lambda }_{{{{{{{{\rm{c}}}}}}}}}\sqrt{2\left(1-\sin {\theta }_{{{{{{{{\rm{M}}}}}}}}}\right)}\)47. The ±0.7 mm uncertainty in both simulations and experiments is the ± 1 pitch length uncertainty associated with pinning to the discrete posts in system SQ1. Adding the hemiwicking height to the meniscus yields the total rise height T, determined as (11.5 ± 0.7) mm and (11.6 ± 0.7) mm from experiment and simulations respectively. These are in agreement with the Dual-Rise prediction in Eq. (4) for H > 0, T = 12.1 mm. Examining Eq. (4) further, we observe that the energy minimisation has reproduced the heuristic balance of forces per unit length of the contact line between capillarity acting upwards, \({\gamma }_{{{{{{{{\rm{lg}}}}}}}}}(rf\cos \theta -1+\phi )\), and weight acting downwards, ρgδT, used previously to estimate T on a single plate22. However, the derivation of the Dual-rise model reveals that this estimate of T is not an estimate of the maximum height obtained, but is actually associated with the centre of mass of the hemiwicked liquid, as we discussed in Section ’Defining Equilibrium’. Although this distinction is minimal for system SQ1 at modest wettabilities, it becomes substantial for highly wettable surfaces.

As the plates are brought closer together, the capillary rise height grows monotonically, while hemiwicking decreases. A typical configuration is shown in Fig. 2a, labelled regime 2. In Fig. 2b, we also see that the total rise height remains independent of the plate separation throughout regime 2. Indeed, there is no difference in total rise height between a single rough plate, and a rough capillary when hemiwicking is present. In the heuristic force balance above, the dominant approximation was that the hemiwicking height was independent of the capillary rise. In this regime, both Dual Rise and the data in Fig. 2b show this assumption to be accurate. Likewise, if we examine the Dual-Rise prediction for C when H > 0 in Eq. (2), aside from a meniscus contribution, C could be derived by considering liquid rising over two pre-hemiwicked surfaces of separation d, in which the contact angle is given by the Cassie-Baxter effective contact angle for the composite liquid-filled surfaces, θ*. Thus in regime 2, we also verify that C can be predicted independently from H. Overall, this explains the range of previous experimental observations of the mutual independence of capillary rise and hemiwicking, across such fields as textiles30,31, bioinspired design29 and porous media26,32.

However, at close plate separations, when the separation and roughness length scales become comparable, a threshold is reached where capillary rise overtakes the top of the hemiwicked column. For system SQ1, Fig. 2b shows this to occur at \({\log }_{10}(d/\delta )\) = 0.5, equivalent to d = 0.75 mm. Here, the independence of capillary rise and hemiwicking breaks down, as suddenly the total rise height changes from being constant, to now increasing as the plate separation decreases. The example of regime-3 shown in Fig. 2a illustrates the absence of hemiwicking. To the best of our knowledge, observations of this regime have not been made previously, despite the largest rise heights occurring here. Regime 3 therefore has particular relevance to the range of applications mentioned previously that aim to exploit or control rough capillary rise1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16.

Often in the rise dynamics literature, the measure for describing whether hemiwicking will be observed is the critical angle θc, defined in Eq. (8). If θ < θc, hemiwicking is observed. Eq. (8) can be derived by considering the energy change when raising liquid above the surface of a reservoir at zero hydrostatic pressure, and in the absence of gravity. However, when there is hemiwicking from the top of a capillary-risen column, the change in gravitational potential energy must also be taken into account. Now, the criterion for hemiwicking becomes more complicated, and in general must be solved numerically by setting H = 0 in Eq. (3). However, if the meniscus is small compared to capillary rise, this results in the condition for hemiwicking on rough plates,

$$\cos {\theta }_{H = 0}=\frac{\cos {\theta }_{{{{{{{{\rm{c}}}}}}}}}}{1-\frac{2\delta }{fD}}.$$
(10)

We may also interpret this equation by asking what is the hydrostatic pressure required to be applied to overcome the capillary pressure favouring hemiwicking48. The capillary pressure favouring hemiwicking is \({\gamma }_{{{{{{{{\rm{lg}}}}}}}}}(rf\cos \theta -1+\phi )/\delta\), and the hydrostatic pressure at the top of the capillary-risen column is − ρgC. Equating these two pressures and substituting either case for C from Eq. (2), produces Eq. (10) in the limit that the meniscus is small. A key feature of Eq. (10) is that the denominator can always be made arbitrarily small, so that hemiwicking is always lost by bringing the plates close together. This represents an important design consideration for systems with closely-spaced plates, such as solar desalinators49, water purification devices50, and liquid-infused carbon capture42. The challenge in these applications is to maximise the liquid-gas surface area through hemiwicking, while maintaining a high plate packing density (close wall separations).

We now test the claim that the observations presented so far and the Dual-Rise model are valid generally. In Fig. 2c, d, we replicate the analysis for system SQ1, but this time for system CY1, featuring cylindrically-pillared surfaces, with dodecane as the rising liquid and a contact angle θ = 0°. Further details of this system are given in Methods, Table 4. An extended validation of the Dual-Rise model is further shown in Supplementary Note 2 (see Supplementary Fig. S3), where we vary the system scale, each pillar dimension, and also include a vertical groove geometry. These are summarised in Supplementary Table 1.

For system CY1, we observe the same three regimes of liquid rise, shown in Fig. 2c. For this system, when hemiwicking is present (regimes 1 and 2), an elongated tail is observed up to large rise heights. The Dual-Rise model for hemiwicking however remains accurate, as shown in Fig. 2d. In this region, CY1 also shows a constant total rise height, T = 22.0 mm. On decreasing the plate separation, we observe the hemiwicking transition to regime 3, at a separation \({\log }_{10}(d/\delta )\) = −0.046, equivalent to d = 0.30 mm. There is an interesting interplay between the two length scales. In the roughness, gravity causes the hemiwicking height to be finite, which is in direct contrast to the complete spreading of perfectly wetting liquid on a single, horizontal plate. Between the plates, this finite hemiwicking height is then able to be exceeded by capillary rise at sufficiently small plate separations. In regime 3, the Dual-Rise model is also shown to accurately capture the simulation observations. Note that for experiments, the small plate separation in this region means that the separation uncertainty, caused by small deviations in the plate alignment and measurement precision, becomes relatively large, so that simulations become the more reliable comparison.

From partially wetting to perfectly wetting systems

In the previous section, we explored how changing the plate separation, roughness parameters, and liquid properties influenced the rise heights. Now, we examine the effect of changing the surface wettability, described via the spreading parameter S (\(S={\gamma }_{{{{{{{{\rm{lg}}}}}}}}}\left(\cos \theta -1\right)\)). This is summarised in Fig. 3 as we study the capillary rise C for system SQ1, where water is used as the rising liquid (λc = 2.7 mm).

Fig. 3: Capillary rise against gravity between two rough plates of variable wetting parameter, S.
figure 3

a Comparison of the capillary rise heights between the: Dual-Rise Model, C, Jurin’s Law, CJ, and the apparent angle approximations, CW (Wenzel approximation) and CCB (Cassie-Baxter approximation), for the simulated square-pillared system SQ1 at a moderate value of the plate separation to roughness depth ratio (d/δ = 5.97). The rising liquid is water (λc = 2.7 mm), and we vary the substrate wettability S (normalised with respect to the liquid-gas interfacial tension γlg). The shaded region indicates the range of possible Wenzel capillary rise predictions when varying the plate separation, x, in Eq. (13). Error bars in the simulated data indicate the ± 1 post uncertainty. b Example equilibria at d/δ = 5.97 in region 3, S/γlg = − 0.66 (θ = 70°), and region 2, S/γlg = − 0.29 (θ = 45°). c Model comparison with the simulated system SQ1 at narrow plate separation (d/δ = 0.87). d Example equilibria at d/δ = 0.87 in region 3 at S/γlg = − 0.66 (θ = 70°), and S/γlg = −0.29 (θ = 45°).

Full size image

In Fig. 3a the plate separation is fixed at a moderate value, d/δ = 5.97 (equivalently d = 1.99 mm). This system exhibits a hemiwicking transition at S/γlg = − 0.58 (equivalent to θ = 65°). At large, negative S (large contact angles) H = 0, with an example of a system in regime-3 shown in Fig. 3b at S/γlg = − 0.66 (θ = 70°). In this region, the meniscus is small, and capillary rise C increases linearly with S. The Dual-Rise model in Eq. (2) matches this observation: in the limit of small menisci, \(C\propto \cos \theta \propto S\). Increasing S across the hemiwicking transition, we see a sudden reduction in the gradient of C, but the linear trend is maintained. An example system in this regime is shown in Fig. 3b at S/γlg = −0.29 (θ = 45°).

As was shown by Eq. (10), hemiwicking can always be entirely suppressed by choosing a small enough plate separation. An example of this type of system is shown in Fig. 3c by choosing d/δ = 0.87 (d = 0.29 mm). No hemiwicking is observed over the entire range of wettabilities, with example liquid configurations shown in Fig. 3d at S/γlg = −0.66 and −0.29.

An important aim of this work is to compare the capillary rise prediction C from the Dual-Rise model with commonly used effective contact angle adaptations to Jurin’s law. We begin with Jurin’s law for smooth surfaces, CJ,

$${C}_{{{{{{{{\rm{J}}}}}}}}}=\frac{2{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}\cos \theta }{d}.$$
(11)

In Fig. 3a (for d/δ = 5.97), we see that CJ is a poor approximation for C, except in two instances. The first (trivial) case is at S/γlg = −1.0 (θ = 90°), in which C and CJ are identically 0. The second however occurs at S/γlg = 0 (θ = 0°). This is because here, hemiwicking is present, so that the capillary rise is perfectly shielded from the surface roughness. In contrast, the system in Fig. 3c (for d/δ = 0.87) never exhibits hemiwicking. At S/γlg = 0, the rising liquid is not shielded from the surface roughness, so Jurin’s law is inaccurate at estimating C.

To adapt Jurin’s law for rough surfaces, a common approximation is to substitute the contact angle θ in Eq. (11) with an apparent contact angle, derived either from a Cassie-Baxter or Wenzel treatment of the surface. When hemiwicking is present, the Cassie-Baxter model would be conventionally employed. Examples demonstrating this are refs. 29,32, with the limitation that they further approximate the Cassie-Baxter angle as 0°, which is not generally the case. The Cassie-Baxter height is given by

$${C}_{{{{{{{{\rm{CB}}}}}}}}}=\frac{2{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}\cos {\theta }^{* }}{d},$$
(12)

where the θ* is the Cassie-Baxter angle for liquid rising over a composite liquid-filled solid texture, defined in Eq. (6). The Dual-Rise model in Eq. (2) reduces to Eq. (12) under the conditions that hemiwicking is present and the meniscus is vanishingly small. These conditions are fulfilled in regime 2 in Fig. 3a, so that CCB accurately approximates C. The common justification of using the Cassie-Baxter model, that capillary rise occurs between two pre-hemiwicked plates, is therefore supported in regime 2. However, when hemiwicking is absent, this approximation breaks down causing CCB to overestimate C, as shown in regime 3 of Fig. 3a, c. A key issue with this approximation is that the region of validity cannot be predicted by the Cassie-Baxter model, so that the hemiwicking state must be known a priori.

In the absence of hemiwicking, the Wenzel approximation models the effect of roughness with the Wenzel apparent contact angle θW, defined in Eq. (9). The Wenzel approximation for rough capillary rise at a plate separation x is

$${C}_{{{{{{{{\rm{W}}}}}}}}}(x)=\frac{2{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}\cos {\theta }_{{{{{{{{\rm{W}}}}}}}}}}{x}.$$
(13)

However, the Wenzel approximation does not reveal the suitable choice of the effective separation x, as the physical details of the roughness are ignored. The choice of x substantially influences the predicted rise height. The minimum reasonable x is when the plate separation is measured between the tops of the surface texture (x = d), whereas the maximum x would be the distance between the texture bottoms (x = d + 2hp). This range leads to the large, grey, shaded regions in Fig. 3a, c. However, the Dual-Rise model suggests that the correct definition of the plate separation in the absence of hemiwicking should be the average total separation D. We label this special case CW(D) simply as CW. In regime 3 of Fig. 3a, CW accurately estimates C, and as hemiwicking is present in regime 2, the Wenzel model becomes invalid.

In Fig. 3c, since hemiwicking is never present, we would naively expect the Wenzel model to be accurate across the range of spreading parameters. However, we find this is not true. CW is accurate at large, negative S, but incorrectly plateaus for S/γlg > − 0.62 (θ < 67°). CW now substantially underestimates C. This discrepancy grows, until at S/γlg = 0, C is a factor of r greater than CW. This error occurs because the Wenzel angle in Eq. (9) is limited to 0∘ for all \(r\cos \theta \ge 1\). In the Dual-Rise model, C in Eq. (2) shows that no such limit occurs in the \(r\cos \theta\) term, arising from the capillary force of the rough surface. Importantly, this reveals that a wide range of published works, ranging from fundamental studies of porous rise to earth science, are using the Wenzel model in conditions where it is invalid (namely \(r\cos \theta > 1\)), see for example refs. 22,28,29,36,37.

We further reflect that there is a contrast between capillary rise on rough and smooth surfaces. According to de Gennes20, in a smooth capillary the rise height plateaus for all spreading parameters where θ = 0° (i.e. S ≥ 0). However, the rough equivalent is not true: the rough capillary rise height does not plateau for all spreading parameters where the Wenzel angle θW = 0°. This contrast arises because on a smooth surface, the contact angle saturation is caused by a capillary force saturation due to a thin film shielding the capillary-rise liquid from the surface wettability. However, on a rough surface in the absence of hemiwicking, the Wenzel angle saturation does not imply a saturation of the capillary force, which instead continues to increase as \(r\cos \theta\).

The volume of liquid raised

When computing the volume of liquid raised in a rough capillary, explicitly accounting for liquid in the roughness is of paramount importance. In Fig. 4, we plot the total volume raised VT, as the sum of capillary, meniscus, and hemiwicking contributions, VC, VM, and VH respectively, for the simulated system SQ2 with water as the rising liquid (capillary length λc = 2.7 mm) at θ = 58°. Experiments and simulations for systems of different geometry are shown in Supplementary Note 2 (see Supplementary Fig. S4).

Fig. 4: The liquid volume raised against gravity upon variation of the plate separation.
figure 4

Predicted volumes from the Dual-Rise model are compared for the simulated, square-pillared system SQ2 with water as the rising liquid (capillary length λc = 2.7 mm) and θ = 58°. The total volume VT is shown, which is decomposed into the individual contributions from: capillary rise VC, hemiwicking VH, and the meniscus VM. The ± 1 post error bars are shown, and the plate separation d is shown relative to the roughness depth δ. Also shown are the capillary volumes calculated using: Jurin’s Law VJ, the Wenzel approximation VW, and the Cassie-Baxter approximation VCB. The three regimes of equilibrium rise are demarked and labelled 1–3.

Full size image

The principal striking feature of Fig. 4 is that VT is constant across the range of plate separations, even though the distributions within the capillary and hemiwicking regions change, including across the hemiwicking transition. This separation independence is validated by the Dual-Rise model, where VT/L = DC + (DM − aM) + 2δH. L is an arbitrary portion of the infinite parallel plates. Upon rearrangement, the separation independence is made clear:

$$\frac{{V}_{{{{{{{{\rm{T}}}}}}}}}}{L}=2{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}r\cos \theta .$$
(14)

A second surprising feature is that the raised volume is substantially larger than would be predicted via all previous models. A smooth approximation \({V}_{{{{{{{{\rm{J}}}}}}}}}=2L{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}\cos \theta\), underestimates the raised volume by a factor of the roughness parameter r, which can be large for real surfaces. Technologies relying on a smooth approximation are therefore considerably underestimating the total raised volume9,35. However, even the Wenzel model, \({V}_{{{{{{{{\rm{W}}}}}}}}}=2L{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}\cos {\theta }_{{{{{{{{\rm{W}}}}}}}}}\), underestimates the raised volume in Fig. 4 by almost 40%, as \(r\cos \theta > 1\). The Cassie-Baxter model, \({V}_{{{{{{{{\rm{CB}}}}}}}}}=2L{\lambda }_{{{{{{{{\rm{c}}}}}}}}}^{2}\cos {\theta }^{* }\), is always unreliable, as the hemiwicked volume is not accounted for.

Indeed, the interaction between the hemiwicked volume and capillary volume is key to explaining the separation independence of VT. The capillary force that raises the liquid depends only on the surface properties, not the plate separation. At equilibrium, this must therefore always be balanced by the same weight of liquid. The weight of the hemiwicked column and meniscus displace an equal weight of liquid from the capillary region. As we treat the liquid as incompressible throughout, this means the raised volume is always independent of plate separation.

We consider again Fig. 2b, d, where the plate separation is increased across the hemiwicking transition, from regime 3 to regime 2. We can now use the separation independence of VT to explain the sudden change in slope of C. On increasing the plate separation, the slope becomes steeper as hemiwicking suddenly emerges. In order to preserve the total volume, liquid must be drained from the capillary region into the hemiwicking region. Thus, C decreases faster upon the appearance of hemiwicking, than before hemiwicking emerges.

Conclusions

In this work, all contributions to equilibrium rough capillary rise are explained and predicted with quantitative accuracy by the Dual-Rise model, a model derived from a rigorous energy minimisation that is valid for surfaces of general roughness. A summary comparing our model accuracy is shown in Table 3, with Jurin’s Law for smooth surfaces, and the Cassie-Baxter and Wenzel approximations for rough surfaces. Table 3 highlights many ways in which these approximations inaccurately predict liquid heights and volumes, and indicates the limited cases where those rough surface approximations are accurate.

Table 3 Summary of model accuracies for hemiwicking H, capillary rise C, total liquid height T, and total volume VT.
Full size table

From this study, a number of interesting questions emerge that depend on the specific roughness geometry. For instance, how does the complex interplay between capillarity, hydrostatic pressure and the roughness geometry determine the curved morphology of the hemiwicking liquid-gas interface, and in particular how does this curvature affect the maximum liquid height? The roughness geometry is also crucial for pinning, leading to a range of metastable rise configurations. Can the pinning forces be predicted in both the hemiwicking and capillary regions?

We anticipate that the Dual-Rise model will play an important role in a broad range of applications in which liquid rise is to be predicted or controlled. In particular, we highlight its relevance in novel sustainability technologies, such as catalytic or carbon capture systems using Liquid Infused Surfaces42, and in understanding and improving the lifespan of concrete structures41.

Methods

System parameters

All experimental and simulated systems are listed in Table 4, indicating the roughness parameters, capillary length relative to the pitch P, and the pitch length P. Where both simulated and experimental equivalents of the same system are used, we match the simulated parameters as closely as possible to the experimental parameters. A small discrepancy is introduced, as an exact translation of the experimental system is not possible due to the simulation being composed of discrete cubic lattice points. This small discrepancy is within the reported error bars. For system CY1, to simulate very close surface separations (\({\log }_{10}(d/\delta )\le 0.12\)) required increasing the system size by 4 times in each direction, indicated as ’Sim. 4 × ’ in Table 4.

Table 4 Surface geometry and liquid parameters used in experiments and simulations.
Full size table

Two different rising liquids are used: water (distilled to a resistance of 18 MΩ, with surface tension γ = 72 mN m−1, density ρ = 1000 kg m−3, and capillary length λc = 2.7 mm); or dodecane (Sigma Aldrich, 99% purity, γ = 24 mN m−1, ρ = 745.2 kg m−3, λc = 1.8 mm).

In experiments, the textured plates were additively manufactured using Accura ClearVue resin (polycarbonate-like material). Plasma-treating the printed plates for 2 min on a high RF setting (Harrick Plasma, PDC-32G) energises the surface and alters the wettability. Plasma-treated smooth polycarbonate has a measured contact angle of 0∘ with dodecane, and 36° with water. With water, the additively manufactured roughness altered the contact angle on different faces of the posts of SQ1. The Dual-Rise model fits experimental rise heights at θ = 58°, which was the contact angle also input into simulations. The quantitative agreement between theory, simulations, and experiments, justifies this choice of θ.

Liquid rise experiments

The textured plates were additively manufactured in a high resolution stereolithography process (3D Systems On Demand). Printed parts had the supports removed, were washed, but had no post-printing thermal cure and as such were left with a natural finish. The plates were 5 cm × 5 cm with a 3 mm thick backbone on which were either printed square cross-section posts 400 μm in diameter with a spacing of 300 μm (or a post-center-to-post-center pitch of 700 μm) or cylindrical cross-section posts 300 μm in diameter with a spacing of 150 μm (or a post-center-to-post-center pitch of 450 μm). Topographic measurements were carried out using a Leica DCM8 confocal profilometer using the 5 × objective, which was sufficient to resolve the post geometries. The target print height was 500 μm and measured values in randomly sampled regions were within 10% of that value. Target pillar pitch values were typically within 2% of the design size. The greatest variation came from post widths where all posts, regardless of shape or size, had a tapered as-manufactured shape, being narrower at the top and wider at the bottom. Mean diameters, taken as an average of the measured top diameter and bottom diameter, were within 10% of design specification, but varied up to 20% from the mean towards the narrower or wider end.

The experimental apparatus holds two of the textured plates, each of the same texture geometry, parallel to one another at a controlled and measured separation. This is accomplished using two micrometers attached orthogonally under one plate mount. One can be used to exactly align the columns of pillars (to better match the simulation) and the other controls the spacing between plates. A reservoir with the liquid can be raised and brought into contact with the lower portion of the plates. Liquid height measurements and profiles are measured using a camera (FLIR CCD camera equipped with an Infinity Photo-Optical Infiniprobe ms lens) viewing down the space between the plates. A bright light is placed on the far side of the plates such that the illumination provides a sharp contrast to the image. Areas occluded by the texture or by liquid appear dark, and all empty space is light. By moving the camera up and down (on an elevator attached to a digital micrometer), or side to side, the heights of the capillary and hemiwicked areas can be measured relative to the height of the liquid reservoir.

The initial plate separation is set to 10 mm. At this distance the separation is much larger than the capillary length for either liquid (water or dodecane), meaning that there is negligible communication between the meniscus that forms on either plate. The camera is centred on the flat liquid region and the elevator micrometer is zeroed. Then images are captured of the meniscus region as well as the maximum hemiwicked regions on either plate. The experiment proceeds as the plates are successively brought closer together, capturing images of the meniscus and hemiwicked regions and recording the camera height positions at one plate spacing before bringing them closer together. The main experimental challenge is the pinning that occurs as the bulk meniscus rises when the plates are brought closer together. Because of the periodic nature of the texture, there is a strong tendency for the meniscus contact line to pin on the top of one row of pillars before snapping up to wet the next row. In order to perturb the system into a lower energy configuration, we tap both the mount holding one of the plates (to perturb the plate spacing) as well as the stage holding the liquid reservoir (to perturb the liquid level). This tapping, especially at close plate separation, can cause the meniscus to jump up one or more rows, and the recorded images are taken at the locations where any further tapping will not move the liquid-gas interface. Further details of how the rise heights were measured from recorded images are shown in Supplementary Note 3.

Phase field simulations

The simulations we perform minimise the free energy of a diffuse-interface model with fluid-surface interactions, in a gravitational field. We choose the diffuse interface model firstly to avoid making assumptions about the liquid-gas interface morphology or topology, requiring no special treatment for interfaces splitting or merging51, and secondly to enable facile interactions between fluids and complex surface topographies52,53.

For the cylinder-pillared systems, we use a ternary phase field model based on refs. 54,55. Here, we use three order parameters, C1(r), C2(r), and C3(r), which define the local composition of the solid, liquid, and gas respectively. Note that the total composition is normalised, so that C1(r) + C2(r) + C3(r) = 1. A value Ci(r) = 0 indicates no quantity of component i is present, whereas Ci(r) = 1 indicates pure component i. We treat the solid in the posts in this diffuse manner, based on a previous model56, to enable the creation of smooth, curved solids, while maintaining the cubic discretisation of the simulation domain. The solid surface at the base of the pillars is treated via a boundary condition, not a diffuse interface treatment.

The total free energy is expressed

$${{\Psi }}[\{{C}_{i}({{{{{{{\boldsymbol{r}}}}}}}})\}]={\int}_{v}\left({\psi }_{{{{{{{{\rm{b}}}}}}}}}+{\psi }_{{{{{\nabla }}}}}+{\psi }_{{{\Lambda }}}+{\psi }_{{{{{{{{\rm{g}}}}}}}}}\right)dv+{\int}_{s}{\psi }_{{{{{{{{\rm{s}}}}}}}}}ds.$$
(15)

where the integrals are over the volume v and solid surface s. ψb is the bulk energy,

$${\psi }_{{{{{{{{\rm{b}}}}}}}}}=\frac{6}{\epsilon }\mathop{\sum }\limits_{i=1}^{3}\left(-{S}_{i}{C}_{i}^{2}{(1-{C}_{i})}^{2}\right),$$
(16)

and ψ∇ is the gradient energy density,

$${\psi }_{\nabla }=\frac{3}{8}\epsilon \left[\mathop{\sum }\limits_{i=1}^{3}-{S}_{i}| \nabla {C}_{i}{| }^{2}\right].$$
(17)

ϵ is the interface width. Si defines the spreading parameter of phase i over the interface between phases j and k,

$${S}_{i}={\gamma }_{jk}-({\gamma }_{ij}+{\gamma }_{jk}).$$
(18)

To enable complete spreading while maintaining simulation stability, the stabilisation term ψΛ is used54,

$${\psi }_{{{\Lambda }}}={{\Lambda }}{C}_{1}^{2}{C}_{2}^{2}{C}_{3}^{2},$$
(19)

where the parameter Λ is set to 50. The gravitational potential energy density, ψg is defined

$${\psi }_{{{{{{{{\rm{g}}}}}}}}}={f}_{{{{{{{{\rm{g}}}}}}}}}{C}_{2}z.$$
(20)

fg is the gravitational force density, and acts as the conversion factor between the dimensional units in experiment and the nondimensional units in simulation: \({f}_{{{{{{{{\rm{g}}}}}}}}}=\rho g{\gamma }^{{\prime} }{P}^{2}/\left(\gamma {P}^{{\prime} 2}\right)\), where ρ is the liquid density, g is the acceleration due to gravity, P and \({P}^{{\prime} }\) are the pitch lengths of the periodic surface roughness in real and lattice units respectively, γ and \({\gamma }^{{\prime} }\) are the liquid-gas interfacial tensions in real and lattice units respectively. The wetting on the solid boundaries at the base of the pillars is achieved using the surface energy density ψs, where

$${\psi }_{{{{{{{{\rm{s}}}}}}}}}=\mathop{\sum }\limits_{i=1}^{3}12{\gamma }_{i{{{{{{{\rm{s}}}}}}}}}\left(\frac{1}{2}{C}_{i}^{2}-\frac{2}{3}{C}_{i}^{3}+\frac{1}{4}{C}_{i}^{4}\right),$$
(21)

where γis is the interfacial tension of component i on the solid surface.

To minimise the free energy numerically, Ψ in Eq. (15) is discretised, as shown previously57, into a cubic array of lattice points, with the grid spacing equal to the interface width ϵ. To create the smooth, solid array of pillars in the diffuse interface method, we firstly initialise component 1 in the desired pattern of cylinders. The rest of the system is filled with pure gas (C3), and the liquid component (C2) is fixed at 0. ψg and ψs are also set to zero. The energy minimisation is then carried out on this initial system using the memory- and computationally efficient L-BFGS algorithm58,59. We truncate the algorithm to 30 iterations, as this allows the 1–3 diffuse interface to form, without allowing the relaxing component 1 to alter the desired shape of the cylinder.

Next, the solid surfaces at the base of the pillars are introduced, and the gravitational energy density switched on. Component 2 (the liquid phase) is initialised in the system in a prescribed configuration. The solid phase (C1) is now fixed while the liquid (C2) and gas phases (C3) are allowed to vary. Ψ in Eq. (15) is now minimised under these constraints. The minimisation is deemed to have converged based on an rms gradient condition: when ∣ ∇ Ψ∣ < 10−5.

For the square pillars, the solid boundaries of the posts conform to the discretisation lattice. This means that we do not need to apply the diffuse solid method, and instead treat all solid boundaries using Eq. (19). C1 is fixed at 0 throughout the minimisation, so the ternary model in Eq. (15) reduces to a binary liquid-gas model.