Topological order from measurements and feed-forward on a trapped ion quantum computer

Abstract

Quantum systems evolve in time in one of two ways: through the Schrödinger equation or wavefunction collapse. So far, deterministic control of quantum many-body systems in the lab has focused on the former, due to the probabilistic nature of measurements. This imposes serious limitations: preparing long-range entangled states, for example, requires extensive circuit depth if restricted to unitary dynamics. In this work, we use mid-circuit measurement and feed-forward to implement deterministic non-unitary dynamics on Quantinuum’s H1 programmable ion-trap quantum computer. Enabled by these capabilities, we demonstrate a constant-depth procedure for creating a toric code ground state in real-time. In addition to reaching high stabilizer fidelities, we create a non-Abelian defect whose presence is confirmed by transmuting anyons via braiding. This work clears the way towards creating complex topological orders in the lab and exploring deterministic non-unitary dynamics via measurement and feed-forward.

Introduction

Long-range entangled quantum states are central to different branches of modern physics. They appear as error correction codes in quantum information¹, emerge as topologically ordered phases in condensed matter, and play a role in lattice gauge theories of high energy physics². Quantum computers and simulators provide new means of exploring such states and tackling their open questions³. A number of quantum algorithms have been designed for these devices, many of which can be decomposed into two steps: a state preparation step and a processing step, in which e.g., unitary dynamics is applied^4,5. For short-range entangled states, the adiabatic theorem guarantees an (approximate) encoding circuit whose depth is independent of the system size. In contrast, long-range entangled states require circuits of extensive depth for their preparation⁶ due to finite Lieb-Robinson velocities, which bound the spread of correlation in unitary dynamics⁷. The stakes are further increased by emerging evidence that scalable digital quantum simulation of (short- or long-range entangled) fermionic systems requires long-range entangled state preparation^8,9,10,11. This situation is problematic: coherence time is a precious resource for near-term quantum computers and simulators and it should not be exhausted during state preparation.

Fortunately, there is a loophole to these constraints imposed by unitarity and locality. Introducing measurement during state preparation violates the assumption of unitarity, such that correlations can be generated instantaneously across the whole system. However, since measurements are random, deterministic state preparation requires conditional quantum gates to be applied based on the outcome of the mid-circuit measurement—a capability known as feed-forward. In effect, measurement allows one to push all the non-constant depth into the classical channel, which is effectively ‘free’ due to the large speed of light and the comparably much larger cost of quantum gates.

The deterministic preparation of an excitation-free state is important for the quantum simulation of topologically ordered systems with non-error corrected devices, but is also a common prerequisite for quantum error correction protocols that realize universal gate sets¹². Moreover, feed-forward is indispensable for the efficient preparation of certain non-Abelian states involving multiple layers of measurement^{13,14,15,16,17,18}.

In summary, to prepare long-range entangled states deterministically and in constant (quantum) depth, one requires feed-forward, mid-circuit measurement and entangling gates, all with high fidelity and fast compared to the coherence time of the platform.

While individual elements of this triad have been demonstrated^{10,19,20,21,22,23,24,25,26,27,28,29}, combining all of these ingredients in one platform to deterministically create long-range entangled states has proven elusive since the inception of this idea more than a decade ago^10,30,31.

Here, we demonstrate the deterministic, high-fidelity preparation of long-range entangled quantum states using a protocol with constant depth (as conceptually represented in Fig. 1), using Quantinuum’s H1 programmable ion-trap quantum computer³². The quantum computer contains 20 qubits encoded in two hyperfine states of ¹⁷¹Yb⁺ ions and is based on the quantum charge-coupled device architecture^33,34. Crucially, the qubit ions in this architecture are mobile. While cross-talk can be a formidable challenge for mid-circuit measurement-based protocols, we will see that the ability to move qubits far apart during mid-circuit measurements transforms cross-talk into a negligible source of error (compared to the two-qubit gate error). To certify this, we measure fidelities and entanglement entropies of a “toric code” ground state on periodic boundaries. A remarkable property of this entangled state is that it admits localized deformations behaving like emergent particles which are neither bosonic or fermionic³⁵. These are called Abelian anyons, due to their exchange statistics being described by commuting phase factors. In addition, we also create the toric code state with two lattice defects, called non-Abelian Ising defects^36,37 which we use to demonstrate anyon transmutation and braiding interferometry.

Fig. 1: Schematic representation of the toric code ground state from wavefunction collapse.

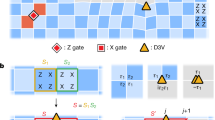
We initialize a system of trapped-ion qubits (encoded in hyperfine states of ¹⁷¹Yb⁺) in a product state where all stabilizers B_p = Z^⊗4 = 1 (blue) are satisfied. We measure A_p = X^⊗4 on every other plaquette, randomly leading to A_p = 1 (gold) or A_p = −1 (black, denoting an e-anyon). We use feed-forward to pair up and annihilate the e-anyons in real time, deterministically producing a clean toric code wavefunction using a finite-depth circuit and nonlocal classical processing.

Results

Toric code preparation with feed-forward

We target the ground state of Kitaev’s toric code Hamiltonian³⁵. For notational convenience, we represent the qubits as living on the vertices of a square lattice³⁸, described by

$$H=-\sum\limits_{p\in {{{{{{{\mathcal{A}}}}}}}}}{A}_{p}-\sum\limits_{p\in {{{{{{{\mathcal{B}}}}}}}}}{B}_{p},$$

(1)

where the operators A = X^⊗4 and B = Z^⊗4 are products of Pauli operators that act on the four-qubit plaquettes of the square lattice and ${{{{{{{\mathcal{A}}}}}}}}$ and ${{{{{{{\mathcal{B}}}}}}}}$ denote the sets of X-type and Z-type plaquettes (cf. Fig. 2a). In the ground state, A_p = B_p = 1 for all plaquettes. Any excited plaquette corresponds to one of the aforementioned anyons: A_p = −1 (B_p = −1) is typically called an e-anyon (m-anyon). Enabled by the effective all-to-all connectivity of the ion-trap, we implement periodic boundary conditions.

Fig. 2: Toric code ground state preparation.

a Definition of the stabilizer operators (1) on the unraveled torus. Numbers denote the different ions and specify the boundary conditions. Plaquettes are labeled by their upper left qubits. The state comprises 4 × 4 qubits and periodic boundary conditions. b Logical Z string operators are Z^hori = Z₀Z₁Z₂Z₃ (Z^vert = Z₀Z₄Z₈Z₁₂) and their vertical (horizontal) translations. $\overline{{Z}^{{{{{{{{\rm{hori}}}}}}}}}}$ and $\overline{{Z}^{{{{{{{{\rm{vert}}}}}}}}}}$ denote expectation values of the logical string operators, averaged over translations. c Expectation values of the stabilizers obtained from collapsing the wavefunction in the single-qubit X- and Z-bases. Error bars denote one standard error on the mean. d Entanglement entropy measurement on 2 × 2 (top) and 2 × 3 regions (bottom). Colored bars denote ${S}_{X}^{(2)}$ for different subsystems of a region with shapes as shown in the inset and γ is defined in Eq. (2). Dashed lines show exact values. Error bars denote one standard error on the mean. The maximum error in the estimates of ${S}_{X}^{(2)}$ for 2 × 2 (2 × 3) regions is ±0.056 (±0.091). Hatched white bars denote average topological entanglement entropies.

This Hamiltonian realizes ${{\mathbb{Z}}}_{2}$ topological order^39,40, with four ground states—while these all satisfy 〈A_p〉 = 〈B_p〉 = 1, they can be distinguished by logical string operators that wrap around the torus.

To be specific, we target the unique ground state with logical expectation values $\left\langle {Z}^{{{{{{{{\rm{hori}}}}}}}}}\right\rangle =\left\langle {Z}^{{{{{{{{\rm{vert}}}}}}}}}\right\rangle =1$, as defined in Fig. 2. The expectation value of the string and commuting plaquette operators certify the quality of the state preparation, with an average of +1 indicating perfect ground state preparation.

To prepare the ground state deterministically and in constant depth, we use a three-step procedure: First, all ions are initialized in $\left\vert 0\right\rangle$, such that $\langle {B}_{p}\rangle =1$. Second, we measure the A_p operator on all odd plaquettes, effectively implementing the projectors $({\mathbb{I}}\pm {X}^{\otimes 4})/2$ with equal probability. This can be done with or without ancillae and we choose to demonstrate both strategies, preparing plaquettes 4, 6, 12, and 14 with an ancilla-free procedure while the measurements on plaquettes 1, 3, 9, and 11 are performed with one ancilla each (Methods, see also Fig. 2 for our labeling convention). Finally, we apply conditional single-qubit Z gates to flip all plaquettes at which A_p = −1 has been measured, which one can physically interpret as pairing up and annihilating the e-anyons. To find the location at which the conditional Z-gates must be applied, we use a simple lookup-table decoder (Methods).

The topology of the toric code requires anyonic defects to come in pairs; however, errors in the syndrome measurement process can result in measuring an odd number of excitations. Therefore, we employ a state preparation strategy—common to many quantum error correction or repeat-until-success protocols—in which odd defect numbers are heralded and the associated data is discarded. We note that unlike post-selection on each plaquette individually, the fraction of retained data is not exponentially small in the system size; thus we can view the discarding of erroneous runs as a scalable part of the state preparation procedure itself, and we report fidelities constructed from the retained data in the main text (see Supplementary Fig. 3 for the raw data).

We test the quality of the state prepared in the above manner in two ways. First, we measure the expectation values of the X^⊗4 and Z^⊗4 stabilizers by performing destructive single-qubit measurements in the X- and Z-basis. Their average plays the role of the energy density of (1) and is closely related to the overlap with the ground state manifold⁴¹. We report an energy density of −0.929 ± 0.004, indicating that a ground state has been prepared with high fidelity. The expectation value of the two logical string operators averaged over translations is close to 1 and equal up to statistical fluctuations, $\overline{{Z}^{{{{{{{{\rm{hori}}}}}}}}}}=0.916\pm 0.0065,\overline{{Z}^{{{{{{{{\rm{vert}}}}}}}}}}=0.914\pm 0.0064$, indicating that the target logical state is indeed responsible for the bulk of the overlap with the ground space manifold. The average expectation of the X-type plaquettes $\langle {A}_{p}\rangle =0.944\pm 0.0049$ exceeds that of the Z-type plaquettes $\langle {B}_{p}\rangle =0.914\pm 0.0063$. This is compatible with the fact that memory errors in the device slightly bias the noise towards Z-type phase flips: The only two-qubit gates in the circuits occur during the measurement of the X^⊗4-operator. Any Z-errors that occur on the data qubits during the ancilla-based measurement circuit are transformed into X-error by the Hadamard gates at the end of the subroutine. In turn, these bit flip errors corrupt the neighboring Z-type plaquettes, while being invisible to the X^⊗4-operators (cf. Supplementary Figs. 1, 3a). To arrive at these numbers, we executed 1240 repetitions of the state preparation procedure of which roughly 10% were discarded via the heralded state preparation procedure. Half of the shots were used to measure the X- and Z-stabilizers, respectively.

A second test for the quality of the state is the topological entanglement entropy^42,43. For short-range entangled phases, order parameters can usually be defined in terms of local linear functionals of the density matrix. For long-range entangled states, by definition, no such observables exist. Instead, it is customary to partition a region into areas A, B, and C and compute the topological entanglement entropy by measuring

$$\gamma =-({S}_{A}+{S}_{B}+{S}_{C}-{S}_{AB}-{S}_{AC}-{S}_{BC}+{S}_{ABC})$$

(2)

where S_X is the von-Neumann entropy of the reduced density matrix of subsystem X. While any state of matter which is related to a product state by a finite-depth cirucit has γ = 0, in a phase with ${{\mathbb{Z}}}_{2}$-topological order (implying the existence of e- and m-anyons), $\gamma =\ln 2$ for all Rényi entropies⁴⁴. Due to their non-linear nature, entanglement entropies are expensive to measure in practice, requiring a number of shots that is exponential in the size of the subsystem. Here, we employ the randomized measurement scheme^45,46,47,48 to measure γ for connected regions of up to six qubits by computing the second Rényi entropies of their subsystems as shown in Fig. 2d (Methods). We report average topological entanglement entropies of $\gamma /\ln 2=0.93\pm 0.055$ and $\gamma /\ln 2=1.05\pm 0.093$ for the 2 × 2 and 2 × 3 regions, respectively, indicating that a state consistent with ${{\mathbb{Z}}}_{2}$ topological order has been prepared.

Anyon transmutation and interferometry

Having established a deterministic procedure to prepare toric code ground states at constant depth with high fidelity, we are now in a position to study simple dynamics on top of the ground state. To this end, we consider a slightly modified geometry, introducing two defects into the system (Fig. 3a)^36,37. This defective state is only slightly harder to prepare than the toric code ground state (Methods), and we report an average expectation value per plaquette of 0.925 ± 0.0039 (Fig. 3b), comparable to the toric code ground state considered before. The geometry with defects lends itself to the study of two types of dynamics.

Fig. 3: Anyon dynamics on a state with two non-Abelian defects.

a Geometry. The lack of the central qubit and the redefinition of the stabilizers leads to two defective plaquettes. b Expectation values of the stabilizers obtained from the state preparation and measurement routine described in “Anyon Transmutation and Interferometry” in the Results section. Error bars denote one standard error on the mean. c Anyon transmutation. A pair of magnetic anyons (m) is created and one partner is transmuted into an electric anyon (e) by moving it across the line connecting the two defects. The maximum and minimum standard error on the mean for the expectation values of stabilizers are ±0.023 and ±0.0066 respectively. Color bars from panel (b) apply. d Anyon Interferometry. A fermionic e − m composite anyon is created next to the defect and a controlled-Z₁₀Z₈Z₄Z₇ braiding operation is applied with the help of an ancilla.

In the first experiment, we study the transmutation of anyons. The elementary excitations of the defect-free toric code are electric and magnetic anyons (the aforementioned e- and m-anyons, respectively) as well as their bound state. While such particles can be moved diagonally through the system and annihilated in pairs, their type is fixed throughout the evolution. The insertion of a defect changes this situation: Moving an anyon across the line connecting the two defective plaquettes allows the particle to skip a square, moving between X-type and Z-type plaquettes, and thus change its nature. We choose to create a pair of magnetic particles and move one of them across the defect on the path shown in (Fig. 3c), performing a measurement on all qubits after each step. We report final stabilizer expectation values of −0.92 ± 0.017 and −0.89 ± 0.020 on adjacent plaquettes. The creation of a single electric-magnetic pair is impossible in a defect-free toric code and is related to the non-Abelian nature of the defect. Indeed, such an e − m composite is a fermion (due to the mutual statistics of e and m anyons), and the defect can be thought of as a Majorana zero mode whose fermion parity can be toggled by pulling out a single fermion⁴⁹. The data indicates that the creation and movement of the anyons does not affect the bystanding plaquettes beyond statistical fluctuation, showing that cross-talk is negligible as it is expected from a quantum charge coupled device in which ions are stored ≥180 μm apart. In principle, we can also trace the anyon non-destructively by performing parity measurements instead of collapsing the full wavefunction at every step. This procedure reduces the required number of shots by a factor that is equal to the number of steps, at the cost of introducing extra gates. The results of this strategy are reported in Supplementary Fig. 4.

As shown in the transmutation experiment, the presence of the non-Abelian defect allows for the creation of a single fermionic excitation (in the form of an e − m composite). Here we explicitly confirm that we have created a fermion by checking that its wavefunction picks up a minus sign upon rotating it by 360^∘. Equivalently, the two anyons making up the composite have non-trivial mutual braiding: the wavefunction acquires a global phase ${U}_{{{{{{{{\rm{braid}}}}}}}}}\left\vert em\right\rangle =-\left\vert em\right\rangle$ when braiding one particle around the other. This phase is naively inaccessible, but it can be measured using the Hadamard test: A controlled version of U_braid is applied, conditioned on the state of an ancilla which is initially prepared in $\left\vert +\right\rangle =(\left\vert 0\right\rangle +\left\vert 1\right\rangle )/\sqrt{2}$. The phase $\left\langle em| {U}_{{{{{{{{\rm{braid}}}}}}}}}| em\right\rangle$ is then directly related to the expectation value $\left\langle X\right\rangle$ on the ancilla. Specifically, in the experiment, we create a single electric-magnetic pair adjacent to the defect by acting with Y₁₀ on the ground state (i.e., $\vert em\rangle := {Y}_{10}\vert \,{{\mbox{gs}}}\,\rangle$) and braid the electric around the magnetic excitation on the path shown in Fig. 3d. We find $\,{{\mbox{Re}}}\,\langle em| {U}_{{{{{{{{\rm{braid}}}}}}}}}| em\rangle =-0.87\pm 0.018$, verifying the fermionic exchange statistics. Similarly, in the absence of the fermionic excitation, we find $\,{{\mbox{Re}}}\,\langle \,{{\mbox{gs}}}\,| {U}_{{{{{{{{\rm{braid}}}}}}}}}| \,{{\mbox{gs}}}\,\rangle =+0.87\pm 0.018$. The strength of the interferometric signal can be attributed to the mobility of the qubits in the device: While conditional dynamics usually requires the use of many SWAP gates to bring the ancilla close to the target qubits, we achieve the same effect here with only four two-qubit gates.

Discussion

We have demonstrated the combined use of mid-circuit measurement, feed-forward and low-error gates to prepare topologically ordered states on periodic two-dimensional geometries deterministically, in constant depth and with high fidelity, providing experimental data from Quantinuum’s H1-1 programmable ion-trap quantum computer⁵⁰. The presented data shows that mid-circuit measurements can now be used with the same fidelity cost as two-qubit gates, considerably broadening the scope of experiment design in the future.

For example, we have considered the efficient preparation of Abelian topological orders and of defects with non-Abelian character within the Abelian phases in this work. This lays the groundwork for the preparation of true non-Abelian topological orders in a quantum device, some of which, surprisingly, require the same overhead as their Abelian counterparts despite their richer properties⁵¹. Namely, only a single round of feed-forward and low-error gates suffices to deterministically prepare such states. Moreover, multiple rounds of measurements and feed-forward can access even more exotic and powerful non-Abelian states^{13,14,15,16,17} which open up new avenues for fault tolerant quantum information processing.

To be clear, we do not see the replacement of unitary encoding circuits on small surface code blocks as the main application of our work. Rather, simulating quantum dynamics on top of long-range entangled states or involving fermions with coherence time-limited near-term devices will profit directly from the scheme presented here. While the present work considered discrete transformations between eigenstates of the system, our demonstration opens up the possibility of studying quenches and variational circuits in topologically ordered systems on digital quantum computers with minimal resources^52,53. These, in turn, can be used to study, e.g., lattice gauge theories at finite temperatures and energies⁵. Since classical simulation of these problems generically requires exponential resources, there is a potential for quantum advantage. While the device noise is small and its characterization agrees well with our experimental findings, the capacity of the H1-1 system must be extended beyond 20 qubits for this to become a reality.

In conclusion, this work has demonstrated a powerful application of measurements and feed-forward. These capabilities open up a multitude of directions for further exploration, ranging from quantum information processing and simulating the ground states and dynamics of many-body quantum systems, to uncovering the emergent structures in monitored circuits^54,55.

Methods

Entropy measurements from randomized measurements

While the deterministic measurement of non-linear quantities, like the entanglement entropy, generally requires full state tomography, recently, robust probabilistic algorithms have been devised^{45,46,47,48,56}. These can be used to measure the second-order Renyi entropy

$${S}^{(2)}({\rho }_{A})=-\ln {{\mbox{Tr}}}\,{\rho }_{A}^{2}.$$

(3)

We follow the protocol from⁴⁸ where it is shown that the purity of a reduced quantum state can be estimated by

$$\,{{\mbox{Tr}}}\,{\rho }_{A}^{2}={2}^{{N}_{A}}\sum\limits_{{s}_{A},{s}_{A}^{{\prime} }}{(-2)}^{D({s}_{A},{s}_{A}^{{\prime} })}\overline{P({s}_{A})P({s}_{A}^{{\prime} })},$$

(4)

where N_A is the subsystem size and $D({s}_{A},{s}_{A}^{{\prime} })$ denotes the Hamming distance between the bitstrings corresponding to the computational basis states s_A and ${s}_{A}^{{\prime} }$. P(s_A) is the probability of measuring s_A in the state ρ_A after applying a random unitary, i.e., P(s_A) = 〈s_A∣Uρ_AU^†∣s_A〉, and the overline denotes the average over random unitaries. Importantly, each of the random unitaries is a tensor product of local unitaries u₁ ⊗ u₂…  which are drawn from the circular unitary ensemble. In principle, one can also choose to simply measure each of the qubits in the X-, Y- or Z-basis with equal probability, at the cost of larger statistical fluctuations²⁵. That is because random Pauli measurements are equivalent to random Clifford gates followed by computational basis measurements and the Clifford group forms a unitary 3-design^56,57.

In the experiment, we compute the purity by averaging over N_U = 72 random local unitary settings, and for each setting we execute N_M = 256 shots to estimate the probability distribution P(s). The parameters N_U and N_M have been chosen by using the grid search procedure as described in⁴⁸ on the emulator of H1-1 ion-trap. We use the unbiased estimator P(PN_M − 1)/(N_M − 1) for evaluating P²(s) in (4) as described in⁴⁷. As discussed in the main text, we discard shots where an odd number of anyons was heralded during the error correction. Even without discarding such shots, we get estimates for $\gamma /\ln 2$ of 0.87 ± 0.055, and 1.00 ± 0.090 for 2 × 2 and 2 × 3 regions respectively.

To evaluate Rényi entropies, ${S}_{X}^{(2)}$, for each subsystem X, we consider different regions of size 2 × 2 and 2 × 3, as shown in the Supplementary Fig. 2a, b. In Supplementary Fig. 2c, d, we show the estimated values of the topological entanglement entropy for each region. The values of ${S}_{X}^{(2)}$, as reported in the main text in Fig. 2d, have been obtained by taking the mean of subsystem Rényi entropies for each region. The error bars for ${S}_{X}^{(2)}$ and γ have been computed by bootstrapping new samples from the given dataset (which is specified by U_N = 72 different randomized measurement settings) and then by evaluating the standard deviation of the resulting distribution.

Effects of measurement error mitigation

While we have not employed any State Preparation and Measurement (SPAM) error mitigation in the main text, we show here the impact of SPAM mitigation on the state preparation procedure.

SPAM error mitigation accounts for the state preparation and read out errors, and in its simplest form, it models the effects of SPAM noise processes on the ideal probability distribution from the quantum device, as

$${P}_{{{{{{{{\rm{noise}}}}}}}}}={A}^{\otimes n}{P}_{{{{{{{{\rm{ideal}}}}}}}}},$$

(5)

where A is the transition matrix that acts locally on each of the n qubits. It is characterized by the probabilities of misreading state $\left\vert 0\right\rangle$ as state $\left\vert 1\right\rangle$ and vice versa. According to prior characterization of the measurement error in the H1-1 ion-trap, a $\left\vert 0\right\rangle$ state on an ion has a 0.1%-chance of being read out as $\left\vert 1\right\rangle$ and there is a 0.5%-chance of $\left\vert 1\right\rangle$ erroneously being read as $\left\vert 0\right\rangle$⁵⁸. We can use that information to construct the transition matrix as,

$$A=\left(\begin{array}{cc}1-0.001&0.005\\ 0.001&1-0.005\end{array}\right).$$

(6)

Note that in (5), we ignore the effects of correlated SPAM errors which occur on multiple sites. We can recover P_ideal by applying ${({A}^{-1})}^{\otimes n}$ on P_noise, and this can done efficiently since the action of transition matrix A is local. The resulting performance of SPAM error mitigation with and without discarding heralded errors can be seen in Supplementary Fig. 5a–d. Without discarding, we get an improvement in energy density from − 0.89 to − 0.91, while SPAM correction boosts energy density from −0.93 to −0.95 using the heralded procedure employed in the main text.

Measurement and decoding of the A _p-operator with and without ancillae

The key advantage of measurement-based over unitary state preparation is the ability to project the state onto an eigenstate of all A_p operators simultaneously. These parity check measurements can be done in one of two ways. More commonly, the parity of the four data qubits on the plaquettes is transferred onto an ancilla using four maximally entangling gates, e.g., to apply the projector $({\mathbb{I}}+{X}^{\otimes 4})/2$, we apply 4 CNOT gates where the control qubit is an ancilla prepared in $\left\vert +\right\rangle$. It is, however, also possible to obtain constant depth circuits without introducing ancillae. In that case, an ancilla-free parity check needs to be executed, using six two-qubit gates. Both procedures are shown in Supplementary Fig. 3a, b. In either case, the state is projected into the even (odd) eigenspace of the stabilizer X^⊗4 upon measuring +1 (−1). However, in the ancilla-free case, we can remove the classically controlled-Z gate to our advantage, as described below. We call the new construction modified ancilla-free parity check. The action remains unchanged when the measurement outcome is +1, but, when the outcome is −1, the action of the modified ancilla-free circuit is given by the projector ${Z}_{{{{{{{{\rm{target}}}}}}}}}({\mathbb{I}}-{X}^{\otimes 4})/2$, where Z_target accounts for the removed classically controlled-Z gate by acting on the target qubit (i.e., the qubit that is measured). The Z_target autocorrects the measured plaquette at the cost of moving a potential error to an adjacent plaquette. This autocorrection ensures that errors can only accumulate on half of the X-type plaquettes and reduces the cost of the subsequent decoding. We emphasize that the use of modified ancilla-free parity checks is done out of convenience - its use is not essential to obtain high-fidelity results.

Since the H1-1 ion-trap is capable of handling up to 20 qubits, using the ancilla-based strategy on four X-type plaquettes allows us to save eight two-qubit gates in the state preparation circuit for free, and those plaquettes are shown in Supplementary Fig. 3c by hatching with slanted(\) lines. The remaining four X-type plaquettes are measured by using the modified ancilla-free measurement circuit and they are shown in Supplementary Fig. 3c by hatching with crossed (×) lines, the red arrows pointing to the target qubits. With this construction, whenever we measure -1 (indicating error or the presence of anyon in the plaquette) on the modified ancilla-free plaquette, the additional Z_target action moves the error/anyon into the diagonally adjacent plaquette in which the arrow is pointing.

To remove the anyon pairs, we have implemented a simple lookup-table decoder which handles each of the 2⁴/2 = 8 error possibilities explicitly. We have implemented a decoder that is compatible with OpenQASM 2.0 for the all the results that we present in the main text⁵⁹. OpenQASM 2.0 does not support conditioning on individual bits in the classical register and this causes a substantial increase in the number of classically conditioned single-qubit gates during the correction. Later in the development, we also considered a more optimal decoder (i.e., with significantly less conditional gates in total and asymptotically linear cost in system size). The resulting energy densities achieved by the former and later decoders are given in Supplementary Fig. 5b and Supplementary Fig. 5e respectively. We find that both decoders give almost the same energy density. We also test the case where every X-type plaquette is prepared by measurement with an ancilla circuit (Supplementary Fig. 3a), measuring four stabilizers using available ancillae and then reuse those ancillae to measure remaining X-plaquettes. Although this implementation requires 4 × (6 − 4) = 8 fewer two-qubit gates, reuse of ancilla qubits in this fashion generally increases the circuit depth, execution time, and potential for memory errors. The results for this procedure are given in Supplementary Fig. 5f showing a slight improvement in the energy density, in particular for the X-type plaquettes, since the noise in the ancilla-based preparation strategy is biased towards corrupting Z-type plaquettes (cf. main text and Supplementary Fig. 3).

We also consider a decoder where we do not measure one of the X^⊗4 stabilizers. Since in the noiseless case, anyonic excitations occur in pairs, we can deduce the state of unmeasured X-type plaquette from the parity of measured stabilizers and apply the corresponding error correction steps. Expectation values of stabilizers for this decoder are shown Supplementary Fig. 5g.

State preparation and dynamics of the model with a defect

The state preparation strategy for the defective model proceeds similarly to the defect-free state. Since the model requires 15 data qubits, we have five leftover qubits on the 20 qubit H1-1 ion-trap which we use as ancilla qubits to prepare the X-type plaquettes 1, 3, and 4 and the two defect-plaquettes. The remaining three X-type plaquettes (cf. Fig. 3a) are prepared using the modified ancilla-free parity check circuits (cf. subsection “Measurement and Decoding of the A_p-operator” in the Methods). Again, we use a simple lookup-table decoder to remove the errors while exploiting the fact that errors never occur in plaquettes which are prepared by modified ancilla-free measurement.

While in the defect-free case only two settings are necessary to measure all stabilizers using single-qubit measurements, for the defective case, we use four settings to obtain one observation for all stabilizers. We measure plaquettes (0, 2, 5, 7, 14), (3, 5, 10, 11, 13), (1, 3, 4, 6, 11), and (0, 6, 8, 12, 14) in the first, second, third, and fourth setting respectively. This splitting has the advantage that each measurement contributes to the expectation value and the corner and defect plaquettes are measured twice (cf. Fig. 3a).

For the anyon transmutation, the sequence X₁₂X₁₃Z₆Z₅ has been applied after the state preparation (cf. Fig. 3c). After each of the single-qubit gates, the corner and the defect stabilizers are measured 1200 times and all other plaquettes are measured 600 times. For the anyon interferometry, the circuit ${H}_{{{{{{{{\rm{anc}}}}}}}}}{Y}_{10}{{{\mbox{CZ}}}}_{7}{{{\mbox{CZ}}}}_{4}{{{\mbox{CZ}}}}_{8}{{{\mbox{CZ}}}}_{10}{Y}_{10}{\left\vert +\right\rangle }_{{{{{{{{\rm{anc}}}}}}}}}\otimes \left\vert \,{{\mbox{gs}}}\,\right\rangle$ has been applied where the control qubit is the ancilla. The real part of the braiding phase is the measured $\left\langle Z\right\rangle$ expectation value of the ancilla at the end of this sequence.

We have also examined the transmutation of a magnetic anyon into an electric anyon while utilizing quantum nondemolition (QND) measurements of stabilizers⁶⁰, see Supplementary Fig. 4. This has the advantage that one can measure the whole transmutation trajectory in one shot, while not destroying the anyon. We construct the circuit such that it begins by preparing the toric code with defects. Then we apply X₁₂, which creates a pair of flux anyons, and measure the stabilizers on plaquettes 1, 4, 6, 8, and 12 using the circuit shown in Supplementary Fig. 3a. Then, we apply X₁₃, to move one of the flux anyon into the defect plaquette and repeat the QND measurement of the same stabilizers. Finally, we apply Z₆ which moves the anyon out of the defect plaquette, and again do a QND measurement of the same stabilizers as above. Afterward, we measure all other stabilizers destructively.

Circuit construction, gate count, and error budget

The native gate set of H1-1 ion-trap consists of the single-qubit gates

$$\begin{array}{rcl}{U}_{1q}\left(\theta =\left\{\frac{\pi }{2},\pi \right\},\phi \right) ={e}^{-i(\cos \phi X+\sin \phi Y)\theta /2},\\ \quad\,\,{R}_{z}(\lambda ) ={e}^{-iZ\lambda /2}\end{array}$$

and the arbitrary-angle entangling gate RZZ(θ) = e^{−iθ/2Z⊗Z 61}. Specifications at the time of the experiment (November and December 2022) indicated average two-qubit gate fidelity of 99.7%, one-qubit fidelity of 99.996%, SPAM fidelity of 99.6%, and memory-error per depth-1 circuit time per qubit of 1−99.97%.

The state preparation circuit for toric code including the decoder requires 484 one-qubit gates and 4 × 4 + 6 × 4 = 40 two-qubit gates. In the case of toric code with defects, after compilation into native gate set, the circuit contains 423 one-qubit gates and 3 × 4 + 5 × 2 + 6 × 3 = 40 two-qubit gates. The circuits were compiled to the native gate set and sent to the device using TKET⁶².

We estimate the global fidelity with the target state using the same randomized measurement data set that we also use to compute topological entanglement entropies (cf. the “Entropy measurements from randomized measurements” subsection in the Methods) by using the framework of shadow density matrices⁵⁶. We construct shadow density matrix for each randomized measurement setting, take its overlap with the target wavefunction and then calculate the mean value. We report a global fidelity with the $\left\langle {Z}^{{{{{{{{\rm{hori}}}}}}}}}\right\rangle =\left\langle {Z}^{{{{{{{{\rm{vert}}}}}}}}}\right\rangle =1$ toric code ground state of $\langle \,{{\mbox{gs}}}\,| {\rho }_{{{{{{{{\rm{prepared}}}}}}}}}| \,{{\mbox{gs}}}\,\rangle =0.80\pm 0.049$.

Multiplying the gate error of all 40 two-qubit gates (0.997⁴⁰ ≈ 0.887), 484 one-qubit gates (0.99996⁴⁸⁴ ≈ 0.981) the memory error on all of the 20 qubits accumulating during 6 depth-1 circuit times (0.9997^6×20 ≈ 0.965) and the SPAM error on 20 + 4 (reused) qubits (0.996²⁴ ≈ 0.9082) leads to a global damping factor of ~0.762 which is compatible with the estimated global fidelity.