Principle of local symmetry in mixed-mode fracture

Abstract

When brittle materials are subjected to uniaxial tensile stress, we observe planar crack propagation perpendicular to the loading direction. However, when additionally subjected to an out-of-plane shear stress, the crack tip/front deviates, leading to fragmentation in the form of twisting facets. Conventional linear fracture mechanics does not adequately describe this effect unless additional criteria are assumed. Among these, the principle of local symmetry, which states that fractures propagate in shear-free directions, is prominent but lacks robust experimental validation. Here we study fractures in hydrogels under mixed load. From the geometry of the evolving crack, we deduce the tension field near the fracture tips and find clear evidence that the principle of local symmetry governs the fragmentation. Our results indicate that the finite size of the fragmentation pattern’s facets and their elastic interactions account for deviations from the principle of local symmetry, providing new insights into fracture mechanics.

Introduction

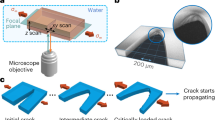
Crack propagation and fracture are ubiquitous but complex phenomena whose physical mechanisms remain largely unknown, mainly because this process occurs at different spatial scales¹. Despite its intrinsic complexity, fracture tips propagate through the combination of three independent directions of loading: perpendicular to the crack plane tip/front (mode I), in-plane shear (mode II), and out-of-plane shear (mode III). Materials are often subjected to combinations of these loads, leading to complicated fracture patterns, see Fig. 1a–c.

Fig. 1: Fracture modes.

The opening mode I (a), the deviation of fractures in mixed-mode I + II, where in-plane shear is applied to a planar fracture generated by the first mode (b), and the fracture fragmentation during mixed-mode I + III, where out-of-plane shear is superimposed on the opening mode (c). d Mixed-mode I + III fracture in a hydrogel, where the initial fracture tip/front becomes segmented into facets, which are tilted at an angle ϕ with respect to the parent planar crack.

Laboratory experiments show that when a brittle fracture tip/front encounters a mixed-mode region, it deviates from its previous planar pattern. Specifically, in mixed-mode fracture I + II, the entire tip/front bends and propagates in a tilted direction (Fig. 1b). In contrast, in mixed-mode fracture I + III, the crack tip/front is segmented into an array of tilted facets while conserving the previous propagation direction, as shown in Fig. 1c. These phenomena occur in a wide range of brittle technical and geological materials^{2,3,4,5,6,7,8,9,10,11,12,13,14,15}.

Crack propagation has traditionally been analyzed within the framework of linear elastic fracture mechanics (LEFM), focusing on the rather general stress field behavior near the crack tip/front. This behavior is characterized by the stress intensity factors K_I, K_II, and K_III for modes I, II, and III, respectively¹⁶. These factors are crucial for quantifying the displacements and stresses that arise under different loading conditions.

In general, the results of linear fracture mechanics need to be complemented by specific criteria for material failure. For example, for mode I load, a crack will grow when¹

$${K}_{{\rm{I}}}\ge {K}_{{\rm{IC}}},$$

(1)

where K_IC is a critical value for the stress intensity factor, known as the material’s fracture toughness.

For mixed-mode load, the criteria for material failure are less obvious, and there is a plethora of failure conditions, which have been reviewed by different authors, e.g.,^8,13. In mixed-mode fracture I + II, a widely accepted criterion is the principle of local symmetry (PLS), which postulates that the fracture deviates from the original path to propagate in a shear-free direction, resulting in a locally vanishing shear stress intensity factor, K_II = 0, and a symmetrical stress distribution around the tip/front. Yet, although widely accepted, the PLS is not well supported by experimental evidence³.

Failure criteria for mixed-mode I + III load are even less clear. Nevertheless, the PLS can be extended to I+III fractures, where the facets tilt in a direction that results in vanishing shear stresses at the tip/front:

$$\left\{\begin{array}{l}{K}_{{\rm{I}}}\ge {K}_{{\rm{IC}}}\quad \\ {K}_{{\rm{II}}}=0\quad \\ {K}_{{\rm{III}}}=0,\quad \end{array}\right.$$

(2)

where, again, K_IC represents the material toughness. Thus, it can be stated that for mixed-mode I+III failure, the fracture forms facets that tilt, causing the local shear mode to vanish.

Using the PLS criterion, Pollard and Cooke^9,14 obtained for the tilt angle ϕ of the facets with respect to the parent planar crack the expression:

$$\phi =\frac{1}{2}{\tan }^{-1}\left[\frac{{K}_{\,\text{III}}^{\infty }}{{K}_{\text{I}}^{\infty }\left(\frac{1}{2}-\nu \right)}\right],$$

(3)

where ${K}_{\text{I}}^{\infty }$ and ${K}_{\text{III}}^{\infty }$ are the stress intensity factors at the tip/front of the planar crack before the segmentation, for modes I and III, respectively. The tilt angle is obtained by assuming an isolated and infinitely long plane facet, and the same tilt angle is obtained by maximizing the opening mode I or minimizing the local shear mode III^9,14.

Indeed, experimental results in mixed mode fracture show facets with tilt angles similar to those predicted by Eq. (3). In particular, pure mode III experiments by Knauss⁶ indicate that ϕ → π/4 when ${K}_{\,\text{III}}^{\infty }/{K}_{\text{I}}^{\infty }\to \infty$, in agreement with Eq. (3). However, Eq. (3) systematically overestimates the experimental results for ϕ, raising doubts about the validity of the PLS in mixed-mode I + III^5,11,14.

This work examines the validity of the PLS for mixed-mode fracture I + III. For this purpose, we generate fractures in brittle hydrogels using an experimental setup capable of independently controlling modes I and III, see Fig. 1d. Using X-ray tomography, we capture the geometries of fractures, enabling a geometric characterization with unprecedented details. From the obtained geometry of the fractures, we determine the stress intensity factors (K) along the crack tips using Finite Element computations, which allows us to assess the validity of the PLS. We show that the finite size of facets and the elastic interactions between neighboring facets cause deviations from the PLS established through Eqs. (2).

Results

Fracture geometry by tomography

The study of mixed-mode I + III fractures requires an experimental setup that allows independent stimulation of both modes, while preventing unstable fracture propagation, so that the state of the fracture can be accurately imaged at different growth stages. This can be achieved through a displacement control setup, which assures that the fracture driving force decreases as the fracture progresses¹⁶, as illustrated in Fig. 2. By employing a conical plate configuration in tests on non-fractured samples, the normal stress (mode I) diminishes for regions of the material away from the center of the cones. The upper holder is equipped with two rings that control the deformation of the sample: an outer threaded ring that allows the sample to be stretched by unscrewing to apply uniaxial tension, and an inner ring that can rotate to twist the sample and apply shear. The upper and lower conical plates feature holes and mushroom-shaped screws to interlock the sample with the plates. This is to prevent the sample from detaching when stress is applied. The module is primarily made of aluminum, except for the columns separating the upper and lower plates, which are made of polyamide, an X-ray low-absorbing thermoplastic.

Fig. 2: Experimental setup.

a The sample is mounted to the measuring module and fixed at the base plate. b, c Two load modes can be applied: b shear (mode III), by rotating the inner ring at an angle α; c tension (mode I), by rotating the outer ring that is equipped with a fine-pitch thread, producing a displacement Δ of the top holder.

Here, we study fractures in brittle hydrogels made of commercial bovine gelatin (250 blooms). Despite significant differences in mechanical strength, the brittleness of gelatin has been used as a simple analog for rocks in geophysical studies^17,18,19. The sample preparation and molding protocol follow the approach used by the authors in a previous study²⁰, with full details provided in the Methods section, along with the mechanical properties of the gelatin.

In the experiments, fractures are initiated by elongating and twisting the sample according to modes I and III, respectively. Before hydrogel gelation, a needle was inserted into the sample, see Fig. 2. This needle allows ambient air to enter the cavity created by the growing fracture. Once the fracture propagation comes to rest, further growth can be stimulated by increasing the load conditions (tension or shear). The initial crack geometry and the successive stages of its development were captured using X-ray tomography at a voxel resolution of 60 μm. The details on the imaging parameters can be found in the “Methods” section.

Figure 3a shows a typical sequence of fracture growth under mixed load. We initiate the experiment by applying stress to the sample (mode I) by adjusting its height using the outer ring of the module. This adjustment creates a small, coin-shaped pre-fracture (see Fig. 3a, leftmost panel). After recording a tomogram of this planar crack, torsion (mode III) is applied by turning the inner ring of the module to the desired angle, such that the fracture propagates under mixed load (modes I + III), leading to out-of-plane fragmentation of the initial planar crack. When the propagation comes to rest, we record a further tomogram. This procedure is repeated to obtain a sequence of tomograms showing the evolution of the fracture propagation. The facets are not connected to each other but by regions that either remain unfractured or fracture at a later stage, thereby preventing fractures from growing in directions opposite to the load applied to the sample^5,11,21,22.

Fig. 3: Sequence of fracture growth and tip/front analysis.

a Sequence of tomograms showing initial flat fracture and subsequent mixed-mode fracture obtained by rotating the sample at an angle α = 30° (background in blue). The fracture expands through successive sample elongations. b 3d image of the fracture, where the color codes the mean curvature of the surface. c Frenet–Serret frame attached to the fracture tip/front. d Inset of a single facet, where the fracture tip/front is represented as a red 3d curve and the Frenet–Serret frame is depicted at a specific point along the tip/front. The Frenet–Serret frame (B, N, T) is given by the binormal B, normal N, and tangent T vectors.

Fracture geometry and local principal axes

To compute the local stress intensity factors, we must determine the fracture tip/front. For planar coin-like fractures, the tip/front of the fracture is a ring that expands as the fracture grows. In contrast, for mixed-mode three-dimensional fractures, the tip/front is a more complicated curve that expands in 3d space.

The fracture tip/front advances only in areas of high stress concentration induced by the curvature of the fracture shape. Therefore, the fracture tip/front can be determined by identifying regions of high curvature on the crack surface. The mean curvature at a surface point determines the local deformations of the surface in space and is defined as the average of the two principal curvatures at that point²³. Experimentally, the mean curvature can be determined from the tomogram, which is a three-dimensional image of the crack. Figure 3b shows a 3d image of the fracture where the color codes the mean curvature of the surface. We see that the fracture’s tip/front corresponds to large values of the absolute mean curvature. We start from the voxels of the largest mean curvature on each facet and apply a spline smoother to determine the entire fracture tip/front^24,25. The result of such a segmentation is shown in Fig. 3c, d.

At each point of the tips of the facet, we compute the Frenet–Serret trihedron, which is an orthonormal basis, (B, N, T), see Fig. 3c, d. Its unit vectors are T, tangential to the tip, N, normal to the tip, and B, forming a right-handed system. Below, we will use the Frenet-Serret trihedra to decompose the stress at the tip/front into the local modes I–III.

Local stress intensity factors

We compute the stress fields in the sample by means of the finite element method (FEM), where the experimentally obtained shape of the crack is used to define the inner boundary of the simulation domain (Fig. 4a). The volume occupied by the sample is triangulated. The simulation domain is given by the cones, the fracture geometry (highlighted in yellow) according to the X-ray tomogram, and the outer cylinder. The boundary conditions for the strain are chosen in agreement with the experiment: the upper cone is vertically displaced and rotated against the lower cone, and the remaining surfaces are assumed load-free. For the FEM simulation, Young’s modulus, density, and Poisson’s ratio are chosen from the rheological properties of the hydrogel, as described in the “Methods” section.

Fig. 4: Computation of the stress intensity factors by finite element method (FEM).

a The sample volume is triangulated. Its boundaries are given by the geometry of the experimental setup (cones and outer cylinder) and by the shape of the fracture (in yellow) that was obtained from the X-ray tomogram. The mesh size is exaggerated for better visibility. In our computation, the mesh size decreases near the fracture surface for better numerical resolution. The strain’s boundary values result from the cones' rotation and displacement relative to each other, which is in agreement with the experiment. At the outer cylinder, stress-free boundary conditions are assumed. b Different paths (1,2,3,4,…, N) along the local normal  −N vector to the fracture tip/front are used to get the components of the stress tensor, σ_BB, σ_BN, and σ_BT as a function of the distance r from the tip/front. c Inset: Stress σ_BN as a function of r, obtained from the FEM simulation with the boundary given by the experiment. Main figure: graphical representation of Eq. (4) for mode II, using the same data as in the inset. From the linear fit, we obtain K_II.

From the stress field obtained by FEM simulation and the Frenet–Serret trihedrons at the fracture tip/front, we compute the components of the stress tensor, σ_BB, σ_BN, and σ_BT in the basis given by the Frenet-Serret trihedron. Here, the stress in B direction corresponds to the local opening mode I, the stress in N to local in-plane shear (mode II), and the stress in T direction to out-of-plane shear (mode III). The corresponding stress intensity factors are then¹⁶:

$$\begin{array}{rcl}{K}_{{\rm{I}}}&=&\mathop{\lim }\limits_{r\to 0}\sqrt{2\pi r}{\sigma }_{{\rm{BB}}}(r)\\ {K}_{{\rm{II}}}&=&\mathop{\lim }\limits_{r\to 0}\sqrt{2\pi r}{\sigma }_{{\rm{BN}}}(r)\\ {K}_{{\rm{III}}}&=&\mathop{\lim }\limits_{r\to 0}\sqrt{2\pi r}{\sigma }_{{\rm{BT}}}(r),\end{array}$$

(4)

where r is the distance from the tip/front along the local normal vector  −N (Fig. 4b).

Mathematically, near the tip/front, the stress can be expanded through²⁶

$${\sigma }_{ij}=\mathop{\sum }\limits_{n=1}^{\infty }K{r}^{n-3/2}{f}_{ij}(n),$$

(5)

where f_ij(n) is a dimensionless function. Thus, the first term of the series, n = 1, contributes a constant to ${\sigma }_{ij}\sqrt{2\pi r}$, and the second term, n = 2, delivers a contribution linear in r. Therefore, near the tip/front, for small r, we expect a linear dependence of ${\sigma }_{ij}\sqrt{2\pi r}$ on r. Based on this argument, we computed the stress intensity factors, K_I/II/III, from a linear fit to Eq. (4). Figure 4c illustrates the procedure for the case of K_II.

We applied this procedure to obtain the local stress intensity factors at each point of the fracture tips/fronts of all facets. The behavior of the local modes along the tips allows us to assess the validity of the PLS. Other well-established methods are also suitable for calculating K_I/II/III—such as the displacement extrapolation method²⁷.

Principle of local symmetry

Figure 5 shows K_I/II/III over the length of the fracture tip/front, as obtained from combining the tomography images and the FEM stress field calculation. In this figure, the top panels (a–c) show the distribution of K values for three different facets of a sample twisted by α = 30°. From these panels, it is clear that although the distributions of K_I, K_II, and K_III vary among the different facets, they exhibit a similar overall behavior. The bottom panels display the data for K_I, K_II, and K_III averaged over all facets of the same fracture, where the length s was scaled for each facet such that s ∈ [0, 1] corresponds to the tip/front along the facet. These panels correspond to the propagating fracture after the sample was twisted by α = 20°, α = 30°, and α = 40°. The error bars in Fig. 5 represent the standard deviation across different facets of the same fracture. Toward the interval boundaries, s ≳ 0 and s ≲ 1, we see larger deviations indicating enhanced dissimilarity of the facets in the lateral regions.

Fig. 5: Stress–intensity factors.

Modes of the stress–intensity factor (K) along the fracture tip/front. In all panels, K_I, K_II, and K_III represent the opening, in-plane-shear and out-of-plane-shear modes, respectively. Panels a–c show K along the tip length for three facets of a system twisted by an angle α = 30°. Panels d–f show the three modes of the stress-intensity factor, K(s), along the normalized coordinate s of the fracture tip/front, where 0 ≤ s ≤ 1 spans a single crack facet. The twisting angles are d 20°, e 30°, and f 40°. The solid lines give the mean stress-intensity factor K(s) averaged over the different crack facets in each sample, and the error bars indicate one standard deviation of the averaged K(s) fracture profiles. For all tests shown in this figure, the samples were elongated by 4 mm and twisted by α = 20°, α = 30°, or α = 40°.

Note that, in principle, all three modes of K can assume positive and negative values. For mode I, K_I > 0 implies fracture opening, and K_I < 0 implies fracture closing²⁸. Along the tip/front, K_I > 0 dominates, as expected for fractured samples. For K_II and K_III, a positive value indicates that local traction aligns with the positive orientation of the normal and tangent vectors of the Frenet-Serret frame (see Fig. 3c).

Despite considerable fluctuation due to the differences between the profiles of the individual facets, we clearly identify trends in Fig. 5: K_I reveals a plateau centered at s ≈1/2 (middle of the facet). As predicted by the PLS, this plateau is characterized by K_I ≈ K_IC (see Eq. (1)). At K_I > K_IC, the crack would propagate farther; for K_I < K_IC, the crack could not have reached this position. Therefore, the plateau level must be K_I ≈ K_IC. We also see that mode I dominates along the fracture tip/front, while shear modes II and III are much smaller in absolute value.

Thus, we find that—apart from fluctuations—the PLS is consistent with the measured data: K_I ≈ K_IC, $\left\vert {K}_{{\rm{II}}}\right\vert \ll {K}_{{\rm{I}}}$, and $\left\vert {K}_{{\rm{III}}}\right\vert \ll {K}_{{\rm{I}}}$.

Facet interaction

The behavior of the stress intensity factors at the fracture tips, s ~1/2 in Fig. 5, supports the validity of the PLS near the centers of the fracture facets. Large fluctuations near the edges of the facets, s ≳ 0 and s ≲ 1, hint at systematic deviations from the PLS due to elastic interactions between the facets, as we will show below. For strongly interacting facets, the stress near the tip/front of fractures cannot be described theoretically²⁹. For more distant facets, Eq. (5) remains valid near the tip/fracture.

First, we compare the stress intensity factors for early and well-evolved segmented fractures. Figure 6a, b shows a crack at two successive stages of a mixed-mode I + III fracture test, with a sample rotation of α = 30°. In the early stages of its evolution, after an initial stretch of the sample by 3 mm, the fracture reveals numerous small facets resulting from the segmentation of the initially coin-shaped fracture with a circular tip/front (Fig. 6a). As the crack progresses, after further stretching to a total of 4 mm, the facets grow and thicken. Furthermore, the coarsening of the facets leads to a reduction in their number (Fig. 6b). The corresponding stress intensity factors along the crack tip/front are shown Fig. 6c, d. We see that the fluctuations in the stress intensity factors near the edges are much greater for developed cracks (Fig. 6d) than for cracks in an early stage of development (Fig. 6c). We hypothesize that the deviation from PLS observed in the well-developed facets of Fig. 5 are due to interactions between the facets.

Fig. 6: Stress intensity factors K of early and developed facets.

Panels a and b show the same fracture at different stages of its evolution as obtained from X-ray tomography, with the red curves indicating the fracture tip/front. The rotation of the sample is α = 30°, panel a: elongation is 3 mm; panel b: 4 mm. Panels c, d show the corresponding averaged stress intensity factors K_I/II/III as a function of the normalized length of the fracture tip/front, s.

Growing facets can be seen as cracks that interact with the initial disc-shaped parent crack and with neighboring facets. Small facets whose tips are distant from one another grow independently. At a later stage, the tips of adjacent facets are less distant. Thus, their mechanical interaction results in a stress amplification, see Fig. 7a. Further growth can lead to facets to structure in echelon configurations, as schematically shown in Fig. 7b, leading to a stress shielding configuration^29,30.

Fig. 7: Facet Interaction.

Illustration of the facet interactions for a growing crack. Small facets formed at an early stage grow independently. At later stages, large facets can align, causing amplification of the stress (panel a). Further facet growth can lead to overlapping configurations, which reduces the stress at the tips due to shielding (panel b).

To better understand the interactions between adjacent facets, which may explain the deviation from the PLS, we consider two simplified model systems, similar to the experimental geometry by Ronsin et al.⁴.

The first model system (A), sketched in Fig. 8a, consists of a rectangular block with a planar parent fracture at one of the edges, subjected to tensile stress σ from the top, and a clamped boundary condition at the bottom face. The planar fracture is the nucleus of a circular secondary fracture that mimics a facet of our experiment. The parent fracture’s tilt, ϕ, allows us to control the degree of mixed mode I + III. Note that this model is engineered to fulfill the PLS, where the facets propagate in the direction perpendicular to the local stress. Thus, any deviations from the PLS are due to finite size effects or parent–facet interaction.

Fig. 8: Model system (A) to study parent–facet fracture interactions.

a System sketch. A planar (parent) fracture tilted at an angle ϕ and a single secondary circular facet are subjected to stress σ at the top face and a clamped boundary condition at the bottom face. The edge of the tip/front is highlighted in red. The normalized length, s, of the fracture tip/front, where 0 ≤ s ≤ 1, covers the crack’s facet. b Stress intensity factors K^(A) at the tip/front, as obtained from finite element method (FEM) calculations. The opening mode, ${K}_{\text{I}}^{(A)}$, displays significant deviations from the principle of local symmetry (PLS) as a consequence of the parent–facet interaction near the edges. Shear modes ${K}_{\text{II}}^{(A)}$ and ${K}_{\text{III}}^{(A)}$ are less affected by the parent–facet interaction and remain close to zero (${K}_{\text{II}}^{(A)},{K}_{\text{III}}^{(A)}\approx 0$).

We compute the stress field with FEM and subsequently the stress intensity factors, ${K}_{\text{I/II/III}}^{(A)}$ at the tip/front of the circular fracture, highlighted in red in Fig. 8a. The details of the numerical simulation are explained in the Methods section. Figure 8b shows the modes of the stress intensity factors for tilt angles ϕ = 20°, 40°.

The mode ${K}_{\text{I}}^{(A)}(s)$ reveals a minimum near the center of the facet, where s ~0.5. For smaller and larger values, ${K}_{\text{I}}^{(A)}(s)$ increases symmetrically. This increase at the edges of the facet is a consequence of the elastic interaction between the circular facet and the planar parent fracture. As expected, the smaller the tilt ϕ, the more significant the interaction between the parent and facet fractures, and the larger the amplification of the opening mode ${K}_{I}^{(A)}$ at the edges. Interestingly, the shear modes are less affected by the parent-facet interaction and fulfill rather well the predictions of the PLS (${K}_{\text{II}}^{(A)},{K}_{\text{III}}^{(A)}\approx 0$).

To isolate the effect of facet-facet interactions on the PLS, we define model system (B), which is the same as model system (A), except for the addition of two lateral facets, as sketched in Fig. 9. The parameters of this model is the tilt, ϕ, of the planar fracture (as in model A), and additionally the distance 2RΛ between the centers of adjacent facets, where R is the radius of the facets.

Fig. 9: Model B to study facet-facet fracture interactions.

The model geometry and boundary conditions are the same as for model A (Fig. 8a), but with three facets at a distance 2RΛ. The normalized length, s, of the fracture tip/front, where 0 ≤ s ≤ 1 covers the middle crack’s facets.

As for model A, we used FEM calculations to obtain the stress intensity factors, ${K}_{\text{I/II/III}}^{(A)}$, at the tip/front of the central facet, highlighted in red in Fig. 9. The difference between models A and B represents the influence of facet–facet interactions. Figure 10 shows the stress intensity factors as predicted by the simplified models A and B, for different tilt angles, ϕ, and facet–facet distance, Λ.

Fig. 10: Facet-facet fracture interactions.

In order to isolate facet–facet interactions, we compare the predictions of stress intensity factors using model B, which includes a parent fracture and neighboring facets (Fig. 9), and model A, which only includes the parent fracture (Fig. 8a). This comparison is made as a function of the normalized fracture tip/front length s, for different parent fracture tilt angles ϕ and closeness between facets Λ. Panels a–c show the difference in the opening mode stress intensity factor, ${\Delta {K}_{{\rm{I}}}={K}_{{\rm{I}}}^{(B)}-{K}_{\text{I}}^{(A)}}$, for a range of distances between facets (from very close, Λ = 0.4, to far away, Λ = 1.6) and tilt angles ϕ = 10°,  20°,  40°. For small tilt angles (ϕ = 10°) and closely spaced facets (Λ = 0.4), the difference ΔK_I is generally positive near the center of the facet (s ≈1/2) and negative near the edges (s ≈0 and s ≈1). This negative difference near the edges indicates stress shielding due to the proximity of adjacent fractures. As the tilt angle ϕ or the distance between facets Λ increases, the influence of neighboring facets on K_I decreases. For less tilted and more distant facets, the edges of the fracture tips face each other, which can lead to stress amplification (compare panels Fig. 10a–c). Panels d–f and g–i show the influence of facet-facet interactions on the shear modes II and III (${\Delta} {K}_{{\rm{II}}}={K}_{{\rm{II}}}^{(B)}-{K}_{\text{II}}^{(A)}$ and $\Delta {K}_{{\rm{III}}}={K}_{{\rm{III}}}^{(B)}-{K}_{\text{III}}^{(A)}$, respectively). It is clear that close neighboring facets induce local shear. As expected, the influence of neighboring facets on the local shear modes decreases with increasing distance between facets, Λ, and with increasing inclination angle, ϕ (reducing shielding).

The top panels of Fig. 10a–c show the difference between the stress intensity factor, ΔK_I, for the opening mode, for a range in the distance between facets (from very close Λ = 0.4 to far away Λ = 1.6), and tilt angles ϕ = 10°,  20°, 40°. For the case of small tilt, ϕ = 10°, and closely spaced facets, Λ = 0.4. Near the center of the facet, s ≈1/2, the difference ΔK_I ≳ 0 while ΔK_I < 0 near the edges of the facet (s ≈0 and s ≈1).

This result can be understood from the proximity of the secondary fractures. For s ≈0 and s ≈1, the central fracture (marked in red) approaches parts of the adjacent fractures, thus effectively shielding stresses, as sketched in Fig. 7b. As expected, the influence of neighboring facets is greatly reduced near the center of the central facet (s ≈1/2). Consequently, in this region, there is hardly a difference between the stress intensity factors of the opening mode, ΔK_I ≈0. Thus, for the opening mode I, the mutual influence of adjacent secondary cracks can be interpreted as geometric shielding of the crack tips, which is particularly pronounced in the vicinity of the crack tip’s ends. For less tilted and more distant facets, the shielding ceases since the edges of the fracture tips face each other, resulting in amplification of the stress, see Fig. 7a for a sketch (compare panels Fig. 10a–c). Similar geometric effects were also reported in refs. ^3,29,30.

The mutual influence of neighboring facets for the shear modes II and III, for different tilt angles, ϕ, and facet-facet distance, is shown in panel d–f and g–i, respectively. We can conclude that the presence of close neighboring facets induces local shear. The function ΔK_II is antisymmetric with respect to s = 1/2, due to the definition of K_II. As expected, the influence of neighboring facets on the local shear modes decreases by increasing the distance between factes Λ, and by increasing the inclination angle ϕ (reducing shielding).

Discussion

Our experimental and numerical investigations provide clear evidence that the PLS governs the fragmentation of brittle hydrogels under mixed-mode I + III loading. By capturing the detailed geometry of evolving cracks through X-ray tomography and computing the local stress intensity factors using finite element simulations, we observed that the opening mode K_I remains dominant along the fracture tips, while the shear modes K_II and K_III are significantly smaller. This observation is consistent with the PLS, which states that fractures propagate in directions that locally cancel shear stresses.

Deviations from the PLS were observed near the edges of the facets, where fluctuations in the stress intensity factors became more pronounced. Through simplified model systems and finite element analyses, we showed that these deviations stem from elastic interactions between adjacent facets. These analyses indicate that facet-facet interactions can either amplify or shield the stress intensity factors near the crack tips, depending on the geometric configuration and the proximity of the facets.

These results suggest that while PLS provides a robust framework for understanding crack propagation in brittle materials under mixed-mode loading, consideration of facet size and elastic interactions is essential for accurately predicting fracture behavior, with direct applications to hydraulic fracturing^31,32,33, geophysical processes^7,9,34, and material strength^35,36.

Moreover, the geometry of the three-dimensional crack can be used as the starting point for simulating crack evolution with methods such as phase-field^10,11,37,38, eigenerosion³⁹, cohesive models⁴⁰, or XFEM⁴¹ to investigate global crack behavior, including facet coarsening.

Finally, we note that applying linear elastic fracture mechanics (LEFM) to soft materials such as hydrogels may be limited by potential deviations from small-deformation assumptions near the crack tip. However, rheological characterization (see “Methods”) shows that the hydrogel exhibits linear elastic behavior, and prior studies have demonstrated that similar hydrogels fracture in a brittle manner with minimal inelastic deformation⁸, justifying the use of LEFM. Future work could explore alternative theoretical frameworks—such as the J-integral^42,43 or the configurational force method^44,45,46,47—which extend beyond the assumptions of LEFM and account for geometric and material nonlinearities. Such approaches may offer deeper insight into deviations from PLS that arise from facet interactions.

Methods

Sample preparation

The hydrogels were prepared by dissolving 10 g of gelatin in a mixture of 0.05 l of distilled water and 0.05 l of glycerin. The solution was heated to 55 °C and stirred until the material was fully dissolved. The solution was then poured into a mold and cured at a temperature of 5 °C for approximately 24 h before unmolding. Including glycerin in the mixture improves the hydrogel’s elasticity. In ref. ⁴⁸, it was suggested that glycerin interacts unfavorably with the collagen chains, creating small water regions that promote the nucleation of overlapping collagen helices, increasing the number of bonds between the chains.

Rheological properties of hydrogels

The mechanical properties of hydrogels were studied on a rotational rheometer Rheometrics RDA-II in the parallel plate geometry, using discs of 50 mm diameter and samples about 10 mm thick. The rheological characterization was performed by small-amplitude oscillatory shear tests in a nitrogen atmosphere.

Initially, a strain sweep test was performed, measuring the loss G^″ and storage modulus ${G}^{{\prime} }$ at a frequency of ω = 5 rad s⁻¹, as shown in Fig. 11a. The result shows that the gelatin hydrogels exhibit linear elastic behavior beyond 10%, supporting the applicability of linear elasticity in the numerical calculations.

Fig. 11: Rheological properties of gelatin.

Panel a shows the storage (${G}^{{\prime} }$) and loss (G^″) modulus resulting from a sweep deformation γ test at a frequency of ω = 5 rad s⁻¹. Note that the linear regimes extend beyond rotational deformations of 10%. Similar results are obtained at other frequencies. Panel b shows a frequency sweep test, at deformation γ = 5%, used to explore the linear regime of deformations (in frequency) and the static shear modulus ${G}_{0}^{{\prime} }={G}^{{\prime} }(\omega \to 0)$.

Figure 11b shows a frequency sweep test in the range from 0.1 rad s⁻¹ to 100 rad s⁻¹, at a strain of γ = 5%. The elastic modulus ${G}_{0}^{{\prime} }$ is then calculated from ${G}^{{\prime} }(\omega \to 0)$, representing the gel’s elasticity under static conditions. At room temperature ${G}_{0}^{{\prime} }=7\pm 1\,\,\text{kPa}\,$. From the elastic modulus, Young’s modulus E is calculated using the relation $E=2{G}_{0}^{{\prime} }(1+\nu )$. Hydrogels are typically considered incompressible (with a Poisson’s ratio of 0.5), but van Otterloo and Cruden have shown that at high gelatin concentrations, Poisson’s ratio decreases¹⁹. For a hydrogel with a gel concentration of 10 wt%, the Poisson’s ratio is ν = 0.43 ± 0.04. Using this value, Young’s modulus is E = 22 ± 4 kPa.

Molding process

The mold consists of three parts. The top and bottom caps remain attached to the sample after curing. These caps are enclosed in a rigid, removable polyamide container, which retains the gelatin until solidification. The container is then removed for the fracture test, leaving the cylindrical walls of the sample with traction-free borders. This rigid mold is coated with silicone oil to prevent the gelatin from adhering during the demolding process. A 2 mm diameter needle is placed in the upper support prior to the curing of the gel. To prevent the flow of the liquid gel through the needle due to capillary forces, a thread is inserted into the needle before the curing process begins. Once the gel has solidified, the thread is removed, creating a seed for the fracture process.

X-ray tomography parameters

The X-ray source was operated at a voltage of 140 kV and a current of 270 μA. Throughout this work, the tomograms were obtained by rotating the samples through 800 steps, with an exposure time of 150 ms per step. Image processing and segmentation were performed with itk-SNAP⁴⁹.

Determination of the tip and SIF

For the computation of the stress intensity factors (K) we need the stress along a path originating from the fracture tip in the direction of  −N. Along this path, the stress distribution varies, as shown in the inset of Fig. 3a in the main article. Thus, selecting an appropriate distance r for the computation of K is non-trivial. At a large distance from the fracture tip, the stress behavior fails to exhibit the expected divergence. Conversely, at very small distances near the tip, although linear elastic fracture mechanics predicts a stress singularity ($\sigma \propto 1/\sqrt{2\pi r}$), the finite-element continuum model inherently yields finite stresses at the crack tip. This issue is in the vanishing quantity ${\sigma }_{\rm{BN}}\sqrt{2\pi r}$ as r → 0 as shown in Fig. 4c in the main article.

To calibrate the segment r, K values are calculated for a coin-shaped fracture subjected to uniaxial tension (σ) and shear (τ), as shown in Fig. 12a. The exact solutions for the stress intensity factors of each mode for this problem are^50,51,52:

$$\begin{array}{rcl}{K}_{I}&=&2\sigma \sqrt{\frac{a}{\pi }}\\ {K}_{II}&=&\frac{4\tau \cos \theta }{2-\nu }\sqrt{\frac{a}{\pi }}\\ {K}_{III}&=&\frac{4\tau (1-\nu )\sin \theta }{2-\nu }\sqrt{\frac{a}{\pi }}\end{array}$$

(6)

where a is the fracture radius, and θ denotes the angular displacement.

Fig. 12: Stress intensity factors calibration.

Panel a shows a scheme of the coin-shaped fracture model under tensile loads (σ = 1 Pa) and shear τ (for simplicity, τ = σ). Not to scale for clarity. The angular displacement along the fracture is given by θ. Panel b shows the representation of the stress intensity factors K (where subindex I, II, and III represents modes of deformation I, II, and III) as obtained by Eq. (6) (lines), and the result obtained from finite element analysis (symbols). In the calculations we use the Poisson modulus ν = 0.43, the dimensions of the cube L = 10 cm, and fracture radius a = 1 cm.

Figure 12b shows the theoretical curves from Eq. (6). To find the suitable distance of r, the calculation is performed at different distance values and those that best fit the theoretical curves from Eq. (6) are selected. Note that the distances may vary between modes. The values of K obtained through the adjusted distance r are shown in Fig. 12b. The numerical results agree well with the theoretical solutions.

Finite element calculations

In this work, we use Comsol Multiphysics to find the stress intensity factors of the crack tip/front. The mesh is created using a tetrahedral volume for the predefined “extra fine” size, and the discretization of the displacement field is quadratic. The stress fields are obtained by considering the hydrogels as isotropic materials and numerically solving the equilibrium equation:

$$\nabla \cdot \sigma =0$$

(7)

where σ is the Cauchy stress matrix with the appropriate boundary condition that resembles the experiments: lower cap fixed and upper cap elongated and rotated. Equation (7) was solved in the spatial (deformed) configuration, using a fracture shape obtained by tomography after waiting long enough for the crack to halt.

Simplified model simulation details

We conducted the simulation using finite element methods based on the configuration illustrated in Figs. 8 and 9. The remote stress applied to the top cap is σ = 2 Pa. The circular facets each have a radius of R = 0.75 cm and are spaced at intervals of 2RΛ, where Λ is a factor controlling the separation between facets. The box has dimensions L_x = L_y = 10 cm and L_z = 20 cm, and the plane fracture is 1 cm long. The box is modeled using the same mechanical properties as the gelatin used in the CT fractures. The distance varied from Λ = 0.4 to Λ = 1.6.