Predicting fracture in disordered network materials using the local intelligent stress threshold indicator

Abstract

Network glass fracture occurs as a sequence of elementary events occurring at weak sites in the glass structure. Fracture is a highly complex process that occurs suddenly and without obvious structural or thermodynamic signs prior to the event’s occurrence. We show that a stress threshold value quantified by local mechanical probing highly correlates with nanoscale crack nucleation in a two-dimensional network glass. Subsequently, a neural network-based predictor, the local intelligent stress threshold indicator (LISTI), links the local stress threshold with the undeformed local structural topology. LISTI yields a reliable heatmap indicating soft spots that strongly correlate with the localized initiation and development of the fracture process. Finally, we show that LISTI can be used to find local zones prone to rearrangement in real-measured two-dimensional silica glass structures.

Introduction

Fracture is a sudden phenomenon with potentially catastrophic consequences for a wide range of materials that carry mechanical loads. A better fundamental understanding of this phenomenon, especially the reliable prediction of fracture initiation that can be connected to the geometric structure of the material in the undeformed state, would significantly improve available methods in material design and eventually lead to advances in structural reliability.

Crystalline solids have a long-range order and may be numerically generated by periodically duplicating a unit cell. However, the presence of easily detectable local dislocations or lattice defects in crystals has driven theoretical and experimental developments over the past century, leading to highly developed methods of crystal plasticity that explain and model how such well-defined defects govern the failure mechanisms of the otherwise perfectly ordered material^1,2. If the topological structure has so many defects that an underlying periodic lattice structure must be abandoned, one may classify the material as disordered or non-crystalline³. Intriguingly, failure of disordered materials also originates from local, nanoscale spots referred to as shear transformation zones (STZs) – one may consider them analogous to dislocations in ordered structures – interacting with one another on a coarser scale^4,5,6,7. Notably, fracture in disordered solids often occurs as STZs are activated sequentially in a short time, also referred to as avalanche events in the literature⁸. While it is generally accepted in the literature that such STZs are somehow encoded in the material structure as “soft spots", a priori identification of such soft spots by correlating them with the local atomic neighborhoods is one of the grand challenges in understanding the mechanics of disordered materials⁹. In fact, without the ability to identify soft spots in a material’s atomic structure, it is practically impossible to define a defect in the same way defects are defined for crystalline solids.

Several strategies to correlate the local atomic structure to plastic rearrangements and fracture have been developed in the last decades. These include methods that correlate deformation with harmonic vibration modes^10,11, non-affine displacement fields^12,13, local identifiers derived only from the geometric constituents of the local atomic neighborhood⁹, as well as experimental identification in colloidal glasses¹⁴. Ding et al.¹⁵ introduced a local quantity called the flexibility volume that quantifies the local atomic free volume with dynamical information from the atomic vibration, showing promising correlations with local rearrangement spots. Milkus and Zaccone correlate non-affine softening with an order parameter describing the local inversion symmetry in the glass structure¹⁶. This centrosymmetry of nearest-neighbor polyhedra was introduced as a parameter that strongly correlates with local mechanical instability¹⁷. Patinet et al.¹⁸ introduced a local probing method receiving a predictive quantity, i.e., the local yield stress, that has revealed the highest correlation with zones prone to atomic-scale rearrangements in deeply quenched computational models. In their methodology, they scan an entire (numerical) material sample, subjecting every local atomic neighborhood to mechanical deformation in different directions until the first inelastic response. It was shown that the local yield stress parameter serves as an outstanding predictor. However, this method requires local stress-strain data from many local mechanical simulations, which come at considerable computational cost.

The main motivation for defect identification and material failure prediction lies in the ability to examine the local topology of a material spot, i.e., exclusively geometric constituents, and predict its susceptibility to structural rearrangement leading to failure. In other words, something that is easily detectable by the human eye in crystals is, to date, well hidden in disordered materials.

From this point of view, neural networks are attractive tools for identifying structural features in disordered materials and correlating them with highly nonlinear catastrophic rearrangements. The first attempts were made by Cubuk et al.¹⁹, who could discern subtle structural features responsible for such heterogeneous dynamics. Fan and Ma²⁰ were able to identify shear transformation zones in a Lennard-Jones glass and a CuZr bulk metallic glass using convolutional neural networks, where the local packing of the atoms was represented using a Gaussian-weighted spatial density map. Recently, Hardin et al.²¹ used a manifold learning method to characterize the local structure in disordered solids, but to date, the derived neural network structural descriptors have not been successfully correlated to localized deformation mechanisms. Lately, Jung et al.²² presented a thorough review of how machine learning techniques, especially graph neural networks and attention-based models, can be systematically utilized to understand the relationship between the structure and the dynamics in glassy systems.

Although glassy network materials respond fundamentally differently to densely packed systems, we demonstrate in this paper that local mechanical probing of the unstrained sample, initially proposed by Patinet et al.¹⁸, also reveals “soft spots" in network glasses. Intriguingly, the prediction ability of this method persists even for larger strains, where fracture has already progressed significantly and large voids are present. Using a two-dimensional representative of silica glass, which was experimentally imaged²³, the concept of scanning and local probing becomes even more critical, as we can investigate and numerically probe atomic structures whose coordinates are derived from real images. With this motivation in mind, we predict zones susceptible to atomic-scale rearrangements in this paper using a neural network-enhanced predictor, which we refer to as the Local Intelligent Stress Indicator (LISTI). The LISTI, which is presented schematically in Fig. 1, builds on the local probing concepts¹⁸ demonstrated in Fig. 1a, b. This way, local mechanical testing is performed within a circular probing window in variable spots $\left({x}^{* },{y}^{* }\right)$ generating a prediction map for the susceptibility of mechanical instabilities for the entire sample. We show that local mechanical probing of network glasses results in outstanding prediction accuracies; however, it is computationally expensive, making a direct application difficult. The LISTI comes with all the physical benefits of local probing, and when appropriately trained, it has no restriction in terms of computational efficiency. Following the concept of local probing, extensive structural feature extraction is possible from only a relatively small number of material samples. The approach then uses neural network methods to predict the local stress thresholds of local structure, as shown in Fig. 1c. The result is a neural network map of the threshold stress for a given material sample (Fig. 1d). We demonstrate the LISTI on a two-dimensional silica model glass, which is in-plane topologically equivalent to experimentally imaged 2D silica bilayer structures²³. Such materials inherit the brittle behavior of the abundant bulk silica glass polymorph and generally experience fracture processes of a somewhat brittle nature. Thus, material failure typically occurs due to avalanche-type events, making event prediction for larger strains particularly challenging. The LISTI allows for real-time investigation of actual material images, which constitutes a direct practical application of the technique.

Fig. 1: Training the local intelligent stress threshold indicator (LISTI) using mechanical probing.

a Local mechanical probing of a two-dimensional network glass sample. A circular material cutout is extracted, affinely deformed, and divided into an outer region where the atoms are frozen and an inner region where the atoms can move freely due to their interaction. b Every local cutout is deformed until the first inelastic response can be identified, indicated by a stress drop occurring at a local critical stress ${\tau }^{(c)}\left({x}^{* },{y}^{* }\right)$. c Scanning the threshold stress $\Delta \tau \left({x}^{* },{y}^{* }\right)$ for the entire sample leads to the threshold stress map. Color coding ranges from red to blue, whereas red refers to low and blue refers to high threshold stress values. The white markers refer to the first eight rearrangements during fracture. We emphasize the accordance of red areas in the threshold stress maps with actual rearrangement spots. d Training the LISTI with geometrical information from local circular material cutouts and the corresponding threshold stress values.

Results

Predicting fracture performing local mechanical probing

LISTI requires an accurate local predictor of material performance and a regressor that captures the relationship between the material structure and the predictor. We chose the local mechanically induced threshold stress as the predictor since low threshold stresses have been shown to correlate with zones that experience rearrangements in densely packed systems¹⁸. This way, a circular window scans the entire sample, performing local mechanical probing, in which the local window is subjected to true shear deformation (as shown in Fig. 1a) until the first local rearrangement occurs (indicated by the stress drop in Fig. 1b). The shear stress threshold $\Delta \tau \left({x}^{* },{y}^{* }\right)$ is defined as the critical stress ${\tau }^{({\mbox{c}})}\left({x}^{* },{y}^{* }\right)$ at which the rearrangement ocurrs minus the initial local stress ${\tau }^{({\mbox{in}})}\left({x}^{* },{y}^{* }\right)$ in the undeformed state, as shown in Fig. 1b. This value is extracted at the scanner position ${{{\boldsymbol{r}}}}^{* }={\left[{x}^{* },{y}^{* }\right]}^{T}$ such that the result of each mechanical deformation protocol is one spot in the threshold stress map shown in Fig. 1d. The blue regions represent local spots with higher local stress threshold values, while the red regions correspond to spots with smaller stress threshold values, i.e., regions that are expected to have higher susceptibility to rearrangement. We present a more detailed description of this local yield stress approach in the Methods section. LISTI correlates the purely structural information at all spots to the threshold stress, as indicated in Fig. 1c, d. Thus, LISTI marries the idea of a purely structural indicator with the remarkable prediction accuracy derived from local mechanical probing.

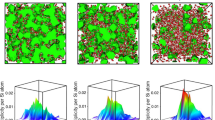
The two-dimensional silica sample presented in Fig. 1a is subjected to pure shear deformation, which was performed by elongating the sample in the first principal direction of shear while compressing the sample in the second principal direction of shear so that the area of the sample remains constant during the entire deformation protocol. Three snapshots at selected strain values where local rearrangements during the deformation protocol occur are depicted in Fig. 2. The location of local rearrangements in the configurations is highlighted in red. The corresponding shear stress-strain relations are shown below the configurations, with the stress drop highlighted in red. Notably, local rearrangements mostly manifest as nano-fracture events in this type of material. Bonds break, leading to nanovoids that may transition into nano-cracks, further increasing the strain. The bottom images in Fig. 2 present the non-affine displacement fields^3,24 of the selected local rearrangement events, which emphasize the idea of little nano-fracture phenomena by revealing dipolar shapes, in contrast to metallic glasses revealing rather quadrupolar shapes³. In particular, this phenomenon can be observed in network glass subjected to pure shear loading, where typically less material flows into the second principal direction of pure shear, while more material flows into the first principal direction. Thus, the local density decreases on average during an event, leading to the formation of small voids within the material^25,26. The local shear stress threshold map is shown behind the non-affine displacement fields in these plots, showing that the occurring rearrangements highly correlate with the predicted regions of low local yield stress, as indicated in red. The actual recorded rearrangement events occurring during remote deformation are also indicated by white marks in Fig. 1c, with the number indicating the sequence in which they occur, again emphasizing the high correlation between the predicted and actual rearrangements. However, the great accuracy of this local probing method comes at a high cost. In fact, ~5⋅10⁵ local molecular simulations are required to generate the rearrangement stress map for this particular sample, with the exact number depending on the chosen scanning grid size, as discussed in the Methods section. This pitfall leads to the local yield stress method being up to a hundred times slower than performing the remote deformation itself.

Fig. 2: Remote deformation of a two-dimensional silica sample.

The upper panel shows the configuration snapshot after the selected atomic-scale rearrangements. The middle panel represents the corresponding nonaffine displacement field after the first rearrangement (a), the third rearrangement (b), and the sixth rearrangement (c). The lowest panel represents the stress(τ)-strain(γ) relations with the corresponding stress drop occurring during the selected rearrangements, colored in red. In the middle panels, the non-affine displacement fields are  plotted together with the local shear stress threshold maps in the background. A high correlation is observed between the actual and predicted zones of local rearrangements in the upper and middle panels. The red color in the prediction maps indicates low threshold stress values, i.e., zones that are expected to be susceptible to rearrangements. The blue color indicates high threshold stress values, i.e., zones that are not expected to be susceptible to rearrangements.

The critical takeaway here is that stress threshold maps are not only applicable to predicting rearrangements in densely packed systems, such as metallic glasses, but are also excellent predictors for glass fracture even at larger strains where significant voids are already present in the material. A more efficient method to obtain these local yield stress maps would, therefore, enable incorporating prediction strategies into larger-scale simulations. The underlying hypothesis is that, in the absence of thermal vibration, there is a deterministic link between the local atomic structure and the local stress threshold, which is embedded in the very fine details hidden in the local atomic configuration. We realize this connection through a generic data-driven algorithm, the local intelligent stress threshold indicator (LISTI), described next.

The local intelligent stress threshold indicator (LISTI)

As shown in Fig. 1d, LISTI takes local topological data as input, represented by purely structural information (i.e., atomic positions and bond connections). The output of LISTI is the stress threshold value Δτ, i.e., the Neural network prediction of the maximum occurring shear stress minus the initial local stress during local probing at the occurrence of the first local instability. For training the LISTI, a pool of local regions and the corresponding shear stress thresholds must be harvested. The data set must be chosen sufficiently large to characterize the unique inelastic features of the disordered material. Notably, the idea of mapping every neighborhood in the material to a material performance value (i.e., the local shear stress value) leads to LISTI being a regression model. The large amount of local material data that can be extracted per material sample leads to the essential advantage that useful predictions can be made by harvesting only a relatively small number of material samples.

The data generation process involves (i) the generation of a set of material samples using molecular dynamics, (ii) the deformation of the material samples to identify the actual rearrangement spots, (iii) local mechanical probing across the material samples to generate stress threshold maps and (iv) a statistical evaluation of its overall accuracy using a relevant prediction quality metric. To construct the LISTI, we evaluate different neural network architectures suitable for predicting the local stress threshold based on purely structural inputs, i.e., atomic coordinates and topological bond information. To test the LISTI, we will statistically evaluate the accuracy of the prediction using two approaches. The first test of the prediction reliability of LISTI is performed by predicting stress threshold values in generated material samples that LISTI has not seen before. These generated samples are statistically equivalent to our first benchmark sample, which is a real material patch experimentally imaged by Lichtenstein et al.²³. The second test of the prediction reliability of LISTI is presented on network structures that are experimentally extracted by Huang et al.²⁷ from another material patch. Notably, LISTI will not be trained on experimentally imaged network structures but on artificially generated statistically equivalent network structures.

The molecular models utilized in this paper are of an empirical nature since they are generated based on a real image of a silica bilayer structure taken by Lichtenstein et al.²³. This flat silica polymorph can be seen as the experimental confirmation of Zachariasen’s network theory²⁸ and provides proof of ring structures in silica glass by images characterized by ring statistics and the topological arrangements of rings in the material. To generate material samples in step (i), whose topology is statistically equivalent to the imaged material data, we use a dual Monte Carlo bond switching algorithm²⁹. The algorithm relies on a Markov Chain Monte Carlo random walk performing a sequence of topological flip transformations starting from a purely hexagonal lattice. The algorithm is further discussed in the Methods section. We generated 50 two-dimensional samples of 10⁴ atoms. Two-dimensional models are sufficient in our case since the topological information from the images is exclusively two-dimensional. The Monte Carlo method ensures that every sample is disordered and unique, while the statistical level of disorder represented by the ring statistics is the same for every sample.

Mechanical deformation of the samples in step (ii) is performed using the athermal quasistatic deformation method^8,30, which is an incremental sequence of deformation and minimization of the potential energy, as further discussed in the Methods section. This allows for a pure investigation of the atomic structure while ignoring any thermal vibrations. This is a reasonable approximation since we consider mechanical effects at temperatures significantly lower than the glass transition temperature. The samples are deformed by incrementally altering the Bravais vectors of the simulation cell. We stretch the simulation cell in the x-direction while compressing it in the y-direction. The ratio of stretching and compressing the cell is chosen so that the area of the cell remains constant throughout the entire deformation protocol. This way, the sample is subjected to a pure shear deformation, where the first and second principal directions of shear are parallel to the axes x₁ and x₂. We recorded all steps at which local rearrangement events occur by detecting the stress drops from the stress-strain relations. The positions of rearrangement are identified by locating the atom that experienced the largest displacement in the configuration during the event.

Quantifying the prediction quality

The local stress threshold maps are evaluated in step (iii) by scanning the samples in their initial, undeformed state, subjecting the probing windows to pure shear deformation, and extracting the maximum stress values at the occurrence of the first stress drop as shown in Fig. 1a, b. This is discussed in more detail in the Methods section. By deforming 50 material samples and performing the corresponding local probing deformations, we can statistically quantify the prediction accuracy for the first n = 6 rearrangement events. Local inspection of the deformation process shows that fracture has already progressed significantly after six events. The predictive accuracy for the first six events is assessed in step (iv) using the modified inverse cumulative distribution function (${{{\mathcal{C}}}}_{{\tau }_{{{\rm{c}}}}}(n)$) described in the Methods section, which takes values ranging from −1.0 to 1.0. Forthwidth, we will refer to this quantifier as prediction goodness. A goodness value of 1.0 refers to a perfect correlation between the prediction of the position of the event and its actual site of occurrence. A value of 0.0 refers to no correlation, i.e., no predictive information, while a value of −1.0 refers to perfect anti-correlation. Again, we present detailed information regarding the evaluation of the prediction goodness in the Methods section.

Figure 3 shows statistics of the goodness parameter in Eq. (1) versus the sequential number n of the event occurring for the first six events of the 50 samples in the data set. The statistics are represented by histograms (in blue) and boxplots (in white) for every event sequence number. The red dashed line shows a goodness value of one, which indicates perfect prediction. The mean goodness values, represented by the blue line in Fig. 3, show that the first few events are expected to be predicted almost perfectly. For later events, the average prediction goodness decreases. This is caused by the strong nonlinearity of the system, leading to strong alterations in the potential energy landscape in the course of inelastic events, which leads to a load redistribution of the whole system. The more inelastic events with increasing strain, the more severe the irreversible changes in the atomic system. Nonetheless, the prediction goodness remains around 0.8 after six rearrangement events, which is already at a deformation state where the fracture process is relatively advanced. From the wider spread histograms and the corresponding box plots in Fig. 3, one also observes that the variance increases with the number of rearrangement events, revealing that the confidence in the prediction estimate decreases with the number of events. This also makes sense because some samples have more advanced fracture processes after n = 6 events (leading to less predictive accuracy), while other samples have less advanced fracture processes at this stage and are therefore closer to their original undamaged structural state (leading to higher predictive accuracy).

Fig. 3: Statistical analysis of prediction goodness for the first six rearrangement events from 50 material samples.

The y-axis represents the prediction goodness parameter $({{{\mathcal{C}}}}_{{\tau }_{c}}(n))$ for each given event (n). The box represents the spread of data between quartiles 1 and 3, while the whiskers extend from the box to the minimum and maximum values of the data.

General LISTI development process

Next, we train the LISTI by selecting appropriate neural network models and test the LISTI’s ability to predict local rearrangements. As shown in Fig. 1d, the input consists of purely geometrical data (i.e., the atomic positions), while the output (i.e., the predictor) is the local shear stress threshold that corresponds to the local configuration. The training dataset is taken from 50 rearrangement stress maps and the corresponding local structural data. Using a 50 × 50 scanning grid, we obtain a total of 1.25⋅10⁵ training samples.

The 50 material samples are divided into a training set of 40 samples (10⁵ data points), a validation set of five material samples (1.25⋅10⁴ data points), and a test set of five material samples (1.25⋅10⁴ data points). Additional ten test samples were generated to test the prediction capability of LISIT. During training, the network parameters were optimized to represent the training set while ensuring that the validation loss remained comparable to the training loss to avoid overfitting. This way, the validation set is used to monitor the variance and bias of the predictions during training, while the test set serves as the final measure of the model’s performance. During an initial training phase, we altered the hyperparameters of the neural networks, such as the number of layers and neurons per layer, to obtain optimal models for the problem at hand. We refer the reader to the Methods section for more information regarding the neural network training procedure, including the definition of the loss function and specific architecture details. We tested three different neural network architectures serving for the LISTI: a recurrent long-short-term memory neural network, a convolutional neural network, and a graph neural network.

A recurrent architecture using long-short term memory cells

The recurrent neural network (RNN) inputs are the center of the corner-sharing SiO₃ triangles in a matrix format in the circular probing region, as shown in Fig. 4a.

Fig. 4: Predicting local stress threshold values using a Recurrent Neural Network.

a The inset of the local probing region (x^*, y^*) represents the details of the atomic structure and the sequence of atoms considered as the input for RNN. The corresponding input is shown in the configuration, with the latter half of the image illustrating the RNN architecture that predicts the shear stress threshold as output. b Training and validation loss versus training epochs. c RNN predictions versus the corresponding actual local stress threshold values for the training set. d RNN predictions versus the corresponding actual local stress threshold values for the testing set. The red lines in (c) and (d) indicate 100% accurate predictions.

The rows refer to the atoms, and the columns refer to their coordinates. The network parameters converged after 1500 training epochs, as indicated by the training and validation loss functions in Fig. 4b. The RNN’s performance is presented in Fig. 4c, where the actual stress threshold values of different samples are plotted versus their neural network-predicted counterparts for the training and validation sets. Figure 4d gives the performance of the RNN model for the test dataset, which was not seen by the network while training; thus, testing the generalization ability of the RNN for an unseen dataset. Notably, these figures present the performance of over 2.5⋅10³ neural network predictions, where points that are located on the red line indicate perfect prediction. The further away from the red line, the worse the prediction accuracy. For this RNN architecture, a clear correlation between target and prediction can be observed from Fig. 4c, although the network systematically overestimates small stress thresholds while it underestimates large stress thresholds. Furthermore, the model was not able to give accurate predictions for the unseen dataset as shown in Fig. 4d. The difference in the deviation of the data points shows that the generalization of the trained RNN is not satisfactory. This might arise due to the model’s inability to differentiate the input data, which is discussed further below. Thus, we conclude that this neural network type can learn and predict the general trends in the stress thresholds from the local structure, but with limitations in its predictive accuracy. Although this incorporation of the RNN has shown some predictive power, there is one major drawback: it only links the sequence of the atomic structure to the output shear stress threshold. This makes the network permutation variant, and it needs to be trained with all the variations of permutation possible for a single structure. This is necessary because even if the sequence of the atoms changes, the coordinates remain the same, ensuring consistent structural information. However, training with all the variations of permutation possible for a single structure requires immense computational resources and is practically unfeasible.

A convolutional neural network architecture

An alternative approach for processing the topology of local atomic structures is to generate images of the local structure to recognize particular patterns and connect them with local shear stress thresholds. We trained a convolutional neural network (CNN) model with the generated images of the local atomic topology as input and the corresponding shear stress thresholds as output, as presented in Fig. 5a. The topologies of the atomic structures are captured as grayscale image data. The silica network is represented by spheres, defining the center of the SiO₃ triangles, and bonds, represented by lines, referring to the corner-sharing connection of the SiO₃ triangles with their respective neighbors. The images have size 220 × 220 pixels while each pixel is assigned a certain level of a grayscale. A sequence of filters scans and transforms the image inputs, followed by a sequence of feed-forward layers with the stress threshold as the final output quantity. The training and validation loss showing network performance of the CNN are presented in Fig. 5b over 300 epochs. Although the training loss decreased over further training, validation loss started to increase, indicating overfitting, even though dropout was used in the model. Further dropouts and regularization resulted in a higher loss, leading to less accurate predictions. Therefore, after comparing multiple variations in the architecture and hyperparameters, the network parameters converged sufficiently after 300 epochs. The accuracy of the local stress threshold predictions is shown in Fig. 5c, where the CNN predictions are plotted against the true values for the training and validation data sets. Notably, the CNN performs significantly better in predicting the local shear stress thresholds than the RNN. Although the correlation between the local shear stress threshold and their CNN predicted counterpart in Fig. 5c is higher than the respective correlation from the RNN in Fig. 4c, we still detect some variations from the perfect prediction line and in particular notice a general bias toward overprediction of the stress threshold.

Fig. 5: Predicting local shear stress threshold values using a Convolutional Neural Network.

a Local probing regions are transferred as an image of the topological structure at the coordinate (x^*, y^*). b Training and validation loss versus training epochs. c CNN predictions versus the corresponding actual local shear stress threshold values for the training set. d CNN predictions versus the corresponding actual local stress threshold values for the testing set. The red lines in (c) and (d) indicate 100% accurate predictions.

A graph neural network architecture

Since our molecular system is composed of corner-sharing SiO₃ triangles so that the network topology results in various rings of different shapes and sizes, we follow Franzblau’s original idea³¹ to represent the silica network directly as a graph. This way, the centers of the corner-sharing SiO₃ triangles define the nodes, while the connections between the triangles define the edges. Thus, the third neural network proposed here is a graph neural network (GNN), where the final output quantity is the threshold stress. GNNs perform computations over network structures based on the idea that entities (in our case, the SiO₃ triangles) exhibit certain relations with their neighboring entities. From a mechanical perspective, this approach originates from the idea that network materials transfer a great portion of mechanical loading over covalent bonding. This way, the neural network model receives not only the coordinates as nodal feature inputs, as implemented in the RNN model above, but also receives additional information between neighboring nodes (SiO₃ triangles) using an adjacency matrix that defines the entire network structure of the local probing region. Furthermore, we note that this graph-based approach also considers long-range interactions to some extent, which is generally present in network glasses, by taking not only direct covalent neighbors into account but also second to up to fifth neighbors in the graph.

Figure 6a visualizes these two inputs and the associated graph representation, followed by the GNN architecture. The training performance is shown in Fig. 6b. Notably, the network considers information flow between adjacent neighbors and walks deeper through the topological structure, visiting multiple neighboring nodes. Furthermore, graph smoothing is avoided, as discussed in more detail in the Methods section. This locality aggregation approach gives each node information about the entire local probing region, physically connecting this neural network model with the idea of local probing. This physical relevance is reflected by the extraordinary performance of the model. The prediction values reveal a high correlation with the corresponding target values. The overall correlation coefficient is 96%, which is significantly higher than the correlation coefficient of the two architectures presented above and is visualized by the correlation plot in Fig. 6c.

Fig. 6: Predicting local stress thresholds using a Graph Neural Network.

a The inset of the local probing region (x^*, y^*) represents the details of the atomic structure and the sequence of atoms that are considered as the input node features for the GNN. The subsequent figures next to the inset depict the atom connectivity derived from the valence information, which serves as the edge vector for the GNN. The latter half of the image illustrates the GNN architecture that predicts the shear stress threshold as a graph-level prediction. b Training and validation loss versus training epochs. c GNN predictions versus the corresponding actual local stress thresholds for the training set. d GNN predictions versus the corresponding actual local stress thresholds for the test set. The red lines in (c) and (d) indicate 100% accurate predictions.

Comparing the prediction quality

Next, we investigate the overall performance of each neural network model in predicting elementary rearrangement events. The results in Fig. 7 illustrate how the goodness parameter, presented in Eq. (1) in the Method section, changes based on the sequence number of failure events. For these first statistics, we combined the training and validation sets for the three neural network architectures. The red dashed line represents perfect prediction, i.e., a prediction goodness parameter of one, whereas the black dashed line represents no correlation or guessing.

Fig. 7: Statistical analysis of the prediction goodness for the first six rearrangement events from the training and validation sets. The y-axis represents the prediction goodness, ${{{\mathcal{C}}}}_{{\tau }_{c}}(n)$, for each given event n.

The lines connecting the means of all the boxplots indicate the trend in the prediction goodness of each neural network as the event number increases. The box represents the spread of data between quartiles 1 and 3, while the whiskers extend from the box to the minimum and maximum values of the data.

The RNN’s prediction goodness is represented in blue in Fig. 7. Although successful at the prediction of the very first events, the wide whiskers of these box plots show less confidence in the estimate for the first rearrangement event than the other networks. This demonstrates that the network struggles to represent the physical relationship between the atomic structure and the local shear stress threshold in the training set. Moving further into the higher strain regions, the prediction accuracy for the RNN model significantly decreases, and very large variability is observed. Some outliers even suggested an inverse correlation between the local atomic structure and the local shear stress threshold for events following the first failure occurrence. This could be attributed to the network’s reliance on the sequence of atoms. Though neighboring sample structures didn’t have a huge variation, there is a considerable difference in the local shear stress threshold. As a result, the network consistently receives local structures that closely resemble neighboring structures, causing the samples to become indistinguishable, leading to bad predictions for later events. However, the network successfully predicted the location of the first event with an average accuracy of 75%, which is significantly higher than many conventional structural predictors, such as local free volume⁹. More details about the comparison between the performance of two conventional structural predictors and LISTI are presented in the Supplementary Note 2.

The red boxplot in Fig. 7 represents the prediction goodness of the CNN model considering the training and validation sets. Despite receiving similar input to the RNN model, the CNN can discern subtle differences in the images and associate them with the local shear stress threshold. The success of CNN models in representing molecular dynamics simulation results can be attributed to their desirable inductive biases, weight sharing, and locality. Consequently, the CNN model achieves an 82% accuracy in predicting the first failure event, which is better than the RNN model. Nonetheless, it struggles to predict rearrangements after the first event. Moreover, the CNN is by far the most computationally expensive model to train. The time taken to train and predict using the CNN model is much longer than the RNN and GNN models; however, it is still much faster than pure mechanical probing for predicting the first event.

The last boxplot in green color in Fig. 7 presents the goodness statistics from the GNN predictions. The distributions show a high correlation with the location of actual rearrangements and a low variation in prediction accuracy, making this network architecture particularly promising for linking the pure topology of the glass network structure with the onset of material failure. In particular, the network can predict the first damage event with an accuracy of 96% and all subsequent events with an accuracy comparable to the purely mechanical local shear stress threshold approach, which requires 2.5⋅10³ molecular dynamics simulations per sample in our case. Furthermore, the GNN regressor shows a high prediction accuracy even at large strains when fracture has already progressed.

Figure 8 showcases the ability of the proposed networks to predict the local shear stress threshold on an unseen test dataset with 15 samples in total. The GNN, with a graph-level prediction, can successfully predict the local shear stress threshold with high accuracy and outperform the other two networks. The GNN predicts the first event, on average, with a goodness of 93% with low variation over different test samples and events. This shows that even for an unseen dataset, the prediction accuracy was high across all the samples. The figure also depicts the average prediction goodness of the other two networks which is 75% and 50% for the Convolutional Neural Network (CNN) and the Recurrent Neural Network (RNN), respectively. Having statistically identified GNNs as the best candidate to be incorporated into the LISTI, we visualize one prediction stress threshold map from the test data set using purely mechanical testing in Fig. 9a and the corresponding stress threshold map using the LISTI in Fig. 9b. The first six rearrangement events are indicated by white circles in Fig. 9a. The striking similarity of these heatmaps again underlines the high prediction goodness of the method when exclusively using topological input data.

Fig. 8: Statistical analysis of the prediction goodness for the first six rearrangement events from the test set.

The y-axis represents the prediction goodness, ${{{\mathcal{C}}}}_{{\tau }_{c}}(n)$, for each given event n. The lines joining the means of all the boxplots showcase the average prediction goodness of each neural network with respect to the sequence of the events. The box represents the spread of data between quartiles 1 and 3, while the whiskers extend from the box to the minimum and maximum values of the data.

Fig. 9: Threshold stress maps for one exemplary test sample.

a Heatmap obtained using local mechanical probing. b Heatmap obtained using the LISTI with the GNN architecture. The color codes of the heatmap are defined such that the normalized shear stress threshold value decreases from blue to red. The normalization of the shear stress threshold values is realized between zero and one. The rearrangement events actually occurring due to macroscopic deformation are indicated by white dots, while the corresponding event number indicates their sequences of occurrence.

The local yield stress method requires 17 h to simulate and predict the location of the first failure event for any given sample on an M1 Ultra chip. Whereas RNN, CNN, and GNN require 2.30, 3.20, and 2.25 h, respectively, to preprocess the data, train on the data, and predict the location of the first failure event for any given sample on an M1 Ultra chip.

Predicting soft spots from a real imaged material patch

We then tested the LISTI on an experimentally imaged 2D silica sample. Notably, our training sample was based on a first smaller material patch imaged by Lichtenstein et al.²³, which was used to extract the topological data of the material in terms of the ring statistics and the ring neighborhood statistics to ensure physically meaningful molecular dynamics models, as discussed earlier and further detailed in the Methods section. Our second experimentally extracted sample is the image of a larger material patch taken by Huang et al.²⁷, as shown in Fig. 10. A square cutout of ~12 × 12 nm, presented in green, was extracted for the simulations. The atomic coordinates were directly extracted from the image, as indicated in the enlarged circular area in Fig. 10b. Since one cannot apply periodic boundary conditions to this square sample, a circular area with a radius of ~5 nm was defined so that the remaining outside area was used as the frozen region during deformation. Figure 10c presents the numerical twin extracted from this green-boxed image area. More information regarding this process is provided in the Methods section.

Fig. 10: Prediction of atomic scale rearrangements in experimental imaged materials.

a Image of a 2D silica sheet grown on graphene (original image data are taken from Huang et al.²⁷ with permission by the publisher). b Circular enlargement of the silica image with the extracted atomic position for the numerical model. c Extracted square region of material with the LISTI stress threshold map shown on the deformed circular region, where blue represents the region with the highest shear stress threshold and red represents the region with the lowest shear stress threshold. d Pure shear deformation state directly after the first rearrangement has occurred. e Non-affine displacement field of the first occurring event.

The benchmark solution for this problem was obtained by applying athermal pure shear deformation to the material sample and recording the atomic trajectories and the actual local rearrangement spots occurring during deformation. Notably, in contrast to the simulations performed with periodic boundary conditions, only the inner circular area was allowed to relax during the minimization steps of the athermal quasistatic deformation. Since the material is somewhat confined in this circular area, only the material response until the first rearrangement event is considered, since unwanted effects coming from the frozen region during deformation increase significantly at very high strains. We performed local probing using LISTI, resulting in a heatmap shown in Fig. 10c, and qualitatively evaluated the prediction accuracy for the first event. The first event in the deformed configuration is encircled in Fig. 10d. The exact first event location is identified by the largest displacement shown in the non-affine displacement field map in Fig. 10e; this location is also plotted by a white dot in the LISTI heatmap. To quantify the accuracy, the first rearrangement event coincides with the predicted soft spot area with a prediction goodness correlation value of 0.96. Since experimental results of this kind are rare, a statistical evaluation of the goodness curve is not possible here. Moreover, since we consider only the first event for the prediction here, we can only extract this one value to quantify the accuracy of the prediction. This excellent result highlights LISTI’s high level of generalization and its ability to understand spots in networks prone to structural failure.

Discussion

We have proposed the local intelligent stress threshold indicator (LISTI), which allows for the reliable and efficient identification of regions prone to rearrangement in disordered network materials. Notably, the smallest local shear stress threshold value for each sample, evaluated by local mechanical probing, has shown a strong correlation with spots prone to rearrangement in network glasses and serves as an excellent indicator for fracture prediction in disordered network materials, while, to this date, existing purely structural indicators have shown a significantly lower correlation with material regions prone to rearrangement. However, LISTI exclusively considers input parameters from the unstrained material topology and, therefore, represents a powerful purely structural predictor candidate.

When training LISTI with information of actually observed rearrangements, one could only consider a few training data spots per material sample. This leads to a computational disaster when training data from the simulation is harvested. Instead, we assess evenly selected material spots across the sample, numerically represented by a discrete grid pattern, in terms of a stress threshold value, which highly correlates with the location of the soft spot. This approach yields abundant training data, even when only a small number of material samples are available. Notably, prediction is not defined by a binary “yes or no” identification in terms of explicit decoding of topological information but by a smooth prediction coefficient map that reveals a surprisingly high correlation with the occurrence of rearrangement spots in the material. We emphasize that LISTI is trained using data obtained from the local shear stress threshold maps, which are evaluated based purely on physical principles. Consequently, its highest performance is expected to be equal to the local shear stress threshold maps, and LISTI will never exceed the predictive ability of the purely mechanical probing method.

In the current study, three different neural network models were tested as the regression model for the LISTI: recurrent, convolutional, and graph neural network architectures. All three models perform reasonably well in predicting events at relatively small strains, specifically the first rearrangement event at the onset of material failure, with the graph neural network demonstrating superior accuracy. The RNN is trained to map the atomic sequence to the shear stress threshold. However, it is susceptible to index permutation and requires training with all variations of sequences. This requires a substantial amount of computational resources, which is practically infeasible. Additionally, the RNN lacks the ability to distinguish between various input samples, as they overlap, and therefore cannot accurately capture the variation between different samples. The CNN, on the other hand, can capture the difference in neighboring samples despite an overlap. However, it cannot be generalized to the unseen dataset since the CNN cannot inherently handle new data combinations due to its variational inductive biases³². The CNN is also computationally more expensive than the GNN. The GNN overcomes all the above-mentioned drawbacks and predicts the rearrangement events with the highest accuracy. For larger strains, the predictive power of the recurrent and the convolutional neural networks degrades quickly, while the graph neural network model maintains reliable prediction accuracy even further into the fracture process at large strains. Since a graph neural network considers the influence of not just its immediate neighbors but also the influence of the neighbors of neighbors, depending on the number of aggregation layers, we see that the phenomenon of fracture in network glasses is not only governed by nearest neighbor states but is significantly influenced by the mechanical truss effects of the covalent bond paths branching throughout the network glass structure.

Although this paper considers network glasses, the GNN could also be implemented to effectively analyze a wide range of glass structures that contain information about atoms and their respective bonds, in other words, glass structures that can be represented as a graph. Another advantage of GNNs is their ability to incorporate information about loading and boundary conditions directly into the feature vector. This allows the network to receive additional information related to the deformation protocols as part of the input. Such an approach can be beneficial when developing models to predict failures resulting from various deformation protocols.

Future work should focus on refining the concept of the LISTI framework and potentially expanding it by incorporating additional predictor candidates. Firstly, incorporating further topological information into the stress threshold, such as statistics of rings³, centrosymmetry of the local region^16,17, could significantly improve the model’s performance, as an additional support for the neural network architecture to learn the underlying mechanical system. Additionally, local mechanical probing could be enhanced by preventing possible overestimations of the local shear stress threshold that may result from the frozen boundary conditions. Future studies could employ various methods addressing this issue, such as the soft matrix method³³.

Methods

Two-dimensional silica samples

Although the experimental benchmark samples for this paper are bilayer structures²³, the topological network information is purely two-dimensional. Thus, it is sufficient to perform the generation and mechanical testing exclusively in a two-dimensional framework.

Artificial network glass samples

The network glass samples required for this research were produced using the Monte Carlo bond switch algorithm, which is a sequence of topological flip transformations starting from a silica crystalline structure³. This algorithm is a Markov Chain Monte Carlo method where the acceptance of every flip transformation is statistically determined by chosen physical constraints of target ring neighborhood statistics and target network heterogeneities. These physical constraints ensure that the generated samples are, from a topological perspective, statistically equivalent to our first benchmark sample, an experimentally imaged material patch by Lichtenstein et al.²³, who identified and extracted atomic coordinates from their two-dimensional silica images. More details about this comparison are provided in the Supplementary Methods. Switching is performed on two lattices: the physical lattice using a Yukawa-type interatomic potential³⁴ and the dual lattice using a harmonic ring-ring potential²⁹. We generate 50 almost square-shaped samples with the dimension of 215 × 215 Ų, containing 9600 atoms. The switching procedure was also performed over the periodic boundary conditions. The generation of the two-dimensional glass models is discussed in detail in Bamer et al.³. The generation was done using our in-house code developed in Julia³⁵.

We also modeled a second two-dimensional silica glass patch, experimentally imaged by Huang et al.²⁷, which served as an additional test sample for the prediction power of LISTI. In contrast to the benchmark sample above, which was used to generate the silica samples, we did not have atomic coordinates; we only had transmission electron microscopy images. We detected the coordinates of the silicon atoms using a Marr-Hildreth operator³⁶. The SiO₃ triangle network structure was identified by detecting the nearest neighbor list. After that, the sample size was iteratively adjusted until the average distance between all Si-Si bonds was 3.05 Å. Subsequently, the oxygen bonds were placed at the center of all Si-Si bonds. Then, the potential energy of the structure was minimized using the Yukawa potential³⁴, applying free boundary conditions in both the x- and y-direction. We checked the nearest neighbor distances between the Si atoms and ensured that the network topology remained equivalent to the original imaged data. The configuration was finally minimized using the Yukawa-type interatomic potential. We note that no rearrangements occurred during this minimization that would result in topological changes.

Athermal quasistatic deformation

The generated material samples were subjected to pure shear deformation using the athermal quasistatic deformation method. The sequence of loading steps was chosen sufficiently small to ensure that all elementary fracture events are captured in the deformation protocol. Every deformation was realized by altering the bravais vectors of the simulation cell and affinely displacing the atomic positions. After the affine deformation step, the potential energy was minimized using the conjugate gradient algorithm. This way, the system remains at a local minimum in the potential energy landscape throughout the entire deformation process. During deformation, these minima transform into saddle nodes at the occurrence of elementary events, and the system drops down into an adjacent minimum. The system was deformed at a strain rate of 1.0⋅10⁻⁴ for a total number of 400 deformation steps to ensure that fracture had sufficiently progressed in all samples. All elementary events were detected by identifying the drops in the resulting stress-strain curve.

Local probing using the shear stress threshold

The local probing method builds on the local yield stress method originally introduced by Patinet et al.¹⁸, which is performed to predict plastic events in densely packed systems. The entire two-dimensional sample is covered by an n_x × n_y grid. We chose a number of 50 for n_x and n_y, resulting in distances of ~4.3 Å in both directions. Local mechanical testing is performed in circular material cutouts from the entire sample, with the center of every cutout being located in the respective grid point, which results in 2.5⋅10³ local samples per global configuration. Every local scanning region is divided into an inner circular region defined by the radius R_free = 11 Å and an outer ring with a thickness that is equal to the cutoff radius of the Yukawa potential, i.e., 10.0 Å. To find the optimal size for the local probing window, R_free, a rigorous parameter study was performed. More details are provided in the Supplementary Note 1. Mechanical deformation is realized by affinely deforming the entire local structure but exclusively minimizing the material inside R_free. This way, one freezes the atoms outside the circular region and the atoms inside can respond freely. We performed true shear deformation protocols in the local regions. In other words, the material circles are deformed to the shapes of ellipses where the original circle and the deformed ellipsoid states have the same area. Following the literature^18,37, one defines the following parameters after mechanical investigation. The local shear stress measured in the undeformed state at the local grid point ${\left({x}^{* },{y}^{* }\right)}^{T}$ is referred to as the initial local shear stress ${\tau }^{({\mbox{in}})}\left({x}^{* },{y}^{* }\right)$. The shear stress at which the first rearrangement occurs is referred to as the critical stress ${\tau }^{({\mbox{c}})}\left({x}^{* },{y}^{* }\right)$. The local stress threshold is defined as: $\Delta \tau \left({x}^{* },{y}^{* }\right)={\tau }^{({\mbox{c}})}\left({x}^{* },{y}^{* }\right)-{\tau }^{({\mbox{c}})}\left({x}^{* },{y}^{* }\right)$, as shown in Fig. 1b. Notably, the local structure of disordered solids is generally anisotropic. Thus, the stress threshold changes when changing the pure shear directions. Consequently, Patinet et al.¹⁸, and Barbot et al.³⁷ also probed rotated local samples and project the shear stress threshold into the remote loading direction. They defined the minimum of all projections as the local yield stress, which improved the prediction accuracy for densely packed systems. After rigorous testing of the method for network glasses, we did not see any prediction improvements when performing this rotation approach. Consequently, we use the shear stress threshold as the predictor, obtained by local probing into the direction that coincides with the direction of the remote deformation.

Prediction goodness

Given the collection of Local shear stress threshold for every sample, we evaluated the cumulative distribution function (CDF), ${F}_{\Delta \tau }\,\left(\Delta {\tau }^{* }\right)$, to estimate the probability that the shear stress threshold falls below a particular threshold stress, Δτ^*. Next, we observed the location of the n actual rearrangement events and identify the corresponding predicted stress threshold Δτ⁽ⁱ⁾, i = 1, …, n at these positions. The CDF value ${F}_{\Delta \tau }\,\left(\Delta {\tau }^{(i)}\right),i=1,\ldots ,n$ returns the percentage of stress thresholds lower than the assigned threshold stress at the actual rearrangement spot. The prediction goodness is identified by the corresponding modified complementary CDF:

$${{{\mathcal{C}}}}_{\Delta \tau }(n)=1-2\,{F}_{\Delta \tau }\,\left(\Delta {\tau }^{(n)}\right)\ .$$

(1)

The modification here is that we subtract twice the cumulative distribution function instead of just once, which would be the conventional complementary cumulative distribution function. This way, the prediction goodness assessment ranges from −1 to 1, with 1 referring to perfect prediction and −1 to perfect anti-correlation.

Neural network models

The chosen neural network architecture must establish a relationship between the local topology in the reference state and the corresponding stress threshold value. This way, local structural information is passed to the neural network, and the predicted threshold stress is returned. These values are then correlated to spots prone to rearrangement at the onset of fracture, as demonstrated in the Results section. Three neural network architectures were proposed to be included in the LISTI: a Recurrent Long Short-Term Memory (LSTM) Neural Network, a Convolutional Neural Network, and a Graph Neural Network.

Recurrent neural networks

We used long short-term memory (LSTM) network³⁸ in this work, which are a special type of Recurrent neural networks (RNNs)³⁹ capable of learning long-term dependencies. LSTMs have the ability to take time and sequence into account and, therefore, have a temporal dimension. They are advantageous for sequential data and have been widely used for time-dependent and sequential problems^40,41,42. Consequently, LSTMs are suitable for processing the sequence of coordinates at the probing locations that are used in local probing. The critical stresses are predicted from this sequence of coordinates.

In this paper, we used the local probing region from the local shear stress threshold method to generate the input sequence for the RNN architecture. Figure 4a represents one such sample with the enlarged image of the local probing region emphasizing the corner-sharing SiO₃ triangles. The coordinates of the Si atoms define the input sequence. Implementation-wise, the input for every probing region is a two-column matrix, whereas every row refers to an Si atom with its two spatial coordinates x and y. The coordinates of all Si atoms within the probing region are organized based on their bond connections. The sequence numbering of atoms is defined from the initial crystalline lattice before the Monte Carlo bond switching procedure. In particular, it is defined along the armchair direction, which is parallel to the x-axis for our initial samples, and the sequence increases from left to right. Once a row is fully indexed, the next row below is selected, and one repeats indexing from left to right. Atomic indexing for one of the local regions can be seen in the illustration in Fig. 4a.

In one local probing region, the number of Si atoms is about 30–38, so padding was required to make the sequence length uniform. In other words, the input matrix is set to a particular standard size whose number of rows must be chosen as large as the maximum occurring number of atoms in the local probing region. In contrast, the number of columns remains two in a two-dimensional system. Therefore, the input shape for each LSTM layer is (38,2), where 38 is the maximum number of Si atoms in the local probing region and 2 represents the X and Y coordinates of each atom. When the network receives an input smaller than the standard size, the remaining rows are padded with a predefined constant number. This is performed by the padding layer, as shown in Fig. 4a. Since this constant number is irrelevant extra information and does not contribute to the network’s understanding of the relationship between structure and stress drop, it must be masked during training. The model should be informed that this portion of the data is padded and should be ignored. To address this, a masking layer is added to hide this information from all the downstream layers. The padding and masking layer is followed by the LSTM architecture, which consists of a single LSTM layer with 128 neurons denoted by L_LSTM. The time dimension or the sequence length of the LSTM layer for our model corresponds to the sequence of Si atoms as mentioned above. Following this, a dense layer with ten neurons, ${L}_{{D}_{1}}$, and an output layer with one neuron, ${L}_{{D}_{2}}$, predicting the shear stress threshold value are implemented, as shown in Fig. 4a. We used the AdaMax optimizer⁴³ to update the gradient during the training procedure. The learning rate was set to 10⁻³. The finalized network is the result of careful hyperparameter tuning. The mean squared error was used as the loss metric to train the RNN architecture and other architectures proposed in this study.

Convolutional neural networks

Convolutional neural networks⁴⁴ have become a predominant machine-learning approach for visual object recognition. Deep CNN architectures have gained wide acceptance in recent years due to their ability to facilitate more non-linear activations for the same effective size as a wider network, thereby improving their accuracy^45,46. Convolution-based algorithms are gaining momentum to study complex patterns in MD simulations, facilitating accurate predictions of material properties while saving a lot of computational time and cost⁴⁷. Since CNNs exhibit translation invariance, unlike RNNs, the order or orientation of the input data doesn’t corrupt the outcome of prediction as long as the structural information remains the same. They also account for locality aggregation, where pixels closer to each other are related than pixels that are farther apart. This ability of CNN enables it to capture the spatial relationship in the data. Therefore, these features make CNNs desirable for the current study.

Typically, the input for a two-dimensional CNN is a fourth-order M × H × W × C-shaped tensor, where M denotes the number of samples, H denotes the height (or the rows) of the data, W denotes the width (or the columns) of the data, and C denotes the depth of the data which, in the case of images, are the color channels. The CNN usually comprises a series of convolutions, pooling, non-linear activation, and dropout layers, each serving a particular purpose. This way, a convolution layer abstracts the given data into distinct feature maps using a two-dimensional array of weights called the filter or kernel. The filter is smaller in size than the input tensor and performs a scalar product with it several times by probing through the rows and columns on a given stride. The feature map is then nonlinearly transformed using functions such as rectified linear units or leaky rectified linear units. Pooling layers help downsample these stacks of feature maps by selecting the predominant features. This is done either by max pooling, which selects the maximum impacting features, or average pooling, which averages over the features in a given probing window. Usually, a CNN has multiple stacks of convolution and activation layers followed by a pooling layer. Furthermore, dropout layers are added to the network to prevent overfitting⁴⁸.

In this study, the CNN uses image information from the local topology of the structure and associates it with the local shear stress threshold. To save the data for training the CNN, the coordinates of the Si atoms and the oxygen bonds are plotted and saved as an RGB image. The color channels are not relevant for training since they don’t hold any relevant information about the structure. Therefore, the images are converted to grayscale, which clearly captures the structure of the sample and also reduces the size of the input, thereby enabling faster training. The pixel intensities of a grayscale image lie anywhere between 0-255 since the images were saved as 8-bit unsigned integers. These images are then normalized using min-max normalization to the range (0,1) in floats. Thus, the input for every pixel into the CNN is a real number between 0 and 1. The input is then passed through a series of 2D convolution layers and 2D max-pooling layers. The convolution layers each had a filter of size 5 × 5 with 32, 64, and 32 filters, respectively, with a stride of 1. The max-pooling is performed with a pool size of 2 × 2. The convoluted and pooled layers are then flattened, followed by three dense layers with 10 neurons each, rectified linear activation units, and a final dense layer with 1 neuron and linear activation. The architecture of the proposed CNN is shown in Fig. 5a.

However, CNNs have a particular limitation regarding generalization over other networks, as they can only work within the range of data they were trained on and cannot handle new data combinations. Additionally, they are restricted to structured rectangular domains and cannot effectively model complex structures on unstructured domains. This is where graph neural networks (GNNs) come into play. GNNs operate on graphs and are designed based on relational inductive bias. Unlike CNNs, GNNs are not limited by structural constraints and can effectively model complex and unstructured domains based on the relationships between entities.

Graph neural networks

Graph neural networks⁴⁹ perform computations over a graph based on the idea that connective entities exist that exhibit certain relations. In other words, GNNs process data that can be represented as a graph. For instance, the atoms and bonds of an atomic structure and their relationship can be modeled as the nodes and edges of the graph^20,50. Especially, network glasses, such as silica glass, have been strongly connected with graph data and classified in terms of graph topologies to identify structures of rings in the material³¹. This emphasizes implementing graph information into an artificial intelligence framework. Each node can influence other nodes further away through multiple convolution operations on a graph. Therefore, the use of graph neural networks in molecular mechanics is a promising direction, and graph convolutional architectures have already been applied to predict molecular^51,52,53 and material^54,55 properties. Graphs can be classified in several ways: they can be directed or undirected, homogeneous or heterogeneous, and static or dynamic. This study uses an undirected, homogeneous, and static graph architecture with padding for unequal input lengths. The influence of the padded nodes was eliminated by the adjacency matrix, as the dummy padded nodes have no connection or influence on the neighboring nodes.

The GNN receives both node features and an adjacency matrix connecting features. The nodes of the graph are the centers of the SiO₃ triangles and were given features h in terms of their spatial coordinates, similar to RNN. The relationship between neighboring nodes was established using the adjacency matrix, as shown in Fig. 6a. The adjacency matrix is computed using the bond information saved during the lattice generation, which gives a value of one if the bond is present and zero if the bond is missing between the given pair of atoms. In Fig. 6a, one local region is presented exemplarily, illustrating how the arrangement of atoms within that area is defined. A small section of the figure is highlighted with an orange circle to provide an example of the adjacency matrix. This matrix depicts all the connections associated with atom number two. From the given matrix, we can see that atom two connects to atom one, three, and six, which is denoted by a value of one, and the atoms without any bond to atom two are assigned a value of zero in the matrix. The influence of its neighbors was considered to determine the future state of the nodal feature h. An aggregation function, which was a graph convolution layer, was used for this purpose in our study. A multi-layer perception was also used as a message-passing function. The aggregation of the node features h, the subsequent message passing, and the update of the node features are written as follows:

$$G=({{{\boldsymbol{h}}}}_{i},{{{\boldsymbol{e}}}}_{ij})\ ,$$

(2a)

$${\alpha }_{ij}={{{\rm{softmax}}}}_{j}\left(\frac{{({W}_{\alpha }^{k}{h}_{i}^{k})}^{T}({W}_{\beta }^{k}{h}_{j}^{k})}{\sqrt{d}}\right)\ ,$$

(2b)

$${h}_{i}^{k+1}={U}^{k}({h}_{i}^{k},{\alpha }_{ij}^{k}({h}_{j}^{k}))\ ,$$

(2c)

$${h}_{i}^{k+1}={M\,L\,P}_{\theta }^{k}\,\left\{{h}_{i}^{k},{\alpha }_{ij}^{k}({h}_{j}^{k})\right\}\ ,$$

(2d)

where h_i is the node feature of the node being updated, h_j is the node feature of the neighboring node, e_ij is the edge tensor, U is the message-passing or the state update function, α is the aggregation function and W_α,β are trainable linear weights.

Firstly, the inputs are fed to two graph convolution network (GCN) blocks, shown in Fig. 6a. The first GCN block consists of two graph convolution layers followed by a dense layer with a rectified linear unit activation function. The second GCN block contains a graph convolution layer and a dense layer similar to the first block. In both blocks, the graph convolution layers are responsible for aggregating the influence of neighboring nodes. The aggregated information was revised by an update function, which can be a mean, a sum, or a neural network-based operation to transform the aggregated information at the nodes. In this case, the update function was dense layers in the GCN block. The aggregated and updated graph is then transformed into a latent vector, which is a low-dimensional representation of a higher-dimensional graph data, by means of a global average pooling operation. The low-dimensional information in the latent vector was then passed on to a feedforward network with three hidden layers consisting of 20, 10, and 5 neurons, respectively. Finally, the output layer had one neuron, which corresponds to the local shear stress threshold. Equivalently to the other two architectures, the AdaMax optimizer⁴³ was used to update the gradients, and the mean squared error was used as the loss metric during the training procedure. The network was trained for 1000 epochs. To ensure optimal performance, the hyperparameters, such as the number of graph convolution layers, the number of units in the latent vector, and the number of layers and neurons in each layer in the feedforward network, had to be carefully chosen.