Introduction

Electricity distribution networks are an important component of critical national infrastructure. The failure of assets in these networks leads to power outages that can cascade through other infrastructure networks and compromise the availability and function of essential services1. Such power outages in the UK are mainly caused by extreme weather events2. As we transition globally to a net zero economy, the demand placed on electricity networks will increase (from electric vehicles, domestic heating, and air conditioning), requiring infrastructure upgrades to increase power supply capacity3. At the same time, climate models project increases in the intensity and frequency of extreme windstorms, which may cause more impacts on electrical infrastructure4,5,6. Maintaining weather-resilience whilst upgrading power systems is crucial: this requires an in-depth understanding of the causes of asset failure during extreme weather to inform the design of climate risk assessments and the stress testing of climate adaptation measures to aid decision-making around investment priorities.

Windstorms are the leading cause of power outages in the UK. They primarily cause power outages through windthrow – the uprooting and breakage of trees and branches in strong winds that subsequently impact overhead lines7,8,9,10. Windthrow is influenced by factors such as antecedent rainfall (or soil moisture), wind direction, and seasonal factors, primarily leaf cover. These variables can modulate the impact of strong winds, as trees uproot more easily in saturated soils9,11, they are more susceptible to falling in strong winds from unusual directions as root systems tend to anchor a tree against the prevailing direction by positioning their centre of mass on the leeward side12, while trees catch the wind more when in leaf leading to a higher vulnerability to strong winds in summer than in winter13,14.

The influence of soil moisture and vegetation on power outages has been well documented by regional studies in the USA. For example, power outage predictions based on machine learning algorithms are shown to improve when including soil moisture and soil characteristics as predictors9,15,16. Similar improvements are obtained by including a measure of leaf cover (LAI – Leaf Area Index) and vegetation characteristics as predictors16,17, while the inclusion of vegetation management practices such as tree trimming also improves predictions9,16,18,19. Less attention has been given to wind direction, although Kabir et al20. found it to be an important predictor for 11 thunderstorms in Alabama, finding that predicted outages were lowest for southerly winds, and gradually increased as wind direction became more northerly.

Predictive skill has also been demonstrated for rainfall during strong wind events18,20,21. Wet conditions may increase the conductivity of tree branches and leaves, increasing the likelihood of circuit trips and overhead line faults. However, it is also possible that its predictive skill may stem from correlations with seasonal factors such as leaf cover (e.g., warmer, wetter storms in summer) and its relationship with wind speeds due to common drivers22,23. Its contribution to power outages, therefore, remains unclear, so we aim to determine if its contribution is causal or merely associated with other important factors. Although proving causation is difficult, building confidence in the cause-effect relationship of predictors is important to justify their inclusion in impact models, particularly if stress testing infrastructure is under changing climate conditions. Since rainfall is projected to increase in warmer climates, incorporating it without a demonstrated causal effect may yield misleading impact projections.

Many studies also suggest the need for several tens of additional meteorological predictors based on data-driven approaches15,24,25,26. This results in large predictor sets that appear to contain high collinearity through correlated variables or multiple variants of the same hazard (e.g., mean and maximum values, exceedances above thresholds). Some studies address this issue using principal component analysis to reduce dimensionality11,17. However, disentangling individual contributions becomes challenging with large numbers of predictors, we therefore prefer a simpler approach that prioritises key predictors. The influence of variables is often quantified in these studies using variable importance metrics and, in some cases, using partial dependence analysis to assess the individual influence of a variable on model predictions. However, the former gives no information on the direction or nature of influence, while the latter does not quantify how a variable compounds the impact of strong winds, which is important for understanding their relative influence.

This study provides an in-depth analysis and quantification of the influence of antecedent rainfall, wind direction, seasonal factors, and accumulated rainfall during storms, which goes beyond current literature to demonstrate their compounding effects on wind-driven power outages and provide causal reasoning for the inclusion or exclusion of predictors. This knowledge is crucial, as the contribution of these factors may become more important in a future warmer climate. We are already experiencing longer growing seasons27, while we expect wetter winters28 and possible changes to storm track orientation and, therefore, wind direction in future windstorms22.

This is the first such study in the UK (and more generally outside the USA), to the best of our knowledge. Current methods developed for the UK rely solely on wind speed to predict power outages29,30 and societal consequences31. Furthermore, such approaches have been used in various regions to assess the projected impacts of climate change on electricity infrastructure32,33 and to examine options for strengthening the resilience of infrastructure30,34. It is therefore necessary to better communicate the role and compound effects of these additional variables for infrastructure impacts as relying solely on wind speed can produce inaccurate forecasts9,29 and, therefore, misleading guidance for emergency response and adaptations that could leave infrastructure maladapted.

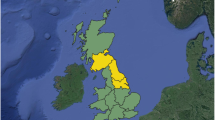
We first demonstrate the influence of each additional variable for wind-driven power outages due to faults in electricity distribution networks. We then use relevant variables to develop better models that illustrate the potential for improved forecasts and climate risk assessments of power outages in UK. We demonstrate our model using data for four UK regions (Fig. 1) managed by a single Distribution Network Operator (DNO). Electricity fault data is provided by the National Fault Interruption Reporting Scheme (NaFIRS) dataset over the period 2006–2018. This records power outages, the affected assets, and the reason for the outage (e.g., wind). Whilst demonstrated here for regions in the UK, this approach can be used more generally in other regions.

Fig. 1: Map of UK regions used in this study.
figure 1

First, we demonstrate the influence of antecedent rainfall, wind direction and season in two larger regions: Midlands (blue—data from Midlands 1 and Midlands 2 is spatially aggregated), Southwest (red—data from Southwest 1 and Southwest 2 is spatially aggregated). Second, we demonstrate improved predictive skill for four smaller regions separately (i.e., Midlands 1, Midlands 2, Southwest 1 and Southwest 2).

Full size image

Results

Drivers of wind-driven power outages

We demonstrate the influence of various drivers of wind-driven power outages for the two larger regions shown in Fig. 1, the Southwest and the Midlands. We follow an event-based approach in which events are defined as the period a cyclone (identified using a tracking algorithm) is within 1000 km of a region. Additional criteria are used to avoid double counting (see “Methods”). For each event, we extract several metrics, including an impact variable—the number of electricity faults (\({F}^{N}\)) within a region, and meteorological characteristics, including the maximum wind gust (\({v}^{X}\)), accumulated rainfall in the 30 days preceding the event (\({R}^{30}\)), the wind direction at the time \({v}^{X}\) occurs and the season the event occurs in. Metrics are estimated using all grid cells within the specified region. We quantify the influence of the meteorological characteristics using conditional probabilities of \({F}^{N}\) exceeding its 95th percentile under various conditions and hazard intensities. Details are provided in the Method section. Furthermore, we also study the influence of accumulated rainfall during a windstorm event (\({R}^{E}\)) as an example of a variable whose predictive skill is potentially a result of confounding factors: these results and their discussion are provided in the Supplementary Discussion.

Influence of maximum wind gust (\({v}^{X}\))

We first examine the relationship between maximum wind gust (\({v}^{X}\)) and the number of electricity faults (\({F}^{N}\)) in a windstorm (Fig. 2). Figure 2 illustrates the positive relationship between the two variables, with stronger \({v}^{X}\) leading to higher \({F}^{N}\). The probability of \({F}^{N}\) exceeding the 95th percentile (\({F}_{95}^{N}\)—dashed blue line in Fig. 2a, b), increases with increasing \({v}^{X}\) in both regions. For example, in the Southwest (Fig. 2c), the probability increases from 0.38 to 0.65 when \({v}^{X}\) exceeds 25 and 30 ms−1, respectively (red line). A similar increase is also seen in the Midlands (Fig. 2d). However, there is considerable dispersion in this relationship. For example, the total number of faults associated with a windstorm with \({v}^{X}\) between 30 and 35 ms−1 varies between 0-850 and 0-700 in the Southwest and Midlands, respectively (Fig.  2a, b). Various factors may contribute to this dispersion; here, we study the contributions of antecedent rainfall, wind direction, and seasonality.

Fig. 2: Influence of maximum wind gust (vX) and antecedent rainfall (R30).
figure 2

Influence of \({v}^{X}\) and \({R}^{30}\) on fault numbers (\({F}^{N}\)) in the Southwest (a, c), and Midlands (b, d). Top row (a, b): scatter plots of \({v}^{X}\) and \({F}^{N}\), the horizontal blue dashed line marks the 95th percentile of \({F}^{N}\). Bottom row (c, d): probabilities of \({F}^{N} > {F}_{95}^{N}\) when conditioned on \({v}^{X}\) alone (black line) and when \({R}^{30}\) simultaneously exceeds its 95th percentile (blue line). Dashed red lines and shaded red areas show the median estimate and 95% confidence interval for the latter probability obtained by shuffling \({R}^{30}\) in annual blocks (see methods). Blue dots indicate statistically significant contributions of \({R}^{30}\). Yellow lines show the likelihood of \({v}^{X}\) exceeding various thresholds while \({R}^{30}\) exceeds its 95th percentile.

Full size image

Influence of antecedent rainfall (\({R}^{30}\))

The probability of a high number of faults (\({F}^{N} > {F}_{95}^{N}\)) is increased when a windstorm occurs after high antecedent rainfall in the preceding 30 days (\({R}^{30}\)). In the Southwest (Fig. 2c), the probability of \({F}^{N} > {F}_{95}^{N}\) increases from 0.38 (black line) when only wind speed is considered, i.e., \({v}^{X}\) exceeds 25 ms−1, to around 0.55 when the same \({v}^{X}\) exceedance follows a period of high antecedent rainfall (\({R}^{30}\) exceeding its 95th percentile, solid blue line). The increase is even greater in the Midlands (from 0.4 to 1.0, Fig. 2d), while at wind speeds of 30 ms−1, both regions see increases of ~0.6 to 1.0. We tested the sensitivity of our results to the thresholds used and note that similar increases are found for more extreme power outages (\({F}^{N}\) > \({F}_{98}^{N}\)) and for varying \({R}^{30}\) thresholds (85th and 90th percentiles). As illustrated in Supplementary Fig. S4, the increase in fault probability is greater for more impactful storms (\({F}^{N}\) > \({F}_{98}^{N}\)), while a positive relationship is seen with \({R}^{30},\) where fault probabilities increase with increasing \({R}^{30}\) percentile.

Correlations do not automatically imply causation. For instance, the increased probability of power outages due to high \({R}^{30}\) could arise from confounding factors such as wind-rain correlations due to their shared drivers22 and seasonality35. These correlations are illustrated by the yellow lines in Fig. 2c, d, which show a probability from 0.2 to 0.4 of \({v}^{X}\) exceeding a specified threshold when \({R}^{30}\) has simultaneously exceeded its 95th percentile. The correlation is higher in the Southwest, possibly due to seasonal differences in monthly rainfall between the regions. In the Southwest, mean monthly rainfall accumulations and the likelihood of \({v}^{x}\) > 25 m s−1 are both highest in winter months and lowest in summer (see Supplementary Fig. S5a, c). The same can be said for \({v}^{x}\) in the Midlands, but there are no pronounced seasonal differences in monthly rainfall there.

To try to rule out seasonality as a possible confounder, we test if the increased probability of power outages due to \({R}^{30}\) can be achieved by chance using bootstrapping in which we shuffle rainfall in annual blocks breaking its association with \({v}^{X}\) and \({F}^{N}\) but conserving its seasonality and temporal correlation. This is repeated 1000 times to calculate 1000 probabilities from which we obtain a median estimate and a 95% uncertainty interval that indicates the sensitivity of the conditional probability to the random shuffling (see methods). Breaking the association between \({R}^{30}\) and other variables removes the increased probability from the median estimate (dashed red line), and we see little difference compared to probabilities when only \({v}^{X}\) is considered (black line). Hence, ignoring the influence of antecedent rainfall can underestimate the risk of power outages. The strength of this conclusion is limited by the large uncertainty interval (red-shaded region). For instance, significant differences (blue dots) are found for only a few \({v}^{X}\) thresholds in the Midlands (i.e., where the blue line lies outside the uncertainty interval), indicating that the increased probabilities can be achieved by chance for most \({v}^{X}\) thresholds. The large uncertainties may be an effect of the aforementioned confounding factors, particularly in the Southwest. It may also be an effect of a small sample size. For example, applying the bootstrapping procedure to this 13-year dataset means there is a 1-in-13 chance of a year with multiple windstorms and power outages randomly coinciding with a wet year. Hence, the sample size potentially limits the possibility of obtaining a significant result in this test, and we are more likely to see \({R}^{30}\) influence being reproduced by chance than in a 30-year power outage dataset, particularly in the Southwest where \({v}^{x}\)-\({R}^{30}\) correlations are higher.

Influence of wind direction

The number of faults in a storm (\({F}^{N}\)) can be higher if the direction of \({v}^{X}\) deviates from the prevailing wind direction. The influence of wind direction in the Midlands region is seen by comparing a wind rose for all events where \({v}^{X}\) > 14 ms−1 (Fig. 3b) to a wind rose for only impactful events where \({F}^{N}\) > \({F}_{95}^{N}\) (Fig. 3d). For all events, winds predominantly vary between westerly and southerly directions around the prevailing south-westerly direction (black dot). Conversely, events where \({F}^{N}\) exceeds \({F}_{95}^{N}\) exhibit a bimodal distribution for wind direction, with impactful events more frequently associated with a direction more westerly or southerly of the prevailing direction. Furthermore, we also see a disproportionate number of impactful windstorm events from the northeast, the opposite of the prevailing direction.

Fig. 3: Influence of wind direction.
figure 3

Wind direction influence on power outages in the Southwest (a, c, e), and Midlands (b, d, f). Top row (a, b) displays wind roses for maximum wind gusts (\({v}^{X}\)) during windstorms that exceed 14 ms−1. The middle row (c, d) shows wind roses for windstorms with high fault numbers (\({F}^{N} > {F}_{95}^{N}\)). Wind rose colours represent \({v}^{X}\), as detailed by the key in panel (a), while the black dots mark the prevailing wind direction. The bottom row (e, f) shows the conditional probability of impactful events (\({F}^{N} > {F}_{95}^{N}\)) given various exceedances of \({{dir}}^{X}\) (deviation from prevailing direction) for \({v}^{X} > 20\) ms−1 (black) and \({v}^{X} > 25\) ms−1 (blue). Dashed lines represent this probability when \({{dir}}^{X}\) is assumed independent of \({v}^{X}\) and \({F}^{N}\); shaded areas show the 95% confidence interval obtained by shuffling \({{dir}}^{X}\) in annual blocks. Dots on solid lines indicate significant probabilities that cannot be achieved by chance.

Full size image

These findings are reflected in the probability of \({F}^{N} > {F}_{95}^{N}\) with varying \({v}^{X}\) and \({{dir}}^{X}\) (the deviation of wind direction from the prevailing direction, see Methods). In the Midlands (Fig. 3f), for \({v}^{X}\) > 25 ms−1, this probability increases from 0.4 to 0.65 as \({{dir}}^{X}\) increases from 0o to 90o (blue solid line). Similar increases occur for \({v}^{X}\) > 20 ms−1 but at larger direction deviations (e.g., \({{dir}}^{X}\) > 130o). Ignoring the influence of \({{dir}}^{X}\) on \({F}^{N}\) in strong winds leads to an underestimation of the estimated risk. Specifically, assuming \({{dir}}^{X}\) is independent of \({F}^{N}\) and \({v}^{X}\) removes this increased probability (blue and black dashed line) and a comparison with the 95% confidence interval confirms the effect of \({{dir}}^{X}\) is not due to random chance. Thus, unusual wind directions are likely a causal factor for power outages in the Midlands region.

We also note that the prevailing wind direction varies seasonally, shifting westerly in summer and south-westerly in winter (Supplementary Fig. S5d), and therefore may correlate with seasonal factors such as leaf cover. However, separate analyses of wind direction in winter and summer show that its relationship with \({F}^{N}\) remains consistent across seasons (Supplementary Fig. S6).

The influence of wind direction on power outages in the Southwest is much weaker. We find no influence when conditioning on events with \({v}^{X}\) > 20 ms−1, although there is an increased probability for \({v}^{X}\) > 25 ms−1 when \({{dir}}^{X}\) > 160o (see Fig. 3e). We find similar results for more impactful events where \({F}^{N} > {F}_{98}^{N}\), but we note that these results are sensitive to regional definitions. To demonstrate this, Supplementary Fig. S7 presents the influence of wind direction for events where \({F}^{N} > {F}_{98}^{N}\) for the four subregions outlined in Fig. 1. The bimodal feature described above, as well as increased probabilities for unusual wind directions, are much stronger in 3 of the 4 regions. This suggests that the higher precision gained with smaller regions may be important for assessing the influence of wind direction.

Influence of seasonal factors (leaf cover)

The influence of season is presented in Fig. 4. We find a seasonal variation in the vulnerability of infrastructure to strong winds that is the inverse of the frequency of such winds. In both regions (Fig. 4a, b), the 3-month rolling probability (see methods) of \({F}^{N}\) > \({F}_{95}^{N}\) given \({v}^{X}\) > 20 ms−1 (solid line) peaks in summer, while its minimum occurs in winter (note the probabilities shown are relative to the maximum value). In contrast, the seasonal cycle of strong wind speeds (probability of \({v}^{X}\) > 20 ms−1 - dashed line) peaks in winter and has its minimum in summer. This contrast is likely due to the seasonality of leaf cover on trees which peaks in summer, making tree limbs heavier and the wind profile of the tree greater. As a result, trees become more susceptible to windthrow, leaving electricity infrastructure more vulnerable to faults, during strong winds in summer.

Fig. 4: Influence of seasonal factors.
figure 4

Influence of seasonal factors on power outages in the Southwest (a, c, e) and Midlands (b, d, f). Top row (a, b) provides the monthly frequency of high-impact events (\({F}^{N} > {F}_{95}^{N}\), left y-axis) and 3-month rolling probabilities (right y-axis): solid lines indicate the probability of high wind events (\({v}^{x}\) > 25 ms−1); dashed line represents the conditional probability of high-impact events given \({v}^{x}\) over 25 m/s. Probabilities are scaled to their maximum value. Middle row (c, d) provides boxplots of \({F}^{N}\) for \({F}^{N}\) > \({F}_{95}^{N}\) in each season, and the bottom row (e, f) provides conditional probabilities of \({F}^{N} > {F}_{95}^{N}\) given \({v}^{X}\) exceeds specified thresholds in each season. The black line shows annual probabilities (shaded area: 95% confidence interval) assuming no seasonal variation. Points on lines indicate significant seasonal differences from annual probabilities.

Full size image

We also find a bimodal pattern in the seasonal distribution of storm frequency where \({F}^{N}\) > \({F}_{95}^{N}\) (Fig. 4a, b). The frequency of these events gradually increases from the end of summer, peaking in winter months, after which their frequency decreases before a second peak in summer. This is likely a consequence of stronger winds in winter and more leaf cover in summer. However, we note that overall \({F}^{N}\) is much higher in winter months than in summer, as demonstrated by boxplots of \({F}^{N}\) in each season (Fig. 4c, d), such that the stronger and more frequent winter storms have a greater overall contribution to power outages.

Since storms are more impactful in summer when trees are in leaf, ignoring this seasonal influence leads to an underestimation of \({F}^{N}\) exceeding \({F}_{95}^{N}\) in summer. For example, in the Southwest region (Fig. 4e), the probability of \({F}^{N} > {F}_{95}^{N}\) given \({v}^{X}\) > 20 ms−1 in summer is 0.35, more than 50% higher than when estimating the same probability from annual data (black line). This difference from the annual probability more than doubles when \({v}^{X}\) exceeds 22 ms−1 (from 0.25 to 0.62), and a significant difference to the annual probability is found for \({v}^{X}\) thresholds between 18 and 23 ms−1. Note that the empirical probability is not shown if there are fewer than 8 events with \({v}^{X}\) above the specified threshold. Similar results are seen in the Midlands region (Fig. 4f): here, the highest probabilities occur in summer, followed by autumn, spring, and winter in line with the seasonal cycle of vegetation. However, a significant difference in the annual probability is only found for summer. We note that the probability of \({F}^{N} > {F}_{95}^{N}\) can be higher in the shoulder months of summer (May, September), thus an optimal method would directly estimate leaf cover prior to a storm using satellite data, for example ref. 24.

Improved prediction of windstorms causing power outages

We now use logistic regression in a leave 1-year out k-fold cross-validation framework to assess if the predictive skill of where \({F}^{N}\) exceeds \({F}_{95}^{N}\) within windstorms can be improved by adding the variables \({R}^{30}\), \({{dir}}^{X}\), and seasonality to a reference model that only considers \({v}^{X}\). We assess these models for the four subregions shown in Fig. 1—Midlands 1, Midlands 2, Southwest 1, and Southwest 2—to provide a more localised estimate of improved predictability and influence for each variable. We find that including the three variables \({{R}}^{30}\), \({{dir}}^{X}\), and seasonality alongside \({v}^{X}\) improves predictive performance in all four subregions. This is demonstrated in Fig. 5, which presents the ROC (receiver operating characteristic) curves and accompanying higher AUC (area under curve) values for the reference model and the model with additional variables.

Fig. 5: Model evaluation.
figure 5

ROC curves for the reference model (black line) and the model that incorporates all four variables (red line) in the four subregions: a Southwest 1; b Midlands 1; c Southwest 2; d Midlands 2. Area under the curve (AUC) values are provided within each panel for both models.

Full size image

The ROC curves illustrate each model’s performance as a binary classifier across various probability thresholds used to assign a predicted probability of a large power outage or not. They show that the model with additional variables (red line) achieves better Hit Rates and False Alarm Rates than the reference model (black line), resulting in better AUC values that provide an integral of model performance across all probability thresholds. The model improvement is further demonstrated using the akaike information criterion (AIC) in Supplementary Table S1, which shows lower, and therefore better, AIC values for the model with the additional variables. Individual contributions to the improvement are highlighted in Supplementary Table S2, which provides the AUC for models when adding one variable at a time alongside \({v}^{x}\). The largest improvements are generally obtained by including the season in all regions. Smaller improvements are obtained by including \({R}^{30}\) and \({{dir}}^{X}\), although the improvements are found in 2 and 3 of the regions for \({R}^{30}\) and \({{dir}}^{X}\), respectively.

Furthermore, we estimate the contribution of each variable to the prediction of \({F}^{N}\) > \({F}_{95}^{N}\) by assessing the influence of each variable in turn alongside \({v}^{X}\) using the model with additional variables. For simplicity, Fig. 6 presents the predicted probabilities of \({F}^{N}\) > \({F}_{95}^{N}\) for 5 separate cases in which \({v}^{X}\) varies from 20 to 40 ms−1: (1) a baseline winter case (black line) where \({R}^{30}\) is its median value and \({{dir}}^{X}\) = 0o (i.e., prevailing direction). We then vary one variable at a time: (2) season = summer (green line); (3) \({R}^{30}\) = 95th percentile (blue line); (4) \({{dir}}^{X}\) = 95th percentile (grey line). We measure a variable’s influence by the difference in probability relative to the baseline winter case as well as the statistical significance (p-value < 0.05) of model coefficients. Coefficients are generally significant, except for \({R}^{30}\) in two of the four regions and \({{dir}}^{X}\) in one.

Fig. 6: Variable contributions to predictive skill.
figure 6

Predicted probabilities of \({F}^{N}\) > \({F}_{95}^{N}\), using the logistic regression model that includes \({v}^{x}\), \({R}^{30}\), \({{dir}}^{x}\), and Season as predictors in the four subregions: a Southwest 1; b Midlands 1; c Southwest 2; d Midlands 2. Probabilities are given for specified values of \({v}^{X}\) (x-axis) under five sets of conditions: (1) a baseline case (black line): Season = Winter, \({R}^{30}\) = median, \({{dir}}^{X}\) = 0o); three further cases where one variable is changed: (2) Season = Summer (green line); (3) \({R}^{30}\) = 95th percentile (blue line); (4) \({{dir}}^{X}\) = 95th percentile (\(\sim\)120o, grey line); and (5) a worst-case scenario (red line) with all above extreme conditions (2, 3, 4) combined. Solid lines indicate statistically significant coefficients (p < 0.05), and dashed lines indicate the opposite. Note: predicted probabilities are not comparable to the empirical exceedance probabilities in previous figures.

Full size image

Our analysis demonstrates that Season has the strongest influence on predicted probabilities in all four regions, followed by \({{dir}}^{X}\) and \({R}^{30}\) (see Fig. 6). For example, under baseline winter conditions with \({v}^{X}\) = 30 ms−1 (black line), the predicted probability (0.2) is three to four times higher in summer (0.6–0.8, green line). In comparison, where coefficients are statistically significant (solid lines), \({R}^{30}\) or \({{dir}}^{X}\) at their 95th percentiles, respectively, increase probabilities 0.5 to 2-fold (blue line) and 2 to 3-fold (grey line) relative to the baseline winter conditions. These contributions align with empirical results; Season’s influence is robust across all regions, while \({{dir}}^{X}\) and \({R}^{30}\) show regional variation, potentially due to regional definitions. Finally, in a worst-case scenario where all above conditions combine (Season = summer, \({R}^{30}\) and \({{dir}}^{X}\) at the 95th percentile) alongside \({v}^{X}\) = 30 ms−1, the predicted probability exceeds 0.9, 4- to 5-times higher than baseline winter conditions (0.2). Notably, the cumulative effect is greater at lower wind speeds (e.g., \({v}^{X}\) = 25 ms−1), warranting further study of the probability and possibility of such a scenario.

Discussion and conclusions

Windstorms are the primary cause of power outages in the UK, largely through windthrow, where trees are uprooted or broken by winds and fall on assets, primarily overhead lines. Previous risk assessments in the UK of network faults during windstorms have relied solely on wind speed, which are shown here and in previous U.S. studies to be insufficient on their own to capture the variance in fault numbers during windstorms (\({F}^{N}\)). Studies have highlighted the predictive skill added by including soil moisture and seasonal factors as predictors, but detailed causal reasoning and quantitative assessment of predictors’ combined effects and interdependencies are lacking. This is critical to avoid flawed guidance for emergency response and costly adaptation measures that may arise from misinferred variable influence. Using a 13-year electricity fault database, we have quantified how antecedent rainfall, wind direction, and season amplify wind-driven power outages in four UK regions. By incorporating these predictors into a logistic regression model alongside wind speed, we have shown that the predictive skill of \({F}^{N}\) is improved compared to a wind speed-only model.

Of the three variables, we find that season provides the largest improvement in the predictive skill of fault numbers (\({F}^{N}\)) across all four regions assessed, while wind direction and antecedent rainfall improve skill in three and two of the four regions, respectively. Importantly, ignoring seasonality, wind direction, and antecedent rainfall contributions can lead to underestimations of fault numbers during impactful storms. For instance, given a maximum wind speed of 30 ms−1, the probability of \({F}^{N}\) > \({F}_{95}^{N}\) is 3–4 times higher in summer than winter, 2–3 times higher with a 120° deviation (95th percentile) from the prevailing wind direction, and 0.5–2 times higher if strong winds follow an extremely wet period (95th percentile). When all conditions align, the probability increases 4-5-fold, and even more at lower wind speeds (e.g., 25 m s−1). We recommend that further work is needed to assess the likelihood of such scenarios.

Our results have limitations, including large uncertainties from the relatively small sample size, which weaken conclusions on the influence of \({R}^{30}\) in particular. The contribution from antecedent rainfall is also complicated by its positive correlation with the wind due to their shared drivers, making it challenging to separate the effects of wet soil conditions from wind-driven impacts on windthrow. In a similar respect, the influence of wind direction may include the effects of other hazards that accompany northerly (e.g., ice accretion) or southerly winds (e.g., thunderstorms) that we have not investigated. However, the role of antecedent rainfall is supported by U.S. studies that highlight its importance in predicting outages9,15,16,20. These results are reinforced by evidence that suggests wet soils reduce soil stability13,36, increasing windthrow risk37, unlike frozen soils, which potentially enhance stability38. Additionally, the role of wind direction is supported by evidence that tree root systems position their centre of mass on the leeward side to counter prevailing winds12. While this provides more stability under typical conditions, it may leave trees more vulnerable to winds from unusual directions.

Contributions from wind direction and antecedent rainfall are also regionally dependent, and our analysis does not include all relevant factors that could explain this. For example, regional differences in vulnerability may arise from different tree trimming practices9,18,19, while static variables such as tree species and soil characteristics are important predictors for windthrow39,40,41,42 and power outage predictions15,16 more generally. Differences may also arise due to the regional aggregations used here. Large regions that combine areas with opposing characteristics may obscure contributions seen on a local scale. Future work should explore local effects in the UK to identify vulnerable areas following similar efforts in the U.S.; such work would benefit-risk assessments and impact forecasts in the UK and more widely.

Although this analysis has accounted for the main meteorological factors behind wind-driven power outages, previous analyses suggest that further improvements may be achieved by including the duration of strong winds9,15 and precise vegetation data like the leaf area index17,25. Previous studies have also used rainfall accumulation during storms to predict outages18,20,21. We assessed the influence of the latter (presented in Supplementary Information), finding a positive relationship with outages and predictive power in the UK regions analysed. However, the causal effect of rainfall during storms is unclear. It also strongly correlates with other predictors (wind, antecedent rainfall, and season), suggesting its quantified effect may arise through inter-variable correlations. These results emphasise the need for caution and in-depth causal analysis when selecting predictors; the inclusion of predictors such as accumulated rainfall due to flawed reasoning could lead to misleading forecasts and risk assessments under future climate conditions. This may be relevant for previous studies that have used data-driven approaches that incorporate several tens of predictors15,20,21,25, often with strong inter-variable correlations (e.g., temperature and rainfall with seasonal factors), which may be unrelated to infrastructure impacts during windstorms.

In conclusion, we argue that the modulation of wind-driven risk of power outages by variables such as soil moisture, wind direction, and seasonal factors requires more attention. Although there are many examples of power outage forecast models in the U.S. that consider multiple hazards, there are no published examples of this elsewhere, and future climate risk assessments of electricity distribution networks, and windstorms, more generally, do not go beyond wind intensities to account for additional variables whose contribution may become more important in a warmer climate. Our results highlight the need to move past this univariate approach to multi-hazard risk assessments for electricity distribution networks and potentially other types of infrastructure impacted by wind, such as rail43,44 and assets underlying insured losses45,46,47,48. This will create more robust impact forecasts to inform emergency response strategies and more informed climate risk assessments for adaptation planning and the prioritisation of investments. The consequence of not doing so may misrepresent risk and lead to maladaptation of infrastructure. This is particularly important for electricity distribution networks that will undergo a huge transformation as we reduce our dependence on greenhouse gases in the future.

Methods

Electricity fault database and regions

UK distribution network operators (DNO) are required by the government regulator to collect data on faults to assets in their network that lead to a power outage. These faults are recorded in a database known as the National Fault and Interruption Scheme (NaFIRs) database. Here we explore data provided by a single DNO that manages networks in four regions: Southwest 1, Southwest 2, Midlands 1, and Midlands 2 (Fig. 1). This database provides information on faults within their distribution network, including date and time of fault, location of fault, cause of fault and the asset that failed. There are various causes of faults included in the database, including wind-related faults as well as faults due to flooding, lightning, and cold weather, which are all attributed to a specific cause by an engineer who responds to a fault. In this analysis, we consider the number of wind-related faults aggregated to a daily timescale during the period 2006–2018. Data is spatially aggregated to the four regions in Fig. 1 as well as to two larger regions that each comprise two of the smaller underlying subregions, e.g., Southwest 1 and Southwest 2 are aggregated to the larger Southwest region, and similarly so for the Midlands region. Specifically, we work with a daily time series of the number of wind-related faults in each region.

Meteorological data

All meteorological data is obtained from the ERA5 reanalysis dataset49 for the period 2006–2018. We extract time series of wind gusts, wind direction, and rainfall for all four subregions and the two combined larger regions. Specifically, at each hourly timestep, we calculate the maximum wind gust, mean rainfall, and mean u and v wind components from all grid cells falling within the boundary of the regions. We note that we have also assessed results using high-resolution gridded rainfall observations from HadUk-Grid50 but found little difference in the results. The analysis follows an event-based approach where an event is defined as an individual cyclone that passes within 1000 km of a given region. Cyclones and their tracks are identified using the Hoskins and Hodges (2002) tracking algorithm at 6-hourly intervals (00, 06, 12, 18 h) for all years analysed.

Framework, event definition, and metrics

Following a similar framework to Dunn et al.29 and Wilkinson et al.31, we apply an event-based analysis in which we assess the relationship between the number of faults that occur over a given region during an event and several characteristics of that event such as the maximum wind gust. Events are defined using cyclone tracks on a daily timescale to match the daily fault data. Specifically, an event is defined as the time period that a cyclone is within 1000 km of a region. As two or more cyclones may fulfil this criterion at a given time and at two separate times on the same day, we apply two further steps to match fault data with an individual cyclone. Firstly, hourly wind data three hours either side of the 6-hourly time steps that cyclones are identified on are assigned to the nearest cyclone at that time (i.e., at 06 h, winds between 04 h and 09 h are assigned to the nearest cyclone within 500 km). Secondly, daily fault numbers are assigned to the cyclone with the highest wind gust on that day.

For each event or cyclone, we identify one impact variable: the accumulated number of faults from each day of the event (\({F}_{N}\)); and three meteorological characteristics. These are simply the maximum hourly wind gust (\({v}^{X}\)) which is a commonly used metric to indicate the overall wind intensity of the windstorm, the accumulated rainfall from the 30 days preceding the event (\({R}^{30}\)) which is used as an indicator of soil moisture conditions, and the deviation in wind direction from the prevailing direction at the time \({v}^{X}\) occurs (\({{dir}}^{X}\)). Lastly, we also assess the season in which the event occurred (Seas = Winter, Spring, Summer, Autumn) as a factor that modulates the influence of \({v}^{X}\). This separation intends to isolate the effect of leaf cover, which will be highest in summer and lowest in winter. This, of course, is a simplistic way to isolate this effect as leaf cover may also be high in months adjacent to summer (e.g., May and September). We, therefore, also present results using a 3-month rolling window centred on each month of the year.

For wind direction, we assess the deviation from the prevailing direction (\({{dir}}^{X}\)) as we hypothesise that the probability of impacts increases as the wind direction deviates further from the prevailing wind direction. Thus, two winds with directions that are +40o or -40o from the prevailing direction should have the same effect. Therefore, \({{dir}}^{X}\) is estimated as the absolute difference from the prevailing wind direction. This limits \({{dir}}^{X}\) to values between 0 and 180o and avoids issues that would arise due to the circular nature of the direction. The prevailing direction is estimated from the mean u and v components associated with all \({v}^{X}\) greater than 20 ms−1. We apply this threshold as we assume that tree root systems grow to anchor against strong winds more so than all winds.

Empirical exceedance probabilities and simulations

We estimate the empirical conditional probability of \({F}^{N}\) exceeding an extreme threshold (\({F}_{{thresh}}^{N}\)) when certain meteorological conditions (\({{MC}}_{i}\)) are met:

$${P}_{i}=\Pr \left({F}^{N} > {F}_{{thresh}}^{N}\quad |{{MC}}_{i}=1\right),$$
(1)

where \({P}_{i}\) is the probability when the meteorological conditions, \({{MC}}_{i}\), in experiment \(i\) are met. \({{MC}}_{i}\) is a binary variable where 1 means the conditions are met, and 0 means they are not met. There are four sets of meteorological conditions (\(i=W,{R},{D},{S}\)) tested, which are: \({{MC}}_{W}\)) \({v}^{x}\) must exceed a specified threshold \({v}_{{thresh}}^{X}\); \({{MC}}_{R}\)) both \({v}^{X}\) and \({R}^{30}\) must exceed their respective thresholds \({v}_{{thresh}}^{X}\) and \({R}_{{thresh}}^{30}\); \({{MC}}_{D}\)) \({v}^{X}\) and \({{dir}}^{X}\) must exceed their respective thresholds \({v}_{{thresh}}^{X}\) and \({{dir}}_{{thresh}}^{X}\); and \({{MC}}_{S}\)) \({v}^{X}\) must exceed \({v}_{{thresh}}^{X}\) within a specified season (Winter, Spring, Summer, Autumn). All thresholds applied are outlined within the results section. Within the analysis we compare the probabilities from \({{MC}}_{W}\) with those from \({{MC}}_{R,D,S}\) to demonstrate whether the probability of extreme \({F}^{N}\) given a wind extreme is different when other conditions are met. Two \({F}_{{thresh}}^{N}\) thresholds are assessed including the 95th (\({F}_{95}^{N}\)) and 98th percentile (\({F}_{98}^{N}\)), as the influence of variables on the number of faults may depend on the windstorm severity.

We also perform empirical simulations to assess if the potential difference in probabilities in \({{MC}}_{R,D}\) compared to \({{MC}}_{W}\) can be achieved by random chance. This is done by shuffling the \({R}^{30}\) and \({{dir}}^{X}\) time series to break their observed link with \({F}^{N}\) and \({v}^{X}\). Specifically, we shuffle the time series in annual blocks (July–June), which captures the main windstorm season and preserves serial correlations and the seasonality of \({R}^{30}\) and \({{dir}}^{X}\). We then estimate the above probabilities with the shuffled data and the observed \({F}^{N}\) and \({v}^{X}\) time series. This is repeated 1000 times to give 1000 probabilities from each random shuffle. The median probability is calculated alongside a 95% confidence interval bounded by the 2.5th and 97.5th percentiles. If the observed probabilities are outside this confidence interval, we conclude that we are 95% confident that they cannot be achieved by random chance and a causal relationship is likely driving the probabilities.

The above approach does not make sense for a categorical variable such as a season. Instead, we compare the probability computed for \({{MC}}_{S}\) to the 95% confidence interval of the probabilities estimated for \({{MC}}_{W}\) (annual probability). In this sense, if the probabilities for \({{MC}}_{S}\) for a given season are outside this confidence interval, we conclude that the probabilities for that season are significantly different from those estimated with annual data. The confidence interval is estimated by applying non-parametric bootstrapping in which we sample 1000 times, with replacement, individual years (July–June), which encompass the main windstorm season to preserve serial dependence within seasons and account for interannual variability. A 95% uncertainty interval is estimated as the interval between the 2.5th and 97.5th percentiles.

Predicting impacts with logistic regression

We use logistic regression to predict the occurrences of \({F}^{N}\) > \({F}_{95}^{N}\). We assess the predictive skill of a reference model considering only \({v}^{X}\) as a predictor, and test whether the prediction accuracy improves when including \({R}^{30}\), \({{dir}}^{X}\), and Season as predictors. In total, we construct two models in each region. Logistic regression is chosen for its simplicity of application and the interpretation of its results. The main aim of the statistical model used here is for inference, to communicate the role of these additional variables, and to demonstrate the potential to improve impact predictions in the UK. It is not our aim to replicate or improve state-of-the-art models that use machine learning algorithms and are applied at a local scale (2 km resolution) in specific regions of the U.S17,19,21,51.

In a logistic regression, the impact \(Y\) is a binary time series (1: \({F}^{N}\) > \({F}_{95}^{N}\), 0: \({F}^{N}\) < \({F}_{95}^{N}\)), the predictors \({v}^{X}\), \({R}^{30}\), \({{dir}}^{X}\) are continuous variables, while season is a categorical variable. The logistic regression model is only fit for events in which \({v}^{X}\) > 20 ms−1. This is because the prediction of extremes using logistic regression comes with an imbalanced classification problem in that there are substantially fewer extreme events than non-extreme events. This can inflate the predictive skill of the model as non-extreme occurrences are much easier to predict. Thus, potential model improvements with the additional variables can be masked by the inclusion of all events in model fitting. However, we note that model coefficients are relatively insensitive to this choice (not shown).

Model performance is tested using a K-fold cross-validation, where K refers to the number of years in the dataset. Specifically, when predicting the probability of \({F}^{N}\) > \({F}_{95}^{N}\) for events where \({v}^{X}\) > 20 ms−1 in a given year, we exclude all events of that year when fitting the model. Our assessment is then based on receiver operating characteristic (ROC) curves, the summary metric known as area under the curve (AUC), and the akaike information criterion (AIC). The ROC curve illustrates each model’s performance as a binary classifier, showing the trade-off between the Hit Rate and the False Alarm Rate across various probability thresholds. For each threshold, the model assigns a predicted probability to the occurrence of a large power outage. As the threshold decreases from 1 to 0, the model becomes more lenient in predicting a power outage, leading to an increase in both the Hit Rate and the False Alarm Rate, represented by the movement of the curve from left to right in Fig. 5. A model that performs better will have a ROC curve that approaches the top-left corner of the plot, indicating high Hit Rates with low False Alarm Rates. The AUC then provides an integral of the model performance across all probability thresholds. A maximum AUC of 1 indicates a perfect model with a 100% hit rate with no false alarms. The closer the AUC is to 1, the better the model.