Introduction

Advances in paleogeographic and paleoclimate models have enabled better understanding Earth’s past, including how life evolved and where mineral deposits may be preserved for use in the energy transition. A key component of these models is accurate tectonic plate reconstructions, which dictate the past configuration of continents and ocean basins. Thanks to open-source tools such as GPlates1 and ever-more detailed geophysical, geological and paleomagnetic records, relative plate motions are reasonably well constrained for the last 250 Myrs2,3,4. However, complexity increases when tying relative plate motions to their actual past latitude and longitude by anchoring the whole network of plate motions to an absolute reference frame. The two prevailing approaches to constructing an absolute reference frame are to measure motions relative to the base of the mantle (a mantle reference frame) or relative to the Earth’s magnetic dipole (a paleomagnetic reference frame), which is assumed to approximately align with the Earth’s spin axis since at least Pangea times (~250 Ma)5,6. The former approach treats deep-rooted mantle hotspots as anchor points and reduces the problem to understanding only the mantle and its interaction with the lithosphere. Mantle hotspot reference frames are particularly useful in numerical simulations of mantle convection, as they enable the isolation of the plate-mantle system. However, a mantle reference frame is not appropriate for understanding climatically sensitive processes, as it does not account for the rotation of the whole plate-mantle system relative to Earth’s spin axis, a process known as true polar wander (TPW). TPW occurs due to mass redistributions within the mantle, which alter Earth’s moment of inertia and cause a uniform motion of the entire mantle and plates relative to the rotation axis7,8. Because the spin axis of the Earth is relatively stable from a celestial reference frame7, TPW also affects the distribution of solar insolation, which is the fundamental driver of Earth’s climate system. Therefore, an absolute reference frame that considers TPW is essential not only for modelling past climate but also for accurately reconstructing any process influenced by past Earth’s atmosphere and surface. A pure paleomagnetic reference frame captures plate motions from the latitudes recorded in inclinations and terrane rotations in declinations preserved in rock magnetism.

Several studies have demonstrated the impact that the choice of reference frame has on paleogeographic and paleoclimate interpretation9,10,11. van Hinsbergen et al.12 measured a difference of up to 15° in paleolatitude between mantle and pure paleomagnetic reference frames and attributed the apparently cooler-than-expected Eocene conditions at Seymour Island, Antarctic peninsula, to TPW shifting its true latitude 12° further south than previously estimated. Similarly, Zhang et al.13 found key differences in Pacific atmospheric circulation cells between paleomagnetic and mantle reference frames for simulated Eocene climates. Other work credits TPW as a possible explanation for the sudden Cenozoic glaciation in North America and Greenland, a phenomenon that cannot be accounted for by climate change or plate motions alone14,15. Anomalously fast continental drifts in the Mesozoic on the order of 1°/Myr has been attributed to TPW rather than conventional plate tectonic processes16,17. Despite these insights, the choice of reference frame often receives insufficient consideration in deep-time climate studies. The Deep-time Model Intercomparison Project (DeepMIP) has relied on a mantle reference frame by default13,18,19. Additionally, many of the plate motion models distributed with the GPlates software1 are in a mantle reference frame, leading to its unintentional widespread use in applications where a paleomagnetic reference frame would be more appropriate. The widely used PALEOMAP paleogeographic reconstructions3 do not clearly specify the type of absolute reference frame used, but appear to be based on the Müller et al.20 mantle reference frame for the last 100 Myrs (Supplementary Fig. S1). Here we emphasise the importance of selecting an appropriate absolute reference frame in any study that involves paleoclimate. We use an efficient, open source, fully 3D dynamical Earth system model to simulate 250 Myrs of climate evolution and evaluate temperature distribution variations between paleomagnetic and mantle tectonic reference frames. Furthermore, we develop a novel approach to preserving ocean gateway and land bridge connectivity in paleogeographic boundary conditions (Fig. 1, see Online Methods). To the best of our knowledge, this is the first study to quantitatively assess these discrepancies using a climate model over 10-100 Myr timescales.

Fig. 1: Implementations of skeletons to preserve ocean gateways and land bridges.
figure 1

Ocean skeletons are shown in black, and land skeletons in red. a Present-day example demonstrating the implementation process. The top-left image shows the digital elevation map at the original resolution, while the top-right map shows the raw re-gridded elevations at the model resolution, which loses key ocean gateway information (e.g., the Panama Isthmus, where the thin land bridge has been lost). To rectify this, a skeleton algorithm traces contiguous ocean and land cells in the high-resolution elevation map (lower left), and the skeletons are imposed over the coarsened elevation map (lower right), restoring the Panama Isthmus. Note that a skeleton is incorrectly traced across the Strait of Gibraltar due to the insufficient resolution of the original elevation map to resolve the narrow strait. b Implementation of skeletons in the paleomagnetic23 (left column) and mantle21 (right column) reference frames at 210 Ma (top), 130 Ma (middle), and 40 Ma (bottom). Note that the skeleton from the paleomagnetic frame is rotated into the mantle frame, preserving its shape and ensuring that the same connections are maintained across both frames.

Full size image

Results and discussion

Global surface air temperatures since 250 Ma

Annual average surface air temperatures (SAT) are used as the primary climatic variable to examine differences between tectonic reference frames. While several other variables could also be used to demonstrate discrepancies between reference frames, SAT is chosen because it is key to many ecological, climatological, and geological processes throughout deep-time. In this study we examine 5 tectonic reference frames: 3 mantle2,21,22 and 2 paleomagnetic22,23 for every 10 Myrs from 250 Ma to present-day. For simplicity, unless specified we hereafter refer only to the results for the hybrid mantle reference frame published in Müller et al.21 as the ‘mantle frame’, and the pure paleomagnetic frame of Merdith et al.23 as the ‘paleomagnetic frame’. However, data and results for a kinematically optimised mantle frame2 as well as the paleomagnetic and mantle reference frames from Torsvik et al.22 are available24 (see Data Availability Statement) and shown in Supplementary Fig. S2–S9.

With CO2 and solar insolation respectively held fixed at 1100 ppm and present-day levels, modelled global mean surface temperature (GMST) varies little across all times and paleogeographies. Mean GMST is 22.4 °C with a standard deviation of 0.3 °C (Fig. 2). This aligns with other studies that control for CO2 and orbital variations over similarly long-time spans25,26,27,28, although Li et al.28 records higher global mean temperatures in the Cretaceous (Fig. 2 blue triangles) driven by land-ocean albedo contrast. Landwehrs et al.27, while showing similar trends for GMST to this study, have considerably lower GMST amplitudes (Fig. 2 red stars), presumably due to the well-documented differences in equilibrium climate sensitivity between Earth system models29,30. It should be noted that each of these other studies uses the PALEOMAP3,31 paleogeographic model for boundary conditions, which has not made clear what absolute reference frame it is based on but appears to use a mantle frame for the last 100 Myrs (Supplementary Fig. S1).

Fig. 2: Global mean surface air temperatures (GMST) for all simulations.
figure 2

The hybrid moving hotspot mantle reference frame21 is shown in yellow, and the pure paleomagnetic frame23 in purple, with variability in GMST due to re-gridding (0.15 °C) shown as error bars (see text). The values from a kinematically optimised mantle frame from Müller et al.2 are indicated by the dotted yellow line. Values for the paleomagnetic and mantle frames described in Torsvik et al.22 are represented by the grey dashed and dotted lines, respectively (see Online Methods). Also shown are GMSTs from similar studies that simulated climate over >100 Myr time series with constant atmospheric CO2 and constant solar forcing26,27,28.

Full size image

To assess the impact of re-gridding on climate, further sensitivity tests were conducted involving 27 simulations at 0 Ma, and 14 each at 40 Ma and 170 Ma (all in the paleomagnetic reference frame). Each input paleo-elevation was incrementally shifted west by a fraction of the width of one cell in the model resolution, mimicking the incidental changes in elevation and coastline shape that may occur when re-gridding elevations from high resolution to the model resolution. Results show that GMSTs vary about the mean by ± 0.15 °C with 98% confidence at the present day (Supplementary Fig. S10) and 170 Ma (Supplementary Fig. S11), and ± 0.10 °C at 40 Ma (Supplementary Fig. S12). We also estimate the uncertainty in regional climate due to re-gridding of elevations. On a regional scale, each model cell deviated from its mean by an average of 0.85 °C with a 95th percentile difference of 2.6 °C (Supplementary fig. S13 and Supplementary Table S1). However, deviations reached up to 19.3 °C due to two cases of an ice-free Arctic at the present day (Supplementary fig. S10 - see Online Methods for further detail).

Considerable regional temperature discrepancies between reference frames

Despite the small influence of paleogeography on global temperature, we find that the choice of reference frame has a profound effect on regional surface air temperatures. Figures 3 and 4 show average temperature differences in the Late Triassic and Early-Middle Jurassic ages, such as at 210 Ma (Fig. 3 top row), display a clear systematic discrepancy. Pangea is positioned up to 13° further north in the paleomagnetic frame, resulting in cooler average zonal temperatures of up to 15 °C near the poles (Fig. 4), and areas of Eurasia and Greenland cooler by >20 °C. This is likely at least partly caused by increased sea-ice and snow cover in northern high latitudes which raises albedo (Supplementary Fig. S14). As Pangea breaks up, the Cretaceous and Cenozoic discrepancies become more balanced (Fig. 4 and Supplementary Fig. S15), however, important regional differences in latitude and SATs persist. For example, zonal average temperatures, particularly in polar regions, show considerable variations of up to 9.4 °C at 70 Ma and 6.6 °C at 60 Ma (Fig. 4). At 40 Ma, western Europe, Greenland, and eastern North America show latitudinal differences of up to 13° (Fig. 3 row 5), resulting in temperature differences of over 20 °C. While some of these differences can be attributed to lower solar insolation in the mantle frame, the more northern position of western Europe and Baltica put these landmasses under the influence of cool winter easterly winds (Supplementary Fig. S16), demonstrating how different reference frames can impact simulated climate in non-linear ways. At 90 Ma (Fig. 3 row 4) we identified fewest latitudinal differences of all the ages tested (up to about 1.5°), yet temperature differences persist, particularly across northern Eurasia, where the mantle frame is warmer by up to 9.5 °C. Some of the differences at 90 Ma illustrate the susceptibility of high latitudes to large temperature swings and possibly the sensitivity to changes in coastline and elevations due to re-gridding (see above sections, Supplementary Fig. S13 and Supplementary Table S1). However, temperature discrepancies of up to 6 °C in mid and tropical latitudes, show the outsized effect that even small geographic rearrangements can have on climate.

Fig. 3: Annual average surface air temperatures for selected ages at 210 Ma, 170 Ma, 130 Ma, 90 Ma and 40 Ma.
figure 3

The first column shows the Merdith et al.23 pure paleomagnetic reference frame, and the second column shows the Müller et al.21 hybrid mantle frame. The third column presents the difference in simulated average surface air temperature between the 2 frames, and the fourth column shows the difference in absolute latitude. Both columns are rotated to the present day for easier comparison. Blue areas indicate regions where the pure paleomagnetic frame is cooler in column 3 and closer to the poles in column 4. Conversely red areas indicate regions where the pure paleomagnetic frame is warmer or closer towards the equator. Grey areas represent crust that is unconstrained in the plate reconstruction model.

Full size image
Fig. 4: Simulated zonal average surface air temperatures over time.
figure 4

The pure paleomagnetic reference frame23 is shown on the top row, followed by the hybrid moving hotspot mantle reference frame in the middle row21, and the difference between the two at the bottom. The difference row highlights cooler temperatures in the paleomagnetic frame in blue and warmer temperatures in red.

Full size image

To illustrate this point further, we select and track four locations on Eurasia, North America, India, and Australia back to 250 Ma (see Fig. 5 and Supplementary Fig. S17 for the chosen locations at present-day). Their paths since 250 Ma highlight the fluctuations in latitude and temperature differences between reference frames. For example, India and Eurasia positions differ between reference frames in latitude by 13° and 11° at 210 Ma respectively, with a corresponding temperature discrepancy at 14 °C and 12 °C, while the point we tracked on North America displays relatively fewer differences with respective latitudinal and temperature discrepancies of 2° and 5 °C (albeit with larger differences to the west and east of our chosen point). Even for the recent Cenozoic period, where the magnitude of TPW is considered small7,17 we identify sizeable differences, such as at 40 Ma (Fig. 3 row 5), with variations of up to 8° latitude and 10 °C in Australia and Europe.

Fig. 5: Paleolatitude and average surface temperature differences for selected representative points on Eurasia, North America, India, and Australia.
figure 5

Triangle and circle markers represent the paleolatitude and temperature differences for the pure paleomagnetic23 and hybrid mantle21 reference frames, respectively. Grey regions show the 95% confidence interval for the paleolatitude of the paleomagnetic reference frame56. Temperature differences in white represent times where the differences fall within the 95th percentile due to re-gridding longitudinally (see Online Methods). See Supplementary Fig. S17 for the present-day locations of each point.

Full size image

Examination of key differences in the Jurassic and Eocene

The TPW-driven differences between reference frames give us an opportunity to examine specific ages in detail to assess whether one reference frame is more suitable than the other. While the most striking differences are in the late Triassic, the estimated atmospheric CO2 and GMST are too different from what was simulated to accurately compare with proxy data. On the other hand, the middle Jurassic (170 Ma) and middle-late Eocene (40 Ma) both have pCO2 and GMSTs similar enough to simulated values32,33 to compare against proxy data.

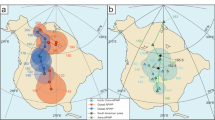
The middle Jurassic (170 Ma) paleomagnetic reference frames suggest cooler conditions in the northern high latitudes and more temperate conditions in the south, while the mantle reference frames suggest cool conditions in both hemispheres (Figs. 3 and 4). The paleomagnetic reference frames align with proxy evidence that suggests cooler northern climates (albeit without permanent ice)34,35,36 and warmer southern climates37,38,39 during this period. Analysis of recently collated databases of glendonite distributions reinforces the suitability of a paleomagnetic reference frame for this time period (Fig. 6a)40,41. Glendonites are remnants of hydrated carbonates that are recognised to form in cool water between −2 to 7 °C42. The paleomagnetic reference frame has a cooler average temperature and smaller spread of air and sea surface temperatures for middle Jurassic glendonite locations (Supplementary Fig. S18). While this does not invalidate the mantle frame, which also has sites with temperatures that fall within the glendonite formation range, we suggest that the cooler northern latitudes and lack of evidence for cold temperatures in the south make the paleomagnetic reference frame a more appropriate fit for the middle Jurassic.

Fig. 6: Comparisons between reference frames with glendonite and crocodilian proxy data.
figure 6

Comparisons are for (a) the Middle-Early Jurassic and (b) the Middle-Late Eocene. Distributions of glendonites40 and crocodilians (https://paleobiodb.org) are plotted on simulated surface air temperatures. The pure paleomagnetic reference frame23 is shown on the top row, with the hybrid mantle reference frame second row21. The differences between simulated air temperatures and latitudinal positions, reconstructed to the present day, are shown in the third and fourth rows. Blue areas indicate regions where the pure paleomagnetic frame is cooler or closer to the poles, and red areas indicate regions where the pure paleomagnetic frame is warmer or closer towards the equator. Crocodilian distributions constrain warm climates with mean annual temperatures above 14.2°44, historically limited to low-mid latitudes65. Glendonites, believed to form in cool water between -2 and 7 °C42, are thus constrained to higher latitudes and cooler regions. The simulated climate in the paleomagnetic frame places glendonites in cooler climates with less variance compared to the mantle frame. Also see Fig. S24 for this data in an orthographic projection.

Full size image

While atmospheric CO2 in the Eocene at 40 Ma was unlikely to be as high as the simulated value of 1100ppm32, the simulated GMSTs are within about 2 °C of those indicated by some proxies43,33, and therefore reasonably close enough to enable comparison. In this case we use crocodilian distribution to compare reference frames. Crocodilians inhabit a critical mean annual SAT range of above 14.2 °C, and prefer warmer temperatures of about 25–35 °C44. Middle Eocene crocodilian fossil locations in the paleomagnetic frame have an average annual SAT of 27.9 °C and SST of 30.9 °C, as opposed to cooler values of 23.2 °C and 25.8 °C in the mantle frame (Fig. 6b and Fig. S19). This corresponds with a mean position of crocodilians 3.4° closer to the equator with a smaller spread of latitudes in the paleomagnetic frame (Supplementary Fig. S19c). Both differences in temperature and latitude are larger than the defined 95% confidence bands (Supplementary Table S1), and therefore we again suggest that the paleomagnetic reference frame is a more appropriate fit for Eocene crocodilians. However, our analysis here has been restricted to just two of many proxy indicators at only two age snapshots. Further work simulating climates across a range of CO2 values is required to understand the more nuanced links to predicted SATs and climate states.

Conclusions

True polar wander influences the absolute locations of continents and oceans in Earth’s past. However, many researchers may inadvertently use a mantle reference frame that is indeed suitable for geodynamic modelling but not for studying Earth’s climate and surface processes, as it intentionally subtracts TPW from its calculations. This research demonstrates that for post-Pangea times, a pure paleomagnetic reference frame, which accounts for TPW, differs from a mantle reference frame in some regions by up to 14° in latitude. This shift results in substantial temporal and geographic disparities, with average surface temperature differing by 5 °C to 20 °C (Figs. 3–5), values that might be amplified by climate feedbacks neglected in our simulations. Analysis of Jurassic glendonite and Eocene crocodilian distributions suggests that a paleomagnetic reference frame, likely better representing true paleolatitude, provides a better fit for proxy data (Fig. 6). However, this study does not account for CO2 variation and solar insolation, so cannot be used to conclusively determine which reference frame performs better. Nonetheless, these findings underscore the critical implications of reference frame choice in modelling deep-time Earth climate.

Methods

Model description

We utilise a coupled atmosphere-ocean global circulation model of intermediate complexity called PLASIM-GENIE, which is created from a coupling of Planet Simulator (PLASIM) with the Grid-Enabled Integrated Earth system model (GENIE)45. The coupled model is run at a 5.625 × 5.625° spatial resolution across 10 vertical levels in the atmosphere and 16 levels in the ocean. The PLASIM atmosphere has the 3D dynamic spectral model PUMA at its core46,47, and is coupled to the land surface and vegetation model, ENTS48. The active models in GENIE are the 3D frictional-geostrophic ocean model, GOLDSTEIN and the 0D dynamic-thermodynamic sea-ice model GOLDSTEINSEAICE, both described in Edwards and Marsh49. Extensive model validation against model intercomparisons and proxy data has been conducted for times since the Pleistocene, albeit mostly through model emulation50,51. Previous studies measured the equilibrium climate sensitivity (ECS) to be 3.2 °C51. This study measured the average ECS to be 3.6 °C by modelling climate at the present day in this model’s boundary conditions at 1x, 2x, 4x, and 8x pre-industrial CO2. As the atmosphere model requires the bulk of computational demands, atmosphere-ocean gearing is enabled52, where for every 10 years of model simulation, nine of those years apply fixed atmosphere-ocean fluxes, being daily averages of the previous (fully coupled) year, with only ocean and sea-ice components of the model running. This allows for a computationally efficient simulation with each simulation taking ~36 h on one CPU to spin up to 3000 model years reaching a quasi steady-state (Supplementary Fig. S20).

Absolute reference frames

Five sets of 26 time-slice simulations are run from 250 Ma to the present-day that differ by the reference frame used to constrain absolute plate positions. Three mantle frames and two for pure paleomagnetic frames are tested:

  1. 1.

    A hybrid mantle reference frame described in Müller et al.21 that constrains motions to a TPW-corrected paleomagnetic reference frame17,21,53,54 from 250 Ma to 100 Ma, and transitions into a moving hotspot reference frame9,55 from 70 Ma to the present.

  2. 2.

    A kinematically optimised mantle reference frame2,56 that takes the above21 absolute reference frame and smooths its motions to minimise net lithospheric rotation and velocity of subduction trench migration.

  3. 3.

    A mantle reference frame that modifies the relative plate motions described above to fit with the reconstructions published in Torsvik et al.22.

  4. 4.

    A pure paleomagnetic reference frame described in Merdith et al.23 that uses reconstructed latitudes from paleomagnetism17 to create an absolute reference frame from global apparent polar wander paths that have been optimised to smooth high plate velocities and consider age uncertainties56.

  5. 5.

    A pure paleomagnetic reference frame published alongside the Torsvik et al.22 reference frame (described in (3))22.

All models used in this study have a similar network of relative plate motions so that the only difference is the absolute reference frame used. Reference frames (1), (2), and (4) use the network of relative plate motions published in Zahirovic et al.57, while the Torsvik et al.22 plate reconstructions (number (3) and (5) above) have their own related but slightly different set of plate rotations. Because TPW is inherent in the paleomagnetic reference frame, and corrected for in the mantle reference frame, we can infer that the difference in absolute location of plates between the two suites of models is largely due to TPW.

In this publication, to simplify our findings and because all tested reference frames support the broad conclusions, we only refer to the Müller et al.21 results as the mantle reference frame, and the Merdith et al.23 results as the paleomagnetic reference frame. However, the results for the Müller et al.2 optimised mantle frame are similar and shown in Supplementary Figs. S2–S5. Similarly, the results that compare the mantle and paleomagnetic references frames from Torsvik et al.22 are given in Supplementary Figs. S6–S9. Comparisons between the Merdith et al.23 and the Torsvik et al.22 paleomagnetic frames, and the Muller et al. (2016) and the Torsvik et al.22 mantle frames, can be found in Figs. S21 and S22.

Uncertainties of paleolatitudes

A complete assessment of error is difficult as tectonic reconstructions use a large array of data which is then fitted, often subjectively, to create a model of past reconstructions. However, assessments of uncertainty in paleomagnetic reference frames are possible by combining apparent polar wander paths from paleomagnetic rock data into one global apparent polar wander path (GAPWaP). The GAPWaP uncertainties for the Merdith et al.23,56 and Torsvik et al.22 paleomagnetic frames were thus used to estimate uncertainty for paleolatitudes in these reference frames.

Uncertainties of simulated temperature differences

As described in the main text, a series of supplementary studies were conducted to estimate the impact of re-gridding the paleogeographic boundary conditions from high to low model resolutions (5.625° x 5.625° in this case). Supplementary Fig. S10 illustrates some of these impacts where the geographic boundary conditions for 0 Ma are shifted east-west by a fraction of one cell width 27 times. While the overall geographies look similar, there are subtle differences in areas near coastlines, continental shelves and mountains. We extrapolated this to be the ‘random’ differences that might also occur when casting the same paleogeography in different absolute reference frames. Note, that we only assessed the random east-west differences as these should have less impact on climate, while any shift north-south would directly change the solar insolation and therefore have a direct impact on climate. While a small shift north or south may also create large changes due to the coarse model resolution, it is difficult to control for this and it does not change the overall message that different reference frames impact simulated climate. We note also that neglected climate feedbacks in the model could amplify the effects of small latitude differences too.

Further sensitivity to re-gridding tests were performed at 40 Ma and 170 Ma in the Merdith et al.23 paleomagnetic reference frame. Overall we ran 27 different simulations at 0 Ma, and a smaller set of 14 simulations for 40 Ma and 170 Ma. Global surface temperature maps for each sensitivity test including the east-west shifts are shown in Figs. S10–S12. While the overall GMST changes between simulations are moderately small, some local changes could be as large as 19 °C (Supplementary Fig. S13). More variations occur on land, particularly in areas that may have shifted in elevation (Supplementary Table S1). The present day also had two interesting cases where the Arctic was ice-free, presenting an example where small changes in geography can have a large impact. In this case we believe it is due to coastlines providing a larger Atlantic flow into the Arctic.

The overall deviation was assessed by first ‘resetting’ the east-west shift so that each simulation was aligned with the other. The deviation from the average temperature across each individual cell is collated and repeated for 0 Ma, 40 Ma and 170 Ma geographies. The complete distribution of deviations is shown in Supplementary Fig. S13. To assess whether differences between reference frames for individual sites are significant, we took a conservative approach and interpreted the 95th percentile of deviations (2.57 °C) rounded up to ± 3 °C as the acceptable threshold of whether temperature differences at any site is unlikely to be due to random differences in elevations/morphology, even when excluding oceans (Supplementary Table S1). If we were only to include values on land, the uncertainty would be higher. Conversely, the uncertainty would be lower if we only considered areas of consistent elevations (see Supplementary Table S1).

Boundary conditions

Elevations for land and shallow marine settings are derived from the paleogeographic maps of Cao et al.58, and deep ocean bathymetry is based on seafloor age grids from Zahirovic et al.57. The paleogeographic maps describe the extent of past elevated regions, continental landmasses, shallow marine environments and ice sheets from the work of Golonka et al.59, updated with data from the paleobiology database (https://paleobiodb.org). A uniform elevation is applied to each paleogeography category, with mountains set to 3000 m, continental landmasses to 500 m, and shallow marine settings to −200 m. For deep ocean bathymetry, the seafloor age grids are converted to depths with the GDH1 age-depth relationship of oceanic crust60 (Fig. 1). For simplicity, and to minimise potential model differences, ice sheets are not imposed in the initial boundary conditions, however, workflows allow for implementation of ice sheets in future work.

As our aim is to assess climatic differences arising from choice of absolute reference frame, paleogeography, as it varies with time and reference frame choice, is our key variable and all other forcing conditions are kept constant between the two sets of simulations. Atmospheric CO2 is set to a constant 1100 ppm as the value approximately corresponds to the long-term average value since 250 Ma32. Solar insolation and orbital forcings are kept constant at present-day values.

A novel skeletonizing approach to preserving sea and land connections

Both geological proxy data and climate modelling suggest ocean gateways have played a key role in global climate change throughout the Mesozoic and Cenozoic61,62,63. However, coarse spatial model resolutions lead to frequent cases of inadvertent gateway openings and closings due to re-gridding of initial geographic boundary conditions into coarse model resolutions (for example, the Panama Isthmus in Fig. 1a). Usually resolved through manual editing, we instead develop a novel and open-source approach using an existing skeletonization algorithm64 that maintains the topological connectivity between elevation maps in different reference frames. This algorithm is applied to land-sea masks of the paleogeographic maps where a medial axis transform produces skeletons of the mask that are then pruned to form traces of contiguous land and water pathways across the Earth. These pathways are applied to the coarse, re-gridded elevation map where water or land cells are imposed to resolve any conflicts between the two maps (Fig. 1a). Skeletons for each age are rotated into their respective reference frames, as opposed to generating a new skeleton for each reference frame. This ensures all skeletons for each age are of the same shape and the preserved gateways and land bridges are the same (see examples for 210 Ma, 130 Ma, and 40 Ma in Fig. 1b).

We also checked to ensure that the enforcement of gateways, or any other aspect of the re-gridding process does not significantly impact albedo by altering the land area. Supplementary Fig. S23 shows that although the re-gridding process reduces land percentage by up to about 10%, the filtering and gateway enforcement only reduces land fraction by 1−2%. Overall, this led to correspondingly small differences in albedo between the two reference frames, and therefore we believe the filtering process was not a primary factor in GMST difference.