Combining quasi-one-dimensional modeling with region-wise structure analysis for rapid technology computer-aided design simulations of gate-all-around MOSFETs

Abstract

The research and development process of semiconductor device technology heavily relies on technology computer-aided design simulations. However, long simulation times remain a significant challenge for research and development engineers. We propose a robust and efficient method to accelerate technology computer-aided design device simulations by generating approximate solutions faster. Since the majority of simulation time is spent preparing an approximate initial solution, our approach achieves orders-of-magnitude faster simulation than the conventional bias-ramping scheme, without incurring additional computational cost. Key techniques such as the quasi-one-dimensional model and the region-wise structure analysis are employed to handle general three-dimensional device structures. The applicability of this method is demonstrated through the simulation of next-generation complementary field-effect transistor inverters and other structures, yielding results 10 to 100 times faster than conventional methods.

Introduction

The silicon complementary metal-oxide-semiconductor field-effect transistor (CMOSFET) technology has continuously evolved for several decades. Starting from the planar MOSFET, the device architecture has evolved to the FinFET^1,2,3 and the gate-all-around (GAA) nanosheet field-effect transistor (NSFET)^4,5,6 to improve the gate controllability. To achieve even higher areal density, it is expected that variants of the GAA NSFET, such as the forksheet field-effect transistor (FSFET)^7,8,9 and the complementary field-effect transistor (CFET)^10,11,12,13, will be adopted as next-generation device architectures in the near future (Supplementary Fig. 1).

Accurate prediction of the electrical performance of transistors is critical for device optimization. Unfortunately, due to their complex internal structures, their electrical performance cannot be easily predicted through simple analytic models. Instead, numerical analysis using computers—Technology Computer-Aided Design (TCAD) simulation^{14,15,16,17,18}—is widely adopted. In the TCAD device simulation, a three-dimensional (3D) device structure is represented by several mesh points where physical laws, including Coulomb’s law (often referred to as the Poisson equation in this context) and carrier continuity equations^19,20, are applied. These coupled equations are solved numerically and the solution describes the device state, capturing its electrical characteristics. By calculating the motion of electrons and holes in the semiconductor device according to these physical laws, the TCAD device simulation enables quantitative prediction of electrical performance. Consequently, the TCAD simulation has become an indispensable tool in the research and development (R&D) process (Supplementary Fig. 2).

However, it is well known that the TCAD device simulations are time-consuming, typically ranging from hours to days for practical structures (Fig. 1a). This prolonged simulation time considerably slows down the entire R&D workflow, as hundreds to thousands of simulation tasks must be performed repeatedly for device optimization (Supplementary Fig. 2). Over the years, users and developers have explored various approaches to accelerate the TCAD device simulations. From a user perspective, the most effective approach is to invest in faster and larger computational facilities, which requires substantial financial resources. From a developer perspective, implementing massive parallelism^21,22 is a viable option. However, this approach increases computational resource usage to achieve shorter runtime. Although individual simulations may be faster, parallelism does not improve the throughput of multiple simulation tasks. In contrast, algorithmic improvements^23,24 offer a fundamental speedup by reducing the number of computational operations needed to reach solution. Therefore, achieving a reliable, orders-of-magnitude speedup in the TCAD device simulation via algorithmic improvements would represent a significant breakthrough. However, due to their limited robustness, previous approaches^23,24 have seen limited adoption in practical applications.

Fig. 1: Accelerated technology computer-aided design (TCAD) device simulation.

a Simulation time versus the number of points for various device structures. The newer the device architecture, the longer the computation time. b Conventional bias-ramping process. c Example of the convergence behavior depending on the bias-ramping step size in the transition from the off-current to the on-current condition. As the step size increases, convergence may not be guaranteed. d Example of the normalized error versus Newton iterations at each bias step when solving the drift-diffusion model, starting from equilibrium to the target bias condition. Each bias step involves several iterations, during which convergence or failure may occur, eventually leading to the target voltage. e Concept of an accelerated TCAD simulation without time-consuming bias-ramping process.

A major bottleneck in TCAD simulations is the bias-ramping process (Fig. 1b). Although only a limited number of bias conditions are of practical interest (for example, for NMOSFETs, the ON condition at V_GS = V_DS = V_DD, or the OFF condition at V_GS = 0 V and V_DS = V_DD), direct computation at these bias points is not feasible due to the nonlinear nature of the governing equations. Instead, the Newton–Raphson method is applied, which is highly sensitive to the initial guess. Since obtaining a sufficiently accurate initial solution at the target bias condition is challenging, the bias voltage is gradually increased from the equilibrium condition to the target value. As illustrated in Fig. 1c, d, convergence is not always guaranteed under non-equilibrium conditions, and each bias step in the bias-ramping process requires several iterations, during which convergence or failure may occur. Following this bias-ramping scheme, the majority of simulation time is spent preparing an approximate initial solution at the target bias point. If a sufficiently accurate initial solution could be reliably generated, direct computation at the target bias would be possible, leading to significant computational savings. This forms the core idea of our acceleration scheme (Fig. 1e).

Recently, there have been several reports on accelerating the TCAD device simulation using pre-trained neural networks^{25,26,27,28,29,30,31,32,33,34,35,36,37,38}. In this approach, neural networks generate an approximate solution for the target bias condition (Supplementary Fig. 3). These studies have demonstrated that solutions predicted by pre-trained neural networks can significantly speed up the TCAD device simulation. This promising approach holds particular potential for industrial applications. However, the key limitation of this approach is its restricted applicability. While a pre-trained neural network can predict approximate solutions well for semiconductor devices within the training dataset, it would be difficult to be applied to devices outside that dataset. Consequently, an additional training phase is required for each new dataset, which incurs a substantial computational cost.

In this work, we present a novel approach that addresses the above-mentioned issue. Our approach aims to perform a TCAD device simulation task orders-of-magnitude faster than the conventional bias-ramping method, without any cost related with the neural network training. The next-generation device architecture, the GAA MOSFET, is selected as the target for acceleration. This seemingly challenging task can be accomplished by developing robust and efficient techniques for generating an approximate solution without relying on the pre-trained neural network. Novel techniques, such as the quasi-one-dimensional (quasi-1D) modeling and the region-wise structure analysis for representing the device structure, are developed for efficient prediction. By integrating these techniques, we demonstrate that the simulation of next-generation CFET inverters and other structures can be performed 10 to 100 times faster than conventional bias-ramping scheme. Furthermore, the proposed method is more robust and broadly applicable than previously reported approaches, without requiring any training phase, as shown in Supplementary Table 1 of Supplementary Note 1.

Results

Quasi-1D modeling

Semiconductors have two types of charge carriers: electrons and holes. Consequently, the standard set of equations for TCAD device simulation includes the Poisson equation and two continuity equations. However, in many cases, a single carrier predominantly determines the electrical performance. For instance, electrons are the primary charge carriers in NMOSFETs, while holes play the dominant role in PMOSFETs. In such cases, solving only two equations—the Poisson equation and a single continuity equation—is sufficient, simplifying the computational workload.

When a 3D device is simulated, the structure is represented by several mesh points, significantly increasing the number of unknown variables. Fortunately, in the core regions of the GAA MOSFETs (as shown in Fig. 2a), the channel direction is well-defined and the integrated carrier density on cross-sections perpendicular to this direction can be effectively modeled. A dimensional splitting approach that separates the 1D channel direction from the 2D cross-sections has been widely employed to reduce the computational complexity in many advanced transport solvers, such as the non-equilibrium Green function solvers^39,40 and the multi-subband Boltzmann transport equation solvers^41,42. Inspired by the success of this approach, we propose a quasi-1D model that solves a 1D continuity equation along the channel direction⁴³. By reducing the problem dimensionality from 3D to 1D, the computational efficiency is greatly improved. Solving the 1D continuity equation directly yields the quasi-Fermi potential along the channel direction⁴⁴, which in turn enables the generation of an initial guess for the electrostatic potential and carrier densities. This eliminates the need for the conventional bias-ramping process.

Fig. 2: Results of the quasi-1D model for an n-type rectangular gate-all-around (GAA) nanosheet field-effect transistor (NSFET).

a Three-dimensional structure of a rectangular GAA NSFET (i) and its doping profile (ii). Both of an NMOSFET and a PMOSFET are considered. The gate length is 12 nm. Comparison of results between the quasi-1D model and the technology computer-aided design (TCAD) simulation for the surface potential (〈ϕ〉_s) and the average potential (〈ϕ〉) (b), the surface quantum potential (${\langle {\phi }_{q}\rangle }_{s}$) and the average quantum potential (〈ϕ_q〉) (c), integrated carrier density (d), and quasi-Fermi potential of the majority carrier (e) along the channel direction. Four gate voltages are considered, while V_DS is fixed to 0.7 V. Comparison of results between the quasi-1D model and the TCAD simulation for the I_D – V_GS curve (f), and the I_D − V_DS curve (g).

Naturally, the Poisson equation for the 3D device structure must also be simplified. This is achieved using the compact charge model⁴⁵, which is detailed in “Methods” and Supplementary Note 2. Following the philosophy of the splitting approach, the Poisson equation is integrated over a cross-section, with careful treatment of the lateral field term. Although the resultant equation involves multiple quantities, they can ultimately be expressed using the electrostatic potential at the semiconductor-insulator interface (the surface potential), the integrated carrier density, and other related quantities. To explicitly derive these equations, we first consider a cylindrical GAA MOSFET with rotational symmetry. Leveraging the universality demonstrated in our previous work⁴⁵, the resultant equations can also be applied to non-cylindrical cross-sections. In addition to the Poisson equation, the compact charge model also incorporates a simplified form of the density-gradient equation⁴⁶, introducing the quantum potential as an additional solution variable. This allows our model to account for the quantum confinement effect.

By solving the quasi-1D model, we can obtain several quantities, such as the integrated carrier density, the surface potential, the average potential over the cross-section, the surface quantum potential, the average quantum potential over the cross-section, and the quasi-Fermi potential along the channel direction. Fig. 2 shows an example of results from the quasi-1D model for an n-type rectangular GAA NSFET. The results for a p-type rectangular GAA NSFET are presented in Supplementary Fig. 7. More information on this section is provided in Supplementary Note 3. With the gate length scaled down to 12 nm, the MOSFET operates as a short-channel device. As shown in Fig. 2b-e and Supplementary Fig. 7a–d, results from the quasi-1D model show good agreement with the TCAD simulation results regardless of the device type (N or P) for several quantities along the channel direction. Furthermore, the quasi-1D model can calculate the current-voltage characteristics similar to the TCAD simulation results (Fig. 2f, g and Supplementary Fig. 7e, f).

In addition to the cross-sectional structure shown in Fig. 2a, Fig. 3 presents quasi-1D model results for GAA NSFETs with different cross-sections. As shown in Fig. 3, the quasi-1D model remains accurate even for structures with rounded corner cross-sections or larger aspect ratios. Since the geometric parameters used in the quasi-1D model, such as cross-sectional area, perimeter, and capacitance values, are extracted directly from the TCAD simulation structures, no additional adjustment is required for new geometries. Only the fitting parameter α (introduced in Supplementary Note 2) may vary depending on the cross-section. For example, α is set to 1.5 for cylindrical cross-sections, and to 1.33 for rectangular GAA structures. For other geometries, α can be adjusted within this range, and a value of 1.33 is used throughout this study. Furthermore, the quasi-1D model is validated for devices with a 10 nm gate length and performs well even in this short-channel regime, as shown in Supplementary Fig. 8. The errors of the results for GAA NSFETs evaluated so far are presented in Supplementary Fig. 9. Although some errors exist, the main objective of this study is to achieve accelerated device simulation. Therefore, perfect accuracy is not necessary, and errors of this scale do not hinder the simulation acceleration. As shown in Supplementary Fig. 10, the acceleration method introduced below was applied to various GAA NSFETs at specific bias conditions, and the acceleration performance was not significantly affected by either the error level or the device structure.

Fig. 3: Results of the quasi-1D model for gate-all-around nanosheet field-effect transistors with various cross-sections

Three cross-sections of an n-type device are considered, with a gate length of 12 nm and a channel thickness of 5 nm. The integrated electron density, quasi-Fermi potential, and I–V characteristics are compared with technology computer-aided design simulation results. a Cross-section with a channel width of 12 nm and a rounded corner. b Cross-section with a channel width of 20 nm and no rounded corner. c Cross-section with a channel width of 20 nm and a rounded corner.

Using the quasi-Fermi potential obtained from the quasi-1D model, we solve the Poisson equation and the density-gradient equation in the 3D structure. Then, an approximate solution for the drift-diffusion (DD) simulation can be constructed. Starting from the approximate solution, the numerical solution is calculated. Therefore, the computational efforts required to obtain the numerical solution at the target bias condition can be reduced significantly.

Region-wise structure analysis

As discussed in the previous section, the quasi-1D model is based on the dimensional splitting approach. However, modern semiconductor devices feature increasingly complex internal structures. In particular, multiple core regions—where the quasi-1D model is effective—are connected through source and drain regions. Consequently, the quasi-1D model alone is insufficient to provide an adequate approximate solution for the entire device. To overcome this limitation, we propose a region-wise structure analysis, which systematically decomposes the device into several regions. The quasi-1D model is applied exclusively to core regions, while parasitic regions are treated separately using appropriate modeling techniques.

Since manual decomposition is not practical for diverse device structures, our region-wise structure analysis is performed directly using the device structure file. The structure file required for the TCAD device simulation can be generated through various methods. The most rigorous approach follows the full fabrication process using TCAD process simulation or emulation^47,48,49, where governing equations are numerically solved. For instance, Fig. 4a illustrates the process emulation results for a CFET inverter. Alternatively, template-based methods^30,50,51 offer a faster way to generate device structures. Regardless of the method used, volume mesh generation—an essential step that partitions the simulation domain into geometric cells—must be performed. As a result, an infinite number of possible device structure files may exist for even a single device in the TCAD device simulation. It is crucial to extract essential and abstract features from a given device structure.

Fig. 4: Process of region-wise structure analysis.

a Results of process emulation for a complementary field-effect transistor (CFET) inverter. b Reconstructed semiconductor regions of the CFET inverter based upon the doping concentration. Only semiconductor regions are shown and each color indicates a different region. c Region graphs of the CFET inverter after analyzing the simulation domain. The six color lines are detected as semiconductor paths connecting two contacts. d The generalized coordinate for the channel regions (i), shared source/drain regions (ii), and test functions in the drain region of the top-tier NMOSFET (iii). e Resultant schematic of the CFET inverter. f Parameter extraction for each channel path. Geometric parameters are shown, while equilibrium electrical parameters are provided in Supplementary Fig. 11.

To eliminate dependence on a specific volume mesh, we introduce an abstract representation of the device structure. Our approach defines a region as a set of adjacent geometric elements that share the same material (Si, SiO₂, ...) and doping polarity (N- or P-type). This definition ensures that the entire simulation domain can be partitioned into multiple regions without ambiguity (Fig. 4b). It is noted that the partitioning method used in this study further subdivides the original regions (Fig. 4b right) while preserving the region boundaries of the original structure (Fig. 4b left). Therefore, the central region and the shared source and drain regions can be distinguished solely based on the original structural regions. The newly divided regions are used to identify MOSFET paths and determine their types, as described below. To systematically extract structural information, we construct a region graph, where each region is represented as a node and adjacency between regions is indicated by edges. In addition to regions, contacts are also included as nodes in the region graph. Fig. 4c illustrates the region graph corresponding to the CFET inverter in Fig. 4a. The region graph enables efficient identification of semiconductor paths between contacts. If a semiconductor path is electrically isolated from a third contact by insulating regions, it can be classified as the channel, with the insulating regions and third contact corresponding to the gate insulators and gate contact, respectively. Furthermore, the doping polarity of the newly partitioned regions is utilized to determine the type of each MOSFET path. It is important to note that a single structure file may contain multiple sub-devices, such as in a multi-stack GAA NSFET, where distinct sub-devices—such as the top, middle, and bottom channels–are typically present. For example, in the CFET inverter, the region graph reveals three NMOSFET channels and three PMOSFET channels. With the region-wise structure analysis, the TCAD device simulator can automatically interpret a given structure file and recognize the role of each region without any user intervention.

A MOSFET channel does not necessarily align with the principal axes (x, y, and z). To address this, the channel direction is determined by computing a generalized coordinate for the channel regions (ψ_ch) that relates the original 3D structure to the quasi-1D model. It is given as a solution of the Laplace equation with the boundary condition of ψ_ch = 0 at the source regions and ψ_ch = 1 at the drain regions, as shown in Fig. 4d (i). For shared source and drain regions, their interfaces with the MOSFET channels are also treated as contacts (Fig. 4d (ii)). The structure with additional contacts shown in Fig. 4d (ii) is a virtual structure and is used solely to extract values required for the quasi-1D model calculation. For example, using the structure shown in Fig. 4d (ii), the conductance matrix (the low-frequency limit of the Y-matrix)⁵² is calculated from a DC (steady-state) drift-diffusion simulation at a low bias condition to describe the parasitic resistances of the shared source and drain regions. It is equivalent to the low-frequency AC (small-signal) drift-diffusion simulation and can be readily extended to the AC drift-diffusion simulation at nonzero frequencies, when capacitances are of interest. This admittance matrix is used solely for the calculation of the quasi-1D model. Test functions, obtained by solving the Laplace equation, are then used to reconstruct an initial guess for the shared source and drain regions (Fig. 4d (iii)). As a result of region-wise structure analysis, the CFET inverter shown in Fig. 4a can be schematically represented as shown in Fig. 4e. The quasi-1D model is solved in the MOSFET channels, while the extracted admittance matrix is used in shared regions. Furthermore, key geometric parameters, such as cross-sectional area, perimeter, capacitance values, and other equilibrium electrical parameters, must be extracted for the quasi-1D model, as shown in Fig. 4f and Supplementary Fig. 11 of Supplementary Note 4. With the above process, the quasi-1D model is now ready to be applied to the CFET inverter example.

Numerical results

The overall flow of our proposed acceleration scheme is summarized in Fig. 5. Despite the complexity of the entire structure, the region-wise structure analysis effectively distinguishes the core MOSFET devices from parasitic regions, enabling appropriate modeling for each part. By applying suitable modeling techniques to these regions, we construct a high-quality approximate solution for the entire structure. This solution is then used to directly initiate the Newton–Raphson iterations for the drift-diffusion model at the target bias condition. A key advantage of our method is that it eliminates the hidden cost associated with neural network training, while maintaining broad applicability across different device structures. In the following paragraphs, we demonstrate the proposed acceleration scheme through realistic examples.

Fig. 5

Overall flow of an accelerated device simulation.

The acceleration scheme has been applied to the CFET inverter shown in Fig. 4a. The device structure file includes both the PMOSFET (bottom-tier) and NMOSFET (top-tier), each of them featuring three stacked channels. In this inverter, the common drain contact serves as an output node and is connected to an infinite load, with its voltage, V_OUT, determined by solving the relevant physical laws. Meanwhile, the input voltage, V_IN, which is the common gate contact voltage, is controlled by the user, while the maximum supply voltage, V_DD, is fixed at 0.7 V. Even for such a complex structure, the quasi-Fermi potential along the channel direction can be accurately predicted, as illustrated in Fig. 6a. The error in the quasi-Fermi potential shown in Fig. 6a, as well as the quasi-1D model results and corresponding errors for the average electrostatic potential and integrated carrier density, are presented in Supplementary Figs. 12, 13, and 14. More information on this section is provided in Supplementary Note 5. Supplementary Fig. 15 presents a 2D cross-sectional comparison between the TCAD simulation and the quasi-1D model, in addition to the comparison of the averaged values along the channel direction. Since key internal quantities such as the quasi-Fermi potential are precisely calculated, even without performing the TCAD device simulation, the quasi-1D model combined with parasitic region analysis produces highly reliable results. For example, the voltage transfer characteristics (V_OUT as a function of V_IN) are effectively reproduced by the quasi-1D model (Fig. 6b), and the current through the inverter is also accurately calculated. The errors of these quantities can also be observed in Fig. 6b. It is important to emphasize that such high accuracy would be unattainable without a consistently derived model directly extracted from the device structure. With the help of ψ_ch and test functions, it is straightforward to assign the quasi-Fermi potential in the 3D structure. The reconstructed 3D quasi-Fermi potential in the drain region of the top-tier NMOSFET is shown in Fig. 6c. Due to the non-vanishing resistance inside the drain region, the bottom channel experiences an additional voltage drop compared to the top channel, which is closer to the drain metal contact. The initial quasi-Fermi potential and the converged solution under a specific bias condition of V_IN = 0.3 V and V_DD = 0.7 V are compared in Fig. 6d. The result shows excellent agreement, with the maximum difference suppressed below 0.1 V. Furthermore, the 1D profiles along the channel direction at the center of the channel cross-section are shown in Fig. 6e, based on the results in Fig. 6d. Additional results for the 3D profile of the quasi-Fermi potential and its corresponding 1D profiles can be found in Supplementary Figs. 16, 17, and 18.

Fig. 6: Results of the quasi-1D model for the complementary field-effect transistor inverter.

a Quasi-Fermi potential of the majority carrier of each channel path obtained from the quasi-1D model and the technology computer-aided design (TCAD) simulation along the channel direction at three bias conditions. b (i) Comparison of results between the quasi-1D model and the TCAD simulation for the voltage transfer characteristics and I − V curve. (ii) Difference in voltage transfer characteristics and the relative error of drain current. c Example of initial electron quasi-Fermi potential using test functions in the drain region of the top-tier NMOSFET. d Comparison of reconstructed initial quasi-Fermi potential and converged quasi-Fermi potential of the majority carrier at V_IN = 0.3 V and V_DD = 0.7 V, and difference between them. e 1D profiles along the channel direction of the quasi-Fermi potential (i) and its difference (ii) at the center of the channel cross-section, based on the results in Fig. 6d.

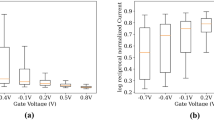
By solving the Poisson equation and the density-gradient equation with the reconstructed initial quasi-Fermi potential, the initial electrostatic potential and carrier densities for the DD model can be obtained at a given target bias condition. Among these, the L₂ and L_∞ norm error of the initial electrostatic potential are presented in Fig. 7a. Five different meshes are considered, and comparisons are made with the converged results under four different bias conditions. Our proposed method provides appropriate initial guesses regardless of the mesh resolution. Thereafter, the device simulation is performed directly at the target bias condition without the bias-ramping process. Fig. 7b presents the total computing time and the number of Newton iterations required for the drift-diffusion simulation when applying our proposed acceleration scheme. Simulations are conducted on the CFET inverter using two different meshes: 381k points and 715k points. Detailed information on the device simulation model and meshes is provided in Methods. With our approach, the solution converges within a small number of Newton iterations (from four to eight) across various bias conditions. Fig. 7c illustrates both the number of Newton iterations of the drift-diffusion simulation and the total computing time required to obtain a solution for a CFET inverter with 715k points at the target bias condition (V_IN = V_DD = 0.7 V). When the conventional bias-ramping scheme is adopted, different maximum step sizes are tested. The actual step size is adaptively determined within this limit, and its optimal value cannot be found a priori. By applying the proposed acceleration scheme, the number of drift-diffusion iterations is reduced by a factor of 17 to 94, and the total computing time is improved by 7 to 39 times, depending on the bias-ramping step size. Furthermore, more details about the acceleration results for the CFET inverter with different mesh resolutions can be found in Supplementary Fig. 19, showing that the simulation acceleration is not significantly affected by the mesh resolution. When considering the total matrix solve time instead of the total computing time, improvements of 11 to 63 times are observed (Supplementary Fig. 20). Furthermore, Fig. 7d compares the acceleration scheme and the conventional bias-ramping scheme across various device structures. In the conventional method, the bias is ramped in two stages—first by ramping V_DD (or V_DS), followed by V_IN (or V_GS)—with multiple maximum step sizes. As shown in Fig. 7d, our accelerated scheme consistently achieves huge performance gain across all device structures, demonstrating its robustness and broad applicability. Results for the total matrix solve time across various device structures are also shown in Supplementary Fig. 21. Moreover, more details about the time required for the structure analysis and the accelerated device simulation are provided in Supplementary Fig. 22. The time required for the region-wise structure analysis is approximately half of that for the acceleration process. This study, however, focused only on the TCAD device simulation aspect when making comparisons with the conventional method.

Fig. 7: Results of the proposed acceleration scheme for the complementary field-effect transistor (CFET) inverter.

a L₂ and L_∞ norm error of the initial electrostatic potential using our proposed method at the target bias condition of V_IN = V_DD = 0.7 V. Five different meshes are considered for the CFET inverter, and converged results under four different bias conditions are used for comparison. b Total computing time and the number of Newton iterations of the drift-diffusion simulation for various bias conditions when using the proposed acceleration scheme. Two different meshes for the CFET inverter are considered. c Comparison of the total computing time and the number of Newton iterations of the drift-diffusion simulation to obtain the solution at the target bias condition (V_IN = V_DD = 0.7 V). In the conventional bias-ramping process, several max step sizes are considered. d Total computing time versus the number of Newton iterations of the drift-diffusion simulation for various device structures.

So far, we have presented numerical results for the CFET inverter. However, our proposed method is also applicable to other structures incorporating the GAA MOSFETs. As an example, we consider a two-input NAND gate consisting of four single GAA MOSFETs, with its schematic shown in Fig. 8a. As illustrated in Fig. 8b, the quasi-1D model not only reproduces the voltage transfer characteristics well, but also calculates the current through the NAND gate accurately. Moreover, similar to the CFET inverter, the accelerated simulation for the two-input NAND gate achieves convergences with a small number of Newton iterations of the drift-diffusion simulation, regardless of the target bias conditions (Fig. 8c). Fig. 8d compares the acceleration scheme with the conventional bias-ramping process for obtaining the solution at the target bias condition (V_A = 0 V and V_B = V_DD = 0.7 V). With the proposed method, the number of drift-diffusion iterations is reduced by a factor of 26 to 116, while the total computing time improves by 10 to 44 times. Additionally, as shown in Fig. 7d, the results of the two-input NAND gate under two different bias conditions further demonstrate the significant performance improvements achieved by our acceleration scheme.

Fig. 8: Results of the proposed acceleration scheme for the two-input NAND gate.

a Schematic of a two-input NAND gate. b Comparison of results between the quasi-1D model and the technology computer-aided design simulation for the voltage transfer characteristics and I–V curve. c Total computing time and the number of Newton iterations of the drift-diffusion simulation for various bias condition when using the proposed acceleration scheme. Two bias condition of A signal are considered. d Comparison of the total computing time and the number of Newton iterations of the drift-diffusion simulation to obtain the solution at the target bias condition (V_A = 0 V and V_B = V_DD = 0.7 V). In the conventional bias-ramping process, several max step sizes are considered.

Conclusions

We have demonstrated that 3D multigate logic transistors can be simulated with high efficiency using advanced techniques to predict an accurate approximate solution. To achieve orders-of-magnitude acceleration in TCAD device simulation compared to the conventional bias-ramping process, we have introduced two novel approaches: the quasi-1D modeling and region-wise structure analysis. The quasi-1D model enables precise estimation of the quasi-Fermi potential, while the region-wise structure analysis allows for efficient integration of the quasi-1D model into complex device structures, reconstructing an initial guess into the full 3D simulation domain. With these techniques, we have successfully accelerated TCAD device simulations of CFET inverters and other structures, achieving significant computational speedup without the additional cost associated with neural network training. The proposed method has been numerically validated in terms of efficiency, accuracy, and robustness across various device structures, demonstrating its broad applicability and practical significance in next-generation semiconductor R&D process.

The proposed method is based on a simplified model, and this study targets GAA MOSFETs, which are currently among the most important device structures in practice. To apply the proposed method to other devices, separate models must be developed for each device. If a simplified model suitable for each device is developed, the proposed acceleration method is expected to be applicable.

Through the quasi-1D model, I–V curves and voltage transfer characteristics of semiconductor devices can be predicted, and several physical quantities along the channel direction can also be obtained. Therefore, instead of the TCAD device simulation, a calibrated quasi-1D model may be sufficient for obtaining approximate results efficiently. However, the purpose of the TCAD device simulation is not simply to evaluate I–V curves. It is necessary for a precise investigation of the physical phenomena inside semiconductor devices. Since TCAD device simulations are time-consuming, the proposed method enables rapid estimation of internal physical quantities at the desired target bias by accelerating TCAD device simulations.

Although the physical models used in the simulations of this work were not fully comprehensive, we demonstrated consistency between the quasi-1D model and the TCAD device simulation results by employing the same physical models. This approach also enabled acceleration of the TCAD device simulation. Accelerated device simulations considering more accurate physical models for modern semiconductor devices, such as the ballistic mobility model and Fermi-Dirac statistics, could be an important and interesting direction for future work.

The proposed method in this work is applicable to DC simulations, and its extension to time-consuming AC and transient simulations is discussed below. Since AC analysis is a post-processing step based on DC simulation, the proposed method can indirectly enhance its efficiency by reducing the time required for the DC simulation. Due to the absence of nonlinearity in AC analysis, direct acceleration is difficult and may require separate techniques. Transient simulation requires the solution from the previous step, and the initial guess for the next step is typically obtained via extrapolation. The quasi-1D model may offer a better initial guess for the next step, which could be worth exploring in the future.

Methods

Compact charge model

The mobile charge density inside a device cross-section is efficiently described in the compact charge model. Along the channel direction (z-direction), consider the semiconductor cross-section whose permittivity, area, and perimeter are ϵ, A^*, and P, respectively, as shown in Supplementary Fig. 4. The Poisson equation integrated over the device cross-section can be written as

$$-\epsilon P{\langle {\phi }_{\perp }^{{\prime} }\rangle }_{s}-\epsilon {A}^{* }\frac{{d}^{2}\langle \phi \rangle }{d{z}^{2}}={A}^{* }\left(q{N}^{+}-q\langle n\rangle \right).$$

(1)

In this equation, the left-hand-side represents the integrated electrical displacement per unit length. ϕ is the electrostatic potential and ${\phi }_{\perp }^{{\prime} }$ is the surface normal component of ∇ ϕ. 〈 ⋅ 〉 is the average over the cross-section, while 〈⋅〉_s is the average over the semiconductor-insulator interface. On the other hand, the right-hand-side represents the integrated net charge density. q is the absolute elementary charge, N⁺ is the net ionized doping density, and n is the electron density. Three average quantities, ${\langle {\phi }_{\perp }^{{\prime} }\rangle }_{s}$, 〈ϕ〉, and 〈n〉, are related through auxiliary relations detailed in Supplementary Note 2. The above equation and auxiliary relations enable a compact expression for the carrier density across the semiconductor cross-section. Other equations that constitute the compact charge model can be derived through appropriate approximations (Supplementary Note 2 and Supplementary Fig. 6).

Quasi-1D model

In the quasi-1D model, the compact charge model and the 1D continuity equation are solved together using the Newton–Raphson method. In the 1D continuity equation, by using the average quantities, such as 〈ϕ〉 and 〈n〉, the Scharfetter-Gummel scheme⁵³ is applied. The mobility models used in the quasi-1D model are implemented to follow the TCAD device simulation, and the same model parameters are used. For the transverse electric field normal to the semiconductor-insulator interface, a correction factor is introduced to calibrate the calculation results.

Process emulation

In our example, the CFET inverter is generated using the process emulator, G-Process^54,55, a topology simulator based on the level-set method. In the level-set-based topology simulation, structural evolution is modeled by iteratively updating the level-set functions to track surface movement^56,57. To enhance computational efficiency, the sparse field level-set method is employed⁵⁸. By representing the surface as a level-set function, surface orientation calculations and surface merging can be efficiently handled, allowing for the implementation of various process emulation functions. G-Process provides a fully 3D environment for advanced semiconductor process emulation, supporting isotropic process simulation, anisotropic process simulation, and chemical mechanical polishing (CMP) simulation. Upon the user’s request, the level-set representation is converted into a device structure with a closed surface using the marching cubes algorithm^59,60, facilitating visualization and meshing.

The CFET inverter, structured with an NMOS-on-PMOS configuration, is designed with a contacted poly pitch (CPP) of 42 nm, aligned with sub-1.5 nm technology nodes⁶¹. It also incorporates the backside power delivery network (BSPDN)^62,63, where buried power rails (BPRs) are used to form the V_DD and V_SS lines. Fig. 4a illustrates the overall fabrication process for the CFET fabrication process with BPRs. The process begins with the deposition of stacked SiGe/Si layers, followed by fin patterning and shallow trench isolation (STI) formation. Next, dummy gates are patterned, and gate spacers are deposited. To prepare for top and bottom source/drain (S/D) epitaxy, a cover spacer is introduced, effectively isolating the exposed Si channel. After the channel is defined, the bottom dielectric isolation (BDI) is formed, followed by bottom S/D epitaxy and contact formation. The same fabrication steps are applied to the top region, ensuring a well-structured device architecture. Finally, the CFET inverter is completed through a series of advanced steps, including the high-k metal gate process, carrier wafer bonding, and BPR formation.

Device simulation

The CFET inverter used in the TCAD device simulation is shown in Fig. 4a. The final structure is generated using a template-based method, accurately replicating the resultant structure from process emulation. To evaluate simulation efficiency, five different meshes are generated for the CFET inverter, consisting of approximately 381k, 715k, 800k, 883k, and 991k points, respectively. Both the top (NMOSFET) and bottom (PMOSFET) devices share a channel width of 12 nm, a channel thickness of 5 nm, and a gate length of 12 nm. The inner spacer and S/D lengths of the top device are 5 nm and 10 nm, respectively, while those of the bottom device are 7 nm and 8 nm, respectively. The S/D doping concentration is 10²⁰ cm⁻³, and the channel doping concentration is 10¹⁶ cm⁻³. The equivalent oxide thickness (EOT) is assumed to be 1 nm. The gate workfunctions are set to 4.4 eV for NMOSFET and 4.9 eV for PMOSFET, respectively. All simulations are conducted at a temperature of 300 K.

All device simulations in this work have been performed using our in-house device simulation framework, G-Device^30,54,55. The simulations are based on the drift-diffusion model, which solves the Poisson equation, electron continuity equation, and hole continuity equation. Furthermore, in order to take into account the quantum confinement effect, a simplified form of the density-gradient equation⁴⁶ is also solved for each carrier. The comparison between the full form of the density-gradient model and the simplified form of the density-gradient model is shown in Supplementary Fig. 5. In this model, a material-dependent coefficient, γ, is set to 1.25 for NMOSFET and 1.8 for PMOSFET, respectively. As described in Supplementary Note 2, we use a penetrating boundary condition⁶⁴ for the density-gradient equation, and an effective decaying length is assumed to be 0.1 nm at the silicon-insulator interface. The Mujtaba mobility model⁶⁵ is used to account for the mobility degradation due to Coulomb impurity scattering, phonon scattering, and surface roughness scattering. Additionally, the high-field saturation model⁶⁶ is considered, where the gradient of the quasi-Fermi potential is used as the driving force. The calibrated results of the drift-diffusion model against the experimental data^4,67 are shown in Supplementary Fig. 23 of Supplementary Note 6. To ensure consistent runtime comparisons, all device simulations have been performed using a single CPU core.

Both the TCAD device simulation and the quasi-1D model used in this work are based on Boltzmann statistics. Although applying Fermi-Dirac statistics is important for modern devices, our in-house device simulator, G-Device, is still under development. In addition, this study does not consider the ballistic mobility model, which is important for modern devices. Instead, the saturation velocity of the high-field saturation model and the parameters of the Mujtaba mobility model were adjusted for calibration with the experimental data. These are current limitations that should be improved in future work, both in TCAD and in the quasi-1D model.