Cellular plasticity model for self-organized phenotypes in multi-cellular robots

Abstract

Robotic systems often struggle to adapt to dynamic, unstructured environments due to top-down design constraints based on human assumptions. Inspired by biological morphogenesis, this study introduces a cellular plasticity model based on Turing patterns, enabling multi-cellular robots to self-organize their cell phenotypes in response to environmental stimuli. The model leverages reaction-diffusion dynamics to capture key cellular plasticity phenomena observed in muscle cells, neurons, and stem cells. Analytical analysis explores equilibrium points, stability, and conditions for emergent Turing patterns, while simulations examine parametric influences on system behavior. Physical experiments with the Loopy platform demonstrate that its cells dynamically self-organize mechanical properties in response to behavioral and environmental demands. This response enables Loopy to achieve similar performance to empirically optimized static parameters in obstacle-free environments and outperform the static configuration in an environment with limited space. This work advances morphogenetic robotics, presenting a scalable framework for decentralized, dynamic adaptation in unmodeled environments.

Introduction

Robotic design often involves navigating an infinite-dimensional design space, where finding a satisfactory solution is inherently challenging without imposing severe constraints^1,2. Traditionally, this problem is addressed through top-down design approaches, relying on human creativity to narrow the design space^3,4,5. However, these approaches often result in robots that fail to adapt to complex, unstructured, and dynamic environments⁶.

In contrast to this top-down design framework, biological systems are remarkably adaptable and develop through morphogenesis, a bottom-up process in which cells independently self-organize their spatial arrangement and phenotypic properties into complex functional structures in response to internal and external stimuli^7,8,9. This research draws inspiration from this biological process, exploring how robots can similarly self-organize their form and function from the decentralized interactions of their components and the environment. While this framework applies broadly to self-organized phenotypes, this study focuses on mechanical properties—such as stiffness and damping—as a specific example of emergent capabilities. Potential applications of this approach include high degree-of-freedom (DoF) robots operating in dynamic, unstructured environments with limited prior information, such as extra-planetary exploration or chemical spill containment.

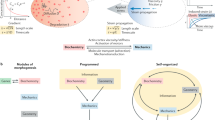
A common framework for describing morphogenesis is Turing patterns, which rely on reaction–diffusion equations to model self-organized pattern formation¹⁰. This framework has been utilized to describe the spontaneous formation of limbs, feathers, seashells, and a multitude of other patterns and structures found in the beauty of the natural world^11,12,13. Robotic systems like Kilobot swarms and Loopy (Fig. 1)^14,15 have leveraged morphogenesis-inspired mechanisms to self-organize the spatial arrangement of decentralized agents. Kilobots, for instance, aggregate in response to chemical gradients, while Loopy’s motor cells respond to chemical concentrations to form a collective cohesive shape. Beyond geometric organization, these systems also demonstrate resilience: Loopy maintains homeostatic stability and corrects self-intersections, while Kilobots reform after damage without explicit programming^14,15. However, despite these advances, both systems primarily focus on static geometric formations and overlook the self-organization of functional properties-such as stiffness, damping, or inertia-and their interactions with the environment^14,15.

Fig. 1: This study develops a cellular plasticity model based on simulated cellular interactions, incorporating reaction–diffusion dynamics and environmental stimuli (left).

These interactions drive the self-organization of Loopy’s cell phenotypes (right, blue vs. red). Specifically, this work focuses on mechanical properties such as stiffness and damping, which adapt to support Loopy’s behavior in response to its shape and environment. Notably, Loopy exhibits a cluster of red (flexible) phenotypes in regions where environmental confinement induces deformation.

At the macroscopic scale of the whole robot, environmental adaptation has been widely studied by evolutionary algorithms, which develop robot populations over generations by selecting high-performing individuals according to predefined fitness functions^16,17,18,19. These methods have been extended to support phenotypic plasticity by allowing robots to switch among multiple phenotypes based on environmental cues, using mechanisms such as gene regulatory networks and evolved mappings between body and controller topologies^20,21. Some approaches also evolve controllers during simulation runtime by randomly updating Boolean network connections and preserving the best-performing configurations²². However, these algorithms require multiple generations of development, limiting their use to simulations and often ignoring the complexities of the natural world²³. Additionally, these algorithms rely on simulating entire populations of robots, which becomes computationally intractable in this work due to the high number of decentralized agents within each robot. Moreover, random mutations could result in catastrophic failures, unsuitable for real-time adaptation in physical robots. Finally, a human designer must specify a fitness function, limiting the self-organization creativity to optimize the human’s limited understanding of the problem^16,17,18,19. This work instead focuses on decentralized, online adaptation within a robot’s lifetime, driven purely by local interactions with real-world environments.

Cellular plasticity, an aspect of morphogenesis, describes how individual cells dynamically adapt their phenotypic properties in response to environmental changes and interactions with neighboring cells²⁴. This adaptive process enables cells to self-organize their functional distributions, collectively supporting the organism’s development and behavior. Observed across diverse cell types—such as muscle cells^25,26,27, neurons^28,29,30, and stem cells^31,32,33—cellular plasticity drives specialization, role adjustment, and cooperative behaviors for collective functionality. However, these responses’ inherent complexity and variability have posed challenges to developing a simplified general model applicable to any phenotype. This has, in turn, complicated the integration of cellular plasticity into bottom-up robotic design frameworks, even though intricate models exist for specific biological processes^34,35,36.

Recognizing this challenge, our work does not aim to develop a universal model that applies to all facets of cellular plasticity. Instead, we focus on distilling core adaptation phenomena from muscle cell hypertrophy, neuron synaptic plasticity, and stem cell differentiation into a simplified model tailored for morphogenetic robots.

Muscle cell hypertrophy describes how muscle cells adapt to various stimuli through several mechanisms. One key mechanism is mechanical load signaling²⁵. When muscle cells experience mechanical stress or damage, they are signaled to enhance their strength and endurance in response. Another crucial factor in muscle cell development is the response to oxygen deprivation²⁶. When muscle cells detect a reduction in oxygen levels, they initiate adaptations to improve oxygen uptake. Furthermore, muscle cells respond to metabolic stress²⁷. For example, when ATP (adenosine triphosphate) levels are low, indicating a high energy demand, muscle cells are triggered to increase mitochondrial production, thus increasing their energy-generating capacity²⁷. These phenomena of muscle cell hypertrophy demonstrate that the growth of functional capacity (oxygen uptake, mitochondria) is stimulated by product (oxygen, ATP) scarcity.

Long-term potentiation (LTP) and long-term depression (LTD) are key processes that enable neurons to adapt their synaptic strength based on signal activity. LTP strengthens the connection between two neurons when presynaptic signals are closely followed by sufficient postsynaptic activation, a process mediated by NMDA receptors and calcium influx²⁸. However, LTP does not occur instantly; it often develops gradually²⁹. Strong, repeated stimuli can sustain LTP for extended periods, lasting days or weeks, although evidence for permanent changes remains limited³⁰. In contrast, weak or brief stimuli produce only transient LTP, whereas prolonged low-frequency signals can lead to LTD, weakening the strength of the synaptic connection. Overall, LTP and LTD reflect a neuron’s ability to adjust its synaptic strength temporarily, depending on the type and duration of stimuli²⁹. These mechanisms demonstrate how neurons dynamically adjust their functional capacity in response to sustained stimuli, strengthening connections through LTP under high stimuli environments and weakening them through LTD under low stimuli environments.

Stem cells, particularly embryonic stem cells, serve as the foundational units for cell development, possessing the unique ability to differentiate into various cell types to increase their functional capacity^31,32,33. Environmental factors, such as the oxygen concentration, temperature, and mechanical stiffness of the extracellular matrix, are examples that guide the differentiation process³². In addition, stem cells inherit intrinsic factors from their parent cells, including epigenetic elements such as histone modifications³³. These factors significantly influence the differentiation pathway of a stem cell, affecting how it develops into a more specialized cell type. As stem cells specialize, they gradually lose their ability to differentiate into multiple cell types³¹. Despite this specialization, these cells retain a degree of adaptability, which allows them to respond to changes and perform specific functions within their designated cell type³³. These phenomena highlight two key aspects of cellular plasticity: that specialization can enhance functional capacity, and that differentiation is shaped by intrinsic (epigenetic) and environmental factors.

Integrating cellular plasticity phenomena from muscle cells, neurons, and stem cells with Turing patterns may provide a scalable, decentralized approach for agents to dynamically adapt their functional capabilities in response to environmental and behavioral demands. Enabling self-organized phenotypes extends morphogenetic robotics beyond spatial formations to the emergence of functional structures in response to environmental and behavioral changes.

This study investigates decentralized strategies for the online self-organization of a robot’s functional capacities, focusing on mechanical properties, through the lens of cellular plasticity and Turing patterns. In doing so, the robot must balance functionality and adaptability to conform to unknown and dynamic environments. This problem includes three components: (1) developing a general cellular plasticity model, (2) analyzing the model’s dynamics and parametric effects, and (3) deploying the model on a robot platform to observe its self-organized mechanical properties in response to diverse morphologies, environments, and behaviors.

In this work, the cellular plasticity model without central control must capture key aspects of cellular plasticity observed in biological systems, precisely: (1) growth spurred by product scarcity, exemplified by muscle cell hypertrophy^25,26,27; (2) functional capacity modulation in response to sustained stimuli, seen in LTP and depression of neuronal synaptic strength^28,29,30; (3) the enhancement of total capacity through specialization, as demonstrated by stem cell differentiation^31,32,33; and (4) the process is self-regulating by adapting to immediate environmental stimuli in real time without relying on fixed set points or a comprehensive environmental model. Next, we utilize the Loopy robot and assume it is in a flat, obstacle-laden environment that is unknown and unmodeled to the robot. Although this study focuses on mechanical properties such as stiffness and damping, the framework is designed to be generalizable to other functional capabilities, with the potential for diverse applications requiring further exploration.

This study builds on our previous work across three fronts. Swarm of One¹⁵ introduced the Loopy platform and demonstrated the emergence of diverse, stable robot morphologies through Turing patterns. Loopy movements³⁷ extended this by showing how decentralized morphogen signaling could produce coordinated rotational behaviors on the same platform. Separately, the cellular plasticity model³⁸ proposed an initial activator–inhibitor framework for phenotypic adaptation, but this was limited to a single cell, without spatial context. In contrast, the present work extends that model into a spatially organized Turing pattern, enabling the self-organization of cell phenotypes—specifically mechanical properties—across multiple cells. This is the first physical demonstration of the cellular plasticity model in a multi-cellular robot, integrated with Loopy’s previously developed morphogenetic capabilities. This study contributes to the literature by:

• Creating a general cellular plasticity model based on Turing patterns for the bottom-up design of robots.

• Providing analytical and simulation analysis of this model’s equilibrium points, stability, and parametric effects on its transient response and spatial patterning.

• Physical experiments demonstrate Loopy’s cells dynamically self-organizing their mechanical properties to environmental and behavioral demands, matching the performance of optimized static properties in obstacle-free environments and outperforming them in a confined environment.

The rest of this work is outlined as follows. Section “Results” provides the model analysis and experimental results. Section “Discussion” discusses key aspects of the results and includes a comparison between the cellular plasticity model and related computational frameworks to contextualize its distinct capabilities. Finally, section “Methodology” describes Turning patterns, the development of the model from singular cells with one ability to multiple cells with many abilities, and the experimental setup.

Results

Utilizing the methodology from the section “Methodology,” this section investigates the cellular plasticity model’s behavior across key scenarios. The analysis begins with the steady-state behavior, stability criteria, and dynamic responses of a single phenotype (i.e., factory) cell to impulse, step, and periodic changes in environmental stimuli (i.e., consumption rates). The analysis then examines the effects of opposition between factories in a multi-factory cell, its emergent phenotype, and total factory capacity, followed by exploring Turing pattern emergence in single and multi-factory cells under varying consumption rate distributions. Finally, the model’s applicability is demonstrated on the Loopy platform, highlighting its ability to generate self-organized mechanical properties from environmental interactions.

Steady state and stability criteria

This experiment analyzes the dynamics of a single-cell system with a single factory–product pair, focusing on steady-state values. The phase portrait of the system, including factory and product nullclines, is shown in Fig. 2, with the nullclines defined by (1) and (2).

$$\frac{{\rm{d}}F}{{\rm{d}}t}=0:F=\frac{D\cdot C\cdot P}{G-K\cdot P}$$

(1)

$$\frac{{\rm{d}}P}{{\rm{d}}t}=0:F=\frac{C\cdot P}{R-I\cdot P}$$

(2)

Fig. 2: A representative phase portrait of a single factory cell’s response with the product (orange) and factory (blue) nullclines, and a single non-zero equilibrium (red star) with parameters of G = K = I = C = 1.0, D = 0.01, and R = 1.5.

P_lim describes the limit product level as the product nullcline approaches infinity, while P_∞ describes the factory nullcline asymptote. The inward direction of the phase portrait signifies a stable non-zero equilibrium.

The system’s equilibrium points are located at the intersections of these nullclines. The phase portrait (Fig. 2) reveals two equilibrium points (red stars): an unstable equilibrium at the origin (0, 0) and a stable equilibrium at (P*, F*). The stable equilibrium is defined by (3) and (4).

$${P}^{* }=\frac{G-D\cdot R}{K-D\cdot I}$$

(3)

$${F}^{* }=A\cdot C,\quad \,\text{where}\,\quad A=\frac{G-D\cdot R}{K\cdot R-G\cdot I}$$

(4)

From (3), the steady-state product level P* is independent of the environmental stimulus C and is fully determined by system parameters. In contrast, the steady-state factory level F* scales linearly with the environmental stimulus, with the gain (A) defined by the system parameters (4). Thus, the factory adjusts dynamically based on the external input. Further analysis of the nullclines reveals that the factory nullcline approaches P = G/K = P_∞ as the factory approaches infinity, while the product nullcline approaches P = R/I = P_lim. Furthermore, for a non-zero equilibrium to exist, it is required that P_∞ < P_lim. This ensures that the system stabilizes at a meaningful level, with alternatives diverging or collapsing to zero. Moreover, G/R > D to ensure positive steady-state values for P* and F* from (3) and (4).

The stability of the equilibrium points is evaluated by analyzing the trace (δ) and determinant (Δ) of the Jacobian matrix at (0, 0) and (P*, F*). Stability is achieved only when both δ < 0 and Δ > 0.

$${\delta }_{(0,0)} < 0:G < C$$

(5)

$${\Delta }_{(0,0)} > 0:D > G/R$$

(6)

$${\delta }_{({F}^{* },{P}^{* })} > 0:\frac{G-{\rm{KP}}^{* }}{AI+1} < C$$

(7)

$${\Delta }_{({F}^{*},{P}^{*})} > 0:G/R > D$$

(8)

From (6), the origin will be unstable, independent of the environmental stimulus (C), by selecting appropriate system parameters to violate (6). In addition, making the origin unstable aids in stabilizing (P*, F*), as it is the reverse condition (8). Furthermore, this condition is repeated from (3) for positive steady states. However, the trace of (P*, F*) may become unstable if C is minor (7), but if D<<, then (G − KP*) ≈ 0, thus stabilizing the system for all C > 0.

Examining system behavior along the axes, from Fig. 2 and (23) and (24), reveals that the product level P always remains positive if it starts positive, as $\frac{{\rm{d}}P}{{\rm{d}}t} > 0$ when P = 0. However, the factory quantity F may become negative, as $\frac{{\rm{d}}F}{{\rm{d}}t} < 0$ when F = 0. Therefore, an artificial constraint must be applied to enforce F > 0 to maintain physical significance.

In summary, this analysis highlights several essential observations. The steady-state product level P* is determined by system parameters, while F* scales linearly with the consumption rate C. In addition, to ensure that the system is stable and maintains biological significance, the model (23) and (24) must meet these additional conditions:

$$\frac{G}{K}={P}_{\infty } < {P}_{lim}=\frac{R}{I}$$

(9)

$$D < < G/R$$

(10)

$$F > 0$$

(11)

Furthermore, this model displays the fourth cellular plasticity phenomenon, self-regulation, where adaptations rely on direct environmental stimulus (e.g., consumption rate C) rather than an environment model. By using real-world stimuli to influence product levels and factory capacities, the robot could adapt to the complexities of unpredictable real-world conditions that a human-specified model might neglect.

System response to impulse and step changes in consumption

Next, to analyze the system response to an impulse and step changes in the consumption rate of the environment, the system with parameter values of G = K = I = 1.0, R = 1.1, and D = 0.01 was subjected to a significant increase in the consumption rate (2 product/time unit) for a short duration (2-time units) and long duration (50-time units) and plotted in Fig. 3 along with the net production rate PR = R − I ⋅ P and steady-state factory (F*) and product levels (P*).

Fig. 3: Product (P) and factory (F) transient response to an impulse (at t = 50) and step (at t = 100) in consumption (C).

In addition to the net production rate, PR = (R − IP). Furthermore, the steady-state factory, product, and production rate are plotted with dotted lines. Parameter values are G = K = I = 1.0, D = 0.01 and R = 1.1.

The first observation of Fig. 3 is that the model exhibited distinct behaviors on different time scales of resource fluctuation. For impulses (at t = 50), the production rate increased rapidly with only a small increase in factory capacity. However, the factory capacity increases significantly for step changes (at t = 100). Furthermore, a higher quantity of the factory persists after the removal of the heightened consumption rate until it eventually decays and the factory capacity returns to the new steady state of the environment.

This response illustrates the first targeted phenomenon: growth driven by product scarcity. Factory growth is initiated only when product levels drop below their steady-state value, as shown in Fig. 3. This behavior is analogous to muscle hypertrophy, where cells increase mitochondrial growth in response to ATP deprivation^26,27. Additionally, the second phenomenon, functional capacity modulation in response to sustained stimuli, is evident as only the step change in environmental demand significantly alters the factory quantity, while the impulse triggers only a temporary production increase. This is similar to LTP/LTD, where sustained activity is required to modulate synaptic strength^28,29,30. Together, these adaptive responses enable cells to effectively handle prolonged and dynamic demand surges while avoiding excessive reactions to transient spikes.

System response to frequency of consumption

This experiment evaluates the model’s response to periodic stimuli by subjecting it to a consumption rate (C) with a constant amplitude and variable frequency. The consumption rate was defined as:

$$C={\rm{Amp}}\cdot \left(1+\sin (2\pi \omega t)\right)$$

(12)

The amplitude (Amp) was set to 1.0, and the frequency in Hz (ω) was logarithmically spaced from 0.01 to 100 Hz. The factory and product responses’ mean values and amplitudes were recorded and plotted in Fig. 4.

Fig. 4: Frequency response of a cell with a single factory.

The factory and product mean, and their amplitudes are plotted. The factory mean marginally changed with frequency, while its amplitude decreased with higher frequencies. The product was unaffected by changes in frequency. Parameter values are G = K = I = 1.0, D = 0.01 and R = 1.1.

The results, illustrated in Fig. 4, reveal that the frequency of the consumption rate had a small effect on the mean levels of the factory and product. In addition, the amplitude of the product response remained very small across all tested frequencies. However, the factory amplitude was large at low frequencies and diminished substantially at high frequencies, consistent with the typical behavior of oscillatory systems, where amplitude decreases as frequency increases. At low frequencies, the factory amplitude increased because the factory had sufficient time to adapt to the periodic input. This adaptation is less pronounced at higher frequencies, where the rapid oscillations do not allow the factory to respond effectively. This characteristic highlights the model’s potential to filter out high-frequency noise, which often appears in dynamic systems, making it desirable for enhancing resiliency to environmental perturbation.

Parametric effects on system time constants

Now that the general behavior of the model has been analyzed, the parametric effects on the model dynamics are examined via simulations to evaluate the time constants of the factory (τ_F) and product (τ_P) in response to step changes in consumption rate. To simplify the analysis, The system is reparameterized from (G, K, R, I, D) to the nullcline asymptotes (P_∞ and P_lim) by dividing (23) by G and (24) by R and keeping D constant and small for stability (D = 0.01). This parameter reduction simplifies analysis from five parameters to two. In Fig. 5, P_∞ and P_lim were varied from [0.1] to [5] with C = 1.0 with the time constant ratio (τ_F/τ_P) plotted as a heatmap.

Fig. 5: Parametric effects on the relative time constants of the product (τ_P) and factory (τ_F), particularly as system parameters near instability τ_F becomes much larger than τ_P.

The orange region displays where the product time constant exceeds the factory time constant. Damped oscillatory modes emerge when P_lim significantly exceeds P_∞, marked by the white region.

Figure 5 shows that as P_∞ and P_lim approach the instability threshold, the relative time constant between the factory and the product becomes very large. As P_∞ and P_lim move away from instability, the factory time constant eventually becomes smaller than the product time constant (the orange region in Fig. 5). Furthermore, as P_lim increases relative to P_∞, the system exhibits a damped oscillatory response (the white area in Fig. 5). This causes the factory capacity (F) to overshoot its steady state, leading to an over-response to stimuli, despite being stable when P_∞ << P_lim. Therefore, due to the model constraint that the factory time constant is slower than the product time constant (τ_F > τ_P), the valid parameter range is restricted to the heat map region. Moreover, this figure can be utilized by a human designer to select the adaption rate of the model, where the higher the time constant ratio, the slower the adaptation.

Effects of opposition on multi-factory cell phenotype and total capacity

To assess the impact of the opposition parameter on factory steady-state levels, we analyzed a system with two factories, for simplicity and ease of visualization. Each factory had identical parameters, and the system was tested under varying consumption rates ([0.1–3.0]) across three scenarios: low-symmetric opposition (O₁₂ = O₂₁ = 0.001), high-symmetric opposition (O₁₂ = O₂₁ = 0.05), and asymmetric opposition (O₁₂ = 0.05, O₂₁ = 0.001). Figure 6 displays the phenotype for each scenario. Blue represents a cell with a greater quantity of the first factory (F₁), and red represents a cell with a greater quantity of the second factory (F₂) for the given environmental stimuli (C₁ and C₂).

Fig. 6: Parametric Effects of Opposition on Emergent Phenotypes.

Effects of low (A), high (B), and asymmetrical (C) opposition rates (O_ij) on the steady-state factory quantities of a multi-factory cell for the given environment stimuli (C₁ and C₂). Blue phenotype indicates cells with a higher concentration of F₁, while red indicates a higher concentration of F₂. Purple indicates a blended phenotype of red and blue. Lower opposition increases the blended region, and asymmetric opposition can favor one phenotype over another, by the increased red region in (C).

The initial analysis of Fig. 6 reveals that when the opposition rates are low (Fig. 6A), there is a smooth blend from red to blue phenotype as the environment transitions from a high stimulus of C₁ to a high stimulus of C₂. However, if the opposition is high (Fig. 6B) and both consumption rates are high, we see a stark switch from bright red to bright blue. Thus, any subtle shift in environmental stimulus from perfectly equal will switch the cell from a blended purple to a red or blue phenotype. Furthermore, from Fig. 6C, by applying asymmetric opposition, the cell can be pre-biased to producing more of one factory than the other for a given pair of environmental stimuli, where the cell more readily specializes to the lesser opposed factory, as demonstrated by more prominent red than blue region.

Next, to analyze the effects of opposition on the total capacity of the multifactory cell, the consumption rates for a cell with two identical factories with symmetric high opposition (O₁₂ = O₂₁ = 0.05) were varied from [0.1] to [3.0], and the total capacity was plotted as a heat map along with contours of total consumption (TotCon = C₁ + C₂) and total capacity (Total capacity = F₁ + F₂).

The results, displayed in Fig. 7, reveal that as the cell specializes—shifting capacity predominantly toward one factory—the total capacity increases. This is most evident along the total consumption line (TotCon = 2.0), where tracing from the 45 deg line (equal consumption rate) outward toward either factory F₁ or F₂ shows a significant rise in total capacity. Specifically, total capacity increases from approximately 9 near the center to over 20 as one factory dominates. This observation underscores the relationship between specialization and total capacity, highlighting how a multi-factory cell can enhance its overall functional capacity by favoring one factory over balanced production.

Fig. 7: Heatmap of the total capacity of a two factory cell relative to the consumption rates of factory 1 (C₁) and factory 2 (C₂).

Black lines are contour lines of total factory capacity, while white lines are contours of constant total consumption (TotCon). Total capacity is minimized when consumption rates are equal, i.e., on the 45-degree diagonal.

From Fig. 6, asymmetric opposition rates can bias cell development into a particular phenotype. This effect is similar to histone modifiers that intrinsically bias stem cell development³³. In addition, these parameters can be utilized by the human designer to influence but not directly control the emergent phenotype. Furthermore, Fig. 7 demonstrates that the model captures the third core phenomenon: specialization increases total capacity due to the total capacity of the cell being minimal when equally supporting the environmental demands. This specialization mechanism underscores the importance of adaptability and efficiency in robotics, indicating that robots initially equipped with multiple functions can dynamically adjust their functional capacity to prioritize higher-demand functions.

Criteria for the emergence of Turing patterns

Next, we will investigate the conditions in which the single factory model will generate a Turing pattern. First, we utilize the conditions from ref. ³⁹ to determine analytically when Turing patterns emerge from the model. Then, we perform a simulation analysis of a 100-cell system to verify the analytics in Fig. 8.

Fig. 8: The emergence of a striping Turing pattern.

A, D display the initial factory quantities with consumption rates of 1.0 and 5.0, respectively. B, E display the factory quantity in each cell over time. C, F display the final factory distribution. A Turing pattern emerges when C is low (C), but when C is high, the pattern is suppressed (F). When the Turing pattern emerges, the total capacity of the cells is marginally greater (3%) than the single-cell scenario (F*). Parameter values: P_∞ = 1.0, P_lim = 1.5, D = 0.1, γ_F = 0.01, and γ_P = 100).

The four conditions for a Turing pattern (19)–(22) applied to the single factory model are listed in (13)–(16).

$${J}_{11} > 0:{P}_{\infty } > {P}^{* }$$

(13)

$${J}_{22} < 0:-IA-1 < 0$$

(14)

$${J}_{11}+{J}_{22} < 0:\frac{G-K{P}^{* }}{AI+1} < C$$

(15)

$$\frac{{\gamma }_{P}}{{\gamma }_{F}}{J}_{11}+{J}_{22} > 0:\left(\frac{{\gamma }_{P}}{{\gamma }_{F}}\right)\frac{G-K{P}^{* }}{AI+1} > C$$

(16)

From these conditions, (13) and (14) are always valid for the given parametric constraints, while (15) is valid from the stability analysis if D is small and C is sufficiently large. Furthermore, (16) is valid if C is sufficiently small or γ_P/γ_F is sufficiently large. Therefore, there exists a range of consumption rates that is sufficiently large for system stability yet small enough to allow a Turing pattern to emerge. Furthermore, this indicates that the Turing pattern may be suppressed if the environmental stimulus is substantial.

Next, to verify the analytical results, 100 identical single factory cells with parameters (P_∞ =  1.0, P_lim = 1.5, D = 0.1, γ_F = 0.01, and γ_P = 100) are uniformly subjected to a consumption rate (C) = 1.0. Each cell started with its product level equal to its factory level at 1.0, except for the 50th cell, which was initialized with a slight increase (1.001) to seed the pattern (Fig. 8A). Next, in Fig. 8B, the emergence of the Turing pattern is shown from near uniformity (pink, left) to striping of the cells (white, purple, right). Lastly, Fig. 8C displays the factory quantities at the end of the simulation, presented in a striping pattern of HIGH–LOW three cells wide. Furthermore, in Fig. 8D–F, the consumption rate is increased to 5.0, and a Turing pattern does not emerge. This aligns with our analytical analysis, where if the consumption rate is high enough, then the Turing pattern effect is suppressed. Furthermore, when the Turing pattern occurred, the system’s total capacity marginally increased by 3% compared to the single-cell case (F*). Figure 8 highlights how cells self-organize their functional capacities into distinct striped patterns of high and low functionality phenotypes when environmental demand is low. Under such conditions, only a subset of cells are recruited to specialize and meet the environmental demand, leaving others free to potentially specialize in alternative functions. This striping effect efficiently distributes functional capacities across the tissue without reducing the total capacity of the collective robot compared to a scenario where cells operate independently without diffusive effects (F*). Conversely, when environmental demand is high, the striped patterns are suppressed, and all cells are uniformly recruited to maximize their functionality and meet the immediate requirements. This dynamic response demonstrates the system’s ability to allocate resources efficiently under low demand while ensuring collective action under high demand, offering significant advantages for self-organizing robots operating in dynamic environments.

Effects of consumption rate distribution on the turing patterns of multi-factory cells

The following experiment assessed how the Turing patterns emerge in cells with multiple factories and spatially varying environmental stimuli. In this experiment, 100 identical cells consisting of two factories of symmetric opposition were subjected to spatially uniform, in-phase, and anti-phase consumption rates between the two factories. Figure 9 displays the results for the simulation with the initial conditions (first column), transience (middle column), and final factory quantities (right column). Furthermore, the self-organized factory quantities are compared to the steady-state factory quantity of a single cell without diffusion (F^ND) and without diffusion or opposition (F*). The cells had parameter values of (P_∞ = 1.0, P_lim = 1.5, D = 0.1, O₁₂ = O₂₁ = 0.02, γ_F = 0.01, and γ_P = 100).

Fig. 9: Environmental stimulation distribution effects on a two-factory Turing pattern.

A, D, G display the initial conditions for uniform, in-phase, and anti-phase distributions. In addition, the steady state without diffusion $F_{i}^{ND}$ and steady state without diffusion or opposition F* for each factory are plotted. B, E, H display the cell phenotype and factory quantities over time. C, F, I display the final factory distributions. In each scenario, the two factory turning patterns self-organize into an alternating striping pattern, where the amplitude of the stripe matches the environment stimulation. The total capacity of the two-factory Turing pattern was marginally greater (<2%) than the unopposed non-diffusive case (F*). However, the total capacity was significantly greater than the opposed non-diffusive case F^ND, (17% for uniform, 24% in-phase, 9% anti-phase). Parameter values: P_∞ = 1.0, P_lim = 1.5, D = 0.1, O₁₂ = O₂₁ = 0.02, γ_F = 0.01, and γ_P = 100.

Analyzing Fig. 9A–C, an anti-phasing turning pattern emerges when both factories are subjected to the same uniform stimulus. This is due to the opposition parameter, where when the natural turning pattern of a single factory starts to emerge, some cells have a high concentration of Factory 1, and others have a low concentration of Factory 1 (Fig. 8). The factories with a high concentration of Factory 1 greatly oppose the growth of Factory 2 in those cells but still require Factory 2’s products. Thus, cells with lower levels of Factory 1 experience less opposition to producing Factory 2. Additionally, they receive increased stimulation from neighboring cells that rely on Factory 2’s product, further accelerating the growth of Factory 2. Therefore inducing the anti-phasing of the factories. This additional reinforcement induces the Turing pattern to emerge much quicker (t = 400) than the single factory case (t = 1500, Fig. 8).

Next, the magnitude of the emergent factory quantities corresponds to the environmental stimuli, as seen in Fig. 9C, F, I. In Fig. 9F, Factory 1 and Factory 2 self-organize into regions of high concentration where their respective stimuli are strong and low concentration where stimuli are weak. Similarly, in the anti-phasing case (Fig. 9I), Factory 1 reaches higher concentrations in regions where its stimulus is strongest, while Factory 2 follows the same pattern. This demonstrates that the Turing pattern aligns with the environmental demand, with the stimulus level directly influencing the pattern’s amplitude.

Next, in terms of total capacity, the total capacity of the tissue with diffusion and opposition is marginally greater (<2%) than that of the unopposed system without diffusion (F*) and significantly greater than that of the opposed system without diffusion (F^ND), (17% for uniform, 24% in-phase, 9% anti-phase). This is due to the anti-phasing of Turing patterns, which minimize the opposition in each cell, allowing it to reach a high factory concentration to support itself and its near neighbors. Therefore, in terms of total capacity, the opposition is synergistic with diffusion, as it allows cells to specialize entirely into their more dominant ability and receive other products from neighboring cells.

Emergence of mechanical properties of the Loopy robot

This experiment evaluates Loopy’s ability to self-organize its mechanical properties across two environments—contained and obstacle-free—and three morphogenetic behaviors: formation, metamorphosis, and morphology rotation. An external script sequentially modifies the underlying reaction–diffusion system parameters to trigger transitions between these behaviors. Loopy begins in a random initial configuration within the contained environment, where it is directed to form a circular morphology, metamorphose into a three-lobed shape, and then rotate its morphology. The environment is then manually switched to obstacle-free, where Loopy continues morphology rotation, stops rotation, and finally returns to a circular morphology through another metamorphosis. Each phase lasts 2 min.

The cellular plasticity model parameters used in this experiment are P_∞ = 1.0, P_lim = 1.5, D = 0.1, γ_F = 0.01, and γ_P = 100. Asymmetric opposition favoring speed (O_ds = 0.001, O_sd = 0.05) is employed to account for the shorter duration of speed stimuli relative to position error, supporting motor speed. To align with the motor’s operating range, position error and speed were scaled by factors of 10 and 20, respectively, while the spring constant (K_s) and damping constant (K_d) were scaled by 100. Each cell was initialized with a quantity of 0.5 for both factories and 1.0 for both products. Furthermore, since the factory quantity may drop below zero, it was artificially limited to 0.1. The morphogenetic behavior parameters are from refs. ^15,37 and displayed in Table 1. To seed the three-lobed formation during the contained metamorphosis phase, consistent with the approach used in section “Results—Criteria for the emergence of turing patterns,” a small activator increase of 0.01 was applied at the start of the phase. This increase was introduced in the motor cell with the highest position error as an ideal case to reduce the error.

Table 1 Morphogenetic behavior parameters

The proposed cellular plasticity model CP is compared to constant stiffness (K_s = 200) and damping (K_d = 200) parameters, PT, empirically tuned for performance (i.e., low position error) in the obstacle-free environment, similar to previous studies^15,37. The CP model is also compared to the PT configuration in an exclusively obstacle-free scenario, PT_free, where the same morphogenetic behaviors are applied. The PT and PT_free configurations were chosen to reflect the human design assumption that Loopy will only be in an obstacle-free environment as made in refs. ^15,37. The PT_free case represents Loopy’s performance under the assumed condition, while PT allows us to examine the performance when the assumption is violated. In contrast, CP showcases the benefits of adaptability in scenarios the designer did not foresee, dynamically adjusting to both expected and unexpected environmental demands.

Each configuration (CP, PT, PT_free) underwent ten trials, and the motor-cell performance: position error, motor speed, and motor failures are displayed in Fig. 12. To accommodate the skewed data distributions introduced by motor failures while still being sensitive to these failures, results are reported using the mean and upper/lower semi-variance⁴⁰ across all cells and trials. Additionally, the data is smoothed temporally with a rectangular kernel of 10 s. An example image of Loopy in each experimental phase is shown in Fig. 11. Furthermore, Fig. 10 illustrates each motor cell’s phenotypes and total capacity (F_s + F_d) from an example CP trial. The following phase-by-phase analysis examines how Loopy’s mechanical properties emerge and adapt under different environments and behaviors, beginning with the contained formation phase.

Fig. 10: An example of Loopy’s cell phenotypes and total capacities across the six phases of the emergence of mechanical properties experiment.

A Red cells exhibit a high concentration of F_s, resulting in low stiffness and high damping, while blue cells have a high concentration of F_d, leading to low damping and high stiffness. Purple cells remain unspecialized, lacking total factory capacity (B), and thus exhibit high stiffness and damping. The red, low-stiffness phenotype dominates during stationary and confined phases, whereas the blue, low-damping phenotype prevails during the rotation phases. In contrast, the purple, high stiffness and damping, phenotype is most prevalent in the obstacle-free stationary phases. These trends demonstrate Loopy’s ability to dynamically adapt its mechanical properties in response to changing morphologies, environments, and behaviors.

Fig. 11: Each Loopy configuration during all experiment phases.

The red circle encompasses cells 3–10 with low stiffness. Yellow jagged are motors that experienced an over-torque failure during that phase.

Fig. 12: Loopy’s average cell performance across ten trials of the six phases of the emergence of mechanical properties experiment.

Each subplot displays the mean and upper/lower semi-variance for position error (A), motor speed (B), and cumulative motor overtorque failures (C). The proposed cellular plasticity method CP had less position error than the performance-tuned configuration PT throughout the six phases due to PT experiencing an average of 4.5 motor failures while CP only experienced 1.1 failures. In addition, CP in the obstacle-free environment performed similarly to the performed-tuned configuration that only experienced an obstacle-free environment PT_free. The proposed method also had the greatest motor speed during the rotation phases. These trends highlight Loopy’s resiliency and ability to adapt to support its behavior in changing environments.

Contained formation phase t = (0, 120)

Initially, as Loopy transitions from random initial conditions to a circular morphology, all cells exhibit a low-damping phenotype (F_d; blue in Fig. 10A) during the rapid formation stage (t = (0, 5)), where motor speed dominates. Once the robot stabilizes and interacts with the container boundaries, when deformations are dominant, phenotypes shift to include low stiffness (F_s, red) and high damping and stiffness (purple) (t = (5, 120)). These low-stiffness phenotypes arise as the robot deforms in the confined environment. The total capacity plot (Fig. 10B) shows that cells 3–10 exhibit increased F_s with further reduced stiffness, corresponding to regions most affected by the container boundaries as shown in Fig. 11.

Figure 12 reveals that the cellular plasticity (CP) method achieves a comparable mean position error to the PT configuration but with significantly lower upper semi-variance. This indicates that, under PT, a small subset of motors experienced disproportionately high errors, while most remained near nominal. In contrast, CP distributed error more evenly across motors, resulting in moderate, consistent performance. This trend aligns with Fig.12C, where an average of three PT motors experienced over-torque failures and became nonfunctional for the remainder of the experiment, compared to less than one motor under CP. These results suggest that PT concentrated mechanical stress on fewer motors, increasing failures, whereas CP mitigated this by distributing stress across the system.

Contained metamorphosis phase t = (120, 240)

During the contained-metamorphosis phase, the phenotype patterns remain similar to those observed during the contained-formation phase. However, the reduced stiffness exhibited by cells 3–10 diminishes as the morphology transitions within the contained environment, resulting in a decreased total capacity (Fig. 10B). This likely occurred because the three-lobed shape was seeded at the cell with the highest position error (cells 3–10); thus, their position errors were reduced, decreasing F_s, and increasing their stiffness.

Like the contained formation phase, the average position error of CP and PT during the contained metamorphosis phase was similar, with CP having a much smaller upper semi-variance (Fig. 12A). However, the upper semi-variance of PT increased during this phase. This was likely due to the cumulative motor failures increasing to an average of 4.5 compared to CP’s  <1 average motor failures (Fig. 12C). This further highlights the resilience of the proposed CP method, which reduces such failures by more evenly distributing position errors, aiding reliable operation even under environmental constraints.

Contained-morphology-rotation phase t = (240, 360)

During this phase, a notable shift in cell phenotypes occurs, with many cells transitioning from low stiffness (red) to low damping (blue), as shown in Fig. 10A, due to the persistent speed of the motor cells. Despite this shift, four stripes of high flexibility remain present due to the confined space deforming the shape. The total capacity increases significantly, as seen in Fig. 10B, likely due to the simultaneous presence of speed and position error stimuli during the morphology rotation, as well as the favorability of the inverse damping factory (F_d) resulting from asymmetric opposition.

Regarding performance, the proposed CP approach’s mean position error and upper semi-variance are similar to PT for this phase. This is likely due to CP often experiencing a motor failure by this stage (Fig. 12C) and self-organizing a few motors to become highly flexible, like in Fig. 10A, which had four flexible groups of cells (red stripes) similar to the average motor failures (4.5) of PT. However, the motor speed of CP was higher than both PT and the unconfined PT_free. These results demonstrate the proposed system’s adaptability, where the cells can rapidly change phenotypes from F_s (low stiffness, red) to F_d (low damping, blue) in response to behavioral changes to exert a more dynamic response, indicated by the higher motor speed.

Free-morphology-rotation phase (t = 360, 480)

During this phase, two of the four high-flexibility phenotypes (red) stripes transition to low-damping phenotypes (blue), as illustrated in Fig. 10A. This transition occurs while maintaining a total capacity comparable to that of the contained-morphology-rotation phase. The shift is likely attributable to the robot exiting the confined environment, which reduces movement restrictions and, thus, deformations. In terms of performance, Fig. 12A shows that the proposed approach (CP) exhibits rapid adaptation, with the position error decreasing to levels comparable to PT_free despite its average of one failed motor. In contrast, the performance-tuned system (PT) fails to recover to the performance of PT_free after being removed from confinement. This is likely due to the average 4.5 motor over-torque failures experienced during earlier phases. These results demonstrate the proposed approach’s adaptability to environmental changes, rapidly achieving performance comparable to the idealized PT_free once unconfined.

Free-rotation-stop phase t = (480, 600)

During this phase, the cell phenotypes shift from low damping (blue) to a striping pattern of low stiffness (red) and high stiffness and high damping (purple), as illustrated in Fig. 10A. This transition corresponds to a notable decrease in total capacity, as shown in Fig. 10B, reflecting the robot’s adaptation to the cessation of rotational movement and small position error (Fig. 12A). However, CP’s position error remains above PT_free due to its average of 1.1 motor failures, but CP has less mean and upper semi-variance position error than PT with its average of 4.5 failed motors.

Free-metamorphosis phase t = (600, 720)

In this phase, the cell phenotypes transition rapidly, initially exhibiting slightly lower damping (blue) as the system responds to the metamorphosis into a circular morphology (Fig. 10A, t = (600, 610)). Once the circular morphology is established, the system settles into a slightly flexible (red) and high-stiffness with high-damping (purple) phenotype-stripped pattern by t = 720. This behavior arises from the sudden morphological shift, which temporarily increases motor speed, leading to a drop in damping. As the circle stabilizes, slight deformations persist, resulting in low position error consumption rates that stabilize into the observed red-purple stripe pattern, consistent with how Turing patterns emerge in Fig. 8.

In terms of performance, CP demonstrates slightly higher position error than PT_free due to CP’s average of 1.1 failed motors. In comparison, PT’s position error and upper semi-variance are significantly higher due to its average of 4.5 motor failures. This highlights the proposed method’s adaptability and resiliency to environmental, morphological, and behavioral changes, in addition to the permanency of failure in long-term autonomy systems.

Discussion

This study introduced a cellular plasticity model to enable the self-organization of phenotypes in multi-cellular robots to support their behavior in dynamic environments. By incorporating reaction–diffusion mechanisms and opposition-driven specialization, the model demonstrated general phenomena observed in various cell types: (1) growth stems from product scarcity in muscle cells, (2) sustained stimuli modulate functional capacity in neurons, (3) specialization increases total capacity in stem cells, and (4) self-regulation occurs without an environmental model. Analytical and simulation analyses highlighted the model’s stability, behavior, and parametric effects, revealing that decentralized interactions can generate phenotype patterns that increase overall capacity through specialization.

The proposed CP model conceptually overlaps with several well-established computational frameworks. Like long short-term memory (LSTM) networks⁴¹, CP maintains an internal state, through factory–product dynamics, that allows it to modulate behavior based on the history of environmental stimuli. It also resembles graph neural networks (GNNs)⁴² in its decentralized structure, where local communication via diffusion enables one-hop neighbor interactions. CP shares conceptual similarities with central pattern generators (CPGs)⁴³, as both systems self-organize from random initial conditions-CPGs producing synchronized oscillations and CP generating spatially patterned functional properties.

Cellular plasticity differs from these frameworks in key ways. Unlike LSTMs and GNNs, it is not trained offline through backpropagation or data-driven optimization^41,42. Also, unlike CPGs, cellular plasticity’s self-organization is spatial rather than temporal⁴³. Most importantly, cellular plasticity is not based on neuron-specific dynamics^41,42,43; instead, it is grounded in fundamental biological principles—reaction–diffusion and environmental stimulation—that generalize across cell types such as muscle cells, stem cells, and neurons. These distinctions position cellular plasticity as a scalable, interpretable framework for decentralized online adaptation that requires neither large datasets nor explicit environmental models. It broadly applies to morphology and behavior and is well suited for embodied morphogenetic systems like Loopy, where form, function, and environmental interaction are tightly coupled.

Since Loopy’s morphology and behavior emerge through decentralized self-organization rather than centralized design, cellular plasticity may be less suited for achieving precisely defined configurations or task-specific specializations. In contrast to data-driven approaches that can be optimized for narrowly defined objectives, cellular plasticity emphasizes general adaptability, trading precision for flexibility in unstructured or unforeseen environments.

Experimental validation on the Loopy robot further demonstrated the practical applicability of this framework, highlighting its adaptability in supporting diverse behaviors in dynamic and unmodeled environments. Notably, the proposed method reduced over-torque failures and improved performance consistency in confined settings compared to performance-tuned parameters.

The Loopy application experiment also revealed a compelling interplay between stiffness and damping, driven by the opposition between the factories F_s (inverse spring constant) and F_d (inverse damping constant). These factories dynamically adjust in opposition to one another: as one increases, the other decreases. Therefore, if a cell experiences deformation, F_s will increase, making it more flexible to the deformation, but due to the opposition, F_d will decrease, making the robot more damped. This, in turn, further reduces the robot’s ability to actively move, increasing the robot’s compliance with the environment. However, the reverse is also true; if the robot begins to move, not only will the damping decrease to aid movement, but F_s will decrease, making the robot stiffer to further support its active movement. This adaptive interplay showcases how cellular plasticity principles enable the self-organization of functional mechanical properties.

This application also highlights the self-organization of cell phenotypes in response to the environment and the robot’s behavior. During the contained formation and metamorphosis phases, the robot’s cells were predominantly red (Fig. 10A, indicating low stiffness and high damping. This phenotype aligns with the robot’s restricted and stationary state, where minimal resistance to deformation and high resistance to movement were advantageous. In the confined and unconfined rotation phases, the dominant phenotype shifted to blue, characterized by low damping and high stiffness, supporting active movement by reducing motion resistance and enhancing structural support. As the robot transitioned from confined to unconfined motion, the proportion of red cells decreased as it became less restricted, further reinforcing that the emergent phenotype mirrored its environment and function. Purple cells (high stiffness and damping) became most prevalent in the free-rotation-stop and free-metamorphosis phases, reflecting the robot’s stationary and unrestricted formation. These results suggest that the proposed approach enables the robot to adjust its mechanical properties to dynamically match environmental and behavioral demands, enhancing its adaptability and resilience in complex and changing conditions.

This study is limited by simplifying complex biological processes to general phenomena and assuming that factories can grow indefinitely given adequate time. Additionally, the lack of experimental validation with robots outside a laboratory environment restricts the empirical confirmation of the model’s applicability. This model is also limited in that it does not eliminate motor failures. Future endeavors aim to address these gaps by undertaking experimental validations with physical robots in unstructured environments to examine the influence of cellular plasticity on the robot’s emergent morphology and behavior. In addition, the model could be enhanced to include a defined factory capacity limit per cell and incorporate a model for cellular division and death. Furthermore, this future model will adjust the parameters of the spawning cell (similar to evolutionary algorithms¹⁶ and stem cell histones³³) to bias specialization towards the additional capacity needed by the parent cell, introducing another layer of adaptive response at a longer time scale.

Methodology

This section describes the Turing pattern framework and the development of the cellular plasticity model from a single cell with a single phenotype (i.e., function) to multiple cells with many phenotypes. Then, it describes the Loopy platform and the application of the cellular plasticity model to self-organize the mechanical properties of the Loopy robot.

Turing patterns

Turing patterns describe the formation of spatial distributions of simulated chemicals or morphogens with a system of reaction–diffusion equations¹⁰. The reaction–diffusion framework is defined by (17), where Q represents morphogen quantities, Γ∇²Q is the diffusion term with Γ being a diagonal matrix of diffusion coefficients, and R(Q) is the reaction function¹⁰.

$$\frac{{\rm{d}}{\boldsymbol{Q}}}{{\rm{d}}t}={\mathbf{\Gamma }}{\nabla }^{2}{\boldsymbol{Q}}+R({\boldsymbol{Q}})$$

(17)

In this framework, the unique interactions within the reaction function differentiate the formation of limbs, feathers, and other natural structures^11,12,13. The reaction function typically utilizes two morphogens: an activator and an inhibitor. The activator morphogen increases the production of both the activator and the inhibitor, while the inhibitor reduces these production abilities¹⁰. Utilizing the activator–inhibitor framework, the mathematical conditions for a Turing pattern to exist are described in (18)–(22) from ref. ³⁹.

$$\,\text{Jacobian: J}\,=\left[\begin{array}{cc}{J}_{11}&{J}_{12}\\ {J}_{21}&{J}_{22}\end{array}\right]$$

(18)

with elements constrained by:

$${J}_{11} > 0$$

(19)

$${J}_{22} < 0$$

(20)

$${J}_{11}+{J}_{22} < 0$$

(21)

$$\frac{{\gamma }_{{\rm{inh}}}}{{\gamma }_{{\rm{act}}}}{J}_{11}+{J}_{22} > 0$$

(22)

where J is the Jacobian of the reaction function about its equilibrium point, γ_act is the diffusion rate of the activator, and γ_inh is the diffusion rate of the inhibitor. This mathematical framework enables synthetic structure formation, the foundation for robotic morphogenesis.

Single-cell single-factory model

Utilizing the Turing pattern framework, the proposed cellular plasticity model for the self-organization of cell phenotypes includes a factory, analogous to an enzyme or organelle, that produces a product molecule consumed by the environment. This factory–product pair represents a cell’s functional capability (i.e., phenotype), where the factory’s size determines the intensity at which the function is performed, and the product quantity indicates its immediate readiness perform the function. This concept maps directly to robotic systems; for example, a motor applying torque to a joint in response to angular error can be modeled as a factory–product pair, where the factory represents the torque gain, and the product represents the available torque, which is consumed at a rate equal to the angular error. Furthermore, the interactions of these components are regulated by the bio-inspired phenomena from the section “Introduction” manifested as feedback loops.

Referring to Fig. 13, at the heart of the cellular plasticity model is the factory quantity (F), which functions as the activator and not only self-replicates at rate G but also produces the inhibitory product quantity (P) at rate R. This inhibitor modulates the factory by slowing product synthesis and factory growth at respective rates I and K. Additionally, the environment consumes the product at a rate of C ⋅ P, where C is the environmental stimulus and the product’s quantity (P), or availability, proportionally affects how fast it can be consumed. Moreover, as the environment consumes the product, the factory is degraded proportionally to the consumption at a rate of (D). The environmental consumption of the product represents a negative stimulus that reduces the product’s inhibitory effect on the factory, allowing it to grow. Therefore, the equilibrium between the factory (F) and product (P) quantities is modulated with the environmental demand (C). This relationship for the cellular plasticity model is mathematically described in (23) and (24).

$$\frac{{\rm{d}}F}{{\rm{d}}t}=(G-KP)F-DCP$$

(23)

$$\frac{{\rm{d}}P}{{\rm{d}}t}=(R-IP)F-CP$$

(24)

Fig. 13: Cellular plasticity model for a single factory cell.

This model utilizes a self-replicating factory that produces a product consumed by the environment. This product also inhibits the production and growth rate of the factory. Moreover, the factory is degraded by the intensity at which the product is consumed.

This model, (23) and (24), describes the first two targeted phenomena of cellular plasticity from the section “Introduction”—growth is spurred by product scarcity, and sustained stimuli modulate functional capacity—via two negative feedback loops depicted in Fig. 1. These loops increase the net production rate (R − I ⋅ P) and net factory growth (G − K ⋅ P) in response to reduced product levels (P), capturing the first phenomenon. Next, suppose the net factory growth feedback loop reacts slower than the net production rate feedback loop. In that case, only prolonged consumption rate changes will significantly modify factory capacity, capturing the second phenomenon. Furthermore, the fourth phenomenon from the section “Introduction,” self-regulation, is demonstrated by this model by not relying on an external environment model to regulate functional capacity.

Single-cell multi-factory model

The cellular plasticity model is extended to include multiple factories (Fig. 14) to reflect how cells and robots often perform diverse functions, such as molecular transport and reaction in cells, or data acquisition, computation, and actuation in robots. However, cells and robots have finite capabilities; if a cell creates proteins to transport molecule A, it reduces capacity to transport molecule B. Similarly, if a robot is overloaded with processing, its data acquisition and actuation capabilities diminish. This resource constraint induces competition, as an increase in one functional capacity reduces the capacity of others. This competition is modeled by introducing an opposition rate O_ij that reduces the net growth rate of the i^th factory proportionally to the quantity of the opposing j^th factory; thus, (23) becomes (25), where N is the total number of factories in the cell.

$$\frac{{\rm{d}}{F}_{i}}{{\rm{d}}t}=({G}_{i}-{K}_{i}{P}_{i}-\mathop{\sum }\limits_{j\ne i}^{N}{O}_{ij}{F}_{j}){F}_{i}-{D}_{i}{C}_{i}{P}_{i}$$

(25)

Fig. 14: Single Cell Multi-Factory Model Diagram.

Expansion of the cellular plasticity model to multiple unique functions within a single cell, via multiple competing factories that oppose each other at a rate of O_ij.

This competition encourages specialization towards higher-demand products, potentially capturing the phenomenon that specialization improves total capacity.

Multi-cellular multi-factory model

Diffusion is crucial in enabling Turing patterns to form spatially organized structures. To account for this, diffusive effects are incorporated into the model, expanding it to include interactions among multiple cells. As a result, (25) and (24) are modified into (26) and (27), where γ_F and γ_P are the diffusion coefficients for the factory and product, respectively:

$$\frac{d{F}_{i}}{dt}={\gamma }_{F}{\nabla }^{2}{F}_{i}+({G}_{i}-{K}_{i}{P}_{i}-\mathop{\sum }\nolimits_{j\ne i}^{N}{O}_{ij}{F}_{j}){F}_{i}-{D}_{i}{C}_{i}{P}_{i}$$

(26)

$$\frac{d{P}_{i}}{dt}={\gamma }_{P}{\nabla }^{2}{P}_{i}+({R}_{i}-{I}_{i}{P}_{i}){F}_{i}-{C}_{i}{P}_{i}$$

(27)

This model captures intracellular competition among factories from opposition and the intercellular cooperation of resource sharing via diffusion, demonstrating how internal interactions and diffusion may contribute to multi-cellular self-organization.

Model constraints

Multiple constraints must be specified to ensure the model captures the cellular plasticity phenomena outlined in the section “Introduction.” The first constraint is that G, K, R, I, D, O_ij, γ_F, and γ_P parameter values are positive constants. Secondly, to ensure that only sustained stimuli lead to changes in functional capacity, the model’s parameters must be constrained such that the factory’s net growth response (i.e., its time constant τ_F), is slower than the production rate’s response, τ_P, to changes in the consumption rate (τ_F > τ_P). Furthermore, the factory (F) and product (P) quantities are also restricted to positive values, as negative values lack physical meaning. The consumption rate stimulus (C) is limited to positive values, thus restricting the model from harvesting environmental resources. Lastly, for Turing patterns to emerge, the diffusion coefficient of the activator must be much smaller than the inhibitor, thus γ_F << γ_P³⁹.

Loopy platform

The Loopy robot, shown in Fig. 1, utilizes the Turing pattern framework and consists of 36 homogeneous, 1-DoF physically linked cells, each constructed from a Dynamixel XM430W210 rotary servo that provides actuation along with position and velocity proprioception¹⁵. These motors are daisy-chained to share power and data communication. Loopy’s motors are controlled in a decentralized manner, with each acting independently and communicating only with its immediate neighbors, without knowing the robot’s overall morphology or position. However, for the convenience of maintenance and development, a central computer simulates the reaction–diffusion system for all cells. The computer then utilizes U2D2 Dynamixel Communicators to transmit motor commands and receive sensor information. Utilizing only local information, Loopy’s cells self-organize into stable morphologies consisting of lobed protrusions, as shown by the three lobes in Fig. 1. These structures are formed using FitzHugh–Nagumo activator–inhibitor dynamics (28) and (29) and a passive morphogen (30)⁴⁴. In this system, q_act is the activator quantity, q_inh is the inhibitor quantity, q_pas is the non-reactive passive morphogen quantity, γ_act γ_inh γ_pas are the diffusion constants, α is the persistent stimulation rate and β is the inhibition rate.

$$\frac{{\rm{d}}{q}_{{\rm{act}}}}{{\rm{d}}t}={\gamma }_{{\rm{act}}}{\nabla }^{2}{q}_{{\rm{act}}}+{q}_{{\rm{act}}}-\frac{1}{3}{q}_{{\rm{act}}}^{3}-{q}_{{\rm{inh}}}+\alpha$$

(28)

$$\frac{{\rm{d}}{q}_{{\rm{inh}}}}{{\rm{d}}t}={\gamma }_{{\rm{inh}}}{\nabla }^{2}{q}_{{\rm{inh}}}+\beta ({q}_{{\rm{act}}}-{q}_{{\rm{inh}}})$$

(29)

$$\frac{{\rm{d}}{q}_{{\rm{pas}}}}{{\rm{d}}t}={\gamma }_{{\rm{pas}}}{\nabla }^{2}{q}_{{\rm{pas}}}$$

(30)

The self-organized morphogen concentrations then guide each motor cell’s desired joint angle, θ_des, in (31), with the balance between diffusion and reaction parameters directly influencing the morphology¹⁵.

$${\theta }_{{\rm{des}}}={q}_{{\rm{act}}}+{q}_{{\rm{pas}}}$$

(31)

For instance, higher inhibition rates (β) reduce lobe size, while increased activator diffusion (γ_act) spreads morphogens across more cells, decreasing the number of lobes¹⁵.

Building on these static formations, Loopy’s morphology can also be made to rotate by introducing simplified active transport through a first-order wave term in the morphogen dynamics³⁷. This allows morphogen concentrations-and thus motor trajectories-to propagate along the robot’s body, producing traveling waves and periodic rotation.

$$\frac{{\rm{d}}Q}{{\rm{d}}t}=\lambda \nabla Q$$

(32)

This modifies the original FitzHugh–Nagumo equations to include active transport between cells, as shown in (33) and (34), where λ sets the transport speed.

$$\frac{{\rm{d}}{q}_{{\rm{act}}}}{{\rm{d}}t}=\left({\gamma }_{{\rm{act}}}{\nabla }^{2}{q}_{{\rm{act}}}\right)+\left(\lambda \nabla {q}_{{\rm{act}}}\right)+{q}_{{\rm{act}}}-\frac{1}{3}{q}_{{\rm{act}}}^{3}-{q}_{{\rm{inh}}}+\alpha$$

(33)

$$\frac{{\rm{d}}{q}_{{\rm{inh}}}}{{\rm{d}}t}=\left({\gamma }_{{\rm{inh}}}{\nabla }^{2}{q}_{{\rm{inh}}}\right)+\left(\lambda \nabla {q}_{{\rm{inh}}}\right)+\beta ({q}_{{\rm{act}}}-{q}_{{\rm{inh}}})$$

(34)

To solve and decentralize the continuous partial differential equations (33), (34), and (30), they are discretized both temporally and spatially, with each motor cell of size s serving as a control volume^15,37. Thus, (33), (34), and (30) become (35)–(37), respectively, for the m^th cell in the loop. These equations are expressed as a sum of diffusion, active transport, and reaction terms, each enclosed in parentheses. The system is then propagated through time (t) using (38), where Δt is the time step.

$$\begin{array}{rcl}\frac{{\rm{d}}{q}_{{\rm{act}}_{m,t}}}{{\rm{d}}t}&=&{\gamma }_{{\rm{act}}}\left(\frac{{q}_{{\rm{act}}_{m-1,t}}-2{q}_{{\rm{act}}_{m,t}}+{q}_{{\rm{act}}_{m+1,t}}}{{s}^{2}}\right)\\ &&+\lambda \left(\frac{{q}_{{\rm{act}}_{m-1,t}}-{q}_{{\rm{act}}_{m+1,t}}}{2s}\right)\\ &&+\left({q}_{{\rm{act}}_{m,t}}-\frac{1}{3}{q}_{{\rm{act}}_{m,t}}^{3}-{q}_{{\rm{inh}}_{m,t}}+\alpha \right)\end{array}$$

(35)

$$\begin{array}{rcl}\frac{{\rm{d}}{q}_{{\rm{inh}}_{m,t}}}{{\rm{d}}t}&=&{\gamma }_{{\rm{inh}}}\left(\frac{{q}_{{\rm{inh}}_{m-1,t}}-2{q}_{{\rm{inh}}_{m,t}}+{q}_{{\rm{inh}}_{m+1,t}}}{{s}^{2}}\right)\\ &&+\lambda \left(\frac{{q}_{{\rm{inh}}_{m-1,t}}-{q}_{{\rm{inh}}_{m+1,t}}}{2s}\right)\\ &&+\beta \left({q}_{{\rm{act}}_{m,t}}-{q}_{{\rm{inh}}_{m,t}}\right)\end{array}$$

(36)

$$\frac{{\rm{d}}{q}_{{\rm{pas}}_{m,t}}}{{\rm{d}}t}={\gamma }_{{\rm{pas}}}\left(\frac{{q}_{{\rm{pas}}_{m-1,t}}-2{q}_{{\rm{pas}}_{m,t}}+{q}_{{\rm{pas}}_{m+1,t}}}{{s}^{2}}\right)$$

(37)

$${Q}_{m,t+1}=\frac{{{\rm{d}}Q}_{m,t}}{{\rm{d}}t}\Delta t+{Q}_{m,t}$$

(38)

From (35)–(38), each cell only depends on its current morphogen concentrations and its immediate neighbor’s concentrations, highlighting the scalability of this system.

Application of cellular plasticity to the mechanical properties of the Loopy robot

To demonstrate the applicability of the proposed cellular plasticity model, we implemented it on the Loopy robot. This system leverages the model to modulate the robot’s mechanical properties-stiffness and damping-self-organized in response to behavioral and environmental stimuli.

The model is applied by defining each cell’s abilities (factories) and their modulation stimuli (consumption rates). In this study, stiffness and damping are the targeted mechanical properties, controlled by the motor’s spring constant (K_s) and damping constant (K_d). The position error (∣θ_des − θ∣) serves as the stimulus for stiffness, while motor speed ($| \frac{{\rm{d}}\theta }{{\rm{d}}t}|$) modulates damping. The inverse spring constant (1/K_s) and inverse damping constant (1/K_d) are defined as the cell’s activator factories (F_s and F_d). This configuration enables mechanical adaptation: increasing position error reduces stiffness, allowing deformation under physical constraints; increasing speed reduces damping, easing motion.

To evaluate how Loopy’s mechanical properties self-organize, it is examined in two environments: obstacle-free and contained (Fig. 15). The obstacle-free environment examines Loopy’s intrinsic ability to develop spatially distributed phenotypes, while the contained environment introduces additional external physical constraints. In addition, Loopy is subjected to three behaviors: formation, metamorphosis, and morphology rotation (Fig. 16). In the formation behavior, Loopy organizes a structured morphology from random initial conditions. Metamorphosis refers to the transition between different morphologies, such as from a circle to a three-lobed shape. Morphology rotation involves propagating morphogens through the robot’s body to produce periodic motor trajectories³⁷.

Fig. 15: The two environments Loopy was immersed in: obstacle-free (left) and contained (right).

The contained environment measures 60 × 80 cm.

Fig. 16: Loopy performs three morphogenetic behaviors.

(1) Formation: transitioning from random initial conditions to an organized morphology; (2) metamorphosis: transitioning from one morphology to another; (3) morphology rotation: propagating morphogens around Loopy to shift which cells constitute different parts of the morphology.

The morphogenetic behaviors are not explicitly programmed but instead emerge from specific parameter changes in the underlying reaction–diffusion system, which modify Loopy’s internal chemical environment. For example, setting γ_pas > 0 enables formation, varying γ_act triggers metamorphosis, and setting λ ≠ 0 induces morphology rotation^15,37. These parameter changes are applied sequentially by an external centralized script that governs transitions between experimental phases. The physical environment is adjusted manually by inserting or removing the bounding frame shown in Fig. 15. Thus, while the robot autonomously self-organizes within each phase, initiating new environments or behaviors—such as formation, metamorphosis, or rotation—is externally induced. The complete cell dynamics are described in Eqs. (39)–(47), where T_app is the applied motor torque.

Inverse spring constant factory–product pair:

$$\frac{{\rm{d}}{F}_{{\rm{s}}}}{{\rm{d}}t}=\left({\gamma }_{F}{\nabla }^{2}{F}_{{\rm{s}}}\right)+(G-K{P}_{{\rm{s}}}-{O}_{{\rm{sd}}}{F}_{{\rm{d}}}){F}_{{\rm{s}}}-D| {\theta }_{{\rm{des}}}-\theta | {P}_{{\rm{s}}}$$

(39)

$$\frac{{\rm{d}}{P}_{{\rm{s}}}}{{\rm{d}}t}=\left({\gamma }_{P}{\nabla }^{2}{P}_{{\rm{s}}}\right)+(R-I{P}_{{\rm{s}}}){F}_{{\rm{s}}}-| {\theta }_{{\rm{des}}}-\theta | {P}_{{\rm{s}}}$$

(40)

Inverse damping constant factory–product pair:

$$\frac{{\rm{d}}{F}_{{\rm{d}}}}{{\rm{d}}t}=\left({\gamma }_{F}{\nabla }^{2}{F}_{{\rm{d}}}\right)+(G-K{P}_{{\rm{d}}}-{O}_{{\rm{ds}}}{F}_{{\rm{s}}}){F}_{{\rm{d}}}-D| \frac{{\rm{d}}\theta }{{\rm{d}}t}| {P}_{{\rm{d}}}$$

(41)

$$\frac{{\rm{d}}{P}_{{\rm{d}}}}{{\rm{d}}t}=\left({\gamma }_{P}{\nabla }^{2}{P}_{{\rm{d}}}\right)+(R-I{P}_{{\rm{d}}}){F}_{{\rm{d}}}-| \frac{{\rm{d}}\theta }{{\rm{d}}t}| {P}_{{\rm{d}}}$$

(42)

FitzHugh–Nagumo with first-order wave equation:

$$\frac{{\rm{d}}{q}_{{\rm{act}}}}{{\rm{d}}t}=\left({\gamma }_{{\rm{act}}}{\nabla }^{2}{q}_{{\rm{act}}}\right)+\left(\lambda \nabla {q}_{{\rm{act}}}\right)+{q}_{{\rm{act}}}-\frac{1}{3}{q}_{{\rm{act}}}^{3}-{q}_{{\rm{inh}}}+\alpha$$

(43)

$$\frac{{\rm{d}}{q}_{{\rm{inh}}}}{{\rm{d}}t}=\left({\gamma }_{{\rm{inh}}}{\nabla }^{2}{q}_{{\rm{inh}}}\right)+\left(\lambda \nabla {q}_{{\rm{inh}}}\right)+\beta ({q}_{{\rm{act}}}-{q}_{{\rm{inh}}})$$

(44)

Passive morphogen:

$$\frac{{\rm{d}}{q}_{{\rm{pas}}}}{{\rm{d}}t}={\gamma }_{{\rm{pas}}}{\nabla }^{2}{q}_{{\rm{pas}}}$$

(45)

Morphogen to formation:

$${\theta }_{{\rm{des}}}={q}_{{\rm{act}}}+{q}_{{\rm{pas}}}$$

(46)

Actuator dynamics:

$${T}_{{\rm{app}}}=-\frac{1}{{F}_{{\rm{s}}}}(\theta -{\theta }_{{\rm{des}}})-\frac{1}{{F}_{{\rm{d}}}}\frac{{\rm{d}}\theta }{{\rm{d}}t}$$

(47)

Furthermore, this system is discretized and decentralized, similar to (35)–(38).