Emerging ferromagnetic materials for electrical spin injection: towards semiconductor spintronics

Abstract

Spintronics is a promising field beyond complementary metal-oxide semiconductors technology. It presents a unique approach to diminishing the energy consumption of memory and logic devices by utilizing spin. The proposed influential memory and logic device is the spin transistor. However, limited spin injection efficiency from the metallic ferromagnetic electrode into the semiconductor layer has been a major obstacle for the advances of spin transistors. Three key properties are critical for magnetic materials in future spintronic devices to improve the spin injection efficiency, namely high spin polarization, robust room-temperature ferromagnetism, and comparable resistance with the semiconductor. Considering these factors, we will explore four major categories of ferromagnetic materials: Heusler alloys, dilute magnetic semiconductors, Si- or Ge-based intermetallic compounds, and two-dimensional ferromagnets. We present a comprehensive overview of the significant milestones for each type of material in terms of their property improvements, functionality achievements, and fundamental applications for spintronics. Finally, we will briefly address the challenges which need to be tackled for practical application in memory and logic devices.

Conventional silicon-based metal-oxide-semiconductor (MOS) devices, which relying on manipulating electron’s charge (specifically one degree of freedom of electrons) are confronted with the significant challenges in miniaturizing of electronic devices due to the fundamental physical limits¹. The exploration of advanced information technology with low-energy consumption and high-speed operation, which complements the existing silicon-based complementary metal-oxide semiconductors (CMOS) technology, is urgently required. Many strategies have already been proposed, such as nanoelectronics, molecular electronics, valley electronics, spintronics, and quantum information technologies^1,2. Among these, spintronics, which exploits the spin degree instead of the charge degree for electrons or holes, has the potential to become an innovative pathway beyond physical limits and satisfy the speed and energy-efficiency needs of the emerging computing paradigm³.

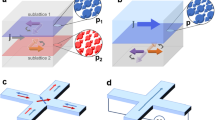
Spintronics is a multidisciplinary field focused on effectively utilizing spin degrees of freedom in solid-state systems^3,4. The term spin refers to either the spin of a single electron, which is characterized by a quantized angular momentum of m_sħ (where m_s = ±1/2 represents the spin magnetic quantum number), or the average spin of a group of electrons as evidenced by their magnetization. The quantized spin angular momentum of electrons exists in two distinct states: spin down ↓ (minority-spin) and spin up ↑ (majority-spin). Spintronics devices are built based on the comprehensive utilization of the spin degree of freedom in certain functional units, such as spin valve, magnetic tunnel junctions (MTJs), spin transfer torque (STT), spin-orbit torque (SOT) and spin field effect transistor (spin-FET). Their structure diagrams are depicted in Fig. 1. These prototypes, even commercial successful spin functionality units, involve a wide coverage of fascinating spin physics, namely injection, transmission, detection, and even manipulation of spins³. Importantly, the injection, transmission and detection of spin degree during the whole operation for a certain spin-based unit governs the success and endurance of ultimate spintronics performance. During this procedure, spin population, coherence and collection should be seriously considered. As for the spin manipulation, the extra driving force from either orbital momentum inter-coupling or external physical stimuli works essentially. This, in turn, creates more possibilities for controlling and tailoring spin activity in addition to simple transmission.

Fig. 1: The milestone discovery of spintronics.

Schematic of (a) spin valve structure based on the giant magnetoresistance effect; (b), magnetic tunnel junction structure based on the tunneling magnetoresistance effect; (c), spin transfer torque switching; (d), spin orbit torque switching and (e) the Datta and Das spin transistor. Images of c and d are reprinted with permission from ref. ⁹ Copyright 2020 Wiley Periodicals, Inc.

The milestone discovery of the giant magnetoresistance (GMR) effect within metallic multilayers (Fig. 1a) in 1988 undoubtedly validated the detectable coupling between charge and spin, which greatly revolutionized the spintronics industry by successful application in Hard Disk Drives (HDD)^5,6. Soon, in 1991, the GMR spin valve was designed by Dieny, which is composed of an additive pinning layer with one ferromagnetic (FM) layer while the other FM layer is free. This valve geometry works efficiently in improving magnetic field sensitivity for HDD that use GMR as read heads. Afterward, in 1995, the introduction of insulating barrier amorphous alumina between counter FM electrodes (Fig. 1b), which demonstrated a large reproducible magnetoresistance signal, marked the tunneling magnetoresistance (TMR) effects⁷ started to play a critical role in spintronics industry. The TMR signal was improved by over 600% once the single crystal MgO was selected as the insulating barrier⁸. The ultrahigh TMR signal not only expands the hard disk recording but also encourages the advancement of magnetoresistive random access memory (MRAM). The recent confirmation of STT (Fig. 1c)⁹ and SOT (Fig.1d)¹⁰ effects have made MTJs more worthwhile for the blossom of low-power and high-density data storage.

As just illustrated, the development of GMR and TMR devices is closely linked to optimizing both metals and insulators under the frame of two-terminal geometry. Semiconductor, which possess unique advantage of gate tunable carrier density, affords distinctive advantage in spin information storage and spin logic computing¹¹. This emerging field has sparked significant scientific interests and high expectations for the development of innovative devices that can convert spin information into an electrical signal, and vice versa. One of the primary objectives of semiconductor-based spintronics is to achieve the realization of a three-terminal device known as the spin-FET, as depicted in Fig. 1e. Spin-FETs offer non-volatile storage, energy efficient and quicker operation than conventional transistors¹¹. More importantly, this device holds significant potential for realizing nonvolatile memory and amplification functionalities within a single unit. However, such devices confront substantial problems including ineffective spin injection from the FM source into the channel and relaxation of spin in the channel which significantly deteriorate the devices’s performance^12,13,14,15. This stands in clear contrast to the conservation of electron charge. Hence, there are still challenges to be addressed in the implementation of such spintronic devices. In this regard, the effective spin injection from FM source into semiconductor channel is of both fundamental and technological importance, making it a crucial solution to be achieved.

This review aims to provide a comprehensive summary of the burgeoning field of electrical spin injection from the perspectives of materials, performances, and applications. After this brief overview of spintronics concepts and developments in section 1, we illustrate the challenges during the electrical spin injection within FM/semiconductor heterostructure in section 2. Section 3 summarizes the FM materials used as spin source/drain. Different types of FM material systems, including Co-based Heusler alloy, dilute magnetic semiconductor Ga_1-xMn_xAs, Si- or Ge-based intermetallic compounds Mn₅Ge_3, and two-dimensional (2D) materials, are discussed based on the magnetic and electronic properties which are applicable to the highly efficient spin injection at room temperature (RT). Finally, we conclude by discussing the future challenges and opportunities for the development of spintronics-based nonvolatile logic-in-memory applications.

Issues and solutions of electrical spin injection in ferromagnet/semiconductor heterostructures

The successful implementation of a spin-FET (Fig. 1e) relies on achieving the following fundamental functionalities^{3,12,13,14,15}: (i) spin injection/extraction into/from a semiconductor channel and (ii) spin-dependent transport via a semiconductor channel. A proposed influential semiconductor-based device is the Datta-Das transistor¹⁶. It features a FET-like structure, with FM metallic contacts (e.g., Ga_1-xMn_xAs) and a non-ferromagnetic semiconductor channel, as illustrated in Fig. 1e. The polarized spins are injected into a 2D electron-gas channel, for example GaAs, where the transport of the polarized spin current is supposed to be ballistic. They are exposed to an electrical field controlled by the gate, which in turn induces an effective Rashba magnetic field for manipulating electrons at a specific velocity. The electrons undergo Larmor precession during this process, and the manipulation of the spin precession angle is achieved through the effective Rashba field. The majority spins’ orientations will be aligned by the gate bias to either the parallel or antiparallel direction with the FM contacts’ magnetization, resulting in correspondingly high or low conductance. It is evident that the spintronic ferromagnet/semiconductor heterostructures play a pivotal role in governing the behavior and performance of devices.

Spin signals have been detected or generated through various means, including electrical, optical, and thermal methods. The spin signals generated and detected via electrical methods, also known as spin-charge conversion, are in harmony with the electric charge operations inherent in CMOS-based integrated circuits. Suppose the efficient spin electrical injection from FM sources into the semiconductor is realized, a spin accumulation signal in the semiconductor can be electrically detected via a change in resistance or potential using Hanle effect measurement or nonlocal SV measurements^17,18,19. Schematic illustration and typical signal results of nonlocal spin valve and Hanle measurements are displayed in Fig. 2a–d, respectively. Typically, the 3-terminal configuration was utilized, with a single FM contact serving as the spin injector and detector. Nevertheless, the 3-terminal geometry is more susceptible to spurious signals, such as Hall or anisotropic magnetoresistance effects, due to the presence of a non-zero charge current at the detector junction. To completely eliminate the possibility of spurious signal, the nonlocal 4-terminal spin transport devices (Fig. 2) are proposed. A spin detection electrode is strategically positioned outside the path of the charge current within this device, thereby furnishing precise insights into spin lifetime and spin polarization in the semiconductor channel.

Fig. 2: Nonlocal SV and Hanle measurements.

a Illustrated in the schematic is the nonlocal measurement of spin voltage, wherein an in-plane magnetic field is applied along the easy axis of the FM spin injector and detector. b Characteristic nonlocal SV signals observed in n-Ge at 4 K. The sweeping direction of the magnetic field is indicated by the black and red arrows, while the relative magnetization directions of the spin injector and detector are denoted by the blue arrows; c Simplified illustration of nonlocal Hanle measurement with an out-of-plane magnetic field applied perpendicular to the FM/semiconductor interface. d Distinctive nonlocal Hanle precession signals were observed in n-Ge at 4 K. The figures are reprinted with permission from ref. ¹⁹ Copyright 2015 by the Royal Society of Chemistry.

As previously mentioned, spins effectively transfer from a FM source into the semiconductor, creating a significant (nonequilibrium) spin polarization of the carriers in the semiconductor. This is a key step in demonstrating many novel spin-FETs. It’s notable that the spin-polarized current in a spin-FET is typically introduced from the FM metal into the semiconductor layer via the diffusive transport through an ohmic contact. The current polarization at the FM metal/semiconductor interface is determined by¹⁴:

$$P=\frac{{P}_{0}}{1+(1-{P}_{0}^{2})\frac{{\sigma }_{F}{\lambda }_{{SC}}}{{\sigma }_{{SC}}{\lambda }_{F}}}$$

(1)

where P₀ represents the polarization at the Fermi level within the ferromagnet; σ_F and σ_SC denote the conductivity of the FM and semiconductor layer, respectively; additionally, λ_F and λ_SC indicate the mean free path travelled by spin carriers before undergoing a spin flipping scattering.

Based on this formula, the restricted spin injection efficiencies have predominantly been ascribed to the following factors, including the limited spin polarization P₀ of electrons within the FM metallic electrodes, the conductivity mismatch problem (σ_{F >>} σ_SC)¹⁴ between the FM electrodes and the semiconductor channel, and the spin transport distance in the channel determined by the semiconductor’s channel length and diffusion profile. Among them, the conductivity mismatch, that refers to the conductivity of the FM metal being approximately 10³ times larger than the semiconductor channel¹⁴, strictly limit the efficient spin injection into the semiconductor considering nearly identical drop in the electrochemical potentials over the spin-up and spin-down electrons channel. To realize such spintronic devices, it is essential to achieve efficient spin injection into semiconductors and further to effectively manipulate the spin transport in them. First, the electrical spin injection and transport in a broad range of semiconductors have been extensively investigated to seek semiconductor materials with long spin lifetime and spin diffusion length¹⁹. Second, to achieve optimal spin injection efficiency, one proposed approach involves the exploration of new materials that demonstrate a significant carrier spin polarization^16,20. Potential candidates including FM oxides and associated Co₂-based Heusler compounds, many of which are anticipated to exhibit “half-metallic” behavior (such as Fe₃O₄ and Co₂MnSi). Such ferromagnets are theoretically expected to have l00% spin polarization at the Fermi level arising from their unique band structure. The valence band for the majority spin ↑ is partially filled, indicating a metallic property, while there exists a gap in the density of states (DOS) for the minority spin ↓, suggesting a semiconducting behavior.

Third, it is essential to solve the “conductivity mismatch” issue and thus achieve optimal spin-injection efficiency. One potential solution involves utilizing FM electrodes that have a resistivity almost equivalent to that of the semiconductor channel, such as diluted magnetic semiconductors Ga_1-xMn_xAs electrodes with a GaAs transport channel^21,22. Another potential solution involves inserting a spin-dependent interface resistance form a Schottky barrier or tunnel barrier^23,24. The Schottky barrier has been experimentally demonstrated using direct FM/semiconductor contacts, such as Fe₃Si/Si or Mn₅Ge₃/Ge heterojunction^25,26,27,28. In this case, the in-situ germanidation or silicidation process of fabricating Fe₃Si or Mn₅Ge₃ layer is favorable for achieving atomically smooth interfaces and thus minimizing Fermi level pinning and defect-induced interface states. The tunneling barrier can be established through a sandwich structure of FM metal/insulator/semiconductor layer, as shown in Fig. 1b. An intermediate thin insulator layer (such as MgO or Al₂O₃) effectively serves to modulate the height of the Schottky barrier²⁴. However, it is challenging to fabricate a superior tunneling oxide that is devoid of pinholes or defects to mitigate the phenomenon of Fermi level pinning. Until recently, the tunneling heterostructures based on 2D van der Waals (vdW) layers such as Co/MgO/MoS₂, Co/TiO₂/black phosphorous, and Fe₃GeTe₂/h-BN/Fe₃GeTe₂ have been reported with improved interfaces and consequently exhibited superior injection performance^29,30,31.

Ferromagnetic materials for electrical spin injection

Spin injection, transport, and detection in ferromagnet/semiconductor heterostructures are crucial for integrating spintronic devices into current production technologies and advancing semiconductor electronics beyond their physical limits. Attaining a high level of spin injection efficiency from FM into semiconductors is an indispensable step for developing spintronic devices. For efficient spin injection, it expects a material that not only possesses high Curie temperature (T_C) and substantial spin polarization, but also seamlessly integrates with existing Si-based CMOS technology. In this section, we will discuss various systems: FM materials with high spin polarization (e.g., half-metallic Heusler alloys Co₂MnGa); FM material with matched conductivity with the semiconductor channel (e.g., dilute FM semiconductor Ga_1-xMn_xAs); a controllable interface between the FM electrodes and the spin transport channel coupled with a Schottky barrier that fulfills the desired interface resistance criteria (for example Si- or Ge-based intermetallic compounds Mn₅Ge₃ on Ge substrates); and 2D vdW heterostructures consisting of 2D FM injector and 2D spin transport channels with improved interfaces for enhanced efficiency of injecting spin.

Half-metallic Heusler alloy

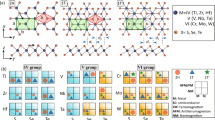
Half-metallic ferromagnets (HMF) represent a promising category of materials that have garnered significant interest for their potential application as spin injectors^32,33. Extensive researches have been conducted on typical half-metallic materials, particularly in ternary Heusler alloys with the composition of X₂YZ or XX’YZ (full Heusler as shown in Fig. 3a) or XYZ (Half Heusler as shown in Fig. 3b). These alloys consist of transition metals (TMs) as X and Y, and group III or IV elements as Z, forming a vast collection of over 1500 compounds³³. The constituent atoms were arranged in an L21-type structure as depicted in Fig. 3a, b. The perfect crystal structure can be conceptualized as a zinc blende-type sublattice constructed by one X and one Z atom while another X atom occupy the remaining tetrahedral hole and Y atom locate in the octahedral hole. In general, half-metallic materials are magnetic due to the contribution of magnetic moments from transition metal atoms. The bonding in these compounds is sufficiently intricate to enable the opening of a gap in the minority spins’ DOS, which is an essential condition for achieving half metallicity.

Fig. 3: The crystalline structure and magnetic moment of Heusler compounds.

Schematic structures of (a) half Heusler (XYZ) and (b) quaternary full Heusler (XX’YZ) compounds. c The magnetic moment per formula unit of Co₂-based Heusler compounds is in direct proportion to the number of valence electrons. This relationship follows the Slater-Pauling curve as illustrated in d. The values of 3 d transition metals and their alloys are provided for contrast. Figures (a, b) reprinted with permission from ref. ³³ Copyright 2021 by Elsevier B.V. Figures (c, d) are reprinted with permission from ref. ³⁵ Copyright 2011 by Elsevier Ltd.

In this section, we will present a selection of representative compounds known as Co₂YZ, including but not limited to Co₂MnSi, Co₂FeSi, and Co₂MnGe. The synthesis and investigation of these Co-based compounds have been ongoing since the 1970s³⁴. It is widely studied that the Co₂YZ’s magnetic properties adhere to the Slater-Pauling rule which accurately predicts their overall spin magnetic moment^35,36,37. The magnetic moment (m) per formula unit can be expressed as m = V_E – 24, where V_E represents the total valence electrons number, encompassing the summation of s and d electrons for transition metals, and s and p electrons for main group elements. As depicted in Fig. 3c, the magnetic moment of full-Heusler materials generally exhibits a linear relationship with the number of valence electrons, with only a few exceptions. Moreover, the majority of these compounds exhibit magnetic moments that are either integer or close to integer values. Furthermore, the T_C of Co₂-based Heusler compounds exhibits a direct correlation with the magnetic moment. Owing to the Slater Pauling behavior of the magnetic moment (as depicted in Fig. 3d), T_C also linearly depends on the number of valence electrons, as illustrated in Fig. 4a. However, this linear tendency is disrupted for materials with 27 valence electrons. These materials, which do not exhibit magnetism, demonstrate superconductivity. Theoretical investigations^35,37 have revealed that the magnetic moments at the Co and Y sites exhibit a simultaneous rise with V_E, resulting in nonlinearity with m. Supposed alterations in the average Heisenberg exchange were to counterbalance the magnetic moments, a linear correlation with V_E would become apparent.

Fig. 4: The T_C and spin-projected DOS of Co₂-based Heusler compounds.

a The T_C of Co₂-based Heusler compounds shows a linear dependence on the number of valence electrons, and therefore, also on the magnetic moment. b Calculated spin-projected DOS for the Co₂MnZ compounds, where Z represents Al, Ga, Si, and Ge. It was observed that all of these compounds exhibit a finite spin-down DOS around the Fermi level. The figure a is reprinted with permission from ref. ³⁷ Copyright 2013 by Springer Science+Business Media Dordrecht. The figure b is reprinted with permission from ref. ³⁹ Copyright 2002 by the American Physical Society.

Based on the plot depicted in Fig. 4a, it is evident that T_C exhibits its highest values in half-metallic compounds with a large magnetic moment or those with a high valence electron concentration as contrasted with the predictions of the Slater-Pauling rule. The theoretical estimation for T_C reach 1185 K in compounds with 6 μ_B which corresponds to 30 valence electrons per unit cell. Co₂FeSi is widely recognized as the Heusler compound with the highest magnetic moment of 5.97 μ_B at 5 K and the most elevated T_C reaching 1100 K³⁸.

The most prominent feature of Co₂YZ lies in the highest polarization which can be attributed to intricate half-metallic band structure that resides near the Fermi level^39,40. The Slater-Pauling behavior is widely recognized as indicative of bulk half-metallicity (100% spin polarization). This phenomenon arises from a metallic spin-polarized band, which is determined by the valence electrons number⁴⁰. Fig. 4b displays the spin-projected DOS of Co₂MnZ and partial DOS plots of Co₂MnGa. The DOS in FM is divided into minority and majority states due to the exchange interaction between Co and Mn atoms. The Fermi level is populated by one spin-band and resides within the bandgap of the other spin-band; thereby achieving the visualization of half-metallicity.

The transport properties are governed by electrons residing on the Fermi surface or within an energy eV_b of the Fermi level particularly applying a bias voltage of V_b. A comprehensive definition of polarization P(n) under low bias can be formulated as follows³⁷:

$$P\left(n\right)=\frac{{{v}_{F\uparrow }^{n}D}_{\uparrow }-{{v}_{F\downarrow }^{n}D}_{\downarrow }}{{{v}_{F\uparrow }^{n}D}_{\uparrow }+{{v}_{F\downarrow }^{n}D}_{\downarrow }}$$

(2)

where v_F represents the Fermi velocity, D_↑ and D_↓ denote the DOS of the majority (spin-up) and minority (spin-down) spin at the Fermi level. The exponent n takes on different values depending on the specific conditions: 0 for electrons ejected in spin-polarized photoemission, 1 for ballistic transport and 2 for diffusive transport or tunneling at low bias. It is theoretically expected that conduction electrons in HMF exhibit 100% spin polarization below T_C on the basis of the polarization definition. This remarkable characteristic renders HMF ideal candidates as spin injector layers in next-generation spintronic devices.

It’s notable the distinctive physical properties of Co-based Heusler alloys are dependent on the crystal structure. For instance, the half metallicity observed in Heusler-alloy films is particularly sensitive to crystal disorder, such as atomic displacement, misfit dislocation, and symmetry break near the surface of the films^37,41. As previously mentioned, within the perfect lattice of Co₂YZ, one Co and Z atoms constitute a zinc blende-type sublattice, while the second Co occupies the tetrahedral voids and Y is situated in the octahedral interstices. When the Y and Z atoms interchange their places (Y-Z disorder), resulting in Y-Z disorder, and eventually the alloy undergoes a transformation into the B2 phase. Furthermore, the presence of X-Y and X-Z disorder ultimately culminates in the emergence of the A2 phase. The anti-site disorder alters the termination of film and consequently diminishes the HMF property in Heusler alloys, leading to a decrease in spin polarization.

Controlling the stoichiometry of Heusler alloy films presents a formidable challenge, often leading to deviations from the anticipated physical properties due to a deficiency or excess of specific atom species^42,43. Furthermore, non-ferromagnetic interfaces have been found to be detrimental for spin injection in some Co-based Heusler alloy films⁴³. Consequently, the measured transport spin polarization of certain Heusler alloy films has been regrettably low. For example, P(n) was found to be 58% in NiMnSb⁴⁴ at 4.2 K as determined by point contact Andreev reflection. P(n) of Co₂MnSi at 10 K was demonstrated as 61% via Julliere’s formula⁴⁵ which still exceeds that of conventional transition metals.

The diminished spin polarization of the HMF may stem from a confluence of the aforementioned factors. Currently, these FM alloys still exhibit lower spin injection efficiencies while the theoretical prediction suggests that the spin injection efficiency for HMF can potentially reach 100%. The experimentally lower efficiency of spin injection in these FM alloys can be attributed to issues such as disorder in crystal structure, non-stoichiometry, and non-ferromagnetic interfaces.

Dilute magnetic semiconductors

The exploration of FM semiconductors has long been appealing owing to their potential applications in spintronics and their seamless integration into semiconductor devices¹⁶. The research on FM semiconductors can be traced back to the 1960s, when typical materials including europium chalcogenides (such as EuS, EuO) and chromium spinels (CdCr₂Se₄), where magnetic elements were arranged periodically in the lattice⁴⁶. The antiferromagnetic super-exchange in EuO is effectively counterbalanced by direct d-f FM exchange between neighboring Eu ions, leading to a resultant T_C = 68 K⁴⁷. Moreover, they demonstrate exceptional physical characteristics, such as a remarkable giant negative magnetoresistance, due to the exchange interaction between band carriers and localized spins. The s-d(f) coupling between spins of itinerant s- and localized d(f)-electrons of Eu ions leads to a significant spin splitting of the bands below T_C, as well as magnetization fluctuations near the T_C induced by the band carriers^46,48,49. Nevertheless, the low TC ( < 100 K, far below RT) has constrained their practical application in spintronics.

During the 1990s, the revelation of ferromagnetism (T_C ~ 110 K) in III-V-based dilute magnetic semiconductors Ga_1-xMn_xAs⁵⁰ sparked significant interest among researchers. It is worth noting that GaAs possesses a zinc blende structure, as depicted in Fig. 5a. The substitution of Mn atoms (Mn_Ga) in GaAs acts as acceptors, inducing the magnetism mediated by holes. The FM interaction in this material is dependent on the p-d coupling between localized spins and hole carriers, as well as significant spin-orbit interactions in p-like orbitals that form the valence band^51,52,53. It implies that the manifestation of Ga_1-xMn_xAs’ ferromagnetism is heavily reliant on the concentration of holes. In the subsequent study, T_C of Ga_1-xMn_xAs was empirically demonstrated escalating in tandem with the increasement of hole concentration, as illustrated in Fig. 5b. These findings align with the Zener model of ferromagnetism proposed by Dietl et al.⁵¹, which posits that T_C is proportional to p^1/3, in which p represents the hole concentration.

Fig. 5: The crystalline structure and T_C dependent carrier density for Ga_1-xMn_xAs.

a The unit cell of Ga_1–xMn_xAs with defects including As_Ga which is the As anti-site and Mn_I representing the Mn interstitial. b Experimentally obtained T_C is plotted as a function of hole density in a series of consistently annealed Ga_1–xMn_xAs samples. The carrier densities are determined through Raman scattering measurements, while the T_C is obtained from SQUID magnetometry. The samples exhibit a wide range of Mn content (0.02 < x < 0.085) and also demonstrate variation in thickness ranging from 300 nm to 1200 nm. The figure (b) is reprinted with permission from ref. ⁵² Copyright 2005 by the Springer Nature.

To achieve effective FM ordering in semiconductor body, a minimum Mn content of approximately 2% is required to ensure a sufficiently high density of holes. However, the incorporation of a significant fraction of Mn atoms into GaAs films poses a formidable challenge because of the limited equilibrium solubility of transition metals in III-Vs, typically amounting to only a fraction of a percent. Therefore, Ga_1-xMn_xAs must be fabricated via a robust nonequilibrium process. Molecular beam epitaxy is commonly used to fabricate Ga_1-xMn_xAs films at relatively low temperatures (T_substrate ≈ 250 °C)⁵⁰. An alternative approach involved the use of ion implantation followed by nanosecond pulsed laser annealing to grow FM Ga_1-xMn_xAs films^54,55. Regrettably, defects such as Mn interstitials and anti-sites act as double donors, thereby offsetting a notable portion of the free holes in Ga_1-xMn_xAs^56,57. In the meantime, Mn interstitials have the capability to form antiferromagnetic coupling with substitutional Mn, resulting in a reduction of the FM moment and a decrease in the T_C.

To elevate T_C, it is crucial to inhibit the formation of Mn interstitial defects and increase the hole concentration. Numerous studies have shown that optimizing the growth and annealing conditions, as well as introducing a capping semiconductor layer, effectively elevate T_C^{58,59,60,61,62,63}. A comprehensive investigation, combining experimental and theoretical approaches, has demonstrated that the out-diffusion of Mn interstitials in Ga_1-xMn_xAs films can significantly augment the hole carrier density and T_C. In recent, the highest recorded T_C for p-type Ga_1-xMn_xAs has reached 190 K with Mn content of around 10%⁶⁰.

The level of spin polarization plays a pivotal role in the majority of spintronic functionalities. The attainment of high spin polarization occurs in a magnetic semiconductor when the Zeeman splitting of the conduction or valence band surpasses the Fermi energy¹⁶. Nevertheless, the magnitude and reliance of the Zeeman splitting on the orientation of the wavevector in magnetization exhibit distinct variations. Consequently, the expected polarization alters dramatically with the angle between the magnetization and current directions as well as the carrier concentration⁶⁴. In theoretical calculations by Ogawa et al., the carrier spin polarization of Ga_1-xMn_xAs is determined as 100% when x is greater than or equal to 0.125⁶⁵. Through the utilization of Andreev reflection spectroscopy, a direct measurement of polarization reveals a polarization of ≥ 85% in Ga_1-xMn_xAs (x = 0.05)^66,67. Furthermore, it can serve as an epitaxially integrated emitter for the purpose of injecting spin-polarized carriers into nonmagnetic structures. The implementation of electrical spin injection from Ga_1-xMn_xAs into nonmagnetic GaAs has been successfully achieved within a device structure, that is integrated with a GaAs-based nonmagnetic light-emitting diode (LED) used as a detector of spin-polarized holes^68,69. However, despite the considerable efforts dedicated to Ga_1-xMn_xAs, the maximum T_C still remains far below RT⁶⁴. Until now, the realization of semiconductors based spintronic devices operating at RT has remained elusive.

Si- or Ge-based intermetallic compounds

The advancement of spintronics, a burgeoning field, relies on the studies on spin injectors with materials having high T_C, high spin polarization, as well as good compatibility with Si-based CMOS technology. As previously discussed, the ultra-low solubility of Mn in the semiconducting host presents a significant challenge in fabricating homogeneous films of dilute magnetic semiconductor with T_C above RT. The half-metallic Heusler alloys are the optimal candidate due to the desired high T_C. But, the intermixing with the substrate and/or lattice mismatch between Heusler alloy films and semiconductor substrate lead to significant reductions in spin polarization. Thus, when considering both high T_C and considerable spin polarization as well as the compatibility with CMOS technology, Si- or Ge-based transition metal alloys, such as Fe₃Si, Fe_1.7Ge, Mn₅Ge₃^{25,26,27,28,70}, which can be directly grown on Si or Ge substrates with high quality interface attracted the researchers’ attention for spintronic application. Here, the physical properties of the representative intermetallic compound Mn₅Ge₃ will be given in this chapter.

Mn₅Ge₃ possesses a hexagonal crystal structure of D8₈ type (space group P6₃/mcm), as illustrated in Fig. 6. The lattice parameters of the relaxed Mn₅Ge₃ unit cell at RT were experimentally determined to be: a = 7.184 Å and c = 5.053 Å⁷¹. The Mn atoms are situated in two distinct crystallographic sites. Mn₁ occupies the position 4 d with 32 symmetry while Mn₂ locates at position 6 g with mm symmetry. The atomic positions are delineated in the rectangular coordinates as follows⁷²:

Fig. 6: The crystalline structure and Magnetic hysteresis curves of Mn₅Ge₃.

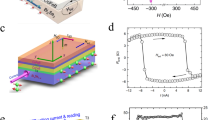
a The top view (left up) and (b), side view (left down) of the crystal structure for Mn₅Ge₃. Colored spheres denote Mn₁(yellow), Mn₂(red), and Ge (blue). c Magnetic hysteresis curves were obtained by applying an external magnetic field in-plane and out-of-plane to Mn₅Ge₃ films of varying thickness. Insets zoom into the positive field branches (ranging from 4000 to 12,000 Oe) in a perpendicular configuration. All measurements were conducted at 15 K. Figures (a, b) are reprinted with permission from ref. ⁷⁷ Copyright 2018 by the American Physical Society. The (c) is reprinted with permission from ref. ⁸⁰ Copyright 2012 by the American Physical Society.

Mn₁ in (4 d) site: ±(1/3, 2/3, 0; 2/3, 1/3, 1/2),

Mn₂ in (6 g) site: ±(x, 0, 1/4; 0, x, 1/4; -x, -x, 1/4) with x = 0.2397,

Ge in (6 g) site: ±(x, 0, 1/4; 0, x, 1/4; -x, -x, 1/4) with x = 0.6030,

The unit cell of Mn₅Ge₃ comprise two periodic atomic layers stacked along the c axis. The planes at z = 0 and z = 1/2 exclusively consist of only Mn₁ atoms which form a 2D hexagonal lattice, whereas the planes at z = 1/4 and z = 3/4 contain equal amounts of Mn₂ and Ge atoms. In principle, there are two possible surface terminations for the Mn₅Ge₃ epitaxial layer, either a Mn termination or a mixed Mn/Ge termination⁷³.

In 1963, it was unveiled that Mn₁ at position 4 d and Mn₂ at position 6 g exhibit distinct magnetic moments, (3 ± 0.1) and (2 ± 0.1) Bohr magnetons respectively, via neutron powder diffraction patterns⁷⁴. However, the polarized neutron diffraction measurements conducted at 77 K in 1964 revealed that Mn₁ atoms have a smaller magnetic moment of 1.7(1)μ_B compared to Mn₂ atoms with 2.7(1)μ_B⁷⁵. Subsequent studies have experimentally demonstrated that the Mn₂ atom carries a larger magnetic moment of 3.23(2)μ_B in comparison to the Mn₁ atom (1.96(3)μ_B)^71,76. The smaller magnetic moment of Mn₁ can be attributed to distinct coordination of Mn and the presence of direct Mn-Mn interactions over a relatively short distance. The moments of Mn atoms in the bulk Mn₅Ge₃ are all aligned ferromagnetically along the hexagonal c axis, resulting in uniaxial anisotropy along the c axis^71,77. The T_C of bulk Mn₅Ge₃ closely approaches RT (296 K), and its saturation magnetization is 2.60(2) μ_B/Mn atom at 4.2 K.

Numerous studies have been conducted on the epitaxial growth of Mn₅Ge₃ films on Ge substrates due to their potential application in spintronics. The epitaxial growth Mn₅Ge₃ was initially achieved by matching the hexagonal (001) basal plane with the (111) plane of the Ge substrate^28,78,79. Mn₅Ge₃ films demonstrate robust ferromagnetism maintaining up to a temperature of T_C = 296 ± 10 K. When the Mn₅Ge₃ film thickness is less than 20 nm, the easy magnetization axis aligns with the hexagonal basal plane, parallel to the interface between Mn₅Ge₃ and Ge. As the film thickness exceeds 20 nm, there is a gradual reorientation of the easy magnetization axis away from the hexagonal (001) plane of Mn₅Ge₃, aligning instead parallel to the c-axis (perpendicular to the sample surface) (Fig. 6c)^70,80. The findings are substantiated by theoretical computations grounded in Kittel’s model which delineates the magnetic behavior of domains in uniaxial thin films. Further analyses suggest that for thicknesses below 10 nm, the magnetization is oriented in-plane with a monodomain-type structure dominated by magnetostatic anisotropy (4πM_S² in which M_S is saturation magnetization). The Mn₅Ge₃ layers display a distinct magnetic structure beyond 20 nm, characterized by a stripe-domain pattern attributed to the robust perpendicular uniaxial magnetocrystalline anisotropy⁸⁰. In ferromagnetic resonance (FMR) experiments, the presence of a stripe domain was evidenced by the emergence of an acoustic FMR mode with a clearly defined resonance field⁸¹. Interestingly, this critical thickness is significantly lower compared to other materials with similar magnetic behavior. For example, it is approximately 50 nm in a Co film.

The T_C of intrinsic Mn₅Ge₃ is limited to 296 ± 10 K. From a practical perspective, it is preferable for spin injectors to possess a magnetic order well surpassing RT. Hence, diverse approaches are employed to boost T_C, such as, Fe, Sb or C co-doping^82,83,84. By substituting one Mn atom with Fe, T_C was elevated to 319 K in FeMn₄Ge₃. Simultaneously, there is a notable increase in spin polarization from 42% in Mn₅Ge₃ to approximately 60% in FeMn₄Ge₃⁸². Similarly, it has been demonstrated that the T_C of Mn₅Ge₃ can be elevated by 14 K through the substitution of Sb for Ge, owing to the heightened magnetic coupling between Mn-3d and Sb-5p⁸⁵.

One common method for improving the T_C in Mn₅Ge₃ is through carbon doping. This pioneering work of Suergers et al. introduced that the incorporation of carbon into Mn₅Ge₃ compounds leads to a significant enhancement of T_C¹⁸. In particular, the textured Mn₅Ge₃C_x films with x = 0.5 demonstrate a significantly increased T_C of 435 K in comparison to bulk un-doped Mn₅Ge₃ which exhibits a T_C of 296 K (see Fig. 7a)^86,87,88. After C doping, there is a discernible reduction in the average magnetic moment of the Mn atom from 2.6μ_B to 1μ_B. A theoretical simulation conducted by Pochet et al. has elucidated that the heightened T_C of Mn₅Ge₃ through carbon doping can be primarily attributed to the emergence of the 90° FM super-exchange between Mn atoms mediated by carbon. On the contrary, the reduction of interatomic distances between Mn atoms, stemming from the robust the strong hybridization between Mn 3 d and C 2p orbitals, is deemed as a secondary effect⁸⁹. Further investigation into the impact of carbon doping on Mn₅Ge₃ was conducted by Spiesser et al. via utilizing scanning transmission electronic microscopy or⁵⁵ Mn nuclear magnetic resonance spectra^86,87,88,90. It has been discovered that carbon enters interstitially in close to the 6(g) crystallographic positions, thereby occupying the 2(b) octahedral voids (Fig. 7b). The magnetic properties of the Mn atoms situated at the corners of a host octahedron are significantly altered by the presence of carbon. Consequently, both the magnetic moment and the magnetocrystalline anisotropy were reduced compared to the pristine Mn₅Ge₃.

Fig. 7: The magnetization curves and atomic lattice of C-doped Mn₅Ge₃.

a Magnetization as function of temperature for C-doped Mn₅Ge₃ thin films with various carbon concentrations. The magnetic field of 1 Tesla was applied in plane. Temperature dependence of the magnetization (triangles) and its derivative (line) for the Mn₅Ge₃C_0.5 film is depicted in the inset. The vertical arrows denote the various local minima corresponding to different T_C for x = 0.5. The figure is reprinted with permission from ref. ⁸⁶ Copyright 2022 by the American Physical Society. b Schematic representation of a hypothetical carbon superstructure in the Mn₅Ge₃C_0.5 lattice. Colored spheres represent different entities, C (black), Mn_I (green), Mn_II (blue), and empty 2(b) sites (light gray). Two distinct types of the Mn_I planes can be identified: one in gray where all 2(b) voids are filled with carbon, and another in pink where all 2(b) voids remain unoccupied. The figure is reprinted with permission from ref. ⁹⁰ Copyright 2022 by the American Physical Society.

As potential candidates for spin-injection, the electronic properties of Mn₅Ge₃ were initially investigated theoretically by Picozzi et al. in 2004. As illustrated in Fig. 8, the full-potential linearized augmented plane-wave computation reveals the pronounced metallic character of Mn₅Ge₃, which is predominantly governed by Mn 3 d contribution from the Fermi level up to a binding energy of 3.5 eV⁷². The spin polarization is determined to be 41% based on the band structure calculations. Soon afterwards, the theoretically predicted band structure was also empirically validated^91,92,93. Subsequently, a variety of studies employing different techniques were conducted to assess the polarization values of Mn₅Ge₃ layers. Point contact Andreev reflection measurements on Mn₅Ge₃ epilayers have revealed a remarkable spin-polarization of 42 ± 5%²⁷. Spin-resolved photoelectron spectroscopy measurements on Mn₅Ge₃ (001)/Ge (111) films using photons with an energy of hν = 21.2 eV have unveiled spin polarization of 15 ± 5% at Fermi energy⁹⁴. It has been discovered that the spin polarization of Mn₅Ge₃ exhibits robust crystallographic anisotropy and heavily depends on the matrix element⁹⁵. Hence, disparities in spin polarization have been observed across various experiments.

Fig. 8: The density of states of Mn₅Ge₃.

Partial density of states of (a), Ge, (b), Mn₁, and (c), Mn₂, and the total density of states is displayed in (d). Majority (minority) spin components are depicted along the positive (negative) y-axis. Fermi energy is defined as zero on the energy scale. The figure is reprinted with permission from ref. ⁷² Copyright 2004 by the American Physical Society.

Due to the immense potential of Mn₅Ge₃ in spintronics, it is essential to study the epitaxial growth of Mn₅Ge₃ films on Ge substrates. In the initial stages, the majority of investigations were directed towards the growth of Mn₅Ge₃ on Ge (111), wherein the solid phase epitaxy (SPE) method was employed to preclude the co-existence of secondary phases^96,97,98. The SPE growth of Mn₅Ge₃ films begins with the deposition of Mn films onto the Ge (111) substrates at RT, followed by thermal annealing at ~450 °C for several minutes to stimulate the inter-diffusion and phase nucleation^28,79,98. Epitaxial Mn₅Ge₃ films have been successfully fabricated, featuring a hexagonal basal plane (001) that aligns parallel to the (111) surface plane of Ge. The atomically abrupt interface was obtained, with virtually no threading dislocations being detectable.

Although extensive researches have been dedicated to investigating the epitaxial growth of Mn₅Ge₃ layer on the Ge (111) substrate, it is also crucial to achieve the epitaxial growth of Mn₅Ge₃ layer on the Ge (001), as it is practically compatible with the Si-based CMOS technology. The initial endeavor to cultivate Mn₅Ge₃ on the Ge (001) substrates utilizing the SPE method was conducted at a substrate temperature of 650 °C. Under such conditions, the Mn₅Ge₃ film manifests itself in the form of a nano-island with (001)_Mn5Ge3 // (001)_Ge^99,100. To effectively enhance the quality of the Mn₅Ge₃ film on Ge (001), non-equilibrium ultrafast solid phase epitaxy (ultrafast-SPE) is employed. In this process, ultrafast annealing is utilized to modify the kinetics and thermodynamics during the growth of Mn₅Ge₃. Consequently, epitaxial Mn₅Ge₃ films were successfully grown on Ge (001) with the in-plane axis [001] of Mn₅Ge₃ (100) plane parallel to the [110] axis of the Ge (001) substrate^101,102,103.

Numerous studies have been dedicated to the development of spin transport devices based on Mn₅Ge₃. As reported, the observation of spin accumulation and precession up to 10 K was documented in Mn₅Ge₃C_0.8/Al₂O₃/n⁺-Ge (10²⁰ cm⁻³) tunneling contacts through the adoption of three-terminal (3-T) Hanle-effect measurements¹⁰⁴. The lifetime of spin at T = 4 K is extracted to be 38 ps and the spin diffusion length is calculated to be approximately 367 nm. However, such a spin signal could potentially be generated by localized states within the tunnel contact through two-step tunneling or impurity-assisted tunneling magnetoresistance. To eliminate such possibilities, investigation into the direct Schottky tunnel contact between Mn₅Ge₃ and As-doped-Ge (111) (10¹⁸ cm^-3) was conducted¹⁷. Utilizing 3 T geometry, which comprises one single FM contact that used as the spin injector and detector, apparent Hanle and inverted Hanle signals with characteristic features of spin accumulation and spin precession were observed up to 200 K. However, the 3-T geometry is highly susceptible to spurious signals, such as Hall or anisotropic magnetoresistance effects, due to the presence of a nonzero charge current at the detector junction. Hence, further research on the non-local spin transport device based on Mn₅Ge₃ films is imperative to propel the advancement of spintronics.

2D ferromagnetic materials

The emergence of 2D materials has attracted much attention due to their tremendous electrical, optical, and magnetic properties and their broad range of applications in spintronics^{105,106,107,108}. The atoms in monolayer 2D materials are typically bound together by robust covalent bonds, while the individual layers are interconnected through the subtle and delicate vdWs interaction¹⁰⁸. Consequently, the distinctive characteristics and adaptability of 2D magnetic materials have provided a captivating platform for the exploration of novel spintronic concepts with exceptional controllability. The initial attempts to isolate magnetic 2D materials were conducted towards the end of 2016, when researchers successfully exfoliated monolayer and few- layer NiPS₃¹⁰⁹, and FePS₃^110,111. The magnetic ordering of these compounds is preserved down to the monolayers limit which was illustrated by the Raman measurements. Then, further breakthrough was made in 2017, with the first experimental confirmation of ferromagnetism via magneto-optic Kerr microscopy in atomically thin CrI₃¹¹² and CrGeTe₃¹¹³, respectively.

To date, a great deal of 2D materials, which are often obtained through mechanical exfoliation, exhibit an intrinsic FM order^112,113,114. Several studies demonstrate that the FM order and the T_C of 2D material depend upon the layer numbers and the thickness of a given material¹¹³. The correlation between the layer number and T_C of recently discovered 2D ferromagnets is illustrated in Fig. 9¹¹⁵. According to the dependence of T_C on the layer numbers, three distinct trends have been identified for three different categories of materials: i) CrX₃ (X = I, Br, Cl) – these materials usually exhibit a significantly low T_C (far below 100 K) at the 2D scale, which marginally increased in their bulk form¹¹⁶; ii) Fe-Ge-Te ternary compounds (Fe₃GeTe₂, Fe₃GaTe₂) – these materials usually exhibit a slight increase in the T_C in the multi-layer structures than the bulk and then a remarkable decrease when down to the monolayer limit^114,117,118. iii) MSe₂ (M = Mn, V et. al) – they surprisingly demonstrate RT ferromagnetism in low dimensionality despite the fact that their bulk crystals do not exhibit FM, unlike most 2D ferromagnets, which derive their magnetic properties from bulk crystals^119,120,121.

Fig. 9: Dependence of the Curie point on the layer number of recently discovered 2D ferromagnets.

Data has been sourced from literature as follows: VSe₂, MnSe₂, Fe₃GaTe₂, Fe₃GeTe₂, (mechanically exfoliated, assisted by SiO₂/Si] or Al₂O₃), and CrI₃, CrBr₃, CrCl₃. The figure is reprinted with permission from ref. ¹¹⁵ Copyright 2024 by the Wiley-VCH GmbH.

In addition to the aforementioned 2D ferromagnets, 2D antiferromagnetic material has also garnered significant attention recently due to their unique properties such as terahertz resonance and no stray fields, particularly suitable for spintronics. Typical representative is the MPX₃ family (M = 3 d transition metals; X= chalcogen atoms) which have similar crystal structures, and have been exfoliated into monolayers^122,123. It’s remarkable the magnetism of these materials exhibits significant variation depending on the transition metal atom M. For instance, Mn-based compounds exhibit a Néel AFM order where the spin states in the nearest neighbor metal atoms have an opposite orientation, while Fe-, Co-, and Ni-based compounds display a zig-zag AFM order where the spin-state of the adjacent metal atom chains along the zigzag direction has an opposite orientation¹²³. Magnetic measurements demonstrated that the Néel transition temperature T_N ranges from 82 to 155 K in bulk Ni, Fe, Mn, and Co based MPS₃ or MPSe₃¹²². Additionally, the magnetic anisotropy energy of this family materials is also significantly different. For instance, FePSe₃ demonstrates a significantly larger magnetic anisotropy energy attributed to its strong Ising-like anisotropy, while MnPSe₃ shows smaller magnetic anisotropy energy attributed to a pronounced XY anisotropy^124,125.

One of the most studied 2D magnetic material is Fe₃GeTe₂ (FGT). FGT possesses a layered hexagonal crystal structure, consisting of Fe₃Ge slabs partitioned by the vdW bonded Te layers. The crystal structure of bulk FGT is depicted in Fig. 10a-b¹²⁶. The Fe atoms within the unit cell are situated in two inequivalent Wyckoff sites, identified as Fe₁ and Fe₂ in Fig. 10a. The magnetic moment of Fe₁³⁺ is about 1.7 μ_B and that of Fe₂²⁺ is about 1 μ_B. As depicted in Fig. 10c, the magnetic coupling parameters governing interlayer Fe₁-Fe₂ coupling and Fe₁-Fe₁ coupling are 20.41 meV and 23.48 meV, respectively, which collectively control the ferromagnetism of FGT. It means the coupling between perpendicular Fe atoms dominates the ferromagnetism in FGT. However, the coupling between Fe and Te atoms also makes contribution to the ferromagnetism. In principle, the distance between adjacent FGT layers hold a pivotal role in tuning the magnetic interactions. Kim and Hu et al. have discovered that the magnetic interaction between adjacent layers of FGT is regulated by the indirect interaction between oxygen p orbitals where oxygen atoms originate from an oxide layer (O-FGT) naturally formed on top of exfoliated FGT^127,128.

Fig. 10: The atomic lattice, exchange coupling and RMCD signal of Fe₃GeTe₂.

The atomic lattice of bulk Fe₃GeTe₂ is depicted in Side view (a) and middle top views (b) showcasing its crystal unit cell marked by dashed rectangular and rhombic shapes¹²⁶. c The schematic diagram illustrates the exchange coupling in Fe₃GeTe₂¹⁰⁸. d Remanent RMCD signal is plotted as a function of temperature across a series of selected few-layer flakes (1 L, monolayer; 2 L, bilayer; 3 L, trilayer; 4 L, four layers; 5 L, five layer); The derived values of the exponent β are depicted as a function of thickness in the inset, revealing a dimensional transition from 3D to 2D Ising ferromagnetism¹¹⁷. The figure a and b are reprinted with permission from ref. ¹²⁶ Copyright 2019 by the American Chemical Society. The figure c is reprinted with permission from ref. ¹⁰⁸ Copyright 2021 AIP Publishing LLC. The figure d is reprinted with permission from ref. ¹¹⁷ Copyright 2018 by the Springer Nature.

The pioneering study of the inherent ferromagnetism in single-layer FGT was conducted by Zhuang et al. in 2016¹²⁹. In their work, density functional theory (DFT) calculations revealed the ease of mechanically exfoliating nanosheets from the bulk phase. The band structure around the Fermi level is predominantly influenced by Fe 3 d orbitals, which leads to the fulfillment of the Stoner criterion and, consequently, itinerant ferromagnetism. In 2018, Fei et al. successfully exfoliated FGT bulk crystals into monolayer onto a gold film which is evaporated on top of SiO₂/Si¹¹⁷. The T_C of monolayer FGT was revealed to be 130 K by X-Ray Magnetic Circular Dichroism (RMCD) measurement. In addition, layer-number-dependent investigations have unveiled a transition from 3D to 2D itinerant ferromagnetism when the thicknesses are decreased to thinner than 4 nm (equivalent to five layers) (Fig. 10d, inset). Subsequently, Deng et al. employed the Al₂O₃-assisted exfoliation method instead of conventional mechanical exfoliation with the aim of protecting the intralayer bonding¹¹⁴. The T_C of monolayer FGT was determined to be 68 K and 30 K through RMCD and remanent anomalous Hall resistance measurement, respectively, which were significantly lower than the one reported by Fei et al.^114,117. Moreover, the itinerant ferromagnetism with an out-of-plane magnetocrystalline anisotropy persists down to monolayer in FGT. However, Min et al. have recently highlighted that the FGT’s ferromagnetism cannot be explained solely by the itinerant picture. Instead, it is suggested to exists in an intermediate regime with both the itinerant and the localized spin states, as derived from the electronic structure calculations¹³⁰. Therefore, the investigation of FGT still needs further demonstration to clarify the controversy about the origin of magnetism and the disparity in the T_C.

As reported, the T_C of FGT depends on many factors, such as the layers number, the fabrication environment and 3 d element doping. FM metallic FGT exhibits a T_C near 220 K in its bulk state¹³¹. The reported T_C exhibited dramatic decreases with the reduced number of layers in FGT when the thickness is less than 25 nm. Layer-number-dependent investigations have revealed a rapid decrease in the T_C from 207 K for five layers to 130 K for the monolayer via RMCD measurement and Anomalous Hall effect measurements^117,132. Moreover, the variation in the probed T_C may stem from diverse synthesis environments of FGT^133,134. Zhang et al. deposited FGT flakes onto three distinct substrates, namely Al, Au, and SiO₂. The substitution of substrate from Al to Au could significantly improve T_C value from 105 to 180 K for 10 nm-FGT film. Such evident modulation of T_C by substrates may be ascribed to the distortion of lattice and the redistribution of charge between the FGT sample and the substrate¹³³. Meanwhile, Deng et al. managed to boost T_C of the monolayer FGT to RT via an ionic gate, much higher than that of the bulk¹¹⁴. Finally, doping with transition-metal atoms is an effective method to tune the magnetic properties of FGT. It was demonstrated the T_C can be improved to 320 K in Fe_3+1.80GeTe₂ layer after the adoption of Fe atoms during the MBE growth^135,136. However, the influence of Co dopant in FGT is complicated. Both the T_C and moment of FGT are gradually suppressed upon Co doping while a certain amount of Co dopant in Fe₅GeTe₂ would improve the T_C to 325 K^137,138.

The electronic properties of 2D FGT were newly investigated by Jung et al.¹³⁰. It has been contended that the FGT’s ferromagnetism cannot be simply explained using the itinerant picture. Rather, it is posited to exist in an intermediate regime with both the itinerant and the localized spin states. FGT demonstrates a robust energy-dependent spin polarization (Fig. 11) arising from the simultaneous presence of itinerant and localized spin states¹³⁰. The spin polarization dependent on energy of a FM electrode has been effectively detected by observing the variation in the TMR value in the spin-valve device configuration of MTJs. The vertical tunneling SV device based FGT electrodes sandwiching wide-band h-BN, WSe₂ or MoS₂ as a NM tunnel barrier have been fabricated^130,139. The observed magnetoresistance ratio (MR ratio) of 160% at 4.2 K for the intrinsic MTJ serves as a compelling validation of the exceptional performance of the device. The spin polarization of 66% was extracted from the MR ratio, corresponding to 83% and 17% of the majority and minority carriers, respectively¹³⁹. By manipulating the electrical bias, it is highly possible to modulate and even reverse the net spin polarization of the injected carriers. This phenomenon ultimately leads to changes in sign of the tunnelling magnetoresistance¹³⁰. Through electrolyte gating, the tunneling MR ratio of FGT/h-BN/FGT MTJ has been significantly improved by 2.5 times, from 26% to 65%, the spin polarization from 0.34 to 0.49¹⁴⁰. Moreover, nonlocal SVs with FGT as the spin source and detector were fabricated and employing multilayer graphene as the spin transport channel. The efficiency of spin injection was approximated to be around 1%, close to conventional nonlocal SVs with transparent contacts between FM electrodes and the graphene channel¹⁴¹.

Fig. 11: The spin polarization and DOS of Fe₃GeTe₂.

The spin polarization (P) dependent on the energy for Fe₃GeTe₂ material (top panel) extracted from the 2D metallic ferromagnetism’s spin-polarized DOS (D↑ and D ↓ ) (depicted in the middle panel). The multilayered FGT’s total DOS (D ↑ +D ↓ ) (depicted in the bottom panel) is derived from DFT +DMFT calculations. The open cyan squares visually represent momentum-averaged intensity of the photoemission spectroscopy measurements for the FGT. The figure is reprinted with permission from ref. ¹³⁰ Copyright 2022 by the Springer Nature.

Although great progress has been made in the development of 2D ferromagnetism and related devices, it is still a great challenge to produce monolayered materials with i) RT FM order, ii) good air stability, and iii) repeatability on a large scale, which are prerequisite to achieve practical applications. Recent discoveries of monolayer MnSe_x (usually, x = 1 or 2) and VSe₂ exhibiting intrinsic ferromagnetism at RT, coupled with the controlled synthesis of pioneering materials Cr₅Te₈ and CrTe₂ along with its exceptional and air-stable FM characteristics, open novel avenues for exploration into 2D magnetism and their applications in spintronic device^{119,120,142,143}. Therefore, we envision that the heterostructures of vdW materials with exceptional spin-related properties at RT will pave the way for the realization of all-vdW-material-based spintronic devices at RT in the future.

Summary and outlook

In summary, we review various FM materials for highly efficient electrical spin injection across the ferromagnet/semiconductor interface, which is expected to become a mainstream technology in future microelectronics. The T_C and spin polarization of various FM/semiconductor materials are summarized in Table 1. (1) Heusler alloys possess the desired high T_C above RT and theoretically 100% spin polarization. Nevertheless, the absence of local ordering structure and intermixing between Heusler alloy films and semiconductor substrate pose a barrier to achieving half-metallic electron transport property at RT, as theoretically predicted in the bulk Heusler alloy. (2) Dilute magnetic semiconductors have comparable resistance with semiconductor channel, which could reduce the interface resistance and further promote the improvement of the spin injection. Nevertheless, a further increase of T_C has always been a major goal in dilute magnetic semiconductors. (3) The Si- or Ge-based intermetallic compounds offer several advantages including considerable spin polarization, the high-quality interface and compatibility with CMOS technology. In essence, the Si- or Ge-based transition metal alloys are deemed to be the most auspicious for application in spintronics. (4) 2D FM materials hold great appeal for spintronics owing to their infinitesimal thickness and exceptional physical properties. However, the air stability and reproducibility of 2D material with desirable performances is still full of challenges.

Table 1 Summary of the T_C and spin polarization in various FM/semiconductor materials

Although the advent of the aforementioned magnetic materials has certainly injected new vitality into the realm of spintronics, the building of spin-based devices operated at RT remains full of challenges. Herein, several strategies are proposed to overcome the main obstacles in applying such spintronics devices in nonvolatile logic-in-memory. First, there is a pressing need for intensive research to advance the development of atomically controlled Heusler films, which has been utilized as a spin source due to their half-metallicity at RT. First principles calculations and materials informatics, based on available databases^32,144, have been utilized to identify pertinent combinations of interfacial atomic bonding, crystalline orientation and surface termination which are aimed at maintaining the atomic ordering in the vicinity of their interface and surfaces. For example, the epitaxial growth of Co₂MnSi on Si has been realized recently which paves the way for high-performance semiconductor spintronic devices¹⁴⁵. In addition, the half-metallicity of Heusler films could enhance better operation ability in STT based devices owing to their intrinsically low Gilbert damping constants for fast magnetization reversal with low switching current density¹⁴⁶. On the other side, a further increase in T_C of dilute magnetic semiconductor can be achieved by non-equilibrium doping in new material system, gate tunability, materials interfaces engineering or proximity effects at ferromagnet/semiconductor junctions, resulting in increased spin and hole densities, ideal for the development of advanced spintronic devices^147,148. Recently, a consensus appears to have emerged in the pursuit of achieving T_C above RT via introducing magnetic dopants into vdW-layered semiconductors, such as Fe-doped MoS₂, V-doped WSe₂, or Cr-doped GaTe¹⁴⁹.

Second, albeit investigations on the above-mentioned magnetic materials in thin films (tens nm) have been ongoing for many years, recent advancements in nanoscale characterization and device fabrication down to the 2D limit (several atomic layers) have created opportunities for exploring novel physical phenomena and developing cutting-edge spintronic devices. Currently, the exploration of integration engineering and the comprehension of the growth process of 2D ferromagnets are still in their nascent stages, despite some initial advancements being achieved. The future prospect for the advancement of spintronics may closely align with development in robust 2D magnetic materials with RT ferromagnetism. With the advent of large-scale growth of advanced 2D materials via chemical vapor deposition (CVD) methods, it is indubitable to anticipate a genuine potential in the new generation of 2D spintronics logic devices on large-scale. For example, the T_C of graphene-based magnetic materials was improved to exceeding RT ( ≥ 300 K) with a saturation magnetization as high as 4.1 × 10⁻⁷ emu·mm⁻² by controlling CVD growth process¹⁵⁰. In addition, the spin transport capabilities also can be improved by utilizing the 2D semiconductor channel, such as MoS₂, black phosphorous or graphene, with the ferromagnetic tunnel contacts^30,151,152. The higher spin diffusion length of ∼13.6 μm was demonstrated in graphene spin devices on standard large-scale substrates^30,31. The outstanding performance in 2D-based FM/semiconductor heterostructure can be attributed to the exclusive features of 2D crystal such as atomic-level thickness control, near-perfect crystallography without dangling bonds, and novel electronic structure-guided interfaces with tunable hybridization and proximity effects, which lead to an entirely new group of spinterfaces¹⁵³. This new aspect has sparked significant interest, prompting both theoretical and experimental endeavors aimed at developing an entirely novel category of vdWs interfaces for efficient spin transmission and dynamic control through exotic heterostructures.

Third, numerous emerging spin-based effects in topological insulators or heavy metals, such as spin pumping via the (inverse) Rashba-Edelstein effect, which has been utilized for generating pure spin current in neighboring nonmagnetic layer through the magnetization precession in FM layer. And the (inverse) Rashba-Edelstein effect has been harnessed for injecting/detecting spin in Rashba interfaces or topological insulator heterostructures¹⁵⁴. Topological insulator (Bi₂Se₃), characterized by spin-momentum-locked surface states arising from strong spin-orbit coupling (SOC), possesses the capability to impart spin current into neighboring materials across the interface through SOT¹⁵⁵. Inversely, the injection of a spin current induces the corresponding spin polarization and charge current. Other types spin-charge conversion can also be achieved through SOC effects of 3D conductors, specifically the observation of the spin Hall effect in the heavy metals (such as Pt, Ta)¹⁵⁶. Such spin-charge conversion phenomena described holds significant implications for the field of spintronics technologies, which center around the generation and detection of spin currents. Therefore, it is highly feasible to achieve low-power and all-electric control of spintronic devices devoid of reliance on magnetic fields. These advancements are poised to expedite the progress of beyond-CMOS device application.

Spintronic devices, which harness the dual degrees of freedom of spin and charge in electrons, have the potential introducing new capabilities to the microelectronics industry. Nevertheless, in order to satisfy the ever-growing demands of chip level integration of magnetism and standard electronics in spintronics, innovation in terms of materials, processes and devices are still indispensable.