Nature’s Master of Ceremony: The Populus Circadian Clock as Orchestrator of Tree Growth and Phenology

Abstract

Understanding the timely regulation of plant growth and phenology is crucial for assessing a terrestrial ecosystem’s productivity and carbon budget. The circadian clock, a system of genetic oscillators, acts as ‘Master of Ceremony’ during plant physiological processes. The mechanism is particularly elusive in trees despite its relevance. The primary and secondary tree growth, leaf senescence, bud set, and bud burst timing were investigated in 68 constructs transformed into Populus hybrids and compared with untransformed or transformed controls grown in natural or controlled conditions. The results were analyzed using generalized additive models with ordered-factor-smooth interaction smoothers. This meta-analysis shows that several genetic components are associated with the clock. Especially core clock-regulated genes affected tree growth and phenology in both controlled and field conditions. Our results highlight the importance of field trials and the potential of using the clock to generate trees with improved characteristics for sustainable silviculture (e.g., reprogrammed to new photoperiodic regimes and increased growth).

Introduction

Even under stable conditions, net ecosystem exchange of contrasting biomes displays diurnal oscillations due to endogenous processes^1,2. Wood formation is the primary responsible for carbon (C) allocation in woody plants, an important ecosystem C sink³. Trees have a seasonal time window for radial growth with unclear drivers, hampering forest productivity and C budget assesments^4,5,6,7,8. Lockhart⁹ theorized cell expansion and division, allowing radial growth, only occur after exceeding a meristem turgor pressure threshold. Indeed, tree growth is limited by species-specific vapor pressure deficit (VPD) and soil water potential (SWP) ranges explaining most diurnal growth variation¹⁰. Since VPD and SWP affect transpiration, and transpiration affects water potential and cell turgor, it is implied tree growth is controlled by the C source and tree water relations (i.e., source-limitation hypothesis)^10,11,12,13. Since VPD increases rapidly with daylength, wood growth is inhibited during sunny days^6,10. Nevertheless, CO₂ assimilation can still occur, even when cambial activity is restrained by unfavorable conditions^6,14. Consequently, a temporal decoupling occurs between wood growth (C sink) and C assimilation (C source) which dominate during rainy cloudy days and night-time, and sunny days and daytime, respectively¹⁰. The number of growth days might more strongly determine annual growth than the growth period (i.e., growing season)^6,15. Trees’ time window for radial growth is thus determined by the C source (i.e., photosynthesis) and limited by tree water relations (i.e., meristem turgor pressure). In addition, it is suggested growth has greater environmental sensitivities than photosynthesis, and these sensitivities are temporally separated on a species-specific basis explained by species’ capacity to timely regulate physiology^6,14,16.

The circadian clock (hereinafter “clock”) allows plants to track time and influences plant physiology and phenology (i.e., the timing, duration, and magnitude of life history phases)^{6,10,17,18,19,20,21,22,23,24,25,26}. Not only does the clock explain species-specific growth patterns (i.e., diurnal growth rate and number of growth days) but also phenological responses (i.e., growth period)^6,23,24. The clock likely correlates the number of growth days and growth period, determining annual tree growth and C uptake^6,15. The extent to which the clock affects trees’ life history phases, related ecosystem processes, a species’ environmental sensitivity (i.e., through resonance, matching internal and external rhythms), and diurnal and annual growth pattern remains unclear^27,28.

The clock is a system of genetic oscillators composed of interconnected transcription-translation negative feedback loops (TTNFLs) reset by signals known as zeitgebers. The mechanism generates cyclic endogenous rhythms adapted to changing environments^{29,30,31,32,33,34,35,36}. The clock shows consistent rhythmicity over a broad temperature range (i.e., temperature compensation), is involved in winter hardiness and freezing tolerance, and sensitizes plants to temperature changes^{32,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55}. Many clock-regulated genes co-regulate plant physiology^32,56. For example, the circadian period shortens with leaf age suggesting involvement of TIMING OF CAB EXPRESSION 1 (TOC1) during leaf senescence⁵⁷. TOC1 is associated with expression of FLOWERING LOCUS T (FT) genes, and involved in xylogenesis (i.e., xylem cell formation)^58,59,60. Edwards et al.⁶¹ showed that expression of LATE ELONGATED HYPOCOTYL 1 and 2 (LHY1 & 2; LHYs, morning-expressed, light-responsive and repressing TOC1) and TOC1 (evening-expressed and repressing LHYs) results in increased biosynthesis of growth regulators cytokinins and auxins during day and night, respectively^62,63. Through fluctuating Cyclin D3 (CycD3) concentrations, cell division, and proliferation tend to be initiated during the evening, while cell elongation and xylem differentiation tend to occur at night. The clock thus gates (i.e., temporally restricts) DNA replication and mitosis to the night when favorable conditions prevent DNA damage and VPD is below radial growth thresholds^9,19,61,64.

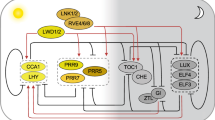
In general, the plant clock is thought to have a conserved architecture^65,66. Various components make up the Populus clock (Fig. 1). Photoreceptors are the most prominent input pathway feature and allow daylight perception. Phytochromes A, B1, and B2 (phyA, phyB1 and phyB2) are dimers allowing daylength tracking^{67,68,69,70,71,72,73,74}. Other photoreceptors, like cryptochromes, become phosphorylated upon interaction with blue light⁷⁵. The ZEITLUPE protein family, containing F-box domains and LOV\PAS-domains with KELCH repeats (ZTL and LKP2), their homologs FLAVIN-BINDING KELCH REPEAT, F-BOX1 (FKF1), and phototropins likewise perceive blue light and play an active role in light-dependent protein degradation.

Fig. 1: Simplified representation of the Populus circadian clock inspired by Bendix et al.²⁶⁶, Fogelmark and Troein²⁶⁷, and Singh et al.²⁶⁸.

Relevant proteins comprising or pertaining to the Populus clock are schematically grouped and colored-coded based on their major physiological function. Proteins related to the photoreception of far-red, red, or blue light are highlighted in pink, red, or light blue, respectively. Key components of the central clock oscillator are encircled or highlighted in white, while other clock-associated proteins are highlighted in light green. Termination arrows indicate negative effects. Proteins known to regulate growth or phenology are highlighted in dark green, and those linked to stress or growth hormones are represented in gray or orange, respectively. The shaded blue outer perimeter denotes key traits influenced by the clock.

The core clock pathway consists of the TTNFL between LHY1 and LHY2 and TOC1, with LHYs encoding for v-MyB myeloblastosis viral oncogene homolog (MYB) transcription factors important in secondary plant metabolite biosynthesis^76,77. TOC1 (aka PRR1) belongs to the PSEUDO-RESPONSE REGULATOR (PRR) gene family^78,79,80.

GIGANTEA (GI) and ZTL are output pathway components and regulate physiological events⁸¹. In Arabidopsis thaliana, ZTL affects gene expression, helps degrades TOC1 and PRR5 proteins, and resetting the clock^81,82,83,84. GI, GIGANTEA-LIKE (GIL), and FKF1 proteins interact in a complex mediating degradation of CYCLING DOF FACTOR (CDF) proteins^85,86. These proteins repress CONSTANS (CO) and FT2 gene transcription by binding to CO and FT promotors^87,88. GI and GIL genes regulate photoperiodic response, short-day (SD) induced growth cessation, and bud set^{85,88,89,90,91,92}. Two Populus CO orthologues exist: CO1 and CO2^59,93. When CO is expressed in A. thaliana, it induces FT expression under long-day (LD) conditions⁹⁴. FT then travels from phloem to shoot apex and initiates flowering^93,95. TEMPRANILLO1 and 2 (TEM1 & 2) prevent flowering, and the CO and TEM balance determines FT levels^94,96. A similar regulatory module may control growth cessation and bud set under SD conditions in Populus⁵⁹. Populus FT paralogs are expressed at different times in different tissues⁹⁷. For example, FT1 is involved in release of winter dormancy bud flush, while FT2 is involved in vegetative growth and bud set^59,85,97,98. Likewise, FT1 and FT2 are mainly expressed in stems and buds, and leaves, respectively^93,99.

EARLY BIRD 1 (EBI1) and its Populus homolog EBI2 encode, like their A. thaliana homologs NFXL1 and NFXL2, for zinc finger proteins with putative transcription factor activity involved in abiotic stress responses^100,101,102. EBI may bind to ZTL affecting transcriptional activation of LHY and TOC1¹⁰³. EBI/NFXL2 thus affects A. thaliana’s clock free-running period and speed³². Genes like LEAFY (LFY), SHORT VEGETATIVE PHASE (SVP), MULTICOPY SUPRESSOR OF IRA 1 (MSI1), REGULATORY COMPONENT OF ABSCISIC ACID RECEPTOR 1 (RCAR1), 12-OXOPHYTODIENOATE REDUCTASE 3 (OPR3) and ALLENE OXIDE SYNTHASE (AOS) also relate to the clock, growth and phenology^{104,105,106,107,108,109}. The floral meristem identity gene LFY controls the inflorescence-to-floral meristem transition^110,111,112. Likewise, SVP regulates floral meristem specifications and transitions¹¹³. SVP affects temperature-responsive regulation of bud break after vernalization and represses expression of FT1 and GA20-OXIDASE1 (GA20ox1)^{106,114,115,116,117}. GA20ox1 is mainly expressed in photosynthesizing tissue and encodes for an enzyme catalyzing the stepwise conversion of C20 gibberellin growth and developmental hormones (GAs)^{116,117,118,119,120}. MSI1 encodes for a WD-40 repeat protein and is associated with flowering, gametophyte, and seed development^{121,122,123,124,125,126,127}. Like SVP, RCAR1 represses bud break while affecting GA20ox1 expression. In addition, RCAR1 regulates abscisic acid (ABA), which inhibits growth and regulates stress^104,105. As elucidated in A. thaliana, the OPR3 and AOS genes encode enzymes regulating the biosynthesis of the growth and stress resistance hormone jasmonic acid (JA)^{107,108,109,128,129,130,131,132,133}.

The effects of gene modification regarding plant yield performance are seldom assessed thoroughly in a real-world environment¹³⁴. This meta-study examines the growth and phenology of transgenic trees exposed to both natural and controlled conditions in Sweden.

The growth and phenology of hybrid WT Populus T89 (WT^T89) trees were compared with independently transformed transgenic and WT Elite864012 (WT^Elite) trees (SI). Their silviculture potential was screened in two large field trials (FEs), with further characterization in five growth chamber experiments (GCEs) and a phenotyping platform experiment (PPE; Fig. 2). To assess statistical significance of growth or phenological changes, we applied generalized additive models (GAMs) allowing determination of when growth or phenological differences become significant and estimation of thresholds at which bud phenological stages occur.

Fig. 2: Schematic roadmap of the growth chamber (GCE; yellow), phenotyping platform (PPE; blue), and field (FE; red) experiments done between 2014 and 2020.

The length of the arrow and dates indicate the duration of each experiment per variable. The black horizontal line with a green star represents a switch from long-day to short-day conditions. The photo on the bottom right shows FE1 in June 2015.

Results

Primary and secondary growth effects

The significance of growth changes in transgenotypes (i.e., independent antibiotic-resistant transgenic lines grouped by the same gene construct) is always reported in contrast to WT^T89 unless indicated (Table 1, SI). The deviation of difference smooth’s Bayesian Wabha/Silverman credible interval above or below the horizontal zero-line in a term plot (i.e., representing WT^T89 growth) visually indicates significant (p < 0.05) differences in transgenotypes’ growth compared to WT^T89 (Fig. 3)^135,136,137.

Table 1 The growth and phenology behavior of (RNAi) transgenic Populus transgenotypes.

Fig. 3: Graphical visualization of a generalized additive model with ordered-factor-smooth interaction smoothers.

Example of the primary growth of P. tremula L. × P. tremuloides trees during growth chamber experiment 1(A). The black solid line represents the primary growth of the reference WT^T89 while the colored solid lines represent the primary growth of two transgenotypes ztl-5 (A; light-green) and ztl-7 (B; yellow). Dots and error bars represent mean and standard error values, respectively. Term plots of a generalized additive (mixed) model with ordered-factor-smooth interaction smoothers modeling the mean primary growth of the respective trees during the experiment (B, C). The horizontal red dotted line represents the mean primary growth of the reference WT^T89. In contrast, the mean primary growth of ztl-5 and ztl-7 are represented by colored solid lines. The difference smooth’s upper Bayesian Wabha/Silverman credible interval (shaded band) is below the horizontal red zero-line in the term plot (i.e., representing the growth of WT^T89) indicating that the growth of ztl-5 is significantly (p < 0.05) different from the growth of WT^T89, whereas the growth of ztl-7 does not differ significantly^135,136,137.

The growth of photoreceptor-related transgenotypes generally differed significantly. The primary and secondary growth of pAtCCR2::LUC PHYA1-1 (aPttPHYA-1; knockdown construct targeting endogenous PHYA) and pAtCCR2::LUC PHYA22-2 (oatPHYAox-22; i.e., overexpressor construct of oatPHYA) carrying transgene A. thaliana promoter COLDCIRCADIANRHYTHMN RNA BINDING2 fused to firefly LUCIFERASE (AtCCR2pro:LUC) was usually significantly slower (Figs. S9–S12)¹³⁸. The primary growth of PHYB-12 and PHYB2KO-6 with downregulated or knocked out the expression of PHYTOCHROME B1 and 2 (PHYB1 and PHYB2), respectively, was usually significantly faster (Fig. S5, S6, S51 and S52). The primary growth of ztl-5 and 7 was significantly slower and faster, respectively (Fig. S1, S2, S9 and S10). The primary and secondary growth of fkf1-11 was significantly slower (Figs. S9–S12).

The growth patterns of core clock-related transgenotypes were condition dependent as lhy-10 displayed both significantly slower (in GCEs) and faster primary and secondary growth (in FEs; Figs. S1–S6, S9–S12, S51 and S52). The growth of toc1-5 and TOC1_OX-7 was usually significantly faster (Figs. S9–S12).

The primary growth of gi-6, gi-13, GIOX-12, and GILOX12 was, except gi-13, always significantly slower (Figs. S5–S8, S51 and S52). In contrast, primary and secondary growth of AtGA20ox1 genotypes under the promoters AINTEGUMENTALIKE1 (MEE1) or RIBULOSE-1,5-BIPHOSPHATE CARBOXYLASE/OXYGENASE SMALL SUBUNIT (RBCS) cloned from Eucalyptus grandis genomic DNA (MEE2) was occasionally significantly faster (Figs. S5–S8, S31, S32, S34, S35, S51 and S52)^139,140. When compared against the growth of WT^Elite in GCE4, the primary and secondary growth of AtGA20ox1 transgenotypes did not consistently grow significantly slower or faster. For example, primary growth of pMEE1::AtGA20ox1-4^Elite and pMEE2::AtGA20ox1-10^Elite, and pMEE2::AtGA20ox1-5^Elite and pMEE2::AtGA20ox1-6^Elite was significantly slower and faster, respectively than WT^Elite (Figs. S33, S36, S53 and S56).

We observed contrasting primary growth patterns between CO1OX-13 and CO2OX-11 in FE2. The former and latter transgenotypes had primary growth that was significantly faster and slower, respectively (Figs. S51 and S52). Primary growth of ft-7 and ft-16 in FE1 and FE2 was usually significantly slower (Figs. S9, S10, S18–S21, S51 and S52). Secondary growth of ft-7 and ft-16 in FE2 was significantly faster, but not for ft-16 in FE1 (Figs. S11, S12, S53 and S54). All EBI1-related transgenotypes (ebi1) and ebi2-6 displayed faster primary and secondary growth, except ebi1-14 in FE2 (Figs. S1, S12, and S51–S64). In contrast, primary and secondary growth of ebi2-7 and ebi2-8 was slower (Figs. S5–S12).

Almost all bud development- or flowering-related transgenotypes had a faster primary growth. From the 12 OPR3-related transgenotypes, including opr3-11 and opr3-7, only opr3-15 had significantly faster primary growth. With an FT RNAi background, opr3_ft-3 and opr3_ft-12, but not opr3_ft-7, explore OPR3 dependence on FT (both FT1 and FT2) and had significantly slower primary growth. Opr3_ft-3 had significantly faster secondary growth in FE2 (Figs. S5, S6, S18 and S19). A similar pattern was observed in the primary growth of AOS-related transgenotypes. aos-10 and aos-13, but not aos-1, had significantly faster primary or secondary growth. aos_ft-10, aos_ft-1, and aos_ft-13 had both significantly slower as faster primary and secondary growth (Fig. S20, S21, and S51–S54). Primary and secondary growth of WT^Elite was usually significantly faster (Figs. S5, S6, S31 and S32).

Phenological alterations

Differences in chlorophyll content index (CCI), bud set, and bud burst between transgenotypes and WT^T89 were analyzed using an ordered-factor-smooth interaction approach and cumulative threshold models (Fig. 4)^141,142. The phenological behavior of transgenotypes is always reported in contrast to WT^T89 (Tables 1 and 2; Fig. 5; SI).

Fig. 4: Graphical visualization of a cumulative threshold model.

Example of the lateral bud burst scoring of P. tremula L. × P. tremuloides trees during growth chamber experiment 3. The black solid line represents the bud burst of the reference WT^T89, while the colored solid lines represent the bud burst of two transgenotypes aos_ft-10 (A; blue) and ft-16 (B; yellow; A). Dots and error bars represent mean and standard error values, respectively. The lateral bud burst was scored following UPOV¹⁹³ using the following scoring values: dormant buds enveloped by scales (0), swelling buds with diverging scales (1), sprouting buds (2), opened buds with leaves clustered (3), diverging leaves with rolled op blades (4), and completely unfolded leaves (5). Term plots of a generalized additive (mixed) model with ordered-factor-smooth interaction smoothers modeling the bud burst of the respective trees during the experiment (B, C, D). The colored solid lines, given for the reference WT^T89, aos_ft-10, and ft-16, represent the predicted probability of having a bud in a specific lateral bud burst stage at a particular moment. The shaded bands around the colored solid lines represent 95% pointwise confidence intervals. The bud burst categories follow UPOV¹⁹³ using the following scoring values: dormant buds enveloped by scales (1; red), swelling buds with diverging scales (2; orange), sprouting buds (3; light-green), opened buds with leaves clustered (4; petroleum-green), diverging leaves with rolled op blades (5; blue), and completely unfolded leaves (6; purple). Let T_ref. represent a rapid increase in the predicted probability of a bud to have completely unfolded leaves. It can be observed that this rapid increase (T_new) is delayed substantially in transgenotype A, as opposed to transgenotype B.

Table 2 Overview of the experiments’ characteristics.

Fig. 5: Representation of lateral bud burst development in different transgenotypes using a cumulative threshold modeling framework.

Examples of lateral bud burst development in P. tremula L. × P. tremuloides trees during growth chamber experiment 3. The black solid lines represent the development of the lateral bud burst in two transgenotypes aos_ft-10 (A; subplot B) and ft-16 (B, subplot A), and the WT^T89 (subplot C), through the linear predictor (i.e., the expected value of a latent variable following a logistic distribution). The black shaded bands around these black solid lines represent 95% pointwise confidence intervals. More specifically, the black solid lines show the factor-smooth interaction effect between Day of the Year and Transgenotype on the linear predictor. Each bud burst category, scored following UPOV¹⁹³, is shown here as colored vertical bars in each subplot: dormant buds enveloped by scales (0; gray), swelling buds with diverging scales (1; red), sprouting buds (2; orange), opened buds with leaves clustered (3; light-green), diverging leaves with rolled op blades (4; blue), and completely unfolded leaves (5; beige). The cumulative threshold model estimates cut points on the latent variable which allows to predict when buds, given a specific transgenotype, are likely to transition from one bud burst category to the next. The first threshold (i.e., the boundary between the first and second bud burst phases; dormant buds enveloped by scales and swelling buds with diverging scales) is by definition always set to −1. In this example, it can be observed that transitions in the lateral bud burst development of transgenotype A occur substantially slower than similar transitions in transgenotype B, or the reference WT^T89. The lateral bud burst development of transgenotype B, on the other hand, is remarkably similar to the reference WT^T89.

pAtCCR2::LUC PHYA22-2 had significantly delayed bud set and significantly higher CCI values (Figs. S13–S16). The delay in bud set and leaf senescence suggests pAtCCR2::LUC PHYA22-2 has an extended growth period without faster primary growth. During GCE1, ztl-5 and ztl-7 had significantly lower and higher CCI values, respectively (Figs. S15 and S16). fkf1-11 was observed to have significantly advanced bud set and lower CCI suggesting faster leaf senescence (Figs. S13–S16). Only lhy-10 had a significantly later bud set from core clock-related transgenotypes (Figs. S13 and S14).

Clock-output-related transgenotypes showed significant phenological differences. gi-13 had significantly delayed bud set and higher CCI, suggesting a prolonged growth period (Figs. S13–S16). Differences were observed in bud set between lines with ectopic expression of AtGA20ox1, and WT^T89 or WT^Elite in the background. The former and latter transgenotypes had significantly delayed or advanced bud set, and advanced or delayed bud burst, respectively (Figs. S37, S38, S41, 42, S45, and S46). Compared to the bud phenology of WT^Elite, only pMEE1::AtGA20ox1-4^Elite and pMEE2::AtGA20ox1-10^Elite differed significantly (Figs. S39, S40, S43, S44, S47, and S48). CO\FT-regulatory-module-related transgenotypes did not differ significantly in their phenology. Only ft-16 had significantly advanced bud set, delayed apical bud burst, and lower CCI, suggesting a shortened growth period (Figs. S13–S16, S25, and S26).

The phenological differences observed in transgenotypes targeting EBI in FE1 are the significantly higher CCI of ebi1-3, suggesting slower leaf senescence, and advanced bud set of ebi2-7 and ebi2-8 (Figs. S13–S16). The bud set in aos-1, aos-10, and aos-13, and aos_ft-1, aos_ft-10 and aos_ft-13 were significantly delayed and advanced, respectively. The apical bud burst in aos-13, and lateral bud burst in aos_ft-10 and aos_ft-13 was also significantly delayed, suggesting aos_ft transgenotype trees have a shortened growth period dependent on FT. We observed a significantly delayed apical and lateral bud burst in WT^Elite (Figs. S22, S23, S25, S26, S28 and S29).

Discussion

Clock-associated genes significantly affected tree growth and phenology across various experimental levels. Our findings highlight the potential of modifying clock-associated genes for silviculture. For example, lhy-10 and toc1-5 grew faster in the field (likely due to their sped-up core-clock TTNFL) indicating trees can be reprogrammed to new photoperiodic regimes by altering their critical daylength or growth period. By safeguarding DNA replication licensing timing through gating and optimizing resonance between cell cycle phases and external environmental rhythms, LHY and TOC1 regulate growth. Downregulation of these genes may lead to a respective decrease and increase in cold hardiness and tolerance, and critical day length^{143,144,145,146}.

Increasing the growth of trees cultivated for biofuel may increase bioenergetic yields^147,148,149. EBI1 appears key to tree growth. ebi1 transgenotypes generally had faster primary and secondary growth. EBI1, associated with stress and photosynthesis protection in A. thaliana, affects the clock period and expression of LHY and TOC1^101,103,150. EBI downregulation may even increase primary growth and early flowering¹⁰³. The only phenological difference observed in the ebi1 transgenotype is that ebi1-3 had a higher CCI, suggesting slower leaf senescence. The growth functions of EBI2 appear similar to EBI1 in Populus albeit with expression at different times and tissues^101,103,150.

Transgenic trees with increased secondary growth have an adaptive advantage under drought conditions and enhanced post-drought recovery⁸. In this light, primary and secondary growth of transgenotypes with AtGA20ox1 expression were generally faster regardless of background line or reporter-promoter construct. The genetic background of AtGA20ox1 transgenotype trees affected tree phenology showing the background can be used as an alternative to promotors for altering growth. MEE1 and MEE2 did not strongly affect growth. AtGA20ox1 overexpression increases growth elongation and period, biomass, and fiber length^115,117. Tree growth even occasionally increased regardless of growth period shortening¹¹⁷. The growth period thus appears less relevant than diurnal growth. The background line strongly affected the bud set irrespective of the promoter.

Trees’ photoperiodic growth constraints can be amended. For example, slower primary growth, delayed bud set, and higher CCI values found in pAtCCR2::LUC PHYA22-2 suggest overexpression of oatPHYA results in a prolonged growth period but hampered primary growth^73,151. Given the lack of differences in pCCR2::LUC^T89 growth, we conclude the pCCR2::LUC construct did not affect growth. The upregulation of oatPHYA, unlike PHYA1, not only positively affected leaf and bud phenology but also secondary growth. Downregulation or knocking out PHYB in PHYB-12 and PHYB2KO-6 generally resulted in trees with faster primary and secondary growth. PHYB is involved in day length, temperature perception, and growth cessation, which might explain why the primary growth of PHYB-12 was slower in FE2 than the PPE¹⁵¹. Primary growth of ztl-5 and ztl-7 was, respectively, slower and faster in GCE1 and FE1. Primary growth of fkf1-11 was slower and leaf senescence in fkf1-11 progressed faster. No changes were observed in PRR7²⁸.

Modification of clock output-associated genes affected tree growth and phenology. All GI-overexpressing transgenotypes had slower primary growth. gi-13 had delayed bud set and significantly higher CCI, suggesting slower leaf senescence. These results contrast the literature suggesting moderate GI downregulation leads to pleiotropic effects in the field^{85,152,153,154}. Trees with GI overexpression also displayed delayed growth cessation and bud set under SD conditions in GCEs. CO1OX-13 and CO2OX-11 in FE2 had faster and slower primary growth, respectively. Likewise, FT downregulation resulted in contrasting growth patterns but generally slower growth. These results suggest CO1, CO2, and FT expression impact Populus growth in natural conditions^59,85,155. In line with Böhlenius et al.⁵⁹, ft-16 had significantly advanced bud set, delayed apical bud burst, and lower CCI. Except for SVPOX-7, all lfy, svp, SVPOX, rcar, or RCAROX transgenotypes had faster primary growth. Our results, suggesting LFY downregulation leads to faster primary growth but no effect on bud phenology, contrast the literature stating upregulation of LFY generally leads to faster primary growth and advanced flowering^110,111,156. Due to its role in temperature regulation of flowering and bud burst, SVP downregulation was expected to delay bud set and advance bud burst¹⁰⁶. RCAR downregulation likewise advanced bud burst^104,106. As expected, msi transgenotype trees lacked a clear phenotype and WT^Elite transgenotype trees generally had a faster primary growth and advanced bud set^125,126,127.

We observed positive growth in trees with downregulation of JA biosynthesis-related genes^108,109,128. OPR3 downregulation positively affected primary growth but FT’s reduced expression overruled this response and generally led to slower primary growth⁵⁹. Primary growth of aos and aos_ft transgenotypes was generally faster and unclear, respectively. Bud set in aos_ft transgenotype was advanced, while apical and lateral bud burst was typically delayed. The implied shortened growth period in aos_ft transgenotype trees is expected due to reduction of FTs in the background⁵⁹.

Phenological differences were sometimes unexpected or lacking. For example, bud burst in lhy-10 was later but no phenological differences were observed in toc1-5. It remains unclear why TOC1 overexpression, nor ZTL downregulation always altered bud phenology^{59,84,143,157,158}.

Tissue-specific clocks exist that differ in their sensitivity to light or temperature compensation mechanism^{28,37,159,160,161,162,163,164}. Roots, for example, have clocks assumed to be slave versions of shoot clocks^{159,161,165,166,167}. Tissue-specific clocks’ sensitivity to environmental changes and importance in tree growth and phenology therefore affects the source-sink limitation paradigm^{28,37,159,160,161,162,163,164,165,166,167,168,169,170}. Dynamic global vegetation models, implicitly assuming plant productivity is C source-limited and underestimating the sensitivity of growth processes to environmental conditions other than photosynthesis, thus need accounting for the clock^{16,171,172,173,174,175}.

New Populus transgenotypes with promising characteristics were introduced here. ebi1-2, ebi1-3, or ebi1-14, for example, generally had faster primary and secondary growth compared to WT^T89 suggesting EBI1 is key to tree growth. Likewise, the effect of different promotors and genetic backgrounds on AtGA20ox1 genotype trees was tested. Indeed, the latter affected phenology. Transgenotypes, such as pMEE1::AtGA20ox1-5^Elite or pMEE1::AtGA20ox1-8^Elite, may therefore both grow fast and survive cold climates, confirming the importance of exposing transgenic trees to real-world conditions to strengthen laboratory research^115,134. It is common forestry practice to transfer southern natural accessions up North. It is now shown core-clock genes’ expression (i.e., LHY1, LHY2, or TOC1) can be used to reprogram trees biotechnologically to a new photoperiodic regime (i.e., latitudinal adaptation) allowing the growth period of targeted accessions to increase. Statistical learning approaches, such as cumulative threshold models, enrich current tree breeding, cultivation, or forestry practices with substantial benefits for chronosilviculture.

The essential takeaway is that transgenic perturbations of genes comprising or pertaining to the Populus clock substantially affected tree physiology across various experimental levels. The clock thus orchestrates tree growth and phenology as if it were Nature’s ‘Master of Ceremony’. Combined with the observation that angiosperm deciduous tree species do not necessarily mirror, or halt, fine- or coarse roots growth in temperature tree species, this confirms the essentiality of Körner’s¹⁶ proposed paradigm shift in plant growth control^175,176.

Methods

Plant material, constructs, and transformations

Transformable wild type P. tremula L. × P. tremuloides Michx. CV. T89 plants were used to perform Agrobacterium tumefaciens-mediated transformations at the Umeå Plant Science Centre (UPSC)^177,178. The transformed plants resulted in circa 68 RNAi transgenic lines targeting 26 genes associated with the clock mechanism (Table S2)^179,180,181. The trees were propagated using in vitro culture and grown in greenhouses until the experiments started. Independent antibiotic-resistant transgenic lines grouped by the same gene construct are hereafter called a transgenotype. The transformation procedures of 31 transgenotypes previously described in the relevant literature are briefly summarized in Table S3 (SI). The transformation procedures for 39 remaining transgenotypes are discussed in detail below. Table S2 provides information on the design, base pairs, gene models, and primer sequences. Following Ibanez et al.¹⁴³ and Jurca et al.¹⁵⁸, plasmids were first constructed by obtaining gene-specific fragments from Populus cDNA. These fragments were amplified with DNA polymerase and primers with specific primer sequences. The gene fragments were then cloned into an entry vector and, using an enzyme mix, recombined into a plant destination vector¹⁸². The resulting plasmids were transformed into A. tumefaciens C58 strain GV3101 and used to transform WT^T89 trees^115,180,181. Independent and stable transgenotypes were selected after exposing the trees to an antibiotic selection marker. Gene expression analysis of c. ten transgenotypes of antibiotic-resistant plants was used to select transgenotypes for further analysis.

Transgenotypes targeting photoreceptor and morning-loop genes

Twelve transgenotypes targeted photoreceptor-related genes. Following Kozarewa et al.¹³⁸, PHYA1 was antisense inhibited in anti-sense transgenotype pAtCCR2::LUC PHYA1-1. pAtCCR2::LUC PHYA22-2* included an over-expression cassette of oatPHYA (*construct number). The antisense transgenotype (pAtCCR2::LUC PHYA1-1) expresses a full-length PHYA cDNA fragment flipped 3′-5′ under the control of the cauliflower mosaic virus (CaMV) 35 s promoter while the oatPHYA (i.e., pAtCCR2::LUC PHYA22-2) was constitutively expressed by 35 s CaMV⁷³. Another promoter-reporter construct of COLD CIRCADIAN RHYTHMN RNA BINDING 2 (pAtCCR2) fused to firefly LUCIFERASE (LUC) was also introduced to these transgenotypes, as well as in a control transgenotype with only the transgene pAtCCR2::LUC T89-5⁶². The transgenotype PHYB-12 and PHYB2KO-6 downregulate and knock out the PHYB gene, respectively, responsible for a plant’s red-light sensitivity. PHYB-12, however, is the result of RNAi, with the gene fragment introduced as two inverted copies with an intron, while PHYB2KO-6 is generated using CRISPR/Cas9-mediated gene editing (i.e., CRISPR, Clustered Regularly Interspaced Short Palindromic Repeats; Cas9, CRISPR-associated protein 9) following Ding et al.^151,183,184. ztl-3, ztl- 5 and ztl-7 are transgenic RNAi transgenotypes constructed following Jurca et al.¹⁵⁸ which repress ZTL expression and hence affect blue-light sensitivity, clock control and the impulse to reset the clock. The transgenotypes targeting the ZTL homolog FKF1, fkf1-10 and fkf1-11, likewise repress FKF1 affecting blue-light reception and flowering. prr7-5, on the other hand, downregulates PRR7, which directly affects the core-loop of the clock. The gene fragments in fkf1-10, fkf1-11, and prr7-5 are designed as two inverted copies of the respective amplified gene-specific fragment with an intron in between.

Transgenotypes targeting core clock-regulating genes

Four transgenotypes included in this study have been described in Ibanez et al.¹⁴³ and Edwards et al.⁶¹. lhy-10 is a transgenotype targeting LHY1 and LHY2. This transgenotype represses the expression of LHY. Likewise, the expression of LHY’s antipodal core clock-regulated gene TOC1 is downregulated in toc1-5. In transgenotypes TOC1_OX-4 and TOC1_OX-7, however, TOC1 is upregulated. The entire TOC1 cDNA in these transgenotypes is constitutively upregulated with varying degrees. In all the above transgenotypes, the core loop of the clock is disrupted with severe alterations in the rhythmicity of the clock as a consequence. Both LHY and TOC1 are key to the clock mechanism.

Transgenotypes targeting genes controlling growth, bud development, and flowering

GI is a prominent gene in the output loop of the clock. Similar to Ding et al.⁸⁵, four transgenotypes were constructed targeting GI and GIL. gi-6 and gi-13 were constructed so that GI is repressed¹⁸⁵. The transgenotypes GIOX-12 and GILOX-12 upregulate GI and GIL, respectively. All four transgenotypes, through the effect of GI on CO and FT, are supposed to have altered timings in their growth cessation, bud set, and flowering⁸⁹. Twelve transgenotypes had ectopic AtGA20ox1 expression driven by two specific promoters. This should lead to increased levels of GAs, as the gene coding for the multifunctional enzyme is relevant in synthesizing GAs¹²⁰. These transgenotypes have WT^T89 or WT^Elite in the background. In addition, the transgenotypes pMEE1::AtGA20ox1-3^T89, pMEE1::AtGA20ox1-4^Elite, pMEE1::AtGA20ox1-5^Elite, pMEE1::AtGA20ox1-8^T89, pMEE1::AtGA20ox1-8^Elite, pMEE1::AtGA20ox1-10^T89 and pMEE1::AtGA20ox1-10^Elite have AINTEGUMENTALIKE1 (AIL1; MEE1 or pAIL1) as promotor (i.e., mainly expressed in meristem and young leaves)^139,186. In contrast, pMEE2::AtGA20ox1-2^T89, pMEE2::AtGA20ox1-5^T89, pMEE2::AtGA20ox1-5^Elite, pMEE2::AtGA20ox1-6^Elite, pMEE2::AtGA20ox1-10^Elite, and pMEE2::AtGA20ox1-11^T89 have RIBULOSE-1,5-BIPHOSPHATE CARBOXYLASE/OXYGENASE SMALL SUBUNIT (RBCS; MEE2 or pEL1.2) cloned from Eucalyptus grandis genomic DNA as promoter (i.e., mainly expressed in photosynthesizing tissue)¹³⁹.

Like FKF1, GI and GIL in Populus may regulate the transcription of CO^85,88,90,91. Two transgenotypes, CO1OX-13 and CO2OX-11, were constructed using RNAi following Hsu et al.¹⁵⁵ and upregulate either CO1 or CO2, respectively. On the other hand, the transgenotype tem1B-5 constructed following Castillejo and Pelaz⁹⁴ upregulates TEM, which repressed the expression of FT. Since the balance between CO and TEM regulates the expression of FT, these upregulating transgenotypes will display different bud burst and flowering times compared to the WT^{T89 93}. ft-16 and ft-7 are two transgenotypes targeting the FT gene^59,97,98. The FT and FT1 gene fragments were introduced in these transgenotypes as two inverted copies with an intron. As a result, the FT gene is downregulated, severely affecting the regulation of bud set and flowering by the CO\FT regulatory module⁵⁹.

Following Eriksson et al.¹⁸⁷, six transgenotypes were constructed with either downregulation of EBI1 or EBI2¹⁸⁸. ebi1-2, ebi1-3 and ebi1-14 repress the former gene, while ebi2-6, ebi2-7 and ebi2-8 repress the latter gene. In A. thaliana, EBI (PttEBI1 orthologue) is associated with ZTL and hence regulates the transcriptional activity of LHY and TOC1. It can be expected that these transgenotypes differ significantly in their growth and phenology from the WT^T89101,102.

More transgenotypes target genes involved in bud development and flowering (e.g., LFY, SVP, MSI1, or RCAR1). lfy-4, for example, a transgenotype with a fragment of the LFY gene, which is involved in the flower-meristem identity, is introduced as two inverted copies with an intron. The LFY gene is downregulated in lfy-4, which should lead to changes in the timing of tree vegetative growth and flowering. Using a similar design, SVP is introduced into svp-3. In this transgenotype, SVP is also downregulated, supposedly affecting the timing of bud development and the temperature-responsive regulation of flowering. SVP is, on the other hand, upregulated in SVPOX-6 and SVPOX-7. In these transgenotypes, the construct consists of a CaMV 35S promoter that drives the expression of the SVP cDNA as a translational fusion to an N-terminal human influenza hemagglutinin (HA) sequence. The upregulation of SVP in these transgenotypes should likewise affect temperature-responsive regulation of bud break after vernalization. The transgenotype msi-1A is a construct for CaMV 35 s promoter-driven upregulation of RNAi to downregulate MSI1 constructed following Englund¹²⁷. Because of MSI1 involvement in WD-40 repeat proteins, the trees likely display altered regulation of flowering, and gametophyte and seed development^{121,122,123,124,125,126,127}. Following Singh et al.¹⁰⁶, RCAR1 is downregulated and upregulated in transgenotypes rcar-10 and RCAROX-18, respectively. Although RCAR1 represses bud break, it also regulates ABA^104,105. Like the transgenotypes targeting RCAR1, twelve other transgenotypes target genes related to JA levels in the trees. Six of these transgenotypes have a fragment introduced of the OPR3 gene encoding for the OPR3 enzyme regulating the biosynthesis of JAs⁸⁷. opr3-7, opr3-11, and opr3-15 simply have the OPR3 fragment introduced as two inverted copies with an intron leading to downregulation of OPR3. Opr3_ft-3, opr3_ft-7 and opr3_ft-12 have the same design but also have FTRNAi in the background, which normally affects the regulation of flowering. Six other transgenotypes target AOS, encoding for a cytochrome P450 protein regulating JA biosynthesis, and are also split into three transgenotypes that downregulate AOS (aos-1, aos-10, and aos-13) or downregulate AOS and have FTRNAi in the background (aos_ft-1, aos_ft-10 & aos_ft-13). Two other wild-type transgenotypes were investigated as alternatives to the reference WT^T89. Both WT^Elite and WT^Elite-884056, described in Stener and Westin¹⁸⁹, are of particular interest to clonal forestry practices in Scandinavia.

Quantitative reverse transcription polymerase chain reactions

This study characterizes transgenotypes related to the aos, aos_ft, fkf1, opr3, opr3_ft, AtGA20ox, prr7, gi and TOC1_OX transgenotypes found in Table S2 (Figs. S57–S67). Gene expression data for most transgenotypes (SI) was determined using quantitative reverse transcription polymerase chain reactions (RT-qPCR) following Jurca et al.¹⁵⁸. Eight hours after dawn (ZT8), we sampled leaves from trees grown in a greenhouse under constant light conditions (i.e., 18:6 h light/dark cycles with a light intensity of 250 μmol m⁻²s⁻¹) and shock froze them in liquid nitrogen. RNA was subsequently extracted from each leaf following the classical cetyltrimethylammonium method of le Provost et al.¹⁹⁰. After treatment with DNase (TURBO DNA-free kit; Ambion, Austin, US), cDNA was synthesized from 1 μg RNA using an iScript cDNA Synthesis Kit (Bio-Rad Laboratories, California, US). RT-qPCR was performed using a CFX96 Real-Time detection system (Bio-Rad Laboratories), gene-specific primers (SI), three to four biological replicates, and two technical replicates. The relative expression of the genes of interest was normalized against the expression of reference housekeeping genes ELONGATION FACTOR 1 ALPHA (EF1a) or 18S rRNA. Further calculations were done relative to WT^T89 or the lowest expressing transgenotype using the 2−ΔΔCT method of Livak and Schmittgen¹⁹¹ and Pfaffl¹⁹². qPCR results were inconclusive for aos and aos_ft transgenotype trees, as well as opr3_ft-12.

Growth chamber experiments

We conducted five growth chamber experiments (GCE1 - GCE5), measuring the growth and phenology of transgenotypes in growth chambers at UPSC according to standard experimental setups outlined in Ibanez et al.¹⁴³, Edwards et al.⁶¹, and Jurca et al.¹⁵⁸ (Fig. 2; Table 2). Following Nilsson et al. ¹⁷⁷, cuttings of P. tremula L. × P. tremuloides were first grown in vitro for 4 weeks. The rooted and in vitro-cultivated transgenic trees were then potted in a 3:1 mix of fertilized peat and perlite and grown for another four weeks under constant LD light, temperature, and relative humidity conditions (i.e., 18:6 h light/dark cycles; 18 °C; and 80% relative humidity, respectively) in the greenhouses at UPSC. The light intensity during this period was 200 μmol m⁻²s⁻¹ (Osram Powerstar HQI-T 400W/D lamps; Osram, Munich, Germany). After the first month, each tree received weekly nutrients (SuperbaS, Supra Hydro AB, Landskrona, Sweden) and water (1.5 l). After a period (Table 2), the trees in GCE2, GCE3, GCE4, and GCE5 were exposed to the same temperature, relative humidity, and irradiance conditions. Still, the light conditions were changed to SD conditions (i.e., 15:9 h light/dark cycles), and dusk time remained unchanged. During each GCE, the primary and secondary growth of the trees was measured weekly. Phenological observations were made on the bud set, and the apical and lateral bud burst in GCE3 and GCE4. The development of the bud set was scored weekly following UPOV¹⁹³ and Ibanez et al.¹⁴³ using the following (opposite) scoring values: a still actively growing shoot and uninitiated bud set (3), initiation of the bud set and cessation of growth (2), formation of the buds (1), and completed bud set (0)^98,143,194. The development of the apical and lateral bud burst was scored following UPOV¹⁹³ and Ibanez et al.¹⁴³ using the following scoring values: dormant buds enveloped by scales (0), swelling buds with diverging scales (1), sprouting buds (2), opened buds with leaves clustered (3), diverging leaves with rolled up blades (4), and completely unfolded leaves (5).

Phenotyping platform experiment

The growth of the transgenotypes was also investigated in a trial at the UPSC tree phenotyping platform (WIWAM Conveyor, SMO, Eeklo, Belgium; Fig. 2; Table 2 in SI). In this trial, hereafter called the phenotyping platform experiment (PPE), the trees automatically move around on a conveyor belt, allowing automatic daily watering, fertilization, and monitoring, and recording of growth parameters. The trees in the PPE were first in vitro-cultivated. The trees were then potted in a commercial mix of fertilized peat and soil (Yrkes Plantjord, Weibulls Horto, Hammenhög, Sweden) and grown for another four weeks under constant LD light, temperature, and relative humidity conditions (i.e., 18:6 h light/dark cycles; 18 °C; and 80% relative humidity, respectively). Afterward, the trees were brought into the phenotyping platform to expose them to similar light and temperature conditions (i.e., 18:6 h light/dark cycles and 20:18 °C warm/cold cycles, respectively) but altered relative humidity conditions (i.e., a relative air humidity of 60%). The red-to-far-red light ratio of the artificial LED lights on the phenotyping platform had an approximate value of 0.9 and an irradiance of 150 to 200 μmol m^-2s⁻¹. The soil in the pots was kept automatically at a target humidity of 1.9 (i.e., a value close to the experimentally determined water capacity), meaning that 1.9 l of water is added for 1 kg of dry soil. All trees were watered and fertilized based on the procedure in Wang et al.¹⁹⁵. After three weeks in the greenhouse, the trees received a weekly dose of 200 ml of 1% Rika-S fertilization (7:1:5 N/P/K; Weibulls Horto, Hammenhög, Sweden). Whilst in the phenotyping platform experiment, the trees were watered twice daily (i.e., according to the target humidity) and fertilized every alternate day with 50 ml of 0.6% Rika-S. In the 7th week, the fertilization dose was increased to 75 ml of 0.6% Rika-S. Additionally, in the 4th and 7th weeks, the trees were treated with Nemasys C insecticide (BASF, Ludwigshafen, Germany). Primary growth of the transgenic trees was measured automatically every alternate day using a light curtain. Secondary growth was also measured every alternate day. However, this was done by automatic photometry of the trees’ sides, top and bottom using three Imperx B4820 RGB cameras. The data were subsequently recorded on a WIWAM computer and made available using the PIPPA web interface (https://pippa.psb.ugent.be/, UGent, Belgium).

Field experiments

Populus transgenotypes were amplified every fourth week until an adequate number of trees was reached. Subsequently, apical shoots of circa five centimeters were cut under sterile conditions and transferred into sterile plastic jars of one liter containing 130 mL MS growth medium (Duchefa Biochemie, Haarlem, Netherlands), adjusted to pH 5.6. Two shoots were transferred to each jar and exposed to cyclic LD light and temperature conditions (i.e., 18:6 h light/dark and 22:18 °C warm/cold cycles, respectively). After roots developed, each tree of c. 15 cm was replanted in a 1 l plastic pot containing a pre-fertilized 3:1 mix of fertilized peat and perlite (Yrkes Plantjord, Weibulls Horto, Hammenhög, Sweden). The potted trees were transferred to a greenhouse with similar environmental settings and treated as described in Johansson et al.¹⁹⁶. After a month, the trees were put outside during the daytime to promote acclimatization to field conditions. Subsequently, they were transported and potted at the field site in Våxtorp.

The growth and phenology of the transgenotypes were tested in two transgenic field trials in Våxtorp (56°25′N, 13°47′E; 39 m.a.s.l.; Laholm municipality, Halland county, Sweden; permits 22-2655|12 and 18-3494|16), which are hereafter called field experiment 1 and 2 (FE1 and 2; Fig. 2; Wang et al.⁹⁸ and Table 2). Before the start of the measurements in 2014 (FE1) and 2018 (FE2), the similarly sized and aged trees were planted in a randomized block design of 18 blocks with 3 × 2.3 m of spacing. In June 2014 (FE1), trees were planted in blocks containing 42 trees, including six WT^T89 individuals and 18 transgenic individuals each representing an unique transgenotype. In October 2016 (FE2), trees were planted in blocks containing 40 trees, including four WT^T89 individuals and 34 transgenic individuals each representing an unique transgenotype. Each time, a row of WT^T89 individuals was planted around the randomized field design. Full-grown larch hedges flanked the long sides of the plots. Stem primary and secondary growth was measured in FE1 and FE2 every alternate month and half a year, respectively. The primary growth of each tree was measured from the base to the top axillar bud using a millimeter-scaled measuring pole. Only in FE1, were weekly phenological observations made on the development of the bud set and leaf senescence. As in the GCEs, the development of the bud set was scored using the scoring scheme of UPOV¹⁹³ and Ibanez et al.¹⁴³. The development of leaf senescence was assessed by measuring the chlorophyll content index (CCI) of five randomly chosen leaves per tree with a chlorophyll content meter (CCM 200 plus, Opti-Sciences). Chlorophyll detoxification is the most prominent feature of leaf senescence and allows trees to remobilize nutrients from their leaves towards more vital plant organs^197,198. Since the CCI is a proxy for chlorophyll concentrations that have, within limits, a close to linear relationship with chlorophyll concentrations, the decline in the CCI can be used as a proxy for the development of the leaf senescence process^199,200. CCI measurements were made at approximately the same day period and using the same leaf side^199,201,202. Further details of the number of transgenotypes per experiment, the (approximate) number of tree individuals per transgenotype, and the duration and frequency of the measurement sampling in the GCEs, PPE, and FEs can be found in Table 2.

Statistical analyses

All growth and phenology data of the trees were analyzed using generalized additive (mixed) models^141,203. These interpretable models assume that the relationship between the response and explanatory variables can be modeled using (non-)linear smooth functions^{203,204,205,206}. The use of smoothers, as well as integrated smoothness selection methods, allows GAMs to have an a-priori-unknown but flexible predictor function of which the complexity is completely determined by the data. As a result, GAMs can unravel hidden relationships in the data whilst accounting for numerous statistical obstacles (e.g., overfitting, non-linear relationships, bias/variance tradeoffs)^{204,207,208,209}. Because it is possible to implement random effects or specified correlation structures within the GAM framework, GAMs can also be used to model spatiotemporal data gathered from repeated observations in multiple individuals and locations over time^210,211. One of the limitations of GAMs, unlike even more flexible statistical models (e.g., GAMLSS; generalized additive models for location, scale, and shape), is that it only focuses on the exponential distribution family and its location parameter μ (i.e., alternatively interpretable as the mean). However, few GAM distributions also allow us to model the distribution parameters σ (i.e., the shape of the response variable’s distribution; alternatively interpretable as the variance).

Generalized additive models with ordered-factor-smooth interactions

To test for significant differences between the growth and phenology of each transgenotype and the growth of WT^T89 in the GCEs, PPE, and FEs, we adopted the GAM with ordered-factor-smooth interaction approach outlined in Wood¹⁴⁰ and Rose et al. ²¹². In this pair-wise comparison of smoothers approach, separate difference smoothers are generated by the GAM for each factor level minus one reference level. In our study, we therefore used GAMs where the growth or phenology of each transgenotype was modeled as difference smoothers, which compare against a reference smoother (i.e., the growth of WT^T89; additional models were made with the growth of WT^Elite as reference smoother solely for the AtGA20ox1 transgenotypes with WT^Elite in the background). Given that all the assumptions of the GAM are met, the deviation of a difference smooth’s upper or lower Bayesian Wabha/Silverman credible interval above or below the horizontal zero-line in a term plot would then visually indicate significant differences in the growth of the transgenotype compared to the growth of WT^T89 (Fig. 3)^135,136,137. R/mgcv’s summary function also provides a quantitative indication of the significance of the (ordered) difference smoothers.

To model the primary and secondary growth of the transgenic trees as a function of their covariates, we used the gam function in R/mgcv^209,211,213. Several GAMs with similar construction but using different distributions were tested. The GAMs with Gaussian location-scale distribution (i.e., gaulss) consistently had the lowest Akaike Information Criterion (AIC), and the Gaussian location-scale distribution was therefore selected to be used in the GAMs modeling tree growth¹⁴². The most suited monotonic link function (i.e., the function linking the distribution parameter to the predictor; “identity”, “log” or “logb” for the mean; “logb” for the variance) varied case by case. For each experiment, and both the mean and variance, primary or secondary growth was modeled with the primary or secondary growth of the individual tree as the response variable. The fixed covariates of the primary and secondary growth were the time (continuous), transgenotype (categorical with up to 34 levels), and tree individual (categorical with up to 20 levels). The interaction term was modeled as an (ordered) random factor-smooth interaction between the covariates time and transgenotype. Random factor-smooth interaction smoothers were chosen because a (difference) smoother was required for each of a large number of transgenotypes and because these smoothers required the same smoothing parameter field^141,214,215. The dependency among observations of the same tree individual was finally incorporated by using the individual as a random intercept (i.e., thus introducing a coefficient for each tree). To reduce overfitting to a minimum, we chose the restricted maximum likelihood (REML) argument as the smoothness selection method^213,216. To test for significant differences between the development of leaf senescence in each transgenotype and the development of leaf senescence in WT^T89 during FE1, a Gaussian GAM was made like those used to test tree growth (Eq. 1). The response variable was, in this case, the chlorophyll content index.

The GAMs modeling primary and secondary growth and leaf senescence are formulated in Eq. 1, where both location and scale parameters are considered. Y_i represents the independent response variable observations on each individual indexed by i, with i = 1,…, n. D represents the distribution of the response variable, and g is the monotonic link function relating the predictor η to the distribution parameters µ_i (location) and σ_i (scale)^{217,218,219,220}. Let t and x denote the covariates time and transgenotype, while ${\boldsymbol{f}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}}\right)$, ${{\boldsymbol{f}}}_{{\boldsymbol{1}}}^{{\boldsymbol{o}}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}},\,{{\boldsymbol{x}}}_{{\boldsymbol{i}}}\right),$ and ${\boldsymbol{\zeta }}$ represent the smooth function of the covariate t_i, the ordered factor-smooth interaction function of the covariates t_i and x_i, and the random effect (i.e., the random effect in the mean for each individual i), respectively.

$$\begin{array}{c}{{\boldsymbol{Y}}}_{{\boldsymbol{i}}} \sim {\boldsymbol{D}}({\rm{\mu }}_{\boldsymbol{i}},{\boldsymbol{\sigma }}_{\boldsymbol{i}})\\ {{\boldsymbol{g}}}_{{\bf{1}}}\left({{\boldsymbol{\mu }}}_{{\boldsymbol{i}}}\right)={{\boldsymbol{\eta }}}_{{\bf{1}}}={{\boldsymbol{f}}}_{{\bf{1}}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}}\right)+{{\boldsymbol{f}}}_{{\bf{2}}}^{{\boldsymbol{o}}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}},\,{{\boldsymbol{x}}}_{{\boldsymbol{i}}}\right)+{\boldsymbol{\zeta }}\\ {{\boldsymbol{g}}}_{{\bf{2}}}\left({{\boldsymbol{\sigma }}}_{{\boldsymbol{i}}}\right)={{\boldsymbol{\eta }}}_{{\bf{2}}}={{\boldsymbol{f}}}_{{\bf{2}}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}}\right)+{{\boldsymbol{f}}}_{{\bf{2}}}^{{\boldsymbol{o}}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}},\,{{\boldsymbol{x}}}_{{\boldsymbol{i}}}\right)+{\boldsymbol{\zeta }}\end{array}$$

(1)

Cumulative threshold models

Cumulative threshold models, or more specifically ordered categorical family GAMs, were made to test whether the bud phenology of the transgenic trees differed significantly from the bud phenology of WT^T89. We tested specifically for differences in the timing of the bud set between the transgenic and WT^T89 trees grown during GC3, GC4, and FE1. We also tested for differences in the timing of the apical and lateral bud burst between the transgenic and WT^T89 trees grown during GC3 and GC4. To test for true significance in the differences, we again used the GAM with an ordered-factor-smooth interaction approach. This time, we modeled ordered categorical data. In an additional step, we computed the predicted probabilities of a bud to be in a specific bud set or bud burst stage at each moment in time (Fig. 4)^141,142. Wood¹⁴¹; p. 176, in fact, notes that “the linear predictor [in this kind of ordered categorical family GAMs] provides the expected value of a latent variable according to a logistic distribution. The probability of this latent variable to be in between certain cut-points (i.e., the categories or stages) then provides the probability of the ordered categorical variable to be of the corresponding stage”.

To model the bud set and bud burst of the transgenic trees as a function of their covariates, we again used the gam function in R/mgcv^209,211,213. Due to the ordered and categorized data, GAMs with ordered categorical distribution (i.e., ocat) and “identity” monotonic link function were subsequently made to model the bud set and bud burst. The bud phenology was modeled with the respective bud set or bud burst for each tree as the response variable. The fixed covariates of the bud set and bud burst were the time (continuous), transgenotype (categorical with up to 19 levels), and tree individual (categorical with up to 12 levels). As for the GAMs modeling growth, the interaction term was modeled as an (ordered) random factor-smooth interaction smoother between the covariates time and transgenotype. A reference smoother was introduced in the ordered categorical GAMs. Random factor-smooth interaction smoothers were also chosen because a (difference) smooth was required for each of the large number of transgenotypes and required the same smoothing parameter^141,214,215. The dependency among observations of the same tree individual was again incorporated using the individual as a random intercept. Term plots, generated with the help of the data_slice and fitted_values functions from R/gratia, provide a visual indication of substantial differences between the predicted probabilities of a bud to be in a specific bud set or bud burst stage at a particular moment²²¹. Equations (2) and (3) provide the cumulative threshold models modeling the bud set and bud burst.

$$\begin{array}{c}{{\boldsymbol{Y}}}_{{\boldsymbol{i}}} \sim {\boldsymbol{D}}({{\mu }}_{\boldsymbol{i}})\\ {\boldsymbol{g}}\left({{\boldsymbol{\mu }}}_{{\boldsymbol{i}}}\right)={\boldsymbol{\eta }}={{\boldsymbol{f}}}_{{\bf{1}}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}}\right)+{{\boldsymbol{f}}}_{{\bf{2}}}^{{\boldsymbol{o}}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}},\,{{\boldsymbol{x}}}_{{\boldsymbol{i}}}\right)+{\boldsymbol{\zeta }}\end{array}$$

(2)

$$\begin{array}{c}{{\boldsymbol{Y}}}_{{\boldsymbol{i}}} \sim {\boldsymbol{D}}({{\mu }}_{\boldsymbol{i}})\\ {\boldsymbol{g}}\left({{\boldsymbol{\mu }}}_{{\boldsymbol{i}}}\right)={\boldsymbol{\eta }}={{\boldsymbol{f}}}^{{\boldsymbol{o}}}\left({{\boldsymbol{t}}}_{{\boldsymbol{i}}},\,{{\boldsymbol{x}}}_{{\boldsymbol{i}}}\right)+{\boldsymbol{\zeta }}\end{array}$$

(3)

Model assumptions

The interpretation of the GAMs, their output, and the extent of the potentially significant differences between their smoothers depends on the degree to which their underlying parametric assumptions are met and reported^{222,223,224,225}. Following Zuur et al.²²⁶ these are, in order of importance, the homogeneity, normality, concurvity, nonlinear dependency, and temporal dependency of the model residuals. The assumption of independent and identically distributed residuals (IID) combines aspects of heterogeneity and dependency and requires assessment. The zero adjusting assumption is not applicable to this study. Failure to meet, or deviations from, the model assumptions might increase type I or II errors or affect the effect size estimation or its significance^227,228. However, a quantitative analysis of the potential error is not straightforward.

All model residuals were extracted using the residuals functions from R/mgcv¹⁴⁰. Several other functions from the same package provided a first indication of the degree to which many of the parametric assumptions are met. The summary function provides approximate p-values on a significant trend in the smoothers and an idea of the model deviance. The model deviance generally proved to be high, adding consideration to the notion that although the hypothesis complexity may increase (i.e., the number of parameters), one can still have low bias and variance (i.e., the interpolation threshold) and that infinite overparameterization can be preferable to any finite number of parameters^229,230,231. Deviations from homogeneity or normality of the residuals could be assessed visually using four diagnostic plots of the normalized quantile residuals provided by the gam.check function²³². The homoscedasticity in the residuals was also further investigated using the check1D, l_densCheck and l_gridCheck1D functions in R/mgcViz²³³. In light of the central limit theory and the rather small sample sizes typical for biological experiments, we used the provided histograms and quantile-quantile plots to assess whether the residuals were normally distributed. The gam.check function, which provides the k-indices and p-values, was used to check the required basis dimensions for the smoothers²³⁴. Low p-values in combination with k-indices lower than one would suggest that the basis dimension of the smoothers was too low. The shapiro.test (Shapiro-Wilk test), ad.test (Anderson-Darling test) and cvm.test (Cramer-Von-Mises test) functions in the R/base, R/nortest, and R/goftest packages were also used to test whether the model residuals followed a normal distribution^235,236,237. Non-linearity in the model residuals was assessed with the bdsTest function (Brock–Dechert–Scheinkmand and LeBaron statistic test) in R/fNonlinear²³⁸. The IID characteristics of the model residuals were investigated by testing for white noise in the error vector using the whitenoise.test function in R/normwhn.test and the standard Box.test function (Ljung-Box test)^239,240,241. Residual temporal autocorrelation was visually assessed using the acf and pacf functions in R/mgcv. Only the raw residual ACF and pACF plots could be provided. Indications of temporal autocorrelation were further investigated by looking for trends or difference stationarity in the residuals. Four tests were used from the R/urca package²⁴². The KPSS (Kwiatkowski-Phillips-Schmidt-Shin), PP (Phillips-Perron), ADF (Augmented-Dickey-Fuller), ERS (Elliot-Rothenberg and Stock Point Optimal), and ADF-GLS tests for the presence of a unit root (i.e., a stochastic trend) in a time series test, were performed using the ur.kpss, ur.pp, ur.df and ur.ers functions, respectively^243,244,245. The additional NP (Ng and Perron) unit root test, giving valid results even when an unknown ARMA process is present, was implemented using the CADFtest function in R/CADFtest²⁴⁶. The potential need to add autoregressive or moving average orders to the GAMs was tested by running the auto.arima function in R/forecast²⁴⁷. Tests were also done to characterize the data further, given that the parametric model assumptions were, according to a strict interpretation, often not met. The Hurst coefficient for long-range dependence and randomness in a system was performed using the WhittleEst function from the R/longmemo package^{248,249,250,251,252}. The skewness (i.e., the asymmetry around the mean of the probability distribution) and kurtosis (i.e., the magnitude in which the tails of a distribution differ from the tails of a normal distribution) were calculated using the skewness, kurtosis and describe functions in the packages R/e1071, R/sur and R/pscyh^253,254,255. Indicative for a “good” model fit is a mean, variance, skewness, kurtosis, and Filliben correlation coefficient of 0,1,0,3 and 1, respectively²⁵⁶. The modality of the data distributions was tested using the dip.test function (i.e., unimodal test) in R/diptest, bimodality_amplitude function (i.e., bimodal test) in R/modes and modetest function (i.e., multimodal test) in R/multimode^257,258,259. Graphical output was made mainly using R/ggplot2 and R/dplyr^{260,261,262,263,264,265}.