Introduction

The rapid expansion of the Internet of Things (IoT) has led to an explosion of data traffic, significantly increasing the demand for robust cryptography. Cryptography inherently relies on stochastic elements, such as random numbers, to ensure the security and robustness of its processes. The random numbers derived from deterministic algorithms using digital hardware and software are considered pseudo-random numbers (PRNs), which are vulnerable to security threats as PRNs can be predicted and manipulated if one gains control over the hardware or software1. In contrast, true random numbers (TRNs) are generated from the natural laws of physics, making them entirely non-artificial and, therefore, capable of ensuring complete security.

A true random number generator (TRNG) is an electronic device that converts such unpredictable phenomena in nature to a bitwise digital signal. In this context, memristors are effective components as a source of unpredictable phenomena as their transition dynamics are inherently stochastic due to thermal noise2,3,4,5,6,7,8,9,10,11,12,13,14,15. Various studies have demonstrated the feasibility of memristive TRNGs2,3,4,5,6,7,8,9, and recently, these TRNGs have been employed in energy-based computing, where their inherent stochasticity helps in finding solutions to optimization problems11,12,13,14,15. Considering such a wide range of potential future applications for TRNGs, the development of high-speed and energy-efficient TRNGs is crucial for accelerating their practical implementation.

For improving the TRNG performance, previous studies have primarily focused on finding more effective entropy sources in memristors and more efficient ways to convert the source information to digital data. For example, Jiang, H. et al. utilized multi-bit counters2, and Woo et al. introduced nonlinear feedback shift register3. These approaches enabled the generation of multiple random numbers from a single memristor switching, thereby improving the TRN rate and energy efficiency. Subsequently, TRNGs have evolved to utilize dynamic changes rather than static ones to achieve faster and more efficient operation. Kim et al. 4 introduced a NbOx-based Mott oscillator, and Woo et al. 15 utilized a similar approach but using a LaCoO3-based memristor exhibiting spin crossover mechanism. Consequently, memristive TRNG achieved improved speed and energy efficiency. However, further improvements in TRNG performance are still necessary, and achieving this will require a new approach beyond traditional ways such as circuit optimization and the exploration of new memristors.

In this study, we propose a physical approach to improve the TRNG performance by manipulating the noise source. The operating principle of the proposed TRNG is based on our previous TRNG using a Mott memristor featured by intrinsic large electrothermal nonlinearities4,16,17,18. When the Mott memristor oscillates, the magnitude of thermal noise is temperature-dependent; high temperature correlates to increased thermal noise19. In this context, we introduced a cell-integrated heater to increase device temperature and, thus, the thermal noise. The heater amplifies the thermal noise and shortens the required time to accumulate sufficient noise for TRN generation. Consequently, the proposed TRNG showed the fastest operation (100 kbit/s) with a high energy efficiency (0.68 μJ/bit), outperforming all previously reported memristor-based TRNGs that have passed the NIST randomness test. Moreover, the heater can be integrated underneath the TRNG, making its array integration feasible without complex electrical interconnection among them. Therefore, we exploit it for a more practical TRNG system. Specifically, we demonstrate an 8×1 TRNG array capable of generating 8 TRNs simultaneously using only 46% of energy per bit compared to the single TRNG. This efficiency could be further improved as the array sizes extended, suggesting the proposed approach is highly applicable in future electronics11,12,13,14,20.

Results and discussions

A resistive heater integration and its performance characterization

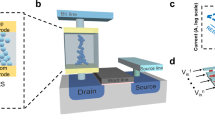
Figure 1a illustrates the cell stack of the heater-embodying Mott memristor fabricated on a SiO2/Si substrate, consisting of a Mott memristor (Ti/NbOx/Pt) and a resistive heater (Pt) separated by a dielectric Al2O3 layer. Details of the device fabrication process are described in the experimental section. The equivalent electrical circuit of the integrated device is shown in Fig. 1b. Here, \({V}_{{\rm{in}}}\) and \({V}_{{\rm{H}}}\) are the voltage sources for the Mott memristor and the heater, and \({R}_{{\rm{M}}}\) and \({R}_{{\rm{H}}}\) are the resistances of the Mott memristor and the heater, respectively. At this configuration, the heater generates Joule heat, which transfers to the Mott memristor through the thermally conducting but electrically insulating Al2O3 layer. Figure 1c shows the thermal circuit of the integrated device (left panel) and its simplified equivalent one (right panel). Here, the θ denotes the thermal resistance of the components, and \({P}_{{\rm{H}}}\) is the electrical power applied to the heater. The \({T}_{{\rm{H}}}\), \({T}_{{\rm{M}}}\), and \({T}_{{\rm{amb}}}\) are the heater, Mott memristor, and ambient temperatures, respectively. The heat is transferred to the Mott memristor through \({\theta }_{{{\rm{Al}}}_{2}{{\rm{O}}}_{3}}\), and is laterally diffused through \({\theta }_{{\rm{L}}}\) while heat is lost to the air and substrate through \({\theta }_{{\rm{air}}}\) and \({\theta }_{{\rm{sub}}}\), respectively. The thermal circuit can be simplified by Wye-Delta transformation, and the equivalent thermal resistance (\({\theta }_{{\rm{eq}}}\)) to the surroundings can be derived21.

Fig. 1: A heater embodying NbOx-based Mott memristor and its electrical characteristics.
figure 1

a A schematic illustration of the device stack where a NbOx Mott memristor and a heater are integrated. b The equivalent electrical circuit of the device. The NbOx Mott memristor and the heater are electrically isolated but thermally connected. c The thermal circuit of the integrated device and its equivalent circuit. d The effective heater temperature estimation scheme. e A \((R/{R}_{300{\rm{K}}}-1)-({T}_{{\rm{H}}}-300{\rm{K}})\) plot for fitting the empirical thermal coefficient of resistance (TCR) of the heater. Each point was obtained by averaging the last three period of resistances in Supplementary Fig. 2. The standard deviation of each points was less than 0.0002. f The heater resistance as a function of the heater voltage (\({V}_{{\rm{H}}}\)) fabricated on the three substrates. g The heater temperature as a function of heater voltage calibrated from (f) using the TCR. h The NDR I \(I-V\) curves of Mott memristors at various \({V}_{{\rm{H}}}\) and the ambient temperatures, fabricated on the three substrates. Here, Set (1) and Set (2) each consist of two NDR curves, one obtained by varying the heater voltage and one by varying the ambient temperature, where the curves in each set are identical. i The thermal resistance representing the heater efficiency and the heat loss (\(1-{T}_{{\rm{M}}}/{T}_{{\rm{H}}}\)) of the integrated device fabricated on the three different substrates.

Full size image

To ensure energy-efficient operation, minimizing heat loss to the surroundings is important, as it directly increases energy consumption. In the integrated device, the heat dissipation mainly occurs through the substrate (i.e., \({\theta }_{{\rm{eq}}}\, \sim \,{\theta }_{{\rm{sub}}}\)). Therefore, we introduced thermally insulating substrates with a higher \({\theta }_{{\rm{sub}}}\) to reduce heat dissipation (finite-element-based simulation results can be found in Supplementary Fig. 1). Then, the heater performance (i.e., the amount of heat generated and transferred to the Mott memristor) was investigated on three substrates: SiO2/Si, Corning Eagle XG, and polyimide (PI) which have distinct thermal conductivities of 130 W/mK, 1.3 W/mK, 1.09 W/mK, and 0.12 W/mK for Si, SiO2, Eagle XG, and PI, respectively22,23,24.

The heater temperature can be estimated by measuring the temperature dependence of resistance:

$$R({T}_{{\rm{H}}})={R}_{0}[1+\alpha \left({T}_{{\rm{H}}}-{T}_{0}\right)]$$
(1)

where \({R}_{0}\) is the resistance at the reference temperature (\({T}_{0}\)) which was 220 Ohms, \(\alpha\) is the temperature coefficient of resistance (TCR). Although \(\alpha\) is well known for bulk metals, its accurate value in the integrated device is unclear due to the size effect of resistivity in a thin film25. Therefore, we first calculated the empirical TCR value of the heater by measuring the heater resistance at various temperatures and calibrated the heater resistance to heater temperature using the TCR, following the process of Fig. 1d. The obtained TCR from the slope was 0.000802 K−1 (Fig. 1e). The details of TCR calculation can be found in Supplementary Fig. 2. Although the TCR value was obtained over a temperature change of 40 K, we assumed that the TCR of the metal remains constant over a wide temperature range, allowing this value to be validly applied within the operating temperature range of the TRNG. Then, the heater resistances as a function of the \({V}_{{\rm{H}}}\) were measured (Fig. 1f). Lastly, the heater resistances were calibrated to the heater temperatures using the TCR (Fig. 1g). On the thermally insulating substrates (Eagle XG and PI) the heater temperature increased more than on the SiO2/Si substrate, implying a higher \({\theta }_{{\rm{eq}}}\) was achieved on the Eagle XG and PI.

The Mott memristor exhibits the negative differential resistance (NDR) behavior, which is highly sensitive to changes in ambient temperature4,26,27. Therefore, to provide an intuitive comparison of how the \({V}_{{\rm{H}}}\) affects the \({T}_{{\rm{M}}}\), we measured the NDR behaviors varying the \({V}_{{\rm{H}}}\), and compared them to the NDR behaviors at various \({T}_{{\rm{amb}}}\). Through this, we can correlate the \({V}_{{\rm{H}}}\) condition and the \({T}_{{\rm{amb}}}\) condition, resulting in identical NDR behaviors. Figure 1h shows the NDR curves measured on the three substrates in various \({V}_{{\rm{H}}}\) and \({T}_{{\rm{amb}}}\) conditions. It includes the reference NDR curves (red line) at \({T}_{{\rm{amb}}}\) = 300 K and \({V}_{{\rm{H}}}\) = 0 V. Also, each panel includes two representative sets of identical NDR curves obtained by varying either \({V}_{{\rm{H}}}\) or \({T}_{{\rm{amb}}}\). On the SiO2/Si substrate, the NDR curves by \({V}_{{\rm{H}}}\) = 6 V (thick skyblue, Set (1)) and \({T}_{{\rm{M}}}\) = 310 K (orange, Set (1)) overlap, indicating that the \({V}_{{\rm{H}}}\) = 6 V condition has an identical effect to the \({T}_{{\rm{M}}}\) = 310 K condition. Similarly, \({V}_{{\rm{H}}}\) = 10 V condition (thick green, Set (2)) was identical to \({T}_{{\rm{M}}}\) = 326 K condition (purple, Set (2)). On the Eagle XG substrate, \({V}_{{\rm{H}}}\) = 1 V condition was identical to \({T}_{{\rm{M}}}\) = 310 K condition, and \({V}_{{\rm{H}}}\) = 2 V was to \({T}_{{\rm{M}}}\) = 351 K. On the PI substrate, \({V}_{{\rm{H}}}\) = 0.6 V and 1 V conditions were identical to \({T}_{{\rm{M}}}\) = 320 K and 350 K conditions, respectively.

Figure 1i summarizes the heater efficiency (\({\theta }_{{\rm{eq}}}\)) and heat loss (\(1-{T}_{{\rm{M}}}/{T}_{{\rm{H}}}\)) of the integrated device on the three substrates. The \({\theta }_{{\rm{eq}}}\) was calculated from the Newton’s cooling law (\({T}_{{\rm{H}}}={\theta }_{{\rm{eq}}}{P}_{{\rm{H}}}+{T}_{{\rm{amb}}}\)) at the equivalent thermal circuit in Fig. 1c. The \({\theta }_{{\rm{eq}}}\) on SiO2/Si, Eagle XG, and PI were 300.37 K/W, 5631.5 K/W, and 16779 K/W, respectively (See Supplementary Fig. 3 for detailed calculations.). Furthermore, the heat loss was reduced from 76.7% on SiO2/Si to 39.8% on Eagle XG and 17.9% on PI. Consequently, the thermally insulating substrates increased the overall thermal resistance of the integrated device, allowing more effective heat utilization.

A heater-embodying Mott TRNG and its operation

A Mott oscillator can be composed by connecting a series load resistor to a Mott memristor, as shown in Fig. 2a4,13,28,29. Here, \({R}_{{\rm{L}}}\) is the load resistance. Figure 2b overlays 100 current oscillations generated from the Mott oscillator on the SiO2/Si substrate when the heater is inactive (\({V}_{{\rm{in}}}\,\)= 1.3 V, \({V}_{{\rm{H}}}\) = 0 V; \({T}_{{\rm{M}}}\) = 300 K) in the top panel and active (\({V}_{{\rm{in}}}\) = 1.3 V and \({V}_{{\rm{H}}}\) = 6 V; \({T}_{{\rm{M}}}\) = 310 K) in the bottom panel. The black lines in each panel are representative ones out of the 100 oscillations. In both cases, the oscillations initially overlapped, gradually dispersed, and eventually became stochastic. This time-varying stochastic behavior is due to the accumulation of thermal noise4. When the \({V}_{{\rm{H}}}\) was applied (bottom panel), the oscillation became more stochastic at an earlier moment than the other case. This stochasticity, caused by the accumulation of thermal noise, is reflected in the variation in the number of oscillation peaks over a given time.

Fig. 2: The enhanced stochastic oscillation of the Mott oscillator by the heater on the SiO2/Si substrate.
figure 2

a A Mott oscillator circuit scheme with the heater. b Oscillation current outputs when the heater is inactive (top panel, gray) and active (bottom panel, red). Each graph includes 100 times of testing results. The black lines are one of the results of each condition. c The oscillation frequency shows a linear relationship with temperature. d The standard deviation (SD) of the peak number within 10 μs and 20 μs of 100 oscillations at various temperatures. e The spike number distribution of 100 oscillations, each lasting 10 μs, at various temperatures, including their FWHMs. The FWHM was increased with temperature implying the oscillation gets more dispersed at elevated temperature.

Full size image

Figure 2c shows the oscillation frequency at various temperatures increased by the heater. Here, the oscillation frequency monotonically increased with temperature26,27,30. Fig. 2d shows the standard deviation (SD) of the peak numbers during 10 μs (red) and 20 μs (blue) varying the device temperature by the heater. The results indicate that as both the oscillation frequency and thermal noise are proportional to the temperature, the SD of the peak number increases with temperature (see Supplementary Note 1 for a more detailed discussion). Consequently, the peak number distribution becomes more dispersed during the given time at high temperatures. Figure 2e shows the peak number distribution during 10 μs at various temperatures modulated by the heater. The full width at half maximum (FWHM) is also shown. The greater the dispersion in the peak number, the more quickly the TRNG can generate the TRN4. When the temperature is increased by the heater, the peak number distribution gets more dispersed having a higher FWHM, indicating that a faster TRNG is achievable at higher temperatures. Unlike peak number deviation, the relative standard deviation of interspike interval (ISI) in the oscillation does not change by temperature making it hard to achieve a faster TRNG exploiting the ISI instead of the peak number (Supplementary Fig. 4). Therefore, controlling temperature to increase peak number deviation is the only viable way to achieve high-performance TRNG in our system.

We built a Mott TRNG comprising an integrated device and a breadboard circuit as shown in Fig. 3a. In the circuit, a falling-edge triggered T flip-flop is used, which receives an oscillation input from the Mott oscillator and returns a binary output depending on the number of oscillation peaks. More detailed system configuration can be found in the experimental section. Please note that the Mott TRNG system in this study is a more compact version than our previous work4, in which the positions of the Mott memristor and the \({R}_{{\rm{L}}}\) was changed. See Supplementary Fig. 5 for more details on the TRNG modification.) The integrated device was placed in the probe station, and it was connected to the breadboard via cable. Figure 3b demonstrates 5 bits (“00110”) of random number generation sample from the TRNG with a 10 μs-long pulse per bit while applying 8 V to the heater. The Mott TRNG operation video can be found in Supplementary Movie 1. We introduced a 2 μs interval between pulses to show the reading result of the T flip-flop. However, this interval can be omitted during actual operation.

Fig. 3: The demonstration of the heater-embodying Mott TRNG.
figure 3

a The overall system configuration including the electrical circuit layout and the optical microscopy image of the components of the proposed TRNG. The integrated device was loaded in the probe station, while the T flip-flop was built on the breadboard. b The 5 bits random number generation demonstration of the TRNG. In the demonstration, the random numbers of ‘00110‘ were generated. c The minimum time required to generate a random number (\({t}_{{\rm{TRNG}}}\)) as a function of \({V}_{{\rm{H}}}\).

Full size image

We evaluated the TRNG rate (\({t}_{{\rm{TRNG}}}\)), which is the minimum time required for the generated bits to become truly random. We collected 100 bitstreams from the TRNG varying the \({V}_{{\rm{H}}}\), and tested them using a monobit test, which is one of the 15 randomness tests in the NIST 800-22 standard31. The test results are summarized in Supplementary Fig. 6. Although the monobit test cannot solely determine whether the random numbers are TRNs, it can quickly examine the randomness of the dataset. In the test, the P-value serves as a measure of the randomness of the dataset, and if the P-value is higher than 0.01, the dataset can be considered a set of random numbers. Figure 3c plots the estimated \({t}_{{\rm{TRNG}}}\) from the monobit test results (i.e., the time for the P-value to be higher than 0.01). The \({t}_{{\rm{TRNG}}}\) decreased with increasing \({V}_{{\rm{H}}}\), confirming that a faster TRNG is viable by increasing the thermal noise in the Mott memristor through the heater. The \({t}_{{\rm{TRNG}}}\) was not dependent on the operating point and frequency controlled by \({V}_{{\rm{in}}}\) (Supplementary Fig. 7). Therefore, \({V}_{{\rm{H}}}\) is the only parameter for reducing the \({t}_{{\rm{TRNG}}}\). However, it should be noted that the oscillation amplitude decreases with increasing temperatures4,26,27. Therefore, at a higher heater voltage for faster operation, an amplifier can be added to address the reduced oscillation amplitude issue and to ensure proper operation of the T flip-flop4.

We collected 55 sets of \({10}^{6}\) random bits (so a total of 55 Mbits) at \({V}_{{\rm{H}}}\) = 8 V, and they passed all 15 NIST 800-22 statistical randomness tests, whose results are summarized in Supplementary Table 1. These results demonstrate \({t}_{{\rm{TRNG}}}\) of 100 kbit/s, which is 2.5 times faster than our previous work4, and the fastest among the volatile memristive TRNGs.

While the heater consumes additional energy, the increased speed may offset this energy consumption. On the SiO2/Si substrate, the total energy consumption was 2.55 μJ/bit, which is compatible with 2.87 μJ/bit of our previous TRNG, although the TRNG speed was improved by 2.5 times4. An effective way to further reduce energy consumption is to improve heater efficiency by using thermally insulating substrates. As a result, the total energy consumption can be reduced to 0.75 μJ/bit and 0.68 μJ/bit on the Eagle XG and PI substrates, respectively. (See Supplementary Fig. 8 and Supplementary Note 2 for the detailed energy consumption comparison.) Additionally, chip packaging, which primarily uses polymers with low thermal conductivity, has a heat-trapping effect. Therefore, it can enhance heat efficiency, similar to the application of PI substrates32. Furthermore, an array integration of the heater can further improve heater efficiency, which will be discussed in the following section.

A heater-embodying Mott TRNG array

IoT devices primarily communicate over the Internet, and securing these communications requires proper authentication. Cryptographic communication requires random tokens, such as nonce, which are generated and refreshed with each authentication. Thus, a large number of TRNs generated in real-time is required. Moreover, the exponential growth in data volume has resulted in a surge of parameters that need to be optimized for computing. This, in turn, necessitates the incorporation of substantial stochastic functions to address large-scale problems. Here, TRNG array is a viable way to generate massive TRNs for these purposes33.

We fabricated an N\(\times\)1 (where N = 1, 2, 4, 8, 16, and 32) size of the heater-integrated TRNG array to demonstrate a massive TRN generation and assess its performance. Figure 4a shows an optical top-view image (left) and a schematic illustration (right) of a representative 8\(\times\)1 array. Here, the heater was integrated parallel to the memristor array beneath it, supplying heat with high efficiency. This is viable as our heater has vertical stack distinguished to previous studies where heater was integrated with lateral device30,34. Fig. 4b shows the thermal circuit of the TRNG array. As the array size increases, more heat is dissipated to the surroundings by the increased heater area compared to a single TRNG. This results in the decrement of the thermal resistance, thereby a higher \({V}_{{\rm{H}}}\) is necessary to reach the target temperature, accompanying more energy consumption (see Supplementary Fig. 9 for more details on the thermal resistance of the array.) However, the energy consumption per bit can be reduced, making the array more energy efficient.

Fig. 4: A Mott TRNG array and its performance.
figure 4

a An optical microscope image of the 8 \({\boldsymbol{\times }}\) 1 TRNG array and a schematic illustration of a part of the array. b The thermal circuit of the TRNG array. c The normalized heater energy (Eheater) and normalized heater energy per TRNG (Eheater/N) as a function of the array size (N). d The monobit test results of eight individual TRNGs obtained from the array. All passed the test in 10 μs. e The energy per bit and the TRN generation rate of the heater-embodying Mott-TRNG, fabricated on the three substrates, as a function of the array size. Symbols are experimentally obtained, and lines are modeled by calculation.

Full size image

Figure 4c plots the experimentally measured normalized heater energy consumption (\({E}_{{\rm{heater}}}\)) and the normalized heater energy consumption per bit (\({E}_{{\rm{heater}}}(N)/N\)). Also, it includes numerical calculation results. (See Supplementary Note 3 for the details of the heater energy consumption.) The \({E}_{{\rm{heater}}}\) increased linearly with N (\({E}_{{\rm{h}}{\rm{e}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}}(N)=N\times {E}_{\Delta }+E(1)-{E}_{\Delta }\)). Here, \(E\left(1\right)\) is the heater energy when N = 1, which includes the original heat loss by \({\theta }_{{\rm{sub}}}\), and \({\theta }_{{\rm{air}}}\), and \({E}_{\Delta }\) is the unit heater energy increased by array size through \(\Delta {\theta }_{{\rm{s}}{\rm{u}}{\rm{b}}}\) and \(\Delta {\theta }_{{\rm{a}}{\rm{i}}{\rm{r}}}\) However, as the array size increases, the original heat loss becomes negligible, and the heater energy consumption per bit (\(={E}_{\Delta }+(E(1)-{E}_{\Delta })/N\)) is reduced and converges to \({E}_{\Delta }\). This suggests that the heater can be more energy-efficiently utilized in the TRNG array.

We demonstrated an 8\(\times\)1 TRNG array of Fig. 4a, generating 100 random numbers simultaneously from each TRNG in the array. The random numbers passed the monobit test, confirming successful TRNG array operation in 10 μs (Fig. 4d). Figure 4e shows the energy consumption per bit (\({E}_{{\rm{bit}}}\)) of the TRNG array and \({t}_{{\rm{TRNG}}}\). The \({E}_{{\rm{bit}}}\) of octuple (N = 8) TRNG on SiO2/Si substrate was reduced to 46% of the single TRNG. Furthermore, on the SiO2/Si substrate and when N = 128 (for 128-bit nonce cryptography35), the energy consumption could be further reduced to 0.981 μJ/bit. The energy consumption could be further reduced on Eagle XG or PI substrates, as they can drastically improve the heater efficiency. For example, the \({E}_{{\rm{bit}}}\) on the PI can be as low as 0.654 μJ/bit when N = 128. We compared the proposed TRNG system on the SiO2/Si substrate to other TRNG works, which passed all the NIST tests with proper data size (≥55 Mbit) in terms of speed, energy consumption, and circuit components (Table 1)2,3,4,15. Our TRNG system outperformed them in all aspects, highlighting the excellence of this work. The heater undergoes a very weak electrical stress that does not cause electromigration issues in the heater36,37. Therefore, incorporating the heater is a reliable solution that enhances performance.

Table 1 Benchmarking of volatile memristor-based TRNG passed all 15 NIST tests
Full size table

In summary, we developed a physical method to improve TRNG by integrating a heater with the NbOx-based Mott memristors and engineering the thermal noise. The proposed TRNG has been improved by directly controlling the thermal noise, representing a novel approach, and as a result, it achieved a speed of 800 kbit/s and energy consumption of 1.2 μJ/bit in an 8 × 1 TRNG array, making it the highest-performing TRNG reported to date.

It would be interesting to envision future advancements in achieving faster speeds and lower energy consumption of the proposed system. Achieving faster speeds can be achieved by increasing the device temperature to further enhance thermal noise; however, it also reduces the NDR region, potentially eliminating the oscillation characteristics. Due to this trade-off, the maximum achievable TRNG rate is likely to have a limit.

On the other hand, there can be more opportunities for energy improvement. In the proposed system, thermal resistance is the crucial factor for achieving high energy efficiency. As demonstrated, introducing a thermally insulating substrate is one solution for high thermal resistance. Additionally, thermal resistance can be enhanced through various methods, indicating the potential for further advancement of the proposed technology. For example, thermal resistance can be further increased by optimizing the heater geometry, such as by implementing a confined cell structure in the phase change memory38. Moreover, device scaling is a fundamental method to increase thermal resistance; if the device feature size is scaled down from 5 μm to 130 nm, the heater energy consumption can be reduced to 0.07% in 128\(\times\)1 TRNG array39. (Table 2 summarizes the estimated TRNG performance, and a more detailed discussion on the device scaling can be found in Supplementary Fig. 10.) When scaled down, the flip-flop limits energy efficiency, and the next step may involve developing an energy-efficient digitalization method.

Table 2 The energy consumption of TRNG systems at different scales and array sizes.
Full size table

In another aspect, there are attempts to utilize heat as information for energy-efficient computing27,40. We remark that heat tunes the stochastic process in the device, and it may be viable to construct a device network modulating stochastic functions through inter-device heat transfer27. As such, this work expands its utility of engineering stochastic processes through heat for next-generation encryption hardware and computing primitives.

Methods

A heater-embodying Mott device fabrication

A (top) Pt/Ti/NbOx/Pt(/Ti)AlOx/Pt(/Ti) (bottom) stack was fabricated using the following procedure. An adhesive 5-nm Ti followed by a 25-nm-thick Pt heater electrode was deposited by e-beam evaporation and patterned by a lift-off process on SiO2/Si, Eagle XG glass, and PI substrates. Then, a 20-nm-thick AlOx layer was deposited by a thermal atomic layer deposition (ALD) at 250 °C using a trimethylaluminium (TMA) precursor and an H2O reactant. Next, an adhesive 5-nm-thick Ti and a 25-nm-thick Pt bottom electrode were deposited using an e-beam evaporator and patterned by a lift-off process. Then, a 35-nm-thick NbOx layer was deposited by a reactive sputtering process at 170 °C in Ar:O2 (13:7, 4 mtorr) mixed gas ambient using a Nb target. Then, a 50-nm-thick Ti top electrode followed by a 15-nm-thick Pt passivation contact electrode was deposited by e-beam evaporation and patterned by a lift-off process. The line width of the patterns was 5 μm.

Mott TRNG system configuration and operation

The TRNG system comprises a Mott oscillator, a heater, and a T flip-flop. The oscillation signal from the Mott oscillator is transmitted to the T flip-flop. The T flip-flop (Texas Instruments, SN74LS73AN) is triggered at the falling edge of the oscillation current signal, which is the identical timing of the voltage decrement at the load resistor. For an experimental demonstration of the proposed TRNG, the Mott oscillator was implemented in a probe station, and the T flip-flop was integrated on a breadboard. The \({V}_{{\rm{cc}}}\), \({\rm{J}}\), \({\rm{K}}\), and \(\mathop{{\rm{CLR}}}\limits^{\bar{} }\) terminals of T flip-flop were sourced to 2.5 V by an EXO K-6135 DC power supply, while the Mott oscillator and the heater were biased by Keithley 4200-SCS. Their signals were transmitted via cables, and they were monitored by Keithley 4200-SCS.

Electrical characterization

All the electrical characterization was performed using Keithley 4200A-SCS.

Device ambient temperature control

The device was placed on a hot chuck (MSTECH, ST1), and the ambient temperature was controlled by a hot chuck controller (MSTECH, MST10000H). The temperature was calibrated by a thermocouple before measurement.

NIST test

The randomness test code was built in the Python environment, referring to the NIST Statistical Test Suite (Special Publication 800-22).