Introduction

Cryogenic computing systems, capable of operating at/below 4 Kelvin temperature, have garnered renewed interest in recent years primarily due to their promise as control processor and memory in large-scale quantum computing systems1,2,3. In addition, they are uniquely suited for exa-scale high-performance computing systems and space applications4,5,6. A suitable cryogenic controller and memory system can facilitate the scaling of quantum computing systems up to thousands of qubits, by solving several existing challenges, including (i) the requirement of a large number of wires and interconnects to connect the qubits with currently used room temperature controller and memory, (ii) the possibility of a large amount of thermal noise propagation from room temperature to noise sensitive qubits, and (iii) the heat and noise generation by the lossy wires and interconnects1,2. Moreover, cryogenic systems based on superconducting devices (such as Josephson junctions and superconducting quantum interference devices (SQUID)) provide unparalleled speed (hundreds of gigahertz) and energy efficiency (sub-atto-joule switching energy)4. This can be extremely useful for developing energy-efficient high-performance computing systems and space electronics.

One of the critical challenges in cryogenic systems is the need for high-speed, low-power memory solutions that can complement the computing infrastructure1. In this quest, superconducting, non-superconducting, and hybrid technologies have been explored1,7,8,9,10,11. However, all of these technologies have unique challenges, and therefore, developing a suitable and scalable memory system for cryogenic applications has remained an ongoing pursuit. Content addressable memory (CAM) and ternary content addressable memory (TCAM) are specialized storage systems that can accelerate certain computing tasks by introducing the capability of comparing input data against stored data12,13. CAM performs searches based on binary data (“0’ and “1”), returning exact match/mismatch output, whereas TCAM allows an additional state (don’t care, “d”) for the input data (Fig. 1a, b). The ternary nature of TCAMs allows for more flexible searches, which is useful in several applications, including pattern recognition, network routing, and database management. Additionally, CAM and TCAM can be empowered to calculate the Hamming distance (HD) between the input search and stored data. This capability allows us to identify nearby matches (the lowest HD implies the closest match) along with the exact matching (HD = 0). CAMs and TCAMs with HD calculation capability can be powerful tools in error detection and correction for both classical and quantum domains, approximate searching, and other data-intensive applications. Additionally, TCAMs have recently been used to accelerate classification tasks, where the TCAM stores the features extracted from the dataset (images, texts, etc.) as the stored data and can provide the search result whenever the features for any search condition are applied as the input data (Fig. 1c)13. Based on the search results, TCAM can predict the classification result. Here, the parallel search capability of TCAMs becomes extremely useful for improving the speed and efficiency of the classification tasks.

Fig. 1: Introduction to content addressable memory (CAM).
figure 1

Illustrations of the search mechanism with a a binary and b ternary CAM. c Block diagram showing the steps how a CAM can be used for artificial intelligence applications such as classification and pattern recognition tasks.

Full size image

TCAMs can also be useful for cryogenic applications like quantum computing by efficiently handling quantum error correction decoding, high-performance computing by improving latency and energy efficiency, artificial intelligence (AI) by accelerating pattern recognition and classification, space exploration by assisting in data storage and retrieval, and decision-making algorithms, and data centers by improving large-scale search operations like database queries and search engines. This paper demonstrated the design and implementation of a cryogenic TCAM with exact search and HD calculation capabilities. Here, we utilize the ferroelectric SQUID (FeSQUID)-based cryogenic memory system that combines the ultra-high speed and energy efficiency of SQUIDs with the voltage-controlled non-volatility of ferroelectric materials. In the proposed TCAM, there are two modes- one for exact searching and another for HD calculation. Due to the use of FeSQUID, we get several advantages from the proposed TCAM when compared with the existing designs (both room temperature and cryogenic), including (i) the exact searching mode provides binary decisions for matching and mismatching without needing any peripheral circuitry, thanks to the superconducting behavior of SQUIDs, and (ii) extremely energy-efficient TCAM operation (1.36 aJ and 26.5 aJ average energy consumption for 1-bit CAM and TCAM search. respectively). Finally, we demonstrate the efficiency and advantages of our proposed TCAM by performing Hyperdimensional Computing (HDC) algorithm-based language recognition task. By implementing the associative memory that supports a highly parallelized search operation for the inference step with FeSQUID-based TCAM arrays, a single 10,000-bit vector comparison consumes just 89.4 fJ. We also demonstrate that the FeSQUID-based TCAM consumes over one order of magnitude less energy compared to the cryogenic 5 nm FinFET SRAM-based TCAM to perform the same operation.

Results

In our proposed TCAM, we use FeSQUIDs as storage elements and heater cryotrons (hTrons) as the access devices to allow write and read operations of any specific FeSQUID in a large array scenario. Here we first introduce these two unique devices.

Ferroelectric SQUID (FeSQUID)

Despite extensive research over the last few decades, a robust method for voltage-controlled gating of SQUIDs remained elusive until the introduction of FeSQUID in 202114. In FeSQUID, a ferroelectric material is employed to modulate the superconducting behavior of the SQUID, which also allows voltage control over the superconductivity. The proposed FeSQUID had a SQUID built with two parallel weak links on top of a ferroelectric material; the structure is shown in Fig. 2a. Ferroelectric materials exhibit non-volatile polarization switching that can be controlled by an external voltage bias. Fig. 2b illustrates the voltage-controlled switching of the ferroelectric polarization (PFE) of a led zirconium titanate (PZT) material at cryogenic temperatures. The internal PFE of a ferroelectric material generates surface charges that, in turn, induce electric fields, effectively injecting direct charge into the system15. Now, when a SQUID is fabricated on top of a ferroelectric layer, the superconducting material screens the charge bound at the interface. The amount of bound charge at the interface directly depends on the remnant polarization (PR) of the ferroelectric. Specifically, negative remnant polarization (\({P}_{R}^{-}\)) increases the surface-bound charge, while positive remnant polarization (\({P}_{R}^{+}\)) decreases it14,16. This alteration in surface charge modifies the carrier density, which in turn affects the critical temperature (TC) of the superconductor and, consequently, the superconducting energy gap (Δ). The relationship between Δ and TC can be described using Bardeen-Cooper-Schrieffer (BCS) theory17,18:

$$\Delta (T)=1.763{k}_{B}{T}_{C}\,\tanh \left(2.2\sqrt{\frac{{T}_{C}}{T}-1}\right)$$
(1)

where T is the temperature and kB is the Boltzmann constant. The Ambegaokar-Baratoff (AB) theory19 further explains how Δ(T) affects the critical current (IC):

$${I}_{C}=\frac{\pi \Delta }{2{q}_{e}{R}_{N}}\,\tanh \left(\frac{\Delta }{2{k}_{B}T}\right)$$
(2)
Fig. 2: Device structures and characteristics of ferroelectric superconducting quantum interference device (FeSQUID) and heater cryotron (hTron).
figure 2

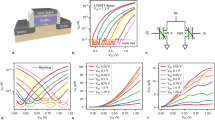
a Device structure and circuit symbol of a FeSQUID. b Polarization-voltage characteristics of a Lead Zirconium Titanate (PZT) ferroelectric. c Current-voltage characteristics for two ferroelectric polarization states. d False colored scanning electron microscope image of a fabricated hTron device. WSi superconductor is used to form the gate and the channel, and SiO2 is used as the dielectric material to separate them. Illustration of gate-controlled switching of a hTron channel when e IG < ISW, keeping the channel in its superconducting state, and f IG > ISW, switching the channel to its resistive state. g Gate current-controlled switching of the hTron channel. Note, the plot uses two separate y-axes---left for gate current (IG) and right for channel current (ICh). While the channel bias current (IB) and the gate switching current (ISW) appear visually aligned, they represent distinct quantities and are not numerically equal.

Full size image

Here, qe is the electron charge, and RN is the normal state resistance of the SQUID. Due to the non-volatile polarization states of the ferroelectric, two distinct levels of IC are observed in the SQUID’s I–V characteristics. Specifically, the \({P}_{R}^{-}\) state of the ferroelectric results in a higher critical current (IC,high), whereas the \({P}_{R}^{+}\) state leads to a lower critical current (IC,low), as shown in Fig. 2(c). This unique voltage-controlled superconductivity of FeSQUID has been leveraged to implement a scalable memory system9, a voltage-controlled Boolean logic family20, and an in-memory computing system21 for cryogenic applications.

Heater cryotron (hTron)

Two-terminal Josephson junction-based superconducting circuits face several challenges, including limited fan-out capability, difficulties in achieving uniform Josephson junction fabrication, scalability constraints due to flux trapping, and high sensitivity to external magnetic fields, among others. To overcome these limitations of Josephson junctions, three-terminal cryotron-based devices were developed, offering gate current-controlled switching of the superconducting channel between its superconducting and resistive states22. A notable member of this family is hTron23, which is capable of driving high impedances (>100 kΩ) and supporting a large number of fan-outs due to its highly resistive state. Unlike Josephson junctions, hTron devices do not rely on superconducting loops, making them free from issues like flux trapping and scalability challenges22. Heater cryotrons have already been used as an access device in different cryogenic memories9,10,24, as an interface between superconductors and semiconductors23, to design logic circuits20,22,25,26, in cryogenic neuromorphic systems27,28,29, and so on.

The hTron is a four-terminal superconducting device driven by current. Two terminals serve as the gate, while the other two form the superconducting channel, as depicted in Fig. 2d. The gate and channel are separated by a dielectric spacer that thermally connects but electrically isolates the two. When no gate current (IG) is applied, the channel remains superconducting, assuming a given channel bias current (IB). However, once IG is applied, the gate becomes resistive, generating thermal phonons that propagate through the dielectric spacer to the superconducting channel. Until IG increases beyond a certain threshold, the superconductivity of the channel persists22. This behavior is shown in Fig. 2e.

When the gate current (IG) exceeds a critical threshold (ISW), enough thermal phonons with sufficient energy (>2δ) are generated and transported to the channel. These phonons become able to disrupt the cooper pairs and suppress the superconductivity of the channel superconductor. Therefore, the channel’s critical current (\({I}_{Ch}^{C}\)) falls below the applied channel bias current (IB). This causes the channel to transition into a high-impedance resistive state, redirecting the channel current (IB) to the external circuit, as illustrated in Fig. 2f, g shows the gate current-controlled switching of the channel between its superconducting and resistive states.

Design principle of FeSQUID-based TCAM

Figure 3a shows the schematic of the proposed cryogenic TCAM. In this section, we discuss the design and working principles of this TCAM. The proposed TCAM is a modified version of FeSQUID-based memory cell, demonstrated in ref. 9. In the FeSQUID-based memory cell, to store one bit of data, one FeSQUID and one hTron are connected in series, and multiple cells are connected in parallel along each row of the memory array. However, in this work, we use two memory cells connected in parallel to each other to design a 1-bit TCAM. The operation of this TCAM cell is controlled by one read word line (RWL), two read bit lines (RBLs), two write word lines (WWLs), and one sense line (SL). The operating principle of the TCAM cell is discussed in detail in the next section. Now, to build a large-scale TCAM, these TCAM cells need to be connected in parallel along the row where the shared RWL in each row will act as the match line (ML) to exhibit the matching/mismatching result (Fig. 3b).

Fig. 3: The proposed cryogenic ternary content addressable memory (TCAM).
figure 3

a Circuit schematic of the proposed TCAM cell. b Illustration of the array-level organization, where data will be stored in a row. c Values of read word line currents (IRWL) for two modes of the proposed TCAM. Definitions of (d) input search data in terms of read bit line currents (IRBL1 and IRBL2) and e stored data in terms of FeSQUID's device states.

Full size image

The proposed TCAM has two modes- one for exact search (binary result) and another for HD calculation (analog result). The mode of the TCAM can be selected by choosing a suitable bias current for the RWL of each TCAM. For exact search mode, the value of RWL current (IRWL) needs to be chosen in a way so that we get superconducting and resistive states from SQUIDS for “0” and “1” data, respectively. According to Fig. 2c, the range for this IRWL is – IC,Low < IRWL < IC,High. Due to the use of the superconducting state of SQUID and the parallel connection of all the TCAMs in a row (as shown in Fig. 3b, if there is any SQUID with a superconducting state, the ML of that row will have zero voltage. This provides us with the binary decision from the ML- either zero or some non-zero voltage for any amount of mismatch or complete matching, respectively. Now, for HD calculation mode, we do not want binary decisions for matching and mismatching; rather, we want analog decisions with different levels of ML voltage for different levels of matching between the input and stored data. Therefore, we need to avoid the superconducting state of SQUIDs, and that’s where the use of FeSQUIDs becomes extremely useful because FeSQUIDs can show either superconducting/resistive states or only resistive state with two different resistance values for two states. In the HD calculation mode, we choose the value of IRWL in a way so that FeSQUIDs show two different resistance values for “0” and “1” states. According to Fig. 2c, the required range of IRWL for this mode is -IRWL > IC,High. Fig. 3c shows the values of IRWL used for two TCAM modes in this work.

The FeSQUIDs are utilized to store the data as the ferroelectric polarization (similar to the memory operation) for the TCAM operations. One FeSQUID stores the data (Data) while the other stores the inverted version of data(\(\bar{Data}\)). To store Data and \(\bar{Data}\), we need to apply suitable voltages across the ferroelectric of FeSQUIDs through the WWLs (VWWL1 and VWWL2). Fig. 3e shows the definition of Data and the corresponding device states. The input search data is applied through a combination of two gate currents (RBL currents, IRBL1 and IRBL2) of the two hTrons, which determine the switching of the hTrons. Fig. 3d shows the values of RBL currents for different input search data (Search and \(\bar{Search}\)).

Wroking principle of FeSQUID-based TCAM

Any TCAM search can be divided into two major operations: (i) storing the data inside the memory through a memory write operation, and (ii) searching any input data against the stored data through a memory read operation. To write data into a FeSQUID-based memory cell, we apply appropriate voltage biases (positive or negative) across the ferroelectric layer. Specifically, we manipulate the polarization state of the ferroelectric material within the targeted FeSQUID cell by employing a V/2 biasing scheme. The appropriate voltage biases (±VWRITE or ±VWRITE/2) are applied to the write word lines (WWLs) and source lines (SLs), such that only the selected memory cell experiences the full ±VWRITE across its ferroelectric layer. In this configuration, half-selected cells located in the same row or column as the targeted cell will experience ±VWRITE/2, while unselected cells, not sharing the same row or column, will experience 0 V. To ensure the write operation affects only the selected cell, the write voltage must be carefully chosen to satisfy the condition \(\frac{1}{2}| {V}_{WRITE}| < | {V}_{C}| < | {V}_{WRITE}|\), where VC is the coercive voltage of the ferroelectric. To satisfy this condition, we have used ±5 V as the value of VWRITE. Please refer to9 for more details on the write operation in a FeSQUID memory array.

As illustrated in Fig. 2c, applying a current within the range IC,Low < I < IC,High to the SQUID will result in either a superconducting (0 V) state for \({P}_{R}^{-}\) or a resistive (nonzero voltage) state for \({P}_{R}^{+}\), depending on the polarization state of the ferroelectric. This property is exploited for the exact search mode by applying a suitable current bias through the SQUID. First, all WWLs and SLs are grounded. Moreover, as seen in Fig. 2c, if a current larger than IC,High is applied, the SQUID will show two different resistance values (and hence, two voltages) depending on the polarization states. This characteristic of SQUID is used for the HD calculation mode. RBL currents are responsible for determining the switching of the hTrons connected in series with each FeSQUID. The search data are represented by the RBL currents.

Based on the application of RWL and RBL currents, the ML voltage will depend on whether the input search matches or mismatches the stored data. Figure 4 shows the working principle of the exact search mode of the proposed TCAM. Here, first, Data and \(\bar{Data}\) are stored in the two FeSQUIDs with the help of WWLs. Then, when Search and \(\bar{Search}\) are applied through the RBL currents (chosen according to Fig. 3d), and the appropriate current is applied to the RWL (chosen according to Fig. 3c), one of the hTrons becomes superconducting while the other remains in a highly resistive state (50 kΩ). For matching conditions (Data = 0 and Search = 0 (Fig. 4a), Data = 1 and Search = 1 (Fig. 4e), the FeSQUID connected in series with the superconducting hTron switches to its resistive state. As a result, the RWL current flows through this branch, and we get a nonzero voltage drop in the ML (shown in Fig. 4g). On the other hand, for the mismatching conditions (Data = 0 and Search = 1 (Fig. 4b), Data = 1 and Search = 0 (Fig. 4d), the FeSQUID connected in series with the superconducting hTron remains in its superconducting state. As a result, we get zero voltage drop in the ML (shown in Fig. 4g).

Fig. 4: Working Principle of the proposed ternary content addressable memory (TCAM) in the exact search mode.
figure 4

Illustration of the working principle of the TCAM when a Data = 0 and Search = 0, b Data = 0 and Search = 1, c Data = 0 and Search = d, d Data = 1 and Search = 0, e Data = 1 and Search = 1, and f Data = 1 and Search = d. Here, “d” represents the don’t care condition in the search bit. g Match line (ML) voltage, power, and energy consumption for 1-bit exact search with the proposed TCAM.

Full size image

Now, for the “d” case in the input search, we apply non-zero currents to both RBLs. As a result, in these cases shown in Fig. 4c, f, both hTrons switch to their resistive states, which leads to the division of the applied RWL current between two branches. The current that flows through each of the branches (IRWL/2) is not sufficient to switch the FeSQUID state to its resistive state. However, since both hTrons become resistive, we get a non-zero voltage drop in the ML (shown in Fig. 4g), irrespective of the stored data in the FeSQUIDs. Fig. 4g shows the value of ML voltages, power consumption, and energy consumption for all the possible combinations of a 1-bit TCAM.

Now, we discuss another capability of our proposed TCAM, which is the HD calculation. Figure 5a shows a 4-bit TCAM where five different combinations of 4-bit data are stored in the TCAM array, and one specific input search data is applied. As explained earlier in this section and in Fig. 4, in the exact search mode, due to the choice of RWl current, we will get zero and non-zero ML voltages for any mismatch and complete match, respectively. However, in the HD calculation mode, we select the RWL current in such a way that the SQUID always receives a current that is larger than its critical currents (IC,Low and IC,High). Therefore, the SQUID never remains in the superconducting state. For the two states, we get two different values of resistance, as shown in Fig. 2c. We design and choose the operating modes of the proposed TCAM in a way that we get the highest ML voltage for the complete matching condition, and the voltage drops with the increase in the mismatch. Fig. 5a shows the ML voltages for this mode for different amounts of mismatch in the 4-bit TCAM. We also extend our simulation to larger TCAM arrays and the ML voltage values for different amounts of mismatch in different sizes of the TCAM arrays in Fig. 5b. The ML voltage for n-bit TCAM can be calculated using the following equation:

$${V}_{ML}=\left({n}_{bits}\times {I}_{RWL}\right)\frac{1}{{n}_{bits}\times \frac{1}{50k\Omega }+{n}_{match}\times \frac{1}{1.8k\Omega }+\left({n}_{bits}-{n}_{match}\right)\times \frac{1}{0.9k\Omega }}$$
(3)

where nbits and nmatch represent the size of TCAM cells in a row and the number of matching bits in that row, respectively. In this equation, we use fixed resistance values for the FeSQUID and hTron devices, derived from experimentally reported data in ref. 14 and23, respectively. While these resistance levels may vary with temperature and biasing conditions, we adopt their experimentally observed mean values to illustrate the fundamental operation of the proposed TCAM architecture. It is important to note that although such variations may influence the ML voltage levels in the HD calculation mode (as shown in Fig. 5b), they do not affect the exact search mode. This is because the binary decision in exact search relies on the superconducting (zero-resistance) and resistive (nonzero resistance) states of the FeSQUID and hTron devices. Thus, even with variations in resistance magnitude, the ML will still yield zero or nonzero voltages corresponding to match and mismatch conditions, ensuring robust binary classification. On the other hand, for the HD calculation mode, although the resistance levels may have variations, we will still have different levels of ML voltage (with different magnitudes) for different degrees of matching. To demonstrate the effect of variation in the resistance levels and the bias current on the ML voltage levels during HD calculation mode, we performed a 10,000-point Monte Carlo analysis, as discussed in the next section. To decode the HD from the ML voltage levels, any cryogenic voltage-based comparator and sense amplifier can be utilized30.

Fig. 5: Working Principle of the proposed ternary content addressable memory (TCAM) in an array scenario.
figure 5

a Match line (ML) voltage levels obtained for different amounts of mismatch between the input search and stored data in a 4 × 4 TCAM array. b Evolution of ML voltage levels for different TCAM array sizes (4-64 bits) and different amounts of mismatch.

Full size image

System-level benchmarking

The TCAM architecture proposed here is particularly well-suited for application in cryogenic environments, where conventional CMOS memory and logic circuits suffer from degraded performance or excessive power dissipation. In quantum computer systems, for example, the TCAM can accelerate quantum error correction (QEC) through rapid, parallel searches of large syndrome-to-correction codebooks stored locally at cryogenic temperatures. This minimizes data transfer overhead between the cryogenic and room-temperature domains and reduces latency in fault-tolerant quantum operations. Similarly, in space-based systems—where ambient temperatures are low and power availability is limited, the TCAM can enable image recognition and decision-making applications by efficiently matching input data against stored templates or classification rules in real time. These cryogenic-specific applications exploit the ultra-low power, non-volatility, and robust binary decision enabled by the superconducting property of the FeSQUID and hTron devices, making it a desirable choice for next-generation in-memory computing under extreme environmental conditions.

With the ever-growing interest in machine learning, the size and data requirements of today’s models are enormous. However, many application scenarios have strict constraints for the system, e.g., in cryogenic environments, embedded systems, or IoT devices. Here, efficient and computationally lightweight algorithms are key. For these reasons, researchers have explored techniques to simplify models by quantizing conventional machine-learning approaches. While reducing the model size, the fundamental requirements of large datasets and large training efforts are unchanged.

For these reasons, an emerging brain-inspired machine-learning concept called Hyperdimensional Computing (HDC) has been proposed and gained rapid interest. In HDC, information is stored as patterns in large vectors with thousands of elements. By utilizing randomness and similarity, HDC is inherently resilient to noisy data and errors in computing operations. This enables the utilization of emerging hardware, which often may suffer from imprecise operation, e.g., due to variability. HDC has been showcased in various classical machine-learning tasks such as language recognition31 (illustrated in Fig. 6a), image classification32, or wafer map defect pattern classification33.

Fig. 6: System-level benchmarking of the proposed ternary content addressable memory (TCAM) while performing the language recognition task.
figure 6

a Illustration of the HDC algorithm for language recognition. The encoded search vector of the sample text that needs to be recognized is compared to all pre-trained class vectors. The most similar (i.e., closest) vector is then inferred as the result. b The inference accuracy of language recognition over the vector size. c Energy consumption of a single vector comparison with 10,000 bits using ferroelectric superconducting quantum interference device (FeSQUID)-based and static random-access memory (SRAM)-based TCAM cells. d Confusion matrix of Hamming distance (HD) calculation in an FeSQUID TCAM block with 15 cells. We performed a 10,000-point Monte Carlo analysis with 5% standard deviation in the resistance levels and the bias current. e Inference accuracy loss due to the injected errors from the resistance variation.

Full size image

The data type of vector elements can be selected, and real numbers, integer numbers, bipolar values, or binary values can be used. Using binary makes HDC very efficient, as the operations can be implemented using basic logic gates. For the similarity metric used during inference, the Hamming distance needs to be calculated, which is a combination of bit-wise XOR and popcount. This can be implemented using TCAM arrays that store the class vector bits and are searched with the bits of the query vector34.

The used vector size affects the inference accuracy of the final model, which is shown in Fig. 6b. For instance, training the language recognition model with 10,000 bits yields an inference accuracy of 97.1% while using half the size yields 95.9%. Estimating the energy consumption of a single vector comparison can be done using the following equation:

$$E={n}_{bits}\,\times 5\,{\rm{\mu}} {\rm{A}}\times {V}_{ML}\,\times 0.3\,{\rm{ns}}$$
(4)

where nbits is the size of the vectors and VML is the match line voltage, depending on nbits and nmatch (see Eq. 3). Here, we consider the switching time of hTron as the only delay during the search operation in the TCAM cell. We use 0.3 ns for the superconducting to resistive switching of hTron devices, as reported in ref. 23. Moreover, the chosen bias current is calibrated with the experimental data of FeSQUID reported in ref. 14. Also, the Eq. (4) only considers dynamic energy since both FeSQUID and hTron operate in the superconducting regime during idle states, and their static power consumption is zero under cryogenic conditions. As most of the vectors in HDC are orthogonal (i.e., a similarity of ≈50%), we assume the number of matching bits to be half of the total number of bits. This gives an energy consumption of 89.4 fJ per vector comparison with 10,000 bits, and 44.7 fJ with 5000 bits.

To put the numbers in perspective, we have implemented a block of TCAM cells using conventional SRAM technology with 5 nm FinFET transistors. Due to the lack of existing superconducting TCAM architectures in the literature, particularly at the circuit level, we selected cryogenic SRAM-based TCAM (circuit schematic is shown in Fig. 7a) as a relevant and available benchmark. Note, cryogenic-compatible SRAM has been actively explored as a practical memory solution for low-temperature environments, and recent efforts have demonstrated functional SRAM-based TCAM architectures operating under cryogenic conditions. Similar to the cryo FeSQUID, we operate the SRAM circuits at 4 K with a supply voltage of 0.7 V. When queried with data, the search lines (SL) will be used to apply the voltage corresponding to the bit “S”. The TCAM cell will respond with one of two cases. For a match (C = S), the data is the same, and the TCAM cell blocks all discharge paths from ML to ground. With an example case of C = 1 and S = 1, this is facilitated as follows. The S1 cell is programmed such that the L node has a low voltage, and the S2 cell has a high voltage at the R node. Even though SL is high, the left discharge path is blocked by L being low, and the right discharge path is blocked by SLB being low. For a mismatch (C ≠ S), the TCAM cell will form a single discharge path inside the cell. For example, with C = 0 and S = 1, the left discharge path will be open as L is high in this case. By connecting multiple SRAM TCAM cells to a shared wire (here ML as shown in Fig. 7b), the discharge rate of the potential of ML is directly proportional to the number of TCAM cells responding with a mismatch. This implements the functionality of the Hamming distance. To transform the discharge rate into a temporal signal, a clocked self-referencing sense amplifier (CSRSA) is used. The CSRSA produces a sharp output signal that can be digitized by a time-to-digital converter. By cutting the large vectors into smaller sections, blocks are formed that calculate the Hamming distance in the analog domain. Hence, the results in Fig. 6c show a decreasing energy consumption for the SRAM-based cells. As fewer blocks are needed when increasing the block size, the comparison of an entire vector becomes more efficient due to the reduction of overhead in the form of fewer sense amplifiers. In our energy estimation scheme for the cryo FeSQUID, the energy depends on VML, which is only subject to the ratio between block size to the number of mismatches, i.e., fixed to 50% here. Still, the energy consumption of cryo FeSQUID is over one order of magnitude smaller than cryo SRAM. For instance, using vectors with 10.000 bits and a block size of 10 bits, SRAM consumes 1.29 × 10−12 J compared to the 8.94 × 10−14 J of FeSQUID. The energy consumption shown in this work is based on the comparison of two 10,000-bit vectors, where one vector is stored in the TCAM cells and the other is applied through the search lines. The energy considered here is only for the active part of the calculation, extracted for one block and then extrapolated.

Fig. 7: Introduction to static random-access memory (SRAM)-based ternary content addressable memory (TCAM).
figure 7

a Schematic of the 16T SRAM-based TCAM cell. b Schematic of the SRAM-based TCAM block.

Full size image

To analyze the impact of resistance variation on the performance of HDC, we first conducted a 10,000-point Monte Carlo study of the ML voltage distributions. For this, we considered a standard deviation of 5% for FeSQUID and hTron resistance levels, and the bias current used in the TCAM array. The match levels (i.e., the Hamming distance) are swept from 0 to 15. This yields the ML voltage distributions for each mismatch level. From the ML voltage distributions, we calculate discrete probability distributions by sorting the voltages of each mismatch level into buckets. The nominal ML voltages are used to calculate the decision boundaries halfway between the respective neighbors. Sorting the voltages into the buckets formed by the decision boundaries yields the discrete probability distributions, which can be abstracted in a confusion matrix. The confusion matrix, shown in Fig. 6d, shows the spread in variation slightly growing for larger Hamming distances.

The formed confusion matrix describes the error behavior, which we then inject into the inference algorithm of HDC. Here we cut the class and query vectors into blocks of the same size and calculate the software Hamming distance first. Using the discrete probability distribution of the respective software, Hamming distance gives a random hardware Hamming distance that is accumulated with all other hardware Hamming distances of this vector comparison. To acquire sufficient statistical data, we run the entire inference algorithm 100 times for each tested vector dimension. Figure 6e shows the results of the inference accuracy loss due to the injected errors from the resistance variation. The loss is calculated by subtracting the inference accuracy with the injected errors from the ideal accuracy. With a vector larger than 5000 bits, the accuracy loss is below one percentage point. As can be seen, the error resilience improves with larger vectors as expected from other HDC works.

Discussion

In this paper, we presented a cryogenic TCAM architecture leveraging the unique properties of FeSQUID technology. The proposed TCAM addresses key challenges faced by current cryogenic computing systems, such as the need for ultra-low power consumption, high-speed operation, and scalability. By combining the non-volatility of ferroelectric materials with the superconducting efficiency of SQUIDs, our design achieves substantial energy savings, with an average energy consumption of 1.36 aJ and 26.5 aJ for 1-bit binary and ternary searches, respectively. In addition to supporting exact match search operations, our TCAM enables Hamming distance (HD) calculation, which opens up new possibilities in error detection and correction, quantum error correction decoding, approximate search algorithms, and AI-based classification tasks. We demonstrate the advantages of FeSQUID-based TCAM array by benchmarking against TCAM with 5 nm FinFET-based cryogenic SRAM array for HDC-based language recognition task. The proposed FeSQUID-based TCAM needs over one order of magnitude lower energy. The parallel search capability and efficient data processing of this energy-efficient TCAM make it highly applicable to a range of cryogenic applications, including large-scale quantum computing, high-performance computing, space exploration, and data-intensive tasks in data centers.

In addition to demonstrating the functionality of the FeSQUID-based TCAM, we recognize the importance of addressing process integration challenges for practical implementation. While ferroelectric materials typically require high-temperature annealing during fabrication, recent advances in low-temperature deposition techniques—such as plasma-enhanced atomic layer deposition—enable their integration within a BEOL-compatible thermal budget. This mitigates potential damage to superconducting layers. Notably, several ferroelectric materials, including PZT35, perovskite oxides36, and antiferroelectric zirconia37,38, have been shown to retain stable polarization and functional properties at cryogenic temperatures down to 50 mK. Moreover, ferroelectric materials have been experimentally integrated with superconducting materials and devices14. Nevertheless, to minimize risks of electrostatic interference—such as unintended modulation of the superconducting energy gap due to ferroelectric polarization, grounded shielding layers, cryogenic trench isolation, and optimized physical layouts can be used. These strategies support the monolithic integration of voltage-controlled FeSQUIDs with superconducting hTrons, enabling scalable, non-volatile, and energy-efficient TCAM architectures suitable for cryogenic computing environments.

Methods

Device modeling and TCAM simulation

To perform the simulation of the proposed TCAM, we utilize Verilog-A-based compact models for FeSQUID and hTron from our previous works. Please refer to9,20, and25 for more details on the modeling methodologies and validation of FeSQUID and hTron, respectively.

To model the voltage-controlled switching of ferroelectric polarization, we use the Preisach model, which is calibrated with the experimental data reported in ref. 14. Then, we use equations (1) and (2) to model the effects of ferroelectric polarization on the superconducting energy gap and critical current of SQUID. Finally, we utilize the resistively and capacitively shunted junction (RCSJ) model to implement the current-voltage characteristics of SQUID, depending on the two polarization states of the ferroelectric material.

For hTrons, we use a phenomenological Verilog-A model, which, at every timestep, compares the applied gate current and channel current with the switching thresholds. Based on the comparison, the model determines whether the channel will remain superconducting or switch to its resistive state. The switching thresholds and other device parameters were taken from the experimental data, reported in ref. 25.

Using these two models, we developed a HSPICE framework to simulate and verify the TCAM design. The results mentioned in Figs. 4 and 5 are obtained using this simulation framework.

System-level simulation

The implementation of the HDC algorithm for language recognition and SRAM-based TCAM blocks is from a previous work34. This allows us to change various parameters such as vector dimension, block size, or supply voltage. The employed supply voltage for the SRAM circuit simulations is 0.7 V. To simulate the transistor at these low temperatures accurately, we have employed a custom cryogenic compact model based on BSIM-CMG. The respective model cards for NMOS and PMOS have been carefully calibrated to reproduce cryogenic measurements of mature 5 nm FinFET technology39.