Introduction

Structure-based drug discovery has traditionally relied on virtual docking, but the advent of machine learning has dramatically transformed the field1,2,3. A breakthrough came with the development of denoising diffusion-based generative models4, leading to highly effective tools such as RoseTTAFold All-Atom5 and Alphafold3 (AF3)6. These co-folding tools can model protein-ligand interactions across a broad and unrestricted range of ligand types. Since then, several other similar tools have emerged, showing docking performances comparable to those of their precursors7,8,9,10.

Historically, molecular docking and ligand-based drug design have relied on physics-based methods grounded in energy force fields and the energetic optimization of protein-ligand interactions11. Early machine-learning approaches were also built on these physical principles12,13. In contrast, modern machine-learning methods–particularly generative co-folding models–operate far more autonomously, enabling the generation of protein-ligand complexes de novo5,6,7. Trained on large structural datasets, these models are expected to internalize the fundamental patterns that govern molecular structure, recognition, and binding.

A central challenge, however, is that machine-learning-based docking predictions typically produce an interacting pose for any ligand, regardless of whether it is a true binder or an inactive compound. Although many models provide scoring metrics to help rank predicted complexes, accurately inferring binding affinities remains difficult. This leads to two fundamental questions: (i) How can we distinguish genuine binding interactions from false positives? (ii) How can predicted poses be ranked in a way that reflects their expected binding affinities? These questions form the core motivation of this study.

Our goal was to better exploit the capabilities of modern deep-learning methods—such as AF36 and Boltz-1/27,10—by applying them to well-characterized drug targets. We show that these diffusion-based methods can accurately recapitulate known binding poses and, with suitable criteria, can differentiate true interactions from artifacts. To this end, we introduce a competitive docking-based scoring strategy that enables the ranking of inhibitors targeting a specific binding site. We further demonstrate how this competitive framework can be extended to virtual screening and de novo drug design.

Results

Overview

The first part of the results evaluated how diffusion-based co-folding models differentiate true inhibitors from inactive compounds, using a dataset of 16 protein targets in addition to the more complex multi-site DNA gyrase. The second part explores the use of diffusion-based tools for ranking inhibitors, introducing a competitive docking strategy applied to all targets. Finally, we present two applications of this competitive docking approach to DNA gyrase: an All-at-Once virtual screening method for hit identification and a strategy for designing de novo inhibitors with improved predicted potency.

Pose convergence can help identify real inhibitors

We used 16 protein targets with diverse biological functions as benchmarks to assess whether denoising diffusion-based models can distinguish true binders from false positives. After reviewing the reference crystal structures for these benchmark proteins (Table S1), we predicted binding poses for several inhibitors lacking experimental structures. Additionally, we included 28 unrelated “off-target” compounds for each benchmark (Table S2). For a given protein target, the off-target set consisted of one inhibitor from each of the other targets in the study, along with compounds that typically bind to proteins entirely unrelated to those analyzed here.

We assessed docking specificity using two criteria: (i) how closely ligands remained within the binding site across predicted models, and (ii) how consistent their poses were with each other (pose convergence), measured by the average RMSD. Overall, true inhibitors bound within approximately 5 Å of the binding pocket and exhibited strong convergence, typically below 2 Å (Fig. 1). In contrast, off-target molecules were positioned further away and showed much greater variation. Notably, across the 16 benchmarks, the pose convergence metric generally outperformed the Bolt-2 binding-likelihood prediction (Fig. 1A, B; Table S3).

Fig. 1: Docking specificity of AF3 across sixteen protein benchmarks.
figure 1

A Pose metric performance: Percentage of true ligands (“on-target” molecules) and false ligands (“off-target’ molecules) with pose convergence < 2.0 Å and distance from the reference binding site < 5.0 Å for each target. B Boltz-2 binding likelihood prediction: Percentage of ligand with predicted binding likelihood > 0.5 for both on-target and off-target ligands across 14 targets. C–J Scatter plots: Ligand pose convergence (RMSD) versus binding site distance for true on-target inhibitors (blue) and unrelated off-target compounds (gray), shown for ten representative targets: kinase CDK2 (C), protease thrombin (D), hydrolase PDE2 (E), kinesin KIF11/EG5 (F), phosphatase PTN11 (G), oxidoreductase DHFR (H), BCL2-like protein MCL1 (I), GPCR HCAR3 (J), lectin GAL3 (K), and PAS-domain EPAS1 (L). Scatter plots on the six remaining targets are provided in Fig. S1.

Full size image

Specificity was especially strong for the kinases CDK2 and TYK2, the PAS-domain EPAS1, the hydrolase PDE2, the phosphatases PTP1B and PTN11, the oxidoreductase DHFR, the lectin GAL3, and the BCL-2-like protein MCL1. In contrast, the weakest specificity was observed for the GPCRs FFA2R and HCAR3, as well as the hydrolase BACE1, and to a lesser extent for the oxidoreductase COX-1, where some off-target molecules were still positioned near the binding site and exhibited low RMSD values. Similar trends were observed with the Boltz-2 model (Fig. S2).

Docking specificity in a molecular system with multiple binding sites

We next asked whether AI-based docking can also help identify the true binding site of a ligand in proteins that have multiple binding pockets. To address this, we selected Mycobacterium tuberculosis (Mtb) DNA gyrase as a model system, given its complex binding landscape and extensive characterization14,15. DNA gyrase contains several inhibitory sites that are targeted by chemically diverse compounds, making it an excellent case study for evaluating the potential of machine learning in drug discovery.

Fluoroquinolones (FQs) are the main class of inhibitors for this enzyme16,17,18, but inhibition can also be achieved by non-FQ compounds19,20, including novel bacterial type IIA topoisomerase inhibitors (NBTIs)21,22,23 and thiophene-based molecules24 (here referred as DNA gyrase allosteric inhibitors).

After validating the available crystal structures (Table S1), we predicted binding poses for several FQs lacking experimental structures, as well as a set of non-FQ compounds. These included ligands that bind DNA gyrase at sites distinct from the FQ pocket, inhibitors of benchmarks, and anti-tuberculous agents known to act on entirely different protein targets (Table S2).

On average, FQs clustered close to their known binding site, with a mean distance of less than 2 Å in models generated (Fig. 2B; Table S3). A similar pattern was observed for non-FQ inhibitors, such as those in the spiropyrimidinetrione class, represented by QPT-1 (QPT) and zoliflodacin (ZLF) (Fig. 2D). These compounds also function through the FQ mechanism by binding at FQ site19,20. NBTIs were consistently positioned within 2 Å of their known binding site, located approximately 10 Å from the FQ site and between the two scissile DNA bonds23,25 (Fig. 2B, E). This result was observed using both AF3 and Boltz-1, but not Boltz-2 (Table S3).

Fig. 2: Docking specificity on Mtb DNA gyrase.
figure 2

A Molecular system: Left panel shows the full DNA gyrase system used for calculation; right panel provides a close-up of the binding site region. The three known binding sites are highlighted: FQ site (green), non-catalytic (NC) site (blue), and allosteric site (pink). The gyrase is displayed as a gray molecular surface and DNA is shown in orange. B AF3 clustering: AF3 successfully separates FQs (green), NC-site binders or NBTIs (blue), and allosteric inhibitors (pink) from unrelated compounds (orange and gray) based on pose convergence and proximity to the FQ site. Similar results were obtained with Boltz-1 (Table S3). C Boltz-2 clustering: In contrast, Boltz-2 fails to achieve this separation, clustering all binders near the FQ site. D-F Docking poses generated by AF3: Close-up views for FQs (D), NBTIs (E), and allosteric inhibitors (F). D–F also presents a chart comparing AF3 pose convergence—defined as the percentage of true inhibitors and other ligands with pose convergence < 2.0 Å and a distance from the reference binding site < 5.0 Å—with Boltz-2 binding likelihood predictions, expressed as the percentage of inhibitors with a predicted binding likelihood > 0.5. A selected set of docked compounds is shown, including zoliflodacin (ZLF), trovafloxacin (TVF), AMK32b (ID8), gepotidacin (GPT), and thiophene 1 inhibitor (TH1). Each 3D image shows five representative AF3-predicted docking poses (i.e., the highest ipTM-scoring model for each seed) alongside the center of-mass of the reference FQ, MFX (gray sphere), superimposed on the reference crystal structure (PDB ID: 5BS8). Carbon atoms are color-coded as in (B), while oxygen and nitrogen atoms are shown in red and dark blue, respectively. The Mg2+ ions are represented as green spheres, the protein as a gray ribbon, and the DNA as an orange phosphate backbone with green–blue base sticks. Both the protein and DNA are shown in transparency. Protein visualizations were generated using PyMOL (The PyMOL Molecular Graphics System, Version 3.0, Schrödinger, LLC).

Full size image

In contrast, regardless of the co-folding model used, thiophene-class allosteric inhibitors were rarely docked at their expected binding site, located approximately 30 Å from the FQ site (Fig. 2F)24. Instead, many of these inhibitors were mislocalized to the FQ or NC sites rather than their true allosteric site (Table S3). When docking was performed in the presence of gepotidacin (GPT) and sparfloxacin (SPF)—used to block the NC and FQ sites, respectively—the allosteric inhibitors remained confined to their correct binding site (Fig. 2F). Notably, poor prediction of allosteric binding site in the absence of occupied primary sites has recently been demonstrated using a dataset of 20 orthosteric/allosteric ligand pairs targeting 17 proteins26.

Finally, although off-target compounds and gyrase ATPase inhibitors adopted plausible binding poses according PoseBusters27 (Table S3), they were, on average, more distant from all three key binding sites of the molecular system under study (Fig. 2D).

Thus, the two criteria, pose convergence and proximity from the FQ site, effectively distinguished the three classes of gyrase inhibitors when using AF3 and Boltz-1 diffusion models. The clustering pattern clearly separated FQs, NBTIs, and allosteric inhibitors—for these latter inhibitors, particularly when the other two binding sites were already occupied by their respective ligands—from unrelated compounds, which were more broadly dispersed across the clusters (Fig. 2).

Competitive docking scoring and pairwise matrix

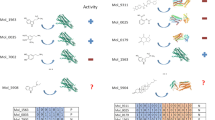
As shown in the previous section, diffusion-based co-folding models generate docking poses for any tested compounds, including those that do not specifically bind to the target protein. In the case of DNA gyrase, when two FQ molecules were docked simultaneously, only one occupied the catalytic FQ site, while the second often stacked against the DNA at the second catalytic site, which is only partially represented in the docking model used here. Furthermore, we previously showed that accurate docking of allosteric inhibitors on DNA gyrase can be achieved when both an FQ and an NBTI are included during docking inference (Fig. 2F). Building on these observations, we implemented a pairwise competitive docking approach to produce a scoring matrix, ranking compounds using a Competitive Docking Score (CDS) (Fig. 3).

Fig. 3: Roadmap of pairwise competitive docking method.
figure 3

Diffusion-based co-folding predictions were performed using a protein model bound to two competing ligands. The ligand that successfully occupies the active site was considered the winner of each competitive docking run. A Competitive Docking Score (CDS) was calculated from at least n independent runs per ligand pair. These scores were compiled into a pairwise matrix to rank ligands based on their cumulative CDS. Expressed as a percentage, the final CDS reflects the win rate across all pairwise docking runs. Protein visualizations were generated using PyMOL (The PyMOL Molecular Graphics System, Version 3.0, Schrödinger, LLC).

Full size image

Competitive docking score correlation with inhibitor affinity

To assess the relevance of CDS rankings, we applied the method to benchmark proteins (Table S4) and compared the results with experimental affinity data reported in the literature28,29,30,31,32 or obtained from the Binding Database33 (Fig. 4).

Fig. 4: Correlation between competitive docking scores and experimental inhibitory activities across studied binding sites.
figure 4

A Rank concordance c-index between experimental inhibitory affinity and computed affinity or ranking, for AF3 pairwise docking strategy method (blue) and Boltz-2 binding affinity prediction (gray). Seventeen targets, containing nineteen binding sites were evaluated, with performance summarized by the rank concordance c-index. B–M Scatter plots show the relationship between the Competitive Docking Score (CDS) using AF3 and experimental pIC50 values for several systems studied. Each plot reports the Pearson correlation coefficient (r). An ordinary least squares regression line is added to illustrate the trend.

Full size image

Using AF3, the rank concordance index (c-index)—a metric particularly relevant to this study, where correctly ordering compounds is more important than predicting their exact inhibitory values—showed strong agreement between CDS rankings and experimental affinities across many targets. Very strong and highly significance correlations were observed for lectin GAL3 (c = 0.89), kinase TYK2 (c = 0.87), protease thrombin (c = 0.86), kinase CDK2 (c = 0.78), GPCR HCAR3 (c = 0.77), kinesin KIF11 (c = 0.76), the DNA gyrase allosteric site (c = 0.76), phosphatases PTN11 and PTP1B (c = 0.75 and 0.74, respectively), and the DNA gyrase FQ site (c = 0.72). Strong correlations were obtained for GPCR FFA2R, PAS-domain EPAS1, BCL-2-like protein MCL1, hydrolase PDE2, and oxidoreductase DHFR (c = 0.66, 0.67, 0.68, 0.67, and 0.68, respectively). Moderate correlations were found for the DNA gyrase NC site (c = 0.62), hydrolase BACE1 (c = 0.62), and oxidoreductase COX-2 (c = 0.67), while COX-1 showed a weak correlation (c = 0.52) (Fig. S3; Table S4).

Importantly, the two systems with the weakest correlations (COX-1 and COX-2) also exhibited low docking pose convergence (Figs. 1 and 2), suggesting that even without competitive docking, inhibitors in these systems could not be reliably docked into the correct binding site.

It could be noted that pairwise competitive docking performed with Boltz-1/2 instead of AF3 generally produced weaker correlations with experimental IC50 values (Table S4), with no significant correlation observed for COX-1, COX-2, PDE2, PTP1B, and TYK2 systems.

We also found that the CDS rankings for COX-1 and COX-2 inhibitors were nearly identical (Pearson r = 0.96), indicating that AF3 could not reliably distinguish between the two cyclooxygenase isoenzymes (Table S5). This limitation is likely due to the high degree of conservation between their binding sites (Fig. S5). To further examine this issue, we tested four major DNA gyrase variants known to confer resistance to FQs by increasing IC50 or MIC values by several-fold30,34. In these cases, docking pose specificity remained largely unchanged, with only minor differences detected (Fig. S6). Similarly, the ranking of FQs using the pairwise competitive docking approach showed only minor shifts compared to the wild-type results (Fig. S6). These findings suggest that substituting one or two amino acids in the catalytic site is insufficient to significantly alter AF3’s binding predictions. This observation is consistent with recently published results showing that co-folding methods are unable to account for intentional perturbations in ligand-protein interaction modeling35.

Competitive docking approach vs. direct AI-based affinity prediction

Boltz-2 includes a machine-learning module for predicting protein-ligand affinity. We compared the performance of this tool with our competitive docking approach by assessing their correlations with experimental data (Fig. 4A). Overall, both methods demonstrated comparable performance across the 19 tested systems, with only minor differences. For instance, Boltz-2 performed slightly better for the BACE1, DHFR, EPAS1, FFA2R, PTP1B, and PDE2 systems, whereas competitive docking showed a slight advantage for the DNA gyrase allosteric site, CDK2, GAL3, HCAR3, PTN11, TYK2, and COX-2 systems.

DNA gyrase as a case study for evaluating CDS rankings

Using DNA-gyrase as a model, the CDS-based ranking method also demonstrates its ability to cluster inhibitors according to their inhibition rank. This capability was observed across all three protein sites. Specifically, ligands with higher CDS values generally corresponded to more potent inhibitors, while those with lower CDS values were typically weaker (Fig. 5A–C and S6; Tables S6–S8).

Fig. 5: Distribution of DNA gyrase inhibitors across IC50 threshold categories, stratified by CDS ranking using AF3.
figure 5

A 21 FQs on Mtb DNA-gyrase, B allosteric inhibitors, C NBTIs, and D 20 FQs on E. coli DNA gyrase. The bar charts show the percentage of inhibitors within each IC50 threshold category, based on their CDS ranking. IC50 thresholds are provided in Table S4. “n” indicates the number of inhibitors in each CDS category.

Full size image

Because DNA gyrase is the primary FQ target in Escherichia coli36, we also measured IC50 values for the inhibition of E. coli growth by 22 FQs and compared them to their CDS rankings (Table S4 and Fig. S7A). Although the overall correlation was modest, a clear trend emerged: FQs with lower IC50 values generally ranked higher in the CDS list (Fig. S7B). Notably, since FQs are known to have limited aqueous solubility37, excluding two FQs predicted to be poorly soluble significantly improved the correlation (Fig. 5D). Importantly, CDS rankings could not be further refined by considering the secondary FQ target in E. coli, as the rankings generated using E. coli topoisomerase IV were nearly identical to those based on DNA gyrase (r = 0.99) (Figs. S7D, E).

All-at-Once docking strategy

To simplify the analysis and reduce computational cost, we evaluated AF3 docking performance by processing entire inhibitor classes in a single run, rather than relying on pairwise competitions. Using DNA gyrase as a model system, we tested three sets of inhibitors with AF3: 21 FQs, 24 NBTIs, and 12 allosteric inhibitors. For the allosteric set, docking was performed in the presence of GPT and SPF to block the other two competing binding sites.

Overall, the All-at-Once strategy yielded less detailed results compared to the pairwise competitive approach (Table S9). While some of the top-ranked compounds based on CDS values showed strong occupancy within the target binding site, several potent inhibitors were not identified among the leading competitors. Moreover, the number of distinct compounds effectively occupying the binding site was too limited for a reliable comparative analysis.

The All-at-Once strategy appears to be effective at identifying strong FQs from weaker FQs and non-FQ compounds. To evaluate its performance in a virtual screening context, we tested it on a compound library of 3155 FDA-approved molecules, including 46 FQs, representing 1.5% of the total library. The library was randomly divided into 124 sets containing 25–26 compounds each, and All-at-Once docking was performed using AF3 (Fig. 6A).

Fig. 6: Roadmap and results for the All-at-Once strategy applied for finding effective FQ molecules in a screening database.
figure 6

A Roadmap of the virtual screening performed on a library of 3155 compounds, including 46 FQs. B Percentage of FQs identified at different levels of the top-ranked compound list. Protein visualizations were generated using PyMOL (The PyMOL Molecular Graphics System, Version 3.0, Schrödinger, LLC).

Full size image

This screening identified 147 top-ranking compounds, including 38 FQs, corresponding to a 25.9% enrichment. The eight FQs not selected as winners are known to have low inhibitory activity against Mtb DNA gyrase37 and mostly belong to the first-generation FQs (Table S10). Applying an additional filter based on pose convergence (cutoff of 2.5 Å) and proximity to the FQ binding site (cutoff of 2.0 Å), as described in Fig. 2, increased FQ enrichment to 77.8% among the 45 remaining compounds. Tightening these thresholds to 1.0 Å further boosted enrichment to 93.5%, with an enrichment factor of 62. These results closely matched the performance obtained with Boltz-2 for hit identification across the 3155-compound library (Fig. 6B).

Applying competitive docking to design more potent FQs

Given that competitive docking can assist in identifying the most effective compounds for a specific target, we investigated how this approach could be employed to design more potent FQs. As proof of concept, and without exhaustive exploration, we selected a set of 414 compounds from several thousand automatically generated using the STONED algorithm38. This selection focused on the chemical space surrounding the five top-ranked FQs identified by AF3 (Table S10). Each de novo compound was then evaluated in competitive docking against STF, the highest-ranked FQ, using the Mtb DNA gyrase model system.

Thirty-one of these newly designed compounds occupied the FQ binding site in at least 70% of the 100 generated models, suggesting a stronger binding potential than STF. Their Tanimoto structural similarity to STF ranged from 0.25 to 0.88 (Fig. S8). Since none of these compounds are listed in the CAS chemical database—indicating they have likely never been synthesized—we further filtered them based on predicted ADME properties. Ultimately, only eight de novo compounds exhibited favorable drug-likeness characteristics, solubility, and chemical synthetic accessibility.

Discussion

Artificial intelligence is rapidly reshaping in silico molecular docking workflows39,40. Machine learning tools based on diffusion models have demonstrated remarkable accuracy in predicting protein-ligand interactions, often outperforming traditional docking programs5,6,7,8,9,10. In this study, we implemented a straightforward pairwise competitive docking approach to rank inhibitors of fifteen different systems, and seventeen total binding sites, using three pre-trained denoising diffusion-based models (Fig. 3).

Importantly, the effectiveness of our competitive docking approach depends on how the used deep learning models adhere to fundamental physical principles—particularly in managing atomic clashes within the generated structures. As AF3 includes a clash penalty in its model ranking, such failures are less frequent in AF3-generated models compared to those produced by Boltz-1 or Boltz-2. The steering versions of both latter models effectively removed atom clashes in the generated models, but without significant improvement in competitive docking performance (Table S4). Hence, overall, AF3-based competitive docking outperformed the steering Boltz models across the studied cases (Fig. S1). Other diffusion-based models, such as RoseTTAFold All-Atoms4, Chai8, or Protenix9, or NeuralPlexer41 should be evaluated to assess their potential in competitive docking scenarios.

Across the analyzed binding sites, the competitive docking approach performed comparably to the recently introduced affinity prediction module in Boltz-2, both in hit-to-lead inhibitor ranking (Fig. 4A) and in screening for hit identification (Fig. 6B). A more robust comparison will require evaluation across additional systems. Notably, in cases where both methods performed poorly—such as the DNA gyrase NC site, COX-1, and COX-2—the competitive docking approach still outperformed Boltz-2. These results highlight competitive docking as a valuable alternative when direct AI-based affinity predictors fail or when addressing particularly challenging systems.

The system-dependent performance of our approach highlights an important limitation of current AI-based co-folding methods: they are not universally reliable across all targets. For example, predictions of fold-switching structures are driven largely by structural memorization rather than by the underlying physics of protein folding42,43. More relevant to our work, protein-ligand predictions generated by state-of-the-art co-folding models are also strongly influenced by pose memorization from the training data44. As a result, co-folding-based docking is expected to perform poorly for ligands or binding sites that were not represented in the models’ training set.

To examine this limitation more directly, we evaluated two GCPR systems whose cryo-EM structures in ligand-bound forms were solved recently: GPER1 and SLC6A3. For both targets, correlations between our pairwise competitive docking results and experimental data were weak, whereas Boltz-2 IC50-based affinity predictions performed better, with concordance indices of 0.6–0.7 (Table S4). These findings indicate that additional case studies are needed to fully how strongly our method–and co-folding approaches in general–depend on the presence of similar ligands or binding environments in the models’ training data. Nevertheless, this limitation may diminish over time as training datasets expand44. Continuous incorporation of newly determined protein-ligand structures will improve reverse diffusion-based models overall and, in turn, enhance the reliability of our competitive docking strategy.

Our scoring procedure, based on competitive docking within an identified binding site, offers a simple and interpretable alternative to more complex tools that depend on external scoring functions45. Although the concept of competitive docking is not entirely new, previous applications have typically focused either on placing multiple ligands side by side within large binding pockets46 or on fragment-based drug design47,48. To the best of our knowledge, using a machine learning-based tool to simulate virtual competition between ligands for the same binding site is a novel strategy. Furthermore, our method provides a streamlined and accessible implementation leveraging machine learning models, with the introduction of novel evaluation criteria based on binding site occupancy. These criteria can be adapted to the specific system under investigation, and we plan to explore this flexibility further in future studies.

However, our competitive docking approach also presents several limitations. Because deep learning-based co-folding models are prone to non-physical artefacts–such as steric clashes, stretched bonds, and chirality violations27,35–the method tends to fail when applied to large or complex ligand molecules. For example, two additional systems we tested, HIV-2 protease (HIV2P) and tankyrase 2 (TNKS2), could not be reliably evaluated due to extensive clashes between the large competing inhibitors (Table S4). Ligand-ligand interactions, rather than ligand-protein interactions, can also pose challenges in competitive docking—particularly in systems with large binding pockets that can accommodate both competing molecules, or in multi-site systems such as the one examined here with DNA gyrase. Computational cost is another constraint, as constructing a full pairwise competitive matrix scales quadratically with the number of ligands. Moreover, the performance of our method appears to depend not only on ligand properties but also on the molecular system itself, consistent with the system-dependent behavior observed throughout our benchmarks.

Given these limitations, it is evident that our current implementation is not broadly generalizable–much like co-folding methods themselves, which are also unlikely to be universally applicable35,44. Its use should therefore be evaluated on a case-by-case basis, taking into account the specific protein system, the class of inhibitor, and the overall molecular size and complexity. Nevertheless, our results demonstrate that, for certain targets, pairwise competitive docking constitutes a complementary and effective strategy for ranking inhibitors. In this way, it expands the computational toolbox available to researchers and medicinal chemists.

We also explored a multi-ligand competition strategy–referred to as All-at-Once–to identify top binders from a mixed set of weak and non-binding compounds. When applied to a library of 3115 compounds, this approach effectively selected strong FQs, while weaker ones were outcompeted during docking (Fig. 6A). Final enrichment of FQs reached 93.5% after applying a filter based on docking accuracy derived from non-competitive predictions. The All at-once strategy offers substantial time savings compared to relying solely on non-competitive docking. Rather than evaluating all 3115 compounds individually, only the 147 candidates selected by the All-at-Once approach needed further analysis for docking accuracy. This efficiency gain becomes even more significant when applying the two-step process to larger compound libraries. Finally, as proof of concept, we applied our pairwise competitive docking method to design improved inhibitors targeting the FQ binding site. Several de novo compounds were selected with eight predicted to have favorable drug-like properties, including ADME profiles, solubility, and synthetic accessibility. These chemically novel candidates merit synthesis and experimental validation in future studies.

In conclusion, we applied three co-folding methods—AF3 and Boltz-1/2—to 17 protein benchmark systems comprising several hundred ligands. First, we showed that ligand pose convergence, measured by RMSD, is a reliable metric for distinguishing true inhibitors from off-target or inactive molecules. Second, our newly developed pairwise competitive docking strategy produced inhibitor rankings that closely reflected experimental inhibition data. The performance of our approach was broadly consistent with Boltz-2’s machine-learning-based affinity predictions, indicating that competitive docking offers a practical alternative for inhibitor prioritization. As with Boltz-2, however, performance remained strongly system-dependent, with concordance indices ranging from 0.5 to 0.9. Therefore, the applicability of the method should be evaluated on a case-by-case basis, considering both the molecular system and the ligand class under study.

Improvements in co-folding models—particularly their ability to generate structures that better conform to fundamental physical principles and avoid steric clashes, along with continued expansion of their training datasets—will likely increase the number of systems for which competitive docking is effective. Finally, we showed that simultaneous docking competition among diverse compounds can robustly identify the strongest binders, providing a promising strategy for virtual screening and hit discovery. Together, these findings open new opportunities for the design of potent inhibitors across a wide range of protein targets.

Methods

Roadmap of the methods

This section begins by listing the biological systems and molecular compounds analyzed in this study. We then describe the metrics used to evaluate ligand poses. Next, we present the pairwise competitive docking approach, illustrated in Fig. 3, followed by the All-at-Once strategy shown in Fig. 6. Finally, we detail the statistical metrics used to assess the correlation between predicted rankings and experimental data.

Biological systems investigated

This study primarily examines the interactions between fifteen proteins and various compounds. The protein systems include two kinases (TYK2, CDK2), two hydrolases (BACE1, PDE2), two phosphatases (PTP1B, PTN11), three oxidoreductases (COX-1, COX-2, DHFR), a PAS-domain (EPAS1), one protease (THROM), a kinesin (KIF11/EG5), a BCL-2-like protein (MCL1), two GPCRs (FFA2R, HACR3), a lectin (GAL3), and the bacterial DNA gyrase. For each system, a crystal reference structure was selected and listed in Table S1.

In ligand-protein inferences using co-folding methods, the protein sequences were derived from the corresponding reference structure of each target. Each protein target was generally examined in its monomeric form. For the COX model system, we included a protoporphyrin IX moiety with a cobalt cation, based on the crystal structure of COX-2 bound to mefenamic acid (MFN) (PDB ID: 5IKR49).

For a more complex test case involving multiple binding sites, we selected bacterial DNA gyrase because of its extensive characterization and the wealth of available literature14,15. To optimize computational efficiency, the system was simplified to include: (i) the N-terminal catalytic core of GyrA (~500 residues); (ii) the C-terminal TOPRIM domain of GyrB (~250 residues); (iii) a 95-residue GyrA fragment completing the active site with the catalytic residue Y129, which forms a transient O-(5’-phospho-DNA)-tyrosine covalent intermediate50; (iv) a 24-mer double-stranded DNA molecule; and (v) two Mg2+ cations.

The DNA sequences were derived from the crystal structure of the Mtb DNA gyrase/DNA complex bound to MFX (PDB ID: 5BS851). Additionally, four major Mtb GyrA variants associated with FQ resistance were incorporated into the docking predictions: G88A, A90V, D94G, and the double mutant A90V + D94G28,34. DNA gyrase and Topoisomerase IV (Topo IV) from Escherichia coli and Staphylococcus aureus were considered using the same double-stranded DNA sequence, corresponding protein fragments, and Mg2+ ions as in the Mtb gyrase model.

Finally, to test the limitations of our pairwise competitive docking method, we added two recently solved GPCRs (GPER1 and SLC6A3) to examine potential memorization issues. Additionally, to assess challenges related to ligand complexity, we included HIV-2 protease (HIV2P) and tankyrase 2 (TNKS2) in the benchmark dataset.

Molecular compounds investigated

A total of 460 compounds were examined, spanning a diverse set of inhibitors across all benchmark targets. These molecules were sourced either from the literature or from BindingDB33. To assess docking specificity, an off-target compound set was included for each protein. For a given target, this off-target set comprised one inhibitor from each of the other targets in the study, as well as six compounds known to bind proteins unrelated to those analyzed here. The SMILES representations and compound names for all molecules investigated are provided in Table S2. These compounds were used in their protonated forms at pH 7.0 predicted with MarvinSketch.

In addition, a library of 3155 compounds was used for in silico screening. This library comprises FDA-approved and pharmacopeia drugs from the commercial collection offered by TargetMol Chemicals Inc. (Massachusetts, USA, Catalog No. L1010). Twenty-two FQs, along with the two negative-control compounds, were purchased from TargetMol Chemicals for experimental IC50 testing against E. coli.

Finally, de novo compounds were generated by exploring the chemical space surrounding the five top-ranked FQs using the STONED algorithm38. For each of the five FQs, 1000 molecules were randomly generated and then filtered using a Tanimoto similarity cutoff of 0.75. This resulted in a total of 420 selected compounds: 75, 70, 80, 107, and 88 for STF, SPF, FRX, TMF, and MFX, respectively. These compounds—each with a Tanimoto coefficient ≥0.75, indicating close structural similarity to the top FQs—were retained for further investigation in this study.

The ADME properties of these compounds were predicted using the SwissADME web server52. The SMILES representations and structural similarity of the de novo compounds to the 5 top-ranked FQs are provided in Table S12. Structural similarity was evaluated using the Tanimoto coefficient calculated from ECFP4 fingerprints generated with RDKit (https://www.rdkit.org).

Machine learning calculations

Boltz-1 and Boltz-2 were installed locally from its official GitHub repository (https://github.com/jwohlwend/bolt). The steered versions of both programs, i.e., that apply physics-based potentials to enhance the physical plausibility of the structures, were also considered10. The AF3 source code was retrieved from GitHub on November 14, 2024 (https://github.com/google-deepmind/alphafold3), and model parameters were obtained directly from Google. Public sequence and structure databases were downloaded from AlphaFold’s storage. Computational resources included: GPU-based model inference using NVIDIA RTX 4080 (16GB), RTX 3090 (24GB) or A40 (48GB), and CPU-based sequence and template searches using an 11th Gen Intel 8-core CPU with 128 GB RAM.

To optimize computational time, multiple sequence alignments were pre-generated for each molecular system, and non-protein components (DNA, ions, and compounds) were incorporated before model inference. At least five randomly selected seed numbers were used, generating a total of a minimum of 25 models per model inference.

Pose evaluation metrics

Docking performance was evaluated by superimposing predicted proteins onto reference crystal structure using PyMol (super command, aligning α-carbons), then ligand heavy-atom root-mean-square-deviation (RMSD) values between docked ligands were computed using DockRMSD53:

$$RMSD=\,\sqrt{\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{d}_{i}^{2}}\frac{}{}$$
(1)

where N is the number of heavy atoms in the ligand, and \({d}_{i}\) is the Euclidean distance in angstroms (Å) between the ith pair of corresponding atoms.

Four performance metrics were evaluated: (i) Accuracy (Å): the mean RMSD between predicted and experimental poses; (ii) Precision (Å): the convergence of docking results, quantified as the mean pairwise RMSD across generated models; (iii) PoseBusters27 quality score: the number of structural quality checks passed; (iv) Per-chain ipTM score: reported for the top-ranking prediction. The per chain interface predicted template modeling (ipTM) score measured the accuracy of the predicted relative positions of the two chains considered within the complex model. ipTM is on a 0–1 scale, with values higher than 0.8 representing high-quality predictions, while values below 0.6 suggest a failed prediction6.

Pairwise competitive docking

To rank compounds based on their binding affinity to a specific binding site, we employed a pairwise competitive docking approach. This method involves running docking predictions with two compounds simultaneously in a single inference step.

Following protein alignment with the reference structure, we measured the center of mass distances between each docked compound and the reference complex. The compound positioned closest to the reference ligand’s binding site was considered to adopt the correct binding pose and was designated as the winner for that site. A 5 Å cutoff was applied, meaning that if the winning compound’s distance exceeded this threshold, the competition was deemed inconclusive. Additionally, docking simulations where the two competing compounds exhibited steric clashes (defined as any interatomic distance below 1.54 Å) were also classified as inconclusive and excluded from further analysis (Fig. 3).

For each pairwise comparison, we typically generated 25 independent docking models using randomized seed values, evaluating outcomes across these 25 generated poses. The results were compiled into a pairwise competition matrix, which was then used to rank compounds based on their Competitive Docking Score (CDS) (Fig. 3). The CDS reflects the percentage of wins for each compound within the matrix.

E. coli growth inhibition screening

Experimental IC50 values were determined for 22 FQs to assess their correlation with the predicted pairwise competitive rankings. Escherichia coli strain ATCC 25922 was grown in LB broth at 37 °C with shaking until mid-log phase (OD₆₀₀ = 0.5–0.7), then diluted to a final assay OD₆₀₀ of 0.01. Test compounds from TargetMol Chemicals Inc. (MA, USA)—including 22 FQs and two negative-control drugs—were prepared as 10 mM or 1 mM stock solutions in DMSO or water, as appropriate. These were serially diluted in 384-well “mother” plates to 50× the final assay concentrations and transferred to assay plates containing either the bacterial inoculum or LB broth for control wells.

Final DMSO concentrations did not exceed 2% (v/v), which did not affect bacterial growth. Plates were incubated overnight at 37 °C in sealed, humidified containers. Growth inhibition was assessed by measuring OD₆₀₀ relative to untreated controls. IC50 values were determined using four-parameter nonlinear regression (GraphPad Prism v10.0) and are reported as mean ± standard deviation from at least three independent biological replicates.

All-at-Once calculations

In addition to pairwise competitions, we evaluated AF3’s docking performance when multiple compounds were processed simultaneously in a single inference run. In this All-at-Once approach, 100 structural models were generated per run. The compound most frequently observed within the FQ binding site was considered the “winner”, and a win rate was calculated for each input compound.

As in the pairwise competition, steric clashes were assessed using the same distance cutoff (1.54 Å). Docking attempts involving a clash were considered inconclusive and excluded from further analysis. Due to the high frequency of atomic overlaps in models generated by Boltz-1, the All-at-Once strategy was implemented exclusively using AF3.

For the virtual screening of the 3155-compound library, including 46 FQs, we randomly divided the dataset into 109 sets of 25 compounds and 15 sets of 26 compounds, yielding 124 All-at-Once runs. The choice of 25–26 compound subsets was dictated by GPU memory limitations. A win-rate cutoff of 30% was applied to identify top-performing competitive compounds for the FQ site. This threshold was selected under the assumption that the presence of four FQs in a single set was highly improbable (estimated probability: 0.04% based on the hypergeometric distribution), while the probability of three FQs occurring in the same set was approximately 0.5%.

Boltz-2x was also applied in virtual screening mode of Mtb DNA gyrase using the 3155-compound library, with compounds ranked according to the binding likelihood predicted by Boltz-2.

Statistical evaluation

The CDSs and rankings obtained were correlated with the experimental inhibition values. Correlations were assessed against available IC50 and MIC values. For DNA gyrase and Topo IV systems, IC50 represents the drug concentration required to inhibit DNA supercoiling by 50%. MIC values correspond to the drug concentration that reduces bacterial growth to 1% or less compared to the drug-free control culture. IC50 values for CDK2, COX-1, COX-2, PDE2, PTP1B, TYK2, and the DNA gyrase were obtained from the literature, whereas inhibitor data for the remaining targets were retrieved from BindingDB33.

To assess statistical correlations, we used three metrics: Pearson’s correlation coefficient (r), which measures the strength of a linear relationship between two numerical variables and is sensitive to the magnitude of differences, Spearman’s rank correlation (ρ), which evaluates monotonic trends based on rank order rather than actual values, and the concordance index (c-index or c), which quantifies the proportion of all comparable pairs for which predictions and experimental outcomes are ranked in the same direction. This latter metric is particularly relevant in our study, where the correct ranking of compounds is more important than accurately predicting their exact inhibitory values.

The c-index was defined using the following formula:

$$c-{\text{index}}=\frac{\#\,{rank}\,{concordant}\,{pairs}}{{total}\,{number}\,{of}\,{usable}\,{pairs}\,}$$
(2)
$$\,=\frac{\mathop{\sum }\limits_{i\ne j}{1}_{(\varDelta exp\left(i,j\right)\times \varDelta {pred}\left(i,j\right))} > 0}{N}$$
(3)

where i and j are the ranks of two observations, Δexp(i, j) represents the difference in experimental ranks, Δpred(i, j) represents the difference in predicted docking ranks, N is the total number of comparable pairs, and a pair (i, j) contributes a value of 1 if the product \(\varDelta exp\left(i,j\right)\) x\(\,\varDelta {pred}\left(i,j\right)\) > 0 (i.e., the predictions are concordant with the experimental outcomes), and 0 otherwise. A 95% confidence interval for the c-index was computed using the bootstrap method with 1000 resamples of the dataset with replacement.

The statistical significance of the r and ρ correlations was determined using a t-test, following the formula:

Pearson t-test:

$$t=r\sqrt{\frac{n-2}{1-{r}^{2}}\,}$$
(4)

where r is the Pearson’s correlation coefficient and n is the number of data points.

Spearman t-test:

$$t=\rho \sqrt{\frac{n-2}{1-{\rho }^{2}}\,}$$
(5)

where n is the number of data points and ρ is Spearman’s rank correlation.

The t-statistic follows a t-distribution with n-2 degrees of freedom, allowing us to calculate a two-tailed p-value.