Color restoration of mural images based on a reversible neural network: leveraging reversible residual networks for structure and texture preservation

Abstract

The Mogao Grottoes in Dunhuang, a treasure of China's and the world's cultural heritage, contains rich historical and cultural deposits and has left precious relics of the history of human art. Over centuries, the Mogao Caves have been affected by natural and human factors, resulting in irreversible fading and discoloration of many murals. In recent years, deep learning technology has shown great potential in the field of virtual mural color restoration. Therefore, this paper proposes a mural image color restoration method based on a reversible neural network. The method first employs an automatic reference selection module based on structural and texture similarity to choose suitable reference mural images for the faded murals. Then, it utilizes a reversible residual network to extract deep features of the mural images without information loss. Next, a channel refinement module is used to eliminate redundant information in the network channels. Finally, an unbiased color transfer module restores the color of the faded mural images. Compared to other image color restoration methods, the proposed method achieves superior color restoration effects while effectively preserving the original structure and texture details of the mural images. Compared to baseline methods, the Structural Similarity Index (SSIM), Feature Similarity Index (FSIM), and Perception-based Image Quality Evaluator (PIQE) values are improved by 7.97%, 3.46%, and 13.98%, respectively. The color restoration of the Dunhuang Mural holds significant historical, artistic, cultural, and economic values, and plays a positive role in the preservation and inheritance of Chinese culture, as well as in the promotion of cultural exchange and mutual understanding.

Introduction

Dunhuang murals are famous for their excellent artistic skills, exquisite paintings and rich themes. In early mural image color restoration efforts, restorers adhered to the principle of cultural relics preservation. They conducted spectral and chemical analyses of mural pigments and employed specific physical and chemical methods and materials to restore the murals' colors. This method necessitated restorers to possess extensive restoration experience and strong professional skills. However, any errors made during the restoration process could result in immeasurable damage to the murals, significantly increasing the complexity and difficulty of the restoration process.

Computer digital image processing methods often do not require direct contact with the mural surface, thus avoiding possible further damage to the mural. This non-invasive feature is crucial for preserving the original state of ancient murals. Therefore, actively utilizing digital image processing and artificial intelligence technology to research the protection, restoration and display of grotto murals is essential for safeguarding cultural heritage and promoting cultural dissemination. Pan et al. [1] utilized digital image processing techniques to simulate the color evolution of murals over thousands of years, laying the foundation for restoring the colors of mural images. Li et al. [2] obtained the color structure of murals through color clustering, determined the original pigments used for each color layer based on pigment domain knowledge, and restored each color layer according to the fading patterns of the pigments under different environmental conditions. The restored color layers were then merged into a single image to achieve color restoration of the murals. Wang et al. [3] cropped mural images and used a Cycle Generative Adversarial Network to learn the transformation between faded and restored mural textures. They extracted texture information from images of different resolutions and combined it to obtain high-resolution color-restored mural images. Xu et al. [4] enhanced the feature extraction and color restoration capabilities of their network for mural images by introducing the Efficient Channel Attention Network module and Deformable Convolution into the Cycle Generative Adversarial Network. Ren et al. [5] proposed a generative adversarial network comprising a parallel dual-convolution feature extraction deep generator and a ternary heterogeneous joint discriminator to restore mural images. Although certain achievements have been made in the digital color restoration of faded Dunhuang murals, the field of deep learning-based mural color restoration is still in its infancy, and the quality and accuracy of restored images need further improvement.

In this work, we propose a color restoration framework based on a reversible neural network, utilizing color transfer techniques to restore the color of faded mural images. Specifically, we select suitable reference mural images for the faded murals based on structural and texture similarity. We introduce a reversible residual network to extract deep feature information from the mural images, and then employ an unbiased color transfer module to transfer the color features from the reference images to the faded murals, thus restoring their colors. Experimental analysis demonstrates that our method can generate high-quality, reasonably color-restored mural images, while effectively preserving the clear content structure and detailed information of the restored images.

The subsequent sections of this paper are organized as follows: Section "Related work" reviews related work on color transfer and reversible networks. Section "The method" details the method proposed in this paper. Section "Experiment" presents the experimental results and discussions. Finally, Section "Conclusions" concludes the paper.

Related work

Color transfer

Color transfer aims to apply the color characteristics of a reference image to a target image, thus giving the target image the color appearance of the reference image. Gatys et al. [6, 7] first proposed using the Gram matrix to store the correlations of feature maps and treat it as the texture representation of an image. They utilized an iterative optimization method to gradually transfer textures, colors, and other style elements from the style image to the content image. Luan et al. [8] constrained style transfer to affine transformations in the local color space and used a regularization term calculated on the Matting Laplacian matrix to optimize the generated image to suppress distortions. However, these methods tend to disrupt the content structure of the original image while transferring color features. Li et al. [9] replaced the upsampling operations in the decoder with unpooling to reduce spatial information loss and suppress structural artifacts. Although this method is effective, it still fails to address the information loss caused by max pooling in the encoder. He et al. [10] performed color transfer by matching high-confidence image block features through nearest neighbor search and combining linear transformation, but this method struggles to accurately distinguish regions with similar local textures and low semantic information. Chiu et al. [11] proposed a PCA-based knowledge distillation model, achieving a balance between content preservation and stylization intensity while realizing realistic style transfer, though this method may produce local artifacts when handling high-frequency details of images. Wu et al. [12] combined a neighborhood adjustment mechanism with contrastive learning to maintain consistency between the generated image and the source image content. Cheng et al. [13] used enhanced image representations based on edge structures and depth maps to control style transfer while preserving the original structure and content details of stylized images. This method introduced a lightweight architecture, the Fire module, to reduce computational costs, but it struggled to extract complete image features. Ma et al. [14] addressed content leakage in stylized images from the perspective of image restoration by iteratively learning bi-directional multi-recovery between content and reference images, though this method still lost detail information due to multiple mutual conversions between image pairs.

Reversible network

Neural flow is a deep generative model that learns high-dimensional observations through a series of invertible transformations. These transformations preserve all information about the data and can accurately restore the data when needed. Dinh et al. [15] first proposed a neural flow framework called NICE, which models complex high-dimensional data distributions through highly nonlinear bijective transformations. In a subsequent study, Dinh et al. [16] introduced Real-valued Non-Volume Preserving transformations to further address the challenges of learning highly nonlinear models in continuous high-dimensional spaces. Kingma et al. [17] proposed a simple generative flow model based on reversible 1 × 1 convolutional networks, but this model requires storing a large number of parameters and intermediate states during training, resulting in high training costs. To address this issue, Gomez et al. [18] first proposed the reversible residual network to mitigate memory consumption in deep neural network training, although this model still contained irreversible components like max pooling and downsampling. Kitaev et al. [19] further applied reversible residual blocks to large Transformer models to improve their efficiency on long sequences. Jacobsen et al. [20] built on Gomez's work by introducing reversible downsampling operations to construct fully reversible networks. Behrmann et al. [21] treated residual networks as the Euler discretization of ordinary differential equations (ODEs) and demonstrated that simply changing the normalization scheme of standard residual networks can construct reversible residual networks. Ma et al. [22] achieved reversible mappings between input and output variables by imposing local connectivity constraints in small "mask" kernels, stacking multiple layers of convolutional flows, and using rotation-ordered masks. An et al. [23] used reversible neural flow models to address content leakage in the image color transfer process. However, due to feature redundancy, the images generated by this method may exhibit color artifacts.

The method

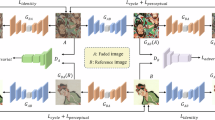
In this work, we adopt a reversible framework different from the traditional encoder-decoder architecture for mural image color restoration. Given a faded mural image, we first calculate the structural and texture similarity scores between the faded image and all reference images. We then select the reference mural image with the highest similarity as the final reference. After increasing the channel dimension of the input image pair using zero-padding, the image pair undergoes lossless deep feature extraction through the forward inference of the Reversible Residual Network (RRN). Next, a Channel Refinement (CR) module is used to eliminate redundant information in the mural image features. Subsequently, an Unbiased Color Transfer (UCT) module transforms the faded features into color-restored features that match the statistical data of the reference features. Finally, the color-restored features are reconstructed into color-restored mural images through the reverse inference of the Reversible Residual Network (RRN). The architecture of the method in this paper is shown in Fig. 1.

Fig. 1

Description of the overall architecture of the proposed network

Reference image automatic selection module

Existing reference-based methods for color restoration of mural images typically rely on human subjective judgment and visual perception to manually select reference images. This manual selection approach is prone to subjectivity and inconsistency, leading to inaccurate color restoration results. Inspired by deep perceptual similarity models [24], we propose an automated reference image selection module based on structural and textural similarity to achieve automated color reference selection. Due to the relative stability and consistency of painting styles and color habits within the same historical period of Dunhuang murals, murals from the same period often exhibit similar structural and color features. Therefore, we use structural and textural similarity as criteria for selecting reference images.

Specifically, we employ pre-trained VGG19 network [25] serves as the backbone for extracting image depth features. The representation of the faded mural image includes the original input image x and the output feature maps from five convolutional layers (conv1_2, conv2_2, conv3_3, conv4_3, and conv5_3):

$$f(x) = \{ \tilde{x}_{j}^{i} ;i = 0,...,m;j = 1,...,n_{i} \}$$

(1)

where m = 5 denotes the number of convolutional layers, n_i is the number of feature maps in the i-th convolutional layer, and $\tilde{x}^{(0)} = x$. The same representation is used for the reference mural image y:

$$f(y) = \{ \tilde{y}_{j}^{i} ;i = 0,...,m;j = 1,...,n_{i} \}$$

(2)

The texture and structure similarity scores are computed simultaneously between the image representations of the faded and reference mural images at the same level. These scores are then weighted and summed to obtain a composite score, which determines the most similar reference image in the reference mural image dataset to the faded mural image that requires color restoration. The texture similarity score and the structure similarity score are calculated using the following equations, respectively:

$$t(\tilde{x}_{j}^{(i)} ,\tilde{y}_{j}^{(i)} ) = \frac{{2\mu_{{\tilde{x}_{j} }}^{(i)} \mu_{{\tilde{y}_{j} }}^{(i)} + c_{1} }}{{(\mu_{{\tilde{x}_{j} }}^{(i)} )^{2} + (\mu_{{\tilde{y}_{j} }}^{(i)} )^{2} + c_{1} }}$$

(3)

$$s(\tilde{x}_{j}^{(i)} ,\tilde{y}_{j}^{(i)} ) = \frac{{2\sigma_{{\tilde{x}_{j} \tilde{y}_{j} }}^{(i)} + c_{2} }}{{(\sigma_{{\tilde{x}_{j} }}^{(i)} )^{2} + (\sigma_{{\tilde{y}_{j} }}^{(i)} )^{2} + c_{2} }}$$

(4)

where $\mu_{{\tilde{x}_{j} }}^{(i)} , \mu_{{\tilde{y}_{j} }}^{(i)} , {(}\sigma_{{\tilde{x}_{j} }}^{(i)} {)}^{2} , {(}\sigma_{{\tilde{y}_{j} }}^{(i)} {)}^{2}$ and $\sigma_{{\tilde{x}_{j} \tilde{y}_{j} }}^{(i)}$ denote the global means, variances, and covariance of $\tilde{x}_{j}^{(i)}$ and $\tilde{y}_{j}^{(i)}$, respectively. c₁ and c₂ are two small positive constants. The final composite score is obtained by using a weighted sum to combine the texture similarity scores and structure similarity scores of the different convolutional layers.

$$D(x,y;\alpha ,\beta ) = 1 - \sum\limits_{i = 0}^{m} {\sum\limits_{j = 1}^{{n_{i} }} {(\alpha_{ij} t(\tilde{x}_{j}^{(i)} ,\tilde{y}_{j}^{(i)} ) + \beta_{ij} s(\tilde{x}_{j}^{(i)} ,\tilde{y}_{j}^{(i)} ))} }$$

(5)

where {α_ij, β_ij} are positive learnable weights, satisfying $\sum\nolimits_{i = 0}^{m} {\sum\nolimits_{j = 1}^{{n_{i} }} {(\alpha_{ij} + \beta_{ij} )} = 1}$. Figure 2 shows the model for calculating the structural texture similarity score.

Fig. 2

Structural texture similarity calculation model

The reversible residual network

Mural images are characterized by rich texture details and vibrant artistic content. Preserving semantic consistency between the generated and source images during color restoration is essential. However, traditional encoders often struggle to extract and maintain image representations without losing content information. To address this challenge, we propose a reversible residual network composed of multiple reversible residual blocks for extracting mural image representations. The forward and backward propagation of this network ensures a one-to-one mapping from input to output. This design enables the network to accurately reconstruct input images, effectively avoiding information loss during feature extraction.

In our design, each reversible residual block takes inputs x₁ and x₂ and produces outputs y₁ and y₂. F and G are the residual functions, and the formula can be expressed as:

$$x_{1} ,x_{2} = split(x)$$

(6)

$$y_{1} = x_{1} + F(x_{2} )$$

(7)

$$y_{2} = x_{2} + G(y_{1} )$$

(8)

The split function divides the input tensor x into two equal-sized parts x₁ and x₂ along the channel dimension. Inspired by Jacobsen et al. [20], we use channel shuffling to reorder the channels, perturbing the channel dimension of the feature map to ensure network reversibility. Reverse inference can then be achieved by subtracting the activation values of the next layer:

$$x_{2} = y_{2} - G(y_{1} )$$

(9)

$$x_{1} = y_{1} - F(x_{2} )$$

(10)

The residual functions F and G consist of three consecutive convolutional layers with kernel sizes of 1 × 1, 3 × 3, and 1 × 1, respectively. A ReLU activation layer is added after the first and second convolutional layers to introduce a nonlinear transformation. In this paper, we omit the normalization layer due to its complexity, which could hinder learning mural image representations. Instead, we focus on extracting richer and more complex feature representations of mural images through cascading multiple reversible residual blocks. Additionally, squeeze layers are inserted between the cascaded reversible residual blocks. These layers the reduce spatial dimensions of feature maps to decrease spatial information while increasing channel dimensions to enhance feature representation capacity. The combination of reversible residual blocks and squeeze layers allows the network to better capture large-scale color and structural information in mural images, while improving computational efficiency and model speed.

Channel refinement module

The shallow features of mural images contain color, texture, and edge information, while the deep features contain rich semantic information. These features are crucial for subsequent color transfer and image reconstruction processes. However, the inclusion of the squeeze layers leads to an exponential increase in channel numbers, causing the reversible network to accumulate numerous redundant features during forward inference. The redundant information will result in apparent artifacts and false colors in the generated restoration image. Inspired by Chiu et al. [11], who used a knowledge distillation model based on Principal Component Analysis (PCA) to extract primary feature information, we construct a channel refinement module. This module effectively handles redundant information and maintains the continuity and integrity of information flow through cascaded reversible residual blocks, aiding in better preservation and restoration of overall structure and details in faded mural images.

The channel refinement module first applies a zero-padding operation to increase the potential dimensionality of the input faded and reference mural image features. Subsequently, it integrates global information within the image using two cascaded reversible residual blocks. Finally, it expands channel information into spatial dimensions of different image patches, enabling the model to effectively utilize existing channel features to express various local and global image characteristics. The channel refinement module is illustrated in Fig. 3, where RRB denotes reversible residual blocks. F_c and F_r represent content and reference image features after eliminating redundant information.

Fig. 3

Channel Refinement Module

Unbiased color transfer module

Mural images exhibit complex color distributions, with unique brushstrokes adding intricate texture details that enhance their artistic and visual appeal. Therefore, it is crucial to comprehensively preserve the fine textures and structural details of the images during the color transfer process. ArtFlow [23] demonstrated that Whitening and Coloring Transform (WCT) [26] can achieve unbiased color style transfer by adjusting color statistics. However, WCT based on Singular Value Decomposition (SVD) tends to lose local detail information and overlook subtle color variations, leading to suboptimal color restoration results for mural images. To address this issue, we employ a Cholesky decomposition-based WCT [27]. Cholesky decomposition breaks down a symmetric positive definite matrix into the product of a lower triangular matrix and its transpose. This method effectively preserves the color correlations between pixels when processing the color covariance matrix, thereby maintaining the overall structure and details of the image and reducing color shift problems during the color restoration process.

Specifically, the content mural image feature F_c is normalized using the Cholesky decomposition to eliminate their statistical correlation and obtain a smoother color representation. The formula is expressed as:

$$C_{c} = F_{c} \cdot F_{c}^{T} ,\,C_{r} = F_{r} \cdot F_{r}^{T}$$

(11)

$$L_{c} = Cholesky(C_{c} ),\,L_{r} = Cholesky(C_{r} )$$

(12)

$$\hat{F}_{c} = L_{c}^{ - 1} \cdot F_{c}$$

(13)

Here, F_c and F_r represent the features of the content and reference image, respectively. Similarly, C_c and C_r denote the covariance matrices of F_c and F_r, while L_c and L_r represent the lower triangular matrices obtained by performing Cholesky decomposition on C_c and C_r, respectively.$\hat{F}_{c}$ denotes the whitened feature of the content image. Subsequently, the whitened content image features are colored to align with the color distribution of the reference image. The final color-restored feature F_res is represented by the following equation:

$$F_{res} = L_{r} \cdot \hat{F}_{c} + \mu_{r}$$

(14)

where μ_r represents the mean value of the features of the reference mural image. Another advantage of the Cholesky decomposition method over SVD is its higher computational efficiency and numerical stability when dealing with faded mural images. Therefore, the unbiased color transfer module used in this paper can achieve image color restoration more robustly and efficiently, while preserving the content structure and texture details of mural images.

Loss function

Three loss functions are used to train the network in an end-to-end manner:

$$L = L_{s} + \lambda_{m} L_{m} + \lambda_{cyc} L_{cyc}$$

(15)

where L_s, L_m and L_cyc denote the style loss, Matting Laplacian loss and cyclic consistency loss, respectively. λ_m and λ_cyc denote the weight parameters of Matting Laplacian loss and cyclic consistency loss, respectively.

The style loss formula is expressed as:

$$L_{s} = \sum\limits_{i = 1}^{l} {\left\| {\mu \left( {\phi \left( {I_{res} } \right)} \right) - \mu \left( {\phi \left( {I_{r} } \right)} \right)} \right\|} + \sum\limits_{i = 1}^{l} {\left\| {\sigma \left( {\phi \left( {I_{res} } \right)} \right) - \sigma \left( {\phi \left( {I_{r} } \right)} \right)} \right\|}$$

(16)

where I_res denotes the restored mural image, I_r denotes the reference mural image, ϕ_i denotes the features of layer i-th of the VGG19 network, and μ and σ denote the mean and variance of the feature map, respectively.

The unbiased color transfer method based on Cholesky decomposition cannot ensure pixel-level consistency in the restoration results, resulting in inconsistent color restoration in semantically similar regions of the restored mural images. PhotoWCT [9] used the Matting Laplacian matrix to maintain pixel affinity. However, the direct application of the Matting Laplacian loss led to a blurring of the generated image due to spatial distortion. Thanks to the bijective characteristics of the reversible network, there is no loss of information in the forward and reverse inference processes, thus avoiding the problems above. The formula for the Matting Laplacian loss is expressed as:

$$L_{m} = \frac{1}{N}\sum\limits_{c = 1}^{3} {V_{c} } [I_{res} ]^{T} MV_{c} [I_{res} ]$$

(17)

where N denotes the number of mural image pixels, V_c[I_res] denotes a vectorized representation of the restored mural image I_res in channel c, and M represents the Matting Laplacian matrix of the faded mural image I_c.

The design of the reversible network allows for forward generation and reverse restoration, which theoretically allows for circular reconstruction of the content mural image $\tilde{I}_{c}$ by transferring the color information of the content mural image I_c to the restored mural image I_res. However, due to the finite precision of floating-point numbers, the reversible operation may introduce numerical errors in the actual execution, leading to apparent artifacts in the generated restored mural image. Therefore, this paper introduces cycle consistency loss to improve network stability and ensure content consistency between the restored and content mural images, calculated using the following formula:

$$L_{cyc} = ||\tilde{I}_{c} - I_{c} ||_{1}$$

(18)

Experiment

Due to the limited number of existing Dunhuang mural images and the rarity of fully preserved murals, directly training models on mural datasets can lead to overfitting and insufficient learning of effective feature representations. To overcome this issue, we adopted a transfer learning approach. Specifically, we first pretrained our network on the large-scale WikiArt dataset [28] to enable the model to learn rich image features. Subsequently, we fine-tuned the pretrained model on the mural dataset to better adapt it to the task of mural color restoration. This strategy of pretraining and fine-tuning allows us to achieve better model performance on the limited mural data and enhance the effectiveness of color restoration.

Datasets

The WikiArt dataset is a publicly available art dataset featuring over 80,000 paintings from various artists, styles, and genres. This dataset covers a range of styles from the Renaissance to modern art, including murals, portraits, and abstract paintings. While the specific content and details of WikiArt images differ from Dunhuang murals, they share similarities in artistic style, color usage, and visual features. By pre-training on the WikiArt dataset, it learns these general visual features, providing a robust foundation for subsequent fine-tuning on the mural dataset. To better simulate the task of mural image color restoration during the pre-training, we applied the degradation method proposed by Wang et al. [29] to images in the WikiArt dataset. This process simulates the fading and discoloration phenomena observed in mural images, enabling us to construct image pairs consisting of faded and original images for pre-training.

Our mural image dataset was curated from The Complete Collection of Chinese Dunhuang Murals. Beiliang Northern Wei [30], The Complete Collection of Dunhuang Grottoes [31], and Dunhuang mural restoration collection [32]. The dataset comprises 1,200 faded mural images and 800 well-preserved, high-resolution reference mural images. To enhance dataset diversity and scale, we applied data augmentation techniques such as cropping, rotating, flipping, and scaling. This resulted in a total of 9,000 curated faded mural images with clear content information and 6,000 reference mural images. Using an automatic selection module based on reference images, each faded mural image was paired with the most suitable reference image. The training-test set ratio was set at 5:1, with the training set consisting of 7500 image pairs and the test set containing 1,500 pairs. All images were standardized to 512 × 512 pixels in size.

Experimental settings

The proposed network architecture consists of 20 reversible residual blocks and two squeeze layers. Experiments were conducted using the PyTorch deep learning framework on a Linux system. We employed the Adam optimizer for training with a batch size of 2 and 100,000 iterations. The initial learning rate was set to 1e-4 with a decay rate of 5e-5. All experiments were conducted on a single NVIDIA RTX 3090 GPU.

When setting the weighting parameters for the loss function, we initially used lower values. Through iterative experimentation and validation, we determined that a cycle consistency loss weight (λcyc) of 10 and a Matting Laplacian loss weight (λm) of 1200 achieved the best balance between color restoration effectiveness and visual quality. The cycle consistency loss plays a role in maintaining accuracy in image content and structure; a smaller weight helps retain sufficient color information in the restored images without overly disturbing the content of the originals. The Matting Laplacian loss focuses on preserving image details and edges; a larger weight suppresses excessive smoothness, resulting in clearer and more refined color restoration images. This balance ensures that the generated images not only retain structural integrity but also capture subtle color variations, thereby enhancing overall visual quality and realism.

Objective evaluation metrics

Image quality assessment is a crucial aspect in validating the effectiveness of color restoration for faded mural images. In this study, we combine full-reference and no-reference evaluation metrics to comprehensively evaluate the quality of color-restored images. Full-reference image quality evaluation metrics are typically used to measure the difference between restored mural images and their original counterparts. On the other hand, no-reference image quality evaluation metrics are more suitable for assessing the perceived quality of mural images when original reference images are not available.

This study employs four full-reference evaluation metrics: Structural Similarity Index (SSIM), Peak Signal-to-Noise Ratio (PSNR), Feature Similarity Index (FSIM) [33] and Gradient Magnitude Similarity Deviation (GMSD) [34]. Additionally, two no-reference evaluation metrics are utilized: Perception-based Image Quality Evaluator (PIQE) [35] and Natural Image Quality Evaluator (NIQE) [36].

SSIM is used to measure the similarity between two images in terms of their structure, luminance, and contrast. The result is a numerical value between 0 and 1, where a higher value indicates greater similarity between the two images. The calculation formula is:

$${\text{SSIM(}}x,y{) = }\frac{{(2\mu_{x} \mu_{y} + C_{1} )(2\sigma_{xy} + C_{2} )}}{{(\mu_{x}^{2} + \mu_{y}^{2} + C_{1} )(\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2} )}}$$

(19)

Here, μ_x, μ_y, σ_x, σ_y and σ_xy are the mean, variance, and covariance of the original mural image x and the restored mural image y, respectively. C₁ and C₂ are constants used to stabilize the computation. SSIM effectively reflects the structural information of images and provides an accurate assessment for structurally similar images.

PSNR is defined based on Mean Squared Error (MSE) and is used to compare the difference between the original mural image and the restored mural image. A higher PSNR value indicates less pixel difference between the two images. The calculation formula is:

$${\text{PSNR = 10log}}_{10} (\frac{{{\text{MAX}}^{2} }}{{{\text{MSE}}}})$$

(20)

where MAX represents the maximum possible value of image pixels, and MSE is calculated as:

$${\text{MSE = }}\frac{1}{mn}\sum\nolimits_{i = 0}^{m - 1} {\sum\nolimits_{j = 0}^{n - 1} {[I(i,j) - K(i,j)]} }^{2}$$

(21)

Here, I(i, j) and K(i, j) denote the pixel values of the original mural image I and the restored mural image K, respectively, where m × n represents the dimensions of the images. PSNR is insensitive to human perception and may not effectively reflect characteristics of the human visual system. Therefore, combining other quality metrics is often necessary for a more accurate assessment of image quality.

FSIM evaluates the similarity between two images by comparing their structural features and gradient magnitudes, making it particularly suitable for assessing the quality of images with intricate details and structures. The index ranges from 0 to 1, where a higher value indicates greater similarity between the images. The formula is expressed as:

$${\text{FSIM}}(x,y) = \frac{{\sum\nolimits_{{i \in\Omega }} {S_{L} (i) \cdot PC_{m} (i)} }}{{\sum\nolimits_{{i \in\Omega }} {PC_{m} (i)} }}$$

(22)

Here, S_L(i) and PC_m(i) represent the local similarity and gradient magnitude similarity at position i of images x and y, respectively, where Ω denotes the set of all pixel positions in the images.

GMSD assesses the similarity deviation between two images based on their gradient magnitude information, exhibiting good sensitivity to detail loss or changes in images. A smaller GMSD value indicates higher similarity in gradient magnitude between the restored mural image and the original mural image, suggesting better image quality. The formula is given by:

$${\text{GMSD = }}\sqrt {\frac{1}{mn}\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {(GMS(i,j) - \mu_{GMS} )^{2} } } }$$

(23)

GMS(i, j) represents the gradient magnitude similarity at position (i, j) of the images. μ_GMS is the average of all GMS(i, j) values, and m and n denote the height and width of the images, respectively. GMSD provides a comprehensive and accurate assessment when evaluating complex and detail-rich images.

PIQE is a no-reference image quality assessment method that measures and evaluates the subjective quality of images by simulating the human visual system. It assesses the noise level of each block by analyzing local gradient variations and integrates these noise levels across all image blocks to derive an overall quality score. Scores range from 0 to 100, with lower scores indicating higher image quality.

NIQE evaluates image quality by analyzing natural scene statistics of images, including local contrast, mean brightness, standard deviation of brightness, among others. It calculates the overall quality score by measuring how much the features of the evaluated image deviate from those in a given reference model. A lower NIQE score corresponds to higher image quality.

Evaluation of automatic reference image selection results

In this section, we evaluate and analyze the results of the automatic reference image selection module. We present pairs of faded-reference mural images used in ablation and comparative experiments, along with additional reference images. Structural and textural similarity scores between all reference images and their corresponding faded images are listed to justify our selection criteria. Figure 4 shows examples of faded mural images paired with reference mural images, arranged from left to right based on decreasing similarity.

Fig. 4

Reference image selection results. a Content b [1] c [2] d [3] e [4] f [5] g [6] h [7].

Table 1 presents the calculated structural and textural similarity scores using Eq. (5). Smaller scores indicate fewer structural and textural differences between the pairs of mural images, indicating higher similarity between them. Combining Fig. 4 and Table 1 reveals that the automatic reference image selection module accurately identifies the most suitable images from a large dataset of references. This approach effectively reduces the subjective impact of manual selection methods based on human visual perception and personal experience. Moreover, it saves time and costs associated with manual screening.

Table 1 Structural texture similarity scores of selected results

Ablation experiments

To verify the effectiveness of each module in the proposed model, we conducted a set of comparative experiments. We restored the colors of faded mural images using the following network structures: the baseline model ArtFlow, VGG19 + UCT, RRN + UCT, and RRN + UCT + CR (Ours). The restoration results are shown in Fig. 5.

Fig. 5

Comparison results of ablation experiments. a Reference, b Input, c ArtFlow, d VGG + UCT, e RNN + UCT, f Proposed Method

As seen in Fig. 5c, ArtFlow is able to maintain the content structure of the image reasonably well but still suffers from issues related to feature resolution and the loss of fine details, especially in areas with complex content structures, such as the Bodhisattva's arm in the second row of Fig. 5c. Additionally, since this method does not address the redundant feature information within the network, color artifacts appear at the edges of the image. For example, red artifacts can be seen on the right edge in the first row of Fig. 5c, and green artifacts are present on the left edge in the third row of Fig. 5c as well as at the seam between the carpet and the floor.

Figure 5d presents the results obtained by utilizing pre-trained VGG19 to extract image features and restoring colors using the UCT module. It is apparent that while the UCT module transfers color information from the reference mural to the faded image, the loss of content information during feature extraction and the presence of image reconstruction errors degrade the content details of the generated image. For instance, in Fig. 5d, the content structure and texture details of the Bodhisattva arm ornaments in the second row and the facial features of the ladies in the third row become blurred.

In Fig. 5e, the reversible residual network is employed to learn mural image representation and reconstruct the color-restored image. The texture structure and content information of the generated image are preserved. However, accumulating channel redundancy information in the network leads to artifacts and false color in the restoration result. There are apparent artifacts on the arms and body parts of the Bodhisattva in the first row in Fig. 5e. The forehead part of the maiden in the third row also exhibits artifacts, and the color restoration results in this area are inconsistent with the rest of the face.

Figure 5f shows the results after adding the channel refinement module. Compared to ArtFlow, the addition of this module effectively reduces artifacts and color distortions in the restored images. Moreover, the introduction of reversible residual blocks and the use of WCT based on Cholesky decomposition significantly help in preserving fine details within local regions of the image. In summary, the proposed network architecture effectively restores the colors of faded mural images while maintaining detailed content information.

The quality evaluation data of the restored images obtained using the four different network structures are shown in Table 2. It can be seen that replacing the VGG19 network with the reversible residual network for feature extraction results in significant improvements in SSIM, FSIM, and GMSD, bringing them on par with the ArtFlow method. This is because the reversible network effectively reduces information loss during feature extraction, leading to stronger retention of the content structure in the restored images. After adding the channel refinement module, the scores of the restored images improved further. Both PIQE and NIQE values are lower than those of the ArtFlow, indicating that the proposed method achieves better visual quality in the restoration results.

Table 2 Ablation experiment evaluation index indicators

Comparison of color restoration results of faded reproduced mural images

Reproduced murals are created by artists who carefully observe the original mural works, understand their composition, lines, colors, and lighting characteristics, and then use corresponding painting materials and techniques to recreate them. This practice helps preserve and pass on the valuable cultural heritage of Dunhuang murals and provides important reference materials for academic research. Reproduced murals typically retain the texture details and color styles of the original murals better, offering clearer and more complete content and texture structures compared to the actual faded murals. However, over time, these reproduced murals also face issues of color fading.

To evaluate the effectiveness of the method proposed in this paper, we conducted color restoration on faded reproduced mural images using our method, S2WAT [37], CAST [38], CCPL [12], and MicroAST [39]. The selected comparative methods were all proposed in recent years and have demonstrated good performance in preserving the original content structure of images during the color restoration process. The comparison results are shown in Fig. 6. Figure 6a depicts the reference murals, Fig. 6b shows the reproduced murals, and Fig. 6c–f display the images restored by the comparative methods. Figure 6g showcases the images restored by the method proposed in this paper.

Fig. 6

Comparison of experimental results of color restoration of faded reproduced murals. a Reference, b Content, c S2WAT, d CAST, e CCPL, f MicroAST, g Proposed Method

S2WAT utilizes Transformers combined with different shapes of window attention outputs to achieve feature extraction, addressing the locality problem of window attention. However, this method still exhibits inconsistent color restoration within regions of the same semantic area. In the fourth row of Fig. 6c, different patches of the geisha's skirt show varying colors. Similarly, in the sixth row of Fig. 6c, the dancer's hair also demonstrates this issue. Although S2WAT maintains the overall content structure of the image, it struggles to preserve fine details in structurally complex areas, such as the ornaments on the bodhisattva's arm in the second row of Fig. 6c. Additionally, as seen in the first row of Fig. 6c, the color restoration results of this method are not accurate. CAST employs domain enhancement to learn the color style representation of artistic images, resulting in better color restoration. However, from the perspective of content structure preservation, this method distorts the mural's line structures, causing deformation in areas with intricate lines. For instance, in the second row of Fig. 6d, the ornaments on the bodhisattva's arm are distorted. Furthermore, in the third row of Fig. 6d, the background area of the geisha is filled with numerous artifacts. CCPL applies contrastive consistency loss to local patches and incorporates a neighborhood adjustment mechanism to ensure content consistency between images during color restoration. Therefore, it excels in preserving image content structure details. However, it achieves the poorest color restoration results, exhibiting color casts and significant lack of color saturation. As shown in the third row of Fig. 6e, the restored image appears predominantly dark purple. MicroAST employs a miniature encoder to extract image features and uses a dual modulation mechanism combining Adaptive Instance Normalization (AdaIN) and Dynamic Instance Normalization (DIN) for color restoration. Although this method completely preserves the content detail information of the murals, it shows noticeable color restoration errors due to its insufficient color feature extraction capability. In the first row of Fig. 6f, the bodhisattva's lotus seat and halo appear cyan instead of green. In the sixth row of Fig. 6f, the dancer's hair color is white. In comparison to the above methods, our method effectively maintains the overall content structure and texture information of the image. It also clearly preserves fine details in structurally complex areas. Moreover, the color restoration results of our method are more accurate, with fuller colors that better align with human visual perception. As seen in the third row of Fig. 6g, the background area of the figures is cleaner, without artifacts present in other methods, demonstrating superior color restoration performance.

The evaluation metrics data for the color restoration results of the reproduced mural images are shown in Table 3. Our method achieves higher SSIM and PSNR values compared to other methods, indicating that the restored results of our work have smaller differences in structural similarity and pixel similarity with the original mural images. FSIM and GMSD values also achieved the best scores, reflecting the advantages of our method in maintaining content structure and detail information. CCPL's FSIM and GMSD values are slightly lower than our method, achieving the second-best results. However, due to the poor visual effect of its color restoration results, its performance on no-reference metrics PIQE and NIQE is inferior to our method. S2WAT loses more mural information, leading to content structure loss and unsatisfactory color restoration effects, resulting in lower objective evaluation metrics compared to other methods.

Table 3 Evaluation of color restoration results of faded reproduced mural images

Comparison of color restoration results of faded real mural images

The real murals are affected by the instability of the chemical properties of the pigments, leading to fading, discoloration, mold growth, and contamination. Additionally, cracks due to the aging of the pigment layer and irregular spot defects and noise caused by pigment flaking present further challenges to the color restoration of real mural images. To further validate the effectiveness of the proposed method in this paper, faded real mural images were selected for color restoration processing. Subsequently, the results generated by this method were compared with those of S2WAT, CAST, CCPL, and MicroAST. The comparison results are illustrated in Fig. 7. Figure 7a shows the reference mural, Fig. 7b displays the faded real mural, and Fig. 7c–f depict restoration images using comparative methods. Figure 7g presents the restoration image using the method proposed in this paper.

Fig. 7

Comparison of experimental results of color restoration of faded real murals. a Reference, b Content, c S2WAT, d CAST, e CCPL, f MicroAST, g Proposed Method

In Fig. 7, S2WAT lacks constraints on semantic information of the image, resulting in the loss of detailed content information in the restored image. For instance, in the sixth row of Fig. 7c, the texture structure of the Thousand-Hand Guanyin's fingers is distorted and blurred. Moreover, due to spot noise interference in the faded murals, this method exhibits incomplete color transfer, as shown in the enlarged region of the background of the Bodhisattva in the fourth row of Fig. 7c. CAST achieves better color restoration, but its ability to preserve the edge structures of images is insufficient, leading to chaotic textures in the restored images. For example, in the first row of Fig. 7d, the red strip decorations on the Bodhisattva's clothing are intermingled. In the sixth row of Fig. 7d, the lines of the Thousand-Hand Guanyin's fingers are distorted, and the restoration in this area appears blurry. Interestingly, CAST is capable of removing point noise from the original mural image, as shown in the fourth row of Fig. 7d. We believe this is achieved because CAST maximizes mutual information between the reference image and the restored image through contrastive learning to learn representations of color style. This process effectively reduces the introduction of noise during color restoration. CCPL excels in retaining content details but struggles with color restoration, exhibiting various color issues in the restored images. Green artifacts appear in the first row of Fig. 7e, while blue artifacts and significant color overflow are visible in the Thousand-Hand Guanyin's finger area in the sixth row. The restoration result in the third row of Fig. 7e shows not only color artifacts but also noticeable color bias. MicroAST preserves the edge structures of complex areas well but is severely affected by noise in the images. This noise is further amplified, destroying the fine texture details of the original image, greatly reducing the visual quality of the color restoration results. Coarse noise in the fourth and sixth rows of Fig. 7f illustrates this issue. Additionally, MicroAST struggles with complete color restoration within the same semantic regions, as observed in the finger area of the sixth row in Fig. 7f. In contrast, our proposed method accurately restores the color of mural images, resulting in more natural and complete color tones, thus achieving superior visual effects. In terms of preserving content details, our method is less affected by noise, with clearer edge structures. However, it also retains the noise information from the original mural images while preserving content structure and texture details.

Table 4 presents the quality evaluation scores for the restoration results of real faded mural images for each method. Our method achieves the highest scores across all evaluation metrics, indicating that it effectively preserves the content information and texture features of the original mural images while achieving high-quality color transfer. The mural images restored by our method are closer to the initial color of the real murals, significantly enhancing the authenticity of the mural color restoration results.

Table 4 Evaluation of color restoration results of faded real mural images

Comparison of color restoration results of faded real mural images

Figure 8 illustrates additional restoration results using our method, and Table 5 presents the corresponding evaluation metric data for the images in Fig. 8. The first set of images demonstrates high accuracy and effectiveness in restoration. The high SSIM and FSIM values indicate strong structural and feature similarity between the restored images and the reference images. The high PSNR values suggest minimal image noise, while the low PIQE and GMSD values indicate good perceptual quality and gradient similarity, respectively. In the second set of restored images, the lower NIQE score suggests good natural quality, but the poorer performance in the other four full-reference metrics may be attributed to significant brightness and contrast differences between the restored and original images, along with retained noise from the original images. In the fifth set of data, we attempted restoration on architectural murals, which exhibit complex structures and rich information compared to human-figure murals. Despite this complexity, we achieved satisfactory color restoration results. Low GMSD and high FSIM values suggest preservation of structural features and texture details. For the seventh set of restored images, high FSIM and low GMSD values indicate good performance in feature similarity and quality. However, higher NIQE and PIQE scores suggest poorer perceptual quality affected by noise.

Fig. 8

Restoration results of the proposed method. a Reference, b Content, c Proposed Method

Table 5 Evaluation of the faded sample—reconstructed sample pairs

Overall, our method demonstrates good restoration performance in most cases, particularly in preserving content structure and texture details. However, further improvements are needed for some images, especially in reducing noise and enhancing perceptual quality.

Conclusions

This paper proposes a mural image color restoration method based on reversible residual networks. We begin by using an automatic reference selection module based on structural texture similarity to address inaccuracies in manual selection methods for reference mural images. Subsequently, leveraging the bijective properties of reversible residual network to realize the lossless extraction of image features, ensuring preservation of image information throughout the transmission process. The channel refinement module eliminates channel redundancy within the network, preventing artifacts in the color restored images. The unbiased color transfer module accurately restores faded mural image colors while better preserving the original content structure and texture details. Compared to the baseline methods, the SSIM, FSIM, and PIQE values improved by 7.97%, 3.46%, and 13.98%, respectively. Comparative evaluations against representative color restoration methods cited in the literature demonstrate superior performance across multiple objective assessment metrics for our proposed method.

By restoring the original colors of Dunhuang murals, we aim to authentically reproduce their historical and cultural value, enhancing public awareness and understanding of Dunhuang cultural heritage. Simultaneously, by creating high-quality digital replicas, the method will also contribute to future academic research and virtual exhibitions. We hope that this method will play an active role in the color restoration of mural images, help restore and protect Dunhuang mural, a valuable cultural heritage, and promote the inheritance and dissemination of Dunhuang culture and art.