Introduction

Dunhuang murals, with their unique artistic style, exquisite painting skills, and profound cultural connotation, have become one of the most precious heritages in the history of human civilization. Some mural images are shown in Fig. 1. In the long history, due to climate change, sand erosion, man-made destruction, and other factors, a large number of murals have been damaged to varying degrees, such as paint shedding, fading, peeling, cracking, and so on1. These factors have seriously restricted the cultural exchange between the East and the West in murals, and have limited the exploration of the historical changes, artistic characteristics, and cultural connotations of Dunhuang murals. Therefore, it is of great significance to explore an effective mural restoration method with the concept of “minimal intervention principle” for the study of mural culture and the development and breakthrough of other painting art categories.

Fig. 1
figure 1

Some mural images.

Full size image

Manual restoration methods play an important role in the conservation of murals. Through observation, we found that the manual restoration of murals can be simply described as a two-step process. The first step is to outline the contours and lines of the missing areas of the murals by highly skilled painters, and the second step is to color the missing areas according to the lines and the surrounding colors. The first step requires the painter to draw the structural information of the missing mural based on personal experience, which requires the painter to be very familiar with the painting style of the mural. The second step requires coloring the missing areas according to the style of the mural based on structural information. These two steps are relatively high technical requirements for mural restorers. Moreover, the manual restoration method is irreversible and tends to restore directly on the mural, which is prone to cause secondary damage to the mural2. Inspired by medicine, the protection staff of cultural relics in many countries and areas apply the protection concept of “minimal intervention” to the restoration task of murals and tend to use digital image restoration methods to complete the restoration of murals.

With the continuous development of computer vision technology, many scholars have proposed image restoration technologies using different strategies in recent years, making digital image restoration technology has made great progress in solving the problem of repairing natural images3,4,5,6,7. Although these methods achieve good performance in solving natural image restoration problems, they are not suitable for the task of mural restoration. The main reasons are: (1) The styles of murals and natural images are very different. Although transfer learning can integrate the prior information in natural images into the restoration task of murals, the unique style displayed by murals is obviously different from natural images. This limits the effectiveness of transfer learning methods. (2) The lines in the mural are uneven, the colors are rich and diverse, and the patterns are complex and changeable. Moreover, the existing feedforward neural network method based on simple convolution cannot capture the rich high-frequency texture information and low-frequency color patch information contained in the mural, which affects the recovery performance of the model.

To alleviate these problems, we propose a new mural restoration framework based on generative adversarial networks (GAN) to solve the large area of irregular shape damage on the mural. The proposed framework adopts the strategy of first contour structure and then texture coloring, which is inspired by the method of manually inpainting murals. This strategy is significantly different from the inpainting strategy for natural images. The framework contains two generative networks to model the two steps in the manual mural restoration method. The first is a coarse-grained network, which is mainly used to reconstruct the semantic information of the lines and contours of the damaged mural. The coarse-grained network simulates the modeling of mural contour and structure restoration during manual restoration. The second is a fine-grained network, which is mainly used to reconstruct fine-grained features to repair texture details and color correction of damaged murals. The fine-grained network simulates the modeling of mural texture details and colorization restoration during manual inpainting. Moreover, the Swin transformer module (SwinT)8,9 can model long-range dependency with the shifted window scheme. The capture of multi-scale features helps to extract information at different granularities10,11. Since different image reconstruction methods have complementary image prior modeling capabilities12,13, we propose a new building block (STMA) that fuses the SwinT module with the multi-scale dilated convolution attention module. To better improve the performance of the network, we also design a new joint loss function to impose guidance on the two-stage training process of the model from multiple dimensions. Experiments show that our proposed mural repair method has better performance. In summary, the main contributions of this paper are summarized as follows: (1) We propose a two-stage GAN mural inpainting framework to solve the large area of irregular shape damage on the mural, which models the manual mural inpainting process and can achieve coarse-to-fine mural inpainting. (2) A novel building block (STMA) is proposed to effectively extract rich contextual information. It combines a Swin transformer module and a multi-scale dilated convolution attention module. (3) The joint loss function designed based on multiple dimensions can not only stabilize the training process of the model but also improve the mural restoration performance of the model.

Methods

Preliminaries: generative adversarial network

Inspired by game theory, Goodfellow et al.14 first proposed GAN. It contains a generative network \(G\) and a discriminative network \(D\). The two networks learn the distribution of data through adversarial training. In the game process between the generative network \(G\) and the discriminative network \(D\), the generative network \(G\) generates realistic samples as much as possible, and the discriminative network \(D\) tries to judge the authenticity of the sample. To realize the process of the game, the following loss function is used when training the GAN,

$$\mathop{\min }\limits_{G}\mathop{\max }\limits_{D}V(D,G)={E}_{x \sim {P}_{{data}(x)}}\left[\log D\left(x\right)\right]+{E}_{z \sim {P}_{(z)}}\left[\log (1-D\left(G(z)\right))\right]$$
(1)

where \(x \sim {P}_{{data}(x)}\), \({P}_{{data}(x)}\) represents the real data distribution. z represents the random noise \(z \sim {P}_{(z)}\), \({P}_{(z)}\) represents random distribution, such as Gaussian distribution.

At present, GAN have been widely used in image inpainting tasks. To generate multiple image inpainting results, a probabilistic diverse GAN (PD-GAN)15 is proposed. PD-GAN is built upon a vanilla GAN that generates images based on random noise. Nazeri et al.16 proposed EdgeConnect by decomposing image restoration tasks into structure prediction and image completion. This method alleviates the problem of image completion when significant portions of the image are missing. By combining the advantages of convolutional neural networks (CNN) and transformers, Wan et al.17 proposed a high-fidelity pluralistic image completion method based on GAN. This method utilizes a transformer to restore coarse textures and enhances local texture details using CNN under the guidance of mask images.

Related work on mural inpainting

As a research hotspot in the field of image restoration, the digital restoration of murals has attracted more and more attention. Several scholars have proposed mural restoration schemes employing different strategies, including the partial differential equation method18,19,20, texture synthesis method21,22, sparse representation method23,24,25, and deep learning method26,27,28,29,30,31. Chen et al.19 proposed an adaptive inpainting method for Dunhuang murals based on the improved curvature-driven model, which solved the defects of the CDD algorithm and shortened the inpainting time. To solve the problem of repairing murals that have fallen off and eroded by diseases, Cao et al.21 proposed a virtual restoration method of murals based on an adaptive local search of sample patches, which makes the composition characteristics of repaired murals more reasonable. Chen et al.25 proposed a mural inpainting method based on Gabor transform and group sparse representation, which alleviates the problems of blurred structure and discontinuous lines in the inpainted murals. Although these traditional methods have achieved good mural inpainting performance, due to the excellent performance of deep learning methods in the field of image reconstruction in recent years, many mural inpainting methods based on deep learning have also emerged. To effectively repair ancient murals, Cao et al.26 proposed a consistency-enhanced GAN to repair missing murals. To utilize the auxiliary information provided by the line drawing, Li et al.27 proposed a line drawing-guided mural restoration method, which decomposed the mural restoration process into two stages: structure reconstruction and color correction. In the structural reconstruction stage, line drawings are used to ensure the authenticity of the large-scale restoration content and the stability of the structure. In the color correction stage, the missing pixels are corrected and the local color is adjusted. The two-stage restoration strategy effectively improves the quality of mural restoration. Considering the problems of insufficient feature extraction and loss of detail reconstruction, Chen et al.28 proposed a GAN mural restoration method based on multi-scale features and attention fusion. From the perspective of attention and loss function, Li et al.29 proposed an approach for inpainting damaged areas of Dunhuang murals based on a recurrent feature reasoning network. To exploit multi-scale information and mask features, Wang et al.30 proposed a Thanka mural inpainting method based on multi-scale adaptive partial convolution and stroke-like masks.

STMA-GAN Network

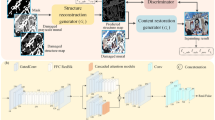
Inspired by the manual restoration mural scheme, we proposed the STMA-GAN model, as shown in Fig. 2. STMA-GAN is built up on a GAN. By modeling the manual restoration process, STMA-GAN is designed as a model that contains two generators and a discriminator. Note that the same discriminator structure is used during the two-stage training process. Among the two generators, one is a coarse-grained network \({G}^{C}\), which is used to model the first step of the manual restoration process to reconstruct the lines and contours of the missing content of the mural, and the other is a fine-grained network \({G}^{F}\), which is used to refine the texture and details of the image reconstructed by the coarse-grained network. Let \({x}_{L}\) and \({x}_{M}\) be the line drawing and mask image. \({x}_{L}\) and \({x}_{M}\) are the inputs to the coarse-grained network. \({x}_{C}\) is the output of the coarse-grained network. It can be represented as:

$${x}_{C}={G}^{C}({x}_{L},{x}_{M})$$
(2)
Fig. 2
figure 2

The overall pipeline of our proposed STMA-GAN.

Full size image

The coarse-grained network consists of an encoder, a stack of STMA blocks, and a decoder. The encoder consists of four convolution-batch channel normalization-ReLU layers (Conv-BCN-ReLU), BCN32 can adaptively combine the information of channel and batch dimension to improve the generalization of the model. The role of the encoder is to encode the input \({x}_{L}\) and \({x}_{M}\) to extract the key features \({F}_{{e}_{i}}^{C}\),

$${F}_{{e}_{i}}^{C}=\left\{\begin{array}{cc}{G}_{{e}_{i-1}}^{C}\left({x}_{L},{x}_{M}\right) & i=1\\ {G}_{{e}_{i-1}}^{C}\left({F}_{{e}_{i-1}}^{C}\right) & i\in \{2,3,4\}\end{array}\right.$$
(3)

where \({G}_{{e}_{i}}^{C}\) is the i-th layer function operation of the encoder. Four stacked STMA blocks form the backbone of the coarse-grained network. This way of stacking building blocks enables the network to extract richer image contextual information. It can be expressed as:

$${F}_{{s}_{j}}^{C}=\left\{\begin{array}{cc}{G}_{{s}_{j-1}}^{C}({F}_{{e}_{4}}^{C}) & j=1\\ {G}_{{s}_{j-1}}^{C}({F}_{{s}_{j-1}}^{C}) & j\in \{2,3,4\}\end{array}\right.$$
(4)

where \({G}_{{s}_{j}}^{C}\) is the j-th function operation of the STMA block. Then, four upsampling-convolution-BCN-ReLU (Up-Conv-BCN-ReLU) layers are used to decode the features from STMA blocks to the initial inpainted image as the output result of the coarse-grained network. Because the deep network structure will make the features disappear in the transmission process from the shallow layer to the deep layer, which weakens the performance of the model to reconstruct the image33,34. To alleviate this issue, skip connections are applied between the encoder and the decoder.

$${F}_{{d}_{k}}^{C}=\left\{\begin{array}{cc}{G}_{{d}_{k-1}}^{C}({F}_{{s}_{4}}^{C}+{F}_{{e}_{4}}^{C}) & k=1\\ {G}_{{d}_{k-1}}^{C}\left({F}_{{d}_{k-1}}^{C}\right)+{F}_{{e}_{4-k+1}}^{C} & k\in \{2,3,4\}\end{array}\right.$$
(5)

where \({G}_{{d}_{k}}^{C}\) is the k-th layer function operation of the decoder. Finally, the output of the coarse-grained network is reconstructed by a convolutional layer \({G}_{\mathrm{cov}}^{C}\),

$${x}_{C}={G}_{\mathrm{cov}}^{C}({F}_{{d}_{4}}^{C})$$
(6)

Similar to the coarse-grained network \({G}^{C}\), the architecture of the fine-grained network \({G}^{F}\) adopts the same design idea. Let \({x}_{m}\) be the binary mask image, the fine-grained network receives \({x}_{m}\) and \({x}_{C}\) as input and outputs the result \(\hat{y}\) as the final repaired mural by the model. It can be represented as:

$$\hat{y}={G}^{F}({x}_{m},{x}_{C})$$
(7)

However, to achieve the refinement of mural texture and detail restoration, a two-staged training strategy and different loss functions are used during training, see the loss function subsection for details.

The discriminator, its role is to determine whether the repair results are good or bad. To stabilize the training of the discriminator, spectral normalization35 is introduced into the discriminator. Spectral normalization can constrain the spectral norm of each layer of the discriminator so that the discriminator satisfies Lipschitz continuity36, which can reduce the blurring effect of the mural repair results and enhance realism5. We use a stack of five convolution-spectral normalization-Leaky ReLU (Conv-SN-LReLU) layers to form the backbone of the discriminator, a single sigmoid function is used for the output of the discriminator.

STMA block

STMA block fuses the Swin transformer module (SwinT) and the multi-scale dilated convolution attention module (MSDA) by the strategy of the split-transformation-merge37.

Splitting: Inspired by ref.13, the feature tensor \({X}_{{in}}\) is fed into a 1 × 1 convolution and split into two sub-feature tensors equally. It can be expressed as:

$${x}_{1},{x}_{2}={Split}({{Conv}}_{1\times 1}({X}_{{in}}))$$
(8)

Following the weight fusion strategy, we obtain the fusion weights by

$${w}_{1},{w}_{2}={Split}({Fuse}({X}_{{in}}))$$
(9)

where \({Fuse}\left(.\right)={Softmax}({MLP}({GAP}(.)))\), GAP represents the global average pooling, MLP represents the multi-layer perceptron. We use the weights \({w}_{1}\) and \({w}_{2}\) to fuse \({x}_{1}\) and \({x}_{2}\) via \({X}_{1}={w}_{1}{x}_{1}\) and \({X}_{2}={w}_{2}{x}_{2}\).

Transforming: The two sub-feature tensors \({X}_{1}\) and \({X}_{2}\) are fed into the SwinT module and MSDA module to perform different transformations, respectively.

$${X}_{s},{X}_{m}={SwinT}\left({X}_{1}\right),{MSDA}({X}_{2})$$
(10)

Specifically, the SwinT module is a Transformer block, which includes a multi-head self-attention mechanism based on a shifted window (SW_MSA) and a multi-layer perceptron (MLP). SW_MSA can use the interactive information between local attention and shift window to better model the long-distance dependency, and it is also beneficial to MLP for further feature transformation38. A LayerNorm layer is added before SW_MSA and MLP, and the residual connection is used to facilitate the transfer of information, see Fig. 3. The SwinT module is computed as:

$$\begin{array}{c}{X}_{1}^{{\prime} }={SW}{{\_}}{MSA}\left({LN}\left({X}_{1}\right)\right)+{X}_{1}\\ {X}_{s}={MLP}\left({LN}\left({X}_{1}^{{\prime} }\right)\right)+{X}_{1}^{{\prime} }\end{array}$$
(11)

where \({X}_{s}\) is the output of the SwinT module. The MSDA module is a multi-scale dilated convolution attention module, which contains convolution operations with different dilation rates. Dilated convolution can systematically aggregate multi-scale contextual information without losing resolution4,39,40. Inspired by this, we use convolutions with different dilation rates to implement multi-scale feature transformation on the input tensor to capture rich contextual information. Convolution operations with larger dilation rates have larger receptive fields, which help extract more semantic information. Convolution operations with smaller dilation rates have smaller receptive fields, which is beneficial in paying more attention to local patterns. The input feature tensor \({X}_{2}\) is evenly divided into four sub-feature tensors \({x}_{{sub}}^{i},i\in \{1,2,3,4\}\) along the channel dimension. Each sub-feature tensor \({x}_{{sub}}^{i}\) is fed separately to the convolution with different dilation rates \(d\in \{\mathrm{1,2,4,8}\}\). We combine convolution operations with different dilation rates in a parallel manner and then concatenated contextual features of different scales from the channel dimension. A standard convolution is used to fuse features at different scales. It can be expressed as:

$${X}_{m}^{{\prime} }={{Conv}}_{3\times 3}({Concat}({ReLU}({{Dconv}}_{3\times 3}^{d}({x}_{{sub}}^{i})),\cdots ,))$$
(12)

where \(\left(d,i\right)\in \{\left(\mathrm{1,1}\right),\left(\mathrm{2,2}\right),\left(\mathrm{4,3}\right),\left(\mathrm{8,4}\right)\}\). Spatially-variant features are calculated by a simple gating mechanism41. The output of the MSDA module can be obtained by weighted feature operation and collaborative attention42.

$${X}_{m}={CoorAtt}\left({X}_{2}* \left(1-{Gate}\left({X}_{2}\right)\right)+{X}_{m}^{{\prime} }* {Gate}\left({X}_{2}\right)\right)$$
(13)
Fig. 3: The structure of the STMA block.
figure 3

a STMA. b MSDA. c SwinT.

Full size image

Aggregating: the feature maps \({X}_{s}\) and \({X}_{m}\) from the SwinT module and MSDA module are finally concatenated as the input of a 1 × 1 convolution which has a residual connection with the input tensor \({X}_{{in}}\). Through the split-transformation-merge strategy, the final output \({X}_{{out}}\) of STMA block is expressed as:

$${X}_{{out}}={{Conv}}_{1\times 1}\left({Concat}\left({X}_{s},{X}_{m}\right)\right)+{X}_{{in}}$$
(14)

Loss function

It is very meaningful to reconstruct the fine-grained texture of the missing area of mural painting. However, there are multiple possible outcomes for reconstructed missing areas. To generate harmonious reconstruction results, we adopt different loss functions at different stages to guide the training of the model. We first train the coarse-grained network separately in an adversarial manner to generate seemingly complete images, and the discriminator also has preliminary discriminative capabilities during this training process. The objective function in this case is:

$$\mathop{\min }\nolimits_{{G}^{C}}\mathop{\max }\nolimits_{D}{L}_{{ad}}\left({G}^{C},D\right)+{\alpha }_{1}{L}_{1}({G}^{C})+{\alpha }_{2}g{L}_{{msssim}}({G}^{C})+{{\alpha }_{3}L}_{{mask}}({G}^{C})$$
(15)

where \({L}_{1}({G}^{C})={||}y-{G}^{C}({x}_{L},{x}_{M})|{|}_{1}\), \(g\) is the Gaussian filtering parameter. \({L}_{{msssim}}\left({G}^{C}\right)=1-{MS}{\rm{\_}}{SSIM}({G}^{C}\left({x}_{L},{x}_{M}\right),y)\). \({\alpha }_{1}\) is a weight factor for \({L}_{1}\). \({\alpha }_{2}\) is a weight factor for \({L}_{{msssim}}.\) \({\alpha }_{3}\) is a weight factor for \({L}_{{mask}}\). The combination of \({L}_{1}\) and \({L}_{{msssim}}\) can ensure the initial quality of the inpainted image43, but it cannot solve the problem of color change and context consistency. To alleviate this issue, we proposed a simple but effective mask loss \({L}_{{mask}}\), it defined as:

$${L}_{{mask}}({G}^{C})={\sum }_{i}{||VG}{G}_{i}\left(y\right)\,\cdot\, {x}_{m}-{{VGG}}_{i}\left({G}^{C}({x}_{L},{x}_{M})\right)\,\cdot\, {x}_{m}|{|}_{1}$$
(16)

where \({VG}{G}_{i}\) denotes the output of the i-th layer of the pre-trained VGG-19 network. We adopted the corresponding activation output from the ReLU1_1, ReLU2_1, ReLU3_1, ReLU4_1, and ReLU5_1 layers.

After the initial training, the fine-grained network is also introduced into the training of the model. Moreover, to reconstruct more refined texture details and colorization, we introduce a histogram loss \({L}_{{hist}}\)44 based on Eq. (15), which is beneficial to guide the pixel distribution of the inpainted image to maintain the original variance and standard deviation. \({L}_{{hist}}={\sum }_{i}\tau {||y}-h(\hat{y}){||}\), where \(h(.)\) is the histogram matching operation, \(\tau\) is the control factor. Therefore, the objective function is given by

$$\mathop{\min }\nolimits_{{G}^{C},{G}^{F}}\mathop{\max }\nolimits_{D}{L}_{{ad}}\left({G}^{C},{G}^{F},D\right)+{\alpha }_{1}{L}_{1}+{\alpha }_{2}g{L}_{{msssim}}+{{\alpha }_{3}L}_{{mask}}+{\alpha }_{4}{L}_{{hist}}$$
(17)

where \({\alpha }_{4}\) is a weight factor for \({L}_{{hist}}\).

Results

Experimental environment and setting

The proposed STMA-GAN is implemented with the Pytorch framework and runs on a platform with a Nvidia ® Tesla V100 SXM2. Part of the datasets for model training and testing were taken from ref. 27 We also obtained 2000 murals through web crawling technology and scanning from the mural album. Finally, the dataset used for model training after manual screening was 3500 murals. 50 murals were used for model testing. For mask images, we adopted the irregular mask dataset publicly available by Nvidia45. This dataset contains a large number of irregular masks with randomized shapes, sizes, and positions. The diversity and complexity of mask images can simulate large areas of random-shaped defects on the mural, such as falling-off blocks and mud stains. We multiply the mural with the binary mask image to simulate the damaged mural. To generate the edges of the mural, we first preprocess the mural using bilateral filtering to smooth out the noise, and then use DexiNed46 to obtain the fine edges of the mural. Figure 4 illustrates some of the murals, line drawings, and binary mask images in the dataset.

Fig. 4
figure 4

Murals, line drawings, and binary mask images.

Full size image

A two-stage training strategy is employed during the training process. However, the multi-stage training strategy can cause the problem of cumulative error in the training process of the model. This is because the results generated by the model during the previous stage of training are used as inputs to the model in the later stage. The output of the model in the previous stage is highly randomized, which can feed bad results into the next stage eventually leading to cumulative errors. To alleviate this issue, we only trained the coarse-grained network in the first stage. After 40,000 epochs, the training process of the coarse-grained network and the discriminator became stable, and the coarse-grained network could generate murals with better structure. Then, the second stage of training is carried out, where the fine-grained network is introduced into the model to train together. Since the coarse-grained network can already generate good results and the discriminator is also well-trained, the fine-grained network also converges faster under their guidance. The proposed model was trained for a total of 1e5 epochs with a mini-batch size of 2. The chosen number of epochs was based on the observation that validation accuracy plateaued after approximately 1e5 epochs, and further training did not significantly improve performance. The Adam optimizer (\({\beta }_{1}\) = 0.0, \({\beta }_{2}\) = 0.9) was used for model training with a learning rate of 1e-3. The weight factor \({\alpha }_{1}\) of \({L}_{1}\) is set to 1, the weight factor \({\alpha }_{2}\) of \({L}_{{msssim}}\) is set to 10, the weight factor \({\alpha }_{3}\) of \({L}_{{mask}}\) is set to 0.1, the weight factor \({\alpha }_{4}\) of \({L}_{{hist}}\) is set to 0.0005. The loss term weights were determined by performing a hyperparameter search on 20 validation murals. In the STMA block, MSDA contains four parallel dilated convolutions with the dilation rates \(d\) set to 1, 2, 4, and 8, respectively. The SwinT module adopts the default parameter of the Swin Transformer.

Comparison experiment

To validate the mural restoration performance of the model, it was evaluated both quantitatively and qualitatively. We compared the proposed model with Edge Connect16, CTSDG47, AOT-GAN4, ref. 27, and MAT48.

For quantitative assessment, PSNR49, SSIM49, and MSE50 metrics were used to evaluate the restored murals from the perspective of image quality. Generally speaking, the higher the values of the PSNR and SSIM metrics and the smaller the value of the MSE metric, the better the quality of the recovered image. FID51 and LIPS52 metrics to assess the characteristics of restored murals from the perspective of data distribution. The smaller the values of these two metrics, the more similar the restored mural feature distribution is to that of the real mural image. Table 1 lists the results of the quantitative comparison of the relevant methods.

Table 1 the results of the quantitative comparison of the related methods.
Full size table

As can be seen from Table 1, our proposed method achieves better results both in terms of distribution-based evaluation metrics and image-based evaluation metrics.

For the qualitative assessment, Figs. 5 and 6 show the results of the restoration of the damaged murals by the relevant methods. As can be seen from Fig. 5, Edge Connect blurs the content of the restored mural, CTSDG causes artifacts in the restored mural, and AOT-GAN do not refine the texture of the restored mural. The ref. 27 method is more effective in the overall restoration of murals. MAT does not restore the color and texture details of the mural well. STMA-GAN achieves better results in the detailing of restored murals. As can be seen from Fig. 6, although Edge Connect, CTSDG, and ref. 27 realize the restoration of the mural, the hanging ornaments next to the figures are not restored. MAT method resulted in the appearance of misplaced image content in the restored murals. AOT-GAN also restored only a small part of the hanging. STMA-GAN not only achieves the restoration of the mural but also the complete recovery of the missing hangings.

Fig. 5: Qualitative comparisons of the related methods.
figure 5

a Ground truth. b Masked image. c Repair result of Edge Connect. d Repair result of CTSDG. e Repair result of AOT-GAN. f Repair result of ref. [27]. g Repair result of MAT. h Repair result of the proposed method.

Full size image
Fig. 6: Qualitative comparisons of the related methods.
figure 6

a Ground truth. b Masked image. c Repair result of Edge Connect. d Repair result of CTSDG. e Repair result of AOT-GAN. f Repair result of ref. [27]. g Repair result of MAT. h Repair result of the proposed method.

Full size image

Ablation study

To better understand the impact of STMA blocks on the performance of the proposed method, we performed ablation experiments. We trained a model without the STMA block (denoted as STMA1-GAN), a model with only the MSDA module in the STMA block (denoted as STMA2-GAN), and a model with only the SwinT module in the STMA block (denoted as STMA3-GAN). Table 2 shows the comparison results of the performance of different models. It can be seen from Table 2 that the performance of the model decreases when the STMA module is removed, no matter from the perspective of data distribution or image quality. The performance of STMA2-GAN and STMA3-GAN is better than STMA1-GAN, which implies that using only a single component of STMA does help to improve the performance of the model, and the SwinT module improves the model performance more. The performance of the STMA-GAN model is the best, the main reason is that SwinT can capture global context information, and MSDA is good at extracting local features. Combining the two can make full use of their respective advantages and capture global and local information at the same time, to improve the performance of the model.

Table 2 Comparative results of ablation experiments.
Full size table

A visual effect comparison result of ablation experiments is shown in Fig. 7. From the overall visual effect, all models have better completed the repair of the damaged mural. However, it can be seen from Fig. 7d that the murals repaired by STMA1-GAN have color deviations. The restored area showed more green color. The color deviation of STMA2-GAN and STMA3-GAN is not very obvious, but the effect of texture detail restoration is not good. STMA-GAN achieves the best visualization results, which suggests that combining SwinT and MSDA can fully utilize their respective advantages. STMA is beneficial to improve the performance of models in color correction and detail restoration. This demonstrates that the STMA block can not only improve the learning ability and feature representation ability of the proposed model but also correct the color of the inpainted mural to some extent.

Fig. 7: Comparison results of ablation experiments on STMA blocks.
figure 7

a Ground truth. b Masked image. c Repair result of STMA-GAN. d Repair result of STMA1-GAN. e Repair result of STMA2-GAN. f Repair result of STMA3-GAN.

Full size image

The loss function also plays an important role in guiding model training, and we performed ablation experiments on the loss function as well. Since \({L}_{1}\) and \({L}_{{msssim}}\) are common combinations, we only explore \({L}_{{hist}}\) and \({L}_{{mask}}\). A model without \({L}_{{hist}}\) is denoted as STMA-GAN1 and a model without \({L}_{{mask}}\) is denoted as STMA-GAN2. As can be seen in Fig. 8, STMA-GAN1 and STMA-GAN2 are weaker than the performance of STMA-GAN, which indicates that the missing \({L}_{{mask}}\) and \({L}_{{hist}}\) reduces the performance of the model. \({L}_{{mask}}\) calculates the differences between mask feature maps, which helps the model to more accurately localize the feature areas that need to be repaired during training. It avoids causing unnecessary modifications to undamaged areas. \({L}_{{hist}}\) calculates the difference in the distribution of gray levels of the murals, which is beneficial to guide the model to optimize the contrast of the murals during training. It ensures that the restored mural is consistent with the ground truth in the grayscale distribution, making the restored mural more natural and realistic. Therefore, \({L}_{{mask}}\) and \({L}_{{hist}}\) are beneficial to guide the training process of the model.

Fig. 8: Comparative results of ablation experiments on loss function.
figure 8

a Comparison results of different models in PSNR. b Comparison results of different models in SSIM. c Comparison results of different models in MSE. d Comparison results of different models in FID. e Comparison results of different models in LIPS.

Full size image

User perceptual study

We also conducted a user study to evaluate the restoration performance of different methods for murals. We invited 20 users to evaluate 50 restored murals restored by different methods. The user scores the restored mural on a scale from 1 to 5 (from worst to best) concerning the original mural provided by us. The final average rating values are presented with two decimal places. Figure 9 shows the user ratings of the restored murals from the perspective of the overall visual effect and detailed textures. The visual effect evaluation of mural restoration is mainly on the naturalness and fidelity of the restored area. From an overall visual perspective, our proposed method received the highest ratings compared to the comparison methods, indicating that the mural restoration results of our proposed method are more acceptable to users. The evaluation of detail texture in mural restoration is mainly to restore the details of the repaired area and realize the smooth transition of the edge. As can be seen from Fig. 9, users also gave high ratings to our proposed method in terms of mural detail restoration, which indicates that our proposed method ensures the clarity of the details of the restored mural.

Fig. 9: User evaluation.
figure 9

a Evaluation performed by users on the restoration results of different methods in terms of visual quality. b Evaluation of the inpainting results of different methods by users in terms of detail textures.

Full size image

Discussion

Image inpainting is essentially an ill-posed inverse problem. Inpainting images with large damaged areas is still a very difficult challenge. According to the above experimental results, our proposed method achieves a relatively ideal visual effect, but there are still some problems when inpainting the more seriously damaged images. From Fig. 10, it can be seen that our proposed method can only repair the general contour of the face and fails to refine the texture details of the face (yellow-bordered area). Moreover, the proposed method also fails to estimate the original image content well (green-bordered area).

Fig. 10: An example.
figure 10

a Masked image. b Ground truth. c Repair result of the proposed method.

Full size image

This means that our proposed model still has some limitations in the image details of refined restoration and model reasoning ability. The marked areas in Fig. 10 are areas where the mural is more severely damaged or where the structural information is more complex. The large amount of missing information leads to the fact that our proposed model cannot rely on the contextual information of the image and the surrounding pixel information to infer the content of the missing area. Although our proposed model can generate restoration results that are consistent with the surrounding area, when the missing area is large and contains complex textures or objects, the model may not be able to generate textures and refined structures that exactly match the surrounding area, resulting in unnatural restoration results. In future work, image prior technology or advanced network backbone can be introduced to further improve the degree of refinement of the repaired image.

In addition, we use supervised learning to train the proposed model. However, the ground truth of the mural is lacking in the actual scene. Creating ground truth for murals is a labor-intensive and time-consuming process that requires expertise in art history, archeology, and possibly digital restoration. This makes it difficult to scale the supervised learning approach to a larger number of murals. Even if ground truth murals are available, they may not always be accurate or comprehensive due to human error, incomplete information, or changes over time. Inaccuracy in labels can lead to poor model performance and misleading results. Here are some potential solutions: (1) Some prior information of the mural is integrated into the training process of the model, to better guide the repair process of the model. (2) Exploring unsupervised or semi-supervised learning methods can mitigate the dependence on labeled data. (3) Utilizing transfer learning from related domains (e.g., image semantic information in general art) can help improve the model’s ability to generalize to complex mural restoration problems. Pre-trained models can be fine-tuned on limited labeled mural data to adapt to specific mural features. (4) Multi-modal or cross-modal learning techniques can leverage information from multiple sources to provide a more comprehensive understanding of murals.

The proposed method is mainly aimed at solving the large area of irregular shape damage on the mural, such as falling-off blocks and mud stains. This makes our method have certain limitations in the task of repairing different types of damaged murals. Murals, as invaluable cultural artifacts, face a wide range of degradation issues, including cracking, peeling, fading, and biological growth. These damages are often compounded by historical factors such as the materials used in their creation, environmental conditions, and human activities. In future work, we will design masks for different types of damaged murals and a unified restoration model for different types of degraded murals.

Inspired by the process of manual mural inpainting, we propose a novel two-stage GAN for mural inpainting. The main goal of the first stage is to use a coarse-grained network to achieve a coarse-grained semantic reconstruction of the damaged mural, to provide a basis for the subsequent finer restoration. The second stage focuses on achieving fine-grained feature reconstruction to restore local features and detailed information in the mural. The proposed STMA block combines the advantages of the Swin transformer module and the multi-scale dilated convolution attention module to enhance the overall learning and restore ability of the model. The training process of the model is guided by introducing different loss functions in the two-stage training strategy to ensure the restored performance of the model. Abundant experiments show that our proposed method can achieve a good restoration of murals.

In our future work, we will further improve the quality of mural restoration in terms of a model learning approach, model training strategy, and multimodal information fusion to promote the digital preservation and communication of cultural heritage. At the same time, to repair murals subjected to different types of damage, we will also design new masks and mural restoration models.