Introduction

Murals, as an essential form of traditional Chinese painting, contain rich historical, cultural, and artistic information, vividly recording the social customs and folk beliefs of multiple ethnic groups across different dynasties1,2,3. As illustrated in Fig. 1d, mural creation typically starts with outlining shapes through line drawing, followed by color rendering and further artistic refinement. Mural line drawings, characterized by their simple ink lines without embellishment or color rendering, utilize variations in line length, connectivity, and smoothness to express the texture and spirit of depicted subjects, thus forming distinct visual rhythms and becoming an independent artistic form. Therefore, line drawings serve as a critical representational technique in Chinese painting, indispensable in Chinese traditional painting, mural art, and folk painting4,5. Currently, line drawings of murals are primarily produced by manual tracing. Artists usually perform field mapping with simple tools under limited lighting conditions, which is time-consuming and requires extensive training. Although the introduction of digital technologies such as 3D laser scanning and digital orthophotography imagery has improved efficiency, the drawing process still largely depends on manual work by skilled professionals. Despite gains in productivity, substantial labor and time investments remain necessary. Furthermore, variations in artistic perception and technical skills among artists result in inconsistent drawing quality, and the limited number of qualified professionals further constrains productivity. Therefore, there is an urgent need for advanced technological solutions to significantly enhance the efficiency and consistency of mural line drawing generation.

Fig. 1: Edge detection and mural line drawings based on deep learning.
figure 1

a General edge detection, b object contour detection, c semantic edge detection, and d mural line drawings.

Full size image

Line drawing generation involves extracting line information from color murals to generate black-and-white images composed solely of lines and blank spaces. Mathematically, line drawing generation can be formulated as a pixel-level classification problem6, where each pixel of a two-dimensional image is classified according to its probability of belonging to line structures. Similar to edge images, mural line drawings depict object contours through black-and-white pixels, emphasizing line and shape representation. However, unlike traditional edge detection tasks7,8,9, which typically focus on high-contrast edges in natural images and consequently lack detailed line features, mural line drawing generation emphasizes the details of lines and textures. Therefore, there is a significant difference between mural line drawing generation and natural image edge detection. Edge detection in natural images relies heavily on large public datasets for training and mainly captures object contours. In contrast, mural data are scarce, and the extraction of mural line drawings requires capturing richer structural features and artistic details, such as intricate clothing patterns (garments, headwear, etc.) and detailed facial expressions (eyebrows, eyes, etc.). Particularly, mural line drawing generation demands more precise and expressive lines aligned with traditional artistic styles. As depicted in Fig. 1a–c, deep learning-based edge detection methods can be categorized into three types: (1) general edge detection10,11, (2) object contour detection12,13, and (3) semantic edge detection14,15. The general edge detection is to identify significant pixel-value changes in images, resulting in detection outputs that contain considerable noise due to the inclusion of all edges. Object contour detection typically simplifies results and excludes internal texture or detail. Semantic edge detection yields concise edges by filtering out irrelevant details. While edge detection in natural images emphasizes contour clarity and object recognition, mural line drawings require finer, artistically meaningful line generation, as demonstrated in Fig. 1d.

In recent years, edge detection techniques have significantly advanced in the fields of computer vision and image processing. Traditional approaches, such as Canny16 and Sobel17, remain widely used and have been optimized across various applications18,19. With the rise of deep learning, CNN-based edge detection methods have become mainstream20, considerably improving accuracy and robustness21,22. Recently, Transformer structures have also been introduced into edge detection tasks, showing significant advantages over CNN-based methods in capturing long-range dependencies23. Moreover, edge detection methods based on generative adversarial networks (GANs) have been developed to generate clearer edge maps and effectively suppress background noise. Additionally, edge detection integrated with hardware optimization has become an important trend, showing great practical value in fields such as intelligent monitoring and autonomous driving24,25.

For line drawing generation, early studies primarily relied on handcrafted features, interactive methods, and various edge detection operators26,27,28, such as the Canny and Sobel operators, to identify adjacent regions in images, forming continuous lines that outline the structural curves of murals. Liu J et al. 29 focused on the Dunhuang Mogao Grotto murals and employed computer-aided interactive techniques to first trace the mural boundaries and then refine the line drawings using a virtual brush. Similarly, He et al. 30 also studied Dunhuang Mogao Grotto murals and adopted a layered interactive approach to progressively generate stroke-based line drawings. In the study by Sun et al. 31, mural image data were sourced from true-color mural images provided by the Dunhuang Academy and publicly available mural artifact images, and 12 real line drawings were manually created. Their method initially applied heuristic routing to detect stroke outlines, followed by high-frequency enhancement filtering to extract internal stroke details, and finally, cooperative representation to generate complete strokes. Although these methods can produce line drawings that meet certain artistic requirements, they heavily rely on manual interaction, resulting in low efficiency and difficulty in handling large-scale data or automated generation tasks.

Benefiting from the powerful feature representation capabilities of deep learning, recent research has focused on designing sophisticated network architectures to learn high-level semantic representations32,33,34,35. Deng et al. 36 proposed a deep structural contour detection framework that integrates edge location and orientation information into a novel loss function, achieving improved accuracy in extracting structural contours from images. In the study by Wang et al. 37, the research focused on Thangka murals, where an edge detection model trained on the natural image BIPED dataset was directly applied to generate Thangka line drawings. Similarly, Wang et al. 38 focused on Dunhuang murals and generated mural line drawings using an edge detection model trained on the BIPED dataset. Their approach introduced a focal Tversky loss function to suppress background pixels near edge pixels and incorporated dilated convolution and spatial attention modules to enhance hierarchical features and enrich scale information. Liu et al. 39 also studied Dunhuang murals, using an edge detection model trained on a natural image dataset to generate mural line drawings. Their approach proposed a residual self-attention and convolution hybrid module to integrate local and global features, thereby improving the extraction of mural line drawings. Peng et al. 40 focused on cultural heritage murals and used deep learning models for line drawing extraction. Their approach introduced a detail-aware bidirectional cascaded network combined with a multi-scale U-Net framework to enhance feature extraction capabilities. In the study by Yu et al. 41, simulated mural samples were created using real mural production techniques to generate realistic line drawings. Their method enhanced mural images and employed Laplacian edge detection combined with a fine noise removal module to extract optimized line drawings. It is evident that due to the lack of publicly available datasets for mural line drawings, most current studies on mural line drawing generation rely on models trained and evaluated using natural image datasets. While this approach is feasible, it has inherent limitations in capturing the rich structural details and artistic features of murals. Mural line drawings require careful consideration of the smoothness and detailed representation of each stroke, imposing higher demands on line extraction and expression. Most existing edge detection methods are not specifically designed for mural line drawing generation, making them insufficient to fully capture mural-specific details and artistic styles. Therefore, effectively adapting existing methods for mural line drawing generation remains a pressing challenge that needs to be addressed.

To address the above challenges, this study proposes an automatic mural line drawing generation method, incorporating edge enhancement, line drawing extraction, and denoising technologies, enabling efficient and accurate extraction of mural lines. Specifically, this method first enhances the mural images’ edge information using contrast-limited adaptive histogram equalization (CLAHE) and bilateral filtering (BF), providing high-quality inputs for subsequent line extraction. Secondly, a neural network for mural line drawings (MLineNet) is employed to extract mural edge features. Finally, a cycle-consistent generative adversarial network (CycleGAN) is introduced to refine and denoise the extracted lines, resulting in high-quality line drawings with clear, natural appearance and rich structural details. Using Dunhuang murals as a primary research subject, a mural line-drawing generation model was constructed based on the proposed method. The reliability and effectiveness of this model were quantitatively verified using multiple evaluation indicators, including structural similarity index (SSIM), texture complexity (TC), line connectivity index (LCI), and a comprehensive score (Q). The final results demonstrate that the proposed method achieves balanced performance in structural similarity, cleanliness, and connectivity of the image, showing good overall effectiveness.

The structure of this paper is as follows: The “Methods” section introduces the overall process of mural line drawing generation and details three key components, including mural edge enhancement, line drawing extraction, and line drawing denoising. The “Results” section presents the generation outcomes of Dunhuang murals, analyzes the performance of different structures, compares the proposed method with other methods, and evaluates our method’s generalization capability through line drawing generation from Baisha murals. Finally, the “Discussion” section summarizes the findings and limitations of this study.

Methods

Overview

The Dunhuang Mogao Grottoes42,43, located in Dunhuang, Gansu Province, China, are one of the largest and best-preserved repositories of Buddhist art in the world. Established in the 4th century Anno Domini, they have undergone continuous development over a millennium and currently consist of 492 caves, with mural paintings covering an area of over 50,000 square meters. The murals encompass a wide range of themes, including Buddhist figure paintings, transformation paintings, narrative paintings, and donor portraits, reflecting not only the spread and evolution of Buddhist beliefs but also the social and artistic styles of different historical periods. Buddhist figure paintings depict various representations of Buddhas, Bodhisattvas, and celestial kings, characterized by smooth lines and vibrant colors, showcasing artistic features unique to each dynasty. Transformation paintings illustrate Buddhist scriptures in visual form, making the teachings more accessible and easier to disseminate. Narrative paintings depict stories from the Buddha’s past lives and karmic tales, promoting Buddhist doctrines and moral principles. Donor portraits portray the patrons who financed the construction of the caves, providing insight into the social structure and clothing culture of the time. These murals are not only treasures of religious art but also serve as invaluable historical, cultural, and social records, holding immense artistic and academic significance. DhMurals171444 is a dataset specifically designed for the study of Dunhuang Mogao Grottoes murals. It comprises 1714 images along with incompletely annotated reference line drawings, aiming to address the limitation of available data caused by natural weathering and human-induced damage to the murals.

This paper proposes an automated method for generating mural line drawings, integrating mural edge enhancement, deep learning-based line extraction, and generative adversarial network-based denoising techniques to efficiently and accurately generate mural line drawings. Based on the DhMurals1714 dataset, this method seeks to mitigate issues of detail loss and blurring in reference line drawings of Dunhuang murals, enabling precise and high-quality extraction of mural line features. As shown in Fig. 2, the proposed approach consists of three key steps: mural edge enhancement, line drawing extraction, and line drawing denoising. First, to improve the quality of mural image edges, CLAHE and BF are applied45, enhancing edge details in the initial images and providing high-quality inputs for subsequent line drawing extraction. Then, in the line drawing extraction stage, the deep learning network MLineNet is employed to extract mural line drawings. This network adopts an encoder-decoder structure, incorporating multi-scale feature fusion and edge-aware optimization strategies to capture lines at various scales while preventing excessive sharpening or information loss. MLineNet generated line drawings effectively reproduce the primary line drawings of murals; however, due to annotation errors and the incompleteness of reference line drawings, noise and false edges still exist, affecting the artistic quality and usability of the extracted lines. To further refine the line quality, this method introduces CycleGAN for unsupervised denoising and correction46. Given the lack of complete and precisely paired ground-truth line drawings, CycleGAN effectively removes noise and restores line smoothness and integrity through unsupervised learning, using only noisy line drawings and incomplete reference line drawings as input. As a result, the CycleGAN refined line drawings not only preserve the structural information of complete lines but also eliminate redundant noise and false edges, making the generated lines more detailed, clear, and natural, aligning with the esthetic standards of mural artwork.

Fig. 2
figure 2

The overall workflow of mural line drawing generation.

Full size image

Mural edge enhancement

Although the reference line drawings in the Dunhuang dataset display the edge structures of images, they suffer from partial detail loss or blurring due to inaccurate annotations. To address this issue, this study applies CLAHE and BF for edge enhancement before line drawing extraction, as shown in Fig. 3. CLAHE and BF are important image enhancement techniques widely used in tasks that improve image details and edge features. In mural image processing, the combination of CLAHE and BF achieves superior edge enhancement effects. CLAHE enhances local brightness differences to make edges more prominent, while BF smooths noise and removes artifacts introduced during enhancement, while preserving the edge features enhanced by CLAHE. The synergy of these techniques demonstrates outstanding performance in mural image edge enhancement, providing a solid foundation for subsequent line drawing extraction.

Fig. 3
figure 3

Visualization of mural edge enhancement.

Full size image

In mural image processing, CLAHE enhances edge features, making edge information clearer while preventing excessive enhancement in high-contrast areas. CLAHE is an improved version of the traditional histogram equalization method, addressing the issue where HE may introduce excessive enhancement and artifacts in high-contrast regions. The key feature of CLAHE is its localized approach, dividing the image into small contextual regions (sub-blocks) for histogram equalization while applying a contrast threshold to each region’s pixels. This prevents the unevenness that global enhancement may introduce. Its formula is as follows:

$${H}^{{\prime} }(i)=\min (H(i),T)+\frac{\sum _{j}\max (H(j)-T,0)}{N}$$
(1)

where \({H}^{{\prime} }(i)\) represents the adjusted pixel value distribution in the histogram, \(T\) is the contrast threshold, and \(N\) is the total number of pixels.

BF preserves edge structures while smoothing image noise by integrating geometric distance and pixel intensity similarity, preventing the edge blurring often caused by traditional linear filtering methods. As a nonlinear filtering technique, BF combines information from the spatial domain and the intensity domain to smooth images while effectively preserving edge features. The core idea is to compute a weighted average of each pixel and its neighboring pixels, where the weight is determined by both spatial distance and intensity differences. The mathematical formulation of bilateral filtering is as follows:

$${I}^{{\rm{{\prime} }}}(x)=\frac{\sum _{y\in {\mathscr{N}}(x)}{G}_{{\rm{s}}}(\parallel x-y\parallel ){G}_{{\rm{r}}}(|I(x)-I(y)|)I(y)}{\sum _{y\in {\mathscr{N}}(x)}{G}_{{\rm{s}}}(\parallel x-y\parallel ){G}_{{\rm{r}}}(|I(x)-I(y)|)}$$
(2)

where \(I(x)\) is the pixel intensity at location \(x\) in the input image, \({\mathscr{N}}{\mathscr{(}}x)\) represents the neighborhood of \(x\), \({G}_{{\rm{s}}}(\parallel x-y\parallel )\) is the Gaussian function in the spatial domain, which measures geometric distance between pixels, and \({G}_{{\rm{r}}}(|I(x)-I(y)|)\) is the range filter, which evaluates intensity or color similarity between pixels. This ensures that neighboring pixels with similar intensities have a greater influence on the central pixel, while regions with significant intensity differences have less influence, thereby preserving edge information.

Line drawing extraction

This study employs MLineNet (as shown in Fig. 4) as the deep learning network for mural line drawing extraction, aiming to automatically produce high-quality line drawings to support cultural heritage digitization, artistic style transfer, computer-assisted painting, and heritage preservation applications. Mural line drawings are not only a form of artistic representation but also essential data for mural restoration, analysis, and research. Existing deep learning-based edge detection models10,35,47 have demonstrated good performance in general edge detection tasks for natural images. These methods often rely on global context modeling, denoising processes based on generative models, uncertainty modeling, or high-precision operator design to improve accuracy and robustness in edge detection. However, these models are mainly designed for general object boundary detection tasks, with a focus on edge localization accuracy and model robustness. Compared with existing deep learning-based line drawing extraction methods37,38,39,40,41,42, MLineNet is designed with the specific characteristics of mural line drawing tasks. It uses an encoder-decoder architecture combined with a multi-scale branch design (H1, H2, H3) and feature fusion to separately extract coarse contours, local details, and global structural features. MLineNet places more emphasis on the clean, connectivity, and structural integrity of lines, rather than solely on edge detection accuracy.

Fig. 4
figure 4

The architecture of the mural line drawing extraction network, named MLineNet.

Full size image

Specifically, MLineNet includes three feature extraction stages within the encoder–decoder architecture, each responsible for capturing coarse contours, enhancing local details, and optimizing overall structural integrity. It incorporates a multi-scale feature fusion strategy to enhance the network’s capacity to represent details at different scales. The network takes an input mural image of size 720 × 720 × 3 and processes it through three stages to progressively extract features at different scales. In the feature extraction phase, the input first passes through two 3 × 3 convolution layers to extract local features and capture the basic edge structure of the mural. Max pooling (3 × 3) is then used to gradually reduce the spatial resolution of the feature maps and capture higher-level global features. For instance, the first stage increases the number of channels to 16 and reduces the feature map size to 360 × 360, while deeper layers further reduce the size to 180 × 180 with an increase in channels, ensuring the model can learn line information at different scales. Since mural line drawings contain rich fine details, such as facial features, clothing patterns, and decorative backgrounds, simple pooling operations may lead to a loss of detail. Therefore, 1 × 1 convolutions are introduced in certain layers for channel compression to preserve detailed features while controlling computational cost. In addition, residual connections are used within the encoder–decoder structure to establish information pathways, allowing lower-level features to be directly transmitted to subsequent layers. This helps mitigate feature loss in deep networks and enhances the retention of detailed lines.

In the decoding phase, MLineNet employs upsampling layers (UpConv) to gradually restore the feature maps to the original input resolution (720 × 720), ensuring that the output line drawing aligns spatially with the input image and retains as much detail as possible. However, simple upsampling is not sufficient to produce high-quality line drawings. To further enhance line quality, MLineNet introduces a feature fusion module during decoding. This module concatenates the feature maps from the different scale branches (H1, H2, H3) as input, where H1 captures coarse contours, H2 enhances local details, and H3 specifically optimizes overall structural integrity, supplementing global framework information and reducing line discontinuities and local deviations. The fusion module consists of depthwise separable convolutions (DWConv, 3 × 3), Smish activation, and PixelShuffle operations. DWConv performs per-channel convolutions to extract local features with low computational cost, while PixelShuffle increases resolution and rearranges the feature structure to preserve detail distribution. Finally, these three features are integrated through a fusion layer to ensure that the generated line drawing maintains global coherence while preserving local detail. The fusion layer is defined as follows:

$$X={\rm{C}}{\rm{o}}{\rm{n}}{\rm{c}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{n}}{\rm{a}}{\rm{t}}{\rm{e}}({H}_{1},{H}_{2,}{H}_{3})$$
(3)
$${X}^{{\rm{{\prime} }}}={{\rm{P}}{\rm{S}}(W}_{{\rm{d}}}\,* \,{\rm{S}}{\rm{m}}{\rm{i}}{\rm{t}}{\rm{h}}(X))$$
(4)
$$Y={{X}^{{\rm{{\prime} }}}+{\rm{P}}{\rm{S}}(W}_{{\rm{d}}}\,* \,{\rm{S}}{\rm{m}}{\rm{i}}{\rm{t}}{\rm{h}}({X}^{{\rm{{\prime} }}}))$$
(5)

where \(X\) represents the concatenated result, \({H}_{1},{H}_{2,}{H}_{3}\) are features extracted at different scales, \({W}_{{\rm{d}}}\) denotes the depthwise separable convolution kernel, Smish is the activation function, and \({\rm{P}}{\rm{S}}\) represents PixelShuffle, which performs pixel rearrangement. \({X}^{{\prime} }\) is the preliminary processed feature map, and \(Y\) is the final fused feature map.

Line drawing denoising

In the automatic generation of mural line drawings, the reference line drawings often exhibit missing or incomplete lines in certain areas. Directly relying on these incomplete annotations for training may lead to a decline in the quality of the generated line drawings, affecting their final visual effect and subsequent applications. To address this issue, we first employed image enhancement techniques and MLineNet during training to extract preliminary line drawings that compensate for the missing information in the reference data. However, although MLineNet can extract relatively complete line structures using deep learning techniques, the imperfections in the reference line drawings may still introduce noise during the extraction process. This can lead to blurred lines in some areas, discontinuous edges, or excessive pseudo-edges in the background. The presence of noise not only affects the overall clarity of the line drawings but may also interfere with subsequent mural studies, artistic style analysis, or digital archiving. Therefore, to further optimize the quality of the generated line drawings, this paper introduces the CycleGAN model to denoise and refine the initially generated noisy line drawings, producing clearer, smoother, and structurally complete mural line drawings.

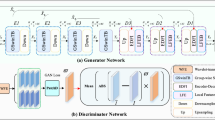
The advantage of CycleGAN lies in its ability to learn the mapping between domains through unsupervised learning from unpaired data. Traditional image denoising methods typically rely on strictly paired datasets, where each noisy image must correspond to a clean target image for the model to learn the denoising mapping. However, in the task of generating mural line drawings, due to the complexity and uniqueness of historical artifacts, it is often nearly impossible to obtain perfectly matched, clean line drawings as supervision signals, making paired data nearly infeasible. Against this backdrop, CycleGAN introduces a cycle consistency loss, constructing a closed-loop structure that maps from the noisy domain to the clean domain and then back again, ensuring that the input image can be as close as possible to the original after two mappings. This mechanism allows the model to effectively learn denoising and structural restoration capabilities even in the absence of paired supervision, making it particularly suitable for practical applications like mural line drawings, where obtaining ideal training data is challenging. Specifically, as shown in Fig. 5, CycleGAN consists of two generators and two discriminators. The input noisy line drawing (source domain X) and the reference line drawing (target domain Y) are not strictly paired. The generator \(G\) maps the source domain X to the target domain Y, while the inverse generator F maps the generated target domain Y back to the original source domain X. The training objectives for generators and discriminators are defined by adversarial loss, where \({{\mathcal{L}}}_{\mathrm{GAN}}(G,{D}_{Y})\) represents the adversarial loss between generator \(G\) and discriminator \({D}_{Y}\) measuring the realism of the generated image \(G(x)\). Similarly, \({{\mathcal{L}}}_{{\rm{G}}{\rm{A}}{\rm{N}}}(F,{D}_{X})\) represents the adversarial loss between the inverse generator \(F\) and discriminator \({D}_{X}\), evaluating the authenticity of the generated image \(F(y)\). The adversarial loss function is defined as follows:

$${{\mathcal{L}}}_{{GAN}}(G,{D}_{Y})={{\mathbb{E}}}_{y\sim {p}_{\text{data}}(y)}[\log {D}_{Y}(y)]+{{\mathbb{E}}}_{x\sim {p}_{\text{data}}(x)}[\log (1-{D}_{Y}(G(x)))]$$
(6)
$${{\mathcal{L}}}_{{\rm{G}}{\rm{A}}{\rm{N}}}(F,{D}_{X})={{\mathbb{E}}}_{x\sim {p}_{\text{data}}(x)}[{\rm{l}}{\rm{o}}{\rm{g}}{D}_{X}(x)]+{{\mathbb{E}}}_{y\sim {p}_{\text{data}}(y)}[{\rm{l}}{\rm{o}}{\rm{g}}(1-{D}_{X}(F(y)))]$$
(7)

where \(x\) is the source domain image (noisy line drawing), \(y\) is the target domain image (reference line drawing), and \({p}_{\text{data}}(x)\) represents the data distribution of source domain images, and \({\mathbb{E}}\) is the expectation operator, which denotes the expected loss over the images. \({{\mathbb{E}}}_{x\sim {p}_{\text{data}}(x)}\) represents the expectation calculation over samples x drawn from the probability distribution \({p}_{\text{data}}(x)\), and \({{\mathbb{E}}}_{y\sim {p}_{\text{data}}(y)}\) follows the same principle. \({D}_{X}\) is the discriminator responsible for determining whether an image belongs to the source domain X, and \({D}_{Y}\) serves the same function for the target domain Y.

Fig. 5
figure 5

Line drawing denoising using CycleGAN.

Full size image

To ensure a reasonable transformation from the source domain to the target domain, CycleGAN introduces cycle consistency loss. This loss ensures that the generated image maintains structural and content consistency with the input image by mapping the transformed image back to its original domain using the inverse generator F, then computing the difference between the original and reconstructed images. The cycle consistency loss function is defined as follows:

$${{\mathcal{L}}}_{{\rm{c}}{\rm{y}}{\rm{c}}}(G,F)={{\mathbb{E}}}_{x\sim {p}_{\text{data}}(x)}[\parallel F(G(x))-x{\parallel }_{1}]+{{\mathbb{E}}}_{y\sim {p}_{\text{data}}(y)}[\parallel G(F(y))-y{\parallel }_{1}]$$
(8)

where \(F(G(x))\) represents the source domain image x mapped through generator G and then back through inverse generator F, and \(G(F(y))\) represents the target domain image y mapped through F and then back through G. The L1 norm (\(\parallel \,\cdot \,{\parallel }_{1}\)) is used to calculate the pixel-wise difference between images. The final loss function consists of both adversarial loss and cycle consistency loss:

$${\mathcal{L}}(G,F,{D}_{X},{D}_{Y})={{\mathscr{L}}}_{{\rm{G}}{\rm{A}}{\rm{N}}}(G,{D}_{Y})+{{\mathscr{L}}}_{{\rm{G}}{\rm{A}}{\rm{N}}}(F,{D}_{X})+{{\mathscr{L}}}_{{\rm{c}}{\rm{y}}{\rm{c}}}(G,F)$$
(9)

By leveraging CycleGAN, this study restores clear and complete mural line drawings from noisy and incomplete images. Through adversarial training and cycle consistency loss, the CycleGAN model effectively removes noise while preserving the structural integrity of the images, ultimately generating high-quality denoised and restored mural line drawings.

Results

In this part of the study, we conducted comprehensive experiments on the DhMurals1714 dataset and further performed generalization validation on the Baisha mural dataset to evaluate the reliability of the proposed automated mural line drawing generation method. The experiments include both qualitative analysis and quantitative comparisons to thoroughly assess the effectiveness of the approach. This section provides a description of datasets, implementation details, and results analysis.

Datasets description

DhMurals1714 is a dataset specifically designed for the study of murals from the Mogao Caves in Dunhuang. It contains a total of 1714 images, each with a resolution of 720 × 720 pixels44. The dataset was created to address the scarcity of usable mural data caused by natural weathering and human damage. Following a random sampling strategy, the dataset was divided into a 7:3 ratio for training and testing, with 1200 images used for training and 514 for testing.

The Baisha mural dataset originates from the Dading Pavilion murals located in Baisha Town, Yulong Naxi Autonomous County, Lijiang City, Yunnan Province48,49. These murals serve as an important source for the study of religious art in Southwest China during the Ming and Qing dynasties and have recently undergone digital preservation and scholarly analysis. The original mural image has a resolution of 5251 × 7406 pixels. By applying a sliding window of 720 pixels with a stride of 680, 70 sub-images of size 720 × 720 pixels were extracted, all of which were used for testing purposes.

Implementation details

The experiments were conducted using an NVIDIA A40 GPU, with PyTorch as the deep learning framework. For training the MLineNet model, we adopted the Adam optimizer to ensure training stability and convergence efficiency. The initial learning rate was set to 0.005 and was dynamically adjusted using a cosine annealing schedule, allowing the learning rate to gradually decrease during training to accommodate multi-scale feature optimization. To improve the model’s generalization ability on the DhMurals1714 dataset, we designed a comprehensive data augmentation scheme. Each training image was augmented with three types of rotation (90°, 180°, and 270°), three scaling factors (2.0, 1.2, and 0.4), and two gamma correction values (0.3030 and 0.6060), resulting in 8 augmented samples per original image. Based on 1200 training images, a total of approximately 10,800 samples (720 × 720 pixels) were generated to simulate the diverse styles of mural line drawings, thereby enhancing the model’s adaptability to unseen data. The training process involved pretraining the model on the BIPED dataset, followed by fine-tuning on the DhMurals1714 dataset to better capture the structural features of Dunhuang mural line art. A batch size of 8 was used, with a total of 60 epochs. An early stopping strategy was applied after 30 epochs to prevent overfitting.

In the training of the CycleGAN model, modeling was also based on the aforementioned 1200 training images with a size of 720 × 720 pixels. To clearly define the source domain (noisy domain) and the target domain (clean domain), we consider the preliminary line drawings as the source domain images (i.e., extracted line drawings with more noise, broken lines, or redundant elements), and the reference line drawings as the target domain images (i.e., reference line drawings) used to guide the generator in learning the denoising mapping. In terms of network structure, the generator adopts a ResNet architecture, while the discriminator uses a PatchGAN network. For loss function design, CycleGAN incorporates both adversarial loss and cycle consistency loss, with the adversarial loss weight set to 1.0 and the cycle consistency loss weight set to 10.0. The optimizer is Adam with an initial learning rate of 0.0002 and a batch size of 2. Training is conducted over a total of 100 epochs, with the learning rate remaining constant for the first 50 epochs and then linearly decaying to 0 over the remaining 50 epochs, in order to stabilize the training process and improve final performance.

Evaluation metrics

To objectively and accurately evaluate the quality of the generated mural line drawings, multiple quantitative evaluation metrics are selected in this study. These metrics comprehensively assess various aspects of the image, including structural similarity, texture complexity and line connectivity, providing a strong basis for model optimization. Specifically, the selected metrics include SSIM, TC, LCI, and Q, which integrates all three indicators.

SSIM50 evaluates the fidelity of the generated image to the original mural image in terms of luminance, contrast, and structural information, reflecting the model’s accuracy in overall structural restoration. A higher SSIM value indicates greater structural similarity and perceptual quality. The SSIM is calculated as follows:

$$\text{SSIM}(x,y)=\frac{(2{\mu }_{x}{\mu }_{y}+{c}_{1})({\sigma }_{{xy}}+{c}_{2})}{({\mu }_{x}^{2}+{\mu }_{y}^{2}+{c}_{1})({\sigma }_{x}^{2}+{\sigma }_{y}^{2}+{c}_{2})}$$
(10)

where \({\mu }_{x}\) and \({\mu }_{y}\) are the mean intensities of images \(x\) and \(y\), \({\sigma }_{x}\) and \({\sigma }_{y}\) are their standard deviations, and \({\sigma }_{{xy}}\) is their covariance. Constants \({c}_{1}\) and \({c}_{2}\) are used to avoid division by zero. SSIM values typically range from 0 to 1, with values closer to 1 indicating higher structural and perceptual consistency.

TC evaluates the simplicity of line patterns in the image. This metric is derived from the contrast feature of the gray-level co-occurrence matrix (GLCM) proposed by Haralick et al. 51. Higher contrast indicates greater gray-level variation and more complex textures. Figure 6 shows two 4 × 4 GLCM examples illustrating structural differences between high and low TC cases. The high-TC matrix (left) is concentrated near the diagonal, indicating smooth transitions and orderly structures, while the low-TC matrix (right) shows more values far from the diagonal, reflecting abrupt gray changes and noisy patterns. To ensure TC increases with visual simplicity, we apply an inverse normalization to the contrast, making the TC value positively correlated with cleanliness:

$${\rm{T}}{\rm{C}}=\frac{1}{1+{\rm{C}}{\rm{o}}{\rm{n}}{\rm{t}}{\rm{r}}{\rm{a}}{\rm{s}}{\rm{t}}}\times 100{\rm{ \% }}$$
(11)
$${\rm{C}}{\rm{o}}{\rm{n}}{\rm{t}}{\rm{r}}{\rm{a}}{\rm{s}}{\rm{t}}={\rm{l}}{\rm{o}}{\rm{g}}\left(1+\sum _{{\rm{i}},{\rm{j}}}{({\rm{i}}-{\rm{j}})}^{2}{\rm{P}}({\rm{i}},{\rm{j}})\right)$$
(12)

where \(P(i,j)\) represents the gray-level co-occurrence matrix, and \(i\) and \(j\) are the grayscale values of the image pixels.

Fig. 6
figure 6

Differences between high and low TC.

Full size image

LCI measures the connectivity and completeness of lines in the image. Based on the theory of connected regions in image processing, it assesses whether the lines form a single or multiple complete structures52. The core idea is to calculate the ratio of the largest connected line region to the total number of line pixels. Figure 7 illustrates two examples of different LCI levels: the high-LCI image has continuous lines forming one main connected region with minimal gaps or noise; the low-LCI image contains fragmented lines with multiple disconnected segments. To better capture local structural consistency in large images, the image is divided into a 9 × 9 grid and the local LCI is computed in each region, with the final LCI being their average:

$${\rm{L}}{\rm{C}}{\rm{I}}=\frac{{N}_{\text{connected}}}{{N}_{\text{total}}}$$
(13)

where \({N}_{\text{connected}}\) is the number of pixels in the largest connected region and \({N}_{\text{total}}\) is the total number of line pixels. The LCI ranges from 0 to 1, with higher values indicating better connectivity and clearer line structures.

Fig. 7
figure 7

Differences between high and low LCI.

Full size image

Finally, the comprehensive evaluation Q is the average of the three aforementioned metrics, providing an overall quality assessment. The closer Q is to 1, the better the model’s overall performance across all indicators. The calculation formula is as follows:

$$Q=\frac{{\rm{S}}{\rm{S}}{\rm{M}}{\rm{I}}+{\rm{T}}{\rm{C}}+{\rm{L}}{\rm{C}}{\rm{I}}}{3}\times 100{\rm{ \% }}$$
(14)

Mural edge enhancement

This study applies edge enhancement processing to Dunhuang mural data prior to line drawing extraction using CLAHE and BF, as shown in Fig. 8. Specifically, (a) represents the original mural, while (b) is the corresponding heatmap, where colors indicate the magnitude of gradient variations—red regions denote higher gradient changes, while blue regions also indicate lower gradient variations. (c) presents the heatmap after CLAHE processing, which enhances local contrast and highlights edge details. (d) shows the result of applying BF filtering after CLAHE, where bilateral filtering effectively reduces texture noise, leading to smoother and more continuous edge information. Finally, (e) is the enhanced mural, in which the primary structural features become more distinct, and edge contrast is improved, providing a more precise input for subsequent line drawing extraction tasks. It is evident that the original heatmap (b) exhibits lower gradient edge structures of the mural, particularly in finer details such as garment textures, ornaments, and background patterns corresponding to hand gestures, where gradient variations are weak, making edge extraction challenging. After CLAHE processing (c), edge details are significantly enhanced, with more pronounced gradient variations in clothing patterns and character outlines, facilitating better feature distinction. Further integration of BF filtering (d) reduces edge noise to some extent, while maintaining relatively smooth and continuous contours, mitigating the texture interference caused by excessive enhancement. The final enhanced mural (e) not only preserves the original artistic characteristics of the mural but also effectively enhances the representation of primary structural elements, making line features more prominent and laying a solid foundation for high-precision line drawing extraction.

Fig. 8: Comparison of mural edge enhancement effects.
figure 8

a Original mural, b mural heatmap, c heatmap after CLAHE, d heatmap after CLAHE and BF, and, e enhanced mural.

Full size image

Line drawing extraction

To verify the effectiveness of MLineNet in the task of mural line drawing extraction, this study extracted line drawings based on the enhanced Dunhuang mural dataset. As shown in Fig. 9, MLineNet’s performance in extracting mural line drawings is illustrated at different feature levels (H1–H3), as well as the final fused output (Y), while Fig. 10 presents the zoomed-in details. Through the encoder–decoder structure, the network first extracts features from low to high levels, and then utilizes multi-scale feature fusion to ensure that details at each scale are fully preserved. Each feature layer corresponds to different image features and details, and after fusion, it ensures a balance between the artistic expression and stability of mural line drawings. Specifically, Fig. 10c presents low-level features, which primarily capture rough outlines and shapes of the mural; Fig.10d reveals more details, particularly in the finer parts of the mural’s lines; Fig. 10e further enhances the overall contour clarity while retaining more detailed information. By fusing these different scales, the final result in Fig. 10f achieves a well-balanced representation of line detail and connectivity. The experimental results show that MLineNet successfully realizes both fine expression and smooth connectivity of lines. Through multi-scale feature fusion, the model not only captures the delicate brushstrokes in murals but also preserves the overall artistic contours of the image. Notably, with the integration of the Fusion layer, the model effectively enhances the hierarchical structure and stability of lines, ensuring that each stroke is clearly presented within complex backgrounds. However, as observed from the results, although details are well preserved, some regions still contain noise.

Fig. 9: Intermediate feature layers and final fusion result of MLineNet.
figure 9

a Mural, b reference line drawings, c H1 heatmap, d H2 heatmap, e H3 heatmap, and f fusion result.

Full size image
Fig. 10: Local comparison of Intermediate feature layers and final fusion result of MLineNet.
figure 10

a Mural, b reference line drawings, c H1 heatmap, d H2 heatmap, e H3 heatmap, and f fusion result.

Full size image

Line drawing denoising

This study adopts CycleGAN to perform denoising tasks for mural line drawings, aiming to recover images with clearer lines and more complete structures from preliminary line drawings with noise. We use the noisy line drawings extracted in the previous steps (Fig. 11c) as source domain images and the reference line drawings (Fig. 11b) as target domain images, training the model in an unsupervised learning manner to learn the mapping from noisy to clean images, thereby achieving effective denoising and structural restoration. Figure 11 presents a visual comparison of several methods, including CycleGAN, as well as three image denoising methods: Non-Local Means (NL-Means)53, Wiener filter54, and Pix2pix55. All methods operate on the same preliminary line drawings, and the comparative results of different denoising methods and local approaches are shown in Figs. 11 and 12. Specifically, (b) shows the reference line drawings, which are handcrafted line drawings extracted from murals, demonstrating the edge structure of the images. However, due to the incomplete accuracy of the annotations in the Dunhuang data, there are some missing or blurred details; (c) shows the preliminary noisy line drawings extracted, containing substantial noise, broken lines, and blurriness, which serve as the input source domain images for the model; (d) presents the NL-Means denoising results, which achieve denoising based on the similarity of image patches but lack in detail preservation; (e) shows the Wiener filter denoising results, where frequency-domain filtering smooths the noise but tends to blur the edges; (f) presents the Pix2pix denoising results, which, as a supervised method based on conditional Generative Adversarial Networks, depend on paired noisy and clean images for training, and while they can remove some noise, the generated results are very close to the reference line drawings and lack detail expression; (g) shows the CycleGAN denoising results, which, as an unsupervised learning method, learn the mapping between the two domains without relying on strictly paired samples, thereby better restoring the structural features and edge information of the images, resulting in clearer lines, smoother edges, and a significant improvement in overall visual quality, especially in maintaining structural similarity, edge clarity, and line connectivity.

Fig. 11: Comparison of line drawings denoising.
figure 11

a Mural, b reference line drawings, c noisy line drawings, d NL-Means, e Wiener, f Pix2pix, and g CycleGAN.

Full size image
Fig. 12: Local comparison of line drawings denoising.
figure 12

a Mural, b reference line drawings, c noisy line drawings, d NL-Means, e Wiener, f Pix2pix, and g CycleGAN.

Full size image

Quantitative analysis of different stages

This study adopts multiple quantitative evaluation metrics to assess the quality of mural line drawings generated by different models for Dunhuang murals. These metrics include the SSIM, TC, LCI, and Q which integrates the three. To systematically analyze the impact of each stage on the quality of line drawing extraction, we conducted stepwise ablation experiments and individually evaluated the contributions of CLAHE + BF, MLineNet, and CycleGAN. These components were ultimately integrated into a complete method (Ours). Specifically, CLAHE + BF serves as a preprocessing step to enhance edge information; MLineNet is responsible for extracting preliminary line structures; and CycleGAN further denoises and improves the naturalness. Through these independent experiments, we analyzed the role of each stage and verified their synergy in the full pipeline. Table 1 presents the quantitative evaluation results for each stage in the Dunhuang mural line drawing task, and Fig. 13 illustrates the radar chart comparison across all metrics.

Fig. 13
figure 13

Radar chart comparison of various evaluation metrics for different stages in Dunhuang mural line drawing generation.

Full size image
Table 1 Quantitative evaluation results of different stages in Dunhuang mural line drawings generation
Full size table

As the base model, MLineNet demonstrated relatively stable performance, achieving an SSIM of 86.58%, a TC of 92.84%, an LCI of 85.37%, and a Q score of 88.26%, indicating its capability to extract complete and coherent mural line drawings. Building upon this, we introduced data augmentation (CLAHE + BF) for improvement, which resulted in an increase in SSIM to 88.19%, LCI to 86.97%, and Q to 89.19%, suggesting that enhanced input helps the model better preserve edge information and improve line connectivity. However, TC slightly decreased to 92.42%, indicating that the augmentation process may introduce pseudo edges and increase texture complexity. After further incorporating CycleGAN, TC improved from 92.84% to 94.21%, confirming its effectiveness in reducing redundant textures. Finally, the complete method (Ours), combining data augmentation and denoising, achieved strong performance across all four metrics, with an SSIM of 89.54%, TC of 93.77%, LCI of 88.14%, and a Q score of 90.48%, demonstrating the overall effectiveness and synergy of the three-stage framework in generating complete, clean, and coherent mural line drawings.

Comparative analysis with other methods

To comprehensively evaluate the performance of different methods in generating Dunhuang mural line drawings, this study selects Sobel and Canny as classical edge detection operators, and DiffusionNet (diffusion probabilistic model for crisp edge detection)10 and TEED (tiny and efficient model for edge detection generalization)11 as deep learning-based comparison methods. Like traditional algorithms, Sobel and Canny can extract the main outlines of murals to some extent, while DiffusionNet and TEED, being deep learning models, offer stronger adaptability in terms of stability and expressiveness in edge detection. The evaluation is conducted from three perspectives: qualitative analysis, quantitative analysis, and human perceptual assessment.

First, we perform a qualitative analysis of the line drawing results. Figure 14 shows the comparison of different methods on Dunhuang murals, and Fig. 15 presents the corresponding enlarged local regions. From the results, it can be observed that the Canny method performs relatively stably in extracting the main contours. However, due to its reliance on fixed gradient thresholds, it often results in the “double-edge problem,” where both sides of a single line are detected as edges, producing redundant double-line structures. The Sobel operator is more sensitive to gradient changes and can capture strong edge signals, but its poor robustness to noise leads to fragmented lines, compromising the overall connectivity of the murals. In contrast, DiffusionNet applies a diffusion mechanism for edge detection, which helps simplify the lines to some extent, though it still suffers from detail loss in complex structures. TEED, as an efficient edge detection model, produces relatively clear overall contours and retains the main edge information well, but some disconnections still occur in fine line structures. The method proposed in this paper demonstrates a balanced performance in terms of structural similarity, simplicity, and connectivity, resulting in a well-rounded overall quality.

Fig. 14: Comparison of different methods in Dunhuang mural line drawings generation.
figure 14

a Mural, b reference line drawings, c Sobel, d Canny, e DiffusionNet, f TEED, and g ours.

Full size image
Fig. 15: Local comparison of different methods in Dunhuang mural line drawings generation.
figure 15

a Mural, b reference line drawings, c Sobel, d Canny, e DiffusionNet, f TEED, and g ours.

Full size image

Secondly, the performance of different methods in generating Dunhuang mural line drawings was quantitatively compared, as summarized in Table 2. Figure 16 presents radar charts of various models across the evaluation metrics, providing a visual comparison of their performance differences. The results indicate that different methods show varying levels of effectiveness across the evaluated indicators. Among traditional edge detection methods, Sobel exhibits noticeable edge omissions in certain regions, leading to a relatively high TC of 94.56%, but the lowest LCI of only 82.19%. Canny achieves SSIM and LCI scores of 84.31% and 84.49%, respectively, yet suffers from the “double-edge problem,” resulting in redundant lines and reduced overall clarity. In contrast, deep learning-based methods generally perform better across multiple indicators. DiffusionEdge, due to its diffusion mechanism, excels in texture complexity with a TC of 96.55%, indicating cleaner lines with less noise. However, similar to Sobel, it has lower SSIM and LCI values of 82.79% and 83.02%, respectively, reflecting losses in detail and structural connectivity. The TEED method shows balanced performance, with an SSIM of 86.13%, TC of 93.37%, and LCI of 87.14%. The method proposed in this study achieves strong overall performance across all metrics, including an SSIM of 89.54%, TC of 93.77%, LCI of 88.14%, and a comprehensive score (Q) of 90.48%. These results indicate that the proposed method maintains a good balance between edge feature similarity, noise control and line connectivity.

Fig. 16
figure 16

Radar chart comparison of various evaluation metrics for different models in Dunhuang mural line drawing generation.

Full size image
Table 2 Quantitative evaluation results of different methods in Dunhuang Mural line drawing generation
Full size table

Finally, to verify the effectiveness of the evaluation metrics (SSIM, TC, LCI) used in the Dunhuang mural line drawing task, a subjective experiment based on human perceptual judgment was conducted. Eight participants were invited to evaluate the line drawings generated by each method in three aspects: similarity, cleanliness, and connectivity, corresponding to SSIM, TC, LCI. A three-point scale was adopted (1 = poor, 2 = fair, 3 = good). The median (MED) and interquartile range (IQR) of the scores for each method were calculated to reflect the overall evaluation level and consistency of judgment. The subjective evaluation results are shown in Table 3. Additionally, the average of the three scores was computed as the overall perceptual score (OPS).

Table 3 Subjective evaluation results (MED, IQR, and OPS) for each method
Full size table

Table 3 presents the detailed subjective evaluation outcomes. Among traditional methods, Sobel received a similarity and connectivity score of 1 and a cleanliness score of 2, with an OPS of 1.17, the lowest among all methods, indicating limited structure recovery and poor line connectivity. Canny achieved a similarity and connectivity score of 2 and a cleanliness score of 1, yielding an OPS of 1.71, slightly outperforming Sobel. DiffusionEdge scored highest in cleanliness (MED = 3) but only 1 in similarity and connectivity, also resulting in an OPS of 1.71. This suggests effective noise removal but a lack of structural preservation and line connectivity. TEED scored 2 in similarity and connectivity and 1 in cleanliness, with an OPS of 1.92, reflecting moderate and stable subjective acceptance. The proposed method (Ours) achieved the highest OPS of 2.83, with a perfect score of 3 in similarity and connectivity and 2 in cleanliness. These results indicate that the method received consistent recognition from participants for preserving structural details, suppressing noise, and maintaining line connectivity. Furthermore, the subjective evaluation results align well with the objective metrics (SSIM, TC, LCI), suggesting that the adopted evaluation system is valid for assessing mural line drawing quality.

Line drawing generation and generalization verification for Baisha murals

The Baisha murals48,49, located in Baisha, Yulong Naxi Autonomous County, Lijiang, Yunnan Province, are an important cultural heritage of the Naxi people, with the Dading Pavilion being one of the core temples. The Baisha murals incorporate diverse cultural elements, including Tibetan Buddhism, Taoism, and Han Buddhism. Their content depicts Buddhist figures, transformation stories, and donor portraits, characterized by bold, flowing lines and rich, vibrant colors. As shown in Fig. 17, compared to the Dunhuang murals, the Baisha murals exhibit a more free and unrestrained overall style, with greater variation in brushstroke thickness, stronger color contrasts, and more intricate background decorations. These stylistic differences are reflected not only in visual features, such as more expressive facial depictions, simplified and dynamic hand gestures, and more complex decorative patterns. The model needs to handle variations in brushstroke thickness and color layers, adapt to interference from intricate background decorations, and ensure the integrity of multi-scale structural information. Therefore, the Baisha murals serve as important historical materials for studying the religious art of southwestern China during the Ming and Qing dynasties, and in recent years, they have been increasingly digitized and studied in depth.

Fig. 17: Comparative details of mural styles in Dunhuang and Baisha murals.
figure 17

a Facial features, b hand gestures, and c background decorations.

Full size image

First, a qualitative analysis was conducted on the performance of different methods in generating line drawings for Baisha murals. Figure 18 shows a comparison of different methods, and Fig. 19 presents zoomed-in results. From the visual comparison, it can be observed that the Sobel and Canny methods exhibit significant limitations in line extraction. The Canny method, which is highly sensitive to local gradient variations, generates noise in both bright and dark regions. It also suffers from the “double-edge problem,” leading to blurred and ambiguous line contours. Although the Sobel method captures the overall structure, it introduces considerable noise, resulting in cluttered line drawings that affect mural clarity and readability. Deep learning-based methods, such as DiffusionNet and TEED, improve line connectivity and structural integrity to some extent. DiffusionNet reduces background interference but lacks detail in fine line extraction. TEED performs better in maintaining global coherence and produces relatively stable lines. However, it still suffers from detail loss and broken lines in complex decorative regions. In contrast, the proposed method demonstrates superior performance on the Baisha mural dataset by effectively preserving line structures while suppressing noise.

Fig. 18: Comparison of different methods in Baisha mural line drawings generation.
figure 18

a Mural, b Sobel, c Canny, d DiffusionNet, e TEED, and f ours.

Full size image
Fig. 19: Local comparison of different methods in Baisha mural line drawings generation.
figure 19

a Mural, b Sobel, c Canny, d DiffusionNet, e TEED, and f ours.

Full size image

In addition, this study conducted a quantitative analysis of the performance of different methods in generating line drawings of Baisha murals. The experimental results are summarized in Table 4. Figure 20 presents a radar chart comparison of the models across various evaluation metrics, visually illustrating their differences. According to the results, among traditional methods, Sobel achieved an SSIM of 80.66%, TC of 88.81%, LCI of 84.77%, and a Q of 84.75%. Canny performed slightly better, with an SSIM of 81.78%, TC of 89.01%, LCI of 85.72%, and Q of 85.50%. Both methods showed relatively lower performance in TC and LCI, indicating limitations in texture simplification and line connectivity, though they retained some capability in structural restoration. DiffusionEdge achieved the highest TC at 95.58%, demonstrating strong suppression of redundant details. However, its SSIM and LCI were relatively lower among deep learning models—78.92% and 82.10%, respectively—resulting in a Q score of 85.53%, indicating overall performance inferior to other deep models. TEED maintained relatively high scores across all metrics, with an SSIM of 82.62%, TC of 93.52%, LCI of 87.99%, and a Q of 88.04%, reflecting a well-balanced overall performance. The proposed method achieved consistently high scores in all four metrics: SSIM of 85.77%, TC of 93.93%, LCI of 88.18%, and Q of 89.29%. These results indicate a good balance between structural preservation, denoising, and line connectivity. Although the model is trained on Dunhuang mural data, it still demonstrates a certain degree of generalization ability when applied to Baisha murals. However, it is important to note that the current model is not specifically designed to accommodate the stylistic differences between different types of murals, such as variations in brushstroke thickness, color complexity, and decorative background styles. As a result, some decorative regions may exhibit issues such as local detail loss or incomplete structural representation. Overall, the proposed method achieved relatively stable results across all metrics, demonstrating strong overall performance in mural line drawing generation.

Fig. 20
figure 20

Radar chart comparison of various evaluation metrics for different models in Baisha mural line drawing generation.

Full size image
Table 4 Quantitative evaluation results of different methods in Baisha Mural line drawing generation
Full size table

Discussion

Line drawing is an essential form of artistic expression in Chinese painting, including traditional ink paintings, murals, and folk art. This study proposes an automated approach for generating mural line drawings by integrating mural edge enhancement, line drawing extraction, and line drawing denoising to achieve efficient and accurate line drawing generation. The main conclusions of this paper are as follows: (1) We propose an automated mural line drawing generation method that leverages CLAHE and BF for edge enhancement, followed by a specially designed neural network for mural line drawings, named MLineNet, for extracting mural line features. MLineNet adopts an encoder-decoder architecture with multi-scale feature fusion to effectively capture features across different scales. A CycleGAN is employed for denoising based on line drawing extraction results, generating high-quality line drawings that accurately capture rich structural details while maintaining clarity and naturalness. (2) Using Dunhuang murals as research subjects, a mural line drawing generation model was constructed based on the proposed method. The reliability of this model was evaluated using SSIM, TC, LCI, and Q. Experimental results showed that the proposed method achieved SSIM, TC, LCI, and Q of 89.54%, 93.77%, 88.14%, and 90.48%, respectively, demonstrating excellent performance in structural similarity, cleanliness, and connectivity. (3) To further validate the robustness and effectiveness of the proposed mural line drawing generation approach, we applied it to Baisha murals, where it achieved a Q value of 89.29%, confirming its generalization ability and adaptability to different mural datasets.

Although the experimental results demonstrate that the proposed method has a certain degree of adaptability and robustness, several limitations remain. First, the model training still relies on annotated line drawing data, which limits its scalability to large-scale, unlabeled datasets. Future work could explore the integration of semi-supervised or unsupervised learning strategies to reduce the dependence on annotated data. Second, for murals with diverse styles or complex structures, the model still encounters issues such as broken lines or missing details in certain regions. Future research could incorporate style-aware modules and adaptive feature modeling methods to enhance the model’s ability to adapt to different mural styles. Additionally, the current validation experiments primarily focus on Dunhuang and Baisha murals, with a relatively limited range of data sources. Future research will aim to extend evaluations to mural datasets with greater geographical and historical diversity, such as the Yungang Grottoes and the Longmen Grottoes, to comprehensively assess the generalization ability and robustness of the method.