Introduction

Three-dimensional (3D) integration technologies and advanced packaging techniques are developing rapidly, driving electronic devices toward higher density, smaller size, and enhanced heterogeneous functional integration1,2,3. The realization of 3D integration and advanced packaging relies heavily on high density interconnect structures. Although through-silicon via (TSV) interposer technology has widely used, the high permittivity of the silicon (ε ≈ 11.9) leads to increased signal transmission loss, making TSV struggle to meet the demands of high-frequency applications4.

Through-glass via (TGV) interposer has emerged as a novel interconnect structure. Owing to the unique material properties of glass (e.g., low dielectric constant (ε ≈ 5.1), high resistivity (>1014 Ω·cm), and chemical stability), TGV provides an ideal platform for high-frequency signal transmission, high-density interconnection, and heterogeneous integration5,6,7,8,9,10,11,12,13. However, the practical applications of TGV still face reliability challenges. Glass has a lower thermal conductivity (0.9–2.2 W/m·K) compared to that of silicon (149 W/m·K). Therefore, TGV exhibits poorer heat dissipation. Additionally, the diameter of TGV is typically larger than that of TSV, thus TGV faces greater challenges with thermal stress mismatch issues.

Studies indicate that thermal loads may cause thermally induced cracks in TGV, due to the CTE mismatch between Cu and glass. Glass substrates near TGV structures may exhibit two types of cracks: radial cracks and circumferential cracks. During heating, the thermal expansion of Cu exerts pressure on the glass substrate adjacent to TGV sidewalls, causing radial cracks near TGV structure14. Circumferential crack is caused by tensile stress generated by TGV on surrounding glass during cooling15. However, the study on stress evolution is currently lacking.

The commonly used methods for residual stress measurement are X-ray diffraction16 and micro-Raman spectroscopy17. However, these two methods are only applicable to crystalline materials and cannot be used for measuring glass, which is an amorphous material. Nanoindentation can measure the stress on the material surface, and since this method only considers the mechanical properties of the material, it is suitable for both amorphous and crystalline materials, and is widely used for small-scale residual stress measurement18,19,20. Finite element analysis (FEA) method is commonly used to investigate the stress distribution within TGV. Li et al. found that thermal stress concentrates primarily at the Cu-glass interface under thermal loading via FEA simulation21. Pan et al. demonstrated through FEA that glass near the edge of the Cu-glass interface in the x-direction experiences the maximum principal stress, which decreases as the heating rate reduces22.

Thermal stress mismatch not only leads to glass cracking but also significant affects on the metal filler within TGV. Since the metal filler is usually Cu, the TGV structure exhibit Cu protrusion under high temperatures23. Okoro et al. observed that the Cu protrusion height increased with prolonged annealing, while the growth rate of Cu protrusion decreased with extend annealing period24. The heating rate significantly influences Cu protrusion behavior. A slower heating rate resulting in more pronounced copper protrusion14. Previous studies have discussed Cu protrusion of TGV structures, and the failure mechanisms have also been explained. However, the research on the systematic research establishing Cu protrusion models for TGV annealed at different temperatures is lacking.

In this paper, annealing experiments on TGV samples under varying annealing conditions were conducted, the residual stress distribution of TGV sample after annealing was measured using nanoindentation. The atomic force microscopy (AFM) was used to characterize the surface morphology of Cu protrusions. The protrusion behavior of TGV samples under different annealing conditions was analyzed. The influence of creep behavior during the annealing process on Cu protrusions was elucidated. Additionally, a numerical model for Cu creep rates under various annealing temperature was established. This paper provides design guidance for residual stress analysis and reliability assessment of TGV structures under thermal loading.

Materials and methods

Sample design

The TGV samples were prepared by the Sky Semiconductor Technology Co., Ltd. The vias in the glass substrate were prepared by laser induced modification method. The vias were filled by Cu to obtain TGV. Subsequently, RDL was electroplated.

The top view of the TGV sample, captured by optical microscopy (OM), is illustrated in Fig. 1a. Cross-section view of TGV sample was observed by scanning electron microscope (SEM), as shown in Fig. 1b. The TGV has a diameter of 70 μm at the upper end and 18.6 μm at the bottom end, presenting a trapezoidal shape. The height is 283.6 μm.

Fig. 1: Sample morphology and experimental methodology.
figure 1

a The top view of TGV sample; (b) cross-section view of TGV sample; schematic diagram of (c) annealing experiment; (d) nanoindentation process; (e) AFM characterization; (f) Finite element model of the TGV sample, and (g) material properties used in the simulation

Full size image

Annealing treatment

The TGV samples were subjected to annealing treatments to evaluate the thermo-mechanical reliability. In the annealing process, samples were maintained at 300 °C, 350 °C and 400 °C for varying durations in a high-temperature vacuum furnace under high vacuum (<1 × 10⁻4 Pa). The temperature was raised from ambient conditions (30 °C) to the target temperature at a constant rate of 10 °C/min. Pan et al. observed the in-situ protrusion of Cu at different heating rates (4 °C/min, 15 °C/min, 30 °C/min, and 50 °C/min)22, and the results showed that more significant creep and plastic deformation occur in the Cu with slower heating rate, therefore the Cu protrusion height increases significantly with a slower ramp rate. Therefore, in order to obtain a more significant Cu protrusion result, the heating rate needs to be reduced.

However, Okoro et al. showed that an increase in the heating rate increases the probability of crack formation. When the heating rate reached ≤ 6.5 °C/min, there was no crack formation in the TGV substrate14. Therefore, in order to observe more significant Cu protrusion results and the formation of TGV cracks, 10 °C/min was selected as the heating rate in this work.

Subsequently, the samples were furnace-cooled to room temperature. The schematic diagram of annealing experiment is shown in Fig. 1c.

Nanoindentation experiment

The residual stress on the glass substrate around TGV structure was measured using nanoindentation, the measurement process is shown in Fig. 1d. As the diamond indenter is pressed into the measurement area to a fixed depth, the residual tensile stress reduces the maximum indentation force required; conversely, when there is residual compressive stress in the measurement area, the result shows the opposite25.

The maximum indentation force required for indenting a material with no residual stress to a fixed depth is denoted as P0. For materials with residual tensile stress and compressive stress, the corresponding maximum forces are PT and PC, respectively. According to previous research, the residual tensile stress σT and residual compressive stress σC can be calculated using Eqs. (1) and (2), respectively19,26.

$${\sigma }_{T}=\frac{{P}_{0}-{P}_{T}}{{A}_{C}}$$
(1)
$${{\rm{\sigma }}}_{{\rm{C}}}=\frac{{P}_{C}-{P}_{0}}{{A}_{C}}$$
(2)

Where Ac is the effective contact area at the measurement location. The Ac is determined using Oliver-Pharr method27, which is given by Eq. (3):

$${A}_{C}=\frac{{P}_{\max }}{H}$$
(3)

Where Pmax is the maximum indentation force, H is nanoindentation hardness.

Atomic force microscope characterization

In-situ atomic force microscope (AFM) characterization was performed to quantitatively map the surface morphological evolution of TGV samples after different annealing periods, as shown in Fig. 1e.

Modeling of TGV sample

The FEA method was employed to simulate the stress distribution of TGV structures under different annealing conditions. A two-dimensional finite element model of the TGV sample was developed using ABAQUS CAE, as illustrated in Fig. 1f. The geometric configuration of the model was designed according to the actual sample. Both sides of the model were constrained in the x-direction. During the simulation, all interacting surfaces were assumed to maintain contact integrity without fracture or delamination.

Figure 1g summarizes the elastic material parameters used in the simulation. The elastic parameters of Cu and glass is chosen according to previous study28. During simulation, the elastic parameters were treated as constants29,30. The stress-plastic strain relationship of Cu in the simulation was selected based on previous literature31,32.

Result and discussion

Effect of annealing on the residual stress of TGV sample

The top view of the TGV samples was characterized using OM before and after performing heat treatments at three temperature levels (400 °C, 350 °C and 300 °C) with variable annealing periods. As evidenced by Fig. 2, circumferential cracks were observed at the edges of the TGV-RDL samples under different annealing temperature after annealing for specific periods. Notably, the time required for crack initiation decreased with the increase in annealing temperature.

Fig. 2
figure 2

Top view of TGV samples annealed at various temperature for different annealing periods

Full size image

The variation of circumferential crack density on TGV samples under different annealing temperatures was statistically analyzed. Crack density was calculated by dividing the number of TGVs exhibiting circumferential cracks by the chip area14, which was 25 mm2.

At 300 °C, after 216 h of annealing, the crack density reached 1.08 cracks/mm2. By 288 h, the crack density increased to 3.44cracks/mm2, with an average propagation rate of 0.03 cracks/mm2·h. At 350 °C, after 5 h, the crack density was 0.32 cracks/mm2. This value reached 4.28 cracks/mm2 at 6 h and further increased to 7.04 cracks/mm2 after 8 h of annealing. At 400 °C, within 20 min, the crack density was 0.2 cracks/mm2. It increased to 1.8 cracks/mm2 after 30 min and reached 7.16 cracks/mm2 by 60 min.

It is evident that the crack density increases with prolonged annealing time. The average crack propagation rate was 2.24 cracks/mm2·h at 350 °C, while at 400 °C, the rate was significantly higher at 10.44 cracks/mm2·h.

Figure 3 shows cross-sectional SEM images of TGV samples under different annealing conditions. It can be observed that after a certain annealing period, cracks appear at the contact point between the RDL edge and the glass substrate. Combined with the results of Fig. 2, it can be concluded that the cracks observed at this location are cross-sections of circumferential cracks. These circumferential cracks initiate from the edge of the RDL and gradually propagate vertically into the glass substrate as annealing periods increase.

Fig. 3
figure 3

Cross-section view of TGV samples annealed at various temperature for different annealing periods

Full size image

After annealing at 300 °C for 216 h, the length of the circumferential cracks reached 6.9 μm. As the annealing time extended to 288 h, the crack length increased to 18.9 μm. After annealed at 350 °C, the length of circumferential cracks increased from 20.7 μm (6 h) to 36.9 μm (8 h). The crack length in TGV annealed at 400 °C increased from 21.2 μm (30 min) to 31.7 μm (60 min).

The residual stress distribution on TGV surfaces is measured using nanoindentation. First, the P0 of glass substrate is defined.

Five glass samples were taken from different distances (10 mm to 50 mm) from the center of the wafer. Each sample was divided into regions such as the sample edge, sample corner, and sample center. Then, within each region, samples were independently randomly selected, with 10 sampling points per region, resulting in a total of 30 sampling points. Nanoindentation was performed at sampling points to compare the maximum indentation force on the glass substrates before and after annealing. Subsequently, the glass samples were annealed at 300 °C, and the nanoindentation testing was continued to record the maximum indentation force.

This process was repeated until the maximum indentation forces at different sampling points on each glass sample converged (with an error of less than 1%), and the average maximum indentation forces across the five glass samples from different distances also converged (with an error of less than 1%). The resulting average maximum indentation force was defined as P0 which was 14.55 mN.

The stress on the glass substrate obtained through cutting and annealing treatment is relatively low, but this does not imply the absence of residual stress on the glass substrate. Therefore, the stress state corresponding to P0 = 14.55 mN is defined as the reference state (Ref. state) of the glass substrate. The residual stress of the TGV structure mentioned in this paper refers to the change relative to the residual stress of this reference state, denoted as Δ residual stress (ΔRS).

Subsequently, the TGV sample was divided into regions such as the sample edge, sample corner, and sample center using the stratified sampling method. Then, within each region, samples were independently randomly selected, with 10 sampling points per region, resulting in a total of 30 sampling points. The test positions on the glass substrate were identified based on the indent array shown in Fig. 1d. Nanoindentation experiments were conducted at these positions to measure the corresponding maximum indentation force and nanoindentation hardness. Finally, the residual stress at each measurement location was calculated based on Eq. (1), Eq. (2), and Eq. (3). The results are shown in Fig. 4.

Fig. 4: The distribution of residual stress on the glass substrate between TGV structure annealed at different temperature.
figure 4

a 300 °C, (b) 350 °C, and (c) 400 °C

Full size image

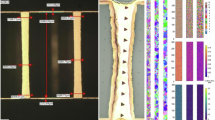
Figure 4a shows the distribution of residual stress values at different positions in the glass substrate adjacent to the TGV structure, which was annealed at 300 °C for varying periods. The x-axis represents the distance from the left TGV-RDL edge.

The residual compressive stress is observed at glass surface near the TGV-RDL edge and gradually decreases as farther from the TGV-RDL edge. This phenomenon can be attributed to the electroplating filling processes of the TGV, which induces residual stress in both the TGV structure and the surrounding glass.

After annealing for 72 h at 300 °C, the residual compressive stress near the TGV edge decreased, and the overall residual stress distribution becomes more uniform. This suggests that annealing at 300 °C for 72 h effectively reduces the residual stress in TGV samples. This phenomenon is attributed to the structural rearrangement of the Cu crystal lattice during annealing. Atomic diffusion-driven dislocation redistribution reduces grain boundary density and defect concentration, ultimately alleviating internal stress.

After annealing for 216 h, the residual compressive stress near the TGV edge transferred into residual tensile stress, which decreases with increasing distance from the TGV-RDL edge. After 288 h of annealing, the residual tensile stress exhibited a sharp reduction due to stress release relaxation caused by glass cracking.

As shown in Fig. 4b, c, TGV samples annealed at 350 °C and 400 °C exhibited similar progresses.

To investigate the evolution of residual stress at top surface of glass substrate near the TGV-RDL edge, the residual stress under different annealing temperatures was measured as a function of annealing periods, as shown in Fig. 5a–c. Besides, the fitting curves of residual stress changes with annealing periods was obtained through an exponential function. According to Fig. 5a, b, the compressive stress was observed on the glass surface near the TGV-RDL edge in the beginning and decreased rapidly until the residual stress reached zero. After that, residual stress changed to tensile stress, and increased slowly. As annealing period extend, the tensile stress exhibited a linear increase.

Fig. 5: The evolution of residual stress at top surface of glass substrate under different temperature.
figure 5

a 300 °C, (b) 350 °C, (c) 400 °C; (d) the residual stress of TGV annealed for different periods to achieves reference state as predicted by the fitting curve

Full size image

Especially, as shown by Fig. 5c, the residual stress on the glass near the TGV-RDL edge annealed at 400 °C indicates excessively increment, the fitted line shows a linear trend at this temperature. Griffith33 proposed that under uniform loading, the overall stress in a material increases gradually. However, due to the presence of a crack, stress becomes highly concentrated at the crack tip. As the external stress increases, the local stress at the crack tip rises rapidly in a linear manner within a certain range. For example, in glass plate crack experiments, the stress concentration factor at the crack tip can exceed 10 times, leading to a sudden linear surge in local stress before fracture, even while the macroscopic stress increases slowly. The underlying mechanism of this phenomenon lies in the stress concentration at the crack tip, which amplifies the effect of the external load. Therefore, the linear increase in residual stress on the glass surface near the TGV-RDL edge means that the crack is about to occur.

After 300 °C/350 °C annealing for 180 h/4 h, the residual stress reaches the critical stress of the glass, initiating crack propagation, which in turn leads to intensified stress concentration and a subsequent linear increase in residual stress evolution. By fitting the residual stress data after 300 °C/350 °C (180 h/4 h) and calculating the intersection point between this fitted line and the fitting curve of residual stress before 300 °C/350 °C (180 h/4 h), the critical stress of the glass is determined to be 549 MPa.

To verify the reliability of the fitting curve in Fig. 5a–c, the TGV sample is annealed at 300 °C for 14.2 h, at 350 °C for 48.3 min and at 400 °C for 10.4 min, exact periods that need to achieve reference state as predicted by the fitting curve, and the residual stress on the glass near the TGV-RDL edge is measured. The result is shown in Fig. 5d.

The result indicates that the absolute errors of the fitting curves at 300 °C, 350 °C, and 400 °C were 0.047 GPa, 0.010 GPa and 0.031 GPa, respectively. Therefore, the fitting curve can accurately predict residual stress of TGV structures across different annealing periods under different temperatures. The results provide theoretical guidance for TGV fabrication techniques and thermal annealing process design, which emphasize precision in residue stress control under thermal annealing.

The stress distribution of the TGV structure after annealing at 300 °C for 72 h was simulated using the FEA method. Figure 6a shows the radial stress distribution of the TGV sample annealed at 300 °C for 72 h and cooled to room temperature, where positive and negative values denote tensile and compressive stresses, respectively. Radial tensile stress is observed in the top glass region between two TGV structures after annealing.

Fig. 6: Finite element simulation results.
figure 6

a Radial stress distribution of the TGV sample annealed at 300 °C for 72 h; (b) Radial stress value at the indent array area

Full size image

The maximum radial stress was found at the contact point between the RDL edge and the glass substrate, indicating that the cracks were easily formed by radial tensile stress at this position. The simulation result was consistent with the phenomenon observed in the SEM image demonstrated in Fig. 3.

The radial stress of the indent array area on the glass of TGV samples annealed at 300 °C for 72 h are shown in Fig. 6b.

Residual tensile stress can be observed in the indent array area after annealing. The stress values decrease with increasing distance from the TGV-RDL edge, which is consistent with the observations in Fig. 4.

The experimental and FEA results suggest that the failure mechanism of TGV sample is due to the significantly higher contraction rate of Cu compared to the glass substrate, the rapid contraction of Cu induces a tendency for delamination from the glass substrate during the cooling stage of the annealing process. However, the adhesion between Cu and glass prevents the delamination. This leads to the generation of tensile stresses within the glass substrate, ultimately resulting in the formation of circumferential crack.

Effect of annealing on the protrusion behavior of TGV sample

Based on previous conclusions, the occurrence of circumferential cracks around the TGV results in the release of internal stress, potentially influencing the protrusion behavior. Therefore, the investigation of the protrusion behavior of the TGV sample only considers the stage where no cracks appeared.

The three-dimensional surface topography of the TGV samples was quantitatively analyzed using AFM, as shown in Fig. 7. The AFM measurements revealed significant morphological variations across the TGV surface, with the most pronounced structural changes observed in the center region. As the annealing time increased, the topography of the TGV exhibited a progressive upward protrusion.

Fig. 7
figure 7

AFM results of TGV samples annealed under various conditions

Full size image

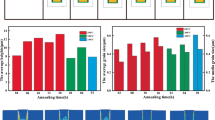
The surface topography height information of TGV samples was characterized using AFM. The protrusion heights of the TGV structures under different conditions were calculated by subtracting the average height of the central line on the TGV surface before annealing from that after annealing, as shown in Fig. 8. The results reveal that the protrusion height of TGV samples increases with the extension of isothermal annealing period, and the change rate of protrusion height gradually decreases as the prolonging of annealing period.

Fig. 8: Protrusion heights of TGV samples annealed under different conditions.
figure 8

a 300 °C, (b) 350 °C, (c) 375 °C, (d) 400 °C

Full size image

The change rate of protrusion height under different annealing temperatures also exhibited distinct characteristics. The protrusion height of the TGV sample annealed at 400 °C for 20 min reached 0.88 μm, while a 50 °C temperature reduction required 1 h annealing to achieve comparable height. Similarly, 5 h annealing at 350 °C yielded 1.39 μm protrusion height, whereas 72 h annealing was needed at 300 °C. These results indicate that the 400 °C condition demonstrated the fastest protrusion height change rate, followed by 350 °C and 300 °C.

The protrusion is composed of plastic deformation and creep deformation during isothermal annealing, which remain irreversible after cooling, resulting in Cu protrusion24. However, during the isothermal annealing stage, the plastic deformation of Cu ceased due to stress relaxation effect, therefore the creep deformation was the dominant mechanism driving protrusion height increase. The change rate of protrusion height, defined as the creep rate, gradually decreases with extended annealing periods and reduction of annealing temperature.

The creep process of materials typically progresses through three distinct stages: decelerating creep, steady-state creep, and accelerating creep. The steady-state creep phase, which persists for the longest duration, plays a critical role in determining the service life of material. In the TGV structures, the appearance of circumferential cracks in the glass substrate leads to premature failure. According to the result of Fig. 8, the Cu does not undergo the accelerating creep stage, as the structural integrity is compromised prior to reaching this phase.

Tobolová et al. demonstrated an empirical relationship between the steady-state creep rate (εr) and temperature (T) through experimental investigation34, as shown in Eq. (4):

$${{\rm{\varepsilon }}}_{{\rm{r}}}=A\exp \left(\frac{-Q}{RT}\right)$$
(4)

Where A is the creep coefficient related to material properties, R is the gas constant, and Q is the apparent activation energy of creep.

The creep rate before TGV failure is defined as the εr of TGV. The εr of TGV samples at a given temperature was determined by fitting the protrusion height versus annealing period and extracting the tangent slope (k) at the point prior to circumferential crack formation.

In order to fit the empirical model, additional experiments were conducted for TGV samples at 375 °C to obtain the protrusion height at varying annealing periods, as shown in Fig. 8c. By fitting the protrusion height curve, the temperature-dependent creep rate of TGV samples at 375 °C was determined as εr375 = 0.2651.

Taking the natural logarithm of both sides of Eq. (4) yields a linear relationship of ln(εr)-1/T, with an intercept of ln(A) and a slope of -Q/R. Subsequently, εr values obtained at 300 °C, 350 °C, and 375 °C were substituted into the linear relationship of ln(εr)-1/T. The fitting line is shown in Fig. 9, yields an R² = 0.9867, indicating excellent agreement with experimental data. Thus, the creep coefficient (A) and apparent activation energy of creep (Q) is obtained as 1.08 × 1018 and 230.02 kJ/mol, respectively.

Fig. 9
figure 9

Fitting line of ln(εr)-1/T

Full size image

To verify the accuracy of fitting line, 1/T = 1/673.15 K−1 (at 400 °C) is substituted into the fitting line to obtain ln (εr), then compare it with the actual creep rate value ln (εr400) = −0.3642, as shown in Fig. 9. The results show that fitting line achieves a RMSE of 1.143.

The temperature-dependent relationship between εr and T for TGV samples is described by Eq. (5).

$${\varepsilon }_{r}=1.08\times 1{0}^{18}\exp \left(\frac{-230.02}{{RT}}\right)$$
(5)

Temporal correlation of residual stress and Cu protrusion height

As shown in Fig. 8, the protrusion heights of TGV samples initially increase rapidly, followed by a slowly increase. Similarly, according to Fig. 5a, b, the residual stress on glass surface near the TGV-RDL edge annealed at 300 °C/350 °C also exhibit progressively declining rates with extended annealing time (before it exhibits a linear increase trend). In contrast, at 400 °C, the residual stress demonstrates a direct linear increase. This phenomenon means that crack is about to occur.

As concluded previously, the tensile residual stress at the TGV-RDL edge originates from rapid contraction of Cu during the annealing cooling stage, resulting in a delamination tendency at the Cu/glass substrate interface, ultimately forming tensile stress.

Since the top region of the TGV can be considered as a cylindrical structure encasing the glass substrate, Lame’s thick-walled/solid cylinder analysis equations can be employed to calculate the in-plane stress within the top glass layer—where the radial stress and circumferential stress in this region are equal in magnitude but opposite in direction. For a glass substrate containing only one TGV, the two-dimensional (2D) thermomechanical stress can be calculated using Eq. (6)35:

$${{\rm{\sigma }}}_{{\rm{tensile}}}\,=\,\frac{-{{\rm{E}}}_{{\rm{Cu}}}{\rm{\varepsilon }}}{1-2{{\rm{\upsilon }}}_{{\rm{Cu}}}+\frac{1+{{\rm{\upsilon }}}_{{\rm{glass}}}}{1+{{\rm{\upsilon }}}_{{\rm{Cu}}}}\frac{{{\rm{E}}}_{{\rm{Cu}}}}{{{\rm{E}}}_{{\rm{glass}}}}}{\left(\frac{{{\rm{D}}}_{{\rm{Cu}}}}{2{\rm{r}}}\right)}^{2}$$
(6)

Here, υglass and υCu are the Poisson’s ratios of glass and Cu, respectively; r denotes the distance from a point in the glass to the center of the TGV; DCu is the diameter of TGV; ECu and Eglass are the Young’s moduli of Cu and glass, respectively; and ε represents the strain of the Cu. Based on these parameters, the stress in the glass under different creep conditions of the copper pillar can be calculated.

Given that υglass, υCu, ECu, Eglass, and DCu are constants, Eq. (6) can be simplified to:

$${{\rm{\sigma }}}_{{\rm{tensile}}}\,\propto \,\frac{{\rm{\varepsilon }}}{{r}^{2}}$$
(7)

This indicates that the residual stress at a specific location in the top glass is directly proportional to the creep strain of the Cu and inversely proportional to the square of the distance from the center of the TGV. According to Eq. (7), the residual stress and the Cu protrusion height was linear fitted, establishing a quantitative correlation model. The results are illustrated in the Fig. 10.

Fig. 10: The linear fitting relationship between residual stress and copper protrusion height under different temperature.
figure 10

a 300 °C, (b) 350 °C

Full size image

Furthermore, the residual stress exhibits a linear increase trend at 400 °C (Fig. 5c) is due to the creep rate at this temperature far exceeds that at 350 °C and 300 °C. Therefore, the residual stress experiences accelerated growth, making TGV samples unsuitable for annealing at 400 °C. For TGV annealing at 300 °C and 350 °C, the annealing time should be controlled within 180 h and 4 h, respectively, to avoid rapid stress accumulation within the glass. It is proposed that the optimal annealing condition is 350 °C for 45 min to 1 h. Based on the fitting results in Fig. 4, the induced stress in the top glass layer around the TGV after annealing under these conditions ranges from –0.036 to 0.059 GPa, indicating a relatively low stress state. Furthermore, compared to annealing at 300 °C, the recommended annealing condition offers a significant reduction in annealing period.

Conclusion

In this study, the stress distribution in glass and Cu protrusion of TGV under different annealing conditions were investigated.

Annealing reduces residual compressive stress in the glass, but prolonged periods lead to residual tensile stress accumulation. Results from FEA align with experimental findings.

Annealing at 300 °C should be ≤180 h and at 350 °C ≤ 4 h to avoid rapid stress accumulation in the glass. The 400 °C condition induces linear growth of residual stress and is not recommended for accelerated annealing. It is proposed that the optimal annealing condition is 350 °C for 45 min to 1 h, which indicating a relatively low stress state and a significant reduction in annealing period compared to 300 °C.

The Cu protrusion height increases with annealing time, but the growth rate decreases. The established Cu creep rate model shows a RMSE of 1.143.

The residual stress in the top glass is directly proportional to the creep strain of the Cu. A quantitative correlation model for the liner relationship residual stress and the Cu protrusion height is proposed.

These results provide theoretical guidance for TGV reliability assessment and thermal optimization design.