Introduction

Surface electromagnetic (EM) waves on two-dimensional interfaces of dissimilar mediums have been a predominant topic of interest among researchers due to their unique features1,2,3. In the optical and near-infrared regime, confined EM waves propagating along the interface between dielectrics and metals are called surface plasmon polaritons (SPPs) and have been widely used in biosensing4, superresolution imaging5,6, and waveguides7. However, metals can be regarded as perfect electric conductors (PECs) in low-frequency ranges, e.g., the far-infrared, microwave, and terahertz regimes. In these low-frequency regimes, SPPs become very weakly confined Zenneck waves, and the evanescent fields can extend over several wavelengths8,9. Fortunately, designer SPPs or spoof SPPs (SSPPs), which mimic the novel properties of SPPs and overcome the aforementioned limits by using structured PECs, were demonstrated in 200410. Metallic/dielectric layers composed of subwavelength, regularly arranged metallic wires known as metasurfaces bind EM fields to individual interfaces with unique anisotropic dispersions that, along with SPPs and SSPPs, play important roles in manipulating near-field light scattering11,12,13,14.

In addition, hyperbolic metamaterials have attracted substantial research interest due to their special dispersions15,16,17, and research has been extended to the metasurfaces because the in-plane propagating properties are well controlled14,18,19,20. Consequently, special properties such as collimation, which were first studied in photonic crystals, have attracted immense interest in metasurfaces11,18,19,21. Such collimating transport exists when the dispersion becomes a flat line, a unique shape between the elliptical and hyperbolic IFCs that has been theoretically studied and experimentally measured at microwave frequencies along a single direction19. The gradual change in dispersion line shape leads to a topological transition and confines the propagation direction of SSPPs, which act as Dyakonov-like waves22,23. However, this unique collimation exists only in one direction at a single frequency in the previous literature, which limits its application.

Another remarkable resonance responsible for asymmetric spectra, known as Fano-resonance, is very famous in photonic systems and has led to numerous applications in electromagnetically induced transparency, slow light, lasing, switching and sensing based on the resulting sharp asymmetrical spectra24,25,26,27,28,29. In particular, high-ordered multipoles, e.g., electric quadrupoles, supported by subwavelength units of the metasurface usually appear as dark modes in contrast to the fundamental electric dipolar mode, which gives rise to the characteristic Fano line shape in the transmission/refection spectra. However, the effects of Fano-resonance on the modes of the metasurfaces bound below the light line have seldom been studied before.

Position sensors play indispensable roles in microfluidics and biology and in the touch screens that are now widely used in daily life. The working principles of recent commercial position sensors include four types: capacitive, resistive, surface acoustic waves (SAWs), and infrared (IR)30,31,32. Their technological limitations include complicated calibration processes due to multilayer construction for capacitive and resistive position sensors, restrictions on device size and substrate materials (piezoelectrics) for SAW sensors, and low sensing resolution for IR sensors30.

In this paper, we study the effects of Fano-resonance on the bound modes in metasurfaces and demonstrate that Fano-resonance can lead to hyperbolic IFCs, especially for lower Q-factor resonance, which acts analogously to symmetrical resonance. We designed a metasurface with Lifshitz-like IFC transitions in different bands in two orthogonal directions corresponding to independent frequencies. Compared with previous work, the existence of independent collimation frequencies for orthogonal directions in our design shows great potential for applications not only in superlenses and wavefront control but also in position sensors19. Accordingly, we built a position-sensing prototype device to demonstrate that the designed metasurface can function as a position sensor by working in tandem with recognition systems. The prototype represents a new kind of position sensor based on surface EM waves that has never been reported before.

Materials and methods

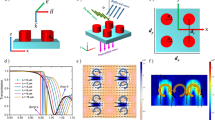
We start with a unit cell composed of a dielectric slab and an anisotropic metallic pattern (H-shape), as shown in Fig. 1, in which the dielectric slab is made of a nonmagnetic material with a relative permittivity of 16 (with 0.001 tangential loss) and a thickness h = 1 mm. The geometrical parameters of the metallic pattern are chosen as follows: period Dx=Dy=5.0 mm, a = b = c = 3.8 mm, w1 = w2=w3=0.4 mm and thickness t = 35 µm. Various EM properties, including SSPP propagation, reflection, and transmission, are strongly influenced both by these geometric parameters and by the relative permittivity of the dielectric slab and are well predicted by their band structures, especially for 2D materials22,33. Therefore, we first evaluated the band diagram of our designed metasurface, as shown in Fig. 2, where Fig. 2a represents the band structure below the light line (blue dash lines), and the inset indicates the first Brillouin zone and highly symmetrical points.

Fig. 1
figure 1

Geometrical details. a Geometry of the designed metasurface with Dx=Dy= 5.0 mm, a = b = c = 3.8 mm, w1=w2= w3=0.4 mm and t = 35 µm. b Top-view depiction of a sample with inset showing the details of a single unit

Full size image
Fig. 2
figure 2

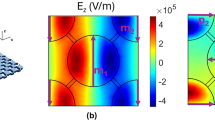
Diagrams for a = 3.8 mm. a Band diagram below light lines with frequency in GHz. The inset shows the Brillouin zone and high-symmetrical points. b–d IFCs of the first three bands in the first Brillouin, respectively, where the gray discs located at the center are the light cones at 3 GHz, 9 GHz, and 12.5 GHz, respectively, the frequency values are marked in GHz, and the frequency increases from blue to orange. e Transmission spectra at normal incidence obtained from simulations (EMT) when the electric field is polarized along the x- and y-directions, corresponding to the black line (point) and the red line (point), respectively. Insets are the Ez distribution at different resonances with values varying from –max (blue) to max (red). f Relative permittivity obtained from EMT, where the gray regions indicate the frequency ranges of hyperbolic IFCs predicted by EMT

Full size image

Further evaluation of the IFCs of the first three bands in Fig. 2b–d has revealed a topological transition of IFCs under a continuous frequency in the first band, where the shape of the IFCs gradually transforms from a closed ellipse to an open hyperbola, becoming a flat line at the transition point. The group velocity of the SSPP modes is perpendicular to the IFCs, which indicates collimation at the transition frequency due to the flat line feature19. Here, we employ the effective medium theory (EMT) to qualitatively facilitate the design of functional metasurfaces.

In most practical cases, the EM response of anisotropic metamaterials can be characterized by the effective permittivity and permeability tensors34,35,36,37. In our case, the permittivity (\(\hat \varepsilon\)) is anisotropic with orthogonal principle axes:

$$\hat \varepsilon = \left( {\begin{array}{*{20}{c}} {\varepsilon _{xx}} & 0 \\ 0 & {\varepsilon _{yy}} \end{array}} \right),$$
(1)

where the coordinates are normalized along the principle axis to diagonalize the matrix, and the subscripts xx and yy denote the x and y-directions, respectively. Notably, only TE modes (electric field polarized along the in-plane directions) are included in the designed metasurfaces due to their special resonances (see details in Supp. Note 3), which are quite different from those of the anisotropic metasurfaces with a metallic substrate, as TM modes are significant in the second case19,38. Next, we simplify the metasurfaces as a truly two-dimensional system and set the wave vector along the z-direction equal to a constant as an approximation, and the shapes of the IFCs of the designed metasurfaces can then be predicted by39:

$$\frac{{k_x^2}}{{\varepsilon _{yy}}} + \frac{{k_y^2}}{{\varepsilon _{xx}}} = k_0^2,$$
(2)

where \(k_x\) and \(k_y\) are the propagation vectors in the x and y-directions, respectively, and \(k_0 = \omega /c\) denotes the wavenumber of the substrate with angular frequency \(\omega\) and light velocity in a vacuum c. The multipolar distributions in our designed metasurface are numerically studied (see Supp. Note 1), concentrating on the electric dipole mode. The effective permittivity along the x and y-directions of the metasurface can be determined through fitting normal incident transmission spectra40,41. By employing Lorentzian dispersion and setting a thickness of 0.1 mm (see Supp. Note 2), the effective permittivity can be expressed as42:

$$\varepsilon _{xx} =163+\frac{8798.42}{6.1^2 - f^2 - 0.032 i \cdot f} \\ \varepsilon _{yy} = 175 + \frac{8377.53}{14.12^2 - f^2 - 0.082 i \cdot f},$$
(3)

where the imaginary parts indicate the loss from the dielectric slab, since a 0.001 tangential loss has been set during simulations, and f represents the frequency (in GHz)43. The normal incident transmission spectra with the electric field polarized along the x and y-directions are shown in Fig. 2d. Here, the red and black points denote the spectra from COMSOL Multiphysics simulations, while the solid lines indicate the homogenized approximation. The simulation and approximation are seen to be in good agreement. Equation (3) has been plotted in Fig. 2f, where the gray regions (6.1–9.6 GHz and >14.12 GHz) predict hyperbolic IFCs and collimation at the transition frequency (6.1 GHz). The band diagram from EMT has been studied (see Supp. Note 3), and the deviation can be understood by considering the strong overlap of frequencies between the different bands and the subwavelength-incompatible geometries at increased frequency, since EMT becomes invalid under such conditions. Therefore, the equation does successfully predict the existence of hyperbolic IFCs; that is, hyperbolic IFCs can be introduced by symmetrical resonance and have good accuracy when the structure is deeply subwavelength.

Unfortunately, the extensive overlap between the frequencies of the second and third bands indicates that there is no independent Lifshitz-like continuous topological transition in this frequency region, while the modes corresponding to the relatively flat IFCs in the second band, as shown in Fig. 2c are difficult to excite individually. There are two approaches to addressing this issue in order to obtain the other independent nondegenerate collimation frequency in the y-direction: one is to break the overlap of frequencies between the bands, and the other is to introduce a new resonance that can be excited by plane EMWs. First, we numerically calculate the modes at the resonance frequencies, as shown in the inset in Fig. 2e, where the mode at the higher frequency is a symmetrical dipole mode with dipole momentum along the y-direction. Consequently, there could be a dark mode protected by symmetry along the y-direction. As shown in Fig. 3a, when our designed H-shape is symmetrical with respect to the y-direction, the electric quadrupole mode (EQM) fails to be excited by the incident EM wave because it is decoupled from the electric dipole mode; however, it is no longer a dark mode once the mirror symmetry along the y-direction is broken, as it will couple with the electric dipole mode in this case. Therefore, our strategy to create nondegenerate collimation along the y-direction is to develop Fano-resonance in our system, that is, to sabotage the y-directional symmetry of the metallic pattern. For simplicity, we decrease only the length of a and keep the other parameters unaltered. The transmission coefficient for this asymmetrical structure when the electric field is polarized along the y-direction can be described by temporal coupled-mode theory44:

$$t_n \, {\mathrm{ = 1}} - \frac{{\left| {\alpha _E} \right|^2}}{{\left( {f - \overrightarrow \omega _d} \right) - \frac{{\left| \kappa \right|^2}}{{\left( {f - \overrightarrow \omega _q} \right)}}}},$$
(4)

where \(t_n\) denotes the normal incident transmission coefficient; \(\alpha _E\) represents the radiative coupling parameter; \(\overrightarrow \omega _d = \omega _d + i\alpha _E^2\) and \(\overrightarrow \omega _p = \omega _p\), where \(\omega _d\) and \(\omega _p\) are the resonant frequencies corresponding to the dipole mode and quadrupole mode, respectively; and \(\kappa\) is the coupling coefficient between these two modes (which is a function of the degree of asymmetry of the pattern) at normal incidence. It is equal to 0 when our structure is symmetrical, which indicates only one dip in the transmission spectrum due to dipole mode, whereas there are two dips for an asymmetric structure.

Fig. 3
figure 3

The introduction of Fano-resonance. a Fano interference between the electric dipole and quadrupole modes at the left and right side, indicating the symmetric and asymmetric case, respectively. b Normal-incidence transmission spectra with different a when the electric field is polarized along the y-direction. c Variation in Q-factor obtained by fitting the Fano line shape as a function of (a)

Full size image

Here, a = 3.8 mm, a = 3.75 mm, a = 3.7 mm, a = 3.65 mm, a = 3.6 mm, a = 3.55 mm and a = 3.5 mm are used as the parameters for the normal incident transmission spectra with the electric field polarized along the y-direction. As shown in Fig. 3b, the asymmetric line shape (Fano line shape) with the symmetry broken along the y-direction has been directly observed. Notably, Equation (4) is not suitable for fitting the transmission in Fig. 3b, because the multipole modes have been defined according to the current contributions of the metallic pattern, in which the effects of the dielectric slab are not fully included, especially in the evaluation of transmission. Nevertheless, it is fruitful for the qualitative prediction of the dip corresponding to the quadrupole and dipole modes and is very correct once only metallic patterns are included (see Supp. Note 10). The Q-factor was evaluated by fitting the transmission spectra with the Fano line shape (see Supp. Note 4), which decreases exponentially as length a decreases, as shown in Fig. 3c. The resonance frequency shows a blueshift, which is also studied (see Supp. Note 5). Recently, Fano-resonance with a high Q-factor has been used in many areas, such as chemical sensing45 and slow light27. However, it is arduous to establish an efficient form to describe the effective permittivity and permeability in this case, and resonances with high Q-factors, above the light line, will couple with modes below46. Therefore, resonances with a lower Q-factor were chosen for our purpose.

The Fano line shape with a low Q-factor behaves like a symmetrical one, in which the effective parameters can be described via Lorentzian expressions. Here, a = 2.6 mm is selected as an example since the Q-factor is <100, as shown in Fig. 3c. The contributions to the radiating power for the case of a = 2.6 mm are dominated by the EQMs, which has been numerically verified (see Supp. Note 1). The contributions of electric multipole modes (including EQMs) to the effective parameters in metamaterials after homogenization has been studied47,48. In particular, the EQMs in a metasurface contribute not only to the effective permittivity in the plane but also to the effective permeability perpendicular to the plane (\(\mu _{zz}\)), which is related to the in-plane permittivity49,50. In addition, interestingly, the bianisotropic property predicts that the corresponding resonant frequency for the in-plane permittivity exists when \(\mu _{zz}\) vanishes, namely, that \(\mu _{zz}\) has no contribution to determining the shape of IFCs in an application in our case49. We note that local constitutive parameters still make sense in the prediction of hyperbolic IFCs, even though the metasurface should be regarded as nonlocal once the EQMs are included. It is known that only in-plane effective parameters can be directly determined via normal transmission spectra, and therefore the effective permittivity can be fitted. With a thickness of 0.1 mm, the expressions read:

$$\varepsilon _{xx} = 163+ \frac{8721.95}{6.68^2-f^2-0.024 i \cdot f} \hfill \\ \varepsilon _{yy} = 175 +\frac{2848.3}{10.65^2-f^2-0.09i \cdot f} \\ \quad+\frac{427.6}{17.1^2-f^2-0.2i \cdot f}$$
(5)

Here, the effect of Fano-resonance on \(\varepsilon _{xx}\) is neglected because the current distribution is concentrated in the y-direction, which has been numerically verified (see Supp. Note 6).The transmission spectra and effective parameters are shown in Fig. 4e, f, respectively, indicating two hyperbolic IFC regions marked in gray, where \(\varepsilon _{xx}\) and \(\varepsilon _{yy}\) have opposite signs. To verify our deduction, the IFCs were numerically evaluated, as shown in Fig. 4b–d. A Lifshitz-like topological transition of the IFCs occurs in the second band with a flat line at the transition frequency, which indicates the other collimation frequency with group velocity along the y-direction. The Lifshitz-like transition of the IFCs for the first band is always retained, as the physical conditions are consistent, and the collimation is very robust as a is decreased. We note that the same phenomenon still occurs even when a has been reduced to 0.4 mm, and thus, the metallic pattern can be regarded as a ‘T-shape’. The IFCs of the first two bands for a = 1.4 mm and a = 0.4 mm have been plotted in Fig. 5.

Fig. 4
figure 4

Diagrams for a = 2.6 mm. a Band diagram below light lines with frequency in GHz. b–d IFCs of the first three bands in the first Brillouin zone, where the gray discs located at the center are the light cones at 3.7 GHz, 10.5 GHz and 13.2 GHz, respectively. Frequency values are marked in GHz, and the frequency increases from blue to orange. e Transmission spectra at normal incidence obtained from simulations (EMT) when the electric field is polarized along the x and y-directions, corresponding to the black line (point) and the red line (point), respectively. Insets are the Ez distribution at different resonances with values varying from –max (blue) to max (red). f Effective parameters obtained from EMT, where the gray regions indicate the frequency regions of the hyperbolic IFCs predicted by EMT

Full size image
Fig. 5
figure 5

IFCs of the first two bands. a, c The IFCs of the first bands for a = 1.4 mm and a = 0.4 mm, respectively. b, d The IFCs of the second bands for a = 1.4 mm and a = 0.4 mm, respectively. The gray discs located at the center are the light cones at 3.7 GHz for (a), (c) and at 10.8 GHz for (b), (d), respectively. Frequency values are marked in GHz, and the frequency increases from blue to orange

Full size image

To summarize our design, we successfully created a continuous Lifshitz-like topological transition for the IFCs in the y-direction by introducing low-Q Fano-resonance to our system. Accordingly, by designing continuous nondegenerate topological transitions in orthogonal directions, two flat IFCs with independent frequencies in orthogonal directions can be achieved. This phenomenon is very stable under variable geometries. Very recently, the modes corresponding to the transition frequency in a single direction were proven to be diffractionless, soliton-like and sensitive to the surrounding environment51. To the best of our knowledge, this study is the first time that collimation has been demonstrated in both orthogonal directions at independent frequencies, which enables many potential applications, especially for position sensors. Meanwhile, recent work on Fano-resonance has mainly concentrated on transmission and reflection spectra, whereas we highlight that Fano-resonances are also accountable for the control of surface modes located below the light line, which introduces a new and previously unreported avenue for manipulating more complicated bands of metasurfaces52,53,54,55. In the next section, we describe the microwave experiment and a sensing prototype, further confirming our results.

Results

Experiment

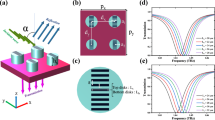
A metasurface consisting of 14 × 14 unit cells and excitation units (total size 8 × 8 cm2) was fabricated. The geometric parameters of the unit cell were chosen as in Fig. 1a, and the excitation unit was composed of microstrip lines to excite surface EM waves (see Supp. Note 7). The details of our real sample are shown in Fig. 1b. The dielectric slab is made of TP1/2, a nonmagnetic material with a relative permittivity of 16 and a tangential loss of 0.001. The metallic patterns were printed in the dielectric slab with 35 µm thick copper and were covered by a negligible thickness of solder on the copper surface to prevent oxidation.

The symmetrical case (a = 3.8 mm) was studied first. Figure 6a shows the distribution of the electric field along the x-direction (Ex), which is measured by locating a receiving antenna ~1 mm above the metasurface when the input frequency is 5.29 GHz along the x-direction. Compared with the IFCs in Fig. 2b, the frequency for the flat IFC agrees well with our simulation results, and the slight difference between the experiment and the simulation is due to the fabrication tolerances and the derivation of relative permittivity. However, we fail to find a collimation frequency upon excitation along the y-direction, and the Ex distribution for a relatively unidirectional propagation frequency (11.63 GHz) in our experiment is plotted in Fig. 6e. The modes composed of x components have been excited, and the Ex distribution is observed in a large area instead of along a narrow trail. Compared with Fig. 2c, d, it is evident that modes in the third band at the same frequency have also been excited, resulting in group velocity along the x-direction.

Fig. 6
figure 6

Measured field distributions. a–d Ex distribution when the metasurface is excited along the x-direction, for a = 3.8 mm, 2.6 mm, 1.4 mm, and 0.4 mm, respectively. e–h Ex distribution when excited along the y-direction, with a = 3.8 mm, 2.6 mm, 1.4 mm, and 0.4 mm, respectively

Full size image

Next, the asymmetric cases were studied. Figure 6b, f depicts the Ex distribution in the case of a = 2.6 mm when the input frequency is 6.04 GHz along the x-direction and 11.51 GHz along the y-direction. Collimation is maintained along the x-direction, which is similar to the symmetric case. However, in contrast to Fig. 6e, mode propagation along a narrow region can be observed in Fig. 6f, which is consistent with the prediction of the IFCs in Fig. 4, where an independent flat line exists for the second band. The cases of a = 1.4 mm and a = 0.4 mm were also studied, where Fig. 6c, g corresponds to a = 1.4 mm and Fig. 6d, h to a = 0.4 mm, respectively. Therefore, two independent collimation frequencies along orthogonal directions in our designed metasurface have been found, proving that hyperbolic IFCs can be introduced by low-Q Fano-resonance. The Ex distributions corresponding to the collimation frequencies were also studied via COMSOL Multiphysics (see Supp. Note 8). The collimation modes are sensitive to the surrounding environment, and the electric field is well confined in a narrow region at the collimation frequency. Based on the physical features, we performed the following experiment to demonstrate that collimation modes can be used to read minor changes in the environment, which is the foundation of position sensors.

To change the environment quantitatively, dielectric cylinders with both radius and height equal to 5 mm were employed, as shown in the inset in Fig. 7a (the dielectric cylinders have relative permittivities of 16.5, 20.5, 36, 45 and 69 from left to right). Here, the metasurface of a = 1.4 mm with excitation along the x-direction is shown in Fig. 7a, b (the former has the cylinder placed at the center of the propagation trail, and the latter has cylinders placed at the sides of the trail). The S21 amplitude was measured for 6.9 GHz along the x-direction and 11.4 GHz along the y-direction, as shown in Fig. 7c, d, respectively, in the case of a = 1.4 mm. For a = 0.4 mm, the cases with 7.9 GHz along the x-direction and 11.2 GHz along the y-direction are plotted in Fig. 7e, f, respectively. The S21 amplitude was considerably reduced when a dielectric cylinder was placed on the propagation trail and fluctuated slightly in the off-trail case, which reveals that interference from the environment of the propagation trail can be registered via S21 amplitude.

Fig. 7
figure 7

The effects of the perturbation. a, b Schematics with cylinders placed at the center and at the sides of the propagation path, respectively. The inset in (a) shows cylinders with relative permittivities of 16.5, 20.5, 36, 45, and 69 from left to right. c–f S21 amplitudes of (c) a = 1.4 mm, field along the x-direction; (d) a = 1.4 mm, field along the y-direction; (e) a = 0.4 mm, field along the x-direction; and (f) a = 0.4 mm, field along the y-direction

Full size image

Position-sensing prototype

The prototype device is composed of two independent microwave sources, four microwave switches, two amplifiers, two detectors, a voltage collector, some coaxial cables and an analysis system, as shown in Fig. 8. The switches are controlled by the program, allowing the ports with the numbers marked on the sample to be periodically opened or closed. For instance, suppose T is the opening time of each switch, and only the four ports labeled 1 are open in the time period 0−T, only the four ports labeled 2 are open in the time period T−2T, and so on. Then, EM waves emitted from the microwave source can periodically scan from port 1 to port 5 with a periodicity of 5 T. The EM waves received from switch 2 and switch 4 are amplified because of the limited coupling efficiency from the plane EM waves to the surface EM waves, and there is substantial loss when transmitting though coaxial cables and switches, so that the power of the EM waves can decay to less than the detection limit of the detectors. The EM wave signal is converted into an AC voltage signal upon reaching the detector after amplification and is collected by the voltage collector. As a result, each row and column is marked by independent numbers, and 25 total points can be identified and distinguished via the recognition system when the amplitude of the signal is decreased by the touch of a finger on the surface. In our recognition system, touch location is mapped on the screen and refreshed each period.

Fig. 8
figure 8

Schematic diagram of the position-sensing prototype, where the black disk on the sample represents the perturbation of the environment, and the coordinates of the perturbation position are analyzed on the computer screen (a real-time demo is shown in Supplementary Video)

Full size image

Since the collimations are very stable under a constant physical state, it is feasible to adjust the geometrical parameters to Dx = Dy = 6.0 mm, a = 3 mm, b = c = 5 mm, w1 = w2 = w3 = 0.4 mm d = 1 mm and t = 35 µm to decrease the collimation frequency along the x-direction due to the limitations of our microwave source. The IFCs of the first two bands under this geometry have been evaluated and plotted (see Supp. Note 9). The real sample is composed of 20 × 20 units, and the excitations were kept unchanged. Two independent collimation frequencies were identified, equal to 4.78 GHz and 9.5 GHz in the x and y-directions, respectively (see Supp. Note 9). The open time T is set to 0.6 s due to the limitations of the switching time of our microwave switch, whose periodicity is 3 s.

In Fig. 8, the black disk denotes the perturbation of the environment at the touch of a finger, as shown in the video (see Supp. Video). The coordinates of the position we touched were successfully mapped on the screen, which establishes that the metasurface based on the given design can function as a position sensor. Other properties, including the touch resolution and the loss of the designed position sensor, have also been discussed (see Supp. Note 9). To the best of our knowledge, this is the first realization of a position sensor based on surface EM waves. Many advantages can be found compared to current position sensors; for instance, this sensor has simpler layers and more easily adjusted resolution than capacitive and resistive sensors and broader optional substrates and wider application ranges than surface acoustic wave sensors30,31,32.

Discussion

In conclusion, we have shown that the Fano-resonance (especially with a lower Q-factor) behaves like a symmetrical resonance and can give rise to hyperbolic IFCs in both EMT and numerical simulation. Then, we created topological transitions of IFCs in orthogonal directions in different bands by decreasing the Q-factor of the Fano-resonance in our system. Thus, the collimating phenomena in both orthogonal directions at the transition frequency were verified both numerically and experimentally. Moreover, a position sensor based on surface EM waves was prototyped and demonstrated. This demonstration was enabled by the fact that the collimated surface modes have great sensitivity to environmental changes in the propagation trails, and it illustrates one of several promising applications.