Observation of the topological aberrations of twisted light

Abstract

When reflected from an interface, a laser beam generally drifts and tilts away from the path predicted by ray optics, an intriguing consequence of its finite transverse extent. For twisted light, such beam shifts manifest even more dramatically: upon reflection, a field containing a high-order optical vortex is expected to experience not only geometrical shifts, but an additional splitting of its high-order vortex into a constellation of unit-charge vortices, a phenomenon known as topological aberration. In this article, we report on the experimental observation of the topological aberration effect, verified through the deformation of vortex constellations upon reflection. We develop a general theoretical framework to study topological aberrations in terms of the elementary symmetric polynomials of the coordinates of a vortex constellation, a mathematical abstraction which we prove to be the physical quantity of practical interest.

Introduction

The reflection of light beams on interfaces is a quintessential problem in wave optics. In contrast to simple geometrical optics laws, where a ray of light reflects of a surface with the same incidence angle but on the opposing side of the surface normal, the reflection of beams in wave optics encompasses a more complex behaviour. Generally, a beam can be mathematically described by a finite spectrum of plane waves. Upon reflection, each of these plane waves individually follows paths determined by geometrical optics¹. However, the changes to the amplitudes and phases of the component plane waves result in a reflected field which is macroscopically different from the incident field. Perhaps the most well-known examples of such phenomena are optical beam shifts, which are spatial and angular deviations of reflected laser beams from their expected ray-optical trajectories^2,3. Such shifts are usually separated into Goos-Hänchen (GH)^4,5 and Imbert-Fedorov (IF)^2,6 shifts, which occur along and orthogonal to the plane of incidence, respectively. These effects have distinct physical origins: while the GH shifts come from the angular variation of the reflection coefficient of the interface, the IF shifts, also known as the spin-Hall effect of light⁷, stem from the rotation of the plane of incidence experienced by elliptically polarised waves upon reflection. The GH and IF shifts have been extensively studied for different types of optical beams and interfaces in a range of contexts, as discussed in detail in Ref. ².

A more subtle topic is the reflection of vortex beams^{2,8,9,10,11,12,13}. Such beams are most well known for their ability to carry orbital angular momentum (OAM), which is accompanied by a twisted phase structure, i.e., a varying phase front transverse to the propagation direction as $\exp (i\ell \phi )$, where ℓ is an integer number and ϕ labels the azimuthal angle^14,15. The wavefronts of such beams consist of ∣ℓ∣ identical helicoids nested on the propagation axis, on which lies a strength-ℓ optical vortex or phase singularity^16,17. Due to the OAM-induced mixing of the spatial and angular GH and IF shifts¹⁸, vortex beams also acquire OAM sidebands upon reflection¹⁹ and feature significant deformations in their intensity profiles^8,9 at critical angles. Beyond beam shifts, Dennis and Götte showed in their seminal work²⁰ that a pure strength-ℓ optical vortex splits into a constellation of unit strength vortices by reflecting at a simple dielectric interface, which they recognised as a topological aberration effect. It is well known, however, that it is impossible to generate perfect higher-order vortices, as the latter are unstable under any kind of pertubation^21,22,23. Therefore, a fundamental question remains open: how do vortex constellations, the actual observable physical objects, experience topological aberrations?

In this article, we address this question first by generalising the framework developed in Ref. ²⁰ to arbitrary uniform aberrations of vortex constellations, thereby addressing typical experimental limitations in the generation of vortex beams. We then show that the aberration of a vortex constellation is captured by a linear transformation of the elementary symmetric polynomials of its coordinates, and that this transformation is related to the angular Wirtinger derivatives of the aberration. Lastly, we detail the experimental observation of the topological aberration of vortex constellations under total internal reflection from a thin Au film-Fused Silica interface, where aberration effects are enhanced due to the resonant excitation of surface plasmons at the interface. With this method, we are able to verify the topological aberration using constellations with up to 3 vortices, in good agreement with the theoretical model developed. Due to the direct link between the vortex dynamics and the properties of the material upon which the light is reflected, our results could be applied to advanced material characterisation techniques. Moreover, the underlying theoretical description of the vortex dynamics might also be applicable to other fields of physics such as Bose–Einstein condensates^24,25, superfuilds^26,27, or topological field theories²⁸.

Results and Discussion

Theory of topological aberrations

We start by considering an arbitrary input field containing a constellation of ℓ_m identical unit-strength vortices. In momentum space, the scalar part of such a field can be written as²⁰

$${\tilde{\psi }}_{I}\, (\, {{{\boldsymbol{\chi }}}}) \,={\sum}_{\ell=0}^{{\ell }_{m}}{\sigma }_{\ell }(| \chi | )\,{\left(\frac{\chi }{| \chi | }\right)}^{\ell }\,,$$

(1)

where χ = (χ, χ^*), with $\chi=({k}_{x}+i{k}_{y})/\sqrt{2}$, and (k_x, k_y) are Cartesian coordinates in momentum space. $\sqrt{2}| \chi |={k}_{\perp }=\sqrt{{k}_{x}^{2}+{k}_{y}^{2}}$ and ${{{\rm{Arg}}}}(\chi )=\alpha={\tan }^{-1}({k}_{y}/{k}_{x})$, where k_⊥ and α are the momentum radial and azimuthal coordinates, respectively. Equation (1) can be seen as a superposition of optical vortices with topological charges 0 ≤ ℓ ≤ ℓ_m, whose background functions σ_ℓ(∣χ∣) determine both the OAM spectrum and the field’s radial features. Furthermore, the constellation coordinates are encoded in the complex roots of the field (1), which is a polynomial of order ℓ_m in χ.

A field of the form given in Eq. (1), i.e. a constellation of vortices, is naturally obtained by attempting to generate a vortex of order ℓ_m experimentally, due to inherent limitations in light-shaping devices and/or subsequent aberrations caused by mirrors, lenses, and other refractive elements. Nevertheless, for small aberrations, which is the case for a carefully assembled experiment, the contributions of ℓ < ℓ_m are small and the constellation is tightly confined to the beam’s central propagation direction. In this case, we can approximate the field in Eq. (1) in real space to the lowest order of each OAM component, obtaining

$${\psi }_{I}({{{\boldsymbol{\xi }}}})={\sum}_{\ell=0}^{{\ell }_{m}}{\bar{\sigma }}_{\ell }{\xi }^{\ell }\,,$$

(2)

where ξ = (ξ, ξ^*), with $\xi=(x+iy)/\sqrt{2}$, and where (x, y) are the Cartesian coordinates in real space. This approximation is valid when the lowest order in the power expansion of σ_ℓ(∣χ∣) is zero, which is the case for Gaussian background fields, for example. However, the approximation breaks when the background fields have components of high-order radial modes, in which case more complicated constellations with both positively and negatively charged vortices may appear^29,30. A detailed derivation of the coefficients ${\bar{\sigma }}_{\ell }$ is provided in the Supplementary note 1³¹.

Upon a spatially uniform aberration such as the reflection from a flat interface, each plane wave component of momentum χ in the angular spectrum (1) is transformed as $\exp (i{{{\boldsymbol{\chi }}}}\cdot {{{{\boldsymbol{\xi }}}}}^{*})\to \,R({{{\boldsymbol{\chi }}}})\exp (i{{{\boldsymbol{\chi }}}}\cdot {{{{\boldsymbol{\xi }}}}}^{*})$, where R(χ) is the momentum-dependent aberration function. In the case of reflection from a flat interface, the aberration function is the reflection coefficient given by the Fresnel coefficients, which also depends on the incident and measurement polarisations^2,20. The resulting field in real space can then be modelled as

$${\psi }_{R}({{{\boldsymbol{\xi }}}}) \,=\int\,{d}^{2}{{{\boldsymbol{\chi }}}}{\tilde{\psi }}_{I}({{{\boldsymbol{\chi }}}})R({{{\boldsymbol{\chi }}}})\exp (i{{{\boldsymbol{\chi }}}}\cdot {{{{\boldsymbol{\xi }}}}}^{*})\,,$$

(3)

which is a Fourier transform in the complex coordinates ξ and χ. Hence, we can expand the aberration in a power series and use the differentiation property of the Fourier transform (FT), which maps the FT of ${\chi }^{m}{\chi }^{*n-m}{\tilde{\psi }}_{I}({{{\boldsymbol{\chi }}}})$ to the n-th order derivatives of ψ_I(ξ). We obtain

$${\psi }_{R}({{{\boldsymbol{\xi }}}}) \,=\, {\sum}_{n=0}^{\infty }{\sum}_{m=0}^{n}{i}^{-n}{C}_{n}^{m}\frac{{\partial }_{n}{\psi }_{I}({{{\boldsymbol{\xi }}}})}{\partial {\xi }^{*m}\partial {\xi }^{n-m}}\,,$$

(4)

$${C}_{n}^{m} \,=\, \frac{1}{n!}\left(\begin{array}{c}n\\ m\end{array}\right){\frac{{\partial }_{n}R({{{\boldsymbol{\chi }}}})}{\partial {\chi }^{m}\partial {\chi }^{*n-m}}\Bigg| }_{\chi,{\chi }^{*}=0}\,,$$

(5)

where $\partial /\partial \xi \,=\, \left(\partial /\partial x-i\partial /\partial y\right)/\sqrt{2}$ and $\partial /\partial \chi \,=\, \left(\partial /\partial {k}_{x}-i\partial /\partial {k}_{y}\right)/\sqrt{2}$ are Wirtinger derivatives³². From Eqs. (2) and (4), we arrive at the final expression for the aberrated field

$${\psi }_{R}({{{\boldsymbol{\xi }}}}) \,=\, {\sum}_{\ell=0}^{{\ell }_{m}}{\bar{\gamma }}_{\ell }{\xi }^{\ell }={\sum}_{\ell=0}^{{\ell }_{m}}{\sum}_{n=0}^{\ell }{i}^{-n}{\bar{\sigma }}_{\ell }n!\left(\begin{array}{c}\ell \\ n\end{array}\right){C}_{n}^{0}{\xi }^{\ell -n}\,,$$

(6)

where ${\bar{\gamma }}_{\ell }$ are the coefficients of the vortex expansion of the aberrated field, derived in detail in the Supplementary note 1³¹.

Equation (6) shows that an aberration decomposes the incoming light field into a superposition of its Wirtinger derivatives, weighted by the Wirtinger derivatives of the aberration function. Interestingly, in the case of the vortex input field of Eq. (1) the derivative modes are simply optical vortices of lower order, in such a way that the aberrated field still contains a collection of ℓ_m phase singularities, but in a deformed constellation, as we illustrate in Fig. 1. This implies that by monitoring the changes in a vortex constellation, one can gain insight into the properties of the aberration function, and thus into features of the light-matter interaction causing the aberration.

Fig. 1: Conceptual picture of the topological aberration effect.

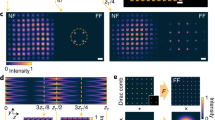
The figure shows the input and reflected fields of a second-order vortex constellation as measured in our experiment. k denotes a plane wave component of the incident vortex, while k₀ is the central wave vector in the beam. The plane of incidence is k_xk_z, and the dashed lines show the ray optics trajectory of the central plane wave k₀, with the angle of incidence θ₀. The input and reflected constellations are marked with black crosses and orange circles, respectively. The intensity scaling does not apply to the magnified regions.

High-order aberrations of vortex constellations

Equation (6) establishes a direct correspondence between the coefficients of the vortex expansions of the incident and aberrated fields. However, the question still remains as to how the coordinates of the singularities within the corresponding constellations compare with one another. This problem is elegantly solved by Vieta’s theorem³³, which we illustrate in the following. Consider an arbitrary constellation of ℓ_m vortices with coordinates (x_j, y_j), which yields a vortex expansion with roots ${\Delta }_{j}=({x}_{j}+i{y}_{j})/\sqrt{2}$ and coefficients c_i to be determined. According to Vieta’s theorem we have that

$${e}_{j}={(-1)}^{\,\, j}\frac{{c}_{{\ell }_{m}-j}}{{c}_{{\ell }_{m}}}\,,\quad 1 \, < \, j \, \le \, {\ell }_{m}\,,$$

(7)

where e_j is the j-th order elementary symmetric polynomial (ESP) of the set of complex roots {Δ}. In terms of ESPs, equation (6) assumes the simple form

$${{{{\bf{e}}}}}_{R}={\hat{R}}_{\chi }{{{{\bf{e}}}}}_{I}\,,$$

(8)

where the vectors e_I and e_R contain the ESPs of the input and aberrated constellations, respectively, with the aberration operator ${\hat{R}}_{\chi }$ acting on the ℓ_m-dimensional subspace spanned by the ESPs. The explicit form for the operator ${\hat{R}}_{\chi }$ is an upper triangular matrix containing the Wirtinger derivatives of the aberration function R(χ) up to the order ℓ_m, as we detail in the Supplementary note 1³¹.

We conclude from Eq. (8) that the aberration of a vortex constellation is fully captured by a linear transformation of its ESPs. Furthermore, an intuitive physical/geometrical interpretation of the ESP transformations is possible by means of Newton’s identities³³, which relate the ESPs to power sums of a set of complex roots. For example, e₁ is proportional to the constellation barycenter, whose transformation contains the GH and IF beam shifts of vortex beams^2,3,18,20. On the other hand, e₂ and e₃ give the second and third moments of the constellation positions with respect to the barycenter, which are related to the variance and the skewness of the constellation, respectively. For higher orders, the ESPs are sums of products of moments of the constellation positions that add up to that order, whose meaning we could not identify.

For clarity, let us explicitly consider the case of ℓ_m = 2. We choose the origin of the reference frame at the barycenter of the input constellation, such that the input field is ψ_I(ξ) ∝ ξ² + e_I2ξ⁰. From Eqs. (6) and (7), we obtain that

$${e}_{R1} \,=\, {\left.2i{R}_{\chi }^{{\prime} }/{R}_{\chi }\right\vert }_{0}\,,$$

(9)

$${e}_{R2} \,=\, {\left.{e}_{I2}-{R}_{\chi }^{{\prime\prime} }/{R}_{\chi }\right\vert }_{0}\,,$$

(10)

where ${R}_{\chi }^{{\prime} }{| }_{0}$ and ${R}_{\chi }^{{\prime\prime} }{| }_{0}$ are the first and second Wirtinger derivatives of R(χ) at χ = χ^* = 0. Equation (9) shows the shift of the barycenter of the constellation by the known Artmann translator of a unit vortex^12,18, which is the first order topological aberration of the constellation. In fact, this result, previously predicted only for perfect input vortices²⁰, holds regardless of the particular geometry or the order of a vortex constellation. Furthermore, equation (10) shows the second-order topological aberration, which amounts to the stretching of the input constellation and its rotation around the barycenter.

Experiment

To observe the aberrations of the vortex constellations, we use the experimental setup depicted in Fig. 2. We use a fibre-coupled diode laser centred at the wavelength λ = 810 nm, operated below the lasing threshold and filtered by a narrow bandpass filter (Semrock, 3nm bandwidth). The beam is then polarised on a polarising beam-splitter (PBS) and divided with a non-polarising 50:50 beam-splitter (BS) into a probe beam, which we prepare with the desired constellation, and a reference beam, used afterwards for the generation of off-axis holograms. Furthermore, the polarisations of the probe and reference fields are set to be identical, and they are controlled by a half-wave plate placed after the BS.

Fig. 2: Experimental setup.

BP, bandpass filter; ND, neutral density filter; M1, retro-reflecting mirror; PBS, polarising beam-splitter; BS, 50:50 non-polarising beam-splitter; HWP1 and HWP2, true-zero order half-wave plates; SLM, spatial light modulator; CMOS, camera sensor. The inset shows a breakdown of our reflecting object, which consists of an Au film assembled on a FS substrate and optically contacted to a FS prism.

To prepare the spatial profile of the probe beam, we shape it on a spatial light modulator (SLM, Holoeye Pluto 2.0) displaying a $\exp (i{\ell }_{m}\phi )$ phase structure, without amplitude modulation, which naturally leads to a constellation tightly confined to the beam centre. We further tune the constellation by introducing wavefront aberrations by means of Zernike polynomials³⁴, ensuring that all the ℓ_m vortices are clearly observable in our apparatus. As an additional precaution, we use a second PBS to prevent any undesired changes in polarisation due to the SLM.

Our aberrating device consists of a 35nm thick Au film assembled on the hypothenuse of a fused silica (FS) right-angle prism, in the so-called Kretschmann-Raether (KR) configuration^35,36. The Au film is deposited on an FS substrate using electron beam-assisted evaporation and optically contacted to the prism with index-matching gel (Thorlabs G608N3). In the KR configuration, a P-polarised input beam can resonantly excite surface plasmons at the interface between FS and the Au film via attenuated total reflection (ATR), enhancing the angular gradients of the reflection coefficient, and hence the topological aberration imprinted on the reflected beam³⁷. By measuring the power of the reflected S- and P-polarised probe beams as a function of the angle of incidence and using a transfer matrix model (See Supplementary Note 3 in ref. ³¹) to numerically fit the results, we determine the resonant ATR angle and the effective permittivity of the Au film to be θ_ATR ≈ 45.02^∘ and ϵ_f = −22.8456 + 1.2619i, respectively. Furthermore, since only P-polarised light excites surface waves, we use the reflected S-polarised field as a good approximation of the input field, allowing both the input and the aberrated constellations to be measured upon reflection. Finally, for our simulations we consider the aberration function R(χ) to be the fitted reflection coefficient for P-polarised light.

To measure the constellation coordinates, we superpose the probe and reference beams off-axis and record the interference patterns with a CMOS camera (IDS U3-3650XLE-M-GL, 2.2 μm pixel size), from which both the intensity and phase profiles are digitally retrieved^38,39. To measure the constellations at different angles of incidence, we rotate the prism using a motorised rotation stage (Thorlabs PRM1/MZ8) while maintaining the camera fixed. The acquired constellations are then shifted in post-processing, so as to centre the origin of the reference frame at the barycenter of the input constellation.

It is worth noting that the measured constellations are affected significantly by interference with stray light coming from the protective glass window on the CMOS sensor, the reflective layers of the beam-splitters, etc., which cannot be eliminated in post-processing due to the propagation direction being almost identical to the probe field. Such interferences deform the input constellation even more than the topological aberration effect, and prevent the accurate observation of the phenomenon. To eliminate these unwanted interference effects, we operated the laser diode below the lasing threshold, shortening the coherence length of the light source to sub-millimetre scale at the cost of requiring precise control of the path length difference between reference and probe beams. Alternatively, a pulsed laser with sufficiently short pulse duration could also be used, provided that the effect of a finite bandwidth is taken into account in the modelling of the aberration function. Finally, we determine the constellation coordinates from the retrieved phase profiles using the algorithm detailed in the Supplementary note 4³¹.

We show in Fig. 3 our experimental results for constellations with 1 ≤ ℓ_m ≤ 3. In Fig. 3a we show the logarithmic Wirtinger derivative of the reflection coefficient, retrieved from the shifts in the barycenters of the constellations using Eqs. (6) and (9). We see that the retrieved derivatives accurately follow the theoretical curves simulated from the measured material parameters under the assumption ${R}_{\chi }^{(n)}{| }_{0}\approx {R}_{{k}_{x}}^{(n)}{| }_{0}/{2}^{n/2}$. Such an approximation is reasonable in our case, since k_xk_z is the plane of incidence, and the constellations are prepared and measured in the same polarisation. We note that, unlike the shifts in the center of mass for the vortex-carrying fields^12,20, the measured barycenter shifts do not depend on the total topological charge ℓ_m. This result is a direct measurement of the first-order topological aberration of a vortex constellation, which, despite its strong correspondence to the GH and IF shifts, had not yet been observed. Furthermore, the barycenter shifts we report are greatly enhanced compared to those of dielectric interfaces, reaching more than 30 wavelengths in magnitude. A similar enhancement of the GH shift has been reported in³⁷ for Gaussian beams, which here we extend to vortex beams and out-of-plane (IF) shifts.

Fig. 3: Measurement results.

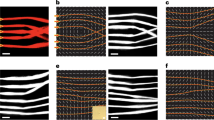
a First, b second and c third Wirtinger derivatives of the reflection coefficient for P-polarised light, retrieved from the measured vortex constellations for 1 ≤ ℓ_m ≤3. In each plot, the real (imaginary) part is shown as filled (hollow) markers for measured data, and as solid (dashed) curves for theoretical simulations. Additionally, in d and e we show the measured vortex constellations of the input field (crosses) and the reflected field (circles) with ℓ_m = 2 in d. and ℓ_m = 3 in e. All error bars are standard deviations calculated from the precision of the singularity positioning, detailed in Supplementary note 5³¹. The measured constellations are shown for the 15 angles of incidence highlighted on the x axis of b and c.

Lastly, in Fig. 3c we show the third Wirtinger derivative of the reflection coefficient, retrieved from the changes in the third-order ESPs of the ℓ_m = 3 constellation. In this case, the experimental results diverge more substantially from the theoretical simulations. By investigating the reflection process with simulated input constellations, we found this discrepancy to be associated to the noticeable radial features in the intensity profile of the field, caused by the lack of amplitude modulation in the mode preparation. A detailed comparison between the measured and simulated fields is provided in the Supplementary note 5³¹. Furthermore, the intensity and phase profiles fields from which the data of Fig. 3 was taken can be found the Supplementary video file⁴⁰.

Measuring the coordinates of a singularity constellation becomes increasingly challenging as the constellation order increases, since the intensity near the singularity positions decreases exponentially with ℓ_m. In our case, properly exposing the holograms near the singularity positions for ℓ_m > 3 requires exposure times that are long enough for the phase between the probe and reference fields to drift due to mechanical instabilities, leading to a decreased accuracy in the determination of the singularity positions. Nonetheless, we show in Fig. 3e the raw constellation coordinates for the set of angles highlighted by an arrow in Fig. 3c. Here, the deformation of the P-polarised constellations as well as the shift of the barycenter can be clearly seen.

In this article, we developed a new framework to describe the topological aberration of vortex constellations and reported on the first observation of the phenomenon predicted more than a decade ago²⁰. We showed that aberrations generally affect the elementary symmetric polynomials of a constellation’s coordinates, from which the angular Wirtinger derivatives of the aberration can be directly retrieved. We demonstrate the effect experimentally by measuring the topological aberrations of vortex constellations with up to 3 vortices upon attenuated total reflection, where aberration effects are enhanced by the resonant excitation of surface plasmon polaritons on the interface between a thin metallic film and a dielectric medium. An exciting perspective for our work is the extension to more complex singular light fields featuring, for example, polarisation singularities¹⁷, spatiotemporal vortices^41,42, vortex knots^29,30 and polarisation knots⁴³. Beyond light waves, we expect our work to inspire connections to other fields of physics where complex vortex constellations and symmetric polynomials appear, such Bose-Einstein condensates, superfluids^24,25,26,27, and even topological field theories²⁸.

Methods