Introduction

Backscattering in the form of analyzing the reflection of light from various objects (including the atmosphere) has been employed for many years1,2, although their investigation for low-power communication is much more recent3,4,5. In backscatter communication systems, a power-constrained wireless device piggybacks its data on ambient wireless signals instead of generating its own radio frequency (RF) waves, which would demand power-hungry components such as mixers, oscillators, and amplifiers. Such a power-efficient and sustainable system architecture has shown to be promising for IoT networks6,7,8. All existing backscatter communication networks operate below 100 GHz and rely on a limited node density9,10,11,12,13, an assumption that will inevitably change as IoT devices become ubiquitous. For instance, consider a dense deployment of IoT nodes in smart factories, plants, and distribution facilities (also called the industrial IoT) or the massive number of sensor and wireless nodes in smart enterprises (e.g., malls, museums, etc.)14. An example of dense IoT settings is illustrated in Fig. 1a. Indeed, enabling several thousands of simultaneous connections for wireless sensors is one of the key requirements for next-generation wireless networks15,16. Scaling backscatter communication to frequencies above 100 GHz can facilitate dense user populations to operate concurrently at orthogonal frequency bands. Further, narrow-beam directional transmission and reception, which is required to combat the high path loss in this regime, provides additional opportunities for simultaneous transmission through space division multiple access. Electromagnetic waves with frequencies between 0.1 and 1 THz combine the best of RF and optical waves: like RF waves, they can be phase modulated and experience lower penetration and reflection losses when compared to optical waves while still providing a large swath of continuous bandwidth and narrow beamwidths (similar to the optical regime)17,18,19. Despite these exciting prospects19,20,21, designing and implementing a backscatter sub-THz device that can establish a retro-directive link and operate over a wide bandwidth while drawing low power has remained a key challenge as the state-of-the-art techniques either employ omnidirectional sub-6 GHz RFID tags, active power-demanding directional arrays22 or retrodirective narrowband architectures at lower frequencies12,13. On the medium access control, localizing the backscatter nodes without any tag cooperation (and thereby power consumption) is yet another challenge towards enabling ubiquitous dense sub-THz backscatter networks. We address these challenges with a novel sub-THz backscatter architecture, exploiting the fundamental properties of leaky-wave devices.

Fig. 1: The system architecture overview.
figure 1

a An illustration of a dense IoT network with many concurrent links for future smart factories and distribution facilities. b An illustration showing multiple retrodirective sub-THz backscatter links. A dual-slot leaky waveguide is impinged by a broadband signal. Depending on the impinging angle, a portion of this signal couples into the waveguide and is guided toward a second slot with the help of embedded mirrors in the cavity. Through the interaction of guided waves with the second slot, a backscattered beam is directed back toward the broadband transceiver creating a retrodirective link without consuming any power. The guided waves are modulated before leakage to piggyback their data on the incident broadband signal. Several concurrent backscatter links can be formed as the signals are separated in both spatial and spectral domains. This allows for joint data communication and localization of wideband backscatter tags in the sub-THz regime.

Full size image

Leaky-wave devices have recently gained considerable attention in the sub-terahertz range23,24,25,26. The main principle is that a signal propagating in a waveguide can couple through an aperture to ‘leak’ out into free space if the guided mode and the free-space mode satisfy a phase-matching constraint on their parallel wave vector components. For the simplest architecture, a metal parallel-plate waveguide (PPWG) with empty space between the plates, with the lowest-order transverse electric (TE1) mode propagating in the waveguide, this phase-matching requirement imposes a constraint on the angle of propagation of the emitted radiation, for a given frequency f:

$$f\left(\phi \right)=\frac{{f}_{c}}{\sin \phi }$$
(1)

where fc is the waveguide cutoff frequency, given by c0/2b, and \(\phi\) is the propagation angle of the free-space mode relative to the waveguide propagation axis. Here, b is the plate separation, and c0 is the vacuum light velocity. This result indicates that the transmitted signal from the waveguide is pointed in a direction determined by the frequency of that signal. This analysis provides an adequate description of the behavior of leaky-wave devices, and this approach has been the basis of implementations in communications23,24 and radar27,28,29,30 in the THz range with demonstrations using bulk optical components21,23,24,25,26,27,28,29,30 and integrated technologies31.

We show here that the leaky-wave transmit-receive reciprocity enables a new foundation for spectrum-agile retrodirective backscatter architectures above 100 GHz. The spectral agility refers to the ability of the leaky-wave backscatter device to piggyback its data on a different part of the frequency band, depending on its location and orientation relative to the THz interrogator.

Results

The idea of a retrodirective frequency-agile sub-THz backscatter link is illustrated schematically in Fig. 1b. Retrodirectivity is the capability of a node to reflect an incident signal toward the source direction without prior knowledge of its direction of arrival while simultaneously imposing a modulation on the reflected signal. As shown in Fig. 1b, a leaky-wave backscatter device modulates sub-THz signals sent from an external transceiver (e.g., an access point) and directionally reflects it back to the transceiver, while embedding information in the phase and amplitude of the backscattered signal. This suggests a key insight: the reciprocal nature of leaky-wave devices could be exploited, not for sensing as in a radar context, but for backscatter communications. In other words, when acting as a receiver, the impinging signals would couple into the waveguide only if their spectral content and their incident angle are related according to Eq. (1). Hence, we devise two symmetrical slots in the leaky-wave backscatter: one for receiving the free-space ambient sub-THz signal (sent from the external transceiver) into the waveguide, and the other for leaking those signals (albeit modulated) back to free space. The embedded mirrors in the waveguide cavity redirect the signals from one slot to the other. Since this operation does not change the spectral content of the signal, the leaked waves are automatically directed toward the transceiver, thereby enabling a retrodirective link between the transceiver and the leaky-wave backscatter without consuming any power.

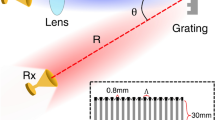
Using a scale-model test bed (see Supplementary Materials), we first measure the angle-frequency features in a parallel-plate leaky-wave device with a single rectangular slot in multiple transmit and receive configurations. As a transmitter, we excite the TE1 mode of the waveguide with a broadband source32 and measure the power spectrum of out-coupled signals at multiple angles using a broadband detector. Similarly, we place the broadband emitter at the same locations and measure the spectrum of in-coupled signals using a detector placed at one end of the waveguide. The results are summarized in Fig. 2a, demonstrating good agreement between the spectral profile at TX and RX modes and confirming the reciprocity in leaky-wave devices. We also observe the peak frequency shifting toward lower frequencies for larger angles, as expected by Eq. (1).

Fig. 2: Angle-Frequency reciprocity in leaky wave antennas enables retrodirective communication.
figure 2

a illustrating the power spectrum at different reception and transmission angles. The inset shows a schematic of the experimental setup. In the TX mode, a single-slot leaky waveguide is excited with a broadband input. We move the broadband RX radially to capture the spectrum of the transmitted signal from the leaky waveguide at different angles. At each configuration, the broadband detector is pointing toward the slot. In the RX mode, we impinge a broadband signal on the leaky waveguide slot and exploit a broadband detector on one end of the waveguide to measure the spectrum of the in-coupled waves. We try different impinging angles and compare the power spectrum as a function of angle in both transmission and reception modes. The results confirm the reciprocity of the angle-frequency relationship for in-coupled and out-coupled waves. b The radiation pattern of the backscattered beam. We observe that the reflected signal is automatically directed toward the transmitter. The top inset illustrates the schematic of the experimental setup, and the bottom inset shows the radiation pattern of the backscattered signal, indicating narrow pencil-shaped beams.

Full size image

We characterize the backscatter, again using a broadband source, but this time with a waveguide with two slots instead of one. Figure 2b illustrates the retrodirectivity of the link between this leaky-wave dual-slot backscatter and an external transmitter/receiver as the scanner. We emphasize that designing this external scanner is outside of the scope of this work, and we use an off-the-shelf THz time-domain system as an interrogator for evaluation purposes. As shown, the backscattered beam has the highest directivity (i.e., power) along the transceiver  angle. The inset shows a few example beam patterns with different incident angles.

Next, we consider the functionality of this backscatter architecture. The coupled waves must be modulated inside the waveguide cavity before they leak out back into the air and toward the transceiver. Designing fast electronically controlled low-power sub-THz modulators with low loss and high modulation depth is itself an active field of research33,34,35,36, and there has been much progress in the design of low-power wideband THz electrical modulators, which is beyond the scope of this paper37,38. Hence, for demonstration purposes, we implement phase and amplitude modulation of guided waves in the waveguide cavity using mechanical components. In particular, we employ an electrostatic MEMS mirror between the parallel plates of the waveguide to dynamically steer waves toward or away from the departing slot, i.e., changing the trajectory of guided waves and thereby modulating the amplitude of the backscattered signal by changing the effective aperture/slot area seen by the guided waves. This is illustrated schematically in Fig. 3a. Using ray optics, we can show that the amount of backscattered power from a rectangular slot with length L and width W can be written as

$${P}_{{bsc}}\propto \frac{1}{C+| \frac{2L}{W}\tan (2{\theta }_{{rot}})|}$$
(2)

where \({\theta }_{{rot}}\) is the amount of MEMS mirror rotation from the optimum orientation, and C is a constant that incorporates internal waveguide losses (see Supplementary Materials). Prior work showed that a trapezoid slot shape can offer better coupling efficiency and high directionality in leaky-wave devices39. Similar ray tracing techniques can be used to characterize the backscattered power with a trapezoid slot shape (see Supplementary Materials). Regardless of the slot geometry, the orientation of the embedded mirror can control the amplitude of the backscattered signal, which then conveys the intended bit stream to the external reader (e.g., access point).

Fig. 3: Modulation and constellation plots.
figure 3

a An illustration showing the phase and amplitude modulation inside the waveguide cavity. We employ an electrostatic MEMS mirror to modulate the trajectory of guided waves; thereby, changing the effective leakage aperture and the amount of out-coupled power, consequently. For phase modulation, we employ a piezo actuator in the cavity and change the trajectory length of the guided waves by a fraction of wavelength to enable the phase shift of interest. b Example constellation plots for multiple leaky-wave backscatters operating at different frequency regimes. Depending on its angular location, each leaky-wave backscatter modulates a portion of the incident broadband signal. The external receiver can recover the data sent by all 3 backscatter tags and simultaneously localize them by mapping the received center frequency to angular locations.

Full size image

We can also embed information in the phase of the signal (as well as the amplitude). We implement phase modulation via a super-resolution piezoelectric with micron-scale displacement. We mount a mirror on this piezo and control the path length of the guided waves (on their trajectory from the receiving slot to the transmitting slot) inside the cavity. This is illustrated in Fig. 3a. As expected, a small displacement of \(\triangle d\) yields the phase change of \(2\pi \frac{\triangle d}{\lambda }.\) We note that changing the MEMS mirror configuration (for amplitude modulation) would also slightly vary the phase, but such variations can be modeled and calibrated in advance. Therefore, with the joint configuration of the MEMS mirror and piezoelectric actuator, we can achieve any arbitrary constellations.

We exploit both amplitude and phase modulations for the leaky-wave backscatter links. Figure 3b demonstrates a few examples of measured constellations. In particular, we broadcast ultra-wideband pulses in space. Three leaky-wave backscatter devices are located within the expanding cone of this beam. Hence, they piggyback their data on a spectral sub-band of the emitted spectrum, depending on their location and orientation. We demonstrate that three leak backscatters can simultaneously send data to a sub-THz reader at the center frequencies of 178 GHz (8-PSK modulation), 220 GHz (16 QAM), and 290 GHz (BPSK). The measured SNR is about 21 dB with an EVM of around 6%. Note that the effective transmit power from the interrogator was − 57 dBm, which is extremely low power. Increasing the data rate will inevitability increase the receiver noise bandwidth according to N = FKTB, where F is the noise factor, K is the Boltzmann constant, T is the temperature in kelvin, and B is the bandwidth. Hence, it is necessary to compensate for the higher receiver noise by increasing the transmit power at the scanner. Fortunately, this will be feasible as our transmit power in these experiments is far below the FCC limit40 and even smaller than the output power available at the emerging THz integrated systems in silicon41,42.

The data rate in our experiments is limited to the speed of the deployed MEMS mirror. We exploit off-the-shelf MEMS devices with a speed of 5 KHz, and they consume less than 1 mW for continuous full-speed operation. For instance, for 16 QAM, this yields to 50 nj/bit. Both the data rate and energy/bit can be significantly improved with custom ICs instead of off-the-shelf components. Indeed, thanks to CMOS integration and fast switching, past work demonstrated low-power Gbps sub-THz transceivers, albeit with omnidirectional front end and mostly in near-field43,44,45,46. Our proposed leaky-wave retrodirective front end can be combined with such low-power modulators from the literature. We will leave the investigation of such an integrated backscatter solution for future work.

We emphasize that our proposed sub-THz backscatter front end enables a retrodirective link at zero power cost and eliminates the need for complicated and power-consuming array architectures, including active phase conjugate arrays22 and Van Atta Arrays12,13 that have been implemented at lower frequencies. Although phase conjugate arrays can form wideband and retrodirective links, they require a local oscillator per radiating element, making the architecture power-hungry. The state-of-the-art heterodyne conjugate arrays at microwave frequencies consume 10 s of mW per element47,48. Exploiting a multi-element array to realize directivity gain can easily yield prohibitively large power consumptions for future IoT nodes. In contrast, Van Atta Arrays are passive structures that exploit transmission lines to create the phase pattern required for retrodictive links at zero power cost (similar to our proposed architecture). However, the Van Atta array requires equal transmission line lengths connecting pairs of antennas. The difficulty in achieving this stipulation increases dramatically as more elements are added to the array. Further, the length of the transmission line is optimized to provide the required phase conjugate at a fairly narrow bandwidth, i.e., the bandwidth around 1% of the center frequency in the state-of-the-art49.

Our experimental results demonstrate three concurrent sub-THz backscatter links in Fig. 3b. We highlight that the backscatter hardware is identical for all nodes in this experiment, i.e., thanks to our frequency-agnostic architecture, backscatter nodes can piggyback their data on different spectral sub-bands simultaneously, according to their location relative to the active scanner. Hence, the next natural question is how many of such concurrent backscatter links can exist.

To answer this question, recall that the reflected signals from backscatter nodes may be separated in space or in frequency. Hence, we first have to understand the spectral band of operation (which we refer to as bandwidth) for a leaky backscatter device at a given location. The bandwidth of a leaky backscatter depends on several factors, including its geometric features and, interestingly, the incident angle of sub-THz excitation waves emitted by the scanner. Indeed, the non-linear frequency-dependent directional transmission/reception causes the out-coupled/in-coupled spectral band to also change with the angle. Particularly, the operating bandwidth for a receiver located at the far field of a typical leaky waveguide device at an angle \(\phi\) relative to the waveguide can be described by50

$${BW}\left(\phi \right)=\frac{{df}}{d\beta }\frac{d\beta }{d\phi }\triangle \phi=\frac{{c}_{0}}{2b\sin \left(\phi \right)\tan (\phi )}\triangle \phi$$
(3)

where \(\triangle \phi\) is the effective angular aperture subtended by the leaky backscatter in radians, \(\beta\) is the wave number of the guided wave, and \(\phi\) is the center of the incident angle. We note that \(\triangle \phi\) captures both the aperture size and distance from the emitter.

Equation (3) suggests that the bandwidth is wider for lower incident angles, i.e., when the backscatter tag is located at lower angles relative to the reader or, given a fixed location of the backscatter, when the tag is orientated in a way that the incident angle (with respect to the plane of the waveguide plate) is smaller. We have measured the half-power bandwidth of a backscatter node located at various angles around a sub-THz emitter. The result is shown in Fig. 4a and compared against the theoretical values suggested by Eq. (3). We observe that the bandwidth of a few  tens of GHz can be achieved for smaller angles. The bandwidth decays non-linearly at larger angles; nevertheless, the bandwidth remains > 1.6 GHz across the entire angular space. We emphasize that achieving such a wide bandwidth for passive RF backscatters has not been reported before.

Fig. 4: Dense leaky-wave backscatter nodes.
figure 4

a The measured half-power spectral bandwidth of a leaky-wave backscatter as a function of the angle of the tag’s angular location. The bandwidth is directly measured from the frequency response of the received time domain signal. We observe that the bandwidth monotonically decreases with larger incident angles. The half-power bandwidth of the backscattered signal can be tens of GHz to a few GHz, depending on the impinging angle. b In a network consisting of multiple leaky-wave backscatters, we can establish several concurrent interference-free links by separating the backscattered signal in the spatial and spectral domains. Since the spectral band at each tag depends on its angular location (i.e., the angle of incident on the tag), to ensure orthogonal multi-tag operation, the emitted signals from the interrogator should impinge on the tags at slightly different angles. Given two backscatter tags (a primary and a secondary), we plot the minimum required angular separation between the two tags as a function of the incident angle on the primary user. We observe that the minimum required angular separation is fairly uniform across space, independent of the location or orientation of the primary user. This angular separation is a difference between the incident angles of free-space waves on the two users. Hence, radial movement of the secondary leaky-wave backscatter away from the primary tag or rotating it both result in increasing the angular separation in this context. This is shown in the top and bottom insets, respectively.

Full size image

Understanding the bandwidth of operation for leaky backscatters has important implications for joint localization and communication as well as for supporting many concurrent links using space division and frequency division multiple access techniques. Specifically, a leaky backscatter tag would modulate its data on a spectral sub-band within the sub-THz regime, depending on its location. Hence, a broadband transceiver can jointly localize the leaky backscatter tag and retrieve the transmitted bits within a single shot without imposing more power or overhead constraints on the leaky device.

The signal reflected from multiple leaky devices can be separated in spatial and spectral filtering: First, the directionality of the backscattered beams helps with separating multi-tag signals in the spatial domain; second, even under a similar line of sight angle, differing by a slight random orientation is sufficient for leaky backscatters to respond to different spectral bands, i.e., differentiating their signals in the spectral domain. Given that the bandwidth is not uniform across all angular locations (as evident from Fig. 4a), it may seem that the supported number of concurrent backscatter devices may be angle dependent too. To investigate this, we look at another metric: The minimum required angular separation between backscatter tags that can yield non-overlapping frequency bands; hence, achieving interference-free concurrent transmissions. We note that the angular separation is with regard to the incident angle of carrier waves impinging on the backscatter device, i.e., it may be due to a difference in the line-of-sight angle of the tags relative to the scanner or due to differences in tags orientation.

The minimum required angular separation between backscatter tags can be modeled based on Eqs. (1, 3), and ray optics principles. We denote the incident angles for the primary and secondary leaky backscatter by \({\phi }_{p}\) and \({\phi }_{s}\), respectively. We estimate the minimum angular separation between the two nodes (i.e., \({\phi }_{\min }\)) that guarantees orthogonal spectral bands for the reflected beams. It turns out that the value of \({\phi }_{\min }\) depends on the angular location of the primary user (\({\phi }_{p}\)) and the effective angular aperture \((\Delta \phi )\). When \(\tan ({\phi }_{p}) > \frac{\Delta \phi }{2}\), we can write (see Supplementary Material for derivation):

$${\phi }_{\min }=\frac{-\left(4\alpha \sin {\phi }_{p}+\triangle \phi \tan {\phi }_{p}-2\right)+\sqrt{{\left(4\alpha \sin {\phi }_{p}+\triangle \phi \tan {\phi }_{p}-2\right)}^{2}-8\alpha (2\alpha {\sin }^{2}{\phi }_{p}-2\sin {\phi }_{p}-\triangle \phi \cos {\phi }_{p})}}{4\alpha \cos {\phi }_{p}}$$
(4)

where \(\alpha=\frac{1}{\sin {\phi }_{p}}[1-\frac{\triangle \phi }{2\tan {\phi }_{p}}].\) This equation suggests that the minimum required angular separation between multiple nodes is a function of the primary users’ angular position (\({\phi }_{p}\)), the effective receive aperture of the backscatter (\(\Delta \phi\)), which itself depends on the distance to the backscatter reader. For example, when \({\phi }_{p}=\frac{\pi }{4}{rad}\) and \(\Delta \phi=\frac{\pi }{36}{rad}\), we get \({\phi }_{\min }=0.083{rad}={4.82}^{\circ }\). This result suggests the possibility of dense spatial reuse in wireless backscatter networks above 100 GHz, with many applications in dense IoT settings such as intelligent manufacturing and automation, smart cities, and smart homes. Figure 4b shows the measured minimum angular separation between two leaky backscatter devices. In these measurements, we place two leaky backscatter devices at a distance of 22 cm from the emitter. Hence, given the dimension of the leaky scatter and slot lengths, we calculate the effective angular aperture of the receiver \((\Delta \phi )\) and embed it in Eq. (4). In experiments, we vary the location of the primary tag starting from ~ 30 degrees to 65 degrees. At each configuration, we move the second backscatter tag apart from the primary node with a step size of 0.5 degrees and find the minimum separation that achieves the successful and concurrent decoding of the two backscatter tags. Using Eq. (4), the theoretical value \({\phi }_{\min }\) is centered at 5 degrees and should slightly decay with the primary user’s angle. From Fig. 4b, we observe good agreement between the theoretical and measured values of \({\phi }_{\min }\).

Interestingly, even though the bandwidth is changing non-linearly with respect to the angle (as shown in Fig. 4a), here, the minimum required angular separation is fairly uniform across space, independent of where the primary user is located. Intuitively, at higher angles, the bandwidth is lower, but at the same time, the frequency becomes a slowly varying function of angle; therefore, the secondary user should be sufficiently far from the primary user to see an orthogonal spectral band. On the other hand, at lower angles, the bandwidth is much wider, but the frequency is a fast-changing function of angle, resulting in a similar value for \({\phi }_{\min }.\) This observation yields an important conclusion that a densely deployed number of such leaky backscatter nodes can be supported independent of the relative positioning of the nodes.

Recall that \({\phi }_{\min }\) is the minimum required angular separation of the incident angles of two backscatter tags for interface-free transmission. Hence, moving the two backscatter nodes apart or rotating one relative to the other increases their angular separation. This is shown in the top and bottom insets, respectively. Hence, we estimate that a maximum of ~ (360/5)(360/5) = 5184 backscatter nodes can be packed and co-exist in the same environment and independently piggyback their data by modulating orthogonal non-overlapping spatial-spectral blocks at the same time. We note that at larger distances, the spectral footprint of each tag will be lower, and hence even more backscatter links may co-exist. Finally, the exact number of supported links also depends on the hardware complexity of the interrogator (i.e., EIRP and output power), which we explain in the Supplementary Material.

Discussion

In conclusion, we presented the first retrodirective ultra-wideband sub-THz backscatter architecture capable of establishing a directional link with an external transceiver operating beyond 100 GHz. Our approach does not rely on conventional active phased arrays that are narrow-band or power-demanding, but rather exploits fundamental properties of leaky-wave devices, including frequency-dependent directional filtering and reciprocity, and achieves frequency-agnostic retrodirectivity at zero power costs. This method enables joint communication and localization of the power-constrained sub-THz backscatters. Each backscatter node modulates a particular spectral band within the spectrum of the emitted sub-THz signal such that there is a monotonic relationship between that spectral band and the location of the backscatter node. Thus, by processing the signal from leaky backscatters, we can uniquely identify their locations as well as retrieve the modulated data embedded in the amplitude or phase of the reflected signal. Although our proof-of-concept demonstration relies on mechanical components for modulation and is, therefore, relatively slow, we also show that our leaky-wave backscatter devices can support wideband channels exceeding 1.6 GHz, regardless of their angular location or orientation. Our design is scalable to multiple leaky backscatters within the angular view of a single sub-THz access point since each node would employ a different portion of the sub-THz spectrum as well as establishing a directional beam, hence minimizing the footprint of interference in both spectral and spatial domains. Recognizing the ever-increasing demand for power-constrained devices, we anticipate that enabling low-power communications in the sub-THz regime will play a key role in future IoT networks.

Methods

Simulation

Our backscatter device was simulated in COMSOL, a Finite-Element-Method (FEM) simulation software package, as illustrated in Supplementary Fig. S2c. The leaky-wave backscatter device is designed with two lossless aluminum plates held in parallel at a separation of 0.95 mm. Two trapezoidal shape slots with longer and shorter widths of 1 mm and 15 mm are cut out of the top plate to serve as the transmit and receive apertures. The slots are identical and have a length, L, of 20 mm. The two modulation devices were employed in the simulation as perfect reflecting surfaces that can change their position and rotation within the waveguide angles (which correspond to phase and amplitude shifts in the radiation profile). The reflecting surface responsible for phase modulation was designed as an off-axis parabolic mirror instead of a flat mirror to better focus the collected radiation and consequently increase the efficiency of the backscatter device. EM signals were injected into one of the trapezoidal apertures (known as the receiving slit) at the optimal frequency and angle designated by Eq. (1). The far-field radiation pattern is then simulated with additional built-in features to measure the devices’ properties, such as coupling efficiency, radiated power, and directivity.

Experimental system

All experimental measurements were performed with a scale model backscatter-transceiver system, as shown in Supplementary Fig. S1 in Supplementary Material. The transceiver was emulated with a THz-TDS system with its transmitter and receiver modules (each equipped with fiber-coupled photoconductive antennas excited by fs-optical pulses) co-located with each other. The transmitter and receiver are mounted to a 2D motorized stage and a custom 3D-printed casing to accurately measure the radiation profile of the backscatter device. The TDS system provides raw time-domain measurements with a flat frequency response between 100 to 400 GHz. Given the lower power output of the transmitter, the maximum transmitted range was 1.2 m (2.4 m roundtrip). This is because the transmitter source has an ultra-low output power. Nevertheless, more realistic transceivers will be able to scale to farther link distances as they would be optimized for a (relatively) narrow spectra range and output power. We have provided a link budget analysis demonstrating this in Supplementary Note 3.

Fabrication

The fabricated backscatter device was constructed out of 6051 polished aluminum with identical dimensions as in our COMSOL simulation. To enable amplitude modulation, we use a mm-sized MEMS mirror, offering continuous rotation in both its x and y directions (with a maximum rotation angle of ± 5 degrees). The average power consumed by the MEMS mirror is less than 1 mW for continuous full-speed operation. For phase modulation, we attach a 90o off-axis parabolic mirror to a linear piezo actuator that provides 5 mm of linear movement with a resolution of 1.25 μm. The amplitude and phase modulation can hence be controlled independently and simultaneously.