Protein complex structure modeling by cross-modal alignment between cryo-EM maps and protein sequences

Abstract

Cryo-electron microscopy (cryo-EM) technique is widely used for protein structure determination. Current automatic cryo-EM protein complex modeling methods mostly rely on prior chain separation. However, chain separation without sequence guidance often suffers from errors caused by cross-chain interaction or noise densities, which would accumulate and mislead the subsequent steps. Here, we present EModelX, a fully automated cryo-EM protein complex structure modeling method, which achieves sequence-guiding modeling through cross-modal alignments between cryo-EM maps and protein sequences. EModelX first employs multi-task deep learning to predict Cα atoms, backbone atoms, and amino acid types from cryo-EM maps, which is subsequently used to sample Cα traces with amino acid profiles. The profiles are then aligned with protein sequences to obtain initial structural models, which yielded an average RMSD of 1.17 Å in our test set, approaching atomic-level precision in recovering PDB-deposited structures. After filling unmodeled gaps through sequence-guiding Cα threading, the final models achieved an average TM-score of 0.808, outperforming the state-of-the-art method. The further combination with AlphaFold can improve the average TM-score to 0.911. Analyzes conducted by comparing some EModelX-built models and PDB structures highlight its potential to improve PDB structures. EModelX is accessible at https://bio-web1.nscc-gz.cn/app/EModelX.

Introduction

Protein structure determination holds pivotal significance in unraveling the structural basis of life activities, and cryo-electron microscopy (cryo-EM) has emerged as a widely embraced methodology for protein structure determination, especially in the realms of vaccine design^1,2,3 and drug discovery^4,5,6. Different from traditional techniques like X-ray crystallography, cryo-EM methodology can be distinguished by its exemption from crystallization and its capability to handle larger proteins^7,8,9. However, to determine protein complex structures from cryo-EM maps, expert interventions are required for template searching, visual inspection on 3D visualization software^10,11, and atomic model refinement procedures^12,13,14. Given the current exponential expansion of cryo-EM structures¹⁵ alongside the continuous influx of newcomers to this field, it is imperative to develop automated modeling tools to remove bottlenecks and mitigate the reliance on human experts.

Automated modeling of cryo-EM protein complex structures can be achieved through homologous template assembly and refinement.^16,17,18 Recently, the success of protein structure prediction methods such as AlphaFold¹⁹ has enabled predicted structures to serve as effective substitutes for homologous templates. Our previous study²⁰ is one of the earliest studies to introduce AlphaFold into protein structure modeling for cryo-EM maps. After that, efforts have been made to assemble protein structures predicted by AlphaFold^21,22,23 or other methods²⁴ to fit into Cryo-EM maps. Nevertheless, the high computational cost of methods like AlphaFold has posed challenges for modeling long proteins, particularly for those exceeding 2000 amino acids. More importantly, the possible mis-predictions of AlphaFold also limited the applications of these methods.

Alternatively, protein complex models can be built by de novo modeling in high-resolution cryo-EM maps without templates. The continuous growth in the proportion (73% in 2023²⁵) of high-resolution (<4 Å) maps within EMDB has provided an increasingly expansive application space for de novo modeling. Most of the existing automated de novo modeling methods require prior chain separation for complex structures. For example, Pathwalking²⁶, MAINMAST²⁷, RosettaES²⁸, DeepMM²⁹, and SEGEM²⁰ can be applied on the manually-segmented maps to build single chain structures. Phenix³⁰ developed automated map sharpening, segmentation, and modeling tools to build a model for any possible segmentation result. DeepTracer³¹ utilized the protein backbone prediction to identify the separate chains before any atom prediction. Unfortunately, the cross-chain interaction and noise densities make it hard to achieve accurate separation, and errors in the prior chain separation would accumulate and mislead the subsequent steps.

Is prior chain separation really necessary for de novo complex structure modeling? A promising alternative is to directly map the protein complex sequence onto the cryo-EM map, which can be converted into a cross-modal alignment task^32,33 to align cryo-EM maps and protein sequences. To accomplish this, the first step is to predict the distribution of Cα atoms, backbone atoms, and amino acid type from the cryo-EM map. The second step is to map each predicted Cα to a position in a unique sequence. During this step, non-homologous chains will be automatically separated since they belong to different unique sequences. The third step is to build and separate homologous chains, which can be done by applying connectivity and symmetry. The major challenge lies in the second step: how to guide Cα-sequence mapping? Fortunately, our previous efforts have successfully pushed the accuracy of amino acid prediction for Cα sites toward over 48%²⁰, making sequence alignment feasible for guiding Cα-sequence mapping.

In this study, we presented EModelX, a fully automated cryo-EM protein complex modeling method, to directly map the protein complex sequence onto the cryo-EM map by cross-modal alignment. This cross-modal setup effectively integrates protein sequence information into the structure modeling process, eliminating the need for prior chain separation. Specifically, a multi-task 3D residual U-Net³⁴ was trained to predict the distributions of Cα atoms, backbone atoms, and amino acid type from the cryo-EM map. The predicted Cαs were then mapped onto protein complex sequence by sequence profile sampling and sequence alignment. Subsequently, the high-confidence Cα-sequence mappings were identified to form the initial model through sequence registration. Finally, the complex structure model was built by filling the unmodeled gaps through a sequence-guiding Cα threading algorithm. To evaluate our method, we curated a benchmark dataset of 99 up-to-date cryo-EM maps (resolution in 2–4 Å). Evaluated on the similarity with PDB structures, EModelX achieved an average TM-score of 0.808, which is higher than all compared methods, including the state-of-the-art method ModelAngelo³⁵. Evaluated on the map-model fitness against cryo-EM density maps, EModelX obtained an average correlation coefficient (CC_box) of 0.646, which is close to 0.687 average CC_box obtained by PDB structures. Besides de novo modeling by EModelX, template-based modeling has also been implemented by combining EModelX with AlphaFold2¹⁹, namely EModelX(+AF). EModelX(+AF) was demonstrated to be able to adaptively refine AlphaFold’s incorrectly folded structures, achieving a better average TM-score of 0.911 and a better average CC_box of 0.669. EModelX was developed in the 2021 Cryo-EM Assisted Protein Structure Modeling Tianchi AI Challenge³⁶ held by China Protein Science Center and Alibaba Cloud Tianchi Platform, where EModelX was validated as the best-performing method among 1917 participated teams by blind-test. EModelX is accessible at https://bio-web1.nscc-gz.cn/app/EModelX.

Results

Overview of EModelX

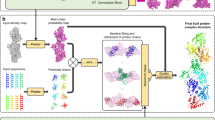
EModelX builds protein complex structure models from the inputs of cryo-EM maps and protein complex sequences. As illustrated in Fig. 1, EModelX starts from normalizing a cryo-EM map to feed it into multi-task 3D residual U-Nets, which predict the distributions of Cα atoms, backbone atoms, and amino acid types. The predicted Cα distribution is then used to propose Cα candidates by point-cloud clustering and non-maximum suppression (NMS). The predicted distributions of backbone and amino acid types are used to sample Cα traces and sequence profiles from the cryo-EM map. Subsequently, a Cα-sequence aligning score matrix is built by sequence alignment on the sampled profiles and protein sequence. The high-confidence aligned pairs are identified and used in the sequence registration to build the initial model, where connectivity and symmetry are applied in separating homologous chains. Residues with insufficient aligning confidence remain unmodeled in the initial model. These unmodeled gaps are filled by sequence-guiding Cα threading, and subsequently, the final model is built by PULCHRA³⁷, and atomic refinement is performed by phenix.real_space_refine³⁸. When combined with AlphaFold, single-chain structures are predicted by AlphaFold2¹⁹ for each sequence (Fig. 1c). Cα traces are both sampled in the predicted Cα atoms and AlphaFold structure. Computing the structural similarity between the sampled Cα traces and AlphaFold traces not only adds a structure alignment item to the Cα-sequence alignment score but also enhances sequence-guiding Cα threading.

Fig. 1: The overview of EModelX’s modeling pipeline.

a Multi-task cryo-EM map interpretation, which aims to interpret cryo-EM maps into distributions of Cα atoms, backbone atoms, and amino acid (AA) types. ${{{{\mathcal{C}}}}}_{in}$ and ${{{{\mathcal{C}}}}}_{out}$ represent the input and output channel of each U-Net module. NMS is the non-maximum suppression algorithm. b Cα-sequence alignment which aims to build an initial model with high confidence by Cα trace sampling and Cα-sequence alignment score, and sequence-guiding Cα threading which tries to fill the unmodeled gaps in the initial model. c Additional inputs for EModelX(+AF), where AlphaFold2 is used to predict single chain structure for each sequence. Computing the structural similarity between the sampled Cα traces and AlphaFold traces not only adds a structure alignment item to the Cα-sequence alignment score but also enhances sequence-guiding Cα threading. d Zooming to the schematic diagram of the 3D-Unet neural network in a.

Models built by EModelX exhibited superior similarities to the PDB structures

EModelX was evaluated on a set of 99 experimentally solved single-particle cryo-EM maps of protein complexes, and compared with Phenix³⁰, MAINMAST²⁷, DeepTracer³¹, and ModelAngelo³⁵. All methods built protein complex structures with inputs of cryo-EM maps and protein sequences. The PDB-deposited structure can be regarded as a quasi-gold standard. Therefore, we first evaluated EModelX and other methods by measuring the similarities of built models to the PDB structures. Details of the benchmark setting and metrics calculation are provided in the Methods section.

We first computed the TM-score by MMalign³⁹ to assess the backbone structure topological similarity between built models and the PDB structures. As illustrated in Fig. 2a, EModelX achieved an average TM-score of 0.808 to PDB structures, outperforming Phenix (0.307), MAINMAST (0.562), DeepTracer (0.538) and ModelAngelo (0.696). Combining with AlphaFold further improves the TM-score of EModelX(+AF) to 0.911. As shown in Fig. 2b, EModelX(+AF) obtained higher TM-scores than other methods in 89 out of 99 test cases. Since the TM-score does not consider protein side chains, following Jamali et al.⁴⁰, we additionally computed sequence recall. Sequence recall is defined as the proportion of the PDB residues that is neighboring (Cα distance ≤3Å) to a modeled residue with the same amino acid type. As depicted in Fig. 2c, EModelX(+AF) consistently outperformed EModelX and other methods, especially for B-factor  >100 Ų. This is reasonable, in regions with lower local resolution, it is challenging to identify side chains. Introducing AlphaFold structures is akin to template-based modeling, which is commonly employed by biologists to solve low-resolution structures. Figure 2d visualizes the model built by EModelX for EMD-24101⁴¹, a cryo-EM map of SARS-CoV-2 Nsp15 endoribonuclease post-cleavage state at 2.2 Å resolution. EModelX’s model exhibits strong similarity to the corresponding PDB structure, achieving a high TM-score of 0.998. Models built by other methods can be found in Supplementary Fig. S2, where ModelAngelo achieved a TM-score of 0.983, slightly lower than that of EModelX.

Fig. 2: The overall performance of EModelX on recovering the PDB structures.

a The average TM-score on the test cases of 99 Cryo-EM maps. Error bars indicate  ± 1.0 standard deviation. b Comparison of the TM-scores between EModelX and compared methods on each test case. c The Sequence Recall for all residues in the test dataset as a function of the B-factor. Each data point represents the average sequence recall on a B-factor interval that contains 1000 residues. d The PDB-deposited structure 7n06 and model built by EModelX for map EMD-24101 of SARS-CoV-2 Nsp15 endoribonuclease post-cleavage state at the resolution of 2.2 Å.

Since MMalign calculates RMSD only on aligned residues, it is necessary to assess EModelX in both the modeling coverage and RMSD simultaneously. Coverage is defined as the portion of MM-aligned PDB residues. Here we additionally reported the performance of EModelX(init), the initial model built without sequence-guiding Cα threading. As illustrated in Fig. 3a, the ablation of sequence-guiding Cα threading resulted in a 19.8% decrease in coverage. By incorporating the AlphaFold structure, EModelX(+AF) improved the average coverage from 83.0 to 92.7%. In contrast, the state-of-the-art (SOTA) method ModelAngelo achieved a lower coverage of 70.0%. EModelX(init) achieved a nearly atomic-level average RMSD of 1.17 Å (Fig. 3b), which was superior to Phenix, MAINMAST, and DeepTracer, and was on par with ModelAngelo. Figure 3c illustrated the joint distribution of RMSD and coverage for each method. We found the distributions of EModelX(init) similar to those of ModelAngelo in both coverage and RMSD, and they were both distributed in the lower part of the plot. In contrast, both EModelX and EModelX(+AF) were distributed in the lower-right part of the plot. Especially for EModelX(+AF), 62 out of 99 maps yielded coverage  >0.9 and RMSD  < 2 Å.

Fig. 3: Comparing EModelX with existing methods.

The average RMSD (a) and coverage (b) on the test cases of 99 cryo-EM maps. Error bars indicate  ±1.0 standard deviation. The coverage is defined as the proportion of residues in the PDB that are successfully aligned to the built model by MM-align. c The scatter plot of coverage and RMSD obtained by compared methods, with their distributions estimated by kernel density estimation (KDE) and illustrated on the corresponding axes. The mean length (d) of segments of continuous forward residues and the forward rate (e) of residue direction on the test cases of 99 Cryo-EM maps. Error bars indicate  ± 1.0 standard deviation. f The PDBdeposited structure and models built by EModelX and compared methods for map EMD-23249 of PCV2 Replicase bound to ssDNA at 3.8 Å resolution. The Cryo-EM density maps are colored in transparent gray. Each chain in a model was rendered by a unique color.

We then evaluated the quality of the local structures built by each method. The mean length of continuous forward segments (proceed in the same direction as PDB structure) can be calculated by phenix.chain_comparison. As shown in Fig. 3d–e, EModelX(init) concurrently achieved the highest mean length (74.1 AA) and forward rate (96.3%), surpassing the SOTA method ModelAngelo (52.5 AA and 95.9% forward rate). Compared to EModelX(init), EModelX shows a decrease in both the mean length and forward rate of continuous residues. This is reasonable, as EModelX tries to fill structure gaps that were unmodeled in EModelX(init), which commonly correspond to low-resolution regions that are challenging to model.

The study on test case EMD-23249⁴² provided an intuitive understanding of the difference between EModelX and compared methods. EMD-23249 is a 3.8 Å cryo-EM map of PCV2 Replicase bound to ssDNA. EModelX built an initial model (EModelX(init)) with atomic level RMSD of 0.78 Å to the PDB structure. The unmodeled region of the initial model was successfully filled in the final model, thus the TM-score was improved to 0.969. By combining AlphaFold, EModelX(+AF) further improved the TM-score to 0.984. In contrast, Phenix and ModelAngelo left some outer regions of the density map unmodeled; obvious topological mismatches can be found between MAINMAST and PDB structure; and both DeepTracer and ModelAngelo suffered errors in chain separation.

Models built by EModelX demonstrated strong map-model fitness to the cryo-EM maps

We have evaluated the performance of EModelX using the PDB structure as the gold standard. However, in real applications, the ground-truth structure for a given map is commonly unknown and there may be errors in the PDB structure. As an alternative, it is of vital importance to evaluate the fitness of the built model to the given map. Therefore, we reported the map-model correlation coefficients (CC) calculated by phenix.map_model_cc⁴³ for each method. However, for 6 out of 99 maps, ModelAngelo failed to build structures that conformed to the cryo-EM maps. Therefore, we excluded these maps, and map-model CC was evaluated in a subset of 93 maps.

CC_box⁴³ can assess the model’s correlation with the whole cryo-EM map. As illustrated in Fig. 4a, EModelX achieved an average CC_box of 0.646, which was superior to 0.420 for Phenix, 0.395 for MAINMAST, 0.567 for DeepTracer, and 0.560 for ModelAngelo. For 37 out of 93 maps, the CC_box value obtained by EModelX reached the average value (0.687) of PDB structures. Similar outperformance can be found in CC_mask, which is defined as the model’s correlation to the map values inside a mask calculated around the macromolecule⁴⁴. EModelX obtained an average CC_mask of 0.738 (Fig. 4b), outperforming other methods (Phenix: 0.702, MAINMAST: 0.355, DeepTracer: 0.616, ModelAngelo: 0.699). For 31 out of 93 maps, the CC_mask value obtained by EModelX reached the average value (0.780) of PDB structures. By combining AlphaFold, EModelX(+AF) further improved the average CC_box to 0.669 and CC_mask to 0.752. EModelX(+AF) yielded higher CC_box values than all compared methods (Phenix, MAINMAST, DeepTracer, and ModelAngelo) in 83 out of 93 test maps (Fig. 4c) and higher CC_mask values than all compared methods in 67 out of 93 test maps (Fig. 4d).

Fig. 4: The EModelX-built models showed strong map-model fitness.

The average CC_box (a) and CC_mask (b) on the subset of 93 maps. Black horizontal lines represent the average value obtained by PDB. Error bars indicate  ± 1.0 standard deviation. Comparison of the CC_box (c) and CC_mask (d) values on each test case between EModelX and other built models. Blue lines represent the linear function y=x. e–g: Test case EMD-32336 at 3.1 Å resolution. e Its PDB-deposited structure (PDB ID: 7w72) and model built by EModelX. f Main chain trace comparison when zooming into two local regions. The sky-blue trace represents EModelX's model and the tan trace shows PDB structure. g Comparison of map-to-model correlation coefficient (CC) per residue on the corresponding zoomed-in regions. h–k: Test case EMD-31339 at 3.2 Å resolution (PDB ID: 7evp). h. Model built by EModelX and the amino acid prediction results of chain C (red) and chain D (green) aligning to the protein sequence (tan). i. Chain C of PDB-deposited structure (tan), EModelX-built model (red), AlphaFold structure (sky-blue). Comparison of map–to–model CC per residue between PDB-deposited structure and EModelX-built model in chain C (j) and chain D (k). l–m: Test case EMD-30946 at 2.9 Å resolution (PDB ID: 7e1y). l Model built by EModelX, and the AlphaFold sub-structure on the PDB-unmodeled region. m Main chain traces of the PDB-deposited structure (tan) and the model built by EModelX (cyan) zooming into the PDB-unmodeled residues in chain D.

The outperformance in CC_box and CC_mask encouraged further exploration of EModelX’s potential to improve some PDB-deposited structures. Figure 4e–m illustrates three test cases as representative examples. The first case is a cryo-EM map of a human glycosylphosphatidylinositol (GPI) transamidase at 3.1Å resolution (EMD-32336)⁴⁵. As depicted in Fig. 4e, the model built by EModelX showed strong global similarity with the PDB structure (TM-score: 0.989). However, when zooming into two local density regions (Fig. 4f), we found two loops of the PDB-deposited structure (tan trace) didn’t fit well in the cryo-EM density. Differently, the EModelX built two short α-helices to fit in the local density respectively. To validate the above local structures built by EModelX, we calculated the map-model CC per residue for the 364th–374th segment and 74th–82nd segment in chain S. As shown in Fig. 4g, EModelX stood relatively stable while the PDB structure suffered drops in the CC value. This case indicated EModelX’s potential to locally improve PDB structure on the map–model fitness.

The second case is a cryo-EM map of a Gp168-beta-clamp complex at 3.2 Å resolution (EMD-31339)⁴⁶. The EModelX-built model was composed of 4 single chains that fit well into the cryo-EM map, as shown in Fig. 4h. However, we noticed that both the C and D chains of the EModelX-built model showed different sequence alignments from the PDB structure. The amino acid type prediction results of EModelX for the C chain and D chain structures could be consistently aligned to the 1st–43rd sequence position. Differently, the PDB structure registered both chain C and chain D to the 12th–54th sequence position. Superimposed in Fig. 4i, the AlphaFold structure and EModelX’s model could both be aligned to the PDB structure. But coincidentally, they shared an 11 AA offset in sequence registration to the PDB structure. Different sequence registrations resulted in different side chain structures, which could influence the map-model CC. As shown in Fig. 4j for chain C and Fig. 4k for chain D, EModelX obtained higher map-model CC than PDB structure in the majority of residues. EModelX yielded higher CC_mask values (0.6524, 0.6574) than the PDB structure (0.6249, 0.6246) in both chain C and chain D. This case suggested that EModelX might improve sequence registration for some PDB structures.

The third case is a cryo-EM map of a Staphylothermus marinus amylopullulanase -SmApu at 2.9 Å resolution (EMD-30946). The PDB-deposited structure did not accomplish the full-length modeling, leaving the 1st–102nd residues of each chain unmodeled. EModelX built a similar (TM-score: 0.954) but more complete model. As depicted in the black square of Fig. 4l, EModelX built multiple β-sheets and loops for the 1st–102nd residues of chain D, which showed strong similarity with AlphaFold structure. Zooming into the black square region, Fig. 4m displayed the EModelX structure of chain D (cyan trace) and chain G (green trace) with the reference of PDB structure (tan trace). The 1st–102nd residues built by EModelX exhibited acceptable fitness (0.524 CC_mask) to the cryo-EM maps. This case demonstrated that EModelX could build reasonable structures for some unmodeled regions of the PDB structure.

Combining AlphaFold improved EModelX’s modeling performance

AlphaFold has been widely used to predict protein single-chain structures, but accurately predicting protein complex structures from sequences alone remains a challenge. By combining EModelX with AlphaFold, EModelX(+AF) is expected to build more accurate protein complex structures.

EModelX(+AF) improved the average TM-score of EModelX to 0.911. To investigate what contributes to EModelX(+AF)’s improvement, we first illustrated the TM-score boxplot at different resolution ranges. As depicted in Fig. 5a, each method suffered TM-score drops as the resolution got worse. Comparing maps with resolution between 3.5–4 Å and 2–2.5 Å, the median TM-score of ModelAngelo suffered a dip of around 44% (0.979 → 0.550), the EModelX’s dropped by about 19% (0.995 → 0.803), while the EModelX(+AF)’s only dropped about 8% (0.993 → 0.917). Accuracy fluctuation in amino acid prediction (0.679 → 0.363 in Supplementary Fig. S3b) should be one of the reasons for performance drops since the Cα-sequence alignment depends on the sequence profiles derived from amino acid prediction. EModelX(+AF) additionally conducted structure alignment between the sampled Cα traces with the AlphaFold traces. Therefore the stable accuracy in Cα atom prediction (0.998 → 0.991 in Supplementary Fig. S3a) should contribute to EModelX(+AF)’s robust performance. However, the single-chain structure predicted by AlphaFold could be also inaccurate. Since AlphaFold2 predicted single chains, our 99 protein complexes were split into 660 single chains for comparison. As shown in Fig. 5b, AlphaFold attained RMSD  < 2 Å in only 386 out of 660 single-chain structures, whereas EModelX(+AF) achieved RMSD  < 2 Å in 548 single-chain structures. The average RMSD for EModelX(+AF) was 1.34 Å, while AlphaFold had an average RMSD of 1.90 Å. This indicated the capability of EModelX(+AF) to rectify the misfolded AlphaFold structures with the assistance of cryo-EM densities.

Fig. 5: EModelX(+AF) demonstrated abilities to rectify the misfolded AlphaFold structures.

a The boxplot of TM-score in different resolution ranges (12, 14, 35, and 38 maps for 2–2.5, 2.5–3, 3–3.5, 3.5–4 Å, respectively). The box extends from the first quartile (Q1) to the third quartile (Q3), with a line at the median. The whiskers extend from the box to the farthest data point lying within 1.5x (Q3-Q1) from the box. Flier points are those past the end of the whiskers. b Comparison of RMSD achieved by EModelX(+AF) and AlphaFold on 660 single chains split from 99 complex structures in our test set. c Comparison of TM-score achieved by EModelX(+AF) and AlphaFold on the 82 hard targets (AlphaFold TM-score  < 0.7). Blue lines represent linear function y=x. d–f: Test case EMD-23970 at 3.8 Å resolution (PDB ID: 7msw). d superimposing PDB structure (blue) with models built by EModelX(+AF), EModelX, and AlphaFold. The models are rendered by Cα distance to the PDB structure. e The Cα distance and B-factor for each residue. Each data point represents an average value of nearby five residues. f CC_mask and B-factor for each residue. g Test case EMD-30612 at 3.7 Å resolution (PDB ID: 7d84). Zooming into chain e, the PDB structure is represented as tan ribbons, the model built by EModelX(+AF) is colored red, and the superimposed AlphaFold structure is sky-blue.

In order to investigate the performance of EModelX(+AF) on the hard targets for AlphaFold, we collected a subset of 82 single-chain structures (AlphaFold TM-score  < 0.7) from the whole test set. Among these hard targets, AlphaFold obtained an average TM-score of 0.636, while EModelX(+AF) achieved an average TM-score of 0.793. As illustrated in Fig. 5c, for 68 out of the 82 targets, EModelX(+AF) obtained higher TM-scores than AlphaFold. We then further studied two representative cases. The first case was on a 3.76 Å cryo-EM map of SARS-CoV-2 Nsp2 (EMD-23970), which was fitted by a single chain structure (PDB ID: 7msw)⁴⁷. The model built by EModelX(+AF) exhibited strong similarity (TM-score: 0.976) with the PDB structure. The removal of AlphaFold led to a TM-score drop of 0.225 (0.976 → 0.751) and the misfolding in the C-terminal domain (lower part of the structure) (Fig. 5d). Further study revealed that the C-terminal domain of the structure corresponds to the high B-factor region in the PDB structure (Fig. 5e). However, in this domain, EModelX(+AF) not only built a model consistent with the PDB structure (Fig. 5e) but also achieved comparable or even better map-model CC (Fig. 5f). It is noteworthy that the AlphaFold structure only exhibited low global similarity to the PDB structure (Fig. 5d, TM-score of 0.593), and EModelX(+AF) achieved improvements utilizing such structure. This is comprehensible, as the structure aligning module of EModelX(+AF) can effectively identify and leverage well-folded local structures from the template. Another case is representative of large protein complexes. It was a 3.70Å cryo-EM map (EMD-30612) of a 34-fold symmetry Salmonella S ring formed by full-length FliF⁴⁸. EModelX(+AF) built a high-quality atomic model for this membrane and achieved a TM-score of 0.987. Zooming into chain P, as depicted in Fig. 5g, the AlphaFold structure exhibited insufficient folding accuracy (TM-score: 0.693). However, EModelX(+AF) successfully rectified the misfolded structure by leveraging information from the cryo-EM map and protein sequence. In summary, EModelX(+AF) showed good robustness to both the poor Cryo-EM density and the poor AlphaFold prediction, which is critical for cryo-EM protein complex modeling.

Discussion

This paper has introduced a fully automated approach to cryo-EM protein complex modeling. The proposed method, EModelX, requires only raw cryo-EM maps and amino acid sequences as inputs, eliminating the need for manual preprocessing. EModelX innovatively employs multi-task 3D residual U-Nets to predict Cα atoms, backbone atoms, and amino acid profiles directly from cryo-EM maps. Subsequently, it utilizes local structure sampling for Cα-sequence alignment. EModelX allows for global alignment of complex multiple sequences, contributing to the efficient and automated modeling of protein complex structures.

The evaluation results for EModelX demonstrate its impressive performance in comparison to existing methods. The initial models generated by EModelX exhibited a remarkable atomic-level average RMSD of 1.17 Å and the final models achieved an average TM-score of 0.808, outperforming the state-of-the-art methods. The correlation coefficient (CC_box) reached 0.646 on average, close to the average CC_box of 0.687 observed for PDB structures. Notably, some EModelX-built models exhibited superior fitness to cryo-EM maps compared to corresponding PDB structures, highlighting its effectiveness in accurately capturing molecular details. Additionally, EModelX is applied to maps that have no deposited PDB structure (Supplementary Note 1). A case study indicated that comparing the structural differences between the EModelX model and the relevant PDB structures may reveal the dynamic changes in molecular conformations across different maps.

There are several promising avenues for future research. First, the concept of end-to-end structure modeling, integrating both experimental cryo-EM data and deep learning, presents an exciting prospect. Exploring methods to seamlessly combine EModelX with E(3)-equivalent neural networks⁴⁹ could enhance the accuracy and efficiency of the modeling process. Second, the development of methods for de novo modeling of protein structures lacking sequence information, and the extension of modeling capabilities to include other molecular complexes such as DNA/RNA-protein assemblies or small molecules, represent important directions for advancing the field of cryo-EM protein complex modeling. Overall, the integration of innovative techniques, as demonstrated by EModelX, sets the stage for continued advancements in the field.

Methods

Benchmark setting

We have curated a non-redundant dataset of cryo-EM maps from EMDB⁵⁰. The collected maps are all single particle cryo-EM maps within 2–4 Å resolution, with unique PDB fitted structure, and released after 2018/1. Subsequently, their fitted PDB structures are downloaded from PDB⁵¹. To build an independent test set, a subset of maps released after 2021/5 were first gathered. Maps in this subset were clustered by cd-hit⁵² at 25% sequence similarity (two maps with any pair of chains  > 25% sequence similarity would be clustered). For each cluster, redundant maps were removed until only one map remained. It resulted in a non-redundant test set of 99 cryo-EM maps (Supplementary Data 1). Maps released before May 2021 were collected for raw training data. Among them, maps that have  > 25% sequence similarity with any test map were also removed, which resulted in a training set of 1529 cryo-EM maps (Supplementary Data 2). It should be noted that all these maps underwent no preprocessing, different from MAINMAST²⁷ and EMBuild²¹ which sharpened the cryo-EM maps by PDB structures. This difference allowed EModelX to be applied on maps that have no deposited PDB structures. Therefore we also gathered a dataset comprising 126 cryo-EM maps that have no deposited PDB structures (Supplementary Data 3).

On the curated benchmark test set. We compared EModelX with four cryo-EM protein structure modeling methods:

• Phenix³⁰ (phenix-1.20.1-4487, release date: Jan 20, 2022) is a software suite for cryo-EM protein structure modeling. It ensembles image sharpening, image segmentation, atomic structure construction, and real space refinement tools to build models.

• MAINMAST²⁷ (version 1.0, release date: Mar 1, 2017) identified the protein backbone structure by mean shift and employed tabu search algorithm in backbone tracing to build single-chain structures from maps sharpened by PDB structures.

• DeepTracer³¹ is a pioneering cryo-EM protein complex structure modeling method. It predicts the locations of amino acids, the location of the backbone, secondary structure positions, and amino acid types to determine protein complex structure.

• ModelAngelo³⁵ (version 1.0.12, release date: Nov 29, 2023) is the state-of-the-art machine-learning approach for automated atomic model building in cryo-EM maps. It combines cryo-EM data with protein sequence and structure information within a graph neural network to construct models of protein complexes with high accuracy, effectively eliminating the need for manual intervention and expertize.

We applied EModelX and these methods to our benchmark test set. It should be noted that EModelX, DeepTracer, and ModelAngelo employed original cryo-EM maps as input, while MAINMAST and Phenix utilized maps sharpened by PDB structure. The implementation details are described in Supplementary Note 2.

We have calculated various metrics to measure modeling performance from different perspectives:

• TM-score is to assess the topological similarity between the backbone structure of built models and the PDB structures. Here MM-align³⁹ and TM-align⁵³ were employed to calculate TM-scores for protein complex models and single-chain models, respectively.

• Sequence Recall is defined as the proportion of the PDB residues that is neighboring (Cα distance ≤3Å) to a modeled residue with the same amino acid type, following Jamali et al.⁴⁰.

• Coverage is the proportion of aligned PDB residues, and the number of aligned PDB residues (Aligned_length) was calculated by MM-align.

• RMSD is the root of the mean squared distance between the Cα atoms of the aligned residue pairs of built models and the PDB structures, and MM-align was used in RMSD computation.

• Mean Length is the mean length of continuous forward segments (proceed in the same direction as PDB structure) and can be calculated by phenix.chain_comparison³⁰.

• Forward Rate is the proportion of modeled residues that proceed in the same direction as PDB structures, and the number of forward residues was calculated by phenix.chain_comparison.

• CC_box: the correlation coefficient between the atomic model and the whole cryo-EM map, calculated by phenix.map_model_cc⁴³.

• CC_mask: the correlation coefficient between the atomic model and the map masked by atomic centers with a fixed radius. It is also calculated by phenix.map_model_cc.

Multi-task cryo-EM map interpretation

The first step of EModelX is the multi-task cryo-EM map interpretation. However, raw cryo-EM maps in EMDB are various in microscope models, electron doses, electron detectors, and experimental procedures, which results in a large variance in density distribution, local resolution, and noise intensity. Therefore, it’s crucial to adopt an image preprocessing step to normalize the maps, making it more suitable for neural network training. Given a raw cryo-EM map ${{{\mathcal{M}}}}\in {{\mathbb{R}}}^{w\times h\times d}$ where w, h, d represents the width, height, and depth of this raw map, we first obtain ${{{{\mathcal{M}}}}}^{{\prime} }\in {{\mathbb{R}}}^{{w}^{{\prime} }\times {h}^{{\prime} }\times {d}^{{\prime} }}$ through transposing the coordinate system of the raw cryo-EM map according to its header file so that it shares the same coordinate system with the PDB-deposited structure, and resizing the transposed map to normalize the voxel size to 1 × 1 × 1 Å by trilinear interpolation. After that we produce the normalized map ${{{\mathcal{N}}}}\in {{\mathbb{R}}}^{{w}^{{\prime} }\times {h}^{{\prime} }\times {d}^{{\prime} }}$ through normalizing the voxel value by:

$${{{{\mathcal{N}}}}}_{xyz}=\left\{\begin{array}{c}0,{{{{\mathcal{M}}}}}_{xyz}^{{\prime} } \, < \, {{{{\mathcal{M}}}}}_{med}^{{\prime} }\\ \frac{{{{{\mathcal{M}}}}}_{xyz}^{{\prime} }-{{{{\mathcal{M}}}}}_{med}^{{\prime} }}{{{{{\mathcal{M}}}}}_{top1}^{{\prime} }},{{{{\mathcal{M}}}}}_{med}^{{\prime} }\, \le \, {{{{\mathcal{M}}}}}_{xyz}^{{\prime} } \, < \, {{{{\mathcal{M}}}}}_{top1}^{{\prime} }\\ 1,{{{{\mathcal{M}}}}}_{xyz}^{{\prime} } \, \ge \, {{{{\mathcal{M}}}}}_{top1}^{{\prime} }\end{array}\right.$$

(1)

where (x, y, z) is the voxel coordinate, ${{{{\mathcal{M}}}}}_{med}^{{\prime} }$ represents the median density value of ${{{{\mathcal{M}}}}}^{{\prime} }$, and ${{{{\mathcal{M}}}}}_{top1}^{{\prime} }$ is defined as the top 1% density value of ${{{{\mathcal{M}}}}}^{{\prime} }$. All voxels in ${{{\mathcal{N}}}}$ range from 0 to 1. The median density value is chosen as the lower boundary considering the sparsity of cryo-EM maps and the top 1% density value is set as the upper boundary to reduce the impact of extreme noise densities on neural network training and inference.

As illustrated in Fig. 1a, the normalized maps were then interpreted as Cα atoms, backbone atoms, and amino acid (AA) type distribution by multi-task machine learning. Specifically, the employed multi-task 3D Residual U-Nets can be formulated as:

$${{{{\mathcal{N}}}}}^{B}={F}_{a}(une{t}_{S}({F}_{s}({{{\mathcal{N}}}}),\, {\theta }_{S}))$$

(2)

$${{{{\mathcal{N}}}}}^{C}={F}_{a}(une{t}_{C}({F}_{s}([{{{\mathcal{N}}}};{{{{\mathcal{N}}}}}^{B}]),\, {\theta }_{C}))$$

(3)

$${{{{\mathcal{N}}}}}^{A}={F}_{a}(une{t}_{A}({F}_{s}([{{{\mathcal{N}}}};{{{{\mathcal{N}}}}}^{B}]),\, {\theta }_{A}))$$

(4)

where ${{{\mathcal{N}}}}\in {{\mathbb{R}}}^{1\times W\times H\times D}$ is the input normalized map, ${{{{\mathcal{N}}}}}^{B}\in {{\mathbb{R}}}^{4\times W\times H\times D}$ represents the predicted backbone distribution map, ${{{{\mathcal{N}}}}}^{C}\in {{\mathbb{R}}}^{4\times W\times H\times D}$ denotes the predicted Cα atom distribution map, ${{{{\mathcal{N}}}}}^{A}\in {{\mathbb{R}}}^{21\times W\times H\times D}$ is the predicted amino acid type classification map, $[{{{\mathcal{N}}}};{{{{\mathcal{N}}}}}^{B}]\in {{\mathbb{R}}}^{5\times W\times H\times D}$ is the channel-wise concatenation of ${{{\mathcal{N}}}}$ and ${{{{\mathcal{N}}}}}^{B},{F}_{s}:{{\mathbb{R}}}^{c\times W\times H\times D}\to \{{{\mathbb{R}}}^{c\times 64\times 64\times 64}\}$ splits a given map into a set of ${{\mathbb{R}}}^{c\times 64\times 64\times 64}$ sub-maps with slide strides of 8 voxels, $unet:{{\mathbb{R}}}^{{C}_{in}\times 64\times 64\times 64}\to {{\mathbb{R}}}^{{C}_{out}\times 64\times 64\times 64}$ is a U-Net³⁴ module with trainable parameters θ, and ${F}_{a}:\{{{\mathbb{R}}}^{{C}_{out}\times 64\times 64\times 64}\}\to {{\mathbb{R}}}^{{C}_{out}\times W\times H\times D}$ produces the assembled prediction results from all sub-maps.

The employed U-Net has been widely used in image segmentation tasks. Regarding our prediction tasks as three 3D image semantic segmentation tasks, U-Net’s max-pooling and up-sampling operation are beneficial for extracting coarser and finer-grained features that are both important for semantic segmentation. Here we implemented our U-Net as 3D Residual U-Net⁵⁴, where the skip-connection⁵⁵ was exploited to alleviate the resolution reduction issues caused by max-pooling and the gradient vanishing problem of deep network. Specifically, the 3D Residual U-Net module $unet:{{\mathbb{R}}}^{{C}_{in}\times 64\times 64\times 64}\to {{\mathbb{R}}}^{{C}_{out}\times 64\times 64\times 64}$ in our method can be formatted as an encoder-decoder model:

$${x}^{(0)}=en{c}^{(0)}(x)$$

(5)

$${x}^{(n)}=en{c}^{(n)}({F}_{p}({x}^{(n-1)}))$$

(6)

$${y}^{(n)}=de{c}^{(n-1)}({F}_{u}({y}^{(n-1)})+{x}^{(N-n)})$$

(7)

$$y=sof\!tmax(de{c}^{(N)}({y}^{(N)}))$$

(8)

where $x\in {{\mathbb{R}}}^{{C}_{in}\times 64\times 64\times 64}$ represents the input map, $y\in {{\mathbb{R}}}^{{C}_{out}\times 64\times 64\times 64}$ is the output map of segmentation result, ${F}_{p}:{{\mathbb{R}}}^{c\times 2W\times 2H\times 2D}\to {{\mathbb{R}}}^{c\times w\times h\times d}$ is the max-pooling operation (w, h, d), ${F}_{u}:{{\mathbb{R}}}^{c\times w\times h\times d}\to {{\mathbb{R}}}^{c\times 2w\times 2h\times 2d}$ is the upsampling operation implemented by strided transposed convolution⁵⁶, the operation ’+’ in Eq. (7) is the skip connection performed by element-wise summation joining, normalized exponential function softmax is performed on the channel-wise, N denotes the total number of encoder/decoder layers, n marks the current layer, and an encoder/decoder module can be unified as:

$${f}_{\!\!out}=ELU(con{v}^{(0)}( \, \, {f}_{\!\!in})+con{v}^{(0,1,2)}( \, \, {f}_{\!\!in}))$$

(9)

where ${f}_{in}\in {{\mathbb{R}}}^{{C}_{in}\times w\times h\times d}$ represents the input feature map, ${f}_{out}\in {{\mathbb{R}}}^{{C}_{out}\times w\times h\times d}$ is the output feature map, $ELU:{{\mathbb{R}}}^{c\times w\times h\times d}\to {{\mathbb{R}}}^{c\times w\times h\times d}$ is the exponential linear unit (ELU)⁵⁷ as an activation function, $con{v}^{(0)}:{{\mathbb{R}}}^{{C}_{in}\times w\times h\times d}\to {{\mathbb{R}}}^{{C}_{out}\times w\times h\times d}$ and $con{v}^{(1,2)}:{{\mathbb{R}}}^{{C}_{out}\times w\times h\times d}\to {{\mathbb{R}}}^{{C}_{out}\times w\times h\times d}$ are cascaded layers and in each layer feature maps are processed by 3 × 3 × 3 convolution  → group normalization⁵⁸ → ELU activation, and similar to Eq. (7) the operation ’+’ is also the skip connection performed by element-wise addition.

After 3D Residual U-Nets prediction, the subsequent step of cryo-EM map interpretation is to propose Cα atom candidates (Fig. 1a). First, we pick a set of voxels satisfying ${{{{\mathcal{N}}}}}_{0ijk}^{C} \, > \, 0.35$ where ${{{{\mathcal{N}}}}}_{0}^{C}$ is the softmax score of Cα class in ${{{{\mathcal{N}}}}}^{C}$ and (i, j, k) represents the voxel coordinate. We then run density-based spatial clustering of applications with noise (DBSCAN) algorithm⁵⁹ with density parameter eps = 10 to efficiently filter out the outlier clusters of Cα voxels that are usually the incorrectly predicted noises. Considering that the ideal distance between Cα atoms is 3.8 Å⁶⁰, the predicted Cα neighbors should also roughly keep this distance. Here we first filter out the non-local maximum Cα voxels in 3 × 3 × 3 Å through the Non-Maximum Suppression (NMS) algorithm, and then adjust the remaining Cα coordinates by:

$${{{{\mathcal{C}}}}}_{n}=\frac{1}{{\sum }_{\delta }{{{{\mathcal{N}}}}}_{0({{{{\mathcal{C}}}}}_{n}^{{\prime} }+\delta )}^{C}} {\sum}_{\delta=(-1,-1,-1)}^{(1,1,1)}{{{{\mathcal{N}}}}}_{0({{{{\mathcal{C}}}}}_{n}^{{\prime} }+\delta )}^{C}\times ({{{{\mathcal{C}}}}}_{n}^{{\prime} }+\delta )$$

(10)

where ${{{{\mathcal{C}}}}}^{{\prime} }\in {{\mathbb{Z}}}^{N\times 3}$ denotes the original coordinates of predicted Cα voxels, N represents the total number of predicted Cα voxels and n is the index of a given Cα, δ ∈ {−1, 0, 1}³ is used to traverse neighbor coordinates, and ${{{\mathcal{C}}}}\in {{\mathbb{R}}}^{N\times 3}$ is the adjusted Cα coordinates.

3D Residual U-Nets Training

In order to train our model, we first annotated the cryo-EM maps in the training dataset according to the PDB-deposited structure. For backbone prediction, we segmented each cryo-EM map into four semantics. A voxel in cryo-EM maps is annotated as a main chain voxel if it contains any main chain atom, otherwise, it is labeled as a side chain voxel when it contains any side chain atom, otherwise, it is assigned as a mask voxel when it is neighbor to any protein atom, otherwise, it is annotated as a non-structural voxel. The introduced mask voxel is to alleviate the unfair bias caused by experimental error in PDB-deposited structures, and it does not participate in the network back-propagation. Similarly, for Cα prediction, a voxel in cryo-EM maps is annotated as Cα voxel if it contains any Cα atom, otherwise, it is labeled as other-atom voxel when it contains any other protein atom, otherwise, it is assigned as a mask voxel when it is neighbor to any protein atom, otherwise, it is annotated as a non-structural voxel. Then for amino acid type prediction, we annotated a voxel neighbor to any Cα voxel as its corresponding amino acid type, all other voxels are assigned as mask voxels and masked out in network back-propagation. Our training loss can be defined as:

$${{{\mathcal{L}}}}={\lambda }_{S}{{{{\mathcal{L}}}}}_{S}+{\lambda }_{C}{{{{\mathcal{L}}}}}_{C}+{\lambda }_{A}{{{{\mathcal{L}}}}}_{A}$$

(11)

where λ_S, λ_C, λ_A is the warming-up task weights that are adaptively adjust from 1, 1, 0 to 0, 0, 1 in our training procedure and ${{{{\mathcal{L}}}}}_{S},{{{{\mathcal{L}}}}}_{C},{{{{\mathcal{L}}}}}_{A}$ can be unified as ${{{{\mathcal{L}}}}}_{CE}$:

$${{{{\mathcal{L}}}}}_{CE}=\sum -{W}_{\hat{y}}log\frac{exp(y=\hat{y})}{{\sum }_{c=0}^{C}exp(y=c)}$$

(12)

where C represents the number of classes, $y\in {{\mathbb{R}}}^{C\times w\times h\times d}$ is the output of corresponding U-Net module, $\hat{y}\in {\{0,...,C\}}^{w\times h\times d}$ is the annotated ground truth label, and ${W}_{\hat{y}}$ is the class weight of $\hat{y}$ that is set according to the ground truth class distribution in order to alleviate the class imbalance problem. Here for ${{{{\mathcal{L}}}}}_{S}$ the class weights are set as 1, 0.3, 0.03, 0 for the class of main chain, side chain, non-structural, and masked voxel, respectively. Similarly, for ${{{{\mathcal{L}}}}}_{C}$ the class weights are set as 1, 0.1, 0.01, 0 for the class of Cα, other-atom, non-structural, and masked voxel, respectively. Nevertheless, for amino acid type prediction we didn’t apply any different class weight for different amino acid types since we do not focus on the prediction of a certain amino acid class and the amino acid class imbalance itself implies natural protein sequence bias. Our neural networks were implemented by PyTorch 1.8.1⁶¹ and trained on Nvidia GTX 3090 Graphics Processing Unit (GPU) with Adam optimizer⁶², learning rate of 1 × 10⁻⁴ and batch size of 8.

Cα-Sequence Alignment

To achieve cross-modal alignment across cryo-EM maps and protein sequences, a naive approach is to map the Cα atom candidates from cryo-EM map to protein complex sequences by scoring how their amino acid types match. However, considering that there are a large number of identical amino acid types in the sequence and there exists prediction error in ${{{{\mathcal{N}}}}}^{A}$, this naive approach is far from correctly aligning Cα candidates to protein sequence. Specifically, we define B as the event that a Cα is predicted as the same amino acid type with a protein sequence position, and A is defined as the event that this Cα matches this protein sequence position in the PDB structure. The probability P(A∣B) can be calculated by Bayes’ theorem:

$$P(A| B)=\frac{P(A)\cdot P(B| A)}{P(B)}$$

(13)

$$=\frac{P(A)\cdot P(B| A)}{P(A)\cdot P(B| A)+P({\overline{A}}_{1})\cdot P(B| {\overline{A}}_{1})+P({\overline{A}}_{0})\cdot P(B| {\overline{A}}_{0})}$$

(14)

$$=\frac{\frac{1}{N}\cdot acc}{\frac{1}{N}\cdot acc+\frac{n-1}{N}\cdot acc+\frac{N-n}{N}\cdot \frac{1-acc}{19}}$$

(15)

$${\approx}^{\frac{n}{N}\approx \frac{1}{20}}\frac{20\cdot acc}{N}$$

(16)

where N is the number of residues, n is the number of residues with identical amino acid types, acc = P(B∣A) is the amino acid prediction accuracy, and event ${\overline{A}}_{0}$ / ${\overline{A}}_{1}$ is defined as that the predicted amino acid type is the same / not the same with its protein sequence position but don’t match in the PDB structure. Eqs. (15) and (16) are derived by the uniform distribution assumption (for computation convenience) that $P(B| {\overline{A}}_{0})=\frac{1-acc}{19}$ and $\frac{n}{N}\approx \frac{1}{20}$. When N is large enough (e.g. N > 1000), $P(A| B)\approx \frac{20\cdot acc}{N}\approx 0$. Therefore, such a naive mapping approach is not sufficient for accurate alignment.

Instead of naive mapping, EModelX leverages Cα trace sampling to enhance the confidence of alignment. As shown in Fig. 1b, the sampled traces are aligned with the sub-sequences of the protein sequence. We define ${B}^{{\prime} }$ as the event that the predicted amino acid types of a trace are identical to a subsequence, and ${A}^{{\prime} }$ is defined as the event that this trace matches this subsequence in the PDB structure. The probability $P({A}^{{\prime} }| {B}^{{\prime} })$ can be calculated by Bayes’ theorem:

$$P({A}^{{\prime} }| {B}^{{\prime} })=\frac{P({A}^{{\prime} })\cdot P({B}^{{\prime} }| {A}^{{\prime} })}{P({B}^{{\prime} })}$$

(17)

$$=\frac{P({A}^{{\prime} })\cdot P({B}^{{\prime} }| {A}^{{\prime} })}{P({A}^{{\prime} })\cdot P({B}^{{\prime} }| {A}^{{\prime} })+{\sum }_{i=0}^{s}P({\overline{{A}^{{\prime} }}}_{i})\cdot P({B}^{{\prime} }| {\overline{{A}^{{\prime} }}}_{i})}$$

(18)

$$=\frac{\frac{1}{N-s+1}\cdot ac{c}^{s}}{\frac{1}{N-s+1}\cdot ac{c}^{s}+{\sum }_{i=0}^{s}\left({i}\atop{s}\right)\cdot \frac{{\prod }_{1}^{i}{n}_{k}\cdot {\prod }_{i+1}^{s}\, (N-{n}_{k})}{{N}^{s}}\cdot ac{c}^{i}\cdot {(\frac{1-acc}{19})}^{s-i}}$$

(19)

$$\mathop{\approx}^{\frac{{n}_{k}}{N}\approx \frac{1}{20},acc\approx {0.5}} \frac{\frac{1}{N-s+1}}{\frac{1}{N-s+1}+{\sum }_{i=0}^{s}\left(\begin{array}{c} i\\ s \end{array}\right)\cdot \frac{1}{2{0}^{s}}}$$

(20)

where s is the length of the sampled subsequence, event ${\overline{A}}_{i}$ is defined as that the sampled trace has i amino acids identical to the subsequence but don’t match in the PDB structure, $acc=P({B}^{{\prime} }| {A}^{{\prime} })$ is the amino acid prediction accuracy, and n_k is the number of residues that have identical amino acid type with the k_th residue in subsequence. Given assumption that acc = 0.5 and $\frac{{n}_{k}}{N}\approx \frac{1}{20}$, when s is large enough, $P({A}^{{\prime} }| {B}^{{\prime} })\approx 1$.

To implement the sampling-enhanced Cα-sequence alignment, EModelX first computes the naive amino acid type matching score ${{{{\mathcal{S}}}}}^{A}$ between the predicted Cα candidates and native protein sequences, which can be formatted as:

$${{{{\mathcal{S}}}}}_{ijk}^{A}={{{{\mathcal{N}}}}}_{{s}_{ij}{F}_{r}({{{{\mathcal{C}}}}}_{k})}^{A}$$

(21)

where ${{{{\mathcal{S}}}}}^{A}\in {{\mathbb{R}}}^{S\times L\times N}$ (S: number of unique sequences, L: max length of sequences, N: number of Cα candidates), s_ij represents the type of j_th amino acid in the i_th unique sequence, ${{{{\mathcal{C}}}}}_{k}$ is the coordinate of k_th Cα candidate, and ${F}_{r}:{{\mathbb{R}}}^{3}\to {{\mathbb{Z}}}^{3}$ is the rounding function.

The subsequent step is to sample Cα local traces. As shown in Fig. 1b, the traces of Cα candidates were sampled based on backbone distribution and Cα distance. Firstly, the Cα neighbor connection likelihood ${{{\mathcal{H}}}}\in {{\mathbb{R}}}^{N\times N}$ is estimated as:

$${{{\mathcal{H}}}}=\frac{{{{{\mathcal{S}}}}}^{D}+{{{{\mathcal{S}}}}}^{B}}{2}$$

(22)

where ${{{{\mathcal{S}}}}}^{D}\in {{\mathbb{R}}}^{N\times N}$ is the distance score, ${{{{\mathcal{S}}}}}^{B}\in {{\mathbb{R}}}^{N\times N}$ is the backbone score, and they are defined as:

$${{{{\mathcal{S}}}}}_{ij}^{D}=\max \left(\min \left(1-\frac{| | {{{{\mathcal{C}}}}}_{i}-{{{{\mathcal{C}}}}}_{j}| -3.8| -0.5}{2},1\right),0\right)$$

(23)

$${{{{\mathcal{S}}}}}_{ij}^{B}=\frac{1}{6}\mathop{\sum }_{k=0}^{5}{{{{\mathcal{N}}}}}_{0{F}_{r}({{{{\mathcal{C}}}}}_{i}+\frac{k}{5}\times ({{{{\mathcal{C}}}}}_{j}-{{{{\mathcal{C}}}}}_{i}))}^{B}$$

(24)

where i and j are indexes of two Cα candidates satisfying $| {{{{\mathcal{C}}}}}_{i}-{{{{\mathcal{C}}}}}_{j}| \in \left[2,6\right),{{{{\mathcal{N}}}}}_{0}^{B}$ is the softmax score of main chain class in ${{{{\mathcal{N}}}}}^{B}$, and F_r is the rounding function.

Subsequently, ${{{\mathcal{H}}}}$ is used to sample local structures ${{{\mathcal{T}}}}\in {{\mathbb{R}}}^{L\times 7}$, where L is the number of sampled structures, and 7 is the length of each sampled local structure. We then estimate the n-hop (n ∈ [1, 6]) connection likelihood ${{{{\mathcal{H}}}}}^{(n)}\in {{\mathbb{R}}}^{N\times N}$:

$${{{{\mathcal{H}}}}}_{{t}_{0}{t}_{n}}^{(n)}=nor{m}_{{{{\mathcal{C}}}}}\left({\max }_{{{{\mathcal{T}}}}}\left( \mathop{\prod}_{i=1}^{n}{{{{\mathcal{H}}}}}_{{t}_{i-1}{t}_{i}}\right)\right)$$

(25)

where $t\in {{{\mathcal{T}}}}$ represents a local structure with length of 7, t_i is the i_th Cα in $t,ma{x}_{{{{\mathcal{T}}}}}$ maintains the maximum value among different $t\in {{{\mathcal{T}}}}$ that share identical for identical (t₀, t_n) pair, and $nor{m}_{{{{\mathcal{C}}}}}$ normalizes ${{{{\mathcal{H}}}}}^{(n)}$ for summing up to 1 in the first channel.

Finally, we compute ${{{\mathcal{S}}}}\in {{\mathbb{R}}}^{S\times L\times N}$ as the Cα-sequence aligning score of predicted Cα candidates to complex sequences:

$${{{{\mathcal{S}}}}}_{ijk}={{{{\mathcal{S}}}}}_{ijk}^{A}+ {\sum}_{n=1}^{6} {\sum}_{{k}^{{\prime} }=0}^{N}\left({{{{\mathcal{S}}}}}_{i(j-n){k}^{{\prime} }}^{A}+{{{{\mathcal{S}}}}}_{i(j+n){k}^{{\prime} }}^{A}\right)\times {{{{\mathcal{H}}}}}_{{k}^{{\prime} },k}^{(n)}$$

(26)

where ${k}^{{\prime} }$ traverses the indices of predicted Cα candidates. ${{{\mathcal{S}}}}$ is updated by n-hop connection likelihood to learn Cα-sequence alignment from n-hop neighboring Cαs. This procedure is named Cα-sequence score propagation.

We have also implemented EModelX(+AF). As shown in Fig. 1c, EModelX(+AF) leverages AlphaFold predicted structure to assist Cα-sequence alignment. Specifically, the Cα-sequence aligning score ${{{\mathcal{S}}}}$ is modified as ${{{{\mathcal{S}}}}}^{{\prime} }$= ${{{\mathcal{S}}}}$ + ${{{{\mathcal{S}}}}}^{T}$, where ${{{{\mathcal{S}}}}}^{T}\in {{\mathbb{R}}}^{S\times L\times N}$ is defined as the structural aligning score. For each $t\in {{{\mathcal{T}}}},n\in [1,6]$ and k = t_n:

$${{{{\mathcal{S}}}}}_{ijk}^{T}=-\!{\min }_{{{{\mathcal{T}}}}}(\delta (t,{{{{\mathcal{P}}}}}_{ijn}))$$

(27)

where ${{{{\mathcal{P}}}}}_{ijn}$ is the [j − n, j − n + 6] sub-structure of AlphaFold predicted structure in i_th unique sequence, and δ is the RMSD calculated by superimposing t and ${{{{\mathcal{P}}}}}_{ijn}$.

Chain and Sequence Registration

After Cα-sequence alignment, the high-confidence Cα-sequence mapping can be identified from the aligning score matrix. We found that the high-confidence mappings showed a strong correlation with ground-truth matches between Cα candidates and protein sequence positions. Therefore, a hierarchical modeling strategy is adopted to first build an initial model based on high-confidence mappings and subsequently fill the unmodeled gaps through Cα threading.

To build the initial model, the chain and sequence registration is necessary to assign chain index and sequence position to those Cαs. Following a greedy strategy, we start from the highest-confidence match of ${{{\mathcal{S}}}}$ to lower ones. For each current match (i, j, k) in ${{{\mathcal{S}}}}$, we iteratively explore its spatial and sequential neighbor match $(i,{j}^{{\prime} },{k}^{{\prime} })$ satisfying ${j}^{{\prime} }=j\pm 1,\, {{{{\mathcal{S}}}}}_{k{k}^{{\prime} }}^{D} \, > \, 0$ and ${k}^{{\prime} }$ = argmax(${{{{\mathcal{S}}}}}_{i{j}^{{\prime} }}$) until no such match could be found. The found matches list, regarded as a Cα trace matching to a protein sub-sequence, would be identified as a high-confidence sequence registration result if its length is long enough (≥9).

The sequence registration is straightforward since we have aligned Cα traces to sequences. However, chain registration can be a combinatorial optimization problem for homologous chains that share the same sequence. Here we leverage connectivity and symmetry to solve this problem. As shown in Algorithm 1, a trace clashes to a chain means that the trace’s sub-sequence has been occupied in the chain. The TOP_CONNECTIVE function proposes the chain to which trace t is most connective. Specifically, a naive greedy strategy is adopted to perform Cα threading for connecting trace t to each chain in given steps (equal to their gap length in sequence order), and the cumulative Cα-sequence aligning scores of connecting results are used to rank these chains and pick the top candidate. The TOP_SYMMETRIC function proposes the chain to which trace t is most symmetric. Specifically, trace t is fused with each chain in ${{{{\mathcal{V}}}}}_{t}$ and is subsequently superimposed to each chain in ${{{{\mathcal{C}}}}}_{t}$. The chain in ${{{{\mathcal{V}}}}}_{t}$ that obtained the lowest RMSD is regarded as the most symmetric chain.

Algorithm 1

Algorithm 1: Chain Registration

Sequence-Guiding Cα Threading

We have built up a high confidence aligned protein complex Cα model with some unaligned structure gaps. For a given gap we thread Cα from one endpoint (Cα that has been assigned with a certain Cα in a high-confidence model) to another. However, it suffers from high computational complexity in long-length gaps. So we employed a strategy of pruning search to accelerate it, which is a modified version of our previous work²⁰. The schematic flowchart of the pruning search algorithm has been depicted in Supplementary Fig. S8, which relies on a scoring function to filter out traces with lower scores within the same structural cluster. The goal of this scoring function is to preserve traces that have: i. higher Cα-sequence aligning scores, ii. higher Cα connection scores, and iii. higher symmetry with corresponding segments in other homomeric chains or AlphaFold structures. Specifically, the scoring functions can be formatted as:

$${{{\mathcal{F}}}}= {\sum}_{j\in s,k\in t}{{{{\mathcal{S}}}}}_{ijk}+ {\sum}_{k\in t}{{{{\mathcal{H}}}}}_{k,{k}^{{\prime} }}-\delta (t,{{{{\mathcal{M}}}}}_{s})$$

(28)

where t is the Cα trace that has been searched, s is the corresponding sub-sequence, ${{{\mathcal{S}}}}$ is the Cα-sequence aligning score, ${{{\mathcal{H}}}}$ is the estimated Cα neighbor connection likelihood, ${k}^{{\prime} }$ is the next Cα of k in t, δ is to calculate the RMSD between t and ${{{{\mathcal{M}}}}}_{s}$. ${{{\mathcal{M}}}}$ for EModelX is another homomeric chain that has built model for sub-sequence s, and ${{{\mathcal{M}}}}$ for EModelX(+AF) is the AlphaFold structure. Cα threading is performed on the unmodeled structure gaps which commonly correspond to local regions at lower resolution. Incorporating AlphaFold can not only provide a more reliable template ${{{\mathcal{M}}}}$ but also enhance Cα-sequence aligning score ${{{\mathcal{S}}}}$ by adding a structure alignment item ${{{{\mathcal{S}}}}}^{T}$ (Eq. (27)). Therefore, it holds promise for enhancing the accuracy of Cα threading.

After sequence-guiding Cα threading, we have built the Cα backbone model of protein complex. Following MAINMAST, we adopted PULCHRA³⁷ as the full-atom construction tool. Finally, the full-atom complex model is refined in the EM density map using phenix.real_space_refine³⁸. Molecular graphics and analyses are performed with UCSF Chimera⁶³.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.