multiDGD: A versatile deep generative model for multi-omics data

Abstract

Recent technological advancements in single-cell genomics have enabled joint profiling of gene expression and alternative modalities at unprecedented scale. Consequently, the complexity of multi-omics data sets is increasing massively. Existing models for multi-modal data are typically limited in functionality or scalability, making data integration and downstream analysis cumbersome. We present multiDGD, a scalable deep generative model providing a probabilistic framework to learn shared representations of transcriptome and chromatin accessibility. It shows outstanding performance on data reconstruction without feature selection. We demonstrate on several data sets from human and mouse that multiDGD learns well-clustered joint representations. We further find that probabilistic modeling of sample covariates enables post-hoc data integration without the need for fine-tuning. Additionally, we show that multiDGD can detect statistical associations between genes and regulatory regions conditioned on the learned representations. multiDGD is available as an scverse-compatible package on GitHub.

Introduction

Single-cell genomics methods have become the main technology to study cellular heterogeneity and dynamics within tissues. They also enable the measurement of multiple molecular features within individual cells, pairing measurements of the transcriptome with epigenome, proteome or genome profiling. These paired multi-modal measurements can be used for deeper characterization of cell states, differentiation processes or genotype-to-phenotype relationships¹. Another example of multi-modal data are unpaired measurements. In these measurements, there is no overlap in cells between modalities. In this work we focus on paired measurements of gene expression and chromatin accessibility, which are increasing in popularity in the biomedical community.

Analysis of paired single-cell multi-omics data typically requires joint dimensionality reduction on multiple types of molecular measurements to identify cell-cell similarities, cell states, and patterns of co-variation between genomic features (also known as vertical integration²). Several statistical models have been proposed for this task, mostly based on factor analysis^3,4,5 or cell-cell similarity embeddings^6,7. Recently, approaches have been proposed to additionally integrate paired data from measurements of individual modalities (i.e. mosaic integration)^8,9,10,11. However, existing methods have primarily been applied to relatively small data sets, while increasing availability of multi-modal data now requires models that can handle tens of thousands of cells from multiple experiments, with the ability to account for technical differences between samples¹². Additionally, methods for vertical integration struggle with imbalance in the dimensionality of feature spaces, especially in the joint analysis of gene expression and chromatin accessibility over hundreds of thousands of genomic regions². Importantly, as the field and its methodologies are still developing, existing analytical approaches predominantly focus on dimensionality reduction for cell clustering, with notably little emphasis on identifying relationships between molecular features¹. This is especially relevant for joint analysis of epigenomic and transcriptomic profiles to associate regulatory regions to changes in gene expression.

To alleviate the problems encountered with large data sets, generative models have been applied to both uni-modal^{13,14,15,16,17,18} and multi-modal^{8,11,19,20,21} data. Deep generative models are powerful machine learning techniques that aim to learn the underlying function of how data is generated. This is of special interest for unsupervised analysis of single-cell data, where the goal is to interpret patterns of variation in high-dimensional and noisy data²². The predominant type of generative model applied in this field is the Variational Autoencoder (VAE)²³: models tailored for scRNA-seq data^13,14,15,16 enable integration of large and complex data sets at lower computational cost²⁴ and have been successfully applied to the analysis of cells across human tissues and in large cohorts^25,26,27. These models do however come with some limitations¹⁸, which are continuously being addressed by a large community. With the current state of model design, it is for example not trivial to integrate new samples from different batches after training as covariates are modeled via one-hot encoding. scArches²⁸ is a tool introduced to solve this problem post-hoc, which applies fine-tuning but does not fully solve the underlying problem.

While the number of generative models available is vast for scRNA-seq single-cell data^{13,14,15,16,17,18,21}, the application to multi-modal single-cell data has just begun. Existing models often employ simplistic architectures, priors for the generative distribution, and encoding of confounding covariates such as batch effects^8,11,19,20. The results are under-performing models, where the suboptimal results are attributed to noise in the data²⁹. Generative modeling can provide much more than a joint integration. As emergent properties, deep generative models can capture underlying relationships between variables and dynamics in high-dimensional data. Straightforward examples of this would be feature interactions and cell state transitions. These properties can be learned without explicit modeling. However, these promising applications of generative models are still under-explored, as many models focus only on a fraction of the actual feature space.

In this work, we propose a new generative model, multiDGD, which aims to provide a basis for improved data integration and analysis of feature interactions. The model is an extension of the Deep Generative Decoder (DGD)¹⁸ for single-cell multi-omics data of gene expression and chromatin accessibility. Unlike VAE-based models, it uses no encoder to infer latent representations but rather learns them directly as trainable parameters, and employs a Gaussian Mixture Model (GMM) as a more complex and powerful distribution over latent space. This introduces several advantages. Firstly, an encoder limits the flexibility and quality of representations. A decoder alone can better recover representations close to the optimum and reduces the number of parameters in the model³⁰. Secondly, the GMM increases the ability of the latent distribution to capture clusters in comparison to the standard Gaussian used in applied VAEs. Another strength of the DGD is its data efficiency. As presented in³⁰, the encoder requires more data to be well-defined than the decoder. Removing the encoder makes the model applicable to not only large but also small data sets. This also translates to the number of features that can be modeled, and makes the DGD amenable to model genome-wide chromatin accessibility data where feature selection is problematic and may not be desirable.

We demonstrate on real world applications that the DGD can learn meaningful representations of complex multi-modal data, with improved performance for dimensionality reduction, cross-modality prediction, and modeling of unseen batches without the need for fine-tuning. Furthermore, we provide a proof-of-concept that multiDGD can be used to predict regulatory associations between genes and peaks based on in silico perturbation.

Results

The model

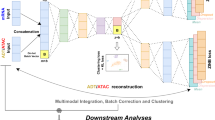
multiDGD is a generative model for transcriptomics and chromatin accessibility data. It consists of a decoder mapping shared representations of both modalities to data space, and learned distributions defining latent space. Figure 1 shows a schematic of multiDGD with its training and inference processes. The novelties compared to scDGD¹⁸ besides the added ATAC-seq modality include the covariate latent model to learn disentangled representations, a branched decoder architecture, and the gene-to-peak analysis functionality to extract learned connections between genes and regulatory regions.

Fig. 1: Schematic of multiDGD’s architecture and generative process.

Representations Z presents the input to the decoder. They are distributed in latent space according to a Gaussian mixture model (GMM) parameterized by ϕ. Z^basal and ϕ present the unsupervised basal embedding and its distribution, respectively. We refer to this part as the latent model. A novelty in multiDGD is the covariate model. Z^cov and ϕ^cov present the supervised representations and GMM for a given categorical covariate. For each data point (cell) i ∈ N, there exists a latent vector of length L, plus 2 dimensions for each covariate modeled. The input is transformed into modality-specific predicted normalized mean counts y through the branched decoder θ. These outputs are then scaled with sample-wise count depths to predict the density of both RNA and ATAC data. Red arrows depict the backpropagation and updating of parameters during training.

The inputs to the decoder are the low-dimensional representations Z of data X. Instead of providing them through an encoder (as in the Variational Autoencoder²³), they are learned directly as trainable parameters³⁰. Single-cell data often creates the need to correct for data shifts like batch effects. Sometimes, we may also want to investigate certain biological axes like developmental stages on their own. In order to provide this functionality in a flexible way, we designed the covariate model, which can disentangle such information from the unsupervised representation. As a result, we can model the molecular representation of cells Z ^basal separately from technical batch effects and sample covariates (Z ^cov). We now have an unsupervised “latent model” (representation Z ^basal and parameterized distribution ϕ) as usual, and additional latent model (Z ^cov, ϕ^cov) which we call the covariate model, trained in a supervised manner. Distributions over latent space are chosen as Gaussian Mixture Models (GMMs). They present a natural choice for data containing sub-populations and can provide unsupervised clustering. Supervision is achieved by assigning GMM components to the covariate classes and optimizing only over the probability densities for the assigned component. This is visualized in Supplementary Fig. 1 and explained in the Methods section in detail. The full representations Z are concatenations of Z ^basal and Z ^cov.

Data is generated by feeding latent representations Z to the decoder. For every ith sample of N data samples (cells), there exists a corresponding representation z_i. The decoder consists of three blocks: the shared neural network (NN) θ^h, and the two modality-specific NNs θ^RNA and θ^ATAC. The modality-specific networks predict fractions of the total counts per cell and modality, y_ij. These are then converted into predicted means of Negative Binomial distributions (a common and natural choice for such over-dispersed count data^31,32) modeling counts by multiplying with the total count s_i. The training objective is given by the joint probability p(X, Z, θ, ϕ)¹⁸, which is maximized using Maximum a Posteriori estimation¹⁸. Both the model and the inference process are explained in more detail in the Methods section and Supplementary Fig. 1.

Benchmarking multiDGD performance and flexibility against other generative models

Below we evaluate multiDGD performance compared to VAE-based alternatives. Machine-learning-based methods have the potential to do more than data integration and latent clustering, and promise to reveal information about regulatory processes captured in the observed data. Since MultiVI⁸ (a VAE-based multi-omics generative model) presents the only one that can model different batches and impute missing data, it is the main focus of our benchmark. Where applicable, we included performances of Cobolt¹¹ and scMM²⁰. scMM does not explicitly model batch effects, which is why a direct comparison on the marrow and gastrulation data was not possible. Cobolt cannot predict counts for novel data and could thus only be used to compare clustering and batch removal performance. Further model limitations are outlined in Supplementary Table 1. All models were used with the same latent dimensionality of 20. We compare performances for three different data sets of paired scRNA-seq and scATAC-seq, derived from human bone marrow¹², human brain³³, and mouse gastrulation³⁴ multi-omics data (see Methods).

Improved count reconstruction and prediction

We first compared data reconstruction performances on held-out test sets (cells) stratified for cell types from the published annotations. Reconstruction performance presents an important metric for evaluating a model’s data integration capabilities. Here, multiDGD consistently outperforms MultiVI on all tested data sets (as well as scMM on the brain data) (Fig. 2A, B and Supplementary Fig. 3 for cell- and feature-wise performances). The improvement in reconstructing ATAC features on the human bone marrow data is partially driven by a strong performance increase on highly variable peaks (Supplementary Fig. 4). Another contributor to this performance increase on ATAC features is the GMM. Supplementary Fig. 6B demonstrates that the test reconstruction performance is strongly decreased for a standard Gaussian latent prior as is common in VAE-based models.

Fig. 2: Performance evaluation on data reconstruction, data efficiency, clustering, and batch effect removal.

Performance evaluations were done on the three data sets marrow, gastrulation, and brain, and three different random seeds. We compared to MultiVI⁸, Cobolt¹¹, and scMM²⁰ where applicable. See the legend under D for color decoding and metric evaluation (arrows in plot titles). All values are presented as mean values +/- SEM. Individual data points for N = 3 are plotted as black dots. A, F Lower is better. A Reconstruction performance on the test RNA data measured by RMSE. B–D, G Higher is better. B Comparison of the reconstruction performance on the test set ATAC data as the AUPRC of binarized data. C Clustering performance of the train representation as the ARI based on clustering derived from the GMM for multiDGD and Leiden clustering for MultiVI. The Leiden algorithm is adjusted for the number of clusters (see Methods). D Batch effect removal of marrow and gastrulation data calculated as 1 − ASW. Brain data annotation contained no batch information. E Data efficiency was evaluated by training bone marrow models on a range of subsets. Test loss ratios were computed for models trained on three random seeds (N = 3). F, G Feature efficiency on the mouse gastrulation test set (N = 5686 cells) was investigated by training multiDGD and MultiVI on the mouse gastrulation data with (in 5%) and without feature selection (all). Performance values were only evaluated on the smaller feature set for comparability. Asterisks indicate significance based on two-sided Mann-Whitney U (MWU) tests (N = 5686). All values are provided in the Source Data. F RMSE for RNA reconstruction performance. MWU test in 5% (p-value 1e-202), all (p-value 0.000). G AUPRC for ATAC reconstruction performance. MWU test in 5% (p-value 0.062), all (p-value 0.021).

We next evaluated the performance of multiDGD for predicting and imputing missing data from one of the two modalities (RNA or ATAC). Predicting data modalities is a natural application of generative models for the case where existing uni-modal data is to be integrated with multi-modal data. In order to assess multiDGD’s predictive capability, we test its performance on the held-out test set given only one modality. Imputations are achieved by optimizing the partial likelihood of the available data (see Methods section ‘Missing modality prediction’). Representations inferred from either the original paired samples or the artificial uni-modal samples are well integrated into latent space (Supplementary Fig. 5). In order to assess the imputation performance of both multiDGD and MultiVI, we measured the relative prediction performance (unseen modality) with respect to reconstruction in form of a loss ratio (Methods section ‘Relative and predictive performance’). This relative performance was similar for both multiDGD and MultiVI, although multiDGD shows a greater variance (Supplementary Table 2). However, the absolute prediction and reconstruction performances of multiDGD for ATAC data are still superior to those of MultiVI (Supplementary Table 3).

Robust performance on small data sets and many features

VAEs have clearly shown their usability and advantage when it comes to the speed at which they can model large data sets due to amortization, although this can come at the cost of posterior approximation³⁵. The encoder-less DGD is naturally suited for data sets with few samples and many features, where autoencoder-based models tend to overfit³⁰. In this work, we briefly revisit this hypothesis by investigating the test performances of MultiVI and multiDGD trained on subsets of the human bone marrow set (Methods section ‘Data efficiency’). To put these into perspective, we compute average test loss ratios as the average test loss from the model trained on a subset over the test loss from the original model trained on the full set. Even though the variance in test loss ratios is much higher for multiDGD than for MultiVI (Fig. 2E), the average loss ratio of multiDGD stays stable for subsets larger than 1%, which corresponds to only 567 cells. MultiVI, on the other hand, performs worse with decreasing number of cells in the training data.

This advantage of the DGD also carries over to data with many features. Typically, in single-cell analysis feature selection is applied before performing dimensionality reduction³⁶, both for scalability and to increase clustering performance¹². While robust methods to select highly variable genes exist for scRNA-seq, there are no robust statistical methods for feature selection in scATAC-seq data sets. Here, accessibility is usually measured over hundreds of thousands of peaks, and several vertical integration methods suffer from this feature imbalance². We compared multiDGD and MultiVI performance on data reconstruction in two scenarios on the mouse gastrulation data. The first one presents the previously presented models trained on data with feature selection (11792 genes, 69862 peaks), the second scenario presents models trained on all measured features (32285 genes, 192251 peaks). We compared performances on only the shared set of features. While MultiVI lost performance for both modalities, multiDGD achieved nearly the same performance as before on ATAC data and even increased its performance on RNA data (Fig. 2F, G).

Expressive representations with improved clustering on annotated data

We next evaluated the latent spaces learned by the models in terms of clustering of cell types and batch effect removal. While multiDGD is not intended for the prediction of cell types, it gives more expressive representations of annotated data than MultiVI. The more complex latent distribution of the GMM clearly benefits the structure of the learned embeddings in terms of clustering and batch effect removal (as seen in Supplementary Fig. 6C, D) compared to a standard Gaussian as a prior. This case study on the human bone marrow set in Supplementary Fig. 6 also suggests that paired data of both modalities compared to models of each modality further improves embedding quality. If cell type annotations are not available, we recommend approximating them through tools such as CellTypist³⁷. Another option if the desired number of GMM components is unknown, is to set an upper bound and learn an effective number of components without the covariance prior (Supplementary Fig. 9).

MultiVI’s shared embeddings of transcriptional and chromatin features are commonly used as input for the Leiden³⁸ clustering algorithm. The DGD intrinsically performs clustering with the Gaussian Mixture Model as the latent distribution (details in Methods sections ‘Architecture’ and ‘Internal clustering’). Measuring clustering performances with the Adjusted Rand Index (ARI) (Fig. 2C), we see a notable variance in performance with random seeds for model initialization, more so for multiDGD than for MultiVI with Leiden clustering. However, the GMM components of multiDGD still learn latent representations whose clustering generally aligns better with the annotated cell type labels (compared to MultiVI, Cobolt, and scMM). Figure 3C visualizes the learned representations and GMM components on the example of the human bone marrow benchmark data (remaining data sets and clustering matrices are shown in Supplementary Figs. 10 and 14). Clustering performance is, in addition, more stable in multiDGD with respect to changing data set sizes than MultiVI. On the human bone marrow data, we observe stable performance for training set sizes of more than 6000 cells, presenting 10% of the original data (Supplementary Fig. 15).

Fig. 3: Latent space visualizations.

Basal and covariate representations from multiDGD (rs=0) on the human bone marrow data and covariate representations from the mouse gastrulation data. Points present representations of cells from the training data. D1 and D2 in covariate representations refer to the first and second dimension of the data. A Covariate representations of the human bone marrow data colored by Site. B Covariate representations of the mouse gastrulation data colored by stage. C UMAP visualization of the basal representations from the human bone marrow data. It is colored by annotated cell types as provided by the data source. GMM component means are indicated by black numbers projected onto their transformed coordinates.

Disentangled representations for improved batch effect removal

Another important feature of generative models for single-cell data is the capability to alleviate batch effects. In multiDGD, batch effects can be removed by disentangling basal and covariate representations as described in ‘The model’ result section. This leads to improved mixing between batches compared to the one-hot encoding in MultiVI (Fig. 2D and Supplementary Fig. 10), although this is to be taken with a grain of salt as the average silhouette width may be skewed due to the different latent distributions. On our benchmark set, we see that the disentangled latent space results in a clear separation of most cell types (Fig. 3C and Supplementary Fig. 10) and a good mixture of the sites at which samples were processed (Supplementary Fig. 13). Supplementary Fig. 6C, D demonstrates the strong positive effect of the covariate model on clustering and batch effect removal. The two-dimensional, separate representation for the batches derived from supervised training (Fig. 3A) mirrors trends found in the general data distribution (see Supplementary Fig. 16). These include site4 showing much more zero RNA counts than all other sites, which can explain why its cluster is distant from the others. In addition, we find that the covariate representation can capture biologically interpretable differences between samples. For example, when modeling the differences between embryos in the mouse gastrulation data set we see time-related structuring of the Gaussian components (Fig. 3B). The early-to-late gastrulation phases from stage E7.5 to E8.0³⁹ appear in chronological order, with stages E8.5 and E8.75 clearly separated. This distance makes sense as the differentiation of early organ progenitors is seen in stages E8.25 to E8.75³⁹.

Integrating new batches without architectural surgery

A novel feature of the DGD is its capability to find representations for previously unseen data. This can simply be unobserved cells from the previously seen covariates, as well as completely new data from novel covariates. The latter is possible thanks to the probabilistic modeling of both the desired ‘molecular’ and covariate components of the representation. We explore the quality of representations and predictions for unseen data by applying the leave-one-out method to train the model. For each batch in the human bone marrow data (defined as the site the data was processed at), we train a multiDGD instance on the training samples of all other batches, providing us with four models. We evaluate these models on their test performances in terms of prediction errors relative to the model trained on all batches. In Fig. 4A, we see a marginal increase in the prediction loss of unseen batches as expected, but overall prediction performance is on par with the model trained on all batches (Fig. 4B) and the unseen batch samples are well integrated into the latent space (Supplementary Fig. 17). So far, unseen covariates have been integrated with approaches such as architectural surgery (scArches²⁸). We include a comparison to scArches applied to MultiVI in the same scheme. However, due to the need for a fine-tuning set, we run scArches on the training portion of the held-out batch, in order to keep the test set independent. This, of course, gives MultiVI+scArches an advantange of additional data. For MultiVI+scArches, the overall reconstruction error decreases compared to MultiVI trained on all batches (4B), highlighting the nature of fine-tuning in scArches. Absolute performance metrics, however, are still inferior to multiDGD (Fig. 4C) and integration into latent space is equivalent (Supplementary Fig. 17), making post-hoc fine-tuning obsolete.

Fig. 4: Model fine-tuning is no longer needed to predict unseen covariates.

All related experiments were performed on the bone marrow data set. For each site (presenting the batches), one model was trained that excluded the site from training. This resulted in four models. Comparisons are done on test predictions with respect to the model trained on all sites (‘full’). scArches was applied with the left-out site from the train set to leave the test set independent. This results in a fine-tuned MultiVI model using all training data (MultiVI+scArches). A Split violin plot of relative test performance for each multiDGD model wrt. the ‘full’ model. The loss ratios are colored by whether the site had been included in training (seen) or not (unseen). Number of samples are as follows (seen, unseen): site1 (5193, 1732), site2 (5391, 1534), site3 (5461, 1464), site4 (4730, 2195). B Comparison of loss ratios for multiDGD and MultiVI fine-tuned with scArches (N = 27700, i.e. test losses for four models). A, B Text above violins present the Kullback-Leibler divergences between the original test losses and the ones derived from the models trained on the incomplete data. C Absolute performance comparison of multiDGD and MultiVI trained on batch subsets. From left to right: Reconstruction performances of multiDGD and MultiVI+scArches for RNA (I) and ATAC (II) data, and batch effect removal (III). Arrows indicate whether higher or lower is better. Dashed lines present the original model performances for training on the full set. Leave-one-out model performances are presented as means +/- SEM with individual points (N=4) as black dots.

Modeling novel covariates

The previous results were derived from integrating novel data (the test set) without any information about the covariate label. We will here refer to this as ‘naive’ integration. This method leads to great prediction results on unseen covariates in terms of count modeling. A caveat of this approach is that we lose information about the differences between covariates. New cells from a previously unseen covariate will be assigned close to one of the seen covariate classes that give the lowest reconstruction loss (Supplementary Fig. 18). The probabilistic modeling of the covariates allows us to include a novel class explicitly without any changes to the decoder. We call this supervised integration. Besides inferring the novel representations, we also initialize a new covariate GMM component for the new class and optimize its mean and covariance along with the representations (Fig. 5A). All other parameters, including the remaining covariate GMM components, remain unchanged.

Fig. 5: Learning a novel GMM component for an unseen covariate class.

A Schematic of how multiDGD infers GMM components (distributions) for novel (not seen during training) covariates. After training, cells from a novel, unseen covariate are integrated by inferring a new GMM component ${c}_{{k}^{{\prime} }}$ for the novel covariates ${K}^{{\prime} }$. All remaining parameters (GMMs ϕ, ${\phi }^{{{{\rm{cov}}}}}({c}_{k\notin {K}^{{\prime} }})$ and decoder) are fixed. For notation see Fig. 1. B Test set reconstruction performance as the negative log probability from multiDGD averaged over features per sample (N from left to right: 1389, 139, 1008, 2411, 739). Error bars indicate the standard error of the mean. The x-axis indicates the covariate class of the test samples, colors indicate the integration method, and include a comparison to the original model trained on all data (seen). Asterisks indicate the significance of distribution differences based on two-sided Mann-Whitney U tests with a threshold of 0.05. All values are provided in the Source Data. MWU (E8.75, seen-unseen(supervised)): N = 739, p-value = 0.030. MWU (E8.75, unseen(naive)-unseen(supervised)): N = 739, p-value = 0.046. C Same as B for the bone marrow data (N from left to right: 1732, 1534, 1464, 2195). MWU results in source data. D Covariate representations of the mouse gastrulation test set from the model trained without stage E8.0. D1 and D2 present the data dimensions. The integration approaches (naive and supervised) are presented as columns. Test representations are colored by the covariate class (stage) in the top row. The bottom row indicates whether the training samples of a class had been seen during training (seen) or not (unseen). E Same as D for the human bone marrow data site 1.

We compared this naive and supervised integration of novel covariates on both the human bone marrow and the mouse gastrulation data. They represent technical and biological covariates, respectively. For most newly integrated covariate classes, test reconstruction errors are again comparable to those derived from the model trained on all covariates (Fig. 5B, C). Covariate representations of the test sets are shown in Fig. 5D, E, and Supplementary Fig. 18. Even though novel components are restricted to the area spanned by existing components, the supervised integration approach still leads to meaningful representations and well-integrated novel components.

Gene-to-peak association with in silico perturbation

An emergent property of multiDGD is the learned connectivity between gene expression and chromatin accessibility data inside the shared representations and decoder. We can use this to perform in silico predictions of where chromatin accessibility is associated with the expression of a given gene or set of genes. As depicted in Fig. 6A, we can silence a given gene X ^j = 0 and compute gradients in latent space in the direction of this perturbing in data space. For every cell used, we have the original representation and a representation after one step of perturbation (Z ^KO). From these representations, we predict the perturbed sample and calculate the differences in prediction $\Delta \hat{X}={\hat{X}}^{{{{\rm{KO}}}}}-\hat{X}$. $\hat{X}$ refers to model predictions.

Fig. 6: Prediction of association between gene expression and peak accessibility.

A Schematic of gene-peak association prediction with in silico perturbation. B Mean absolute effect of perturbation on peak accessibility (∆X, y-axis) within 10 kb window around transcription start site (TSS) of silenced genes. The rolling average and 95% confidence interval of perturbation effect over the distance to TSS is shown for silencing of 862 highly variable genes (HVGs), with window size of 100 bps. C Comparison of HiChIP signal around 3 genes (CLEC16A, CD69, ID2) with ∆X from silencing of the gene in naive CD4+T cells. For each gene, the top track shows the Enhancer Interaction Score (EIS) calculated from HiChIP data using the gene promoter as viewpoint (see Methods), for HiChIP on primary naive CD4+ T cells (positive HiChIP, green) and on the muscle cell line HCAMSC (negative control HiChIP, blue). The bottom track (red line) shows the scaled ∆X for the prediction of peaks associated with the expression of the gene of interest. The location of the transcript for the gene of interest is shown on top of each plot. T-cell-specific enhancer regions are highlighted in gray. D Barplots of Area under the Precision Recall Curve (AUPRC, y-axis) for prediction of HiChIP enhancer regions from ∆X or Spearmann correlation between gene expression and peak accessibility in the selected cell type (x-axis). We show AUPRC for predicted associations in bone marrow CD4+ T cells of CD4+ T cell HiChIP signal (dark green) or HCAMSC HiChIP signal (blue), and for predicted associations in CD14+ monocytes of CD4+ T cell HiChIP signal (light green). For multiDGD, we display the mean AUPRC and 95% confidence interval obtained by performing analysis on 3 models trained with different random seeds (N=3) with individual points as black dots.

First, we evaluated the ability of this in silico perturbation method to recover the association between gene expression and accessibility around the transcription start sites (TSS) of 2073 highly variable genes. When silencing a set of highly variable genes in the bone marrow data set, we observe significantly higher mean $\Delta \hat{X}$ at peaks in the proximity of the TSS as expected. $\Delta \hat{X}$ then gradually flattens for peaks over 2000 base pairs away (Fig. 6B).

Next, we investigated whether we could recover associations between genes and peaks overlapping distal enhancers. As ground-truth data for gene-enhancer interaction, we used H3K27ac HiChIP data measuring physical contacts between active chromatin and promoters in primary CD4+ T cells⁴⁰. We predicted the effect on chromatin openness from silencing three genes with CRISPR-activation-validated T-cell-specific enhancers captured by HiChIP (CLEC16A, CD69, ID2)⁴⁰. We observed high perturbation effect in naive CD4+ T cells in several regions with HiChIP evidence (Fig. 6C), which were not captured by HiChIP in a muscle cell line (negative control for cell-type-specific interactions). In addition, the enhancer prediction accuracy was significantly lower when considering perturbation effect in a different cell type (CD14+ monocytes) (Fig. 6D). These results suggest that multiDGD is capturing cell-type-specific enhancer-gene links. In all cases, multiDGD prediction outperformed gene-peak associations derived from Spearmann correlation of gene expression and peak accessibility, where performance was close to random (Fig. 6D, Supplementary Fig. 19). We note here that $\Delta \hat{X}$ is not independent of mean availability (Supplementary Fig. 21). Nevertheless, perturbation effects of a given genomic region are stronger when perturbing their matched genes compared to random genes (Supplementary Fig. 20). We further observed instances of high $\Delta \hat{X}$ in absence of HiChIP signal (Fig. 6). While these might be false positives driven by noise in the scATAC data, it is possible that multiDGD could be capturing indirect effects of gene expression on accessibility.

Finally, we sought to leverage in silico predictions with multiDGD to investigate the correspondence between the expression of transcription factors (TFs) and their effect on accessibility of peaks containing their DNA binding motifs. We tested the effect of silencing 41 TFs on chromatin accessibility, using a categorization of ‘activators’ or ‘repressors’ from Gene Ontology (GO) terms⁴¹. When measuring the perturbation effects at peaks containing TF binding motifs, we found that silencing activator TFs tends to lead to significantly higher fractions of closing peaks compared to silencing of annotated repressors (Fig. 7A). For 36 out of 41 TF perturbations, we found a significant difference in mean $\Delta \hat{X}$ between peaks containing TF binding motifs and matched random peaks (T-test p-value  < 0.01). However, we observe broad variation in perturbation effects for different TFs. We measure the strongest chromatin closing effects in response to silencing (indicating a positive correlation between accessibility and expression) for TFs with reported activation effects on a broad set of metabolic genes involved in stress response, including NRF1⁴² and HIF1A⁴³. For about one third of the TFs annotated as activators based on GO terms, we detected perturbation effects at TF binding peaks consistent with repressive activity (i.e. chromatin opening upon TF silencing), in line with the observations in ⁴¹. In several cases these discrepancies could be explained by conflicting GO terms, where the same TF is reported to have both activator and repressor function in different cellular contexts (e.g. ELF4⁴⁴, IRF1⁴⁵, POU2F1-2⁴⁶). We frequently observe perturbation changes in both directions for this class of TFs, with mean $\Delta \hat{X}$ varying between cell types (Supplementary Fig. 22B). PBX1, for example, is generally regarded as a transcriptional activator in the context of cancer, but can play a dual role in hematopoiesis⁴⁷. In our data this factor is specifically expressed in HSCs and erythroid progenitors (Supplementary Fig. 22A). While its in silico silencing leads to chromatin closing in most cell types, we predict chromatin activation in HSCs and granulocytic-myeloid progenitors (G/M prog, GMP). This is in line with evidence from mouse studies suggesting that PBX1 KO leads to premature derepression of GMP transcripts in myeloid progenitors⁴⁷. These results further support the idea that multiDGD is learning cell-type-specific patterns of regulation and that coupling the generative model with in silico perturbation can be used to interpret the interplay between molecular features in cells.

Fig. 7: Prediction of association between gene expression and peak accessibility of transcription factors.

A Violin plots of fractions of closing peaks (∆X < 0) for in silico silencing of transcription factors (TFs) annotated as activators (red, 32895 cells, 34 TFs) or repressors (blue, 7226 cells, 7 TFs). The black box and white point denote the interquartile range and median of the distribution, respectively. The p-value for a two-sided 2-sample T-test comparing the mean of the distributions is shown on top. B Mean ∆X in response to TF silencing for 34 predicted activators and 7 annotated repressors. We show the mean effect for all affected cells over a set of 10,000 peaks containing TF binding motifs (red points) or over a set of 10,000 peaks sampled at random amongst the peaks containing at least one TF binding motif (gray points) with the standard error of the mean. Asterisks denote TF perturbations for which the difference in mean effect between TF binding peaks and random peaks is significant (two-sided 2-sample T-test p-value < 0.01). All values are provided in the Source Data.

Discussion

We present multiDGD, a novel generative model for single-cell multi-omics data. We demonstrate its use as a tool for dimensionality reduction and cross-modality prediction, but also new functionalities. Firstly, it enables the integrated modeling of unseen batches without the need for fine-tuning methods such as scArches²⁸. Secondly, it contains a built-in analysis of gene-peak associations. This is possible due to the emergent properties of generative models, which enable us to combine integration and analysis of data in a single framework. We have thus focused on comparing to existing generative models for multi-omics data^8,11,20 in this work. Among these, however, only MultiVI provides functionalities such as batch effect removal, which is critical for our analysis. We show that multiDGD presents a strong improvement compared to MultiVI⁸, which is based on VAEs and presents a popular generative model architecture used in single-cell analysis. Our model outperforms MultiVI in terms of data reconstruction, cross-modality prediction, and cell type clustering (if labels are given). Part of the performance increase in modeling ATAC data may be due to the use of raw counts rather than binarised data, preserving more information⁴⁸. However, we attribute much of the general performance increase in comparison to MultiVI to the more complex latent distribution and the removal of the encoder. The performance increase in modeling RNA and ATAC counts can also be seen in the prediction of unseen cells and of missing modalities, although the variance in prediction performance is higher for multiDGD. One potential reason for this could be the over-denoising in MultiVI, which would also contribute to generally lower performance.

Even though multiDGD also outperforms the Leiden algorithm on MultiVI latent dimensions in terms of cell type clustering and learns meaningful embeddings, sampling from the prior over component means in the initialization leads to a high variance in clustering performance. We are eager to investigate how to stabilize this behavior. Potential directions are to initialize the component means from origin as well or to re-sample representations during training to avoid local minima.

As single-cell multi-omics profiling becomes more robust and accessible, models for analysis will need to efficiently handle multi-sample data sets. They will further have to be able to disentangle technical batch effects from biological differences between cell types. We have introduced probabilistic modeling of covariates for the DGD. Probabilistic modeling of covariates improves basal representations, successfully captures interpretable sample-specific differences, and enables the integration of unseen data from different categories without architectural surgery. We have demonstrated this application and show that multiDGD can easily predict an unseen covariate with nearly the same performance as if it had been trained on it, but without any fine-tuning. We believe this feature will facilitate the construction and re-use of large multi-omics atlases.

Multi-omics data sets, however, are often still small compared to scRNA-seq data sets¹. The number of genomic peaks frequently outnumbers the amount of sequenced cells. Here we show that multiDGD shows clear advantages in modeling small data sets with high-dimensional spaces compared to data-hungry VAEs. We envision these capabilities will be of great value in allowing us to consider genome-wide epigenetic profiles for targeted analyses of data subsets of interest, such as specific lineages.

The goals of multi-omics analysis of course go way beyond efficient and high-quality embedding of cells. What is really desired is to further our understanding of gene regulation. Since we can incorporate larger decoders in multiDGD compared to VAE-based methods, explaining non-linear relationships may become easier. The resulting reconstruction performance increase certainly enables more reliable analysis at the feature level. We made use of this in the prediction of gene-peak associations based on in silico perturbations. Genetic modulators of chromatin accessibility can be found experimentally through gene knockouts⁴⁹, which could be strongly accelerated by predictions of promising candidates. We demonstrated meaningful associations in proximal interactions around 2073 highly variable genes (Fig. 6B, Supplementary Fig. 20) and distal interactions with 3 genes with experimentally validated enhancers (Fig. 6C, D). Additionally, we showed that the model can capture the effect of activating and repressing 41 transcription factors at DNA binding sites (Fig. 6E, F). We recognize that at the current state, this gene-peak linkage prediction is a proof of concept, with several open questions to be investigated. For example, the extent by which multiDGD captures direct or secondary interactions remains to be determined, and whether different types of association can be distinguished. Further investigation is also needed to determine whether the magnitude of perturbation changes is meaningful. Nevertheless, our results emphasize the potential of generative models as tools to capture interactions between molecular layers.

Altogether, multiDGD provides a strong performance increase on data reconstruction, incorporates modeling of covariates, and provides a unified framework for integration and analysis of genomic features. We see this as a significant next step in the evolution of single-cell multi-omics modeling.

Methods

Data

This work makes use of single-cell multiome data sets from human bone marrow, human brain tissue and mouse gastrulation stages.

Acquisition

The human bone marrow multiome data set from ref. ¹² was downloaded from NCBI GEO⁵⁰ under accession GSE194122 on September 12, 2022. For human brain data, we used the annotated data from ref. ³³. The annotated mouse gastrulation set used was taken from ref. ³⁴.

Preprocessing

Human bone marrow data was used directly without any preprocessing. It comprises counts for 13431 gene transcripts and 116490 chromatin accessibility peaks. The 69249 cells represent 22 different cell types and were sequenced at four different sites. The sites are here interpreted as different batches.

The raw human brain counts were collected into an AnnData object according to 10X HDF5 Feature Barcode Matrix Format. This data set contains 3534 cells with a total of 274892 features. We performed feature selection by excluding features that were not present (meaning counts of zero) in at least one percent of all cells. The result was 15172 transcripts and 95677 peaks. For cell type annotation, we chose the ATAC cell type annotation with 16 different types. From this data, we used no batch annotation.

For the mouse gastrulation data, we again performed feature selection based on the percentage of cells. The original number of features were 32285 for transcripts and 192251 for peaks. We excluded features that were only present in five percent of the cells and arrived at 11792 gene expression features and 69862 chromatin accessibility features. The total number of cells in this data is 56861 with 37 different cell types. This data contains a temporal component and thus makes the definition of batches more difficult. Nevertheless, we chose the gastrulation stage as the batch and expect this variable to only be partially removed from the latent representation as cell type appearance is not independent of the stage.

Feature selection is not homogenous due to the differences in data sources. The human bone marrow data was already preprocessed. The processing scheme for the remaining two raw datasets were chosen in such a way that they resulted in similar ranges of features. Additionally, the high thresholds chosen allows for evaluating MultiVI and multiDGD in terms of feature efficiency due to the large difference between the number of features before and after filtering. Additionally, the use of differently processed datasets presents a valuable test of multiDGD’s general applicability. An overview of all dataset sizes is given in Table 1.

Table 1 Summary of datasets used in this work

Data splits

In order to adequately compare model performances across methods and random seeds, we created data splits for training, validation and testing. All three data sets were split into a train set comprising 80% of the samples and validation and held-out test sets with 10% of the samples each. The splits were generated by randomly selecting samples stratified by the cell type compositions; i.e. each data split contains the same ratios of cell types.

The model

multiDGD is an extension of the Deep Generative Decoder (DGD)¹⁸ for single-cell multiomics data. The core model consists of a decoder and a parameterized distribution over latent space. This is presented by a Gaussian Mixture Model (GMM) here. Since there is no encoder, inference of latent representations is achieved by learning representations as trainable parameters. This process is described in detail in ref. ¹⁸. multiDGD additionally offers the option of disentangled covariate representations. For this purpose, multiDGD learns not only a set of representations Z and distribution parameters ϕ, but also ${Z}^{{{{{\rm{cov}}}}}_{v}}$ and ${\phi }^{{{{{\rm{cov}}}}}_{v}}$ for every vth covariate. The corresponding graphical model is depicted in Supplementary Fig. 1. The following sections will describe the model and associated processes in more detail.

Relevant notation

See Table 2.

Table 2 Summary of relevant symbols used to describe the DGD

Probabilistic formulation

The training objective is given by the joint probability p(X, Z, θ, ϕ)¹⁸, which is maximized using Maximum a Posteriori estimation¹⁸. This can be decomposed into:

$$p(X,Z,\theta,\phi )=p(X| Z,\theta )\,p(Z| \phi )$$

(1)

p(X∣Z, θ) in this model is presented as the Negative Binomial distribution’s mass of the observed count x_i for cell i given the predicted mean count and a learned dispersion parameter r_j for each feature j

$$p({x}_{i}| {z}_{i},\theta,{s}_{i})={\prod}_{j=1}^{D}p({x}_{ij}| {z}_{i},\theta,{s}_{i})$$

(2)

and

$$p({x}_{ij}| {z}_{i},\theta,{s}_{i})={{{\mathcal{NB}}}}({x}_{ij}| {s}_{i}{y}_{ij},{r}_{j}),$$

(3)

where ${{{\mathcal{NB}}}}(x| y,r)$ is the Negative Binomial distribution. Here we calculate the probability mass of the observed count x_i,j given the negative binomial distribution with mean s_iy_i,j and dispersion factor r_j. The predicted mean s_iy_i,j is given by the modality-specific total count s_i of cell i and the decoder output y_i,j. This output y_i,j describes the fraction of counts for cell i and modality-specific feature j, i.e. the predicted normalized count. These equations are valid for each modality (RNA and ATAC) separately, as we have a total count S per modality.

The joint probability p(X, Z, θ, ϕ) that is maximized in the DGD¹⁸ further contains the objective for the representation to follow the latent distribution, p(Z∣ϕ). Since ϕ is a GMM, this results in the weighted multivariate Gaussian probability density

$$p({z}_{i}| \phi )={\sum}_{k=1}^{K}{\pi }_{k}{{{{\mathcal{N}}}}}_{L}({z}_{i}| {\mu }_{k},{\Sigma }_{k})$$

(4)

with K as the number of GMM components and ${{{{\mathcal{N}}}}}_{L}({z}_{i}| \mu,\Sigma )$ as a multivariate Gaussian distribution with dimension l (the latent dimension), mean vector μ and covariance matrix Σ.

For new data points the representation is found by maximizing p(x_i∣z_i, θ, s)p(z_i∣ϕ) only with respect to z_i, as all other model parameters are fixed. More of this in a later section.

Architecture

Decoder

The decoder in multiDGD is of hierarchical nature and will here be described in two sections: the shared network θ^h from latent space Z to the hidden state H, and the modality-specific networks ${\theta }^{{{{\rm{mod}}}}}$ from H to their respective data spaces ${X}^{{{{\rm{mod}}}}}$. All layers in the networks consist of a linear layer followed by Rectified Linear Unit (ReLU) activation, except for the last layer in θ^mod. The widths and depths of the networks are defined by hyperparameters. The activation of the last layer in ${\theta }^{{{{\rm{mod}}}}}$ depends on the type of count scaling applied. Per default, the predicted normalized count means ${y}^{{{{\rm{mod}}}}}$ are scaled with the count depth ${s}^{{{{\rm{mod}}}}}$. The count depth presents the sum of all counts per modality. In this case, the predicted count means are achieved through softmax⁵¹ activation of ${y}^{{{{\rm{mod}}}}}$. The probabilistic modeling of the counts and the corresponding objective function are described in the following section.

Count modeling

In multiDGD, counts of both gene expression and chromatin accessibility are modeled with Negative Binomial distributions (see Equation (3)). For probabilistic modeling of outputs, we include ‘output modules` which entail additional learned parameters and loss functions matching the probability distribution used. For the Negative Binomial output module, the necessary additional parameters are the feature-specific dispersion factors r. For each feature in a given modality, we learn a dispersion factor to describe the shape of this individual feature’s distribution. The loss function in this module is given by the negative log probability mass function of the Negative Binomial given an observed count. This provides us with the reconstruction loss of the given modality.

$${{{{\rm{Loss}}}}}_{{{{{\rm{recon}}}}}_{i}}^{{{{\rm{mod}}}}}=-{\sum}_{j=1}^{M}\log {{{\mathcal{NB}}}}({x}_{i}^{\,j}| {\hat{x}}_{i}^{\,j},{r}^{\,j})$$

(5)

GMM (basal)

The Gaussian Mixture Model (GMM) presents the complex distribution over latent space in this model. It is a parameterized distribution which determines the shape of the latent space and is optimized in parallel to decoder and representation during training. The GMM consists of a set of K multivariate Gaussians with the same dimensionality as the corresponding representation. For the purpose of simplicity, we let multiDGD choose K based on the number of unique annotated cell types. This parameter is of course flexible and allows for tailored latent spaces depending on the desired clustering resolution. The objective for the representations is given as

$${{{{\rm{Loss}}}}}_{{{{{\rm{rep}}}}}_{i}}^{{{{\rm{basal}}}}}=-\log p({z}_{i}| \phi )=-\log {\sum}_{k=1}^{K}{\pi }_{k}{{{{\mathcal{N}}}}}_{l}({z}_{i}| {\mu }_{k},{\Sigma }_{k})$$

(6)

Trainable parameters include the means μ and covariances Σ of the components and the mixture coefficients w, which are transformed into mixture weights π through the softmax function. These parameters are in turn also learned with respective priors introduced in ref. ¹⁸. The means μ follow the softball prior¹⁸ similar to a mollified Uniform. Weights w are described by a Dirichlet prior as is common in Bayesian Inference. Empirically, variances of Gaussian distributions follow the inverse Gamma distribution. As a result, the negative log covariance can be approximated by a Gaussian. The composition of the prior loss is thus given as follows.

$${{{{\rm{Loss}}}}}_{{{{\rm{prior}}}}}^{{{{\rm{basal}}}}}= -\log p(\phi )=-\log p(\mu,w \,,-\log \Sigma )\\=\, -\log \left(p(\mu )\,p(w)\,p(-\log \Sigma )\right)$$

(7)

$$p(\mu )=\, \prod\limits_{k}{p}_{{{{\rm{Softball}}}}}({\mu }_{k}| {{{\rm{scale}}}},{{{\rm{sharpness}}}})\\ p(w)=\, \prod\limits_{k}{{{\rm{Dir}}}}({\mu }_{k}| \alpha )\\ p(-\log \Sigma )=\, \prod\limits_{k}\prod\limits_{l}{{{\mathcal{N}}}}\left(-\log {\Sigma }_{k,l}| -\log 0.2\times \frac{scale}{K},1\right)$$

(8)

Altogether, these losses form the objective for both the representations and the GMM and will be referenced as the latent loss

$${{{{\rm{Loss}}}}}_{{{{\rm{latent}}}}}^{{{{\rm{basal}}}}}={\sum}_{i}^{N}{{{{\rm{Loss}}}}}_{{{{{\rm{rep}}}}}_{i}}^{{{{\rm{basal}}}}}+{{{{\rm{Loss}}}}}_{{{{\rm{prior}}}}}^{{{{\rm{basal}}}}}$$

(9)

Supervised GMM (covariate)

The difference between the GMM for the basal latent space and the covariate space is merely the training scheme. As mentioned above, training for covariate representation and GMM is supervised. This results in a change in the objective as only probability densities of components assigned to a sample’s label are taken into account.

$${{{{\rm{Loss}}}}}_{{{{{\rm{rep}}}}}_{i}}^{{{{\rm{cov}}}}}=-\log p({z}_{i}| \phi,{c}_{i})=-\log {{{{\mathcal{N}}}}}_{l}({z}_{i}| {\mu }_{k={c}_{i}},{\Sigma }_{k={c}_{i}})$$

(10)

This means that the conditional probability p(z_i∣ϕ) is solely dependent on the component with index identical to the numerical label c_i ∈ 0, …, C with C as the number of unique covariate labels.

Representations

Representations are treated as trainable parameters. However, they formally do not belong to the model architecture since they represent the low-dimensional embedding of data.

Representation (basal)

For each sample x_i with i ∈ N, there exists one representation z_i. The basal representations Z ^basal represent the main embedding of data X, which aims to model the desired biological attributes of the data in low-dimensional space. As this structuring is unknown, Z ^basal is inferred in an unsupervised setting. As described in ref. ¹⁸, the representations are updated once per epoch with the gradients derived from reconstruction and distribution losses.

Representation (covariate)

Covariates represent experimental variables we wish not to influence Z ^basal. In order to separate these influences, we model these attributes in distinct two-dimensional spaces Z ^cov. Here, it is necessary to follow a supervised training approach for successful disentanglement. This process is described in the corresponding section for the covariate GMM.

Initialization and default parameters

The decoder contains two layers in the shared network and two in the modality-specific ones. All layers except the last one in modality-specific networks have 100 hidden units (layer_width). The last layer in a modality-specific network receives $\max({{{\rm{layer}}}}\_{{{\rm{width}}}},\sqrt{{M}^{{{{\rm{mod}}}}}})$ hidden units. M refers to the number of data features. Depth and width hyperparameters can of course be altered and should be considered depending on the number of samples and features available. Weights and biases are initialized per default using PyTorch’s Kaiming Uniform⁵² method. In the Negative Binomial output module, dispersion parameters are initialized with a default value of 2.

Representations are generally initialized at origin, meaning they all start from zero vectors. One could also initialize from a pre-defined matrix, for example an l-dimensional Principal Component Analysis (PCA) or sampling from the prior. However, linear mappings are not always representative of the true underlying structure. In the default settings, the latent dimensionality l is set to 20, and covariate representations receive two dimensions.

The GMM is generally initialized with Softball prior scale 2 and hardness 5 and a Dirichlet α of 1. The prior over the covariance matrix Σ is defined by the number of mixture components as in ref. ¹⁸ with $0.2\times \frac{{{{\rm{scale}}}}}{K}$. The default GMM contains a single Gaussian. This setting is used if no ‘observable-key’ is provided for the basal latent space in model initialization. However, we do recommend to use cell type annotations or predictions as this will increase the flexibility and complexity of the basal representation and will provide an intrinsic clustering of the model. If an observable is given, the number of unique classes will be used as the number of components in the basal GMM ϕ. For the covariate GMM ϕ^cov, the number of components is equal to the number of unique categories in the covariate.

Training

The general training algorithm remains as presented in¹⁸, with an extension due to the covariate latent model and presence of multiple modalities (Box 1).

The training data is iterated over in mini batches with a default batch size of 128. Each set of parameters receives their on Adam⁵³ optimizer with betas (0.5, 0.7) and learning rates of 1e − 4 for the decoder and 1e − 2 for representations and GMMs. As a proxy for the prior over θ, a weight decay of 1e − 4 is applied. The default maximum number of epochs is set to 1000, with early stopping applied at the earliest in epoch 50, taking into account the last 10 epochs.

The loss is presented as

$$-\log p(x,z,\phi,\theta )={\sum}_{{{{\rm{mod}}}}}{{{{\rm{Loss}}}}}_{{{{\rm{recon}}}}}^{{{{\rm{mod}}}}}+{{{{\rm{Loss}}}}}_{{{{\rm{rep}}}}}^{{{{\rm{basal}}}}}+{\sum}_{cov}{{{{\rm{Loss}}}}}_{{{{\rm{rep}}}}}^{{{{\rm{cov}}}}}+{{{{\rm{Loss}}}}}_{{{{\rm{prior}}}}}$$

(11)

Positive definite parameters such as the Negative Binomial dispersion factors and the GMM covariances are learned as their logarithmic counterparts for numerical stability and enforcing the positive constraint.

Validation

Validation is performed in parallel to training. Representations for the validation set are equally initialized at origin and optimized every epoch. In the validation loop, only the representation parameters of the validation set are updated, and covariate representations are inferred in an unsupervised manner.

Testing and prediction of new data

With testing and predicting, we refer to the inference stages after the model parameters θ and ϕ have been trained and are regarded as frozen. Firstly, the best mode (i.e. GMM component) is found for each new sample X. The best mode is given by the maximization of p(x∣z, θ, ϕ)∏_kp(z ∣ ϕ_k) with respect to k. This step is the memory-critical process as for each new data point X_m with m ∈ M, K losses have to be computed. In the case of present covariate models, this problem becomes combinatorial. In total, $M\times K\times {\prod }_{q=1}^{Q}{C}_{q}$ losses have to be computed, with C_q representing the number of covariate classes for covariate q.

After the best modes have been determined, the representations Z_m are optimized for a set number of steps, per default 10. This process is very fast and negligible compared to the total run time as long as the number of cells is in the thousands¹⁸.

Integrating unseen covariates (naive)

Because the covariate models are probabilistic, the method for integrating unseen covariate classes presented here works just like predicting new data. The unobserved covariate label might not have received its own distribution, but the model is capable to find the best covariate representation given its prior knowledge. One could see this as the unseen class being determined as a linear combination of the observed ones.

Integrating unseen covariates by modeling a new covariate component (supervised)

There is also the option of inferring an additional GMM component alongside the new covariate label. This is done by initializing a new GMM with as many additional components as novel covariate classes. In this work, it is limited to one additional component. The new number of components is then C + 1. The first C components of the new GMM receive the means and covariates from the trained GMM and are frozen (i.e. fixed and cannot be changed). As a result, only the last and new component will be inferred. This is again achieved by supervised learning of the test samples given their covariate labels, where we ensure that the novel GMM component ID and novel covariate class numeric label match.

Missing modality prediction

We again start from a trained model with all internal parameters (decoder and GMM) fixed. For the new samples, representations are initialized as described above. The only change to the simple data inference is that only the loss of the observed modality is used to infer representations. After inference, the predictions for all features are generated, so we get a completed picture of the sample.

Internal clustering

The GMM is naturally equipped to cluster sample representations. Part of the objective calculation is to get a K-length vector for every representation containing the probability densities of said representation under each component k ∈ K. The ${{{\rm{argmax}}}}$ of this vector returns the index of the component with highest probability.

Gene-to-peak association with in silico perturbation

Figure 6A depicts the mechanism of the gene2peak feature of multiDGD. Intuitively, we associate features to each other across modalities by predicting the effect of silencing a given gene or set of genes X^j∈RNA on the reconstructed peak accessibility profiles ${\hat{X}}^{i\in {{{\rm{ATAC}}}}}$. To simulate the effect of silencing gene j on chromatin accessibility, we consider cells in which X^j∈RNA > 0. Then for each cell i we generate a pseudo-expression profile X_KO where ${X}_{{{{\rm{KO}}}}}^{j\in {{{\rm{RNA}}}}}=0$. In order to predict the downstream affects of this perturbation, we need to compute the basal representations of the changed state ${Z}_{{{{\rm{KO}}}}}^{{{{\rm{basal}}}}}$. We therefore compute the loss for only perturbed features ${X}_{{{{\rm{KO}}}}}^{j\in {{{\rm{RNA}}}}}$ and backpropagate it to get a gradient pointing from Z ^basal to ${Z}_{{{{\rm{KO}}}}}^{{{{\rm{basal}}}}}$. As a result, we have the original representation Z ^basal and the perturbed representation ${Z}_{{{{\rm{KO}}}}}^{{{{\rm{basal}}}}}$. From these, $\hat{X}$ and ${\hat{X}}_{{{{\rm{KO}}}}}$ are predicted, and the perturbation changes $\Delta \hat{X}$ are computed as $\Delta \hat{X}=\hat{X}-{\hat{X}}_{{{{\rm{KO}}}}}$.

Box 1 Simplified algorithm of multiDGD’s training procedure

Model search

Hyperparameter optimization

Architectures and training parameters can vary strongly in both VAE and DGD. For a comparison of tools rather than Machine Learning methods, we chose the default settings for both MultiVI and multiDGD. The default settings for multiDGD are derived from design knowledge gained in ref. ¹⁸. Additional parameters such as model depth of the hierarchical DGD were found experimentally. The final default parameters are described in the section above. MultiVI models were trained with one, two and three layers in the encoder and decoder each. The best architecture was chosen for each individual data set. multiDGD does not have an encoder, but shared and modality-specific networks. We tested different depths of one to three layers for the shared and modality-specific feed-forward networks. A summary of our parameter search can be found in Supplementary Fig. 2.

Training

For each of the data sets included in this work, we train three instances of each method with random seeds 0, 37 and 8790.

Model selection

For each data set, the best model from hyperparameter optimization was chosen based on the validation loss. This refers to the negative log density for multiDGD and the ELBO for MultiVI.

Benchmark models

We compared the performance of our method to MultiVI⁸, Cobolt¹¹, and scMM²⁰ when direct comparison was possible. All three models are VAE-based methods, and we used their default parameters except for the latent dimensionality. Here, we set it to 20 for all models in order to achieve comparable embeddings. See ‘Software and Hardware’ for the package versions of all three methods used.

Performance evaluation

Reconstruction

Reconstruction performance metrics were chosen based on their compatibility for both MultiVI and multiDGD. Expression count reconstructions could be compared directly as both methods model the counts with Negative Binomial distributions. We thus report RMSE and MAE of the test predictions.

$${{{\rm{RMSE}}}}=\sqrt{\frac{1}{D\times N}{\sum }_{j=1}^{D}{\sum }_{i=1}^{N}{({x}_{ji}-{\hat{x}}_{ji})}^{2}}$$

(12)

Chromatin accessibility is modeled differently in the two approaches. While multiDGD uses Negative Binomials, MultiVI models the peak counts as probabilities of being open. We thus binarize the observed counts and calculate the area under the precision-recall curve (AUPRC). It is a sensible metric for imbalanced data.

Clustering

multiDGD can naturally cluster samples based on the probabilities of the GMM components for a given representation. This is not possible with MultiVI’s standard Gaussian prior, so it is common practice to perform Leiden³⁸ clustering on the latent space. We compare GMM and Leiden clustering through the Adjusted Rand Index (ARI) with respect to the cell type annotations. For a fair comparison, we adjust the Leiden algorithm such that it results in a similar number of clusters as the DGD, which is based on the number of unique cell types in the data. For bone marrow and brain data, the default scanpy Leiden parameters were used. For the gastrulation set, the resolution was set to 2. The ARI is the adjusted-for-chance version of the Rand index, which is related to clustering accuracy. This metric takes values between zero and one, with one representing perfect clustering according to the reference.

Batch effect removal

The batch effect is measured as the Average Silhouette Width (ASW). It is given as

$${{{\rm{ASW}}}}=\, \frac{1}{N} {\sum}_{i}^{N}\frac{b(i)-a(i)}{\max \{a(i),b(i)\}}\\ {{{\rm{with}}}}\,a(i)=\, \frac{1}{| {C}_{I}| -1}\sum\limits_{j\in {C}_{I},\,j\ne i}d(i,j)\\ {{{\rm{and}}}}\,b(i)=\, {\min }_{J\ne I}\frac{1}{| {C}_{I}| }\sum\limits_{j\in {C}_{I}}d(i,j)$$

(13)

a(i) presents the mean distance between point i and all other points belonging to the same cluster. d(i, j) is the distance between points i and j. b(i) is the smallest mean distance of i to all points belonging to different clusters. This metric ranges between minus one and one. A value of one indicates a perfect clustering and a value of minus one indicates that samples would better fit into other clusters. For interpretability, we report 1 − ASW as the batch effect removal metric, where larger values indicate better performance.

Data efficiency

In order to test model data efficiency, we created subsets of the largest data set in our study, with 1, 10, 25, 50 and 75% of the training data. We trained both multiDGD and MultiVI instances on all these subsets with the hyperparameters determined for the full set and for the same three random seeds 0, 37, and 8790 as before. The performance of models on the subset is evaluated by the relative test losses, which we refer to as test loss ratios $\frac{1}{N}\mathop{\sum }_{i}^{N}\frac{{{{{\rm{Loss}}}}}_{i}^{{{{\rm{trained}}}}\,{{{\rm{on}}}}\,{{{\rm{subset}}}}}}{{{{{\rm{Loss}}}}}_{i}^{{{{\rm{trained}}}}\,{{{\rm{on}}}}\,{{{\rm{full}}}}\,{{{\rm{set}}}}}}$ for every random seed.

Feature efficiency

For this experiment, we chose the mouse gastrulation data as it had previously been used with stringent feature selection and offered the most additional features of all three data sets. The data with feature selection (features that were present in at least five percent of cells) contained 11792 genes and 69862 peaks. The full data set with all measured features is comprised of 32285 genes and 192251 peaks. We trained instances for both multiDGD and MultiVI on the full data set with random seed 0.

In order to assess in what way training on all features affected the models’ performances, we evaluated the reconstruction performances of RNA and ATAC data on the features previously selected for training (‘5%‘).

Relative and predictive performance

Relative and predictive performances are measured as the mean ratio of prediction (or novel/comparative) error over reconstruction error $\frac{1}{N}\mathop{\sum }_{i}^{N}\frac{{{{{\rm{Loss}}}}}_{i}^{{{{\rm{pred}}}}/{{{\rm{recon1}}}}}}{{{{{\rm{Loss}}}}}_{i}^{{{{\rm{recon}}}}0}}$. Prediction refers to the data generation of the missing modality in the unpaired samples. Data generation of the original, paired samples is described as reconstruction. In relative performance, we compare the reconstruction performance of a novel or changed setting (recon1) to the original reconstruction performances (recon0).

Gene-peak association

All gene-peak association predictions were performed on the test set of the bone marrow data (6925 cells).

For the prediction of perturbation effects around transcription start sites (Fig. 6B), we selected a sample of highly variable genes in the RNA data for the test set, using the method implemented in scanpy. We then ran the in silico silencing for all the sampled genes and measured the mean perturbation effect on chromatin ($\Delta \hat{X}$) across all perturbed cells on peaks located within 10kb of the TSS of the silenced gene (using gene annotations from Ensembl v108). Of note, the mean perturbation effect across cells in TF binding sites is partially dependent on the total number of cells expressing the silenced gene in the test set (R² = 0.45, p-value = 0.0029), suggesting that the estimates for perturbation effects might be more reliable with more support data.

For validation of gene-peak association predictions in distal enhancers (Fig. 6C, D), we downloaded H3K27ac HiChIP data from primary T cells⁴⁰ from the Gene Expression Omnibus (GSE101498). Raw .hic files were converted to matrices of interaction signal between any two genomic bins of size 10kb using Juicebox tools⁵⁴, replicating the workflow and parameters described in⁵⁵. We then computed the mean enhancer interaction signal (EIS) between 2 replicate samples for naive CD4+ T cells and HCAMSC cells using as viewpoint the bins containing the promoter of the gene of interest. We calculated cell-type-specific gene-peak associations the absolute predicted change $| \mathop{\sum }_{i}^{| {{{\rm{idx}}}}(ct)| }\Delta {\hat{X}}_{{{{\rm{idx}}}}(ct)}|$ where ct stands for cell type and idx(ct) is the subset of the indices for this cell type. We evaluate the ability to recover enhancer-gene interactions from HiChIP data with ROC curve analysis, where we consider a genomic bin to be an enhancer region if the EIS is higher than the 75% quantile computed over the whole locus.

For the TF perturbation analysis (Fig. 7), we considered a list of transcription factors annotated as activators or repressors based on mining GO terms⁴¹. We identified peaks containing TF binding motifs using the JASPAR database (release 2022). We then restricted our analysis to TFs which had matches in less than 80% of all peaks and that were expressed in at least 250 cells in the test set. We computed $\Delta \hat{X}$ for silencing of each TF and computed the mean $\Delta \hat{X}$ across 10k peaks sampled amongst the peaks containing TF binding motifs, and across 10k peaks sampled amongst all peaks containing at least one TF binding motif. This strategy to select the null ‘random’ set was used to exclude peaks with extremely sparse counts at distal intergenic locations, which might represent an unfair comparison for this analysis.

Visualization

We applied UMAP⁵⁶ to dimensionality reductions used in visualizations.

Reproducibility

Our results, including figures, can be produced by utilizing the code available on GitHub (https://github.com/Center-for-Health-Data-Science/multiDGD_paper) and the processed data and trained models available on Figshare (https://doi.org/10.6084/m9.figshare.23796198.v1).

Software and hardware

All code is written in Python (version ≥ 3.9.12) and executed on a cluster with x86_64 architecture and NVIDIA TITAN RTX and NVIDIA TITAN X GPUs. The machine learning framework used was PyTorch⁵⁷ version 1.10. Training progress was monitored and logged using weights and biases (wandb)⁵⁸. MultiVI was used as part of the scvi-tools⁵⁹ package with version 0.19.0. For Cobolt and scMM, we applied version v1.0.1 and release 1, respectively. The scanpy⁶⁰ package was used for parts of the analysis.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.