Introduction

The recent surge of research in non-Hermitian physics1,2,3,4,5,6 has uncovered a wide array of phenomena that transcend the realm of traditional Hermitian systems. Non-Hermitian systems exhibit a remarkable sensitivity to their boundary conditions, exemplified by the non-Hermitian skin effect (NHSE)7,8,9,10,11,12,13,14,15,16,17,18. Featured by the gathering of a significant number of eigenstates at system boundaries, the NHSE breaks the extended Bloch-wave behaviors and challenges the conventional notion of bulk-edge correspondence by displaying distinct spectral shapes under periodic and open boundary conditions19,20,21,22,23,24. In addition to the skin effect, the interplay between non-Hermiticity and spatial inhomogeneity, such as domain walls, disorders, or impurities/defects, offers intriguing insights into wave behaviors and introduces additional richness to localization phenomena in generic non-Hermitian systems. They include impurity-induced topological bound states25,26, non-Hermitian quasi-crystals27,28, and the counterintuitive accumulation of eigenstates known as scale-free localization29,30,31,32,33,34, where eigenstates concentrate near defects while the localization length scales with the entire system size. Electric circuits22,35,36,37,38 offer a powerful platform for simulating various lattice models, where the lattice Hamiltonian is represented by an adjacency matrix that adheres to Kirchhoff’s law in current networks. Non-reciprocity can be modeled using active devices39, facilitating the realization of the NHSE in topolectric circuits21. The key asymmetric element is implemented using a negative impedance converter through current inversion, known as the INIC device.

The skin localization and the remarkable spectral sensitivity have been harnessed for innovative functionalities such as optical funneling40, high-precision sensor devices35,41,42, and optomechanically induced transparency43. Yet, the collective localization of all eigenstates inherent in the NHSE poses the challenging task of engineering a uniform distribution of spatial non-Hermiticity across the entire system. Furthermore, it restricts the tunable freedom of wave dynamics, such as localization length, position, and proportion of eigenstates. The pivotal question is: Can we precisely tailor wave localization in a controllable manner within generic lattice systems?

In this work, we uncover a novel type of localization of eigenstates, termed scale-tailored localization (STL) (See Table 1). Unlike Anderson localization resulting from wave interference or NHSE arising from intrinsic point gaps10,11,17, STL emerges due to the presence of long-range asymmetric coupling, giving rise to localized modes with distinctive characteristics: both their number and localization length scale exclusively with the coupling range. Consequently, the energy spectra are partitioned into two distinct sectors: point- (or arc-) shaped spectra corresponding to modes barely affected by the long-range coupling, and loop-shaped spectra associated with the scale-tailored localized states. This is in stark contrast to the NHSE, where skin localization requires a uniform distribution of non-Hermiticity (e.g., gain/loss or nonreciprocity) across the entire lattice, and the skin depths of the eigenstates are fixed and governed by the non-Bloch band theory7,9. From a practical standpoint, STL customizes wave localization without the complexity of a full-scale implementation of non-Hermiticity. The scale-tailored localized modes, unlike the scale-free localized modes induced by local non-Hermiticity31,32,33, exhibit resilience in the thermodynamic limit.

Table 1 Comparison of four distinct wave-localization phenomena based on localization length, position, physical origin, and fate in the thermodynamic limit
Full size table

In our setup, we implement a unidirectional electrical circuit with a rolled boundary condition controlled by electric switches, where unidirectional coupling is achieved through a simplified version of active devices, the voltage followers (VFs)34. The scale-tailored localized modes can be transformed into skin modes or vice versa with the changing of the asymmetric coupling range, accompanied by the self-adaptation of the localization length of all scale-tailored localized states. We then identify the STL by measuring the admittance spectra in the non-Hermitian electrical circuits. Our results indicate that long-range asymmetric coupling (non-Hermiticity) can serve as a powerful tool to manipulate wave localization and offer a feasible platform for exploring the intriguing properties of scale-tailored localized states.

Results

Scale-tailored localization

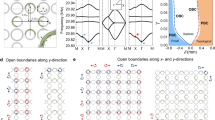
We start by introducing a minimal model that exhibits STL. It has unidirectional hoppings on a one-dimensional (1D) lattice with rolled boundary conditions, as depicted in Fig. 1a. The Hamiltonian for this model is expressed as:

$$\hat{H}={\sum}_{n=0}^{N-2}t{\hat{c}}_{n}^{{{\dagger}} }{\hat{c}}_{n+1}+t{\delta }_{t}{\hat{c}}_{N-1}^{{{\dagger}} }{\hat{c}}_{p}.$$
(1)

Here, N represents the length of the lattice. \({\hat{c}}_{n}^{{{\dagger}} }\) and \({\hat{c}}_{n}\) are the creation and annihilation operators on the n-th site. t is the strength of the unidirectional hopping between neighboring sites and set to be the energy unit t = 1 in the following. Our model features an additional long-range asymmetric hopping connecting the end site and the inner p-th site with coupling strength δt. The coupling range is l = N − p. The special case of p = 0 and δt = 1 or δt = 0 corresponds to the periodic or open boundary condition.

Fig. 1: Scale-tailored localization (STL) in the unidirectional hopping model.
figure 1

a Upper panel: Sketch of the lattice model with rolled boundary condition. Bottom panel: Different regimes (marked in different colors) of eigenstates’ localization with respect to the coupling strength δt. STL (inv. STL): the induced second-type eigenstates are localized on the left (right) boundary; Bloch: all second-type eigenstates are extended. b Eigenenergies for different combinations of (N, l) in the complex plane with δt = 0.1 (solid circles) or δt = 10 (empty diamonds). The cases of (N, l) = (40, 5), (40, 10), and (40, 20) are marked in red, purple, and pink, respectively. For reference, the black unit circle represents the spectra under periodic boundary conditions. c Spatial distributions of the second-type eigenstates for several typical values of δt with fixed (N, l) = (40, 20). d The perfect overlapping of rescaled spatial distributions by the coupling range l for different (N, l). e Rescaled spatial distributions by the total system size N with δt = 0.1 and l = 5.

Full size image

In the presence of the additional coupling, the eigenvalues and eigenstates of the system are

$$\left\{\begin{array}{l}E=z,\hfill \\ \left\vert \Psi \right\rangle={({\psi }_{0},{\psi }_{1},\cdots,{\psi }_{N-1})}^{T}={(1,z,\cdots,{z}^{N-1})}^{T},\hfill\end{array}\right.$$
(2)

with z given by the roots of the following equation:

$${z}^{p}\left({\delta }_{t}-{z}^{N-p}\right)=0.$$
(3)

The energy spectra are highly sensitive to the boundary conditions, as evident from the solutions. For periodic boundary conditions (δt = 1 and p = 0), the solutions are \({z}^{(m)}={e}^{i\frac{2\pi }{N}m}\) (m = 0, 1, . . . , N − 1), and all eigenstates are extended Bloch states. The eigenenergies are uniformly distributed on the unit circle. In contrast, for open boundary conditions (δt = 0), there exists a unique N-fold degenerate solution E = 0. All eigenstates coalesce into the state \(\left\vert \Psi \right\rangle={(1,0,...,0)}^{T}\) residing at the first site of the lattice. This degeneracy arises from N × N Jordan-block form of the Hamiltonian, which leads to an N-th order exceptional point (EP). In our subsequent studies, we focus on the more general cases with δt ≠ 0 and p ≠ 0. The solutions can be classified into two distinct types. The first type corresponds to a p-fold degenerate solution z = 0, representing a p-th order EP with eigenstates localized exclusively at the first site. The second type consists of l non-degenerate solutions given by \({z}^{(m)}=\root l \of {{{{\delta }_{t}}}{e}^{i{\theta }_{m}}}\), where \(m=1,2,\cdots \,,l,{\theta }_{m}=\frac{2\pi }{l}m\), and l is the number of rolled sites. Interestingly, the first-type solutions can be regarded as remnants of the N-th order EP, unaffected by the additional long-range coupling. In contrast, the second-type solutions result from such long-range coupling, with eigenenergies and wavefunctions given by:

$$\left\{\begin{array}{l}{E}_{m}=\root l \of {{\delta }_{t}}{e}^{i{\theta }_{m}},\hfill \\ \big\vert {\Psi }^{(m)}\big\rangle={\left(1,\root l \of {{\delta }_{t}}{e}^{i{\theta }_{m}},\cdots,{\left(\root l \of {{\delta }_{t}}{e}^{i{\theta }_{m}}\right)}^{N-1}\right)}^{T}.\hfill\end{array}\right.$$
(4)

These l eigenenergies are evenly distributed on a circle of radius \(\root l \of {{| {\delta }_{t}}| }\), dependent solely on the settings of the long-range coupling. The entire energy spectra are composed of both the isolated EP at the center and loop-shaped parts circling around, separated in the complex plane, as shown in Fig. 1b.

We proceed to examine the localization properties of the second-type eigenstates in Eq. (4). They have the same spatial profile but different site-dependent phase factors. The localization length ξ can be extracted from the spatial profile via \(| {\psi }_{n}^{(m)}| \sim {e}^{-\frac{| n-{n}_{0}| }{\xi }}\), with n0 the localization center. When the additional coupling is weaker than the unidirectional hopping ∣δt∣ < 1, all l states accumulate at n0 = 0 with localization length

$$\xi=-\frac{l}{\log | {\delta }_{t}| }.$$
(5)

If the coupling is stronger than the unidirectional hopping ∣δt∣ > 1, they accumulate at the last site n0 = N − 1 with localization length \(\xi=\frac{l}{\log | {\delta }_{t}| }\). Figure 1c illustrates the eigenstates’ profiles for several typical values of δt with fixed (N, l) = (40, 20). The more ∣δt∣ deviates from 1, the stronger the localization becomes. A duality exists between ∣δt∣ and \(| \frac{1}{{\delta }_{t}}|\) with equal localization length but opposite localization directions. At δt = 1, they become extended across the whole lattice. The different localization regimes of the second-type eigenstates are summarized in Fig. 1a.

The analysis above clearly indicates that even an infinitesimal long-range coupling can trigger eigenstates’ localization, underscoring its non-perturbative nature. Intriguingly, the localization length of the second-type eigenstates is directly proportional to the coupling range l and is irrelevant to the total system size N, which differs from the scale-free localization29,31,32,33. Upon rescaling these eigenstates by the coupling range, their spatial profiles become perfectly identical, as depicted in Fig. 1d. We refer to this type of accumulation as STL. The case ∣δt∣ > 1 is termed inverse STL due to the opposite localization direction. In comparison, Fig. 1e shows the eigenstates’ rescaling with respect to the total system N. In the thermodynamic limit, the scale-free localized modes become extensive, while the scale-tailored localized modes maintain a fixed and finite localization length.

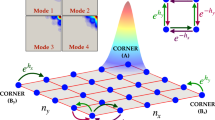
The mechanism and generality of STL

The STL exhibits unique characteristics that set it apart from other localization phenomena, as outlined in Table 1. Figure 2 sketches the physical mechanism of several typical localizations. In Anderson localized systems, the eigenstates have finite localization lengths due to wave interference in disordered media, impeding wave propagation. The non-Hermitian skin effect, scale-free localization, and STL are specific to non-Hermitian systems. For the skin effect, the skin modes are confined to the system boundary, with finite localization lengths governed by the generalized Brillouin zone. The skin effect accompanies spectral collapses from Bloch bands of periodic boundary conditions and requires the intrinsic point-gap topology or spectral winding. In contrast, the scale-free localization is the eigenstates’ accumulation near an impurity, with their localization length proportional to the system length, \(\xi \sim {{{\mathcal{O}}}}(N)\). In the simplest scenario, the presence of a local non-Hermitian impurity gives rise to an \({{{\mathcal{O}}}}(1/N)\) correction to the eigenspectra and eigenstates. In STL, the long-range coupling introduces a new length scale l. Heuristically, the long-range coupling can be treated as a non-local non-Hermitian impurity that generates closed paths within the one-dimensional lattice. The wave propagation at the junction (e.g., the p-th lattice site of the model (1)), satisfies a self-consistency condition f (zl, δt) = 0 (e.g., zl = δt in Eq. (3)). While the specific form of f (zl, δt) depends on model details, the self-consistency condition yields l states characterized by a localization length of \(\xi \sim 1/\log | z| \sim {{{\mathcal{O}}}}(l)\). The highly size-dependent spectral properties of the critical NHSE44,45 can be visualized from the extreme case of STL when l = N with N the system length.

Fig. 2: Schematics of several typical localization phenomena.
figure 2

a Anderson localization in disordered lattice resulting from wave interference. b Non-Hermitian skin modes localized at the system boundary due to nontrivial point gap. c Scale-free localization induced by a local non-Hermitian impurity. d Scale-tailored localization (STL) arising from long-range asymmetric coupling.

Full size image

While we have presented the simplest unidirectional coupling model for illustrative purposes, it is worth noting that the phenomenon of STL induced by long-range asymmetric coupling is expected to be quite general and applicable to other models as well, such as the Hatano-Nelson model and Hermitian lattice chain (details in Supplementary Sections I, II and Supplementary Figs. S1–S4). This holds true regardless of whether the original system possesses skin modes or not. Moreover, scale-tailored localized states can emerge both at the system boundary and in the vicinity of long-range impurities (details in Supplementary Section III and Supplementary Fig. S5). The STL persists in the presence of multiple long-range asymmetric couplings (details in Supplementary Section IV and Supplementary Figs. S6, S7). These couplings induce various scale-tailored eigenstates of different length scales. We have further verified the occurrence of STL in 2D (details in Supplementary Section V and Supplementary Figs. S8, S9) and in interacting systems46,47,48 (details in Supplementary Section VI and Supplementary Fig. S10). The presence of STL, which involves the reshaping of a fraction of the eigenspectra and eigenstates (scaling with the coupling range l), implies the potential for effectively manipulating wave localization by suitably tailoring the long-range couplings in the system.

Now, let us consider the most general case with lattice Hamiltonian

$$\hat{H}={\sum}_{n=0}^{N-j-1}\left[{\sum}_{j=1}^{{M}_{L}}{t}_{jL}{\hat{c}}_{n}^{{{\dagger}} }{\hat{c}}_{n+j}+{\sum}_{j=1}^{{M}_{R}}{t}_{jR}{\hat{c}}_{n+j}^{{{\dagger}} }{\hat{c}}_{n}\right]+{\delta }_{t}{\hat{c}}_{N-1}^{{{\dagger}} }{\hat{c}}_{p},$$
(6)

where tjL (tjR) represents the hopping towards the left (right) side, with the largest range being ML (MR). δt denotes the asymmetric coupling with range l = N − p. We can analytically solve the eigenspectra and eigenstates of Hamiltonian (6) and establish a general criterion for the occurrence of STL (details in the Methods, Supplementary Section II and Supplementary Figs. S3, S4). We take the Bloch spectra under periodic boundary conditions \(E={\sum}_{j=1}^{{M}_{R}}\frac{{t}_{jR}}{{z}^{j}}+{\sum }_{j=1}^{{M}_{L}}{t}_{jL}{z}^{j}\). For a given E inside the Bloch spectra, there exist M = MR + ML solutions zi(i = 1, ⋯  , M), which can be ordered by their moduli ∣z1∣ ≤ ∣z2∣ ≤ ⋯ ≤ ∣zM∣. Note that there must exist solutions with unit modulus because E is chosen from the Bloch spectra. If the (MR + 1)-th root has unit modulus:

$$| {z}_{{M}_{R}}| \, < \, | {z}_{{M}_{R}+1}|=1,$$
(7)

then there are l scale-tailored states when adding an asymmetric coupling.

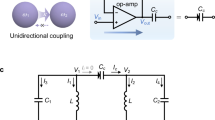
Unidirectional electrical circuit

We implement the unidirectional-hopping model using an electrical circuit that combines passive and active devices, as illustrated in Fig. 3a–c. Each unit cell in the circuit comprises an LC resonator with a capacitor C0 = 10pF (except for the last one with C3) and an inductor L = 220 μH, a VF, and a connecting capacitor C1 = 220pF which couples two neighboring nodes. To achieve the rolled boundary condition or the long-range coupling, we activate the p-th switch while leaving the other switches off. The coupling strength in the long bond is controlled by capacitor C2. The key element responsible for unidirectionality is the VF with mismatched input and output currents. This active device utilizes an operational amplifier (OpAmp) to replicate the input voltage at the output, as depicted in Fig. 3b. The voltage or current at the input and output ends satisfy the relation:

$${V}_{\!\!{{{\rm{out}}}}}={V}_{\!\!{{{\rm{in}}}}},\quad {I}_{{{{\rm{in}}}}}=0.$$
(8)
Fig. 3: Implementation of unidirectional electrical circuit and observation of STL.
figure 3

a Experimental design of the unidirectional circuit array. Each unit cell consists of an LC resonator with a capacitor C0 = 10pF and an inductor L = 220 μH, a VF, and a connecting capacitor C1 = 220pF. b VF as the active device with mismatched input and output currents. c The fabricated circuit board with 20 unit cells. The long-range coupling is controlled by electrical switches. d Eigenvalues of the admittance matrix with different (N, l) = (20, 4) (red), (20, 6) (blue), (20, 9) (pink), and (20, 15) (green). (e1–e4) Spatial profiles of all scale-tailored localized eigenstates (corresponding to the eigenvalues distributed on the circle) of the admittance matrix with different (N, l). The experimental results (solid diamonds) align with the theoretical results (hollow circles). e5 Rescaled spatial distributions divided by the coupling range l of the scale-tailored localized eigenstates. Other parameters are: ω = 2π × 100kHz, C2 = 10pF, C3 = 220pF.

Full size image

A printed circuit board comprising 20 units is fabricated, as displayed in Fig. 3c. Based on Kirchhoff’s law, for a given alternating current (AC) input current with frequency ω, the circuit lattice is described by

$${{{\bf{I}}}}(\omega )=J(\omega ){{{\bf{V}}}}(\omega ),$$
(9)

where J represents the admittance matrix (or the circuit Laplacian). The current and voltage vectors are defined as I = (I0, I1, ⋯  , IN−1) and V = (V0, V1, ⋯  , VN−1), respectively, with In and Vn denoting the input current and voltage at node n. The admittance matrix J and its eigenvalues play a role similar to the Hamiltonian (up to some trivial constant term) and its associated eigenenergies. In our circuit, the capacitor at the last unit is set to C3 = 220pF, and the coupling capacitor is C2 = 10pF, corresponding to δt = 0.0454 in the unidirectional model (1). The AC input current has a frequency of ω = 2πf = 2π × 100 kHz, and the coupling range l is adjustable using switches.

Experimental demonstration of STL

By measuring the voltage responses at all nodes in the network when subjected to a local current input, the admittance eigenvalues and eigenstates can be accessed. To demonstrate the scaling rule with the coupling range, we examine four representative cases: l = N − p = 4, 6, 9, 15, while maintaining a fixed lattice size of N = 20 by activating the corresponding switches. In Fig. 3d, we present the measured admittance spectra in the complex energy plane. For each l, the spectra consist of two distinct types: l states evenly distributed on a circle with a radius of \({({\delta }_{t})}^{1/l}\), and the remaining N − l states enclosed within this circle. These N − l states primarily reside at the first site, arising from the p-fold degenerate exceptional point, which is highly sensitive to perturbations. Imperfections or non-uniformities in the capacitors/inductors can cause the exceptional point to split and spread along the imaginary axis (details in Supplementary Section VII, Supplementary Fig. S11 and Supplementary Table S1). In contrast, the states distributed on the circle display resilience.

In Fig. 3e1–e4, we present the spatial profiles of eigenstates (with their corresponding eigenvalues distributed on the circle) of the admittance matrix for different combinations of (N, l). Notably, for each l, the eigenstates display nearly identical profiles, with small deviations due to unavoidable circuit noises or device errors. These eigenstates decay from the left boundary exponentially with a finite spanning. As the coupling range l increases, the eigenstates gradually become more delocalized. Furthermore, by rescaling their distributions with the prefactor of l, we observe perfect overlapping of their profiles for all combinations of (N, l), as depicted in Fig. 3e5. It indicates that the localization length scales as \({{{\mathcal{O}}}}(l)\), thus confirming the nature of the scale-tailored localized states.

The reconstruction of the scale-tailored states from the admittance matrix involves N2 voltage response measurements, which is cumbersome and indirect. Instead, these eigenstates can be obtained through the measurement of the non-local voltage response, as illustrated in Fig. 4a. An AC current feed is injected at the far right end of the circuit using an AC voltage source connected through a shunt resistance Rs = 10 kΩ. Each additional resistor R0 and capacitor Cr per unit cell is used only for circuit stability and facilitating frequency adjustment. When the driving frequency approaches the system’s eigenfrequency corresponding to a scale-tailored eigenstate, the measured voltage response directly yields the profile of the scale-tailored eigenstate (See “Methods”). Intriguingly, despite the current being fed at the far right end, the measured voltage response peaks strongest at the far left end, as shown in Fig. 4b. This counterintuitive enhancement underscores the exotic localization behavior of the scale-tailored eigenstate. In fact, the localization length ξ can be extracted from the voltage response:

$$\xi=\frac{1}{\log \left[\frac{1}{N-1}{\sum }_{n=0}^{N-2}\frac{| {V}_{n}| }{| {V}_{n+1}| }\right]},$$
(10)

where Vn represents the voltage response at the n-th node. As shown in the inset of Fig. 4b, the linear scaling of ξ with the coupling range l is further confirmed.

Fig. 4: Direct measurement of the scale-tailored localized states.
figure 4

a An input AC current is fed at the far right end of the circuit using an AC voltage source connected through a shunt resistance Rs = 10 kΩ. b Voltage response at all nodes relative to the current feed. The inset displays the localization length ξ extracted from the voltage responses. Experimental data are marked by colored symbols for different configurations: (N, l) = (20, 6) (red diamonds) with (R0, f) = (82 kΩ, 174 kHz), (20, 11) (blue triangles) with (R0, f) = (22 kΩ, 175 kHz), (20, 16) (green crosses) with (R0, f) = (16 kΩ, 176.5 kHz), which align with theoretical expectation (black lines). Other parameters are: C0 = 10pF, C1 = 220pF C2 = 30pF, C3 = 200pF, Cr= 1.5 nF, L = 470 μ H.

Full size image

Discussion

We have established STL as a novel localization mechanism stemming from long-range asymmetric couplings, going beyond the well-known paradigms of Anderson localization due to wave interference and skin localization arising from intrinsic non-Hermitian point gaps. Leveraging the high feasibility of electric-circuit arrays and the adjustability of nonreciprocity through VFs, we have further observed the scale-tailored localized states in electrical circuits, accompanied by the separation of energy spectra in the complex plane. Our framework highlights the non-perturbative nature of non-Hermitian couplings, resulting in dramatic changes in energy spectra and eigenstates. With wave localization fully tailored by the long-range coupling, our study opens new avenues for the versatile manipulations of peculiar wave phenomena in various open systems and other experimental platforms, including photonic20,40, ultracold atoms49, and metamaterials19.

Methods

Analysis of STL

The unidirectional-hopping model in Eq. (1) is a special case of the more generic Hatano-Nelson model50 with nonreciprocal couplings:

$$\hat{H}={\sum }_{n=0}^{N-2}({t}_{L}{\hat{c}}_{n}^{{{\dagger}} }{\hat{c}}_{n+1}+{t}_{R}{\hat{c}}_{n+1}^{{{\dagger}} }{\hat{c}}_{n})+{t}_{L}{\delta }_{t}{\hat{c}}_{N-1}^{{{\dagger}} }{\hat{c}}_{p}.$$
(11)

Here, tR and tL represent the hopping to the right and left side, respectively. The eigenvalues and eigenstates for the above model can be obtained as:

$$\left\{\begin{array}{l}E={t}_{L}{z}_{i}+\frac{{t}_{R}}{{z}_{i}},\hfill \\ \left\vert \Psi \right\rangle=\mathop{\sum }_{i=1}^{2}\left\vert {\Psi }_{i}\right\rangle={\sum }_{i=1}^{2}{c}_{i}{(1,{z}_{i},{z}_{i}^{2},\cdots,{z}_{i}^{N-1})}^{T},\hfill \end{array}\right.$$
(12)

where z1 and z2 satisfy z1z2 = tR/tL = η, and z1 is given by the roots of the following equation:

$${z}_{1}^{N+1}-{\left(\frac{\eta }{{z}_{1}}\right)}^{N+1}+{\delta }_{t}\left[{\left(\frac{\eta }{{z}_{1}}\right)}^{p+1}-{z}_{1}^{p+1}\right]=0.$$
(13)

Without the additional long-range coupling, i.e., δt ↦ 0, Eq. (13) reduces to \({z}_{1}^{2(N+1)}={\eta }^{(N+1)}\), from which we obtain N solutions \({z}_{1/2}^{(m)}=\sqrt{\eta }{e}^{\pm i{\theta }_{m}}\) with θm = [mπ/(N + 1)](m = 1, ⋯  , N). These roots form the generalized Brillouin zone7. The eigenstates are skin modes localized at the left or right boundary when ∣tR∣ < ∣tL∣ or ∣tR∣ > ∣tL∣, respectively.

When δt deviates from 0 and exceeds a critical value, part of the skin modes is reshaped by the long-range coupling. For simplicity, we focus on the case of N, p ≫ l (l = N − p), that is, the coupling range l is the smallest length scale of the system. When δt > rl, the solutions of Eq. (13) can be categorized into two types. The first type consists of p solutions satisfying \(| {z}_{1}|=| {z}_{2}|=\sqrt{\eta }\). Specifically, they are \({z}_{1/2}=\sqrt{\eta }{e}^{\pm i\theta }\), where θ is determined by real solutions of \({r}^{l}\sin [(N+ 1)\theta ]={\delta }_{t}\sin [(p+1)\theta ]\). These solutions represent the skin modes that are nearly unaffected by the long-range coupling. The second type has l solutions satisfying \(| {z}_{2}| < \sqrt{\eta } \, < \, | {z}_{1}|\). In this case, Eq. (13) reduces to \({z}_{1}^{N-p}={\delta }_{t}\), which leads to l solutions \({z}_{1}^{(m)}=\root l \of {{\delta }_{t}}{e}^{i{\theta }_{m}}\) with \({\theta }_{m}=\frac{2m\pi }{l}(m=1,2,\cdots \,,l)\). The localization length of the second-type eigenstates is determined by the settings of the long-range coupling. They correspond to STL or inverse STL for ∣δt∣ < 1 or ∣δt∣ > 1 with localization length \(\xi=\mp \frac{l}{\log | {\delta }_{t}| }\propto l\).

The criterion of STL

Here, we investigate the generic non-Hermitian model described by Hamiltonian (6) with an additional non-local coupling, as sketched in Fig. 5a. The solution of the eigenvalue equation \(\hat{H}\left\vert \Psi \right\rangle=E\left\vert \Psi \right\rangle\) are

$$\left\{\begin{array}{l}E={\sum }_{j=1}^{{M}_{R}}\frac{{t}_{jR}}{{z}^{j}}+{\sum }_{j=1}^{{M}_{L}}{t}_{jL}{z}^{j},\hfill \\ \left\vert \Psi \right\rangle={\sum }_{i=1}^{M}{c}_{i}{\left(1,{z}_{i},{z}_{i}^{2},\cdots,{z}_{i}^{N-1}\right)}^{T}.\hfill \end{array}\right.$$
(14)

Here M = MR + ML, and c1, ⋯  , cM are superposition coefficients determined by the boundary constraints \(\det [{H}_{B}]=0\). For a given E, there exist M solutions zi(i = 1, ⋯  , M), which can be ordered as ∣z1∣ ≤ ∣z2∣ ≤ ⋯ ≤ ∣zM∣.

Fig. 5: Sketch of generic 1D lattice models and the criterion of STL.
figure 5

a A generic 1D non-Hermitian lattice model. The largest hopping ranges to the left and right are ML and MR. The additional asymmetric coupling is marked in red. b Sketch of the criterion of STL. The (MR + 1)-th roots of the Bloch spectra reside on the unit circle (red circle).

Full size image

We focus on the relevant case with N ≫ l ≫ 1 and discuss the existence condition of STL (details in Supplementary Section II). The dominant terms in the determinant are \(\det [{H}_{B}]={A}_{1}+{A}_{2}+{B}_{1}\), with

$${A}_{1}= {\left({z}_{{M}_{R}+1}{z}_{{M}_{R}+2}\cdots {z}_{M}\right)}^{N}{G}_{a} \\ \times {\sum}_{{i}_{1}\ne \cdots \ne {i}_{{M}_{R}}=1}^{{M}_{R}}{(-1)}^{\tau ({i}_{1}\cdots {i}_{{M}_{R}})}\left[{f}_{1}({z}_{{i}_{1}})\cdots {f}_{{M}_{R}}({z}_{{i}_{{M}_{R}}})\right],$$
(15)
$${A}_{2}= {\left({z}_{{M}_{R}}{z}_{{M}_{R}+2}\cdots {z}_{M}\right)}^{N}{G}_{a}^{{\prime} } \\ \times {\sum}_{{i}_{1}\ne \cdots \ne {i}_{{M}_{R}}=1}^{{M}_{R}-1,{M}_{R}+1}{(-1)}^{\tau ({i}_{1}\cdots {i}_{{M}_{R}})}\left[{f}_{1}({z}_{{i}_{1}})\cdots {f}_{{M}_{R}}({z}_{{i}_{{M}_{R}}})\right],$$
(16)
$${B}_{1}= -{\delta }_{t}{z}_{{M}_{R}+1}^{p}{\left({z}_{{M}_{R}+2}\cdots {z}_{M}\right)}^{N}{G}_{b} \\ \times {\sum}_{{i}_{1}\ne \cdots \ne {i}_{{M}_{R}}=1}^{{M}_{R}}{(-1)}^{\tau ({i}_{1}\cdots {i}_{{M}_{R}})}\left[{f}_{1}({z}_{{i}_{1}})\cdots {f}_{{M}_{R}}({z}_{{i}_{{M}_{R}}})\right].$$
(17)

Here, \({G}_{a},{G}_{a}^{{\prime} }\) and Gb are finite polynomials depending on the specific model. If ∣B1∣ ≫ ∣A2∣, which requires

$${\delta }_{t}| {z}_{{M}_{R}+1}{| }^{p}\gg | {z}_{{M}_{R}}{| }^{N},$$
(18)

then the boundary constraints yield A1 + B1 = 0. Consequently,

$${z}_{{M}_{R}+1}=\root l \of {{\delta }_{t}\eta }{e}^{i{\theta }_{m}},$$
(19)

where

$$\eta=\frac{{G}_{b}}{{G}_{a}},$$
(20)

and \({\theta }_{m}=\frac{2m\pi }{l}\) with m = 1, ⋯  , l. Since Ga and Gb are finite polynomials, \(| {z}_{{M}_{R}+1}{| }^{l}=| {\delta }_{t}\eta | \sim {{{\mathcal{O}}}}(1)\), indicating there are l scale-tailored localized states.

Substituting Eq. (19) into Eq. (18), the condition (18) simplifies to

$${\delta }_{t} > | {z}_{{M}_{R}}{| }^{l}.$$
(21)

This governs the existence of l scale-tailored localized states with \(|{z}_{{M}_{R}+1}|=\root l \of {{\delta }_{t}\eta }\) under the condition N ≫ l ≫ 1. Notably, for sufficiently large \(l,|{z}_{{M}_{R}+1}|\to 1\), and the eigenenergies of these scale-tailored states approach the Bloch spectra (energy spectra under periodic boundary conditions):

$$E={E}^{(PBC)}={\sum}_{j=1}^{{M}_{R}}\frac{{t}_{jR}}{{({e}^{ik})}^{j}}+{\sum}_{j=1}^{{M}_{L}}{t}_{jL}{({e}^{ik})}^{j},$$
(22)

where k ∈ [0, 2π]. Moreover, the condition Eq. (21) holds regardless of the magnitude of δt only if \(| {z}_{{M}_{R}}| < 1\). Thus, the criterion can be formulated in terms of the Bloch spectra: for any E ∈ σPBC, there exist ML + MR solutions zi, sorted by their moduli \(\left\vert {z}_{1}\right\vert \le \left\vert {z}_{2}\right\vert \le \ldots \le \left\vert {z}_{{M}_{L}+{M}_{R}}\right\vert\). Note that for the Bloch spectra, there must exist a z-solution of unit modulus. If these solutions zi further satisfy \(\left\vert {z}_{{M}_{R}}\right\vert < \left\vert {z}_{{M}_{R}+1}\right\vert=1\), then l scale-tailored localized states appear upon introducing the additional long-range coupling of arbitrary strength, as sketched in Fig. 5b.

Circuit Laplacian and impedance matrix

The circuit Laplacian relates the input current and voltage at all the nodes via Kirchhoff’s law, I (ω) = J (ω)V (ω). For the circuit array shown in Figs. 3a and 4a, the circuit Laplacian is given by:

$$\begin{array}{rcl}J(\omega )&=&-i\omega \left(\begin{array}{cccccccc}\mu &{C}_{1}&\cdots \,&0&0&\cdots \,&0&0\\ 0&\mu &\cdots \,&0&0&\cdots \,&0&0\\ \cdots \,&\cdots \,&\cdots \,&\cdots \,&\cdots \,&\cdots \,&\cdots \,&\cdots \\ 0&0&\cdots \,&\mu &{C}_{1}&\cdots \,&0&0\\ 0&0&\cdots \,&0&\mu &\cdots \,&0&0\\ \cdots \,&\cdots \,&\cdots \,&\cdots \,&\cdots \,&\cdots \,&\cdots \,&\cdots \\ 0&0&\cdots \,&0&0&\cdots \,&\mu &{C}_{1}\\ 0&0&\cdots \,&{C}_{2}&0&\cdots \,&0&\mu \end{array}\right) \\ &=&\widetilde{J}(\omega )-i\omega \mu {I}_{N\times N}.\hfill\end{array}$$
(23)

Here \(\mu=\frac{1}{{\omega }^{2}L}-({C}_{1}+{C}_{0})\) in Fig. 3, and \(\mu=\frac{1}{{\omega }^{2}L}-({C}_{1}+{C}_{0}+{C}_{r})-\frac{1}{i\omega {R}_{0}}\) in Fig. 4. The capacitors C0 and C3 are set to satisfy C1 + C0 = C2 + C3 in our circuit. IN×N is the N × N identity matrix. JN−1,p = − iωC2 represents the long-range coupling. Compared to the theoretical model in Eq. (1), we have the coupling strength t and tδt set by the capacitors C1 and C2 in the circuit array. In the experiments illustrated in Fig. 3, each unit cell is composed of an LC resonator, a capacitor, and a VF (OpAmp OP07) with a gain bandwidth product of 600 kHz. In Fig. 4, each unit cell incorporates an additional resistor (R0) and a capacitor (Cr), with the VF (OpAmp OP27G) having an 8 MHz bandwidth product. We plug the circuit unit into the circuit motherboard, allowing for easy adjustment of both boundary coupling and lattice size. To mitigate crosstalk between adjacent inductors, we maintain a distance of approximately 4 cm between two lattice sites.

To access the admittance eigenvalues and eigenstates, we perform voltage-response measurements with respect to a local current input for all nodes in the network. These responses are encoded in the impedance matrix G:

$${{{\bf{V}}}}(\omega )=G(\omega ){{{\bf{I}}}}(\omega ).$$
(24)

Specifically, with an input AC current In at the n-th node and the measured voltage response \({V}_{m}^{n}\) at the m-th node, the impedance matrix element Gmn is given by:

$${G}_{mn}=\frac{{V}_{m}^{n}}{{I}_{n}}.$$
(25)

The admittance matrix J (ω) and the impedance matrix are related through J (ω) = G−1(ω). In the experimental setup shown in Fig. 3, the AC current is provided by an AC voltage source (NF Wave Factory1974) through a resistance of Rs = 2 kΩ, and the voltage response is measured using a lock-in amplifier (Zurich Instruments UHF).

Besides the reconstruction of the admittance matrix, direct access to the scale-tarilored eigenstates is possible through the non-local voltage measurements as in Fig. 4a. The impedance matrix \(G\left(\omega \right)\) (the inverse of the admittance matrix \(J\left(\omega \right)\)) encodes information about the eigenmodes. It can be expressed as

$$G\left(\omega \right)=\left(\begin{array}{cc}{G}_{0}&{G}_{1}\\ 0&{G}_{2}\end{array}\right),$$
(26)

where G0 is a p × p upper triangular matrix with elements being \({[{G}_{0}]}_{i,j}=\frac{-1}{{J}_{i,i+1}}{\left(\frac{-{J}_{i,i+1}}{{J}_{i,i}}\right)}^{j-i+1}\). G1 is a p × l matrix defined by \({[{G}_{1}]}_{i,j}={\left(\frac{-{J}_{i,i+1}}{{J}_{i,i}}\right)}^{p-i}{[{G}_{2}]}_{0,j}\). G2 is an l × l matrix:

$${G}_{2}={\sum}_{n=p}^{N-1} \, \frac{1}{{j}_{n}}\frac{{{\psi }_{nR}^{{\prime} }\psi }_{nL}^{{\prime} {{\dagger}} }}{{\psi }_{nL}^{{\prime} {{\dagger}} }{\psi }_{nR}^{{\prime} }}$$
(27)

with \({\psi }_{nR,i}^{{\prime} }={\psi }_{nR,p+i}\) and \({\psi }_{nL,i}^{{\prime} }={\psi }_{nL,p+i}\). Here, ψnR or ψnL(n = p, ⋯  , N − 1) is the right or left eigenvector with eigenenergy jn of the admittance matrix \(J\left(\omega \right)\), representing the scale-tailored eigenstates. We denote the eigenfrequency of the electric circuits as \({\omega }_{c}^{\left(m\right)}\), determined by det \(\left[\,{J} \left({\omega }_{c}^{\left(m\right)}\right)\right]={0}\). When the driving frequency approaches an eigenfrequency \({\omega }_{c}^{\left(m\right)}\), the eigenvalue associated with a scale-tailored eigenstate satisfies \({j}_{m}\left(\omega \to {\omega }_{c}^{\left(m\right)}\right)\to 0\) and Ji,i = − jm. We thus have

$${ \left[{G}_{1} \left(\omega \to {\omega }_{c}^{ \left(m\right)}\right)\right]}_{i,j}=\frac{1}{{j}_{m}}\frac{{\psi }_{mL,p+j}^{*}}{{\psi }_{mL}^{{\prime} {{\dagger}} }{\psi }_{mR}^{{\prime} }}{\psi }_{mR,i}$$
(28)

with i = 0, ⋯  , p − 1, and j = 0 ⋯  , l − 1. The matrix G2 reduces to

$${\left[{G}_{2}\left(\omega \to {\omega }_{c}^{\left(m\right)}\right)\right]}_{i,j}=\frac{1}{{j}_{m}}\frac{{\psi }_{mL,p+j}^{*}}{{\psi }_{mL}^{{\prime} {{\dagger}} }{\psi }_{mR}^{{\prime} }}{\psi }_{mR,p+i}$$
(29)

with i = 0, ⋯  , l − 1, and j = 0 ⋯  , l − 1. This indicates that when the driving frequency approaches the eigenfrequency \({\omega }_{c}^{\left(m\right)}\), the x-th \(\left(x=p,\cdots \,,N-1\right)\) column of the impedance matrix directly yields the scale-tailored eigenstate ψmR, i.e.,

$${\left[G\left(\omega \to {\omega }_{c}^{\left(m\right)}\right)\right]}_{x}=\frac{1}{{j}_{m}}\frac{{\psi }_{mL,x}^{*}}{{\psi }_{mL}^{{\prime} {{\dagger}} }{\psi }_{mR}^{{\prime} }}{\psi }_{mR} \sim {\psi }_{mR}.$$
(30)

Therefore, the scale-tailored eigenstates can be accessed by measuring the voltage response related to the input AC current at the far-right end of the circuit under \(\omega \to {\omega }_{c}^{(m)}\).