Introduction

The kagome lattice, a two-dimensional lattice of corner-sharing triangles, is known for its geometrical frustration and exotic electronic structures, including Dirac points, saddle-point van Hove singularities (VHSs), and a flat band. A prominent example of kagome metals is the recently discovered AV3Sb5 family (A = K, Rb, and Cs), which contains a V kagome lattice1,2,3,4,5,6,7,8,9,10,11,12,13. CsV3Sb5 exhibits superconductivity below a transition temperature (Tc) of 2.5 K, along with three-dimensional charge density waves (CDW)5,6,7,8, pair density wave7, and a Z2 topological band structure2,3. The CDW states in these materials are linked to the electronic nematicity and chiral flux phases featuring the time-reversal symmetry breaking10,11. Suppressing the CDW states through pressure or chemical doping leads to the reduction of intertwined orders and emergence of new electronic states12,13. This raises a fundamental question: can the novel electronic states emerge in an intrinsic kagome metal without CDW order?

Here, we report the discovery of a new kagome metal, CsTi3Bi5, which features a Ti-based kagome lattice and adopts the same crystalline structure as AV3Sb5. High-quality CsTi3Bi5 crystals exhibit superconductivity with an onset superconducting transition temperature Tc of ~4.8 K but notably lack a CDW transition, as demonstrated by transport and magnetic susceptibility measurements. Scanning tunneling microscopy/spectroscopy (STM/STS) and Josephson STS reveal two distinct superconducting gaps on the surface of CsTi3Bi5 crystal. In the superconducting state, the superconducting gaps break the sixfold rotational symmetry of the crystal down to twofold. In the normal state, the quasiparticle interference (QPI) patterns also show C2 symmetry, indicating a nematic ordered phase with the same nematic direction as in the superconducting state. Our findings provide a new materials platform for the exploration of the electron liquid crystal phases and the interplay between electronic nematicity and superconductivity.

Results

CsTi3Bi5 (CTB) has a layered hexagonal crystal structure in the space group P6/mmm (Fig. 1a), which is isostructural to the vanadium-based kagome metal AV3Sb5. The perfect kagome layer of Ti atoms is coordinated by a hexagonal net of Bi1 atoms located at the center of the hexagons, which is sandwiched between two additional honeycomb layers of Bi2 atoms above and below the Ti triangles in the kagome plane. The upper and lower Bi2 layers are separated by a large distance and are thus weakly bound to the middle Ti kagome layer.

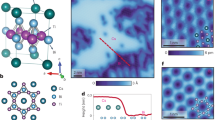
Fig. 1: Atomic structure analysis of the CsTi3Bi5 crystal.
figure 1

a Schematic structure of the CsTi3Bi5 crystal with Cs atoms in purple, Bi atoms in light orange, Ti atoms in azure. The dashed lines represent a unit cell. The perfect kagome net of Ti atoms is mixed with a net of Bi1 atoms. b XRD pattern of an as-prepared CsTi3Bi5 single crystal with the corresponding Miller indices (00l), showing the high quality of the crystal. Inset is a photograph of the as-prepared CsTi3Bi5 single crystal with a regular hexagonal morphology and sharp edges. The size of the crystal is over 4 mm. c Laue diffraction pattern along the [001] direction of CsTi3Bi5, demonstrating excellent crystallinity. d Atomic resolution HAADF-STEM Z-contrast image of CsTi3Bi5 viewed along the [210] projection, with the atomic model overlaid.

Full size image

We synthesize the CTB crystals through a modified self-flux method. A typical crystal with a lateral size of over 4 mm and regular hexagonal morphology is shown in the inset of Fig. 1b. The corresponding X-ray diffraction (XRD) pattern confirms the pure phase and the excellent crystalline nature of the as-grown single crystal with a preferred [001] orientation (Fig. 1b and Supplementary Fig. 1). The clear Laue diffraction spots (Fig. 1c), along with the rocking curve obtained from the (008) reflection showing a full-width-half-maximum of ~0.04° (Supplementary Fig. 2), demonstrate the high-quality single crystal nature of the as-grown CTB. The lattice parameters a, b, and c are measured to be 5.839, 5.839 and 9.295 Å by the single crystal diffraction, which is larger than a and b (5.548 Å) but slightly smaller than c (9.349 Å) of CsV3Sb5 crystals (Supplementary Fig. 3). The temperature-dependent XRD patterns of CTB powders prepared by grinding the single crystals into microscale granules show the negligible structural difference (Supplementary Fig. 4). The layered structures are confirmed by the atomic resolution high-angle annular dark field (HAADF) scanning transmission electron microscopy (STEM). The Z-contrast image of CTB viewed along the [210] projection is shown in Fig. 1d, with the structural model overlaid. The image clearly reveals the perfect crystalline structure of the CTB sample without noticeable structural defects or impurity phases. Atomic-resolution chemical analysis via the electron energy-loss spectroscopy (EELS) and X-ray energy dispersive spectroscopy (EDS) spectrum imaging in STEM unambiguously shows clear atomic layers of Ti, Cs, and Bi atoms (Supplementary Figs. 5, 6), in full agreement with the single-crystal structure of CTB. The EDS analysis of the bulk CTB crystal, measured in a scanning electron microscope (SEM), provides a semi-quantitative average stoichiometric ratio of Cs:Ti:Bi ~0.9:3.0:4.9 (Supplementary Fig. 6). These characterizations demonstrate the high-quality of the as-synthesized CTB.

Superconductivity in CTB was detected by the zero-field cooled magnetic susceptibility under various magnetic fields for H//c (Fig. 2a) and H//ab directions (Supplementary Fig. 7). Under an applied field of 5 mT, a diamagnetic transition is observed and is suppressed by the increasing magnetic field, which indicates the superconducting signature (Fig. 2a). However, we note that the superconducting volume fraction is very low, about 7% under 5 mT. To explore the origin of such a low superconducting volume fraction, we measured the magnetization under ultra-low fields. We find that the volume fraction rapidly increases from 10% under 0.3 mT to ~60% under 0.001 mT at 1.8 K (Fig. 2b), indicating that the superconducting phase is extremely sensitive to the applied magnetic field. The superconducting volume fraction above 60% together with the pure phase of the crystal demonstrate that the superconductivity is bulk in nature. The onset superconducting transition temperature deduced from the M–T curves is ~4.8 K (Fig. 2b), which is significantly higher than vanadium-based kagome superconductors. The existence of the superconducting phase is not only unambiguously confirmed by the shielding signal, but also confirmed by electrical transport measurements. The in-plane resistivity versus temperature curve shows a metallic behavior (Supplementary Fig. 8) with a superconducting transition at onset Tc ~ 4.8 K and zero-resistivity at ~3.6 K (Fig. 2c).

Fig. 2: Superconductivity of the CsTi3Bi5 crystal.
figure 2

a The magnetic susceptibilities under various magnetic fields for H//c, showing the diamagnetic transition which is suppressed by the increasing magnetic field. The superconducting volume fraction is low, about 7% at 5 mT. b The magnetic susceptibilities under ultra-low fields, showing that the volume fraction is rapidly increased from 10% at 0.3 mT to ~60% at 0.001 mT measured in a device that screens out the earth’s magnetic field. c Temperature dependence of resistivity below 5 K. d The dI/dV spectrum shows a superconducting gap with Δ1 ~ 0.7 meV (Vs = −3 mV, It = 1 nA, VMod = 50 μV). e The Josephson effect of superconducting gap in (d) by using an SC tip (Vs = −3 mV, VMod = 50 μV, It is labeled for each spectrum in unit of nA). The dI/dV linecut (g) shows a uniform spatial distribution of Δ1 in the surface region of (f). The lower panel of (f) is a magnified image, showing the honeycomb lattice of the Bi surface (Vs = −10 mV, It = 2 nA). h The dI/dV spectrum shows a superconducting gap with Δ2 ~ 0.3 meV (Vs = −3 mV, It = 1 nA, VMod = 50 μV). i The Josephson effect of superconducting gap in (h) by using an SC tip. (Vs = −3 mV, VMod = 50 μV, It is labeled for each spectrum in unit of nA). The dI/dV linecut (j) shows a uniform spatial distribution of Δ2 in the surface region of (k). The lower panel of (k), shows the honeycomb lattice of Bi surface (Vs = −3 mV, It = 1 nA).

Full size image

To further investigate the superconducting order, we applied the STM/STS and Josephson STS on the surface of the CTB. The low-temperature cleavage results in two distinct cleaved surfaces, where the Cs-terminated surfaces show a hexagonal lattice while the Bi-terminated surfaces show a honeycomb lattice structure (Supplementary Fig. 10). Fourier transforms (FT) of the STM topography images show the absence of the density wave order, in sharp contrast to AV3Sb5 superconductors5,6,7. When the temperature cools below 60 mK, which is much lower than the transition temperature of 4.8 K, the dI/dV spectra obtained at various cleaved CsTi3Bi5 surfaces mainly exhibit two types of spectral gaps with gap-edge peaks at the energies symmetric with respective to EF (Fig. 2d, h). In order to establish the superconducting origin of these energy gaps, we directly probed the superfluid condensate for the superconducting phase coherence by constructing a Josephson STM equipped with a superconducting (SC) tip (see Methods and Supplementary Fig. 11). When the SC tip was approached closer to the sample surface, a sharp zero-bias peak due to the Josephson tunneling of Cooper pairs gradually emerged. Both the small and large spectral gaps exhibit Josephson effects, strongly demonstrating that both types of symmetric gap originate from the superconducting gaps in CTB (Fig. 2e, i and see Supplementary Fig. 11 for details)14.

From the dI/dV spectra collected in 390 surface regions in three CsTi3Bi5 samples, we obtained an averaged gap size for the large gap Δ1 = 0.77 ± 0.07 meV and the small gap Δ2 = 0.33 ± 0.12 meV, respectively (for details see Supplementary Fig. 12). It should be noted that the small superconducting gap in some surface regions without Cs adatoms is much weaker than that in the other surface regions. These two distinct superconducting gaps are spatially separated by the superconducting domains. The dI/dV line cut collected in the large-gap surface regions, where the honeycomb lattice of the Bi surface is well resolved, reveals that Δ1 (Fig. 2f, g) is spatially uniform inside the surface domain. Similarly, Δ2 is also nearly uniform inside the small-gap surface regions (Fig. 2j, k). The size of the superconducting domains ranges from hundreds to tens of nanometers (Supplementary Fig. 13). The strong spatial inhomogeneity of the superconducting gap obtained at the surface of CsTi3Bi5 crystal indicates a possible emergence of surface superconductivity. We note that the tunneling conductance dI/dV curves in the large superconducting gap regions can be well-fitted by the Dynes function (Supplementary Fig. 14). In addition, the superconducting gap is robust against the nonmagnetic adatoms and impurities (Supplementary Fig. 15).

Although CTB shows a small volume fraction in the magnetic susceptibilities for the magnetic field on the order of mT, the possibility that the superconductivity originates from CsBi2 impurity phase is ruled out for the following reasons: (1) The quality of our CTB single crystals is extremely high and the impurity concentration is extremely low. Such a low impurity concentration cannot induce superconductivity with as high as 60% volume fraction when the external magnetic field is on the order of µT (Fig. 1b). (2) The magnetic susceptibilities of CsBi2 impurity should show an isotropic response to the out-of-plane and in-plane field, which is in sharp contrast to the measured anisotropic behaviors of CTB (Supplementary Fig. 7). (3) The superconducting gaps are obtained by STM/S and Josephson STS on the Cs and Bi terminated surfaces of CTB free of CsBi2 impurity or clusters (Fig. 2f, j and Supplementary Fig. 11a), and most of the scanned surface regions with clean and flat topography are superconducting (Supplementary Fig. 11). These intriguing properties point to a highly unusual and novel superconducting ground state in CTB.

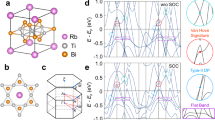
In sharp contrast to vanadium-based AV3Sb5, the smooth resistivity versus temperature curve shows no obvious density-wave-like phase transitions, consistent with the STM topography at low temperatures. This indicates the stability of the pristine lattice structure of CTB and demonstrates the absence of the translational-symmetry-breaking CDW formation that is commonly observed in AV3Sb5. Thus, it is interesting to explore whether the CTB shows purely rotational-symmetry breaking states. To investigate the intriguing symmetry-breaking superconducting states, we collected dI/dV spectra at a base temperature of 30 mK by applying an in-plane magnetic field (B//) and studied the superconducting gap as a function of θ defined as the azimuthal angle of B// with respect to the a-axis of the kagome lattice (Fig. 3a). We observed significant variations of the superconducting gap size with the direction of B//. At B// = 1.0 T and θ = 6°, 66°, and 96°, typical dI/dV spectra at the same spatial location clearly show that the superconducting gap Δ1 determined by the distance between the two coherence peaks varies with the angle θ (Fig. 3b). The angular dependence of Δ1 based on an extensive dataset exhibits the twofold symmetry, with minima around θ = 0° and 180° coinciding with the crystal a-axis, and maxima around θ = 90° and 270° (Fig. 3c). To directly show the twofold symmetric feature, we plot the data in polar coordinates and with respect to the underlying kagome lattice (Fig. 3d) where the long axis of Δ1 (green dotted line) nearly coincides with the vertical direction of the crystal a-axis (Γ-K direction in the momentum space). Similarly, in the small-gap surface regions, the angular dependence of Δ2 also shows a twofold symmetric feature (Fig. 3e–g). The long axis of the twofold Δ2-θ dependence (Fig. 3g) is nearly the same as in the case of Δ1. Therefore, the preferential direction of the C2 symmetry axis of the superconducting gap demonstrates convincingly the rotational-symmetry breaking superconducting state in CTB (more data are shown in Supplementary Fig. 16), which shares an intriguing analogy to the nematic superconducting state observed in the iron-based superconductor FeSe15.

Fig. 3: Rotational symmetry breaking in the superconducting state of CsTi3Bi5 single crystals.
figure 3

a Schematic of the dI/dV measurement in a rotating the magnetic field in the ab plane of CsTi3Bi5 crystal. The orientation angle θ is defined as the angle between field B// and the crystal a-axis. b dI/dV spectra at B// = 1.0 T and θ = 6°, 66° and 96°, showing the sixfold symmetry breaking of Δ1 (Vs = −3 mV, It = 1 nA, VMod = 50 μV). c Angular dependence of Δ1, showing the twofold symmetry with field orientation. The error bars denote the difference among spectra obtained at different positions in the same surface region. d Polar plot of Δ1, showing that the long axis of the twofold Δ1-θ distribution is nearly aligned with the θ = 90° direction. The contour line in the polar plot denotes the sinusoidal fit of the data. e dI/dV spectra at B// = 1.5 T and θ = 6°, 66°and 96°, showing the sixfold symmetry breaking of Δ2 (Vs = −3 mV, It = 1 nA, VMod = 50 μV). f Angular dependence of Δ2, showing the twofold symmetry with field orientation. The error bars denote the difference among spectra obtained at different positions in the same surface region. g Polar plot of Δ2, showing that the long axis of the twofold Δ2-θ distribution is almost aligned with θ = 90° direction. The contour line in the polar plot denotes the sinusoidal fit of the data. h A panorama of dI/dV spectra for the small gap at different field orientations, showing that the low-energy electronic states exhibit rotational symmetry breaking beyond the superconducting gap size. The dashed lines are guides to the eye for the C2 symmetry. Each dI/dV spectrum ranges from −1 mV to 1 mV and is normalized.

Full size image

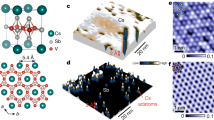
In addition to the superconducting gap size, the line shapes of dI/dV spectra show a twofold behavior as well (Fig. 3h and Supplementary Fig. 17), suggesting that the nematic order extends beyond the superconducting state. Motivated by such observations, we warmed up the sample to 4.8 K near the normal state where the superconductivity is almost suppressed (Supplementary Fig. 18). The large-area STM topography, T(r), shows a clean Bi surface with a few types of randomly-distributed point defects (e.g., at E = 40 mV in Fig. 4a). The QPI features around point defects are too weak to be observed in the STM topography. Only six Bragg peaks of nearly equal intensity consistent with the crystal symmetry are visible in the power spectral density of the FT of STM topography T(q) (e.g., at E = 40 mV in Fig. 4b). In contrast, the QPI around point defects in the dI/dV maps, g(E, r) (e.g., E = 40 mV in Fig. 4c), is much stronger and its FT, g(E, q), shows rich QPI patterns (e.g., at E = 40 mV in Fig. 4d).

Fig. 4: Rotational-symmetry breaking in the normal states of the CsTi3Bi5 crystal.
figure 4

a, b The STM topography of Bi surface T(r) and the magnitude of drift-corrected Fourier transform (FT) T(q), showing isotropic six Bragg peaks (Vs = 40 mV, It = 500 pA). c, d dI/dV map g(40 mV,r) and the magnitude of drift-corrected FT g(40 mV,q), revealing the C2 symmetric QPI patterns (Vs = −40 mV, It = 500 pA, Vmod = 5 mV). The flower-like QPI pattern along the Γ-K1 direction highlighted by the red dotted line shows higher intensity than those along the Γ-K2 and Γ-K3 directions. The C2 symmetric QPI patterns observed only in the dI/dV maps indicate an electronic nematicity at the Bi surface. Right panel of (d): the angle dependence of the extracted QPI intensity, displaying the symmetry breaking from C6 to C2. e g(E,q) at E = −320 meV, −30 mV, 10 mV, and 320 meV, respectively, showing that the C2-symmetric QPI patterns disappear at the relatively large energy beyond the Fermi surface. f Calculated CEC at E-EF, exp = 40 meV showing five pockets from bands of distinct orbital characters as labeled, where EF,exp denotes the experimental Fermi level determined by ARPES measurements31. The five scattering wave vectors correspond to q1, q2, q3, q4, and q5. g QPI simulation based on (f). h QPI simulation based on (f) with orbital-dependent anisotropic spectral weight.

Full size image

Around the zone center Γ point, there is a small hexagon, a larger hexagon rotated by 30°, and an even larger fragmented circle delineated by six arcs. The intensities of these QPI features have the approximate sixfold (C6) symmetry. Intriguingly, a C2 symmetric petal-like pattern is clearly seen in g(E, q) in Fig. 4d, whose intensity along the direction Γ-K1 is much stronger than those at the corresponding locations in the other two directions (Γ-K2 and Γ-K3). The FT intensity as a function of angle displays a clear symmetry-breaking pattern from C6 to C2 (right panel of Fig. 4d). The long axis of twofold QPI intensity (Γ-K direction) is in the same direction as the large gap direction of the C2 symmetric superconductivity (Fig. 3d, g), indicating that the rotation-symmetry breaking persists across the superconducting transition.

The QPI patterns are robust against the scanning direction (Supplementary Fig. 19) and reproducible with different STM tips (Supplementary Fig. 20) over an identical region. Since the C2 symmetric features are absent in topography but present in the dI/dV maps on selective contours rather than in all the QPI patterns, we attribute their origin to a genuine nematic electronic phase instead of structural distortions. To further determine the energy scale over which the electronic states break the rotation symmetry and the nematic order, we collected energy-dependent dI/dV maps g(E,r) and the corresponding FT images g(E,q). We find that the C2-symmetric features in g(E,q) are suppressed at the sample bias below ~−120 mV and above ~280 mV (Fig. 4e and Supplementary Fig. 21). These energy scales are surprisingly high and may be indicative of the role played by the orbitals in the observed nematic order.

In conjunction with the QPI measurements in the normal states, we have also studied the angular-dependent magnetoresistance (AMR) under an in-plane magnetic field of 5 T at different temperatures. As the magnetic field is rotated within the kagome plane (θ = 0° corresponds to the magnetic field perpendicular to the current direction), we observe a pronounced twofold rotational symmetry of the in-plane magnetoresistivity (Supplementary Fig. 22a). Surprisingly, the magnitude of this twofold symmetry, characterized by the AMR ratio (Δρ/ρmin = [ρ(θ, T) − ρmin(T)]/ρmin(T) × 100%) (Supplementary Fig. 22b), is extremely large, reaching up to 67% at 2 K, which is about 10 times larger than that of CsV3Sb57,14. Although the AMR ratio decreases with increasing temperature, it remains at about 20% at 90 K. It should be noted that we have observed the twofold symmetry AMR under an in-plane magnetic field of 0.02 T at 2.2 K (Supplementary Fig. 22c), which is further evidence of the nematicity in the superconducting state16,17

Note that although the rotational symmetry is broken at the onset of the CDW transition in AV3Sb56,10,18,19, the electronic state in the CDW phase is not nematic because of the simultaneously broken translation symmetry. In order to gain microscopic insights for the absence of the CDW order and the emergence of electronic nematic order, we performed first-principle density functional theory (DFT) calculations of the electronic structure for the CTB crystal (details given in Supplementary Fig. 23). While the band structure carries a nontrivial topological Z2 invariant analogous to the vanadium-based kagome metals AV3Sb52,8, the low energy orbital-resolved band dispersion (Supplementary Fig. 23b, c) reveals substantial differences. First of all, the strength of the SOC is much stronger due to the heavier Bi atom and causes a ~ 400 meV downward shift of the Bi pz band near the zone center and large splitting of the Dirac crossings at the K points (highlighted by the light-yellow shade in Supplementary Fig. 23a). Furthermore, the Fermi level is pushed below the two VHS of the in-plane \({d}_{{xy}}/{d}_{{x}^{2}-{y}^{2}}\) orbitals at M points (highlighted by the light-yellow shade in Supplementary Fig. 23a), signifying dramatically altered carrier density of the “135” (AV3Sb5 prototype structure) transition-metal d-orbitals for a broadened physical landscape of the kagome metals. Moreover, the out-of-plane \({d}_{{xz}}\)/\({d}_{{yz}}\) dominated bands are significantly modified near the M points compared to AV3Sb5 due to the large hybridization and SOC, such that the corresponding VHS are removed. These important changes in the electronic structure intertwined with the stable phonon spectrum20,21 provide a microscopic origin for the stability of the pristine kagome lattice in CsTi3Bi5 and the absence of the 2a0 × 2a0 CDW order observed in all AV3Sb5.

We then analyzed the orbital contribution to the anisotropic QPI patterns. There are four bands crossing the Fermi level as determined by the DFT calculations with similar dispersions in the kz = 0 and kz = π planes (Supplementary Fig. 23a). Correspondingly, the constant-energy contours (CEC) near the Fermi level consist of four sheets with different orbital contents as shown in Fig. 4f. The QPI patterns imaged by the STS conductance map g(V, q) can thus be compared directly to the joint density of states calculated for the electronic states on the CEC. Figure 4d, g illustrate such a comparison between g(40 meV, q) and the simulated QPI from the calculated band states of CTB in the kz = 0 plane (calculations show that the energy band is only weakly qz dependent). The detected QPI patterns mainly originate from five dominant scattering branches (q1,2,3,4,5) (marked in Fig. 4g, details see Supplementary Fig. 24): intra-band scattering of the Bi pz orbital (q1), inter-band scattering between the Bi pz orbital and the Ti \({d}_{{xy}}/{d}_{{x}^{2}-{y}^{2}}\) orbitals (q2), inter-band scattering between the Bi pz orbital and the \({d}_{{xz}}\), \({d}_{{yz}}\) orbitals (q3), intra-band scattering of \({d}_{{xy}}/{d}_{{x}^{2}-{y}^{2}}\) orbitals (q4), and intra-band scattering of Ti-\({d}_{{z}^{2}}\) orbital (q5). Accordingly, we extracted the QPI intensity data from Fig. 4d and derived four polar plots (Supplementary Fig. 24b). It can be easily identified that the q2, q3, and q4 branches break the rotational symmetry but q1 preserves the rotational symmetry.

To confirm the orbital dependence of these anisotropic QPI results, we intentionally introduced spectral weight anisotropy to simulate the QPI patterns (Fig. 4f) due to electronic states that weakly break the rotational symmetry. Specifically, the thicknesses of the Ti-\({d}_{{xz}/{yz}}\) and \({d}_{{xy}/{x}^{2}-{y}^{2}}\) Fermi pockets along one Γ-K1 direction were set to be larger than the ones along other directions, showing anisotropic spectral weights in the calculated CEC (Supplementary Fig. 23c). Corresponding QPI simulations based on the CEC with anisotropic spectral weight (Fig. 4h) show reduced symmetry that breaks the sixfold crystal rotation in the isotropic thickness case (Fig. 4g) down to a twofold rotational symmetry, which is similar to the experimental results (Fig. 4d). Moving away from the Fermi level, we can similarly simulate the quasiparticle energy dispersion and compare to the experimental data. In the cut of a series of g(E,q), the energy dispersions of four branches q1, q2, q3, and q4 are obtained. The q1, q2, and q4 branches show electron-like dispersions with distinct Fermi vectors, while q3 exhibits a hole-like dispersion (Supplementary Fig. 24e). The calculated dispersions based on DFT match well with the experimental observations, confirming our determination of the orbital branches (Supplementary Fig. 24f). To study the symmetry-breaking feature of each branch, we compared the coherent quasiparticle weights of the three branches along two equivalent q directions, Γ-K1 and Γ-K3 (Supplementary Fig. 24e). The q1 branch shows the same weight along the two q directions, while the q2, q3 and q4 branches show stronger weight along the Γ-K1 direction than that along the Γ-K3 direction. This is consistent with a higher spectral weight for the Ti-\({d}_{{xz}/{yz}}\) and \({d}_{{xy}/{x}^{2}-{y}^{2}}\) bands along the Γ-K1 direction than that in the other directions, pointing to the importance of the orbital dependence in the electronic nematic order. It should be noted that the orbital-dependent electronic nematic order is intrinsic. Therefore, the anisotropic features are observed in both superconducting and normal states.

Discussion

In summary, we have successfully fabricated high-quality single crystals of Ti-based kagome metal CTB and discovered superconductivity with an onset Tc ~ 4.8 K for the first time. The observation of the Josephson effect on cleaved surfaces using a superconducting STM tip demonstrates the superconducting ground state in CTB. Through a combination of angular-dependent STS and spectroscopic imaging, we find that the electronic states of CTB spontaneously break the rotational symmetry of the crystal and exhibit a nematic order in both the superconducting and normal states. The Ti-based “135” kagome metals thus provide a new materials platform for the much-needed exploration of the electron liquid crystal phases and the interplay between electronic nematicity and superconductivity.

Methods

Single crystal growth of CsTi3Bi5

Single crystals of CsTi3Bi5 were grown from Cs liquid (purity 99.98%), Ti powder (purity 99.9%) and Bi shot (purity 99.999%) via a modified self-flux method. The mixture was placed into an alumina crucible and sealed in a quartz ampoule under Argon atmosphere. The mixture was heated to 1000 °C and soaked for 24 h, and subsequently cooled at 2 °C/h. Finally, the single crystal was separated from the flux, and the residual flux on the surface was carefully removed using a Scotch tape. Except for the sealing and heat treatment procedures, all other preparation procedures were carried out in an argon-filled glovebox in order to avoid the introduction of air and water. The obtained crystals have a typical hexagonal morphology with a size of over 3 × 4 × 0.3 mm3 (Fig. 1b). The layered structure and stoichiometric ratio of CsTi3Bi5 were confirmed by the SEM and energy-dispersive X-ray spectroscopy (EDS) (Supplementary Fig. 6).

Sample characterization

XRD patterns were collected using a Rigaku SmartLab SE X-ray diffractometer with Cu Kα radiation (λ = 0.15418 nm) at room temperature. The X-ray single crystal diffraction was carried out by Bruker D8. Temperature-dependent XRD measurements were carried out by Rigaku Smart X-ray diffractometer with Cu Kα radiation (λ = 0.15418 nm) and the cooling sample stage. SEM and EDS analyses were performed using a HITACHI S5000 with an energy dispersive analysis system Bruker XFlash 6|60. Magnetic susceptibility was determined by a SQUID magnetometer (Quantum Design MPMS XL-1). The superconducting transition of each sample was monitored down to 1.8 K under external magnetic fields from 1 μT to 0.3 mT. Electrical resistivity data were collected on a Quantum Design Physical Properties Measurement System (PPMS). The cross-sectional sample along the [210] projection was prepared using a focused ion beam system. Atomic-scale STEM imaging and EELS spectrum imaging were carried out on an aberration-corrected Nion U-HERMES100 dedicated STEM, operated at an acceleration voltage of 60 kV. The STEM-EDS spectrum imaging was performed on an aberration-corrected JEOL GrandARM2 microscope, operated at an acceleration voltage of 300 kV.

Scanning tunneling microscopy/spectroscopy

The samples used in the STM/S experiments were cleaved at low temperature (13 K) and immediately transferred to an STM chamber. Experiments were performed in an ultrahigh vacuum (1 × 10−10 mbar), ultra-low temperature STM system with vector magnetic field capability at a base temperature of 30 mK (Unisoku 1600). All the scanning parameters (setpoint voltage Vs and tunneling current It) of the STM topographic images are listed in the figure captions. Unless otherwise noted, the dI/dV spectra were acquired by a standard lock-in amplifier at a modulation frequency of 973.1 Hz, the modulation bias (Vmod) is listed in the figure captions. Non-superconducting tungsten tips were fabricated via electrochemical etching and calibrated on a clean Au(111) surface prepared by repeated cycles of sputtering with argon ions and annealing at 500 °C. To remove the effects of small piezoelectric and thermal drifts during the acquisition of dI/dV maps, we apply the Lawler–Fujita drift-correction algorithm22, which aligns the atomic Bragg peaks in STM images to be exactly equal in magnitude and 60° apart.

Vector magnetic field

The vector magnetic field was applied using the zero-field cooling technique, after which we carefully approached the tip to the surface to find the same region to perform tunneling spectroscopy. The direction of in-plane field was calibrated by using the vortices of standard superconductors. We noted that the superconducting gap in Fig. 3 could survive up to in-plane magnetic field higher than bulk Hc, which may result from the local effect of STM/S measurements23.

Surface identifications

Due to the weak bonding between the Cs layer and Bi layer, cleaving at low temperatures exposes both Bi-terminated and Cs-terminated surfaces (Supplementary Fig. 10a). The Cs-terminated surface (when free from reconstruction) exhibits a hexagonal lattice (Supplementary Fig. 10b), while the Bi-terminated surface exhibits a honeycomb lattice (Supplementary Fig. 10c), consistent with the crystal structure in Fig. 1. To circumvent the complexity of reconstruction at the Cs terminated surface, we focus on the Bi surface. We applied the STM manipulation method to sweep the top Cs atoms away to expose the large-scale Bi surfaces7.

Fabrication and characterization of superconducting tip

The SC tips were fabricated by picking up a nanoflake at the sample surface, a method which has previously been used for construction of cuprate SIS junctions24. In that case, a tungsten tip was used to dip into the clean surface of the sample more than 15 nm in depth, held for 5 s at a voltage of 1 V, then withdrawn to its original position. The CTB nanoflake shaped like a truncated cone with base radius R ~ 10 nm, top surface radius r ~ 4 nm, and height h ~ 3 nm, will stick to the apex of the tungsten tip. The stable CTB-coated tips were usually obtained after repeating the “dip process” many times in several as-cleaved clean surface regions.

DFT calculations

First-principles calculations based on DFT with projector augmented-wave pseudopotential method25 are implemented through Vienna ab initio simulation package26. Exchange correlation energy is treated by Perdew–Burke–Ernzerhof parameterization of generalized gradient approximation27. The convergence criteria of atomic forces and total energy in structural optimization are less than 1 meV/Å and 10−7 eV/atom, respectively. The cutoff energy of plane wave is taken as 500 eV. The Γ centered 8 × 8 × 8 Monkhorst–Pack k-point grid is used in the self-consistent cycle. We use the Wannier90 package28 to fit Wannier functions and construct tight-binding model, and calculate the surface spectra by using the surface Green’s function method with WannierTools package29. Calculations of structures’ irrep assignments and parity are performed through the vasp2trace program30.