Introduction

The quantum Hall effect is known to host a wide range of correlated and symmetry–protected phases. Coulomb repulsion plays a central role in it, shaping the structure of QH edge channels1, inducing (pseudo) spin–polarized QH ferromagnets2, or generating fractional quantum Hall states3 with anyonic excitations that may be useful for topological quantum computation4.

In 2015, a surprise came with the observation of the pairing of electrons in QH interferometers. Choi and co-workers5 found in GaAs Fabry–Pérot interferometers (FPIs) defined by two quantum point contacts (QCPs) in series6 an anomalous Aharonov–Bohm (AB) effect with halved flux–periodicity, h/2e. The specific configurations identified were the presence of at least two QH edge channels in the FPI, that is, a bulk filling factor νB > 2, and interference from the outer channel while the inner one forms a closed loop. Strikingly, this electron pairing was confirmed by quantum shot noise that evidenced an effective charge e* ~ 2e (refs. 5,7), pointing conspicuously toward correlated electron–pair transport.

The analogy with Cooper pairing in superconductors is tantalizing, however, the resemblance is only apparent since there are no attractive, non–Coulombic interactions, nor evidence of a macroscopic condensate. On the theoretical front, most efforts to date have failed to describe this baffling phenomenon8,9,10. Yet, an effective dynamical pairing via the exchange of neutralons10 has been put forward, but cannot capture all phenomenology5,7,11.

Here, we opt for a different platform–the graphene QH FPI12,13,14,15 to uncover new insights into this phenomenon. By leveraging the high–tunability of its plunger gate12 and conducting systematic out–of–equilibrium transport measurements, we establish a new QH edge channel spectrometry that allows us to identify the exact channels involved coherently in the electron pairing. This spectroscopy allows us to conclude that pairing consistently occurs when the number of edge channels exceeds one. The pairing’s weight significantly grows with an increase in the filling factor, ultimately leading to visible frequency beating in the pajama map at a filling factor higher than 2. Furthermore, at filling factor νB = 3, we uncover evidence of correlated transport involving three electrons over the three distinguishable edge channels. Our systematic exploration of the flux and energy bias parameter space gives key insights into a complex interplay between edge channels and their interactions.

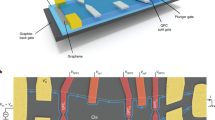
The QH FPIs are made with hBN–encapsulated graphene deposited onto a graphite gate acting as a back–gate electrode. Two QPCs are electrostatically defined by a set of two palladium split–gate electrodes12,16. The FPIs are equipped with a plunger–gate electrode to tune the effective area enclosed by the QH edge channels. Several 1D ohmic contacts17 allow us to source and drain current and probe voltages across the FPI. Figure 1a shows an atomic force microscopy topography of the device studied in the main text, which has an FPI cavity area of 2.2 ± 0.2 μm2. Importantly, the FPI is defined by the pristine, non–etched edges of the graphene flake, ensuring confinement of the QH edge channels to within a few magnetic lengths of the crystal edge, without any edge reconstruction18, as well as by split and plunger gates. All experiments are performed at a magnetic field of 14 T and a temperature of 0.01 K. Partial pinch–off of the inner channel as overlaid in Fig. 1a, b yields conductance oscillations shown in Fig. 1c with negative slope in the magnetic field, B, versus plunger gate voltage, Vpg, plane, which is characteristic of AB quantum interference for a flux periodicity of h/e12,19.

Fig. 1: Inner edge channel interference at Vbg = 1.8 V (νB = 2.26).
figure 1

a Atomic force microscope image of hBN encapsulated graphene. Ohmic contacts (rough surface), plunger gate and quantum point contact (QPC, smooth surface) are in yellow. Inner and outer edges are depicted with black and red. Dashed blue line marks invisible graphene. Diagonal conductance GD = I/VD, where I and VD are current and diagonal voltage. Scale is 1 μm b Schematic of edge configuration. c Pajama map, with QPC transmission T1 = 0.67 and T2 = 0.66, reveals AB--dominated interference19. Inset: Fast Fourier transform (FFT). d GD versus Vpg from  −4.7 V to  −4.5 V at zero bias VDC. e, f Checkerboard extracted from Supplementary Movie 1, and its calculated counterpart (Methods). g Oscilations at 0 < Vpg < −5 V, with bias dependence in Supplementary Movie 1. h Gate spectroscopy, sliding FT (with a 0.175V window) on oscillations at VDC = −28 μV. Full bias dependence in Supplementary Movie 2. First harmonic (blue line) diverges at \({V}_{{{\rm{pg}}}}^{{{\rm{c}}}}\); second and third harmonics in dashed red and yellow. Inset: FFT at Vpg = −1.3 V shows three frequency peaks. i, Lobe structures: first (blue), second (red), and third (yellow) harmonic (Methods). Inset: Thouless energy ETh versus inverse harmonic index.

Full size image

Results

Gate–spectroscopy fingerprint of QH edge channels

The considerable advantage of graphene FPI over conventional semiconductors is the absence of a bandgap, which allows one to achieve a very large electrostatic tuning of the charge carrier density ranging from the electron states to the hole states. Figure 1g illustrates this tunability with conductance oscillations versus plunger–gate voltage, Vpg, from −5 to 0V, reflecting the quantum interference of the inner channel at νB = 2 (same configuration as in Fig. 1a, b). The Fourier transform of these oscillations in a small sliding window gives the plunger–gate dependence of the oscillation frequency12. The resulting gate–spectroscopy shown in Fig. 1h reveals three peaks of decreasing amplitudes (see inset) that relate to the first harmonic frequency fpg and the next two harmonics 2fpg and 3fpg. This indicates quantum interference occurring over two and three turns of the inner channel loop, thus providing a clear signature of the interferometer’s high coherence. Importantly, each peak diverges at the same plunger gate voltage \({V}_{{{\rm{pg}}}}^{{{\rm{c}}}}=-0.28\,{{\rm{V}}}\), which corresponds to the expulsion of the inner channel from under the gate when the filling factor under the gate reaches νpg ~ 1. This divergence is channel–specific12 and provides an unambiguous indicator of the QH edge channels involved in the interference.

One new aspect of our measurement approach is the systematic acquisition of IV curves at every point of the interference patterns in Fig. 1c, g, enabling us to simultaneously explore the complete parameter space of energy, plunger gate voltage, and magnetic field (see the plunger gate–dependent oscillations at various bias voltages in Supplementary Movie 1). Figure 1c, g are extracted from the bias–dependence data at zero bias. The bias voltage dependence of the oscillation frequency yields a checkerboard pattern illustrated in Fig. 1e in a restricted gate voltage range, reflecting the additional phase shift acquired by the injected electrons at finite energy. This checkerboard pattern can be accurately simulated in Fig. 1f, as outlined in the Methods section. In turn, this enables us to compute the Fourier transform of the oscillations at each bias voltage (see oscillation frequency dispersion at various bias voltages in Supplementary Movie 2) and to extract the bias voltage dependence of each harmonics displayed in Fig. 1i. The resulting oscillatory lobe structure of each harmonic is best fitted with a Gaussian decay for the energy relaxation (see ref. 12), and provides the Thouless energy of the interferometer edge ETh = hv/L = 135 ± 4 μV (bias–oscillation period), where L = 3.4 ± 0.2 μm is the length of the interfering channel between two QPCs and v is the edge velocity. The harmonics then yield ETh/N (see Fig. 1i inset), where N is the respective harmonic index, providing an assessment of v = (1.1 ± 0.1) × 105 ms−1 consistent with our previous work12.

Electron pairing on two coherently coupled channels

Electron pairing emerges in our interferometer in the presence of two edge channels by interfering with the outer channel while keeping the inner channel localized in the interferometer cavity (see inset schematics in Fig. 2a). Gate spectroscopy shown in Fig. 2a reveals the pairing frequency (orange dashed line) that is almost twice that of the inner channel interference unveiled previously in Fig. 1h. Since an area variation of one flux quantum at a fixed magnetic field) is ΔA = ϕ0/B = αΔVpg = α/fpg, where α is the (non–linear) lever arm of the gate and ΔVpg = 1/fpg the plunger–gate oscillation period, a frequency doubling therefore signals an abnormal flux periodicity of h/2e similar to that reported in GaAs5,7,11.

Fig. 2: Gate–spectroscopy of outer edge channel interference.
figure 2

Conductance oscillations were measured by partitioning the outer edge channel with QPC transmission of T1 = 0.91 and T2 = 0.94 at Vbg = 1.8 V (νB = 2.26). a Gate spectroscopy, FFT amplitude of the oscillation versus Vpg and frequency f at VDC = − 55.5 μV. FFT is slided over the whole plunger gate voltage range with a 0.2V window. Supplementary Movie 3 shows the dependency of this gate–spectroscopy on the bias voltage. The black and red dashed lines represent the frequency dispersion of the inner fi (determined from Fig. 1h) and outer fo edges, respectively. The orange dashed line, calculated as the sum of fi and fo, coincides with the strong signal attributed to pairing fp. Inset schematics show the edge channel configuration, with the red dashed line indicating the partitioned outer channel and the orange wavy line representing inter–channel interaction. b The lobe structures of pairing (orange–colored) and the outer channel (red–colored), extracted from bias–voltage dependent gate–spectroscopy in Supplementary Movie 3. c The pajama map, measured at zero bias VDC = 0V, shows frequency beating that persists across the entire bias–voltage range (Supplementary Movie 4). Inset: 2D FFT reveals two frequencies–the outer channel fo and pairing fp. fp is shown as the sum of the fo (red arrow) and fi (black arrow).

Full size image

The frequency doubling is also evidenced by the presence of a residual peak at half the frequency highlighted with a red dashed line that coincides with the frequency of the outer channel h/e–periodic interference, the latter being independently characterized by its spectroscopy at a different filling factor where pairing is sub–dominant (Supplementary Fig. 9). Inspecting the plunger–gate evolution of those frequencies, we see that both pairing and outer channel frequencies diverge at \({V}_{{{\rm{pg}}}}^{{{\rm{c}}}}=-0.96\,{{\rm{V}}}\), a value corresponding to a filling factor underneath the plunger gate νpg = 0.05, in agreement with the expulsion of the outer channel from the plunger gate area.

However, unlike the harmonics in Fig. 1h, the pairing frequency is not exactly twice that of the outer channel: At Vpg = −4.8 V, one finds 105 V−1 and 45 V−1, respectively. To understand this discrepancy we add on the gate–spectroscopy the inner channel frequency (first harmonic measured in Fig. 1h) as a black dashed line in Fig. 2a, which leads us to a central finding of this study: The pairing frequency is not double the AB frequency but the sum of the distinct inner and outer channel frequencies. This is seen with the orange dashed line in Fig. 2a, which is constructed from the sum of the black (inner channel) and red (outer channel) dashed lines, and which fits remarkably well with the pairing frequency dispersion. Here the different frequencies for the inner and outer channels stem from their slightly different positions with respect to the plunger and QPC split gates, as discussed in the following, and thus their different effective areas.

This finding is particularly striking and insightful as it demonstrates that, although localized, the inner channel influences the quantum interference of the outer channel and such an unusual pairing frequency. The system therefore behaves as if a correlated excitation propagates on both inner and outer channels, thereby accumulating the sum of the AB phases of both channels \(\varphi=\frac{h}{e}{\oint }_{inner}{{\bf{A.dl}}}+\frac{h}{e}{\oint }_{outer}{{\bf{A.dl}}}\), where A is the vector potential.

Examining the bias voltage–dependence of this gate–spectroscopy displayed in Fig. 2b shows that the pairing mode and the outer channels exhibit nearly the same bias voltage periodicity, that is, Thouless energy, confirming the fact that the pairing frequency is not a harmonic of the outer channel interference. Here, it is evident that pairing prevails over the h/e–periodic contribution from the outer channel.

We delve further into the evolution of pairing with respect to changes in filling factor and bias voltage in Supplementary Fig. 9. At a low filling factor (Vbg = 1.2 V, νB = 1.7), pairing is present but with notably lower prominence at all bias voltages (Supplementary Fig. 9a,d). However, pairing significance increases and becomes dominant as the filling factor rises (Supplementary Fig. 9b, c, e,f). The influence of bias voltage on the relative weight of each frequency becomes particularly noticeable when pairing and outer frequencies have similar amplitudes, as observed at Vbg = 1.58 V (νB = 2, Supplementary Fig. 9e).

Notably, the zero–bias pajama map depicted in Fig. 2c displays a distinct discontinuity in the tilted AB constant phase lines, deviating from the standard pattern shown in Fig. 1b. The Fourier transform reveals two contributions associated with the pairing frequency and the outer edge frequency, as shown in the inset.

Phase jumps

Taking into account these two oscillation frequencies, a simple frequency beating can describe the observed regular discontinuities. Figure 3 demonstrates how to reproduce such discontinuities in pajama maps obtained from the outer edge interference at Vbg = 1.2 V (νB = 1.7), as illustrated in Fig. 3c.

Fig. 3: Experimental and simulated analysis of phase jumps in the pajama maps measured at Vbg = 1.2 V (νB = 1.7).
figure 3

a The pajama map, obtained by partitioning the inner edge channel, suggests GD oscillation with a single–frequency from the inner edge fi. b Calculated pajama map with the frequency fi derived from the panel a. c Observed pajama map when partitioning the outer edge channel, where the dominant oscillations (black arrows) provides the frequency associated with the bare outer edge fo. d Calculated pajama map using the frequency fo. e The pajama map determined by pairing oscillation frequency GD(fi + fo). Pairing frequency is calculated by summing up fi and fo. f The diagonal conductance GD beating in the pajama map occurs due to the simultaneous presence of two oscillations with pairing frequency GD(fi + fo) and outer edge frequency GD(fo).

Full size image

We first simulate in Fig. 3b the oscillation of the inner channel data shown in Fig. 3a. In the data shown in Fig. 3c, a distinct negative constant phase line (see black arrows) correlates with the frequency of the bare outer channel, allowing for the extraction of its frequency, which we simulate in Fig. 3d. We then compute a signal whose frequency is the sum of the inner and outer ones in order to simulate the pairing contribution in Fig. 3e. Adding now the pairing contribution and the outer contribution as occurring in the interferometer leads to Fig. 3f, in which a beating pattern naturally emerges and remarkably fits the data Fig. 3c.

Details regarding methods and simulations for other filling factors can be found in Supplementary Figs. 5-6. Additionally, differences in the relative weight of pairing at various bias voltages result in diverse beating patterns and apparent phase jumps20, as shown in Supplementary Fig. 9j-l. This bias–dependent frequency superposition is also visualized in Supplementary Movie 4.

Similarly, the apparent complexity of the checkerboard patterns can also be fully replicated by summing those of the pairing mode and the bare outer edge, using the relative amplitude of each component extracted at zero bias. Four checkerboard patterns, shown in Supplementary Fig. 10a,c,e,g, are obtained by partitioning the outer channel at different filling factors on the νB = 2 and νB = 3 plateaus (e.g. pairing and tripling regime). Employing the functional form described in the Methods but considering only the first harmonic, we have successfully simulated the checkerboard patterns seen in Supplementary Fig. 10b, d, f, h,l.

Electron tripling on three coherently coupled channels

The observation of pairing naturally raises the question of whether the inclusion of an additional third channel could lead to a threefold increase in frequency, namely, electron tripling, although this has not been observed thus far in GaAs5,7,11,21.

To address this question we set our QH FPI to bulk filling factor 3 and, akin to the case of pairing, we partitioned the outer channel, while having the middle and inner channels localized (Fig. 4a). Figure 4c reveals a new frequency in the plunger gate spectroscopy, highlighted with the violet dashed line, which is almost three times higher than that of the outer channel: At Vpg = − 3.9 V, one finds 179 V−1 and 45 V−1, respectively. By overlaying the spectral dispersion of the inner (black), middle (blue), and outer (red) channels, each separately identified, we can calculate the sum of the three. The violet dashed line denotes this sum and significantly aligns with the tripling frequency. As for the case of pairing, the tripling frequency therefore results from the sum of the three distinct AB phases of the three edge channels, each characterized by a different effective area.

Fig. 4: Electron tripling and pairing.
figure 4

a, b Schematic of edge channel configurations: interference with the outer channel (a) and the middle channel (b). Inner, middle, and outer edges are represented in black, blue, and red, respectively. Dashed lines denote the partitioned edges. The orange wavy line depicts the middle–--outer edge interaction, and the violet wavy line illustrates the interactions among all three edges. c Gate spectroscopy, derived from the conductance oscillations when partitioning the outer edge channel at Vbg = 2.5 V (νB = 2.93) with QPC transmission T1 = 0.59 and T2 = 0.5. Sliding FT was performed with a 0.45 V window. The top axis is the filling factor beneath the plunger gate. Frequencies for inner fi, middle fm, and outer fo edges are marked with black, blue and red dashed lines. The orange dashed line (pairing1, fp1) is the sum of fm and fo, and the violet dashed line (tripling, ft) is the sum of all three channel frequencies. Data were taken at VDC = 0 V, with a full set of their bias voltage dependence provided in Supplementary Movie 5. Prominent signals between 1 < νpg < 2 (above 250 V−1) are associated with electron tripling ft. Weaker signals at low frequencies (~100 V−1) correspond to fo and fp1. In this regime, the inner edge has been already expelled from beneath the plunger gate, while the middle and outer edges remain beneath the plunger gate and are slightly displaced from the graphene crystal edge (supplementary information section VI for details). d, Gate–spectroscopy obtained from outer edge channel interference, with T1 = 0.78 and T2 = 0.81, at VDC = − 55 μV. The orange dashed line here (pairing2, fp2) corresponds to the sum of fm and fi. Full bias voltage–dependent gate spectroscopy is in Supplementary Movie 6. Lobe structures for all the channels are detailed in Supplementary Fig. 3.

Full size image

The coherent mixing and contributions of the three channels result in a pajama pattern shown in Supplementary Movie 7 that is even more complex than that for the pairing. Importantly, a non–negligible pairing contribution shown in the orange dashed line in Fig. 4c remains present and comes from the sum of the outer and middle channel frequencies. This suggests that pairing occurs only between the partitioned channel and the nearest neighbor channel, the middle one in this case. To ascertain this deduction, we have carried out another gate–spectroscopy in a different configuration in which we partitioned the middle channel, fully transmitted the outer channel, and localized the inner channel (see Fig. 4b). The resulting spectroscopy displayed in Fig. 4d clearly shows a pairing contribution coming from the sum of the middle and inner channels frequencies, confirming that this pairing occurs between partially transmitted and fully localized nearest neighbor channels.

Interestingly, the amplitude of the pairing peak is weaker in this configuration (also confirmed at slightly different filling factors in Supplementary Fig. 4b), while the middle and inner frequencies are visible. Here, the difference with the previous configurations at filling factor 2 is that the pairing involves channels belonging to two different Landau levels, that is, the zeroth and the first ones. Consequently, the edge channels are more spatially separated due to the large cyclotron gap compared to the case of pairing between the outer and middle edges which both belong to the zeroth Landau level. The fact that pairing intensity increases with smaller separations between channels strongly suggests that inter–channel Coulomb interactions play a crucial role in pairing and tripling.

Real-space distance between edge channels

A key question to assess the Coulomb interaction quantitatively is the real space distance between edge channels. As in optical interferometry, our gate–spectroscopy provides a very accurate measurement of the interfering path, which can in turn lead to the edge channel–to–gate distance δ(Vpg) by integrating the Vpg–dependence of an edge channel frequency (see Methods). The integration of frequency dispersion in Fig. 2a provides the representative edge distance between two channels at νB = 2, as shown in Fig. 5a. Additionally, Fig. 5b displays the distances among the three edges at νB = 3. Strikingly, despite a relatively smooth electrostatic potential around local top gate, the outer (red line) and middle (blue line) channels are very close, with a distance LMO comparable to or even smaller than the magnetic length \({l}_{{{\rm{B}}}}=\sqrt{h/2\pi eB}\), implying strongly interacting channels. For instance, we obtain LMO = 5.6 nm at Vpg = − 3 V with a magnetic length lB = 6.7 nm at B = 14 T. On the other hand, the inner channel (black line) that belongs to the first Landau level is located at \({L}_{{{\rm{IM}}}}\, \sim 35\,{{\rm{nm}}}\) (at Vpg = −3 V) away from the middle channel. This distance can be accounted for by the large cyclotron gap between the zeroth and first Landau levels of graphene. On the contrary, along the graphene crystal edges of the FPI, the QH edge channels are known to be all confined on a scale of the order of lB to the crystal edge18,22. We can thus outline the spatial structure of edge channels as well as the many–body Landau level spectra at the crystal edges and the pn junctions in our FPI with the schematics in Fig. 5c. This provides novel and accurate measurements of the inter–channel distances, which are crucial for a further theoretical assessment of Coulomb interactions between the channels. It is also consistent with our observation and interpretation of weaker pairing between the middle and inner channels at νB = 3 discussed above.

Fig. 5: Interferometric determination of edge channel–to–plunger gate distance.
figure 5

a δ represents the distance between edge channel-to-plunger gate. Black and red lines show δ as a function of plunger gate voltage at Vbg = 1.8 V, obtained by integrating each plunger gate frequency dispersion in Fig. 2a. The top schematics illustrate edge channel configurations in three plunger gate regimes. Calculation details are in the Methods section. b δ for three edge channels at Vbg = 2.33 V (νB = 2.8), derived from Fig. 4c. The distance LMO between the outer and middle channels is less than a magnetic length lB, whereas the inner is at a distance \({L}_{{{\rm{IM}}}} \sim 35\,{{\rm{nm}}}\) from the middle due to the large cyclotron gap between the zeroth and first Landau levels. c The center schematic illustrates an edge configuration with a partitioned outer edge channel (dashed red line), while the inner and middle edges are shown in the black and blue lines, respectively. The FPI is defined by gates surrounding the QPC and plunger gate (color-coded in yellow), with the crystal edge delineating the remainder. The top and bottom schematics illustrate the energy dispersion of the Landau levels along the crystal-defined and gate-defined edges, highlighting noticeable differences in edge positions. Previous studies (Refs. 18,22) have assessed the crystal edge dispersion, revealing edge channels confined to a few magnetic lengths from the crystal edge. At the pn junction, gaps of broken symmetry states open in the zeroth Landau level when the local filling factor νB(x) reaches every quarter filling, i.e., νB(x) = −1, 0, and 1 (refs. 36,37).

Full size image

Discussion

Inter–channel interactions typically result in fractions of the electron charge being redistributed in edge magnetoplasmons23,24,25,26,27. For two co–propagating channels with strong mutual interactions (or with equal edge velocities), electrons decompose into fast (charged) and slow (neutral) plasmonic modes, each evolving in both channels. Their dynamics, solved through the matrix scattering approach23 for edge magnetoplasmons, does not give rise, according to Ref. 8, to any dominant multiple electron tunneling whose contribution to dc transport vanishes at νB = 2 and νB = 3. A more recent theoretical work10 has taken into account charge discreteness and has considered the limit where all edges are totally pinched off at the QPCs. It has predicted that an electron entering the FPI generates neutral plasmons, so–called neutralons, which are absorbed by a second tunneling electron; this exchange of neutralons induces a dynamical attractive interaction, thus enhancing the average Fano factor, which could potentially reach 2. In addition to the assumption of strong pinched QPCs, this enhancement requires non–universal interaction parameters, thus couldn’t yet explain the robustness of pairing observed in various experimental contexts. In addition, correlated tunneling of three electrons or more is neglected as they are less probable, which seems plausible at higher filling factors as well. Note that at νB = 3 one expects strong enough inter–edge interactions to induce two neutral modes that could enhance neutralon exchange thus pairing dynamical attraction. The present observation of tripling at νB = 3 doesn’t favor such a mechanism, and can therefore, more generally, provide a selective criterion for theoretical explanations.

A possible scenario would consist of two or three electrons entanglement mediated by inter–edge interactions. It was shown in Ref. 28 that two electrons entangled through a double dot tend to bunch in the singlet state, leading to a doubled Fano factor, but to antibunch in the triplet state. In our setup, distinguishable edge states and valley components could offer alternative degrees of freedom to the spin.

Besides, it is worth mentioning a recent report on pairwise electron tunneling into large quantum dots29, reminiscent of the FPI configuration. In this context, some theoretical models predict a possible attraction–pairing–of localized electrons resulting from the minimization of the screened Coulomb interaction30, and even three electrons bunching in very specific configurations31.

A different explanation of the frequency doubling and tripling based on charging effects32,33, which has long obscured AB–dominated interferometry19, certainly deserves careful consideration. For strong capacitive coupling between the interfering edge and the bulk, designated by the Coulomb–dominated (CD) regime, and similarly to a single–electron transistor, the conductance should not depend on the magnetic field and rather oscillates with the gate voltage, which changes the occupancy of the device, leading to vertical lines in the B, VG plane. The interfering phase varies continuously according to the relation θ = −2πνϕ/ϕ0, thus is doubled or tripled at νB = 2 or νB = 3 respectively. In our FPI at νB = 2, we have observed, for the inner channel, a noteworthy crossover from the CD regime to the AB regime, with an increase in the filling factor on the h/2e2 quantum Hall plateau, as illustrated in Supplementary Fig. 8. Nonetheless, the pairing phenomenon gets simultaneously weaker (stronger) when the inner channel is CD (AB) (see Supplementary Fig. 8a,b,c,d). Moreover, a larger QH FPI with a size of 15 μm2 exhibits pairing exclusively at νB = 2, without the presence of the inner or outer channel frequencies (see Supplementary Fig. 2). In that case, no signature of the CD regime is observed, most likely due to a smaller charging energy. In addition, the theoretical analysis in Ref. 32 is valid in the presence of edge reconstruction, so that highly dense localized states in compressible stripes are close enough to the edges to feel strong edge–bulk interactions. Nonetheless, we have shown the absence of edge reconstruction at the crystal edges of our devices, thus pointing towards an incompressible bulk18. Although the question remains open, these concordant observations suggest that the CD regime is not related to the pairing and tripling phenomena, in agreement with the conclusions of Ref. 5. Beyond the edge–bulk interactions, interactions between the chiral edges need to be more carefully considered and could lead us to revisit the interpretation of such a transition9.

A concurrent work20 with a similar observation of frequency doubling proposes an explanation based on phase shifts induced by the discrete addition of charges in the inner channel strongly coupled to the outer one. The key idea is that the charge on the outer edge, which controls the FPI phase θ, is itself dependent, through inter–edge coupling, on the inner edge charge. In this model, the ground–state energy variations are expanded with respect to those of the charges on both channels. Thus, contrary to8,9, the plasmonic modes are ignored; which could be justified for a short enough inner edge where electron–hole pairs creation costs high energy. This also differs from modeling interactions by Gaussian fluctuating phase in order to fit the observed voltage dependence of the AB oscillations in Fig. 1a. In principle, one could generalize the same argument to νB = 3. Nonetheless, we don’t attribute the observed discontinuities in the pajama to phase jumps renormalized by inter–edge interactions, but rather to beating between AB oscillations of the outer channel and a pairing mode. The way these discontinuities vary with the bias voltage (see Supplementary Movie 4) would also question their emergence from a charge addition mechanism.

In addition, it is not yet established that a pure electrostatic approach could account for the electron transfer 2 by 2 observed in large quantum dots29 and for shot noise measurements in interferometers based on GaAs devices5,7. Indeed, for symmetric ac voltages at two QPCs, the Fano factor is given universally by the charge of the dominant tunneling process, independently on the form, strength and range of interactions, but can be increased by non–equilibrium excited states34 (as in Ref. 9). The argument in Ref. 20 is also based on a well–defined charge number for the outer edge, which is questionable for almost open QPCs for which pairing has been observed as well7. Therefore, correlated phenomena beyond this electrostatic approximation might enter into play in this electron pairing and tripling observed in QH interferometers.

Methods

Sample fabrication

The hBN–encapsulated graphene heterostructure was assembled from exfoliated flakes using the van der Waals pick–up technique17 and deposited onto a graphite flake serving as the back–gate electrode. The substrates are highly doped Si wafers with a 285nm thick SiO2 layer. The flake thicknesses are 27 nm for the graphite, 45.5 nm for the bottom hBN, and 27.5 nm for the top hBN. Contacts and electrostatic gates were patterned using e–beam lithography, and Cr/Au was deposited for the contacts after etching the heterostructure with a CHF3/O2 plasma. Pd was deposited for the electrostatic gates, preceded by a slight O2 plasma etching to remove resist residues on hBN and ensure a homogeneous electrostatic potential beneath the gate.

Measurements

All measurements were performed in a dilution fridge with a base temperature of 0.01 K at 14 T. The measurement setup and filtering are described in Refs. 12 and 22. Systematic current–voltage characteristics were measured in a four–terminal configuration as illustrated in Fig. 1a with an acquisition card (NI–6346 from National Instruments). IV curve takes about 10 s, with oversampling enabling us to average about 1000 samples per data point. The diagonal voltage drop across the interferometer was measured with a differential FET amplifier (DLPVA–100–F–D from Femto GmbH). A homemade multichannel 20–bit digital–analog converter (DAC) was used to adjust the various gate voltages, with noise levels below 7.5 nV/\(\sqrt{{{\rm{Hz}}}}\), and a long time resolution of 1ppm. The DAC electronic includes an ultra–stable voltage reference LTZ1000 from Linear Technology. Differential resistance data were obtained by numerically differentiating the current–voltage characteristics.

Checkerboard pattern

In the presence of a single harmonic numbered n, the oscillation dependence with bias voltage can be described by the functional form12:

$${G}_{n}^{{{\rm{osc}}}}= {A}_{n}\left[\beta \cos \left(n\times \left(2\pi \frac{\varphi }{{\phi }_{0}}-\frac{2L}{\hslash v}eV\beta \right)\right)\right.\\ \left.+\overline{\beta }\cos \left(n\times \left(2\pi \frac{\varphi }{{\phi }_{0}}+\frac{2L}{\hslash v}eV\beta \right)\right)\right]\exp \left(-\frac{{(eV)}^{2}}{{\sigma }_{n}^{2}}\right),$$
(1)

where β and \(\overline{\beta }\) are asymmetry parameters describing how symmetric is the voltage drop on the two sides of the interferometer. An is the nth harmonic oscillation amplitude. eV is the voltage applied between the source and drain. L is the length of the interfering channel between two QPCs, v is the edge channel velocity, and φ is the AB flux picked up by the electrons. The phenomenological Gaussian energy decay describing phase fluctuations of the interfering edge channel due to Coulomb interactions or the electric noise in the non–interfering edge channels35 fits best our data. The checkerboard pattern in Fig. 1e is very well reproduced by the sum of the three first harmonics \({G}^{{{\rm{osc}}}}={\sum }_{n}{G}_{n}^{{{\rm{osc}}}}\), with β = 0.4, \(\overline{\beta }=0.6\), A1 = 0.25e2/h, A2 = 0.052e2/h, A3 = 0.0125e2/h, σ1 = 100 μeV, σ2 = 80 μeV, and σ3 = 65 μeV, as shown in Fig. 1f. In the presence of several edge channel contributions to the oscillations, the oscillation dependence of edge channel i with bias voltage can be described by:

$${G}_{i}^{{{\rm{osc}}}}= {A}_{i}\left[{\beta }_{i}\cos \left(2\pi \frac{{\varphi }_{i}}{{\phi }_{0}}-\frac{2L}{\hslash {v}_{i}}eV{\beta }_{i}\right)\right.\\ \left.+\overline{{\beta }_{i}}\cos \left(2\pi \frac{{\varphi }_{i}}{{\phi }_{0}}+\frac{2L}{\hslash {v}_{i}}eV{\beta }_{i}\right)\right]\exp \left(-\frac{{(eV)}^{2}}{{\sigma }_{i}^{2}}\right),$$
(2)

with the same notation as above. Checkerboard patterns in Supplementary Fig. 10 are very well reproduced by the sum of the outer and pairing conductance \({G}^{{{\rm{osc}}}}={G}_{o}^{{{\rm{osc}}}}+{G}_{p}^{{{\rm{osc}}}}\) without harmonics.

Gate–to–edge channel distance from gate–spectroscopy

The gate–spectroscopy is a direct measure of the capacitance coupling between the gate and the interfering edge channels12. Assuming a distance δ between the gate and the interfering channel as drawn in the left inset in Fig. 5a, the lever arm of the gate is given by \(\alpha ({V}_{{{\rm{pg}}}})={L}_{{{\rm{pg}}}}\frac{\,{{\mbox{d}}}\,\delta ({V}_{{{\rm{pg}}}})}{\,{{\mbox{d}}}\,{V}_{{{\rm{pg}}}}}\), where Lpg = 1.5 μm is the gate edge length12. As a result, one can compute the displacement distance δ by integrating the gate–voltage dependence of the frequency of the considered channel: \(\delta ({V}_{{{\rm{pg}}}})=\frac{{\phi }_{0}}{B{L}_{{{\rm{pg}}}}}\int_{{V}_{{{\rm{pg}}}}^{{{\rm{c}}}}}^{{V}_{{{\rm{pg}}}}}{f}_{{{\rm{pg}}}}(V)\,{{\mbox{d}}}\,V\), using ΔA = ϕ0/B = αΔVpg = α/fpg. Figure 5b displays the resulting distances for the three channels at νB = 3 computed from Fig. 4c.