Nearly perfect spin polarization of noncollinear antiferromagnets

Abstract

Ferromagnets with high spin polarization are known to be valuable for spintronics—a research field that exploits the spin degree of freedom in information technologies. Recently, antiferromagnets have emerged as promising alternative materials for spintronics due to their stability against magnetic perturbations, absence of stray fields, and ultrafast dynamics. For antiferromagnets, however, the concept of spin polarization and its relevance to the measured electrical response are elusive due to nominally zero net magnetization. Here, we define an effective momentum-dependent spin polarization and reveal an unexpected property of many noncollinear antiferromagnets to exhibit nearly 100% spin polarization in a broad area of the Fermi surface. This property leads to the emergence of an extraordinary tunneling magnetoresistance (ETMR) effect in antiferromagnetic tunnel junctions (AFMTJs). As a representative example, we predict that a noncollinear antiferromagnet Mn₃GaN exhibits nearly 100% spin-polarized states that can efficiently tunnel through low-decay-rate evanescent states of perovskite oxide SrTiO₃ resulting in ETMR as large as 10⁴%. Our results uncover hidden functionality of material systems with noncollinear spin textures and open new perspectives for spintronics.

Introduction

Materials with high spin polarization have been of significant interest for applications in spintronics—a research field that exploits the spin degree of freedom for information technologies¹. Qualitatively, spin polarization can be understood as the extent to which the spin of electrons is aligned with a certain direction. Quantitatively, however, the spin polarization is not uniquely defined and can be referred either to the uneven number of up-spin and down-spin electrons at the Fermi energy or to the unbalanced (spin-polarized) currents carried by electrons with opposite spin orientations². Even in the latter case, the transport spin polarization appears to be different as determined from spin-dependent tunneling³ or ballistic transmission^4,5 experiments. Nonetheless, whatever the definition is used, a high degree of spin polarization, ideally 100%, is beneficial for spintronics. This is due to a stronger electric response that can be achieved in transport measurements. For example, half-metals—ferromagnetic materials that have only one spin state at the Fermi energy and thus 100% spin polarization⁶ (independent of the definition)—are supposed to exhibit an infinitely large tunneling magnetoresistance (TMR) if used as electrodes in magnetic tunnel junctions (MTJs)⁷.

The recent interest and progress in antiferromagnetic (AFM) spintronics^8,9 puts forward the spin degree of freedom in AFM metals and the AFM Néel vector as a state variable. For AFM metals, however, the concept of spin polarization and its relevance to the measured electric response becomes even more subtle. Most antiferromagnets host $\hat{P}\hat{T}$ and/or $\hat{T}\hat{t}$ symmetries, where $\hat{P}$ is space inversion, $\hat{T}$ is time reversal, and $\hat{t}$ is half a unit cell translation, which makes their band structures spin-degenerate and thus spin polarization vanishing. There exists however a class of antiferromagnets that have broken $\hat{P}\hat{T}$ and $\hat{T}\hat{t}$ symmetries and thus exhibit a spin-split band structure, including certain types of noncollinear^10,11 and collinear^12,13,14,15 antiferromagnets. Due to the alternating local crystallographic environment along the two magnetic sublattices the latter were dubbed altermagnets¹⁶. Recently, it has been proposed that the concept of altermagnetism can be extended to accommodate noncollinear spins and multiple local structure variations¹⁷.

In antiferromagnets with violated $\hat{P}\hat{T}$ and $\hat{T}\hat{t}$ symmetries, Kramers’ spin degeneracy is broken even in the absence of spin-orbit coupling, and hence these materials can support longitudinal spin-polarized currents along certain crystallographic orientations^11,18,19. Due to this property, while the net magnetization of these antiferromagnets is zero, their transport spin polarization is not, which allows using them as ferromagnets in spintronic devices. It is not obvious, however, how the net transport spin polarization of the antiferromagnets is related to their resistive response of a spintronic device such as, e.g., an AFM tunnel junction (AFMTJ)^{20,21,22,23,24,25}. In fact, it has been predicted that a large TMR in AFMTJs can occur even if the net currents are spin-neutral, i.e., the net transport spin polarization is zero²⁰. The TMR effect in these junctions relies on the conservation of the transverse momentum in the process of tunneling and controlled by matching the spin-polarized Fermi surfaces of the two AFM electrodes. As a result, the net spin polarization of the electrodes is less relevant, while the spin polarization of conduction channels plays an essential role²⁰.

In this work, we define an effective momentum-dependent spin polarization and reveal an unexpected property of many noncollinear antiferromagnets to exhibit nearly perfect spin polarization in a broad area of the Fermi surface. As a result, using these non-collinear antiferromagnets in AFMTJs leads to an extremely high (extraordinary) TMR effect.

Results

Spin polarization

Conduction channels are defined as propagating Bloch states in a metal electrode which are determined by transverse wave vector ${{\boldsymbol{k}}}_{{\|}}$, band number n, and spin ${{\boldsymbol{s}}}_{{{\boldsymbol{nk}}}_{{\|}}}$. Since ${{\boldsymbol{k}}}_{{\|}}$ is conserved in the tunneling process, it is the spin state of conduction channels in the electrodes that controls the TMR effect in AFMTJs.

The spin state can be quantified in terms of the net spin ${{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{\|}}}$ of conduction channels at the transverse wave vector k_||:

$${{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{||}}}=\mathop{\sum }\limits_{n}{{\boldsymbol{s}}}_{n{{\boldsymbol{k}}}_{{||}}}=\mathop{\sum }\limits_{n}\frac{{l}_{z}}{2\pi }\int \left\langle {\psi }_{n{\boldsymbol{k}}}\left|{\boldsymbol{s}}\right|{\psi }_{n{\boldsymbol{k}}}\right\rangle \delta \left({E}_{n{\boldsymbol{k}}}-{E}_{F}\right)d{k}_{z}$$

(1)

Here l_z is the lattice constant of the electrode along the transport z direction, $\left\langle {\psi }_{n{\boldsymbol{k}}}\left|{\boldsymbol{s}}\right|{\psi }_{n{\boldsymbol{k}}}\right\rangle$ is the spin expectation value for band n of energy E_nk and eigenfunction ψ_nk at wave vector ${\boldsymbol{k}}=\left({{\boldsymbol{k}}}_{{\|}},{k}_{z}\right)$, and E_F is the Fermi energy. For collinear AFM metals, spin ${{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{\|}}}$ is allowed to have only two directions: up, i.e., parallel to the Néel vector (that is parallel to one of the AFM sublattices), or down, i.e., antiparallel to the Néel vector. Its magnitude, ${s}_{{{\boldsymbol{k}}}_{{||}}}\equiv |{{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{\|}}}|={N}_{{{\boldsymbol{k}}}_{{\|}}}^{\uparrow }-{N}_{{{\boldsymbol{k}}}_{{\|}}}^{\downarrow }$, is determined by the number of conduction channels ${N}_{{{\boldsymbol{k}}}_{{\|}}}^{\uparrow,\downarrow }$ for up- (↑) and down- (↓) spin electrons at ${{\boldsymbol{k}}}_{{\|}}$. In this case, the net spin determines the spin polarization of conduction channels given by ${p}_{{{\boldsymbol{k}}}_{{\|}}}=\frac{{s}_{{{\boldsymbol{k}}}_{{\|}}}}{{\sum }_{{\boldsymbol{n}}}{{|}}{{\boldsymbol{s}}}_{{n{\boldsymbol{k}}}_{{\|}}}{{|}}}=\frac{{N}_{{{\boldsymbol{k}}}_{{\|}}}^{\uparrow }-{N}_{{{\boldsymbol{k}}}_{{\|}}}^{\downarrow }}{{N}_{{{\boldsymbol{k}}}_{{\|}}}}$, where ${N}_{{{\boldsymbol{k}}}_{{\|}}}$ is the total number of conduction channels at ${{\boldsymbol{k}}}_{{\|}}$.

For collinear sublattice magnetizations, in the absence of spin-orbit coupling, spin is conserved in the tunneling process, and therefore transmission at ${{\boldsymbol{k}}}_{{\|}},T({{\boldsymbol{k}}}_{{\|}})$, is controlled by matching the spin components of the wave functions in the electrodes. For example, for an AFMTJ with parallel (P) Néel vectors of the two AFM electrodes, $T({{\boldsymbol{k}}}_{{\|}})$ is large, while for antiparallel (AP) Néel vectors, $T({{\boldsymbol{k}}}_{{\|}})$ is small due to a mismatch of the spin states in the AFM electrodes. As a result, the total transmission for the P state (T_P) is larger than that for the AP state (T_AP), leading to a non-zero TMR ratio, ${TMR}=({T}_{P}-{T}_{{AP}})/{T}_{{AP}}$.

On the contrary, for noncollinear AFM metals, spin is not a good quantum number and, in general, is not conserved in the tunneling process (even in the absence of spin-orbit coupling). The spin magnitude and direction vary depending on ${{\boldsymbol{k}}}_{{\|}}$ and n. Nevertheless, one can define an effective spin polarization,

$${{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{||}}}=\frac{{{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{||}}}}{{\sum }_{n}|{{\boldsymbol{s}}}_{{n{\boldsymbol{k}}}_{{||}}}|},$$

(2)

as a vector that has different magnitudes and orientations at different ${{\boldsymbol{k}}}_{{\|}}$. Due to being ${{\boldsymbol{k}}}_{{\|}}$-dependent, the effective spin polarization is different from the conventional spin polarization which is defined with respect to a global spin-quantization axis. As seen from the definition, the spin polarization magnitude, ${p}_{{{\boldsymbol{k}}}_{{\|}}}\equiv {{|}}{{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{\|}}}{{|}}$, is equal to 100% when spins ${{\boldsymbol{s}}}_{n{{\boldsymbol{k}}}_{{\|}}}$ are parallel in all conduction channels n at ${{\boldsymbol{k}}}_{{\|}}$ or only one conduction channel is present. This situation is reminiscent of the collinear case, where spin is conserved in the process of tunneling. As a result, matching the net spins ${{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{\|}}}$ in the electrodes can be used as the necessary requirement for large transmission $T({{\boldsymbol{k}}}_{{\|}})$ in the areas of the Brillouin zone where ${p}_{{{\boldsymbol{k}}}_{{\|}}}$ is close to 100%. On the contrary, at those ${{\boldsymbol{k}}}_{{\|}}$ where there are a few conduction channels with non-collinear ${{\boldsymbol{s}}}_{n{{\boldsymbol{k}}}_{{\|}}}$, spin is not conserved and thus ${{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{\|}}}$ could not serve as a proper measure of TMR in the spirit of Julliere’s formula⁷.

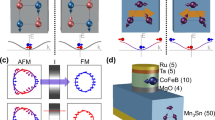
An important implication following from this observation, is the possibility of having a 100% spin polarization in non-collinear antiferromagnets. To illustrate this property, we consider a simple tight-binding model of a Kagome lattice with magnetic moments forming a noncollinear AFM configuration, as shown in Fig. 1a. This magnetic structure mimics a noncollinear two-dimensional (2D) antiferromagnet with broken $\hat{P}\hat{T}$ and $\hat{T}\hat{t}$ symmetries. Assuming one orbital per atom with exchange-split on-site energies ${E}_{i}^{\uparrow,\downarrow }={E}_{i}\pm \frac{\Delta }{2}\left(i=\mathrm{1,2,3}\right)$ and spin-independent nearest-neighbor hopping t, we arrive at the band structure $E({\boldsymbol{k}})({\boldsymbol{k}}={k}_{x},{k}_{y})$ that consists of six bands with k-dependent spin expectation values, as shown in Fig. 1b (see Methods for details of the calculation). Figure 1c, d show magnitudes ${p}_{k}\equiv {{|}}{{\boldsymbol{p}}}_{k}{{|}}$ and polar angles φ of the calculated transport spin polarization ${{\boldsymbol{p}}}_{{k}_{y}}$ (here we assume x-direction for transport) as a function of transverse wave vector k_y and the Fermi energy E_F. It is seen that while ${{\boldsymbol{p}}}_{{k}_{y}}$ is oriented in different directions (Fig. 1d), its magnitude is nearly 100% (indicated by red color in Fig. 1c) in a broad range of E_F. Only at small E_F, ${{|}}{{\boldsymbol{p}}}_{{k}_{y}}{{|}}$ is significantly reduced due to the overlap of bands with different spin orientations (Fig. 1c). Qualitatively, the large spin polarization is sustained in a broad range of k_y and E_F and only at small values of the spin splitting Δ it gets reduced (Supplementary Fig. S1²⁶).

Fig. 1: Spin polarization of a noncollinear Kagome antiferromagnet.

a Kagome lattice with non-collinear AFM structure of magnetic moments. b Calculated band structure of the Kagome lattice for Δ/t = 1.5. Arrows indicate the spin expectation values. Spin magnitudes are shown in color. c, d Map of the spin polarization vector ${{\boldsymbol{p}}}_{{k}_{y}}$ as a function of k_y and E_F for the Kagome lattice (a) for $\Delta /t=1.5$. ${{\boldsymbol{p}}}_{{k}_{y}}$ vectors lie in the x-y plane $({p}_{z}=0)$. Their magnitudes ${p}_{k}\equiv {{|}}{{\boldsymbol{p}}}_{k}{{|}}$ (c) and polar angles φ (d) are depicted in color.

Extraordinary TMR

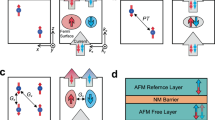
In three-dimensional (3D) spin-split antiferromagnets, the Fermi surface can form regions with 100% spin polarization in a two-dimensional (2D) Brillouin zone (2DBZ) perpendicular to the transport direction. These fully spin-polarized Bloch states can generate a very large TMR effect in the associated AFMTJs (Fig. 2e). The mechanism of such TMR is schematically illustrated in Fig. 2f showing conduction between left and right AFM electrodes for parallel (P) (top) and antiparallel (AP) (bottom) Néel vectors in k-space. The electrodes have fully spin-polarized conduction channels indicated in Fig. 2f by two crossing ellipses with the spin polarization vector having different orientation θ (indicated by varying color). If electronic states in these channels dominate transmission, TMR in such AFMTJ is expected to become virtually infinite. This is due to the spin-state match of the 100% spin-polarized conduction channels in the left and right electrodes for parallel-aligned AFMTJ and the spin-state mismatch for antiparallel. In contrast to the ordinary TMR in conventional MTJs with ferromagnetic (FM) electrodes (Fig. 2a, b) and in AFMTJs with collinear exchange-split AFM (altermagnetic) electrodes (Fig. 2c, d), where the spin polarization is defined with respect to the global quantization axis, the predicted TMR effect (Fig. 2e, f) relies on of the momentum-dependent spin polarization of a non-collinear antiferromagnet, which may have different orientations at different ${{\boldsymbol{k}}}_{{\|}}$ (Eq. 2). While such TMR seems qualitatively similar to the ultimately infinite TMR in MTJs with ideal half-metallic electrodes, there is a conceptual difference between the two effects. In nominal half metals, the fully spin-polarized conduction arises from the presence of only one-spin bands at the Fermi energy, resulting in the global 100% spin polarization of the electric current, whereas in non-collinear antiferromagnets, the fully spin-polarized conduction occurs only within a given ${{\boldsymbol{k}}}_{{\|}}$-defined conduction channel with the global spin polarization of electric current being incomplete (or even possibly zero). Therefore, since the mechanism of the giant TMR effect in non-collinear AFMTJs is conceptually different from the ordinary TMR in collinear MTJs and AFMTJs, we dub it extraordinary TMR (ETMR).

Fig. 2: Schematics of different types of tunnel junctions and TMR effects.

a Schematics of a conventional MTJ where two ferromagnetic (FM) electrodes are separated by a tunnel barrier. b Mechanism of TMR in a conventional MTJ. Conduction (indicated by block arrows) between left and right FM electrodes for parallel (P) and antiparallel (AP) magnetization (indicated by large arrows). Red and blue circles denote the Fermi surfaces of the ferromagnet for up-spin (small red arrows) and down-spin (small blue arrows) electrons. Angle θ refers to the spin orientation with respect to the magnetization in the left electrode. c Schematics of an AFMTJ with collinear exchange-split AFM electrodes (C-AFMTJ). d Mechanism of TMR in C-AFMTJ. Conduction between left and right AFM electrodes for P and AP Néel vectors (indicated by double-arrows). Red and blue ellipses denote the Fermi surfaces of the antiferromagnet for up- and down-spin electrons. Angle θ refers to the spin orientation with respect to the Néel vector in the left electrode. e Schematics of an AFMTJ with non-collinear AFM electrodes (NC-AFMTJ). f Mechanism of ETMR. The NC-AFM electrodes have fully spin-polarized conduction channels within the area indicated by crossing ellipses with the spin polarization vector having different orientation θ (indicated by varying color). Electrons in these channels can efficiently tunnel through a tunnel barrier due to its low-decay-rate evanescent states supporting transmission. Matching (mismatching) of the 100% polarized conduction channels in the two electrodes for the P (AP) state produces ETMR.

To provide the required efficient tunneling of the fully spin-polarized states, low-decay-rate evanescent states in the tunneling barrier need to support their transmission. Therefore, for observing ETMR, in addition to 100% spin-polarized conduction channels in the AFM electrodes, their distribution in the 2DBZ needs to be matched to the distribution of the low-decay-rate evanescent states in the insulator at the Fermi energy. Thus, we identify two important properties which may exhibit non-collinear AFM metals and the associated AFMTJs: nearly 100% transport spin polarization and ETMR.

Spin polarization of Mn₃GaN (001)

In the following, we demonstrate that these properties can be observed in practice. As a representative example of a noncollinear antiferromagnet, we consider antiperovskite Mn₃GaN, and show, based on density-functional theory (DFT) calculations (see Methods for details), that this antiferromagnet hosts conduction channels with nearly 100% effective spin polarization in a broad area of the Fermi surface. We then show that these highly spin-polarized states in antiperovskite Mn₃GaN match the evanescent states with low decay rates in perovskite oxide SrTiO₃ resulting in ETMR as large as 10⁴ % in Mn₃GaN/SrTiO₃/Mn₃GaN (001) AFMTJs.

Mn₃XN-type (X = Ga, Sn, Ni …) antiperovskite crystals have a cubic structure similar to perovskites, except the positions of anions and cations being interchanged. The frustrated Mn-kagome lattice in the (111) plane favors a noncollinear AFM ordering, resulting in interesting spin-dependent properties^{27,28,29,30,31}. Figure 3a shows the atomic and magnetic structure of Mn₃GaN, where Mn magnetic moments form a 120° chiral configuration within the (111) plane (Fig. 3b). Such a Γ_5g noncollinear AFM structure breaks $\hat{P}\hat{T}$ and $\hat{T}\hat{t}$ symmetries, resulting in a spin-polarized Fermi surface (Supplementary Fig. S2²⁶) and hence spin-polarized conduction channels.

Fig. 3: Atomic structure, spin texture and effective spin polarization at the Fermi surface of Mn₃GaN.

Atomic and magnetic structure of antiperovskite Mn₃GaN in the noncollinear ${\Gamma }_{5g}$ AFM configuration in 3D view (a) and projected to the (111) plane with ${\hat{{\rm{M}}}}_{\bar{1}10}$ and ${\hat{C}}_{\bar{1}10}$ symmetries indicated (b). Components of spin ${{\boldsymbol{s}}}_{{n{\boldsymbol{k}}}_{{\|}}}=({s}_{{n{\boldsymbol{k}}}_{{\|}}}^{x},{s}_{n{{\boldsymbol{k}}}_{{\|}}}^{y},{s}_{n{{\boldsymbol{k}}}_{{\|}}}^{z})$ (c) and spin magnitudes ${s}_{{n{\boldsymbol{k}}}_{{\|}}}\equiv {{{|}}{\boldsymbol{s}}}_{n{{\boldsymbol{k}}}_{{\|}}}{{|}}$ (d) for five bands (labeled by index n) contributing to the Fermi surface of Mn₃GaN and plotted in the 2DBZ of Mn₃GaN (001). Components of the effective spin polarization ${{\boldsymbol{p}}}_{{\boldsymbol{k}}_{{\|}}}=({p}_{{{\boldsymbol{k}}}_{{\|}}}^{x},{p}_{{{\boldsymbol{k}}}_{{\|}}}^{y},{p}_{{{\boldsymbol{k}}}_{{\|}}}^{z})$ (e) and polarization magnitude ${p}_{{{\boldsymbol{k}}}_{{\|}}}\equiv {{|}}{{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{\|}}}{{|}}$ (f).

Figure 3c shows the calculated spin components ${{\boldsymbol{s}}}_{{n{\boldsymbol{k}}}_{{\|}}}=({s}_{{n{\boldsymbol{k}}}_{{\|}}}^{x},{s}_{{n{\boldsymbol{k}}}_{{\|}}}^{y},{s}_{{n{\boldsymbol{k}}}_{{\|}}}^{z})$ for each of five bands (labeled by index n) contributing to the Fermi surface of Mn₃GaN (001). While all bands are spin textured, the largest contribution to the total spin ${{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{\|}}}={\sum }_{n}{{\boldsymbol{s}}}_{n{{\boldsymbol{k}}}_{{\|}}}$ (Fig. 3c, rightmost panels) comes from bands 3 and 4 that have the largest Fermi surfaces (Fig. 3c, panels labeled by n = 3 and n = 4). Band 3 has a pronounced cross feature in its spin texture, while band 4 reveals the largest spin values along the diagonal lines close to the corners of the 2DBZ (Fig. 3d). It is notable that for all bands, ${s}_{{{\boldsymbol{k}}}_{{\|}}}^{z}$ vanishes along the diagonals, [110] and $[\bar{1}10]$, in the 2DBZ (Fig. 3c, third row). This is due to mirror symmetry ${\hat{M}}_{\bar{1}10}$ and two-fold rotation symmetry ${\hat{C}}_{\bar{1}10}$ (Fig. 3b) supporting transformations of the spin component ${s}_{{{\boldsymbol{k}}}_{{\|}}}^{z}$ at wave vector ${{\boldsymbol{k}}}_{{\|}}=({k}_{x},{k}_{y})$, as follows from ${\hat{{\rm{M}}}}_{\bar{1}10}{s}_{{k}_{x}{k}_{y}}^{z}={-s}_{{k}_{y}{k}_{x}}^{z}$ and ${\hat{{\rm{C}}}}_{\bar{1}10}{s}_{{k}_{x}{k}_{y}}^{z}={-s}_{{-k}_{y}-{k}_{x}}^{z}$. As a result, ${s}_{{{\boldsymbol{k}}}_{{\|}}}^{z}$ is antisymmetric with respect to diagonals [110] and $[\bar{1}10]$ of the 2DBZ and zero at the diagonals (see also Supplementary Fig. S3²⁶).

All these features lead to the net spin texture with the largest ${s}_{{{\boldsymbol{k}}}_{{\|}}}{{\equiv }}{{|}}{{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{\|}}}{{|}}$ appearing around the ${k}_{x}=0$ and ${k}_{y}=0$ lines in the 2DBZ, forming a cross pattern, and at the diagonal lines close to the corners of the 2DBZ (Fig. 3d, rightmost panel). This spin texture is mirrored by the momentum-dependent spin polarization ${{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{\|}}}$. As seen from Fig. 3e, the ${p}_{{{\boldsymbol{k}}}_{{\|}}}^{i}(i=x,y,z)$ components are reminiscent to the ${s}_{{{\boldsymbol{k}}}_{{\|}}}^{i}$ components (Fig. 3c, rightmost panels), and the cross pattern featuring the distribution of ${s}_{{{\boldsymbol{k}}}_{{\|}}}$ (Fig. 3d, rightmost panel) is mimicked by the distribution of ${p}_{{{\boldsymbol{k}}}_{{\|}}}{{\equiv }}{{|}}{{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{\|}}}{{|}}$ in Fig. 3f.

The most important observation following from these results is nearly 100% spin polarization in a broad area of the 2DBZ of Mn₃GaN (001), especially around the ${k}_{x}=0$ and ${k}_{y}=0$ lines away from the zone center (Fig. 3e). This feature emerges due to bands 3 and 4 having nearly the same spin orientation around these lines and no other bands appearing in these regions (Fig. 3c). The somewhat reduced spin polarization near the zone center is caused by overlap of the non-collinear spin states in bands 1, 2, 3, and 4. Interestingly, we observe that some regions in the 2DBZ of Mn₃GaN (001) exhibit a persistent spin texture, where spins in relatively broad region of the 2DBZ are pointing in the same direction (Supplementary Fig. S4). We note however that this persistent spin texture is not symmetry enforced like that predicted in Ref. ³², but results from specific type of interactions intrinsic to a particular non-collinear antiferromagnet.

ETMR in Mn₃GaN/SrTiO₃/Mn₃GaN (001) AFMTJs

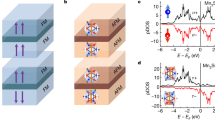
As was discussed above, the appearance of 100% spin polarized states in a non-collinear AFM metal can be detected via the ETMR effect using an AFMTJ that supports efficient tunneling of these states. This requires an insulator whose complex band structure exhibits the distribution of the lowest-decay-rate evanescent states in the 2DBZ similar to the distribution of the 100% spin-polarized conduction channels in the AFM electrode. It appears that perovskite SrTiO₃ (Fig. 4a) satisfies this condition³³. Figure 4b shows the lowest decay rate ${\kappa }_{{{\boldsymbol{k}}}_{{\|}}}$ of the evanescent states in SrTiO₃ (001) in the 2DBZ (see Methods for details of these calculations). It is evident that the distribution of ${\kappa }_{{{\boldsymbol{k}}}_{{\|}}}$ exhibits a cross pattern alike the distribution of the spin polarization ${p}_{{{\boldsymbol{k}}}_{{\|}}}$ in Mn₃GaN (001) (Fig. 3f). Such matching between the high-${p}_{{{\boldsymbol{k}}}_{{\|}}}$ and low-${\kappa }_{{{\boldsymbol{k}}}_{{\|}}}$ areas in the 2DBZ suggests that a Mn₃GaN/SrTiO₃/Mn₃GaN (001) AFMTJ can be employed to detect the perfectly spin-polarized states in Mn₃GaN by measuring the ETMR effect.

Fig. 4: ETMR effect in Mn₃GaN/SrTiO₃/Mn₃GaN (001) AFMTJ.

a Atomic structure of perovskite oxide SrTiO₃. b The lowest decay rate ${\kappa }_{{{\boldsymbol{k}}}_{{\|}}}$ of the evanescent states of SrTiO₃ (001) in the 2DBZ calculated at the energy close to the bottom of the conduction band. c Atomic structure of the AFMTJ. The Néel vectors of the Mn₃GaN electrodes lie in the [111] plane (not shown) and can be parallel or antiparallel. d Layer-resolved density of states (LDOS) for parallel Néel vectors. Calculated ${{\boldsymbol{k}}}_{{\|}}$-resolved transmission in the 2DBZ for the AFMTJ for parallel (P) (e) and antiparallel (AP) (f) alignment of the Néel vector in Mn₃GaN electrodes. g Total transmission and ETMR ratio as functions of energy.

Due to similar atomic structures and lattice constants, high-quality crystalline Mn₃GaN/SrTiO₃/Mn₃GaN (001) AFMTJs are feasible in practice. In fact, epitaxial Mn₃GaN films have been grown on SrTiO₃ revealing high crystallinity of their interface structure³⁴. Figure 4c shows the atomic structure of the AFMTJ that is used in our calculations. Here a 3-unit-cell SrTiO₃ (001) barrier layer is placed between 2.5-unit-cell Mn₃GaN layers. The layers are connected across Mn₂N/TiO₂ interfaces which have the lowest energy among other interfaces³⁵. We find that a wide band gap of SrTiO₃ is well maintained across the junction (Fig. 4d). The Mn₃GaN/SrTiO₃/Mn₃GaN (001) structure in Fig. 4c is then used as the scattering region of the AFMTJ connected to two semi-infinite Mn₃GaN (001) electrodes for transmission calculations (see Methods for details).

We find for the P state, where the Neél vectors of the two electrodes are parallel, ${T}_{P}({{\boldsymbol{k}}}_{{\|}})$ is strongly enhanced in a cross-pattern area of the 2DBZ, resulting from the high-${{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{\|}}}{\small{-}}{\rm{low}}{\tiny{-}}{\kappa }_{{{\boldsymbol{k}}}_{{\|}}}$ matching (Fig. 4e). We note that, as follows from Supplementary Section E, the interface structure of the AFMTJ maintains bulk-like features of the spectral density (Supplementary Fig. S5a) and its spin polarization (Supplementary Fig. S5b) in Mn₃GaN and the decay rate in SrTiO₃ (Supplementary Fig. S5c). In contrast, for the AP state, where the Neél vectors of the two electrodes are antiparallel, while the largest ${T}_{{AP}}({{\boldsymbol{k}}}_{{\|}})$ also appears at the cross-pattern area, it is significantly reduced compared to ${T}_{P}({{\boldsymbol{k}}}_{{\|}})$ due to reversed ${{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{\|}}}$ in the two electrodes (Fig. 4f). As a result, the total transmission T_AP is much smaller than T_P, producing TMR as large as ~1.8 × 10⁴% (Fig. 4g). This TMR value is gigantic, significantly larger than the values known for conventional MTJs and reminiscent to an infinitely large TMR expected for MTJs based on ideal half-metallic electrodes. In fact, estimating the spin polarization P of the electrodes with Julliere’s formula⁷ ${TMR}=\frac{{2P}^{2}}{1-{P}^{2}}$, we obtain P ≈ 99.99%. This extraordinary behavior of the Mn₃GaN/ SrTiO₃/Mn₃GaN (001) AFMTJ is due to the property of antiperovskite Mn₃GaN to exhibit fully spin-polarized electronic states that can efficiently tunnel through perovskite SrTiO₃ while preserving their spin state—the signature of the ETMR effect.

We note that in our calculation, the Fermi energy (E_F) of the AFMTJ lies near the conduction band minimum (CBM) of SrTiO₃ (Fig. 4d), while it is expected to appear well within the band gap of the insulator. This is due to the underestimated band gap of SrTiO₃ resulting from the well-known deficiency of DFT to correctly describe the excited states. Such a shortage, however, does not affect our main conclusions, since the ETMR appears not only for E = E_F but also in a broad energy window around E_F (Fig. 4g). Especially, we obtain even larger ETMR value of ~2.3 × 10⁵% at E = E_F −0.25 eV, well inside the band gap of SrTiO₃, indicating the validity of our results. This enhancement of the ETMR ratio at E = E_F −0.25 eV followed by some reduction at E = E_F −0.5 eV (Fig. 4g) clearly correlates with the appearance of 100% spin polarization in the 2DBZ of Mn₃GaN at different energies (Supplementary Fig. S6). In addition, we find that the cross feature of the evanescent states persists much deeper in the band gap of SrTiO₃ (Supplementary Fig. S7²⁶), suggesting that independent of the band offset between Mn₃GaN and SrTiO₃, matching between the highly polarized conducting channels in Mn₃GaN and low decay rate evanescent states in SrTiO₃ is well maintained. Note that the TMR ratio is reduced for energies above the CBM of SrTiO₃, which is expected since at the energies within the conduction band of SrTiO₃, the tunneling mechanism of conduction breaks down (Fig. 4g).

We also note that our calculations neglect the effects of spin-orbit coupling which may lead to spin mixing affecting the spin polarization and ETMR. We find, however, that taking spin-orbit coupling into account does not change our main conclusions. This is evident from Supplementary Section H, which shows the effects of spin-orbit coupling on the spin polarization of bulk Mn₃GaN (Supplementary Figs. S8a, b) and ETMR in Mn₃GaN/SrTiO₃/Mn₃GaN AFMTJ (Supplementary Figs. S8c–f ). While quantitively SOC reduces the ETMR ratio from 1.8 × 10⁴% to 2.6 × 10³%, qualitatively the ETMR effect remains huge driven by the nearly perfect spin polarization of Mn₃GaN.

Discussion

In addition to the AFM ${\Gamma }_{5g}$ phase, there is another common noncollinear AFM configuration of antiperovskites known as the ${\Gamma }_{4g}$ phase^36,37. The AFM ${\Gamma }_{4g}$ phase is obtained from Γ_5g by rotating all magnetic moments about the [111] axis by 90°. The corresponding distribution of ${{\boldsymbol{s}}}_{{{\boldsymbol{k}}}_{{\|}}}$ in Mn₃GaN in the AFM Γ_4g state mirrors this rotation (Fig. 5a, leftmost panel). This spin rotation, however, does not change the patterns of ${s}_{{{\boldsymbol{k}}}_{{\|}}}$ and ${p}_{{{\boldsymbol{k}}}_{{\|}}}$ (Fig. 5b, c, leftmost panels) which remain the same as those for the Γ_5g phase. Therefore, the ETMR effect is also expected for Mn₃GaN/SrTiO₃/Mn₃GaN (001) AFMTJs with Mn₃GaN electrodes in the AFM ${\Gamma }_{4g}$ phase.

Fig. 5: Effective spin polarization of different noncollinear antiferromagnets.

Calculated components of spin polarization ${{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{\|}}}=({p}_{{{\boldsymbol{k}}}_{{\|}}}^{x},{p}_{{{\boldsymbol{k}}}_{{\|}}}^{y},{p}_{{{\boldsymbol{k}}}_{{\|}}}^{z})$ (a) and spin polarization magnitudes ${p}_{{{\boldsymbol{k}}}_{{\|}}}\equiv {{|}}{{\boldsymbol{p}}}_{{{\boldsymbol{k}}}_{{\|}}}{{|}}$ (b) for Mn₃GaN in the ${\Gamma }_{4g}$ phase, Mn₃Ir $({\Gamma }_{4g})$, Mn₃Pt $({\Gamma }_{4g})$, Mn₃NiN $({\Gamma }_{4g})$, Mn₃SnN $({\Gamma }_{5g})$, and Mn₃Sn.

Apart from Mn₃GaN, other noncollinear AFM metals can be used as electrodes in AFMTJs. Figure 5 shows the calculated spin texture and effective spin polarization at the Fermi surface for different noncollinear antiferromagnets. It is evident that all of them exhibit a nearly perfect spin polarization in a substantial portion of the 2DBZ. The effective use of this high spin polarization in the TMR experiment requires an appropriate choice of a crystalline insulator to match its low-decay-rate evanescent states to the highly polarized states in the antiferromagnet. Especially promising in this regard is Mn₃NiN which has ${p}_{{{\boldsymbol{k}}}_{{\|}}}\approx 100\%$ in a wide cross region around the 2DBZ center ($\bar{\Gamma }$ point) (Fig. 5c). This feature allows the use of the tunneling barriers, such as SrTiO₃ and MgO, in the respective AFMTJs: while the former supports efficient transmission along the ${k}_{x}=0$ and ${k}_{y}=0$ lines in the 2DBZ (Fig. 4b), the latter exhibits lowest decay rates around the $\bar{\Gamma }$ point³⁸. On the other hand, using a conventional MgO barrier in AFMTJs with Mn₃Sn electrodes seems not the best choice, due to the nearly zero spin polarization around the $\bar{\Gamma }$ point in Mn₃Sn (Fig. 4c). This may be a reason why the TMR in Mn₃Sn/MgO/Mn₃Sn AFMTJs appeared to be relatively low²⁴.

The are a few important requirements for observing the predicted ETMR effect. AFMTJs must have identical AFM electrodes to provide matching between their spin states in the momentum space. High quality and crystallinity of AFMTJs are required for conservation of transverse momentum ${{\boldsymbol{k}}}_{{\|}}$ in the process of tunneling. Defects in the barrier, such as oxygen vacancies, should be avoided because they can lead to diffuse scattering between different ${{\boldsymbol{k}}}_{{\|}}$ thus suppressing ETMR (similar to TMR in conventional MTJs³⁹). Also, measurements well below the Néel temperature are desirable, due to temperature-driven fluctuations of magnetic moments being detrimental for ETMR. Finally, measurements at a low bias voltage are required, since ETMR is expected to decrease with bias due to the mismatch of spin states at different energies.

We would like to emphasize that the momentum dependent spin polarization that is defined in this work is not the same as the transport spin polarization of non-collinear antiferromagnets in the diffusive transport regime^10,11. While the latter represents the net spin polarization of charge carriers when transport occurs along certain crystallographic directions and is defined with respect to a global quantization axis, the former has, in general, different quantization axes for different transverse wave vectors. As a result, even in those cases when the net spin polarization is zero, the effect resulting from the momentum-dependent spin polarization does not generally vanish. Observing this requires, however, ballistic transport regime which can be realized in AFMTJs or in metallic structures whose dimensions are comparable or less that the mean free path of electrons, such as, for example, an atomically sharp domain wall recently observed in antiferromagnets⁴⁰. Moreover, the concept of momentum dependent spin polarization is relevant not only to noncollinear antiferromagnets, but also to all materials hosting noncollinear spins in the momentum space. Particularly, nonmagnetic systems with broken space inversion symmetry are known to exhibit noncollinear spin textures due to spin-orbit coupling⁴¹. These systems may reveal a sizable ${p}_{{{\boldsymbol{k}}}_{{\|}}}$ that can be efficiently utilized in ballistic spintronic devices.

Overall, the unique property of noncollinear antiferromagnets to sustain a nearly perfect transport spin polarization opens unprecedented opportunities for spintronics. Functionalizing this property in AMFTJs allows an efficient electric detection and control of the AFM Néel vector as a state variable. While the latter can be achieved via the predicted ETMR effect, the former is envisioned due to the potentially strong spin-transfer torques in these AFMTJs^42,43. Therefore, noncollinear AFMTJs have potential to become a new standard for spintronics providing stronger magnetoresistive effects, few orders of magnitude faster switching speed, and much higher packing density than conventional MTJs.

Lastly, future generations of magnetic logic and memories are expected to operate at a sub 10 nm length scale that is comparable to or less than the mean free path of electrons. At these dimensions, ballistic transmission controls transport properties of materials, and thus the predicted nearly perfect spin polarization carried by electrons with noncollinear spins can be efficiently exploited in ballistic spintronic devices. Thus, our work opens a new paradigm for the investigation and application of spin-textured materials by employing momentum-dependent transport spin polarization.

Methods

Tight-binding model for a Kagome lattice

We consider a 2D Kagome lattice with non-collinear magnetic moments, as shown in Fig. 1a. Our tight-binding (TB) model assumes one orbital per atom with on-site spin splitting (Δ), spin-independent first-nearest neighbor hoping (t), and magnetic moments oriented along the local axes given by the unit vectors ${{\boldsymbol{m}}}_{j},j=\mathrm{1,2,3}$. The TB Hamiltonian in real space is given by

$$H=-t\sum _{\left\langle j{j}^{{\prime} }\right\rangle \alpha }{c}_{j\alpha }^{\dagger }{c}_{{j}^{{\prime} }\alpha }+\frac{\varDelta }{2}\sum _{j\alpha }\left({\boldsymbol{\sigma }}\cdot {{\boldsymbol{m}}}_{j}\right){c}_{j\alpha }^{\dagger }{c}_{j\alpha },$$

(3)

where ${c}_{j\alpha }^{\dagger }$ and ${c}_{j\alpha }$ are the creation and annihilation operators for site j and spin α, σ represents a vector of the Pauli matrices $({\sigma }_{x},{\sigma }_{y},{\sigma }_{z})$, and summation 〈$j{j}^{{\prime} }$〉 runs over the nearest-neighbor sites. Matrix elements of the TB Hamiltonian in the momentum space can then be written as follows:

$${H}_{\alpha {\alpha }^{{\prime} }}^{\, j{j}^{{\prime} }}\left({\boldsymbol{k}}\right)=\sum _{i}{e}^{i\, {\boldsymbol{k}}\cdot ({{\boldsymbol{R}}}_{i}+{{\boldsymbol{r}}}_{{j}^{{\prime} }}-{{\boldsymbol{r}}}_{j})}{H}_{\alpha {\alpha }^{{\prime} }}^{\, {jj}{\prime} },$$

(4)

where ${H}_{\alpha {\alpha }^{{\prime} }}^{\, {jj}{\prime} }$ are matrix elements of Hamiltonian (3) in real space, ${{\boldsymbol{r}}}_{j}$ is the position vector of atom j in the unit cell of the Kagome lattice, and ${{\boldsymbol{R}}}_{i}$ is the coordinate on the lattice cell i. With the three non-equivalent lattice sites, the TB matrix (4) has rank of 6. Its eigenvalues and eigenfunctions ψ_nk are calculated numerically using the built-in function Eigensystem in Mathematica v13.1. The spin expectation values for each Bloch state ψ_nk are calculated in the standard way: ${{\boldsymbol{s}}}_{n{\boldsymbol{k}}}=\frac{\hbar }{2}\left\langle {\psi }_{n{\boldsymbol{k}}}\left|{\boldsymbol{\sigma }}\right|{\psi }_{n{\boldsymbol{k}}}\right\rangle$, where ${\boldsymbol{k}}=({k}_{x},{k}_{x})$. To obtain the spin polarization of conduction channels at the Fermi energy E_F, we assume that x is the transport direction. Then ${{\boldsymbol{p}}}_{{k}_{y}}$ for a given transverse wave vector k_y is defined by

$${{\boldsymbol{p}}}_{{k}_{y}}\left({E}_{F}\right)=\frac{{\sum }_{n}{{\boldsymbol{s}}}_{n{k}_{y}}}{{\sum }_{n}\left|{{\boldsymbol{s}}}_{n{k}_{y}}\right|}$$

(5)

where the spin expectation values are

$${{\boldsymbol{s}}}_{n{k}_{y}}({E}_{F})=\frac{a}{\pi }\int {{\boldsymbol{s}}}_{n{\boldsymbol{k}}}\delta \left({E}_{n{\boldsymbol{k}}}-{E}_{F}\right)d{k}_{x}.$$

(6)

DFT calculations

Calculations are performed within density functional theory (DFT) using a plane-wave pseudopotential method implemented in Quantum-ESPRESSO⁴⁴. The ultrasoft pseudopotentials⁴⁵ and the generalized gradient approximation (GGA)⁴⁶ for exchange-correlation potential are employed in the calculations involving noncollinear magnetism. The plane-wave cut-off energy of 52 Ry and a 12 × 12 × 12 k-point mesh in the irreducible Brillouin zone are used to achieve self-consistency in the electronic structure calculations for bulk antiferromagnets and a 12 × 12 × 1 k-point mech in the calculations involving Mn₃GaN/SrTiO₃ (001) and Mn₃GaN/SrTiO₃/Mn₃GaN/SrTiO₃ (001) supercells used for AFMTJs with parallel and antiparallel Néel vector, respectively. The relaxed in-plane lattice parameters of SrTiO₃ a = b = 3.94 Å are assumed. Internal coordinates and the c-lattice constant of the supercell were relaxed until the force on each atom was less than 0.001 eV/Å. The resulting bond length between the Mn and O atoms at the Mn₂N/TiO₂ terminated Mn₃GaN/SrTiO₃ interface was found to be 2.087 Å.

The spin expectation values for each Bloch state and spin polarizations of the conduction channels are obtained using a 50×50×50 k-point mesh. The layer-resolved spectral density (i.e. the layer- and ${{\boldsymbol{k}}}_{{\|}}$-resolved density of states) of the relaxed Mn₃GaN/SrTiO₃/Mn₃GaN (001) structure is calculated using supercell calculations involving periodic boundary conditions with gaussian broadening of 0.01 eV using 50 × 50 k-points. The effects of spin-orbit interaction on spin polarization of bulk Mn₃GaN (001) and ETMR in Mn₃GaN/SrTiO₃/Mn₃GaN (001) AFMTJs are evaluated using fully relativistic PAW pseudopotentials and discussed in Supplementary Information (Section H), while in the main text, these effects are neglected.

The quantum-transport calculations are performed using PWCOND code^47,48 implemented within Quantum ESPRESSO. In the calculations, the relaxed Mn₃GaN/SrTiO₃/Mn₃GaN (001) structure is considered as the scattering region, ideally attached on both sides to semi-infinite Mn₃GaN leads. The ${{\boldsymbol{k}}}_{{\|}}$-resolved transmission is obtained using 100 × 100 k-points in the 2D Brillouin zone. The total transmission as a function of energy is calculated using 50 × 50 k-points in the 2D Brillouin zone.

The decay rates of evanescent states in SrTiO₃ are obtained from its complex band structure calculated using PWCOND. An arbitrary wave vector consists of a component parallel to the interface, ${{\boldsymbol{k}}}_{{\|}}$, which is conserved during tunneling, and a component perpendicular to the interface, k_z. For each ${{\boldsymbol{k}}}_{{\|}}$, we calculate the dispersion relation $E=E({k}_{{\boldsymbol{z}}})$, allowing complex k_z=q+iκ. The imaginary part κ is the decay rate, so that the corresponding wave functions decay as $\sim {e}^{-\kappa z}$.

The figures are plotted using Matplotlib and FermiSurfer⁴⁹.