Introduction

Geotechnologies are an important instrument for monitoring, assessing, and forecasting processes within Earth systems, and the anticipation of the utility of spatial analysis and modeling in a variety of environmental disciplines and applications has been consistently high since the early 21st century1,2,3,4,5,6,7. Beyond its role as a means to enhance our understanding of nature, geospatial predictions have evolved into indispensable instruments for supporting local management practices towards environmental risks and natural disaster threats, guiding the planning and prioritization of technical, financial, and political decisions8,9,10. On a larger scale, spatial modeling results serve as crucial information for forecasting and understanding the consequences of socioeconomic development and climate change scenarios in alignment with achieving Sustainable Development Goals, facilitating coordinated responses to global challenges11,12.

With the rise of the availability of observational information from various domains, including remote sensing, implementing data-driven models, namely machine learning (ML) and deep learning (DL) algorithms, has gained significant popularity in geospatial tasks. Using mathematically similar approaches, ML and DL models have found applications in the whole diversity of territory analysis needs, such as land cover monitoring and natural resources inventorying5,13, accounting of ecosystems’ functioning14 and biodiversity assessments15,16, as well as disaster management, including fires3,17, floods18, and droughts19. With this domain flexibility, ML and DL approaches overcome the limitations of models based solely on physical equations requiring complex and specific process descriptions, which, with ensured computational efficiency, makes data-driven solutions exceptionally relevant for operational use20. However, the quality of data-driven spatial predictions and the potential challenges in consistently providing trustworthy results have recently garnered significant attention.

One of the most important concerns lies in the very nature of data-driven modeling-that is, the belief that knowledge can be obtained through observation and, further, out of the insights6. Other questions relate to the nuances of the practical implementation of various techniques of spatial analysis and prognosis and efficient and fair data handling, not least driven by the existing gap between domain specialists and applied data scientists, both underrepresented in each other’s fields.

The core aspect of geospatial modeling, distinguishing it from other data-driven applications, is the multitude of specific features characterizing environmental processes, which exhibit dynamic variability across spatial and temporal domains4. The limitations shaped by this context are reflected in numerous research. It has been shown that ignoring the spatial distribution of the data led to the deceptively high predictive power of the model due to spatial autocorrelation (SAC), while appropriate spatial model validation methods revealed poor relationships between the target characteristic-aboveground forest biomass and selected predictors21. Unaddressed spatial dependence between training and test sets influences the model generalization capabilities, as was shown in the example of the Earth observation data classification22. Another aspect is that in some cases, the locations of observation data differ from prediction areas, while strong clustering of samples poses challenges for data-driven model performance evaluation23. The temporal dynamics of the data used for spatial predictions is discussed as an important question to be considered, for instance, in exploring phenomena affected by environmental changes due to natural or anthropogenic impact. With that, the difficulty of balancing spatial and temporal variability of tracked features might arise to capture target phenomena consistently rather than making predictions using generally irrelevant dependencies based on the unreliable observation timeline5,24,25. Therefore, ML and DL spatial modeling implementation could be constrained by data issues, diminishing the reliability of output results, the model’s suitability for extrapolation beyond the training information, and, ultimately, its ability to accurately represent real-world processes.

Accounting for the spatial-temporal patterns of the data used for training at the model building is not the end of the journey toward model inference and its implementation beyond specific case studies. Understanding the accuracy of predictions is obligatory for applying a trained model, yet many studies lack statistical assessment and necessary uncertainty estimations, raising a question about the reliability and sufficiency of the results26. Uncertainty estimation is especially important in ML and DL geospatial applications where input data distribution may differ from the distribution of the data sample used for model building27. This phenomenon is called the out-of-distribution problem, giving the bias for spatial modeling28. For instance, the covariate shift of input features, the appearance of new classes that were not in the training sample, and the label shift can be observed. On the other hand, a change in labels while the distribution of input features remains the same can be another problem29. This urges both suitable and efficient approaches to measuring uncertainty correctly, as well as to account for it at the experimental planning and model development stages30.

Given the unique potential of geospatial predictions to mitigate sustainability threats, an overview of common challenges in data-driven geospatial modeling and the relevant approaches and tools to tackle these issues is of significant scientific and practical value. In addition to the existing literature background6,7,24,31,32, this scoping review aims to comprehensively address the limitations of data-driven geospatial modeling at both stages of model building and model deployment to capture the spatial distribution of target features. To discuss multidisciplinary issues laying in the specifics of spatial environmental data on the one hand and ML model development and deployment on the other, we gathered information using published materials from journals indexed in WoS and Scopus databases related to spatial environmental problems and information sources relevant to computational and data science fields. In addition to this, we covered the recent advances published in AI-related conferences, giving the pace of development in the AI field and simultaneously providing access to the best available solutions in terms of quality and efficiency.

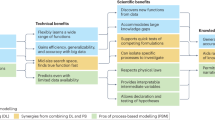
This paper is structured as follows. Providing a general pipeline for geospatial data-driven modeling, we give focus to challenges associated with using nonuniformly distributed real-world data from various environmental domains, including those from open sources. We further address data imbalance, SAC and unaccounted uncertainty limiting the reliability and robustness of spatial model predictions, aiming to provide a practical guide to support geospatial AI-based solutions in both research and practice (Fig. 1). Finally, we overview key areas for growth in data-driven spatial modeling, considering the development of ML and DL technologies and new technologies for data collection.

Fig. 1: General workflow for the tasks, including the geospatial modeling process and common issues relevant to each stage.
figure 1

The pipeline includes challenges typical for geospatial modeling and requires approaches to handle them. At each step of the modeling process, we have identified the main challenges, metrics, and solutions. Illustrated prediction and uncertainty rasters were created from the SoilGrids open data distributed under the Creative Commons CC-BY 4.0 (https://www.isric.org/explore/soilgrids).

Full size image

Data-driven approaches to forecasting spatial distribution of environmental features

This review focuses on geospatial data-driven approaches, meaning that models are built with parameters learned from observations’ data and aim to simulate new data minimally different from the “ground truth” under the same set of descriptive features. Among the standards guiding the implementation of data-driven model applications in general, CRISP-DM33 is the most well-known, which includes the following steps:

  • Understanding the problem and the data.

  • Data collection and feature engineering.

  • Model selection.

  • Model training, involving optimizing hyperparameters to fit the data type and shape.

  • Accuracy evaluation.

  • Model deployment and inference.

There are, however, other workflows with more detailed guidelines tailored to specific problems or more mature fields of data-driven modeling34. Recently, guidelines and checklists have been proposed for ecological niche modeling tasks helping to improve the reliability of outputs24,35, suggesting a standardized format for reporting the modeling procedure and results to ensure research reproducibility. It emphasizes the importance of disclosing details of each prediction-obtaining step, from data collection to model application and result evaluation. Similar logic can be applied to the other applications involving spatially distributed environmental data, giving nuances to each step.

Determined by the domain, for instance, conservation biology and ecology, natural resource management, climate monitoring, modeling of hazardous events occurrences, or others, collection of the observation data and the following preprocessing can be selected. This step involves gathering ground-truth data from specific locations and combining it with relevant environmental features, e.g., Earth observation images, weather and climate patterns, or other georeferenced characteristics. Importantly, while data describing various environmental processes require specific approaches for their pattern accounting, noise, and outlier elimination, most domains face the same issue: a lack of completeness and independence of observations in spatial gathering from point-based measurements.

The choice of a data-driven algorithm for the geospatial task depends on many factors, including the type of target variable, the amount of available information and calculation resources, and specific use cases of the trained model. Classification algorithms are employed for predicting categorical target variables for purposes of various domains, e.g., identification of land cover and land cover change5, cropland specifics36, pollution sources37, hazardous events susceptibility38,39, habitat suitability40, and others. Regression algorithms are applied to forecast the distribution of continuous target variables—for instance, soil41 and water42 quality characteristics’ assessment, vegetation data such as forest height43 and biomass44. Importantly, the same problem can be solved using both classification and regression approaches.

The chosen model could be used for the search for dependencies of the target feature distribution with descriptive features and their derivatives, while advances in DL methods allow considering spatial context as the feature per se5. Appropriate accuracy scores are selected based on the task, with a focus on controlling overfitting, while in the case of geospatial modeling, spatial bias is required to be considered. Notably, evaluation of the model performance against “gold standard” data with expert annotations is again limited by the availability of benchmark datasets and their reliability considering spatial and temporal dynamics of environmental phenomena32.

Finally, as an output of the data-driven spatial prediction tasks, model inference involves building maps with spatial predictions for the region of interest. Therefore, obtaining spatially distributed results of data-driven geospatial modeling is often called mapping15,17,19,21. For the deployment of the model, it is essential to understand the reliability of model outputs, which could be determined by the level of certainty of the model’s estimations.

In summary, while the general pipeline for data-driven modeling is well-established, geospatial tasks present cross-domain challenges due to the complexity of environmental data dynamics, limiting the direct application of the algorithms. Addressing these challenges is discussed further.

Imbalanced data

The problem of imbalanced data is one of the most relevant issues in environment-related research with a focus on spatial capturing of target events or features. Imbalance occurs when the number of samples belonging to one class or class (majority class[es]) significantly surpasses the number of objects in another class or class (minority class[es])45,46.

Despite real-world data often being imbalanced, most models assume uniform distribution and complete input information47. Thus, a nonuniform input data distribution poses difficulties when training models. The minority class occurrences are rare, and classification rules for predicting them are often ignored. As a result, test samples belonging to the minority classes are misclassified more frequently compared with test samples from the predominant classes. In geospatial modeling, one of the most frequent challenges is dealing with sparse or nonexistent data in certain regions or classes48,49. This issue arises from the high cost of data collection and storage, methodological challenges, or the rarity of certain phenomena in specific regions.

For instance, forecasting habitat suitability for species—species distribution modeling (SDM)—is a common task in conservation biology, and it relies on ML methods, often involving binary classification of species abundance. Although well-known sources such as the GBIF (the Global Biodiversity Information Facility) database50 provide numerous species occurrence records, absence records are few, while it is additionally difficult to establish such locations from the methodological point of view51. Another case is the capturing of anomalies, particularly relevant for ecosystem degradation monitoring, while related spatial tasks often involve the challenge of overcoming imbalanced data. For example, in pollution cases, such as oil spills occurring on both land and water surfaces, accurate detection and segmentation of oil spills from image analysis is vital for effective leak cleanup and protection of ecosystems having limited capability to resilience in front of anthropogenic loads. However, despite the regular collection of Earth surface images by various satellite missions, there are significantly fewer scenes of oil spills compared with images of clean water52. Similarly, detecting and predicting of hazardous events, such as, for instance, wildfires, struggle from the same problem53.

Weiss and Provost54 demonstrated that decision tree models perform better with balanced training datasets, as imbalance between classes can lead to skewed decision boundaries. The impact of class imbalance is closely tied to the sample size: smaller training sets lack sufficient minority class representation, making it challenging for the model to capture underlying patterns. Japkowicz55 found that increasing the training set size reduces the error rate associated with class imbalance, as larger datasets provide a more complete view of minority classes, enhancing the model’s capacity to differentiate between classes. Thus, given adequate data and manageable training times, class imbalance may have a minimal effect on overall model performance.

Approaches to measuring the problem of imbalanced data

Measuring class imbalance is essential for understanding the characteristics of a dataset, selecting appropriate modeling techniques, and making informed decisions, thus, approaches to quantifying class imbalance are extensively elaborated. One common and most straightforward method is to examine the class distribution ratio directly, which can be as extreme as 1:100, 1:1000, or even more in real-world scenarios. The minority class percentage (MCP) calculates the percentage of instances in the minority class. Gini index (GI) measures inequality or impurity among classes, indicating imbalance56. Shannon entropy (SE) is another way to measure non-uniformity or data substance and can be linked to imbalance through the entropy of the class distribution56. The Kullback-Leibler (KL) divergence measures the contrast between probability distributions, showing how close the observed class distribution is to a hypothetical balanced distribution57. In summary, higher values of GI, SE, and KL indicate a higher imbalance.

When dealing with class imbalance, it is crucial to use appropriate quality metrics to reflect model performance accurately. Standard accuracy metrics may mislead, especially when there is a significant class imbalance—for example, a model that always predicts the major class yielding a high accuracy but performs poorly for the minority class58. The F1 score, combining precision and recall, is a better alternative and is commonly used for imbalanced data. Another useful metric is the G-mean, which balances sensitivity and specificity and provides a more reliable performance assessment, especially in imbalanced datasets55,59.

Enhancing geospatial models with imbalanced data

The general problem of imbalanced data in ML is extensively observed46,47, while approaches relevant to geospatial modeling specifically are also worth discussing. Approaches to tackling imbalanced data problems in geospatial prediction tasks can be divided into data-level, model-level, and combined techniques.

Data-level approaches

Tabular data In terms of working with the data itself, the class imbalance problem can be addressed by modifying the training data through resampling techniques. There are two main ideas: oversampling the minority class and undersampling the majority class57,60, that can be applied randomly or in an informative way. Informative oversampling and undersampling may involve processing the data based on the location, such as generating artificial minority samples considering geographic distance or deletion of geographically close points of the majority class correspondingly. Figure 2 illustrates the issue of imbalanced data and solutions, including oversampling and undersampling techniques.

Fig. 2: Handling imbalance data for artificial species distribution generated data.
figure 2

A Point data generation using virtualspecies198 R package based on annual mean temperature and annual precipitation, obtained from WordlClim2 database. B Oversampling the minority class by SMOTE method with smotefamily199 R package. C Achieving a balanced dataset through random undersampling of the prevalent class. The image was created using the open-source Geographic Information System QGIS. Basemap is visualized from tiles by CartoDB, distributed under CC BY 3.0, based on the data from OpenStreetMap, distributed under ODbL (https://cartodb.com/basemaps). Boundaries used are taken from geoBoundaries Global Database (www.geoboundaries.org), distributed under CC BY 4.0.

Full size image

More complex methods for handling imbalanced data involve adding artificial objects to the minority class or modifying samples in a principled way. One popular approach is the synthetic minority oversampling technique (SMOTE)57, which combines both oversampling of the minority class and undersampling of the majority class. SMOTE creates new samples by linearly interpolating between minority class samples and their K-nearest neighbor minority class samples.

Being one of the most widely used in ML applications, the SMOTE technique has recently seen various modifications61,62. Since there are more than 100 SMOTE variants in total63, here we focus on those relevant to geospatial modeling. One widely used method for oversampling the minority class is the Adaptive synthetic sampling approach for imbalanced learning (ADASYN)64,65. ADASYN uses a weighted distribution that considers the learning difficulties of distinct instances within the minority class, generating more synthetic data for challenging instances and fewer for less challenging ones66. To address potential overgeneralization in SMOTE56,61, Borderline-SMOTE is proposed. It concentrates on minority samples that are close to the decision boundary between classes. These samples are considered to be more informative for improving the performance of the classification model on the minority class. Two techniques, Borderline-SMOTE1 and Borderline-SMOTE2, have been proposed, outperforming SMOTE in terms of suitable model performance metrics, such as the true-positive rate and an F-value67. Another approach is the Majority Weighted Minority Oversampling Technique (MWMOTE), which assigns weights to hard-to-learn minority class samples based on their Euclidean distance from the nearest majority class samples68. The algorithm involves three steps: selecting informative minority samples, assigning selection weights, and generating synthetic samples using clustering.

As for the limitations of discussed data-level approaches, oversampling, and undersampling may, given that they are widely used, lead to overfitting and introduce bias in the data56,63. First of all, it is difficult to understand the optimal class distribution given a dataset, while there is the risk of information loss when under-sampling the prevalent class and the risk of overfitting when over-sampling the minority class. Additionally, these techniques do not address the root cause of class imbalance and may not generalize well to unseen data60.

Image data Computer vision techniques applied to Earth observation tasks have gained their popularity in the analysis of remote sensing data69,70,71,72, therefore, examining approaches to overcoming data imbalance problems on the image level warrants a separate discussion.

Data augmentation is a fundamental technique for expanding limited image datasets73. It revolves around enriching training data by applying various transformations, such as geometric alterations, color adjustments, image blending, kernel filters, and random erasing. These transformations enhance both model performance and generalization. Geospatial modeling frequently uses data augmentation strategies to address specific challenges. For instance, experts employ a cropping-based augmentation approach in mineral perspective mapping, which generates additional training samples while preserving the spatial distribution of geological data74. DL-based oversampling techniques such as adversarial training, Neural Style Transfer, Generative Adversarial Networks (GANs), and meta-learning approaches offer intelligent alternatives for oversampling75. Neural Style Transfer stands out as a captivating method for generating novel images by extrapolating styles from external sources or blending styles among dataset instances76. For instance, researchers have harnessed the power of Neural Style Transfer alongside ship simulation samples in remote sensing ship image classification. This dynamic combination enhances training data diversity, resulting in substantial improvements in classification performance77. GANs, on the other hand, specialize in crafting artificial samples that closely mimic the characteristics of the original dataset. For instance, GANs have been used for data augmentation in specific domains, such as roof damage detection and partial discharge pattern recognition in Geographic Information Systems78,79. In the context of landslide susceptibility mapping, a notable research study introduces a GAN-based approach to tackle imbalanced data challenges, comparing its effectiveness with traditional methods such as SMOTE80.

Taking it a step further, researchers have unveiled a deeply supervised Generative Adversarial Network (D-sGAN) tailored for high-quality data augmentation of remote sensing images. This innovative approach proves particularly beneficial for semantic interpretation tasks. It not only exhibits faster image generation speed but also enhances segmentation accuracy when contrasted with other GAN models like CoGAN, SimGAN, and CycleGAN81.

It is worth noting that these advanced oversampling techniques are considered to be highly promising and not limited to image applications only82. Limitations of the discussed methods are mostly related to the model generalization and computational resources required to process image data.

Model-level approaches

Cost-sensitive learning Cost-sensitive learning involves considering the different costs associated with classifying data points into various categories. Instead of treating all misclassifications equally, it takes into account the consequences of different types of errors. For example, it recognizes that misclassifying a rare positive instance as negative (more prevalent) is generally more costly than the reverse scenario. The goal is to minimize both the total cost resulting from incorrect classifications and the number of expensive errors. This approach helps prioritize the accurate identification of important cases, such as rare positive instances, in situations where the class imbalance is a concern83.

Cost-sensitive learning finds application in spatial modeling, scenarios involving imbalanced datasets, or situations where the impact of misclassification varies among different classes or regions. Several studies have shown it is effective in this context84,85,86.

Boosting Boosting algorithms are commonly used in geospatial modeling because they are superior in handling tabular spatial data and addressing class imbalance85,87. They effectively manage both bias and variance in ensemble models.

Ensemble methods such as Bagging or Random Forest reduce variance by constructing independent decision trees, thus reducing the error that emerges from the uncertainty of a single model. In contrast, AdaBoost and gradient boosting train models consecutively and aim to reduce errors in existing ensembles. AdaBoost gives each sample a weight based on its significance and, therefore, assigns higher weights to samples that tend to be misclassified, effectively resembling resampling techniques.

In cost-sensitive boosting, the AdaBoost approach is modified to account for varying costs associated with different types of errors. Rather than solely aiming to minimize errors, the focus shifts to minimizing a weighted combination of these costs. Each type of error is assigned a specific weight, reflecting its importance in the context of the problem. By assigning higher weights to errors that are more costly, the boosting algorithm is guided to prioritize reducing those particular errors, resulting in a model that is more sensitive to the associated costs60. This modification results in three cost-sensitive boosting algorithms: AdaC1, AdaC2, and AdaC3. After each round of boosting, the weight update parameter is recalculated, incorporating the cost items into the process88,89. In cost-sensitive AdaBoost techniques, the weight of False Negative is increased more than that of False Positive. AdaC2 and AdaCost methods can, however, decrease the weight of True Positive more than that of True Negative. Among these methods, AdaC2 was found to be superior for its sensitivity to cost settings and better generalization performance with respect to the minor class60.

Combining model-level and data-level approaches

Modifications of the discussed techniques could be used as well. For instance, several techniques combine boosting and SMOTE approaches to address imbalanced data. One such method is SMOTEBoost, which synthesizes samples from the underrepresented class using SMOTE and integrates it with boosting. By increasing the representation of the minority class, SMOTEBoost helps the classifier learn better decision boundaries, and boosting emphasizes the significance of minority class samples for correct classification57,90,91. As for limitations, SMOTE is a complex and time-consuming data sampling method. Therefore, SMOTEBoost exacerbates this issue as boosting involves training an ensemble of models, resulting in extended training times for multiple models. Another approach is RUSBoost, which combines RUS (Random Under-Sampling) with boosting. It reduces the time needed to build a model, which is crucial when ensembling is the case, and mitigates the information loss issue associated with RUS92. Thus, the data that might be lost during one boosting iteration will probably be present when training models in the following iterations.

Despite being a common practice to address the class imbalance, creating ad-hoc synthetic instances of the minority class has some drawbacks. For instance, in high-dimensional feature spaces with complex class boundaries, calculating distances to find nearest neighbors and performing interpolation can be challenging56,57. To tackle data imbalances in classification, generative algorithms can be beneficial. For instance, a framework combining generative adversarial networks and domain-specific fine-tuning of CNN-based models has been proposed for categorizing disasters using a series of synthesized, heterogeneous disaster images93. SA-CGAN (Synthetic Augmentation with Conditional Generative Adversarial Networks) employs conditional generative adversarial networks (CGAN) with self-attention techniques to create high-quality synthetic samples94. By training a CGAN with self-attention modules, SA-CGAN creates synthetic samples that closely resemble the distribution of the minority class, successfully capturing long-range interactions. Another variation of GANs, EID-GANs (Extremely Imbalanced Data Augmentation Generative Adversarial Nets), focus on severely imbalanced data augmentation and employ conditional Wasserstein GANs with an auxiliary classifier loss95.

Autocorrelation

Autocorrelation is a widespread statistical characteristic observed in features across geographic space, indicating that the value at a specific data point is influenced by the values at its neighboring data points96. Within the environmental domain, autocorrelation is frequently observed resulting from the spatial continuity of natural phenomena, such as temperature, precipitation, or species occurrence patterns97,98. However, the data-driven approaches applied for the tasks of spatial predictions assume independence among observations. If SAC is not properly addressed, the geospatial analysis may result in misleading conclusions and erroneous inferences. Consequently, the significance of research findings may be overestimated, potentially affecting the validity and reliability of predictions7,99.

On the contrary, there could be environment-related tasks where autocorrelation is explored as the interdependence pattern between spatially distributed data not to be mitigated. For instance, based on an assessment of SAC catching regional spatial patterns in the LULC changes, a decision-support framework considering both land protection schemes adapted financial investment and greenway construction projects supporting habitats was developed100. Other examples are the enhancement of a landslide early warning system introducing susceptibility-related areas based on catching autocorrelation of landslide locations with rainfall variables101, and an approach to assessing the spatiotemporal variations of vegetation productivity based on the SAC indices, valuable for integrated ecosystem management102.

While the definition of SAC varies, in general, it integrates the principle that geographic elements are interlinked according to how close they are to one another, with the degree of connectivity fluctuating as a function of proximity, echoing the fundamental law of geography96,103. Essentially, SAC outlines the extent of similarity among values of a characteristic at diverse spatial locations, providing a foundation for recognizing and interpreting patterns and connections throughout different geographic areas (Fig. 3).

Fig. 3: The difference in SAC on the example of geochemical maps; raster and point data are obtained from USGS Open-File Report200.
figure 3

A There appears to be a strong positive SAC, with high concentrations of Aluminum (in red) and low concentrations (in blue) clustered together. B The Bismuth distribution map shows more scattered and less distinct clustering, indicating weaker SAC. The central and eastern regions show interspersed high and low values, suggesting a negative or weaker SAC. The image was created using the open-source Geographic Information System QGIS. Basemap is visualized from tiles by CartoDB, distributed under CC BY 3.0, based on the data from OpenStreetMap, distributed under ODbL (https://cartodb.com/basemaps). Boundaries used are taken from geoBoundaries Global Database (www.geoboundaries.org), distributed under CC BY 4.0.

Full size image

Spatial processes exhibit characteristics of spatial dependence and spatial heterogeneity, each bearing significant implications for spatial analysis:

  • Spatial dependence. This phenomenon denotes the autocorrelation amidst observations, which contradicts the conventional assumption of residual independence seen in methods such as linear regression. One approach to circumvent this is through spatial regression.

  • Spatial heterogeneity. Arising from non-stationarity in the processes generating the observed variable, spatial heterogeneity undermines the effectiveness of constant linear regression coefficients. Geographically weighted regression offers a solution to this issue104,105.

Numerous studies have ventured into exploring SAC and its mitigation strategies in spatial modeling. There exists a consensus that spatially explicit models supersede non-spatial counterparts in most scenarios by considering spatial dependence106. However, the mechanisms driving these disparities in model performance and the conditions that exacerbate them warrant further exploration107,108. A segment of the academic community contests the incorporation of autocorrelation in obtaining spatial predictions, attributing potential positive bias in estimates as a consequence. These studies advocate explicit incorporation of SAC only for significantly clustered data109. Additionally, while the issue of SAC has been extensively discussed in the past, the analytical approach that neglects spatial dependence is prone to artificially enhancing the estimated model performance. This oversight is frequently observed in various studies related to Convolutional Neural Networks (CNNs), revealing a potential flaw in their validation procedures110.

Another concept is the residual spatial autocorrelation (rSAC), which manifests itself not only in original data but also in the residuals of a model. Residuals quantify the deviation between observed and predicted values within the modeling spectrum. Consequently, rSAC evaluates the SAC present in the variance that the explanatory variables fail to account for. Grasping the distribution of residuals is vital in regression modeling, given that it underpins assumptions such as linearity, normality, equal variance (homoscedasticity), and independence, all of which hinge on error behavior106.

Approaches for measuring spatial autocorrelation

To ensure a logical flow, the first step is to determine whether the data display SAC. The practice of checking for SAC has become standard in geography and ecology97. Various methods are used for this purpose, including 1) Moran’s index (Moran’s I), 2) Geary’s index (Geary’s C), and 3) variogram (semi-variogram)111.

Moran’s I typically depict a decline, reaching 0 or lower at specific distances, indicating an absence of SAC. A value of 0 or below suggests a random spatial distribution for the variable. Similarly, Geary’s C values near 0 signify an absence of SAC or spatial randomness, akin to what one would expect from a randomly distributed variable. Conversely, higher Geary’s C values, especially those exceeding 1, imply positive SAC. This indicates that the variable exhibits similarity or clustering at different locations, revealing a distinct spatial pattern in the data112.

A widely used mathematical tool to assess the spatial variability and dependence of a stochastic variable is a variogram. Its primary purpose is to measure how the values of a variable alter as the spatial separation between sampled locations increases. In simpler terms, it quantifies the extent of dissimilarity or variation between pairs of observations at different spatial distances, playing a pivotal role in spatial interpolation, prediction, and mapping of environmental variables like soil properties, pollutant concentrations, and geological features113.

The latest research includes new methods and modifications of previously known approaches. Recently, Moran’s index has been extended to include interval data and small data cases, as cited in the sources114,115. Eigenequations were employed to transform spatial statistical measures into spatial analysis models based on Moran’s index. The theoretical foundation of SAC models was explored using normalized variables and weight matrices116. A more efficient and sensitive procedure for computing SAC was also proposed, known as the Skiena A algorithm and statistic. This algorithm is much faster than the computations for either Moran’s I or Geary’s C117. Ongoing discussions and analyses are also examining issues such as the scale effects of SAC measurement, which are contributing to a deeper understanding of SAC and its applications in different domains118,119.

Addressing spatial autocorrelation

The most common ways to eliminate the influence of SAC in the data on the prediction quality include proper sampling design, careful feature selection method, model selection, and spatial cross-validation, which we discuss further.

Sampling design

SAC is significant for clarification of spatial variability of environmental features. However, excessive SAC presence in georeferenced datasets can lead to redundant or duplicate information120. This redundancy stems from two primary sources: geographic patterns informed by shared variables or the consequences of spatial interactions, typically characterized as geographic diffusion.

In geospatial modeling tasks utilizing remote sensing data, the primary aim is usually to estimate the characteristics of areas that haven’t been directly studied. Regular sampling methods often provide the best results for this purpose. Classical sampling theories often assume that each member of a target population has a known chance of being selected, which is not always practical or efficient for spatially correlated data. Instead, using a grid to select a subset of the population can improve the accuracy of estimates like the mean of a geographic landscape by accounting for spatial patterns121,122. Spatial sampling strategies can help address SAC by minimizing the effects of correlation among nearby measurements122. Various strategies based on stratified or adaptive sampling123,124,125 can be used to reduce the risk of overestimating the overall population parameters due to strong SAC within specific areas.

The size of the sample also plays a key role in spatial modeling. In quantitative studies, it affects how broadly the results can be applied and how the data can be handled. In qualitative studies, it is crucial to establish that results can be applied in other contexts and to discover new insights126. The relationship between SAC and the best sample size in quantitative research has been a popular topic, leading to many studies and discussions120,127,128. Currently, there are debates within the scientific community regarding the effective sample size—an estimate of the sample size required to achieve the same level of precision if that sample was a simple random sample. While Brus129 claims that effective sample size calculations are inappropriate for some cases, Griffith122 shows that effective sample size is meaningful even with a random sampling selection implementation.

Exploring the details of sampling in relation to SAC reveals many layers of understanding:

  • The employment of diverse stratification criteria elicits heterogeneous impacts upon the amplitude of SAC130.

  • The sampling density and SAC critically influence the veracity of interpolation methodologies131.

  • Empirical findings suggest that sampling paradigms characterized by heterogeneous sampling intervals - notably random and systematic-cluster designs - demonstrate enhanced efficacy in discerning spatial structures, compared with purely systematic approaches132.

To summarize, the selection of an appropriate sampling design is essential for addressing the challenges posed by SAC. By carefully considering the spatial arrangement of samples, researchers can effectively reduce autocorrelation’s impact. Consequently, a proper sampling design can markedly improve the accuracy of predictive models in spatial analysis.

Variable selection

SAC can be influenced significantly by selecting and treating variables within a dataset. Several traditional methodologies, encompassing feature engineering, mitigation of multicollinearity, and spatial data preprocessing, present viable avenues to address SAC-related challenges.

One notable complication arises from multicollinearity amongst the selected variables, which can potentiate SAC133. Multicollinearity can be detected using correlation matrices and variance inflation factors (VIFs)134. To address multicollinearity, one can eliminate variables with high correlations, apply dimensionality reduction techniques like principal component regression, carefully select pertinent variables, and develop novel variables that capture the essence of highly correlated variables135. Another approach for addressing this challenge is the consideration of rSAC across diverse variable subsets, followed by the deployment of classical model selection criteria like the Akaike information criterion136.

In ML and DL, emerging methodologies have embraced SAC as an integral component. For instance, while curating datasets for training Long Short-Term Memory (LSTM) networks, an optimal SAC variable was identified and integrated into the dataset137. Furthermore, spatial features, namely spatial lag and eigenvector spatial filtering (ESF), have been introduced to the models to account for SAC138.

A novel set of features termed the Euclidean distance field (EDF), has been innovatively designed based on the spatial distance between query points and observed boreholes. This design aims to seamlessly weave SAC into the fabric of ML models, further underscoring the significance of variable selection in spatial studies139.

Model selection

Selecting or enhancing models to mitigate SAC impact is crucial. Spatial autoregressive models (SAR), especially simultaneous autoregressive models, are effective in this regard97. SAR may stand for either spatial autoregressive or simultaneous autoregressive models. Regardless of terminology, SAR models allow spatial lags of the dependent variable, spatial lags of the independent variables, and spatial autoregressive errors. Spatial errors model (SEM), incorporates spatial dependence either directly or through error terms. SEMs handle SAC with geographically correlated errors.

Other approaches include auto-Gaussian models for fine-scale SAC consideration97. Spatial Durbin models further improve upon these by considering both direct and indirect spatial effects on dependent variables140. Additionally, Geographically Weighted Regression (GWR) offers localized regression, estimating coefficients at each location based on nearby data141. In the context of SDM, six statistical methodologies were described to account for SAC in model residuals for both presence/absence (binary response) and species abundance data (Poisson or normally distributed response). These methodologies include auto covariate regression, spatial eigenvector mapping, generalized least squares (GLS), (conditional and simultaneous) autoregressive models, and generalized estimating equations. Spatial eigenvector mapping creates spatially correlated eigenvectors to capture and adjust for SAC effects112. GLS extends ordinary least squares by considering a variance-covariance matrix to address spatial dependence142.

The use of spatial Bayesian methods has grown in favor of overcoming SAC. Bayesian Spatial Autoregressive (BSAR) models and Bayesian Spatial Error (BSEM) models explicitly account for SAC by incorporating a spatial dependency term and a spatially structured error term, respectively, to capture indirect spatial effects and unexplained spatial variation143.

Recently, the popularity of autoregressive models for spatial modeling as a core method has slightly decreased, while classical ML and DL methods have been extensively employed for spatial modeling tasks. Consequently, various techniques have been developed to leverage SAC’s influence effectively. The common approach is to incorporate SAC with the usage of autoregressive models during the stages of dataset preparation and variable selection. This approach is presented in greater detail in the previous subsection. On the other hand, combining geostatistical methods with ML is gaining popularity. For example, the combined usage of an artificial neural network and the subsequent modeling of the residuals by geostatistical methods to simulate a nonlinear large-scale trend was applied144.

Spatial cross-validation

Spatial cross-validation is a widely used technique to account for SAC in various research studies21,99,145. Neglecting the consideration of SAC for spatial data can introduce an optimistic bias in the results. For instance, it was shown145 that random cross-validation could yield estimates up to 40 percent more optimistic than spatial cross-validation.

The main idea of spatial cross-validation is to split the data into blocks around central points of the dependence structure in space146. This ensures that the validation folds are statistically independent of the training data used to build a model. By geographically separating validation locations from calibration points, spatial cross-validation techniques effectively achieve this independence147.

Various methods are commonly employed in spatial cross-validation, including buffering, spatial partitioning, environmental blocking, or combinations thereof21,146. These techniques aim to strike a balance between minimizing SAC and avoiding excessive extrapolation, which can significantly impact model performance146. Buffering involves defining a distance-based radius around each validation point, excluding observations within this radius from model calibration. Environmental blocking groups data into sets with similar environmental conditions or clusters spatial coordinates based on input covariates148. Spatial partitioning, known as spatial K-fold cross-validation, divides the geographic space into K spatially distinct subsets through spatial clustering or using a coarse grid with K cells146. Another approach was recently proposed, taking into account both geographic and feature spaces designed for situations when the sample data are different from the prediction locations to support the ability of the validation set to reflect the differences between training and test sets23.

An alternative discussion109 argues that both standard and spatial cross-validation are not fully unbiased for estimating mapping accuracy, and the concept of spatial cross-validation itself has been criticized. The study showed that standard cross-validation overestimated accuracy for clustered data, while spatial cross-validation severely underestimated it. This pessimism in spatial cross-validation is mainly due to only validating areas far from calibration points. To obtain unbiased map accuracy estimates in large-scale studies, probability sampling and design-based inference are recommended. Furthermore, clearer definitions are needed to distinguish between validating a model and validating the resulting map. The pessimistic results might also indicate limited model generalization.

In summary, spatial cross-validation techniques could be suitable to address SAC in data-driven spatial modeling tasks, while providing a transparent and precise description of the methodology of the model accuracy assessment and inference obtaining in a step-by-step manner is of high importance. Selecting the most suitable technique and its corresponding parameters should result from thoughtful consideration of the specificity of the research problem and the corresponding dataset. Thus, the development of “generic” evaluation methods is requested.

Uncertainty quantification

Uncertainty quantifies the model’s prediction confidence level (Fig. 4). Two primary types of uncertainty exist aleatory uncertainty, which arises from data uncertainty, and epistemological uncertainty, which originates from knowledge limitations149. Sources of uncertainty may stem from incomplete or inaccurate data, inaccurately specified models, inherent stochasticity in the simulated system, or gaps in our understanding of the underlying processes150. Assessing aleatoric uncertainty caused by noise, low spatial or temporal resolution, or other factors that cannot be considered can be challenging. Therefore, most research is focused on epistemic uncertainty related to the modeling process.

Fig. 4: Example of uncertainty quantification for spatial mapping provided within the project SoilGrids25.
figure 4

A Maps of one of the target variables—soil pH(water) in the topsoil layer. B Maps of associated uncertainty calculated as ratio between the inter-quantile range and the median for the same territory. The image was created using the open-source Geographic Information System QGIS. Basemap is visualized from tiles by CartoDB, distributed under CC BY 3.0, based on the data from OpenStreetMap, distributed under ODbL (https://cartodb.com/basemaps). Boundaries used are taken from geoBoundaries Global Database (www.geoboundaries.org), distributed under CC BY 4.0. SoilGrids data are publicly available under the CC-BY 4.0 (https://www.isric.org/explore/soilgrids).

Full size image

However, despite the importance of the confidence of ML model predictions, many researchers do not consider this aspect of modeling. Often, the authors compare the metrics of several models and optimize hyperparameters, but the uncertainty of the models obtained remains beyond the scope of research. While the main steps of the machine learning pipeline are well-developed, including preprocessing, model selection, training, and validation, there is a notable gap in uncertainty quantification. There are no straightforward criteria for evaluating and reducing uncertainty, underscoring the need for more widely accepted methods to address this critical aspect.

Approaches to uncertainty quantification

In data-driven modeling, several approaches are used to estimate the uncertainty of model predictions, the most popular of which are calibration errors, sharpness, proper scoring rules, and methods related to prediction intervals151. However, only a few of them are utilized in spatial modeling.

In ML, model calibration refers to the alignment between predicted probabilities and the actual likelihood of events occurring. A well-calibrated model predicts probabilities that accurately reflect the actual probabilities of outcomes. Therefore, calibration is critical in probabilistic models, where the output includes probability estimates. Calibration ensures that these probabilities are reliable and can be interpreted as accurate confidence levels152.

Several metrics are employed to assess the calibration performance of probabilistic forecasts. One of the most used metrics is Mean Absolute Calibration Error, which measures the average absolute discrepancy between predicted and observed probabilities across the entire probability space. Another metric is the Miscalibration Area, which quantifies the extent of calibration discrepancies by measuring the area between the predicted and observed cumulative distribution functions153. Several other metrics are related to the measurement of calibration error: Static Calibration Error, Expected Calibration Error, and Adaptive Calibration Error154.

Proper scoring rules (PSR) are functions based on calibration and sharpness, offering a systematic approach to assessing the accuracy and reliability of predictive models. Among PSR methods, the negative log-likelihood155, continuous ranked probability score (CRPS), and interval score are prominent indicators used to quantify the quality of probabilistic predictions.

In geospatial modeling, one of the common approaches for UQ is quantile regression156. It allows one to understand not only the average relationship between variables but also how different quantiles (percentiles) of the dependent variable change with the independent variables. In other words, it helps to analyze how the data is distributed across the entire range rather than just focusing on the central tendency. Quantile regression is particularly useful when dealing with data that may not follow a normal distribution or when there are outliers in the data that could heavily influence the results.

For instance, to quantify the uncertainty of models for nitrate pollution of groundwater, Quantile Regression and Uncertainty Estimation Based on Local Errors and Clustering were used157. Quantile Regression was also used for the UQ of four conventional ML models for digital soil mapping: to estimate UQ authors analyzed Mean Prediction Intervals and prediction interval coverage probability (PICP)158. Another widely used technique for UQ is bootstrap, which is a statistical resampling technique that involves creating multiple samples from the original data to estimate the uncertainty of a statistical measure159.

Visualization methods for UQ in geospatial modeling hold a distinct place compared to other areas of ML160. Researchers emphasize the significance of visually analyzing maps with uncertainty estimates, especially for biodiversity and policy conversation tasks161. Visualization techniques such as bivariate choropleth maps, map pixelation, Q-Q plots, and glyph rotation to represent spatial predictions with uncertainty can be used162.

Reducing the uncertainty in data-driven spatial modeling

One the model level, two primary groups of approaches to reduce uncertainty could be selected: those related to Gaussian Process Modeling and those associated with ensemble modeling.

Gaussian Process Regression, also known as kriging, is commonly used for UQ in geospatial applications, providing a natural way to estimate the uncertainty associated with spatial predictions163. Another approach, known as Lower Upper Bound Estimation, was applied to estimate sediment load prediction intervals generated by neural networks164. For soil organic mapping, researchers compared different methods, including sequential Gaussian simulation (SGS), quantile regression forest (QRF), universal kriging, and kriging coupled with random forest. They concluded that SGS and QRF provide better uncertainty models based on accuracy plots and G-statistics165. However, Random Forest demonstrated better performance of prediction uncertainty in comparison with kriging in soil mapping in another study166, although predictions of regression kriging were found to be more accurate, that can be related to the architecture of these models.

Model ensembling is a powerful technique used in ML to address uncertainty. The diversity of predictions in an ensemble provides a natural way to estimate uncertainty. More robust estimates can be achieved through ensembling methods like weighted averaging, stacking, or Bayesian model averaging167. Ensembling mitigates uncertainties associated with individual models by computing the variance of predictions across the ensemble168. To address issues like equifinality, uncertainty, and conditional bias in predictive mapping, ensemble modeling and bias correction frameworks were proposed. Using the XGBoost model and environmental covariates, ensemble modeling resolved equifinality and improved performance169. A comparison of regional and global ensemble models for soil mapping showed that regional ensembles had less uncertainty despite similar performance to global models170.

Key areas for focus and growth

In this review, we highlight the multifaceted challenges encountered in geospatial data-driven modeling. To complement the discussed issues and solutions and account for the rapid development of ML-based data analysis and modeling techniques, we present a curated collection of tools in the form of an open GitHub repository https://github.com/mishagrol/Awesome-Geospatial-ML-Toolkit. This repository aims to serve as a comprehensive resource for researchers and practitioners in the field to enhance geospatial ML applications addressing the observed context of the environmental data specifics. We warmly invite the community to utilize this collection and contribute to it.

Below, we outline the major points of growth that can lead to new seminal works in the area. Referring to the general pipeline of data-driven processing, we identify new datasets, new models, and new approaches to ensure the quality of work required for the industry deployment of the applied science solutions and address the issue of interpretability of data-driven predictions.

New generation of datasets

It is crucial to enhance data quality, quantity, and diversity to ensure that models are reliable in capturing the spatial distribution of target environmental features. Establishing well-curated databases in environmental research is of utmost importance as it drives scientific progress and industrial innovation. When combined with modern tools, these databases can contribute to developing more powerful models. In general, better data naturally lead to a reduction of biases related to the imbalance and autocorrelation, as large amounts of high-quality data allow for better identification of such effects and constructing models that overcome them. For example, more samples from a scarcely class conclude quality improvement for imbalanced data, while dense sets of points lead to a more natural introduction of autocorrelation in spatiotemporal models. Moreover, such samples can lead to more precise uncertainty estimation.

A specific area of interest is the cost-effective and efficient semi-supervised collection of the data, which can have labels only for a part of the objects presented in the dataset. Although currently underdeveloped, this data type holds significant potential for expansion and improvement. In computer vision and natural language processing, the superior quality of recently introduced models often comes from using more extensive and better datasets. Internal Google dataset on semi-supervised data JFT-3B with nearly three billion labeled images led to major improvements in foundation computer vision models171,172. Another major computer vision dataset example is LVD-142M with about 142 million images173, while a pipeline that can be used to extend the size of existing datasets to two orders of magnitude is provided. In natural language processing, a recent important example is training large language models174. It uses a preprocessed dataset with 2 trillion tokens. The adoption of climate data is more closely related to geospatial modeling. Due to the increasing number of available measurements, it now also allows the application of DL models. For a variant of a Transformer model175, SEVIR dataset176 led to better predictions. Also, the possibility of forecasting precipitation with higher spatial resolution at the nowcasting timeline from 5 to 90 min ahead using the DL approach was shown177. To achieve results with superior accuracy and usefulness, radar measurements at a grid with cells of 1 × 1 km, taken every 5 min for 3 years, were processed, while in total, around 1 TB of data were used. Other openly available datasets have been released as well, with a focus on enhancing the computer vision models178. While the idea of automated data collection appears in ref. 179, existing systems contribute little to gathering huge amounts of labeled data even with large and complex systems180.

A natural further step is integrating diverse data sources. Combining datasets from various domains, such as satellite imagery, meteorological and climatic data, and social data, such as social media posts that provide real-time environmental information for specific locations, can be beneficial. By developing multimodal approaches capable of processing these diverse data sources, the community can enhance model robustness and effectively address the challenges discussed in this study and the existing literature. Currently, most of the related research combines image and natural language modalities181, while other options are possible.

New generation of models

The introduction of new modeling approaches may be driven by several factors, including addressing the known limitations outlined in the current review and responding to technological advancements. For example, while the ongoing progress in technology results in improved data sources, such as higher-resolution gridded datasets and dense geolocated observation data, it also poses challenges in adapting geospatial models based on classical ML algorithms to handle large volumes of information effectively. Incorporating DL methods is a potential solution, although they come with challenges related to interpretability and computational efficiency, especially when dealing with large volumes of data. We anticipate the emergence of self-supervised models trained on large semi-curated datasets for geospatial mapping in environmental research, similar to what we have seen in language modeling and computer vision. Such approaches have also been applied to satellite images182 including, for example, a problem of the estimation of vegetation state71 and assessment of damaged buildings in disaster-affected area183.

Active learning stands out as a powerful strategy, enabling the model to selectively label instances during training. This becomes especially useful when addressing complex tasks like multiclass classification in geospatial modeling. For example, a comprehensive active learning method was proposed for multiclass imbalanced streaming data with concept drift184.

A promising approach to handling the multi-dimensional dynamic context of environmental processes for solutions requiring spatial resolution is physics-informed ML20. Such techniques enable the consideration of the interaction between environmental features and address their mutual dynamics185, while, at the same time, a combination of data-driven and process-based methods within physics-informed learning helps to overcome specific struggles of the methods, such as complications in tackling episodic data observations from the one side and computational intractability from the other186. A significant advantage of working on such combined models is the introduction of physically meaningful research hypotheses and domain-specific knowledge, which data-driven solutions lack so are often criticized for187.

As mentioned above, UQ is essential in building and using data-driven modeling. Developing deep neural networks has led to several new methods for estimating uncertainty. Some primary methods include Monte Carlo dropout, sampling via Markov chain Monte Carlo, and Variational autoencoders26. These methods have already been used in research on earth system processes modeling using ML, but they have yet to be widely applied in environmental spatial modeling. For instance, Bayesian techniques have been used in weather modeling, particularly wind speed prediction and hydrogeological calculations, to analyze the risk of reservoir flooding188. Probabilistic modeling was employed to assess the uncertainty of spatial-temporal wind speed forecasting, with models based on spatial-temporal neural networks using convolutional GRU and 3D CNN. Variational Bayesian inference was also utilized189.

Industry-quality solutions: deployment and maintenance

A shift to using geospatial solutions for decision-support suggests placing applied research outcomes in this field in a product-oriented context. It means that a question of deployment in a production environment arises after constructing a model. From this perspective, several aspects could be formulated as points for growth and support of the technology for operational use to address real-world challenges, enhancing the deployment: accounting of shifts in data sources, supporting of models’ adaptability and consistency of performance, and development of environments helping to improve processing of the data and ensure continuous operation.

An important challenge arises from the aging of data-driven models caused by changes in environmental factors such as, for instance, the changing climate190, so climate patterns evolve over time, and the model may become less accurate if it’s not regularly updated with current data. On the contrary, shifts in the output variables are also could be the case, e.g., alterations of land use and land cover191. Monitoring and considering such changes is essential to either discontinue using an outdated model or retrain it with new data192. The monitoring schedule can vary, guided by planned validation checking or triggered by data corruption and new business process implementations. Other approaches lay in the model-related accounting solutions, such as incorporating concept drift into the maintenance process193, using advanced DL methods, and introducing uncertainty estimation and anomaly detection into Quality Assurance and Quality Control (QA/QC) routines. Another aspect is the collection and introduction of domain-specific benchmark data, which would assist in the interpretability of data-driven approaches and support the reliability and transparency of applications.

Another issue constraining training and inferencing data-driven models is the requirement of the infrastructure to ensure continuous data flow. That makes the availability of advancing computing power and cloud-processing infrastructure, along with the development of specialized frameworks for geospatial data-driven applications, critical problem194. While some solutions have already been available for the community, such as the Google Earth Engine195, there is an urgent need for libraries to provide datasets, samplers, and pre-trained models specific to environmental domains and ML methods. A related question is a discussion about balancing between model generalization power and model complexity196,197. While the model generalization could be achieved in many ways, including larger volumes of data or the introduction of scarce-data learning approaches such as transfer learning, domain adaptation, and physics-informed learning supported with techniques of accounting of spatial bias provided in the current review, all of the solutions raise a question of the available energy resources, which is yet to be addressed and considered to be method and scenario-dependent.