Introduction

Polar topologies play host to various novel physical properties, including enhanced conductivity1,2, negative capacitance3,4, sub-terahertz collective dynamics5, and nonlinear light-matter interactions6. The design and detection of domains with distinct topological structures have become central topics in the field of ferroelectrics7,8,9. By now, various types of topological polar structures have been identified, such as flux-closure10, vortex11,12,13, skyrmion14, meron15, Solomon ring16. However, nearly all of these topological features are formed in ferroelectric thin films and/or grown on substrates. Polar topological structures in free-standing films are called for due to their increased flexibility17 and additional degrees of freedom for controlling domain topology through stretching, bending, and torsion8,9,18,19. Additionally, the possibility of generating polar topologies in non-ferroelectric materials remains largely unexplored.

Simultaneously, moiré systems formed by 2D materials with a twisted angle have emerged as fertile grounds for exploring emergent novel phenomena20,21,22,23,24,25,26. Analogous to 2D atomic layers, free-standing oxide films with much flexibility18,19,27,28,29 can also be employed to construct moiré patterns, which harbor the potential for inducing unique structures and properties. However, characterizing the interfaces and associated local structures within twisted bilayers poses a significant challenge. At present, atomic-scale polar displacements and nanoscale polarization and electric field can be determined by aberration-corrected scanning transmission electron microscopy (STEM)-based methods, like high-angle annular dark-field (HAADF) imaging and diffraction analysis based on 4D-STEM3,4,14,17,30,31. Nevertheless, most of these techniques can only acquire 2D projections of polarization structures within one sample, making it difficult to reveal the structure variation in the normal direction of twisted bilayers.

Ptychography is a high-resolution coherent diffractive imaging method used to retrieve object potentials encoded in diffraction intensities collected at series of probe positions (so-called 4D dataset)32,33,34. In multislice ptychography, samples are segmented into slices at various depths, and the potentials of each slice are reconstructed from the recorded coherent diffraction intensities35,36,37,38. Leveraging its advanced lateral resolutions and depth sectioning capabilities, multislice electron ptychography has revealed intriguing structure phenomena in various material systems39,40,41,42,43,44,45,46.

In this study, we demonstrate the occurrence of polar vortices in twisted free-standing bilayers of the paraelectric material, SrTiO3, using multislice electron ptychography. The vortices are organized into in-plane arrays, while in the stacking direction, the vorticity alternates between clockwise and counterclockwise directions.

Results

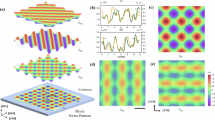
As shown in Fig. 1a, the twisted bilayer is formed by stacking two flakes of free-standing films of SrTiO3. These films are grown on a SrTiO3(001) substrate with a sacrificial layer of Sr2CaAl2O6. The thickness of each free-standing layer is 17 nm. The low magnification annular dark-field image (Supplementary Fig. 1) shows moiré fringes, which are characteristic of twisted bilayers. In order to get a clear image of both stacking layers, HAADF is first used by tuning the beam defocus. As shown in Supplementary Fig. 2, the contrast decreases as the focal point of the electron probe goes from the upper layer to the lower layer. This contrast variation can be attributed to the channeling effect in the upper layer, yielding a much clearer contrast for the upper layer compared to the lower layer. Atomic columns in the HAADF image of the upper layer are slightly stretched (the first image in Supplementary Fig. 2), which can be attributed to electron scattering of the lower layer. These observations indicate the challenge of decoupling the atomic structures of the two stacking layers, making accurate analysis of the bilayer’s atomic structure a difficult task.

Fig. 1: Ptychographic reconstruction of twisted SrTiO3 bilayer.
figure 1

a Schematics illustrating the sample preparation process and experimental setup for electron ptychography. Besides is a structure model of twisted SrTiO3. Sr, Ti, and O atoms are represented by green, blue, and red spheres, respectively. b Total phase images of the upper (left) and lower layer (right) recovered using multislice ptychography. Scale bar, 2 nm. The structure model of SrTiO3 is overlaid on the phases. c Total phase image summed over the slices of the two layers, revealing the moiré pattern in the stacking region. Regions with AA and AB stacking sequences are marked with yellow and red circles, respectively. Scale bar, 2 nm.

Full size image

In contrast, multislice ptychography overcomes the channeling effect caused by dynamic scattering and enables the recovery of object functions for each depth section of the sample in the electron beam direction. During ptychographic reconstructions, the entire moiré system is divided into 4-Å-thick ‘slices’. Therefore, both upper and lower layers contain about 40 slices, ensuring identification of structural variations between and within the layers. Supplementary Movie S1 provides the recovered phase images of all the slices. Figure 1b presents the total phase of each layer, allowing for the measurement of a twist angle of 4.1°. The upper layer covers a larger region than the lower one, therefore the entire field of view encompasses both the twisted bilayer region and the single-layer region. Moiré patterns are clearly visible in the total phase image obtained by summing the slices in the two layers (Fig. 1c). The coincidence regions in the moiré pattern are labeled by circles: those marked with yellow circles exhibit the AA (Sr-Sr, TiO-TiO) stacking sequence, maintaining the periodicity of bulk SrTiO3, while regions marked with red circles display the AB (Sr-TiO, TiO-Sr) stacking sequence, resembling antiphase boundaries. The integrated phase value of Sr and Ti columns are plotted as a function of depth (Fig. 2a and Supplementary Fig. 3) and used to calculate the depth resolution, which is 2.3 nm based on the full width at 80% of maximum (FW80M) of the phase depth profile. As shown in Fig. 2a, the depth position of the interface is identified as the intersection point between the depth profiles of atomic columns in the two layers, which is 15.6 nm (the 40th slice) below the top surface (the 1st slice). The phase image of the interface is displayed in Fig. 2b. Due to the limited depth resolution, the intensity of the atomic columns in the two layers is blurred into one another near the interface. The depth range containing information of both layers is determined based on the minima points of the profile depth profiles near the interface, which is 12.4 nm (the 32nd slice) to 18.8 nm (the 48th slice) marked with dashed lines in Fig. 2a. Slices in this region are excluded for the following polarization mapping.

Fig. 2: Polar vortices forming in the two stacking layers.
figure 2

a Depth profiles of the phases integrated over Sr atomic columns in the nonoverlapping region (between AA and AB stacking regions) of the moiré patterns. The position of the interface is indicated with a black star (the 40th slice). The interface region is indicated with dashed lines. b Phase image of the interface (the 40th slice). c, e Polar displacement mapping in the depth of 12.0 nm (top layer) (c) and 23.2 nm (bottom layer) (e). Regions with AA and AB stacking sequences are marked with yellow and red circles, respectively. The 10-pm arrow in (e) is a reference for the magnitude of the polar displacement. d, f Vorticity (∇⨯P)[001] distribution corresponding to (c) and (e). The vorticity is in the unit of 1010 C/m3. Scale bars, 2 nm.

Full size image

Based on the recovered phases at different depths, the positions of O and TiO columns at different depths are determined by Gaussian peak fitting. These positions were then used to calculate the polar displacements, which are defined as the relative displacement between each TiO column and its four nearest O columns (δO-Ti). The polar displacements of the slices in the upper layer are displayed in Supplementary Fig. 4, while those in the lower layer are displayed in Supplementary Fig. 5. Supplementary Movie S2 is used to show the variation process of the polarization in depth.

Polar vortices emerge in both upper and lower layers. In the upper layer, vortices are formed at the depth of 11.2 nm and maintain such an arrangement to the depth of 12.0 nm (Supplementary Fig. 4). The polarization mapping in Fig. 2c specifically focuses on the section at a depth of 12.0 nm. Here, the vortices exhibit counterclockwise (CCW) rotation. The vortices have a diameter of approximately 7–10 unit cells and are distributed between the regions with the same stacking sequence. Figure 2d shows the vorticity, which is calculated as the z-component of the curl of the polar displacement (∇⨯P)[001]. Vortices with CCW rotation form the regions with positive vorticity. Between the regions with different stacking sequences, vorticity is mainly negative. Moving to the lower layer, polar vortices form a regular array in the depth of 23.2 nm, approximately 7 nm below the interface (Fig. 2e, f). The core positions of the CCW vortices shift laterally compared to the upper layer, which can be caused by a non-periodic strain field and terraces at the interface.

Figure 2c reveals that polar vortices are only present in the bilayer region of the upper SrTiO3 layer. The magnitude of the relative displacement is analyzed separately for the bilayer region and single-layer region of the upper layer. As Supplementary Fig. 6 shows, relative displacements in the single-layer region of the upper layer are much smaller compared to those in the twisted bilayer region. This observation suggests that the emergence of the polar vortex is closely linked to the elastic interactions between the bilayers across the interface, which will be discussed in detail later. To provide a comparison, we conduct reconstruction on a dataset simulated with rigid bilayers of SrTiO3, which have no polarization and no elastic interactions across the interface. Simulation parameters, such as the voltage, convergence semi-angle, scan step size, detector pixel size, and electron dose, are chosen to be the same as the experiment. Supplementary Fig. 7 presents the mapping of relative displacement at two different depths near the interface. The polarization mapping of all the slices is shown in Supplementary Movie S3. Neither the upper nor the lower layer exhibits polar topological features, as seen in the experimental results. Supplementary Fig. 8a provides the magnitude of the relative displacements between TiO and O (or Sr) atomic columns (δO-Ti and δSr-Ti) calculated from all the recovered slices. The ground truth of δO-Ti and δSr-Ti is zero, so the results can be viewed as the measurement accuracy. It can be observed that the values of δO-Ti and δSr-Ti in the simulation are at the same level and smaller than the experimental ones, thereby confirming the existence of the polar vortex observed in the experiment. We also compared experimental values of δSr-Ti and δO-Ti. As shown in Supplementary Fig. 8b, δO-Ti is significantly larger than δSr-Ti, indicating the displacement of oxygen predominantly contributes to the formation of polar vortex.

For further validation of the reliability of ptychographic reconstruction, we performed experiments on a different bilayer sample with the same thickness for comparison. Figure 3a shows the projected phase image summed over all the slices. Supplementary Fig. 9 shows the total phase images summed over the upper layer and lower layer. The depth position of interface is determined using the same method mentioned above, which is 17.8 nm below the top slice (marked on the depth profiles shown in Fig. 3b). Different from the interface of the main sample we studied (Fig. 2b), the interface of this sample contains obvious amorphous layer (Fig. 3c). Figure 3d provides the relative displacement δO-Ti in one of the slices outside the interface region, which exhibits no regular features. All the depth sections of δO-Ti, showcasing the absence of any polar vortex signature, are shown in Supplementary Movie S4.

Fig. 3: Ptychographic reconstruction of a different twisted SrTiO3 sample with an amorphous layer at the interface.
figure 3

a Total phase image summed over all the slices. b Depth profiles of the phases integrated over Sr atomic columns in the nonoverlapping region of the moiré patterns. The position of the interface is marked with a black star. The interface region is indicated with dashed lines. c Phase image of the interface (the 22nd slice). d Mapping of δO-Ti at the slice labeled with ii in (b). The 10-pm arrow in (d) is a reference for the magnitude of the polar displacement. Scale bars in (a), (c), and (d) are 4 Å.

Full size image

Besides forming an in-plane vortex array, the polarization also evolves along the depth direction. Figure 4a shows an evolution process of the reversal of vortex rotation occurring in the lower layer. In the depth of 19.2 nm, polar vortices with CW rotation form a regular array (a local region is shown in the top left image of Fig. 4a, and the whole region is shown in Supplementary Fig. 5). Some CCW vortices also exist near the CW vortices, creating pairs of vortices with opposite vorticity. As the depth increases, vortices first vanish and then reappear with the opposite rotation directions, forming a CCW vortex array in the depth of 23.6 nm (bottom right image of Fig. 4a and Supplementary Fig. 5). Throughout this process, the vortex cores remain nearly unchanged.

Fig. 4: Evolving polar vortices in the depth direction.
figure 4

a Depth variation of the experimental polarization distribution in a small region in the lower layer. The corresponding regions in Fig. 2f are indicated by a green square. The relative depth values are labeled on the top of each image. Scale bar, 2 nm. b Depth variation of the polarization from a phase-field simulation. Scale bar, 2 nm. The color maps of (a) and (b) stand for the vorticity in the unit of 1010 C/m3.

Full size image

To investigate the underlying mechanism of the polar vortex, we carried out phase-field modeling (details in Methods). Our findings reveal that incorporating flexoelectricity is necessary to reproduce the experimental observations, indicating its significant role in introducing polar vortex in paraelectric SrTiO3. Supplementary Fig. 10 shows the detailed influence of flexoelectric coefficients on the polarization distribution in phase-field simulation. Previous studies have demonstrated the importance of flexoelectricity in introducing polarization in defects47,48 and superlattice49. The flexoelectric coefficients used in our simulation (f11 = 1 V, f12 = 0 V, f44 = 3 V) align well with the experimental measurements50,51. Figure 4b shows the depth sections of polarization in a region with identical size as presented in Fig. 4a, which bears a close resemblance to the experimental observation. Phase-field simulation is also used to shed light on the 3D polar texture of the vortex (Supplementary Fig. 11), especially the z-component of the polarization, which can not be determined in the experiment due to the limited depth resolution.

The distribution of polarization is found to be closely tied to the lattice rotation. Figure 5a shows the distribution of lattice rotation (measured using geometric phase analysis52) and the corresponding polarization displacement in the depth of 19.2 and 23.2 nm in the lower layer. More details about the depth variation of lattice rotation and strain ɛxx are shown in Supplementary Movie S5. Most CCW vortices are located in the region with CCW lattice rotation, while CW vortices are located in the region with CW lattice rotation. The relationship is further highlighted through the line profiles of vorticity and rotation in Fig. 5b. As the direction of the vortices reverses, so does the lattice rotation. This regularity is validated by phase-field modeling. Figure 5c shows the simulated lattice rotation and polar displacement at two different depths, while Fig. 5d presents their line profiles. The concurrent change in the sign of vorticity and lattice rotation matches well with the experiment, confirming the strong correlation between the directions of vortex and lattice rotations.

Fig. 5: Relationship between polar vortex and lattice rotation.
figure 5

a, c Experimental (a) and phase-field modeling results (c) of lattice rotation and polarization in two depths with CW and CCW vortex arrays. b, d Profiles of the vorticity and lattice rotation across the lines marked in (a) and (c). Positive values mean counterclockwise lattice rotation. Scale bars, 2 nm.

Full size image

In summary, we unravel the formation of polar vortices in the twisted film of paraelectric SrTiO3. Using multislice electron ptychography, the structures of the overlapping layers are distinguished, allowing the study of the 3D variation of polarization. It is found that polar vortices evolve into different rotation manners in the depth direction, and the emergence of the vortex array is tightly related to the lattice rotation. Our work demonstrates that with the existence of the flexoelectric effect, polar topologies can also be generated in paraelectric materials. Multislice electron ptychography serves as a powerful imaging tool to investigate the interesting phenomena in twisted functional materials. With more sampling on the beam direction of the reciprocal space, multislice ptychography is promising to achieve better depth resolution53,54 and reveal the evolution of the z-component of the polarization.

Methods

Preparation of twisted bilayer SrTiO3 film

Pulsed laser deposition (248 nm KrF excimer laser) was used to grow the epitaxial heterojunctions SrTiO3/Sr2CaAl2O6 on SrTiO3 (001) substrates. The substrate temperature and oxygen partial pressure used to grow the Sr2CaAl2O6 (SAO) layer is 740 °C and 15 Pa, respectively. The substrate temperature and oxygen partial pressure used to grow the SrTiO3 film were 710 °C and 10 Pa, respectively. During the deposition, the energy density of the laser beam focused on the targets was 2 J cm-2 and 1.9 J cm-2 for Sr2CaAl2O6 and SrTiO3, respectively. The laser pulse rate was 3 Hz. The sample was annealed at 710 °C for 10 min under an oxygen partial pressure of 100 Pa.

To transfer the free-standing film to the TEM grid, polymethyl-methacrylate (PMMA) was coated onto the as-grown film. The tape was then attached to the surface of PMMA. Then, the sample was immersed in deionized water at 120 °C until the SAO layer was dissolved. During this process, the whole film cracked into pieces and some of them attached to the surface of others. Next, the surface of the film was attached to the carbon film side of a TEM grid, and the PMMA outside of the grid was cut. At last, the PMMA was removed by acetone vapor.

Experimental data collection and reconstruction

The electron microscopy experiment was conducted in a probe aberration-corrected FEI Titan Cubed Themis G2 operated at 300 kV. The convergence semi-angle is 25  mrad. The nominal collection angle range of the ADF image shown in Fig. 1b is 25–153 mrad. 4D datasets used to do multislice ptychography were acquired using an electron microscope pixel array detector (EMPAD). Each diffraction pattern contains 128 × 128 pixels, and the pixel size is 0.026 Å-1. The probe was under-focused about 30 nm with respect to the top surface of the sample and scanned over a raster grid with a step size of 0.52 Å. The dataset was acquired under a beam current of about 20 pA and a dwell time of 0.96 ms (0.1 ms for acquisition time and 0.86 ms for readout time), resulting in a dose value of 4 × 104 e/Å2.

A homemade program named EMPTY (Electron Microscopic PTYchography) mentioned in our previous work38 was used for the ptychographic reconstruction. When doing multislice ptychography, diffraction patterns were padded with zero to 160×160 pixels to generate a real space pixel size (sampling interval of recovered object phases) of 0.24 Å. Object was separated into 85 slices, and the slice thickness was 4 Å. Six probe states were used to account for the partial coherence of the illumination55,56. Probe positions were refined using the gradient descent method57. The regulation factor used to avoid ambiguity in multislice electron ptychography was initialized as 1.0 and gradually decreased after reaching convergence. Final reconstruction was achieved after 1500 iterations.

Simulation of ptychography dataset

A homemade multislice simulation program was used to generate the 4D dataset used for ptychographic reconstruction. The reliability of the program was verified in our previous work. The voltage, convergence angle, and pixel size of diffraction patterns are the same as in the experiment. The thickness of the twisted SrTiO3 bilayer model is 30 nm in total, which is close to the sample used in the experiment. The scan step size is 0.468 Å. Poisson noise was added to diffraction patterns, corresponding to a beam of 30 pA and a dwell time of 1 ms. During reconstruction, the slice thickness of the sample is also 4 Å.

Analysis of reconstructed phase images

The Python package Atomap was used to locate atomic columns in phase images. After finding Sr, TiO, and O columns, the polar displacement of each unit cell was calculated as the deviation between the TiO column and the center of four neighboring O columns. Geometric phase analysis was calculated using Strain + +.

Phase-field simulation

A three-dimensional ferroelectric polarization vector P = (Px, Py, Pz) was chosen as the order parameter. The temporal evolution of P was obtained by solving the time-dependent Ginzburg-Landau equation:

$$\frac{\partial {P}_{i}({{\boldsymbol{r}}},t)}{\partial t}=-L\frac{\delta F}{\delta {P}_{i}({{\boldsymbol{r}}},t)}\left(i=x,y,z\right)$$

in which L denotes the kinetic coefficient, F denotes total free energy functional, r denotes spatial coordinate, and t denotes evolutionary time. Meanwhile, total free energy functional F includes contributions of Landau energy, gradient energy, electric energy, flexoelectric energy, elastic energy, and electrostrictive energy, respectively:

$$F=\iiint \left({f}_{{Landau}}+{f}_{{Gradient}}+{f}_{{Electric}}+{f}_{{Flexo}}+{f}_{{Elastic}}+{f}_{{Es}}\right){dV}$$

which can be given by

$${f}_{{Landau}}= {\alpha }_{{ij}}{P}_{i}{P}_{j}+{\alpha }_{{ijkl}}{P}_{i}{P}_{j}{P}_{k}{P}_{l}+{\alpha }_{{ijklmn}}{P}_{i}{P}_{j}{P}_{k}{P}_{l}{P}_{m}{P}_{n} \\ + {\alpha }_{{ijklmnrs}}{P}_{i}{P}_{j}{P}_{k}{P}_{l}{P}_{m}{P}_{n}{P}_{r}{P}_{s}$$
$${f}_{{Gradient}}=\frac{1}{2}{G}_{{ijkl}}{P}_{i,j}{P}_{k,l}$$
$${f}_{{Electric}}=-\frac{1}{2}{\kappa }_{0}{E}_{i}{E}_{i}-{P}_{i}{E}_{i}$$
$${f}_{{Elastic}}=\frac{1}{2}{C}_{{ijkl}}{\varepsilon }_{{ij}}{\varepsilon }_{{kl}}$$
$${f}_{{Es}}=-{q}_{{ijkl}}{\varepsilon }_{{ij}}{P}_{k}{P}_{l}$$

where \({\alpha }_{{ij}}\), \({\alpha }_{{ijkl}}\), \({\alpha }_{{ijklmn}}\) are Landau coefficients, \({G}_{{ijkl}}\) gradient coefficients, \({f}_{{ijkl}}\) flexoelectric coefficient, \({C}_{{ijkl}}\) electrostrictive coefficient, \({q}_{{ijkl}}\) elastic constant, and \({\kappa }_{0}\) background dielectric permittivity. \({\varepsilon }_{{ij}}\) denotes the strain component and Ei the electric field component derived from Ei = \({-\varphi }_{,i}\), where φ is the electric potential. Each energy expression can be found in previous literature. In addition, the mechanical (\({\sigma }_{{ij},j}=0\)) and electric (\({D}_{i,i}=0\)) equilibrium conditions must be satisfied for the body-force-free and body-charge-free systems in simulation. A finite element method was employed to solve the above equations to obtain spatio-temporal evolution of polarization, stress, and electric field.

For simplicity, a set of 500Δx × 500Δx × 20Δx uniform meshing is used in this model, where Δx represents 0.5 nm. Periodic boundary conditions are set up along the in-plane directions ([100] and [010]). A close-circuit electric boundary condition was applied on both top and bottom surfaces. A fixed displacement boundary condition was employed on the bottom of the film, while the stress on the top surface was free. The amplitude of the initial random noise of P was set as 0.001 C/m−2 for the following polarization evolution.

To simulate the periodic strain field in twisted bilayers, the estimated in-plain strain was applied with sinusoidal waveform, which can be derived from elastic theory:

$${\varepsilon }_{{xx}}={\varepsilon }_{{yy}}=-\frac{A}{2}\left(\cos \frac{2\sqrt{2}\pi }{k{l}_{0}}x+\cos \frac{2\sqrt{2}\pi }{k{l}_{0}}y\right)\cdot \cos \frac{2\pi z}{{l}_{z}}$$
$${\varepsilon }_{{xy}}=\frac{1}{2}\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)=\frac{A}{2}\left(\cos \frac{2\sqrt{2}\pi }{k{l}_{0}}x-\cos \frac{2\sqrt{2}\pi }{k{l}_{0}}y\right)\cdot \cos \frac{2\pi z}{{l}_{z}}$$
$$\omega =\frac{1}{2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) \\ =\frac{\sqrt{2}}{4}A\left(\cos \frac{2\sqrt{2}\pi }{k{l}_{0}}x+\cos \frac{2\sqrt{2}\pi }{k{l}_{0}}y\right) \cdot \cos \frac{2\pi z}{{l}_{z}},\,[z\in (0,\,hz)]$$

where εxx, εyy are IP tensile strain along x and y direction, εxy is IP shear strain, ω represents IP lattice rotation. A is the strain amplitude which is set to 0.005, kxl0, and kyl0 are periods of the in-plain strain where l0 is the lattice parameter. kx = ky = 6 were assumed to achieve the same vorticity and period of vortices. lz refers to the period of the strain distribution in the z-direction, and hz represents the thickness of the film. Here we set lz = 2hz. It is worth noting that in the phase-field simulation, we only considered the strain inside the material, so z = 0 does not mean the real surface of the sample.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.