Introduction

Combinatorial optimizations are ubiquitous in industry and technology1. The potential of quantum computers for these problems has been extensively studied2,3,4,5,6,7,8,9,10. However, it is unclear whether they will deliver advantages in practice before fault-tolerant devices appear. With only quadratic asymptotic runtime speed-ups expected in general11,12,13 and low clock-speeds14,15, a major challenge is the number of qubits required for quantum solvers to become competitive with classical ones. Current implementations are restricted to noisy intermediate-scale quantum devices16, with variational quantum algorithms17,18 as a promising alternative. These are heuristic models—based on parameterized quantum circuits—that, although conceptually powerful, face inherent practical challenges19,20,21,22,23,24,25. Among them, hardware noise is particularly serious, since its detrimental effect rapidly grows with the number of qubits. This can flatten out the optimization landscape—causing exponentially-small gradients (barren plateaus)24 or underparametrization25—or render the algorithm classically simulable20. Hence, near-term quantum optimization solvers are unavoidably restricted to problem sizes that fit within a limited number of qubits.

In view of this, interesting qubit-efficient schemes have been explored26,27,28,29,30,31,32. In refs. 26,27, two or three variables are encoded into the (three-dimensional) Bloch vector of each qubit, allowing for a linear space compression. In contrast, the schemes of refs. 28,29,30,31,32 encode the m variables into a quantum register of size \({{\mathcal{O}}}\left(\log (m)\right)\). However, such exponential compressions both render the scheme classically simulable efficiently and seriously limit the expressivity of the models28,31. Moreover, in refs. 28,29,30,31,32, binary problems are relaxed to quadratic programs. These simplifications strongly affect the quality of the solutions. In addition, the measurements required by those methods can be statistically demanding. For instance, in a deployment with m = 3964 variables30, most of the measurement outcomes needed did not occur and were replaced by classical random bits, leading to a low quality solution compared to state-of-the-art solvers. To the best of our knowledge, no experimental quantum solver has so far produced non-trivial solutions to problems with m beyond a few hundreds8,9,10,33. Furthermore, the interplay between qubit-number compression, loss function non-linearity, trainability, and solver performance in general is mostly unknown.

Here we explore this territory. We introduce a hybrid quantum-classical solver for binary optimization problems of size m polynomially larger than the number of qubits n used. This is an interesting regime in that the scheme is highly qubit-efficient while at the same time preserving the classical intractability in m, leaving room for potential quantum advantages. We encode the m variables into Pauli correlations across k qubits, for k an integer of our choice. A parameterized quantum circuit is trained so that its output correlations minimize a non-linear loss function suitable for gradient descent. The solution bit string is then obtained via a simple classical post-processing of the measurement outcomes, which includes an efficient local bit-swap search to further enhance the solution’s quality. Moreover, a beneficial, intrinsic by-product of our scheme is a super-polynomial suppression of the decay of gradients, from barren plateaus of heights 2−Θ(m) with single-qubit encodings to \({2}^{-\Theta ({m}^{1/k})}\) with Pauli-correlation encodings. In turn, the circuit depth scales sublinearly in m, as \({{\mathcal{O}}}({m}^{1/2})\) for quadratic (k = 2) compressions and \({{\mathcal{O}}}({m}^{2/3})\) for cubic (k = 3) ones. All these features make our scheme more experimentally- and training-friendly than previous quantum schemes, leading to significantly higher quality of solutions.

For example, for m = 2000 and m = 7000 MaxCut instances, our numerical solutions are competitive with those of semi-definite program relaxations, including the powerful Burer-Monteiro algorithm. This is relevant as a basis for quantum-inspired classical solvers. In addition, we deploy our solver on IonQ and Quantinuum quantum devices, observing a good performance even without quantum error mitigation. For example, for a MaxCut instance with m = 2000 vertices encoded into n = 17 trapped-ion qubits, we obtain estimated approximation ratios above the hardness threshold r ≈ 0.941. We note that previous experiments addressed instance sizes of a few tens for MaxCut8,33 and up to few hundreds for combinatorial optimization in general9,10, but attaining significantly lower solution qualities. Our results open up a promising framework to develop competitive solvers for large-scale problems with small quantum devices.

Results

Quantum solvers with polynomial space compression

We solve combinatorial optimizations over \(m={{\mathcal{O}}}({n}^{k})\) binary variables using only n qubits, for k a suitable integer of our choice. Such compression is achieved by encoding the variables into m Pauli-matrix correlations across multiple qubits. More precisely, with the short-hand notation [m] : = {1, 2, …m}, let \({{\boldsymbol{x}}}:={\{{x}_{i}\}}_{i\in [m]}\) denote the string of optimization variables and choose a specific subset \(\Pi :={\{{\Pi }_{i}\}}_{i\in [m]}\) of m ≤ 4n − 1 traceless Pauli strings Πi, i.e., of n-fold tensor products of identity (\({\mathbb{1}}\)) or Pauli (X, Y, and Z) matrices, excluding the n-qubit identity matrix \({{\mathbb{1}}}^{\otimes n}\). We define a Pauli-correlation encoding (PCE) relative to Π as

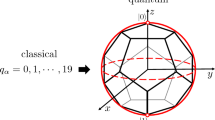
$${x}_{i}:=\,{\mbox{sgn}}\,\left(\langle {\Pi }_{i}\rangle \right)\,{{\mbox{for}}}\, {{\rm{all}}}\,i\in [m],$$
(1)

where sgn is the sign function and \(\langle {\Pi }_{i}\rangle :=\left\langle \Psi \right\vert {\Pi }_{i}\left\vert \Psi \right\rangle\) is the expectation value of Πi over a quantum state \(\left\vert \Psi \right\rangle\). In Supplementary Note 2, we prove that expectation values of magnitude Θ(1/m) are enough to guarantee the existence of such states for all bit strings x. In practice, however, we observe magnitudes significantly larger than Θ(1/m)) (see Supplementary Fig. 1). We focus on strings with k single-qubit traceless Pauli matrices. In particular, we consider encodings \({\Pi }^{(k)}:=\left\{{\Pi }_{1}^{(k)},\ldots,{\Pi }_{m}^{(k)}\right\}\) where each \({\Pi }_{i}^{(k)}\) is a permutation of either \({X}^{\otimes k}\otimes {{\mathbb{1}}}^{\otimes n-k}\), \({Y}^{\otimes k}\otimes {{\mathbb{1}}}^{\otimes n-k}\), or \({Z}^{\otimes k}\otimes {{\mathbb{1}}}^{\otimes n-k}\) (see left panel of Fig. 1 for an example with k = 2). That is, Π(k) is the union of 3 sets of mutually-commuting strings. This is experimentally convenient since only three measurement settings are required throughout. Using all possible permutations for the encoding yields \(m=3(\begin{array}{c}n\\ k\end{array})\). In this work, we deal mostly with k = 2 and k = 3, corresponding to \(m=\frac{3}{2}n(n-1)\) and \(m=\frac{1}{2}n(n-1)(n-2)\), respectively. The single-qubit encodings of refs. 26,27, in turn, correspond to PCEs with k = 1.

Fig. 1: Quantum optimization solvers with polynomial space compression.
figure 1

Encoding: An exemplary MaxCut (or weighted MaxCut) problem of m = 9 vertices (graph on the left) is encoded into 2-body Pauli-matrix correlations across n = 3 qubits (Q1, Q2, Q3). The color code indicates which Pauli string encodes which vertex. For instance, the binary variable x1 of vertex 1 is encoded in the expectation value of \({Z}_{1}\otimes {Z}_{2}\otimes {{\mathbb{1}}}_{3}\), supported on qubits 1 and 2, while x9 is encoded in \({Y}_{1}\otimes {{\mathbb{1}}}_{2}\otimes {Y}_{3}\), over qubits 1 and 3 (see Eq. (1)). This corresponds to a quadratic space compression of m variables into \(n={{\mathcal{O}}}({m}^{1/2})\) qubits. More generally, k-body correlations can be used to attain polynomial compressions of order k. The Pauli set chosen is composed of three subsets of mutually-commuting Pauli strings. This allows one to experimentally estimate all m correlations using only 3 measurement settings throughout. Quantum-classical optimization: we train a quantum circuit parametrized by gate parameters θ using a loss function \({{\mathcal{L}}}\) of the Pauli expectation values that mimics the MaxCut (or weighted MaxCut) objective function (see Eq. (2)). The variational Ansatz is a brickwork circuit with the number of 2-qubit gates and variational parameters scaling very mildly with m (see Fig. 2), and circuit depth sublinear in m. This makes both experimentally- and training-friendly (see Fig. 3). Solution: once the circuit is trained, we read out its output x from the correlations across single-qubit measurement outcomes on its output state. Finally, we perform an efficient classical bit-swap search around x to find potential better solutions nearby. The result of that search, x*, is the final output of our solver.

Full size image

The specific problem we solve is weighted MaxCut, a paradigmatic NP-hard optimization problem over a weighted graph G, defined by a (symmetric) adjacency matrix \(W\in {{\mathbb{R}}}^{m\times m}\). Each entry Wij contains the weight of an edge (i, j) in G. The set E of edges of G consists of all (i, j) such that Wij ≠ 0. We denote by ∣E∣ the cardinality of E. The special case where all weights are either zero or one defines the (still NP-hard) MaxCut problem, where each instance is fully specified by E (see MaxCut problems). The goal of these problems is to maximize the total weight of edges cut over all possible bipartitions of G. This is done by maximizing the quadratic objective function \({{\mathcal{V}}}({{\boldsymbol{x}}}):={\sum }_{(i,j)\in E}{W}_{ij}(1-\,{x}_{i}\,{x}_{j})\) (the cut value).

We parameterize the state in Eq. (1) as the output of a quantum circuit with parameters θ, \(\left\vert \Psi \right\rangle=\left\vert \Psi ({{\boldsymbol{\theta }}})\right\rangle\), and optimize over θ using a variational approach17,18 (see also Supplementary Note 9 for alternative ideas on how to optimize the state). As circuit Ansatz, we use the brickwork architecture shown in Fig. 1 (see “Numerical details” for details on the variational Ansatz). The goal of the parameter optimization is to minimize the non-linear loss function

$${{\mathcal{L}}}=\,\,{\sum}_{(i,j)\in E}\,\,\,{W}_{ij}\tanh \left(\alpha \,\langle {\Pi }_{i}\rangle \right)\tanh \left(\alpha \,\langle {\Pi }_{j}\rangle \right)+{{{\mathcal{L}}}}^{({\mbox{reg}})}.$$
(2)

The first term corresponds to a relaxation of the binary problem where the sign functions in Eq. (1) are replaced by smooth hyperbolic tangents, better suited for gradient-descent methods27. The second term, \({{{\mathcal{L}}}}^{({\mbox{reg}})}\) (see Regularization term), forces all correlators to go towards zero, which is observed to improve the solver’s performance (see Supplementary Note 1).

However, too-small correlators restrict the \(\tanh\) to a linear regime (\(\tanh (z)\approx z\) for ∣z∣ << 1), which is inconvenient for the training. Hence, to restore a non-linear response, we introduce a rescaling factor α > 1. We observe a good performance for the choice α ≈ n⌊k/2⌋ (see Supplementary Note 3). Once the training is complete, the circuit output state is measured and a bit-string x is obtained via Eq. (1). Then, as a classical post-processing step, we perform one round of single-bit swap search (of complexity \({{\mathcal{O}}}(| E| )\)) around x in order to find potential better solutions nearby (see “Numerical details”). The result of the search, x*, with cut value \({{\mathcal{V}}}({{{\boldsymbol{x}}}}^{*})\), is the final output of our solver.

Our work differs from refs. 28,29,30,31,32 in fundamental ways. First of all, as mentioned, those studies focus mainly on exponential compressions in qubit numbers. These are also possible with PCEs since there are 4n − 1 traceless operators available. However, besides automatically rendering the schemes classically simulable efficiently28,31, exponential compressions strongly limit the expressivity of the model, since L-depth circuits contain \({{\mathcal{O}}}(L\times \log (m))\) parameters. This affects the quality of the solutions. Conversely, our method operates manifestly in the regime of classically intractable quantum circuits. Secondly, as for experimental feasibility, while the previous schemes require the measurement of probabilities that are (at best) of order m−1, our solver is compatible with significantly larger expectation values (see Supplementary Fig. 1). Third, while in refs. 28,29,30,31 the problems are related to quadratic programs28, Eq. (2) defines a highly non-linear optimization.

Circuit complexities and approximation ratios

Here, we investigate the quantum resources (circuit depth, two-qubit gate count, and number of variational parameters) required by our scheme. Due to the strong reduction in qubit number, an increase in required circuit depth is expected to maintain the same expressivity. We benchmark on graph instances whose exact solution \({{{\mathcal{V}}}}_{\max }:={\max }_{{{\boldsymbol{x}}}}{{\mathcal{V}}}({{\boldsymbol{x}}})\) is unknown in general. Therefore, we denote by \({r}_{{{\rm{exact}}}}:={{\mathcal{V}}}({{{\boldsymbol{x}}}}^{*})/{{{\mathcal{V}}}}_{\max }\) the exact approximation ratio and by \(r:={{\mathcal{V}}}({{{\boldsymbol{x}}}}^{*})/{{{\mathcal{V}}}}_{{{\rm{best}}}}\) the estimated approximation ratio based on the best-known solution \({{{\mathcal{V}}}}_{{{\rm{best}}}}\) available (see Numerical details).

In Fig. 2 (left panel), we plot the gate complexity required to reach \(\overline{r}=16/17\approx 0.941\) without doing the final local search step (to capture the resource scaling exclusively due to the quantum subroutine) on non-trivial random MaxCut instances of increasing sizes, for the encodings Π(2) and Π(3). For rexact, this value gives the threshold for worst-case computational hardness. By non-trivial instances, we mean instances post-selected to discard easy ones (see Numerical details). The results suggest that the number of gates scales approximately linearly with m. The same holds also for the number of variational parameters, which is proportional to the number of gates. In turn, the number of circuit layers scales as \({{\mathcal{O}}}(m/n)\). For quadratic and cubic compressions, e.g., this corresponds to \({{\mathcal{O}}}({m}^{1/2})\) and \({{\mathcal{O}}}({m}^{2/3})\), respectively. These mild scalings translate directly into experimental feasibility and model training ease. In fact, we observe (see Supplementary Note 5) that the number of epochs needed for training also scales linearly with m. Moreover, in Supplementary Note 6, we prove worst-case upper bounds on the number of measurements required to estimate \({{\mathcal{L}}}({{\boldsymbol{\theta }}})\). These bounds scale with the problem size as \(\tilde{{{\mathcal{O}}}}(m\,{(6| E|+m)}^{2})\) for even k and \(\tilde{{{\mathcal{O}}}}({m}^{1-1/k}\,{(6| E|+m)}^{2})\) for odd k.

Fig. 2: Gate complexity and performance.
figure 2

Left: Number of two-qubits gates (in bubble plot) needed for achieving an average estimated approximation ratio \(\overline{r}\ge 16/17\approx 0.941\) (over 250 non-trivial random MaxCut instances and 5 random initializations per instance) without the local bit-swap search (quantum-circuit’s output x alone) versus m, for quadratic and cubic compressions. The larger the bubble, the greater the fraction of instances requiring the corresponding number of gates. A linear scaling is observed in both cases. Right: Median r (now including the local bit-swap search step) over random initializations for three specific MaxCut instances of different sizes as functions of the compression degree k. Intervals indicating the highest and lowest observed values are also displayed. The m = 800 graph is planar and used 10 random initializations, while the m = 2000 and m = 7000 ones are random graphs and used 10 and 5 initializations, respectively (see Table 1 for graph details). For a fair comparison, the total number of parameters is kept the same for all k. The horizontal lines denote the reported results of the leading gradient-based SDP solver35 (dotted lines) and the powerful Burer-Monteiro algorithm36,37 (dashed lines). Our solver outperforms the former in all cases and even the latter for m = 2000 at k = 6 and 7.

Full size image

In Fig. 2 (right), in turn, we plot solution qualities versus k, for three MaxCut instances from the benchmark set Gset34 (see “Numerical details”). The total number of variational parameters is fixed by m (or as close to m as allowed by the circuit Ansatz) for a fair comparison, with the circuit depths adjusted accordingly for each k. In all cases, r increases with k up to a maximum, after which the performance degrades. This is consistent with a limit in compression capability before compromising the model’s expressivity, as expected. Remarkably, the results indicate that our solutions are competitive with those of state-of-the-art classical solvers, such as the leading gradient-based SDP solver35, based on the interior points method, and even the Burer-Monteiro algorithm36,37, based on non-linear-programming. Moreover, our quantum solver (including the overhead in parameter initializations for the training) makes a smaller number of queries to the loss function than Burer-Monteiro (see Supplementary Note 7). Importantly, while our solver performs a single optimization followed by a single-bit swap search, the Burer-Monteiro algorithm includes multiple re-optimizations and two-bit swap searches (see Supplementary Note 7). This highlights the potential for further improvements of our scheme. All in all, the performance seen in Fig. 2 is not only relevant for quantum solvers but also suggests our scheme as an interesting heuristic for quantum-inspired classical solvers.

Intrinsic mitigation of barren plateaus

Another appealing feature of our solver emerging from the qubit-number reduction is an intrinsic mitigation of the infamous barren plateau (BP) problem due to the curse of dimensionality23,38,39,40,41, which constitutes one of the main challenges for training variational quantum algorithms. BPs are characterized by a vanishing expectation value of \(\nabla {{\mathcal{L}}}\) over random parameter initializations and an exponential decay (in n) of its variance. This jeopardizes the applicability of variational quantum algorithms in general19. For instance, the gradient variances of a two-body Pauli correlator on the output of universal 1D brickwork circuits are known to plateau at levels exponentially small in n for circuit depths of about 10 × n23. Alternatively, BPs can equivalently be defined in terms of an exponentially vanishing variance of \({{\mathcal{L}}}\) itself (instead of its gradient)42. This is often more convenient for analytical manipulations.

In Supplementary Note 10 we prove that, if the random parameter initializations make the circuits sufficiently random (namely, induce a Haar measure over the special unitary group), the variance of \({{\mathcal{L}}}\) is given by

$${{\rm{Var}}}({{\mathcal{L}}})=\frac{{\alpha }^{4}}{{d}^{2}}{\sum}_{(i,j)\in E}{w}_{ij}^{2}+{{\mathcal{O}}}\left(\frac{{\alpha }^{6}}{{d}^{3}}\right)\,,$$
(3)

with d = 2n the Hilbert-space dimension. Interestingly, the leading term in Eq. (3) appears also if one only assumes the circuits to form a 4-design, though it is unclear how to bound the higher-order terms without the full Haar-randomness assumption. For 1D brick-work random circuits, the unitary-design assumption is approximately met at depth \({{\mathcal{O}}}(n)\)43,44. In practice, for our loss function, we observe convergence to Eq. (3) at depths of about 8.5 × n. This is illustrated in Fig. 3 for linear, quadratic, and cubic compressions, where we plot as a function of m the average sample variance \(\overline{\,{\mbox{Var}}\,({{\mathcal{L}}})}\) of \({{\mathcal{L}}}\) over 100 non-trivial random MaxCut instances and 100 random parameter initializations per instance. As shown in the inset, a depth of roughly 1.05 × n is needed to reach r > 0.941 on average with the circuit’s output alone, while barren plateaus are reached at roughly 8.5 × n.

Fig. 3: Loss-function variance decay.
figure 3

Main: Average sample variance \(\overline{\,{\mbox{Var}}\,({{\mathcal{L}}})}\) of \({{\mathcal{L}}}\), normalized by \({\alpha }^{4}{\sum }_{(i.j)\in E}{w}_{ij}^{2}\), after plateauing, for the encodings Π(1), Π(2), and Π(3), as a function of m (in log-linear scale). Error bars are not shown since they are too-small to be visible in this scale. The agreement with the analytical expression in Eq. (3) is excellent (the dashed, blue curve corresponds to the first term of the equation, which decreases as 2−2n). Since \(n={{\mathcal{O}}}({m}^{1/k})\), this translates into a super-polynomial suppression in m of the decay speed of \(\overline{\,{\mbox{Var}}\,({{\mathcal{L}}})}\) for k > 1. Inset: average variances of the entries of the gradient of \({{\mathcal{L}}}\) as functions of the number of layers, for quadratic compression (Π(2)). Each curve corresponds to a different n. Note the decay of the plateau (rightmost) values with n. The black crosses indicate the depths needed to reach average approximation ratios > 0.941 (computational-hardness threshold) with the quantum-circuit’s output x alone, i.e., excluding the final bit-swap search. In all cases such ratios are attained before the variances have converged to their asymptotic, steady values.

Full size image

One observes an excellent agreement between \(\overline{\,{\mbox{Var}}\,({{\mathcal{L}}})}\) and the first term of Eq. (3) for large m. As m decreases, small discrepancies appear, especially for k = 2 and k = 3. This can be explained by noting that α ~ 1.5 for k = 1 whereas α ~ 1.5 × n for k = 2 and k = 3 (see Supplementary Note 3) so that the second term in (3) scales as 2−3n for the former but as n6 2−3n for the latter. Hence, as m (and so n) decreases, that term requires smaller m to become non-negligible for the former than for the latter. Remarkably, the scaling \(\overline{\,{\mbox{Var}}\,({{\mathcal{L}}})}\in \Theta ({\alpha }^{4}\,{2}^{-2n})\) in n translates into a super-polynomial suppression of the decay speed in m when compared to single-qubit (linear) encodings. This means, for instance, that quadratic encodings feature \(\overline{\,{\mbox{Var}}\,({{\mathcal{L}}})}\in \Theta ({\alpha }^{4}\,{2}^{-2\sqrt{m}})\), instead of \(\overline{\,{\mbox{Var}}\,({{\mathcal{L}}})}\in \Theta ({\alpha }^{4}\,{2}^{-2m})\) displayed by linear encodings. Importantly, the scaling obtained still represents a super-polynomial decay in m. Yet, the enhancement obtained makes a significant difference in practice, as shown in the figure by the orders of magnitude separating the three curves.

Experimental deployment on quantum hardware

We demonstrate our quantum solver on IonQ’s Aria-1 and Quantinuum H1-1 trapped-ion devices, for two MaxCut instances of m = 800 and 2000 vertices and a weighted MaxCut instance of m = 512 vertices. Details on the hardware and model training are provided in Experimental details, while the choice of instances is detailed in Numerical details (see Table 1). We optimize the circuit parameters offline via classical simulations and experimentally deploy the pre-trained circuit. Figure 4 depicts the obtained approximation ratios for each instance as a function of the number of measurements for the quadratic (Π(2)) and cubic (Π(3)) Pauli-correlation encodings. For each instance, we collected enough statistics for the approximation ratio to converge (see figure inset). The circuit size is limited by gate infidelities. For IonQ, we found a good trade-off between expressivity and total infidelity at a total of 90 two-qubit gates. Quantinuum’s device displays significantly higher fidelities, which allows for larger circuits, but we used the same number of gates for comparison. This is below the number required for these instance sizes according to Fig. 2 (left), especially for k = 2. However, remarkably, our solver still returns solutions of higher quality than the Göemans-Williamson bound in all cases, and than the worst-case hardness threshold in 4 out of the 5 experiments. As a reference, the largest MaxCut instance previously solved experimentally with QAOA2 had m = 414 and average and maximal approximation ratios 0.57 and 0.69, respectively (see Table 4 in ref. 33).

Table 1 Benchmark instances used in this work
Full size table
Fig. 4: Trapped-ion experimental implementation.
figure 4

Main: estimated approximation ratios for our scheme deployed on IonQ's Aria-1 (I) and Quantinnum H1-1 (Q) devices as functions of the number of measurements (per each of the three measurement settings). Three problem instances (see main text for details) are shown: one weighted MaxCut instance of m = 512, solved with quadratic compression using n = 19 qubits (purple pentagons), one MaxCut instance of m = 800, solved with quadratic compression on n = 23 qubits (red circles) and cubic compression on n = 13 qubits (yellow triangles), and another MaxCut instance of m = 2000, solved with cubic compression on n = 17 qubits (blue squares). The black horizontal lines indicate the Goemans-Williamson threshold (dotted), at r ≈ 0.878, and the worst-case computational-hardness threshold (dashed), at r = 16/17. Inset: loss function \({{\mathcal{L}}}\) (at fixed, optimized parameters) versus number of measurement shots (same shot range as in main figure), for the m = 2000 instance with cubic compression. The solid, pink curve corresponds to our numerical simulation, while the blue dots are the experimental data for the implementation on Quantinuum (the highest-fidelity one).

Full size image

Discussion

We introduced a scheme for solving binary optimizations on m decision variables using a number of qubits polynomially smaller than m. Pauli correlations across few qubits encode each binary variable. The circuit depth is sublinear in m, while the numbers of parameters and training epochs are approximately linear in m. Moreover, the qubit-number compression brings in the beneficial by-product of a super-polynomial suppression of the decay in m of the variances of the loss function (and its gradient), which we have both analytically proven and verified numerically. A drawback of our multi-qubit encoding, however, is a slight deterioration in sample complexity as compared to the single-qubit case (for ∣E∣ linear in m, from \(\tilde{O}({m}^{2})\) to \(\tilde{O}({m}^{3})\) in the worst case), but this is not severe in view of the advantages mentioned above. As a matter of fact, these features, together with an educated choice of non-linear loss function, allow us to solve large, computationally non-trivial instances with high quality.

Numerically, our solutions for m = 2000 and m = 7000 MaxCut instances are competitive with those of state-of-the-art solvers such as the powerful Burer-Monteiro (BM) algorithm. Moreover, in all the cases analyzed our algorithm makes a smaller number of queries to the loss function than BM (see Supplementary Note 7). Experimentally, in turn, for a deployment using 17 trapped-ion qubits, we estimated approximation ratios beyond the worst-case computational hardness threshold 0.941 for a non-trivial MaxCut instance with m = 2000 vertices. We stress that these results are based on raw experimental data, without any quantum error mitigation procedure to the observables measured. Yet, our method is indeed well-suited for standard error mitigation techniques45,46,47, the use of which may enhance the solver’s performance even further.

While the focus here has been on MaxCut problems, the technique can be extended to generic Quadratic Unconstrained Binary Optimization (QUBO) problems, which can be mapped to a MaxCut problem through a simple change of variables. In addition, since MaxCut is NP-hard, any NP problem can be mapped to a MaxCut instance with a polynomial overhead in m. Although for certain problems this overhead may be in practice significant, we emphasize that our approach is still advantageous over any scheme based on quantum MaxCut (or QUBO) solvers with standard encodings requiring as many qubits as decision variables. Besides, the framework can also be extended to polynomial unconstrained binary optimization (PUBO) problems48 using as loss function a higher-order polynomial of the hyperbolic tangents and without any increase in qubit number. This is in contrast to conventional PUBO-to-QUBO reformulations, which incur in expensive overheads in extra qubits49. Interestingly, for problems with specific structures, such as the traveling salesperson problem, PUBO reformulations exist that are more qubit-efficient than the corresponding QUBO versions50. Combining such reformulations with our techniques could allow for polynomial qubit-number reductions on top of that.

We note that, although slightly higher than with single-qubit encodings, as mentioned, our worst-case sample complexity upper bound is significantly better than in VQAs for chemistry. There, the sample complexity of estimating the loss function (the energy) scales as the problem size (number of orbitals) to the eighth power for popular basis sets such as STO-nG51. In addition, further improvements to our sample complexity are possible via optimization of hyperparameters (α and β) in a problem-dependent way. Moreover, the circuit depth and training run-time may be further improved by suitable pre-training strategies, such as those based on classical tensor-network simulations52. Another potentially relevant tool for pre-training is given in Supplementary Note 9, where we derive parent Hamiltonians whose ground states give approximate MaxCut solutions via our multi-qubit encoding. Such Hamiltonians may be used for QAOA schemes2 to prepare warm-start input states for the core variational circuit.

Finally, an important question is whether our scheme can lead to quantum advantages over classical solvers. This will depend on both hardware advances and algorithmic developments, such as in the circuit Ansatz, regularization term, hyper-parameters, and circuit optimizer. Particularly intriguing are the role of entanglement in our solver and its relationship with classical schemes where, instead of a quantum circuit, generative models are used to produce the correlations (see Supplementary Note 4). For the latter, the fact that our circuits become hard to simulate classically as the number of qubits increases gives our approach interesting prospects. These are all exciting open questions to study in the future. All in all, our work offers a promising machine learning framework to explore quantum optimization solvers on large-scale problems, using either near-term quantum devices or quantum-inspired classical techniques.

Methods

MaxCut problems

The weighted MaxCut problem is an ubiquitous combinatorial optimization problem. It is a graph partitioning problem defined on weighted undirected graphs G = (V, E) whose goal is to divide the m vertices in V into two disjoint subsets in a way that maximizes the sum of edge weights Wij shared by the two subsets—the so-called cut value. If the graph G is unweighted, that is, if Wij = 1 or Wij = 0 for every edge (i, j) ∈ E, the problem is referred to simply as MaxCut. By assigning a binary label xi to each vertex i ∈ V, the problem can be mathematically formulated as the binary optimization

$${{\mbox{maximize}}}_{{{\boldsymbol{x}}}\in \{-1,1\}^{m}} \sum\limits_{i,j\in[m]} W_{ij}(1-\,x_i\,x_j) \,.$$
(4)

Since ∑i,j∈[m]Wij is constant over x, Eq. (4) can be rephrased as a minimization of the objective function xTWx. This specific format is known as a quadratic unconstrained binary optimization (QUBO). For generic graphs, solving MaxCut exactly is NP-hard53. Moreover, even approximating the maximum cut to a ratio \({r}_{{{\rm{exact}}}} > \frac{16}{17}\approx 0.941\) is NP-hard54,55. In turn, the best-known polynomial-time approximation scheme is the Goemans-Williamson (GW) algorithm56, with a worst-case ratio rexact ≈ 0.878. Under the Unique Games Conjecture, this is the optimal achievable by an efficient classical algorithm with worst-case performance guarantees. If, however, one does not require performance guarantees, there exist powerful heuristics that in practice produce cut values often higher than those of the GW algorithm. Two examples are discussed in “Best Solutions known” in “Numerical details”.

Regularization term

The regularization term in Eq. (2) penalizes large correlator values, thereby forcing the optimizer to remain in the correlator domain where all possible bit string solutions are expressible. Its explicit form is

$${{{\mathcal{L}}}}^{({\mbox{reg}})}=\beta \,\nu {\left[\frac{1}{m}{\sum}_{i\in V}\tanh {\left(\alpha \langle {\Pi }_{i}\rangle \right)}^{2}\right]}^{2}.$$
(5)

The factor 1/m normalizes the term in square brackets to \({{\mathcal{O}}}(1)\). The parameter ν is an estimate of the maximum cut value: it sets the overall scale of \({{{\mathcal{L}}}}^{({\mbox{reg}})}\) so that it becomes comparable to the first term in Eq. (2). For weighted MaxCut, we use the Poljak-Turzík lower bound \(\nu=w(G)/2+w({T}_{\min })/4\)57, where w(G) and \(w({T}_{\min })\) are the weights of the graph and of its minimum spanning tree, respectively. For MaxCut, this reduces to the Edwards-Erdös bound58ν = ∣E∣/2 + (m − 1)/4. Finally, β is a free hyperparameter of the model, which we optimize over random graphs to get β = 1/2. Such optimizations systematically show increased approximation ratios due to the presence of \({{{\mathcal{L}}}}^{({\mbox{reg}})}\) in Eq. (2) (see Supplementary Note 1).

Numerical details

Choice of instances

The numerical simulations of Fig. 2 (left) and Fig. 3 were performed on random MaxCut instances generated with the well-known rudy graph-generator59 post-selected so as to filter out easy instances. The post-selection consisted in discarding graphs with less than 3 edges per node on average or those for which a random cut gives an approximation ratio r > 0.82. The latter is sufficiently far from the Goemans-Williamson ratio 0.878 while still allowing efficient generation. For the numerics in Fig. 2 (right) and the experimental deployment in Fig. 4 we used 6 graphs from standard benchmarking sets: the former used the G14, G23, and G60 MaxCut instances from the Gset repository34, while the latter used G1 and G35 from Gset and the weighted MaxCut instance pm3-8-50 from the DIMACS library60 (recently employed also in27). Their features are summarized in Table 1.

Best solutions known

For the generated instances, the best solution is taken as the one with the highest cut value between the (often coinciding) solutions produced by two classical heuristics, namely the Burer-Monteiro36 and the Breakout Local Search61 algorithms. For the instances from benchmarking sets, we considered instead the best-known documented solution. The corresponding cut value, \({{{\mathcal{V}}}}_{{{\rm{best}}}}\), is used to define the approximation ratio achieved by the quantum solution x*, namely \(r={{\mathcal{V}}}({{{\boldsymbol{x}}}}^{*})/{{{\mathcal{V}}}}_{{{\rm{best}}}}\).

Variational Ansatz

As circuit Ansatz, we used the brickwork architecture shown in Fig. 1, with layers of single-qubit rotations, parameterized by a single angle, followed by a layer of Mølmer-Sørensen (MS) two-qubit gates, each with three variational parameters. Each single-qubit gate layer contains rotations around a single direction (X, or Y, or Z), one at a time, sequentially. Furthermore, we observed that many of the other commonly used parameterized gate displays the same numerical scalings up to a constant.

Quantum-circuit simulations

The classical simulations of quantum circuits have been done using two libraries: Qibo62,63 for exact state-vector simulations of systems up to 23 qubits, and Tensorly-Quantum64 for tensor-network simulations of larger qubit systems.

Optimization of circuit parameters

Two optimizers were used for the model training. SLSQP from the scipy library was used for systems small enough to calculate the gradient using finite differences. In all other cases, we used Adam from the torch/tensorflow libraries, leveraging automatic differentiation to speed up computational time. As a stopping criterion for Adam, we halted the training after 50 steps whose cumulative improvement to the loss function was less than 0.01. For both optimizers, the default optimization parameters were used.

Classical bit-swap search as post-processing step

As mentioned, a single round of local bit-swap search is performed on the bit string x output by the trained quantum circuit. This consists of sequentially swapping each bit of x and computing the cut value of the resulting bit string. If the cut value improves, we retain the change. Else, the local bit flip is reverted. There are altogether Θ(m) local bit flips. A bit flip on vertex i affects Θ(d(i)) edges, with d(i) the degree of the vertex. Hence, an update of only Θ(d(i)) terms in \({{\mathcal{V}}}({{\boldsymbol{x}}})\) is required per bit flip. The total complexity of the entire round is thus Θ(∣E∣).

Experimental details

Hardware details

The experiments were deployed on IonQ’s Aria-1 25-qubit device and on Quantinuum’s H1-1 20-qubit device. Both devices are based on trapped ytterbium ions and support all-to-all connectivity. The VQA architecture of Fig. 1 was adapted accordingly to hardware native gates. We used alternating layers of partially entangling Mølmer-Sørensen (MS) gates and, depending on the experiment, rotation layers composed of one or two native single-qubit rotations GPI and GPI2 (see Table 2). Since the z rotation is done virtually on the IonQ Aria chip, parameterized RZ rotation was also added at the end of every rotation layer without any extra gate cost.

Table 2 Details about the experimentally deployed instances
Full size table

The native gates in Quantinuum’s H1-1 chip are the double parameterized U1q gate, a virtual z rotation, and the entangling arbitrary-angle two-qubit rotation RZZ. In our experiment, the circuit pre-trained for the m = 2000 vertices instance using IonQ native gates was transpiled into a Quantinuum native gates circuit with the same number of 1 and 2-qubit gates.

Resource analysis

We run a total of four experimental deployments. The three selected instances were trained using exact classical simulation with Adam optimizer, as detailed in Numerical details. In an attempt to get the best possible solution within the limited depth constraints of the hardware, the stopping criteria were relaxed to allow 150 non-improving steps. This resulted in a total number of training epochs considerably larger than the average case scenario (see Supplementary Note 7). Table 2 reports the precise quantum (number of qubits and gate count) and classical (number of epochs) resources, as well as the observed results.