ChromatinHD connects single-cell DNA accessibility and conformation to gene expression through scale-adaptive machine learning

Abstract

Gene regulation is inherently multiscale, but scale-adaptive machine learning methods that fully exploit this property in single-nucleus accessibility data are still lacking. Here, we develop ChromatinHD, a pair of scale-adaptive models that uses the raw accessibility data, without peak-calling or windows, to link regions to gene expression and determine differentially accessible chromatin. We show how ChromatinHD consistently outperforms existing peak and window-based approaches and find that this is due to a large number of uniquely captured, functional accessibility changes within and outside of putative cis-regulatory regions. Furthermore, ChromatinHD can delineate collaborating regulatory regions, including their preferential genomic conformations, that drive gene expression. Finally, our models also use changes in ATAC-seq fragment lengths to identify dense binding of transcription factors, a feature not captured by footprinting methods. Altogether, ChromatinHD, available at https://chromatinhd.org, is a suite of computational tools that enables a data-driven understanding of chromatin accessibility at various scales and how it relates to gene expression.

Introduction

Changes in DNA accessibility are a major hallmark of gene regulation^1,2, and techniques that combine chromatin accessibility with RNA sequencing are opening up novel avenues to explore the interplay between transcription factor binding and chromatin state changes in influencing gene expression³. These methods not only facilitate the dissection of intricate gene regulatory networks⁴, but they also illuminate the extent of intercellular and intracellular variability in transcriptional and epigenomic states^5,6. Furthermore, these techniques have great potential for both fine mapping⁷ and functional understanding⁸ of non-coding genetic variation.

One of the very first steps of analyzing chromatin accessibility typically involves binning the raw data into putative cis-regulatory elements (CREs), using peak-calling^9,10,11,12, predefined regions^4,13 or sliding windows with a predefined size^14,15,16. This critical preprocessing step is based on the idea that distinct modular regions evolved in the genome whose activity is regulated in a coordinated way across cell types through transcription factor (TF) binding, chromatin modifications, nucleosome displacement and/or chromatin interaction changes¹³. The CRE, often referred to as an enhancer or promoter, is in this way seen as the fundamental functional unit of gene regulation, and multiple such functional units often act in a combinatorial way to regulate gene expression⁷. Discretizing accessibility information into such putative CREs facilitates downstream data analysis because common statistical methods for differential expression, batch correction, dimensionality reduction, correlation analysis, differential TF binding, and predictive modeling of gene expression can rapidly consume a CRE-based count matrix^{11,12,17,18,19,20,21}.

However, there is increasing evidence that reducing gene regulation to a coordinated process involving ‘peak-defined’, modular CREs may be an oversimplification. Multiple studies have highlighted inconsistencies and limitations of peak calling across cell types and methods^10,11, both within and outside of canonical CREs^6,13,15,16. From an experimental perspective, there is by now an extensive body of evidence indicating that gene regulation involves very different scales²²: combinatorial TF binding localized at a few dozen base pairs^23,24, nucleosomal interactions at 100 bp scale²⁵, and genome organization^26,27 combined with hub formation at kilobase scale or higher^28,29. These scales indicate that a priori summarization at the CRE level, typically encompassing several hundred base pairs, may be too reductive to illuminate the full regulatory landscape underlying gene expression.

To address this, we developed ChromatinHD, a suite of computational methods that performs predictive and differential analysis of single-nucleus (sn) (ATAC + RNA)-seq data using the raw fragment data. Rather than making a priori assumptions about how the data should be structured, ChromatinHD uses neural network architectures and probabilistic modeling to automatically determine the functional regions and appropriate resolution to describe those regions in a cell type/state and position-specific manner. We apply ChromatinHD to show that there are inherent biases to current CRE-centric approaches, which affect the functional and mechanistic interpretation of chromatin data. Compared to these approaches, our scale-adaptive models are better at linking putative regulatory regions to gene expression and identifying differentially accessible regions (DARs) that are more strongly enriched for functional binding sites and functional genetic variation. This enhanced performance is primarily due to the scale-adaptive nature of our models, which select regions of various sizes (from 25 bp to multiple kilobases) based on their dynamic accessibility profiles rather than just the magnitude of accessibility. Finally, we highlight how ChromatinHD captures information on (1) the juxtaposition between DNA contact on the one hand and enhancers that co-predict gene expression on the other, pointing to preferential genomic conformations driving gene expression, and (2) dense TF binding that is visible through changes in fragment sizes but not captured by typical footprinting approaches. Altogether, our data-driven, scale-adaptive approach provides the same interpretability as CRE methods but extracts more fundamental gene regulatory information that would be missed otherwise.

Results

ChromatinHD enables scale-adaptive sn(ATAC + RNA)-seq analysis

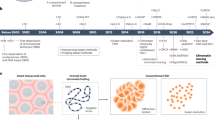
By contemplating raw sn(ATAC + RNA) data, it is clear that the reorganization of open chromatin occurs at scales ranging from 50 base pairs, onto 500 base pairs and several kilobases (Supplementary Fig. 1). Furthermore, numerous changes frequently occur at the periphery of peaks, are discordant within peaks, and, although this is harder to visualize, it may be that both fragment size information and co-occurrence of fragments could provide valuable information about how these accessibility changes modulate gene expression (Supplementary Fig. 1). With this in mind, we designed two scale-adaptive models that can capture these different features to link regions to gene expression (ChromatinHD-pred, Fig. 1a) or determine differentially accessible regions by using sn(ATAC + RNA) data as input (ChromatinHD-diff, Fig. 1b).

Fig. 1: Central concepts behind ChromatinHD-pred and ChromatinHD-diff.

a ChromatinHD-pred inputs raw fragments in a neural network architecture, that will (1) transform the positions of each fragment close to a TSS (e.g. -10kb or -100kb) into a positional encoding, (2) transforms this positional encoding into a fragment embedding, typically with a smaller number of features, using one or more non-linear neural network layers, (3) pools the fragment information for each cell and gene. b ChromatinHD-diff uses cell type/state annotations derived from, for example, single-cell RNA-seq to construct a complex multi-resolution cell type/state-specific probability distribution. To do this, we apply several bijective transforms on the cumulative density function (CDF), to ultimately be able to estimate the likelihood of observing a particular cut site using the probability density function (PDF). c Three nested regions exemplifying how ChromatinHD models capture predictive and differential accessibility at different scales. Raw data of the same regions is presented in Supplementary Fig. 1. Red and blue Δcor represents regions that are respectively positively and negatively associated with gene expression. d Summarized relative performance for various tasks: accuracy of prediction (pred.), correlation between predictivity and CRISPRi sensitivity (CRISPRi), enrichment for transcription factor binding sites (TFBSs), enrichment for eQTLs (eQTL), enrichment for genome-wide association study variants (GWAS), and an average of the relative performance across tasks (all). Only methods that were second-best performing for any of the tasks are shown. Full details for each task is shown in Figs. 2 and 3. e The average of the relatively performance against the top performing method across all tasks (from d) for individual datasets. Source data are provided as a Source Data file.

In ChromatinHD-pred, we use raw chromatin accessibility fragments as input to predict gene expression (Fig. 1a). This enables pinpointing which accessibility features, such as the position, fragment size and other fragments in the same cell, might be linked to gene expression. To make the model automatically choose the relevant scale in the data, we leveraged concepts from transformer models³⁰, which convert absolute positions of objects, typically text, into a positional encoding that can then be consumed more readily by downstream neural networks. In our case, these objects correspond to individual Tn5 cut sites relative to the canonical transcription start site (TSS) of a gene. ChromatinHD provides this positional encoding to a neural network that will learn which resolution is most relevant, and pool information across different fragments from the same cell to predict gene expression (Fig. 1a, Methods). Using a perturbation-based interpretation scheme, ChromatinHD-pred can then assess which regions are linked to gene expression, with predictivity changing locally (~50 bp), regionally (~500 bp), and/or globally (>1 kb) (Fig. 1c).

ChromatinHD-diff learns the difference in accessibility between different cell types, individuals, or conditions (Fig. 1b), which can provide information about the activity of TFs⁴. Current tools typically do this by aggregating information across cells into pseudobulk, followed by a statistical model, e.g. a Wilcoxon rank-sum test, t-test, logistic regression, or more complex generalized linear models^11,19,31. To make this approach scale-adaptive, we leveraged concepts from normalizing flows^32,33, which are used to model complex probability distributions with a tractable likelihood that can be used for scalable statistical training and inference. In summary, ChromatinHD-diff will model the probability of finding a Tn5 insertion site using a series of reversible transforms that transform a simple uniform distribution into a complex distribution. Each of these transforms works at a different resolution (ranging from ~1 kb to ~25 bp), and the optimal resolution of both baseline and differential accessibility will be automatically selected in a data-driven way by including a Bayesian regularization term in the loss function (Methods). As such, ChromatinHD-diff models how the distribution of insertion sites changes between conditions locally within ~50 bp, regionally within ~500 bp and globally within >1 kb (Fig. 1c).

ChromatinHD outperforms current methods for analyzing sn(ATAC + RNA)-seq data

We set out to comprehensively evaluate whether ChromatinHD’s scale-adaptive approach would more optimally capture the relevant genomic regions in the data compared to CRE-based approaches, which involve defining CREs using peak calling, window scanning or predefined regions¹², followed by differential accessibility or predictive modeling using the cell-by-CRE count matrix. We benchmarked ChromatinHD models on five tasks: quality of linking regions to target gene expression, correspondence to CRISPRi-validated regions, detection of functional transcription factor binding sites (TFBSs), and detection of accessibility changes in genome-wide association studies (GWAS) or expression quantitative trait loci (eQTLs). While a detailed description follows in the proceeding sections, summarized over all tasks we found that ChromatinHD’s scale-adaptive approach outperformed the next best CRE approach consistently on each task (Fig. 1d). Furthermore, the top performing CRE-approach was very task-dependent, showcasing that these methods or parameter settings are often created for specific tasks that do not necessarily generalize across tasks. For instance, while peak summits were most effective in identifying the most differential TFBSs, they fell short in capturing natural variation and linking regions to genes (Fig. 1d). Window-based methods, on the other hand, could somewhat effectively associate regions with gene expression, as observed previously¹⁶ but faced challenges in identifying differentially accessible regions (DARs) (Fig. 1d). Additionally, while CREs defined by the ENCODE consortium worked well in tasks involving human immune cells, they struggled when used in other non-immune or non-human contexts (Fig. 1e). In contrast, our data-driven models emerged as a universally superior method for analyzing accessibility data, surpassing all other compared methods across a variety of tasks and datasets.

We zoomed in on evaluating the task of linking accessibility to gene expression, to identify what causes this difference in performance. In typical workflows such as Signac¹¹, ArchR¹⁹ or window-based approaches^15,16, this is done using some type of regression between the CRE accessibility and the gene expression with linear or logistic regression models. To provide a harmonized benchmarking, we therefore evaluated different methods according to their ability to predict gene expression using standard linear, regularized, or non-linear approaches (Methods), on either left-out test cells of the same dataset or cells from an independent test dataset. As a baseline, we also included methods that look at the accessibility within the promoter and/or gene body that are used as a proxy for gene activity¹⁹. Note that the correlation between single-nucleus RNA-seq and ATAC-seq can never be perfect due to the sparsity of both assays (Supplementary Fig. 1)^11,16, and that this comparison is best investigated in a relative way, rather than focusing on the absolute values of the correlation. We found that ChromatinHD’s scale-adaptive approach consistently outperforms all other methods on test cells (Fig. 2a) and test datasets (Fig. 2b). This performance difference is consistent across genes and visible both when the correlation or the out-of-sample R² is used (Supplementary Fig. 2a). Following earlier observations, window-based approaches slightly outperform CRE-based approaches^15,16, followed by MACS2 peaks merged over different cell types¹¹.

Fig. 2: ChromatinHD-pred improves linking putative regulatory regions to gene expression.

a Accuracy for prediction of gene expression on unseen cells from the same dataset. b Accuracy for prediction of gene expression on a different dataset from the same cellular context. The blue box highlights the difference in performance between ChromatinHD-pred and the second-best performing method. c Example of interpretation of a ChromatinHD-pred model on the IRF1 gene in the pbmc10k dataset, highlighting (with arrows) how the predictivity of a region is often located in the periphery and outside of peaks, or is variable within peaks. Also shown is the predictivity on two test datasets (pbmc10k_gran, pbmc3k). Only windows where at least 0.2 fragments per 1000 cells are present are shown, padded on both sides with 800 bp to show the genomic context. d, e Correlation between smooth region importance (predictivity for ChromatinHD-pred, correlation for CRE-based methods) and CRISPRi fold enrichment in 50 bp windows. Colors in (e) denote different genes as shown in (d). f Two example regions where ChromatinHD-pred corresponds to the CRISPRi enrichment, while CRE-based methods fail. False positives and false negatives are defined as the difference between the z-scores of the CRE-based region importance with the z-scores of ChromatinHD’s predictivity. Source data are provided as a Source Data file.

Using a perturbation-based interpretation, ChromatinHD determines which regions in the genome exactly provide predictive information to the model by censoring fragments at multiple scales (Fig. 2c). Based on this, we determined that there is extensive predictive information both outside and inside of peaks. In the pbmc10k dataset and utilizing the top predictive peak caller, 19% of the information on gene expression is contained outside of peaks, about 56% of the top 5% predictive regions do not fall within a peak, 16% of peaks contain both positively and negatively associated regions for gene expression, and the peak’s summit does not align with the most predictive region for 31% of the top predictive peaks (Supplementary Fig. 2b–d). This intra- and inter-CRE heterogeneity can be clearly seen in individual examples (Fig. 2c, Supplementary Fig. 2e, f). In the cases where peaks are a good representation of the predictive regions, ChromatinHD-pred matched the performance of peak-based methods (Supplementary Fig. 2e). We confirmed that the performance improvements and predictive regions are generalizable in independent test datasets (Fig. 2b, c). Furthermore, we found that the relative performance difference of ChromatinHD-pred compared to other methods is consistent across genes even if they are lowly expressed, have low accessibility, or low dispersion (Supplementary Fig. 3a–d). Moreover, despite the sparsity of the snATAC-seq data, our interpretation scheme still managed to identify specific predictive regions (Supplementary Fig. 3e, f) and had a robust difference in performance (Supplementary Fig. 3g).

To assess whether ChromatinHD-pred identifies regions that are causal for gene expression, we compared ChromatinHD’s predictivity to CRISPR-interference (CRISPRi) data, which can directly measure how silencing of a region by dCas9-KRAB affects gene expression³⁴. We performed this comparison for 4 genes for which extensive (>80% of accessible regions covered) CRISPRi tiling data was available in K-562 cells and which are differentially expressed within a multiome dataset of haematopoiesis³⁵, as to best match with this cell line’s erythroleukemic phenotype. We found that across all genes and various resolutions, prioritized ChromatinHD regions are better correlated with CRISPRi sensitivity than other approaches (Fig. 2d, e). Particularly striking is the lower performance of peak-based approaches, which was driven by several instances where the CRISPRi-sensitive region fell right outside of the peak, for example within the broader HDAC6 promoter affecting GATA1 expression or was embedded within a larger peak with mixed CRISPRi sensitivity, for example the KLF1 promoter and first intron (Fig. 2f). Altogether, this highlights the importance of a peak-free approach for linking putative regulatory regions to gene expression.

A standard ChromatinHD-pred analysis with training and interpretation for 5000 differentially expressed genes at a window of 200 kb around the transcription start site can be performed overnight using consumer-grade GPUs (Supplementary Fig. 2g). This is comparable to that of window-based analyses but has a higher computing time requirement than standard peak-based analyses, being ultimately a trade-off between computation and accuracy for linking relevant regions to target gene expression (Supplementary Fig. 2h). We performed an ablation analysis by removing individual elements from the model and tracking performance. This confirmed that the model utilizes multi-scale information, with non-linearities, the positional encoder, library size normalization, residual layers, and early stopping all contributing to the performance increase (Supplementary Note 1).

Next, we compared differentially accessible regions (DARs) identified by ChromatinHD-diff and standard DAR calling approaches, and found that DARs were very dissimilar, with less than 50% overlap between peak-based, window-based, and ChromatinHD-diff approaches (Fig. 3a). This lack of overlap was especially evident when comparing closely related cell states, such as various stages of differentiation, indicating the prevalence of multiscale effects among related cellular conditions (Supplementary Fig. 4a).

Fig. 3: ChromatinHD-diff detects functional differential accessibility within and outside of canonical cis-regulatory elements.

a Similarity between differentially accessible regions (DARs) identified by various methods according to overlap between individual positions (Jaccard) and overlap between regions (F1). b Magnitude of enrichment of transcription factor binding sites (TFBSs) in DARs for which the TF is differentially expressed in the cluster. c Ratio between the number of TFBSs identified in differential MACS2 summits versus differential ChromatinHD-diff regions. TF-cluster combinations were selected as those with differential expression (z-score > 3) and differential binding (odds-ratio > 1.5). d DARs in granulocyte precursors containing a GATA2 TFBS identified by ChromatinHD-diff, and whether it is also identified by alternative methods. Shown is ChIP-seq data (fold-change over control) of GATA2 in K-562 cells. e DARs in hematopoietic stem and progenitor cells (HSPCs) containing an ERG binding site according to MACS2 summits, and whether it is also identified by alternative methods. ERG binding peaks in TSU-1621MT cells⁹⁰ are shown. f DARs in erythroblasts containing a differential GATA1 TFBS identified by ChromatinHD-diff, and whether it is also identified by alternative methods. Shown is the ChIP-seq data (fold-change over control) of GATA1 in K-562 cells, and the CRISPRi fold-change enrichment of gRNAs in K-562 cells for high-vs-low bins of the gene’s expression. g Magnitude of enrichment of eQTLs or GWAS variants in DARs. h–j Examples of GWAS variants located in a ChromatinHD-diff DAR but not identified by alternative methods, highlighting how such variants can be located in the periphery of peaks in (h), outside of peaks in (i) or at a specific location within peaks in (j). Shown below is a putative mechanism for these variants based on allele-specific binding (ASB) and changes in binding affinity using ADASTRA v5.1.3⁹¹. Source data are provided as a Source Data file.

In assessing the DARs, we first focused on their efficacy in uncovering cell-type-specific TFBSs. Leveraging the differential expression of TFs as a proxy for relevant cell-type-specific TFs (Methods), we found that the enrichment of TFBSs was consistently highest in ChromatinHD-diff DARs compared to alternative DAR approaches on all datasets (Fig. 3b). In practice, this means that ChromatinHD-diff can find substantially more differential TFBSs, on average 33% in the hspc dataset, compared to the next best approach (Fig. 3c). This increase in sensitivity was especially marked for TFs that are active during transient differentiation stages, such as in multipotent progenitors, granulocyte-monocyte progenitors, and granulocyte progenitors (Supplementary Fig. 4b). For instance, ChromatinHD-diff identified over three times as many differential GATA2 binding sites in granulocyte precursors³⁶ (Fig. 3c). We attribute this to the fact that regions targeted by this TF inherently possess limited overall accessibility in granulocyte precursors, yet significantly differ in accessibility (Fig. 3d, Supplementary Fig. 4c). The few TFs for which peak-based DAR methods performed better were almost exclusively restricted to so-called stripe factors, known to stably bind the genome across cell types despite changes in TF gene expression³⁷ (Supplementary Fig. 4b), and indeed being strongly associated with highly accessible, but only slightly differentially accessible, peaks, as shown for the stripe TF ERG³⁷ (Fig. 3e, Supplementary Fig. 4d). Most TFs fall between these two extremes and bind both peak and non-peak regions (Fig. 3f, Supplementary Fig. 4e), explaining the increased enrichment in ChromatinHD-diff DARs. Importantly, we found that many of the binding sites outside of canonical peaks are clearly linked to gene expression as validated by CRISPRi (Fig. 3f, Supplementary Fig. 4e), and are bound by the corresponding TF as validated by ChIP-seq (Fig. 3f, Supplementary Fig. 4c). This underscores the complexity of TF binding patterns and the necessity of scale-adaptive models for a comprehensive understanding of the relationship between TF activity and gene regulation.

We further evaluated the DARs based on their enrichment for natural variants with impact on either diseases/traits or gene expression in the relevant context (such as immune diseases/traits for immune datasets). ChromatinHD DARs are more strongly enriched for both types of natural variation, with an average odds-ratio of 5.5 compared to the next best approach (MACS2 shared peaks, 4.8) (Fig. 3g). GWAS QTLs that were uniquely located within ChromatinHD DARs were associated with atypical differential accessibility in the periphery of larger peaks (rs443623, Fig. 3h), broad accessibility changes (rs875741, Fig. 3i), and intra-CRE variability (rs7668673, Fig. 3j). We validated some of these associations using allele-specific binding data complemented with changes in predicted binding affinity (Fig. 3h–j).

As before, data-driven differential modeling of snATAC-seq data comes with a computational cost, with a full ChromatinHD-diff analysis of 5000 genes with 200 kb regions taking about 5 hours using a consumer-grade GPU (Supplementary Fig. 4f). We performed an ablation analysis to confirm that the likelihood on test cells increases when larger scales are added to the model, indicating that the model is utilizing its scale-adaptive abilities (Supplementary Fig. 4g). The appropriate scale is selected through a Bayesian regularization approach, which we validated and optimized by comparing train- and test-cell likelihoods (Supplementary Fig. 4h).

Change in accessibility, and not the magnitude of accessibility, is an indication of functionality

Based on observations made in individual examples (Fig. 2c, d), we explored two main biological reasons on why our ChromatinHD approach performs better across tasks: its size-adaptability, and its ability to decouple changes in accessibility from the baseline accessibility at a region.

We found that DARs identified by ChromatinHD are very variable in size, ranging from a few dozen base pairs to several kilobases, a feature that is distinct from most CRE-based approaches that typically have more uniform, smaller or larger DAR sizes (Fig. 4a). By stratifying DARs across various lengths, indicators of functionality were present in DARs of every size (Fig. 4b), even very small (<20 bp) and very large (>1 kb) regions. CRISPRi did have a stronger preference towards larger regions, possibly because of the bulkiness of the dCAS9-KRAB complex, while this size-dependency was much less pronounced on other tasks (Fig. 4b). Altogether, this shows that there is not a predefined size for a CRE, and that size-adaptability, as implemented in ChromatinHD models, is a key aspect of single-nucleus accessibility data analyses.

Fig. 4: Size-adaptability and decoupling of baseline and differential accessibility are critical for understanding functional accessibility changes.

a Size distribution of differentially accessible regions (DARs) for different methods overlaid with that of ChromatinHD-diff (blue). b Various features of DARs split by DAR size: the number of differential genomic positions, number of differential regions, CRISPRi fold enrichment (in the hspc data), GWAS odds ratio (in the hspc data using reported immune GWAS variants), eQTL odds ratio (in the hspc data using CAVIAR fine-mapped GTEx variants), and average transcription factor binding sites (TFBSs) odds-ratio for differentially expressed TFs (in the pbmc10k data). c, d Enrichment for various measures of functionality split by average accessibility and differential accessibility. Differential accessibility is defined as either the standard deviation of the accessibility landscapes across cell types defined by ChromatinHD-diff (CRISPRi, GWAS and eQTL) or as the log-fold change between the accessibility in a cell type versus the average (TFBS). e Comparison between differential positions identified by ChromatinHD-diff versus those of the best performing alternative, MACS2 per cell type merged together with a Wilcoxon rank-sum test. Shown are the % of positions that a method identifies as differential within a mean/variance bin (according to ChromatinHD-diff). Highlighted is the false-discovery rate, i.e. the percentage of positions which have a low change in accessibility (<1.6 fold-change) according to ChromatinHD-diff among those that are predicted to be differential by the peak-calling approach, and false-negative rate, i.e. the percentage of positions which are not differential by the peak-calling methods among those that were found differential by ChromatinHD-diff within the particular window of baseline and differential accessibility. Source data are provided as a Source Data file.

A key assumption made by peak-based methods is that the magnitude of accessibility is an indication of a region’s functionality. Still, individual examples demonstrate that a region’s predictivity (Fig. 2c) or change in accessibility (Fig. 3h–j, Supplementary Fig. 4e) is not necessarily correlated with the absolute level of accessibility. Leveraging ChromatinHD-diff’s ability to decouple differential accessibility from baseline accessibility (Fig. 1c), we contrasted regions according to their baseline accessibility and dynamics of accessibility, the latter being characterized as the magnitude of differential accessibility over all cell types. We found that once baseline accessibility passes a threshold, CRISPRi sensitivity, cell-type-specific TFBSs, GWAS variants, and eQTLs targeting differential genes are all primarily enriched within dynamically accessible regions rather than highly accessible ones (Fig. 4c). For cell-type-specific TFs, the enrichment is strongest in regions with intermediate accessibility, a feature that may be TF-dependent and relates to a TFs ability to remove nucleosomes (Supplementary Fig. 5a)³⁸, but which is shared across different datasets (Supplementary Fig. 5b). This shows that, apart from eQTLs targeting non-differentially expressed genes (Fig. 4d), the sensitivity of a region to some ‘perturbation’ including natural variation, dCAS9-KRAB, or TFs, is primarily determined by its ability to dynamically respond to these changes, rather than its magnitude in accessibility. In CRE-based approaches, baseline and differential accessibility are modeled together, and consequently many differential regions are misinterpreted as false-negatives because of low accessibility, while many non-differential positions are seemingly identified as false-positively differential because of high accessibility (Fig. 4e). This decoupling between accessibility magnitude and accessibility dynamics is also important for predictive models, given that about 51% of information is gained outside of peaks once regions are normalized by baseline accessibility (Supplementary Fig. 5c), compared to only 19% without such normalization (Supplementary Fig. 2b).

ChromatinHD identifies a 1-5 kb outward juxtaposition between co-predictive regions and DNA contact

Because ChromatinHD-pred uses a nonlinear multilayer mapping between one or more fragments and gene expression, it can capture information that goes beyond the position of individual cut sites, such as the presence of other fragments within the same cell (Fig. 1e) or the size of the fragments (Fig. 1d). We first assessed whether ChromatinHD can capture dependencies between fragments within the same cell, by comparing a model that can only additively share information across fragments with a model that can do so in a non-additive way. Even though the co-occurrence of multiple fragments close to a TSS is a rare occurrence (Supplementary Fig. 6a), we found that the non-linear model performs better (Out-of-sample- R² ratio > 1.25, 75.2%) or approximately equal (0.8 > Out-of-sample-R² ratio > 1.25, 20.2%) for the large majority of genes (Fig. 5a). The genes that featured an increase in performance were typically those that already had a high predictive performance with the additive model, indicating that prediction reaches a saturation point which can be overcome by sharing information from multiple fragments.

Fig. 5: A 1-5 kb shift in co-predictivity and DNA contact highlights preferential DNA conformations connecting two co-predictive regions.

a Predictive test-set accuracy of additive and non-additive ChromatinHD-pred models across all genes (n = 5000). Percentage of genes with out-of-sample-R² ratio higher or lower than 1.25 are indicated. b Examples of co-predictive regions for BCL2. Immune-related GWAS SNPs are shown and colored according to haplotype (LD r² > 0.9). c Odds-ratio for finding high co-predictivity (higher than median) and high Hi-C signal (higher than median) within a slice of genomic distances (1kb-10kb, 10kb-20kb, …) performed for the original Hi-C data (Hi-C max-pool distance = 0), and for max-pooled Hi-C data where we took the maximal Hi-C signal at various genomic distances around the original position. B-cell genes were defined as being differentially expressed in naive, memory or plasma cells compared to all other cell types in the dataset. d Hi-C pileups of potential DNA contact points (C1 and C2) close to two co-predictive regions (E1 and E2, distance 20-25 kb, corΔz-score > 0). Shown is the relative Hi-C signal centered on the co-predictive pair divided by a random pair around the same gene with the same genomic distance. The numbers 1-8 refer to various putative conformations of enhancers and contact points, further described in panels (e–l). e–l Illustrations of how different distances between predictive regions and DNA contact points from d may inform on DNA conformation. m Difference in log contact frequency between up and down-regulated genes in B-cells. n–o Same as d but with E1-E2 distances of 5–10 kb and 45–50 kb respectively. Source data are provided as a Source Data file.

To determine whether two regions in the genome are co-predictive for gene expression in the same cells, we correlated the predictive accuracies between pairs of genomic windows (100 bp) across cells, allowing us to identify co-predictivity as a measure of putative cooperation between regions (Fig. 5b, Supplementary Fig. 7a–c). We found that the majority of co-predictive pairs work synergistically, meaning that if fragments from two positions co-occur in a cell, they are typically in agreement on how the gene will be expressed (Supplementary Fig. 6b). In addition, positive co-predictivity was higher within shorter genomic distances (<20 kb) (Supplementary Fig. 6c) and the region around the TSS had a slightly higher average co-predictivity compared to up- or downstream regions (Supplementary Fig. 6d). Also, genes that gained performance in the non-additive model typically had strong co-predictivity with the TSS (Supplementary Fig. 6e,e.g. KLF12, TNFAIP2, CCL4, Supplementary Fig. 7a-c). It is thereby worth noting that co-predictivity can inform on how seemingly distinct genetic variation can converge through a shared mechanism. For example, the first BCL2 intron contains 3 SNPs not in linkage disequilibrium (R² < 0.4) in distinct co-predictive, negatively predictive regions, all associated with granulocyte numbers^39,40,41, suggesting that these distinct genetic variants work through a common regulatory hub to regulate downstream gene expression (Fig. 5b).

With co-predictivity, we have a readout on cooperativity between regions that is conceptually distinct from both DNA contact frequencies^26,42,43,44 and DNA proximity⁴⁵. Several recent studies have shown how these latter read-outs can produce seemingly paradoxical results, with the physical proximity between specific enhancer and promoter pairs decreasing upon active transcription, while DNA contact frequencies increase^46,47,48. This decreased proximity between the DNA may be related to the establishment of a high protein concentration environment⁴⁹. However, whether this is a general genome-wide feature of mammalian gene regulation is not well understood.

The high-resolution, genome-wide readout provided by co-predictivity may help reconciling these seemingly non-intuitive observations. We compared ChromatinHD’s co-predictivity matrices from the pbmc10k dataset with Hi-C data at 1 kb resolution²⁶ originating from GM12878, a B-cell-like cell line. When investigating the Hi-C signal of individual co-predictive pairs, we found that these are often close but not exactly overlapping with physically contacting regions, frequently missing each other by 1 or several kilobases (Supplementary Fig. 6f). Indeed, if we compared co-predictivity with max-pooled Hi-C signal, we found that the overlap is the highest at about 2-5 kb of max-pooling (Fig. 5c). This confirms that DNA contact is more frequent than random in (co-)predictive regions (of ~1 kb), but that it is much higher in the adjacent regions, potentially to accommodate protein and RNA complexes required for gene regulation.

We next studied whether the juxtaposition of co-predictivity and DNA contact depends on their orientation, because this could help disambiguate different 3D conformations, and therefore help us understand how this interaction is established or maintained (Fig. 5d–l). Assuming a given genomic distance between a co-predictive region pair (initially 20kb-25kb), a DNA contact at respectively -2kb and +2 kb of the two co-predictive regions would be indicative of a loop which exposes the two co-predictive regions outward (Fig. 5e). Indeed, after normalizing with random non-co-predictive regions, we found that the DNA contact is the strongest for such a configuration (Fig. 5d, e), compared to the less frequent - but still enriched - contacts overlapping with the co-predictive regions themselves (Fig. 5f), juxtaposed in the same orientation (Fig. 5g) or juxtaposed to inside of the loop (Fig. 5h).

When zooming out to assess larger distances between enhancers and contact points (Fig. 5d), we found a preference for the co-predictive regions to be located outside of the contact points (Fig. 5i), with DNA contact being less likely than even random if they would result in the two regions being on opposite sides (Fig. 5j), or deep (>20 kb) on the inside of the loop (Fig. 5k). Interestingly, we also saw an enrichment for situations where only one of the regions is close to a contact point as long as both co-predictive regions are located on the same side of the loop, indicative of further looping and hub formation (Fig. 5l)^50,51. The dependency between co-predictive regions and DNA contact points changed depending on whether the regions were active in a cell, as co-predictive regions regulating genes highly expressed in B-cells showed a more outwards dependency pattern in the B-cell-like cell line (i.e. Fig. 5e), compared to the inwards pattern (i.e. Fig. 5h) for genes downregulated in B-cells compared to all other leukocytes (Fig. 5m). This suggests that this juxtaposition itself is dynamic between cell types, and likely important to regulate gene expression.

The general pattern of DNA contact between co-predictive regions was consistent across different sets of distances (Fig. 5d, n, o, Supplementary Fig. 6g, h) and was further validated on a recently published Hi-C dataset with higher resolution⁴³ (Supplementary Fig. 6i, j). Although the outwards pattern was enriched across all distances (Fig. 5h), the inward pattern was strongly disfavored when the distance between enhancers was small (<15 kb, Fig. 5n, Supplementary Fig. 6g), while being slightly positively enriched at a larger distance (>25 kb, Fig. 5o, Supplementary Fig. 6h), potentially because the larger stretch of DNA allows more physical freedom regarding how co-predictive regions can interact. Interactions between promoters and enhancers produced an asymmetric contact pattern, with DNA contact particularly preferred on the inside of the gene body with the strongest enrichment still at the 1-5 kb inward juxtaposition (Supplementary Fig. 6k).

Altogether, by connecting co-predictivity analysis with Hi-C data, we revealed how co-predictive regions make contact in a slightly juxtaposed way, and that this juxtaposition is oriented in such a way to prefer looping and further hub formation. While this confirms and reconciles some of the results observed at individual loci^46,47,48, it also shows how ChromatinHD’s co-predictivity data provides a view on cooperativity between DNA that is complementary to both DNA contact and DNA proximity analyses.

The mechanism by which enhancer-enhancer and enhancer-promoter interactions are created and maintained is still controversial⁵². First, we found that contacts in the same orientation are consistently enriched even over longer distances (Fig. 5d), indicating that some contacts between co-predictive regions may form independent of looping extrusion (Fig. 5g). When contrasting highly and weakly co-predictive regions, we found that binding of looping factors RAD21, CTCF and YY1 are not enriched directly within highly co-predictive regions, but are enriched close (RAD21, CTCF, ~500 bp) or farther away (YY1, ~1.5 kb) to the co-predictive region, contrasting with the enrichment cell-type-specific TFs centered at the predictive region itself (Supplementary Fig. 6l). This further confirms the juxtaposition between co-predictivity and DNA contact, and that several mechanisms: CTCF-cohesin, YY1 and cohesin-independent, may all be at play to form or stabilize these interactions.

ChromatinHD identifies submononucleosomal fragments as indicative of dense TF binding and active gene regulation

Differences in fragment size is an additional feature that ChromatinHD enables us to consider (Fig. 1d). This could be relevant since such differences have already been linked to distinct chromatin states and nucleosome positioning^53,54. To test this, we censored fragments of a particular length and assessed the effect of the model’s ability to predict gene expression. We found that, while the predictivity of a fragment size is correlated to the number of fragments of that size in the data, there are clear relative differences corresponding to nucleosomal or sub/super-nucleosomal fragment sizes (Fig. 6a). Averaged over all genes, nucleosomal fragments (160-190 bp) were about 3 times less predictive than submononucleosomal fragments (80-120 bp) (Fig. 6a, b). We note that despite these relative differences, nucleosomal fragment sizes still contributed significantly to a model’s predictive performance and every fragment size was, on average, still positively correlated with gene expression at similar levels (Fig. 6b).

Fig. 6: ChromatinHD learned a complex dependency between predictivity and fragment size.

a Relationship between the abundance of a fragment size bin (± 10 bp) and the overall loss in predictive accuracy (predictivity, Δcor) when fragments of these sizes were removed from the data. b Abundance, normalized predictivity (predictivity divided by abundance) and average effect of different fragment size bins. The effect is defined as the difference in predicted gene expression between the original data and when the respective fragment is removed. Fragment sizes were split into footprint, mono-, mono, mono + , di-, di + , tri, tri+ and multi fragments by taking the middle point between the local maxima and minima of normalized predictivity. c Motif enrichment for windows with mono− (80-120 bp) versus TF footprint (0-80 bp) fragments, compared to the overall enrichment of a motif in predictive windows. d Relationship of the # of (indirectly) bound TFs within a 100 bp window according to ENCODE GM12878 data (x-axis) and predictivity as defined by ChromatinHD-pred (blue), # of footprints according to HINT-ATAC on the pbmc10k data (red), ratio of Mono− versus TF footprint fragments (green) and overall number of fragments (orange). Shown is the mean and standard error of a spline fit using R’s gam function with smoothing parameter sp = 1. ChIP-seq data of top 30 TFs (ordered by the correlation between predictivity and number of binding sites within 100 bp windows); data for all TFs is shown in Supplementary Fig. 8a. Source data are provided as a Source Data file.

Surprisingly, we saw a split in predictivity within nucleosome-free fragments, with TF footprint fragments (10-60 bp) being much less predictive than larger submononucleosomal fragments (60-120 bp, Mono−), despite the former being most frequent (Fig. 6a) and typically strong indicators of TF binding by establishing footprints in the DNA^53,55,56,57. We hypothesized that this may be due to the fact that TF footprint fragments mainly straddle isolated binding events on the genome, whereas the most predictive regions are at locations with concentrated direct and indirect TF binding, larger DNA protection, and therefore fragments that straddle longer regions²². To assess this, we contrasted motifs enriched in predictive regions to motifs enriched in regions with a high submononucleosomal versus TF footprint ratio. We found that nearly all TFs enriched in predictive regions are also enriched in high submononucleosomal regions (Fig. 6c). Only CTCF, a critical chromosomal organization regulator and the most common TF used in footprinting analyses^56,58, showed a clear preference towards TF footprint fragments. To find further experimental evidence, we cross-referenced with TF footprints inferred using HINT-ATAC⁵⁵ on the same ATAC-seq data, and TF ChIP-seq data from GM12878, a B-cell-like cell line¹³. We found the number of TFs that bind (in)directly within a 100 bp window to be strongly positively correlated with both the predictivity of a window and the ratio of submononucleosomal versus TF footprint fragments, increasing linearly even for regions with dozens of bound TFs (Fig. 6d). This was true both when we focused on TFs enriched in B-cells, as to best match the ChIP-seq cell line (GM12878) with the primary cells under study (PBMCs) (Fig. 6d), but also when we considered all TFs (Supplementary Fig. 8a). This increase in predictivity coincided with a decrease in the number of fragments, which further confirms the ambiguous relationship between the magnitude of accessibility with functionality of a region (Fig. 4). Indeed, low accessibility can both mean high nucleosome occupancy (and therefore low expression) or high TF occupancy (and therefore typically high expression). By considering the raw fragments in its model, ChromatinHD-pred can differentiate between the two cases that would seemingly look similar when one pools fragments within peaks.

The use of footprinting methods has been controversial, particularly given several observations of functional binding events that do not leave footprints⁵⁹. Our analysis highlights that dense (indirect) binding of TFs may mask the local footprint signal, despite these densely bound regions being the most predictive for gene expression. Indeed, we found that the number of detected footprints stagnates and even decreases with an increasing number of TFs that bind to the respective regions (Fig. 6d, Supplementary Fig. 8a), an observation further confirmed on DNase I hypersensitivity datasets⁵⁶, which typically have a higher sensitivity to detect footprints (Supplementary Fig. 8b). Altogether, this shows that while footprinting methods can detect individual TF binding events, they are less able to distinguish densely bound regions from weakly bound ones, and in fact tend to be negatively biased towards the former. In contrast, although ChromatinHD does not provide direct evidence of TF binding, it is better able to detect these densely bound regions because the subtle shift in fragment sizes makes the model more predictive for gene expression.

Discussion

A central challenge in understanding eukaryotic gene regulation is learning how various chromatin state scales are integrated to regulate a gene’s expression⁶⁰. An important advance toward addressing this challenge is the development of multi-omic profiling assays which directly link gene expression to other genomic read-outs in the same cell³, as these can inform both on TF binding and long-range interactions and how they affect gene regulation¹². However, this potential has so far mainly been exploited with methods using CREs as the main preprocessing step, which, we reasoned, may be too reductive to capture the full multiscale underlying gene regulation. To address this, we developed ChromatinHD, a suite of two scale-adaptive machine-learning models and interpretation tools that can contribute to learning how chromatin accessibility relates to gene expression.

By staying close to the actual biochemistry, i.e. raw fragments, combined with two scale-adaptive machine learning models, we showed that accessibility data contains information both outside and inside canonical CREs. Although we do find that predictive changes in accessibility tend to indeed be restricted to specific regions in the genome, our study mainly calls into question whether the use of a priori defined CREs and/or window sizes are suitable as a summarization approach to comprehensively study gene regulation, complementing observations made in recent studies using windows^15,16 and footprinting⁶. The high probability that both false-positive regions are included and functional false-negative regions excluded (Fig. 4), means that summarization at the CRE level induces an undesirable bias that can negatively affect the prioritization of regions for gene regulation, the identification of relevant TF binding sites and the fine mapping of relevant genetic variants. By being able to select regions of various sizes and by decoupling baseline from differential/predictive accessibility, ChromatinHD models can better delineate regulatory regions across all five tasks we studied (Fig. 1). Our study thereby confirms the importance of dynamic accessibility that has been recently recognized for resolving GWAS variants⁶¹, but expands this idea for CRISPRi sensitivity, cell-type-specific eQTLs, and TF binding.

Furthermore, the high resolution offered by both ChromatinHD and deep Hi-C data also allowed us to identify a juxtaposition of 1-5 kb between DNA contact and enhancer activity, which is likely related to preferential chromatin conformations underlying gene regulation. Our data is consistent with previous observations made for individual loci^46,47,48, and suggests that these juxtapositions occur across the whole genome in vivo in mammalian DNA. ChromatinHD-pred also revealed a strong preference for longer submononucleosomal fragments to better predict gene expression, a chromatin accessibility feature that is indicative of a very active regulatory environment with potentially high (in)direct protein binding, but which is less well captured by footprinting methods. Both of these examples highlight how an unbiased, data-driven approach is useful to uncover additional, often hidden, layers of complexity underlying gene regulation. As such, our study is consistent with recent studies that have shown similar potential, albeit using window-based approaches¹⁶, and footprinting analysis⁶.

The improved expressivity of ChromatinHD models come with stronger computational requirements, particularly compared to peak-based approaches, although a typical analysis can still be performed within one day. Moreover, the current two ChromatinHD models only cover two major use cases of accessibility - linking regions to gene expression and differential modelling - and extensions should still be developed that include dynamics³, multiomics velocity⁵, impact of genetic variation⁷ or integrates spatial information⁶². Combining co-predictivity with emerging nascent RNA sequencing techniques⁶³ may also shed light on the mechanisms underlying active transcription and bursting. To enable the community to use and extend ChromatinHD, we made the PyTorch models, training and interpretation tools available as a python package (https://chromatinhd.org), making them easily deployable and extensible. With this package, users will be able to train, infer and interpret the models. For downstream analyses, e.g. gene regulatory network inference⁴ or velocity analysis⁵, users can directly plug the identified predictive regions in these tools.

Methods

ChromatinHD

Documentation can be found at https://chromatinhd.org. ChromatinHD is available as a Python package at https://github.com/DeplanckeLab/ChromatinHD and PyPI (https://pypi.org/project/chromatinhd/).

Data preprocessing

All nine multiome datasets (pbmc10k, pbmc10k_gran, pbmc10kx, lymphoma, e18brain, pbmc3k, alzheimer, liver and hspc) were preprocessed in the same manner. Raw fragments, mapped either to the GRCh38 or mm10 genomes, and the raw expression counts at the gene-level, were obtained from the 10X Genomics website (https://www.10xgenomics.com/resources/datasets; pbmc10k, pbmc10k_gran, lymphoma, e18brain, pbmc3k, alzheimer), or GEO (liver: GSE218468⁶⁴, hspc: GSE209878³⁵). Cells were filtered on containing at least 1000 UMIs and 200 genes with at least 1 UMI. We selected the 5000 most variable genes for downstream analysis by ordering on the normalized dispersion calculated by scanpy⁶⁵. We obtained potential transcription start sites (TSS) for each gene from biomart⁶⁶, and picked the appropriate transcription start site for a gene as the one with the highest number of ATAC-seq cut sites in the 200 bp window around the putative TSS using ChromatinHD’s select_tss_from_fragments function. From this TSS, we extended either 10 kb or 100 kb up- and downstream to define a gene region. We used memory-mapped files (for short-term storage) and zarr store⁶⁷ (for long-term storage) to store the fragment information in an efficient sparse data format with fast access to fragments from a particular minibatch of cells, and to which cell, genes or cell-by-gene combinations these fragments belong. This data format contains index pointers⁶⁸, indicating the first index at which the fragments from a particular cell begin.

ChromatinHD-pred

As input, ChromatinHD-pred (Fig. 1a) uses a matrix containing the start and end positions of the fragments X and a mapping M for each fragment indicating to which cell and region each fragment belongs. The goal of a ChromatinHD-pred model is to create a model that uses the positions of all fragments in a predefined window around the TSS in a cell to predict the (relative) expression of the gene in that cell. Each model is independently parameterized per gene. While a network could in theory learn this from the raw positions, ChromatinHD uses a positional encoding, as used in sequence models⁶⁹, to more efficiently present the positions to the downstream neural networks. This positional encoding will convert an integer position of start and end Tn5 insertion sites into a set of continuous features. This encoder allows downstream linear and activation functions to easily learn to prioritize certain positions. Given a scale i ∈{200, 400, 800, 1600, 3200, 6400}, and w, l, r respectively the width, left bound and right bound of the window around the TSS, we used a set of knots ${{{{\rm{k}}}}}_{{{{\rm{j}}}}}={{{\rm{l}}}}+{{{\rm{ij}}}}$, $\forall {{{\rm{j}}}}\in \{0,\ldots,{{{\rm{n}}}}\}$ with ${n}_{i}={{{\rm{\lceil }}}}\frac{w}{l}{{{\rm{\rceil }}}}$. The positional encoding of a position x was calculated using the 1st order B-spline basis function N_i,1 defined as:

$$\begin{array}{c}{{{{\rm{N}}}}}_{{{{\rm{j}}}},0}\left({{{\rm{x}}}}\right)=\left[\begin{array}{cc}1 & {{{\rm{if}}}}\,{{{{\rm{k}}}}}_{{{{\rm{j}}}}}\,\le \,{{{\rm{x}}}} \, < \,{{{{\rm{k}}}}}_{{{{\rm{j}}}}+1}\\ 0 & {{{\rm{otherwise}}}}\hfill\end{array}\right.\\ {{{{\rm{N}}}}}_{{{{\rm{j}}}},1}\left({{{\rm{x}}}}\right)=\frac{{{{\rm{x}}}}-{{{{\rm{t}}}}}_{{{{\rm{j}}}}}}{{{{{\rm{k}}}}}_{{{{\rm{j}}}}+1}-{{{{\rm{k}}}}}_{{{{\rm{j}}}}}}+\frac{{{{{\rm{k}}}}}_{{{{\rm{j}}}}+2}-{{{\rm{x}}}}}{{{{{\rm{k}}}}}_{{{{\rm{j}}}}+2}-{{{{\rm{k}}}}}_{{{{\rm{j}}}}+1}}\end{array}$$

(1)

The positional encodings for both cut sites were concatenated, creating a final positional encoding consisting of $2\sum {{{{\rm{n}}}}}_{{{{\rm{i}}}}}$ dimensions. A visual representation of this positional encoding, along with an analysis of alternative encodings is provided in Supplementary Note 1.

Next, the positional encoding is transformed into a fragment embedding by a single linear layer bringing the number of dimensions down from $2\sum {{{{\rm{n}}}}}_{{{{\rm{i}}}}}$ to m = 100 (Supplementary Note 1), followed by a ReLU and linear layer. Adding additional layers to the fragment embedder resulted in a slight drop in test cell predictive performance (Supplementary Note 1). The advantage of a B-spline basis function over e.g. radial basis-function kernels for positional encoding is that they are zero for the majority of j. We used this sparsity property to optimize both the forwards and backward pass of the fragment embedder by only calculating the first linear layer for non-zero positional encodings.

Next, the information coming from one or more fragments for each cell is pooled by summing the respective fragment embeddings, creating a cell embedding. If a cell has no fragments, its cell embedding is set to all-zero. To this embedding, we concatenated the z-scored library size of the cells, to help the model disambiguate between the true lack of a fragment at a particular position with the low efficiency of transposition within a cell. This final cell embedding with $2\sum {{{{\rm{n}}}}}_{{{{\rm{i}}}}}+1$ dimensions is subsequently used to predict relative gene expression using 5 blocks each consisting of (1) a linear layer, (2) a ReLU activation function, (3) a Layernorm which will shift and scale all m dimensions on a per-cell basis to mean 0 and standard-deviation 1, (4) a residual connection which adds the result from the previous block to the result of the current block. All linear layers within the block maintain the same number of hidden dimensions m, except the layer in the final block which maps from m to 1 to ultimately predict relative gene expression. The importance of each of the elements within these blocks was validated within an ablation analysis (Supplementary Note 1).

To train the model, we split the data into train, validation and test cells according to a 3:1:1 split. We trained using minibatches of cells (n = 1000) and calculated for each epoch the correlation between predicted and observed gene expression on the validation set for each gene. Once validation performance increased relative to the previous epoch, we performed early stopping of the training for that particular gene. As loss function, we used the negative correlation between the MAGIC imputed gene expression data (k = 30)⁷⁰ versus the predicted gene expression. Parameters were optimized using a ADAM⁷¹ with a learning rate of 10⁻⁴.

ChromatinHD-diff

To learn how the accessibility changes between different cell types/states we defined a likelihood for observing a Tn5 insertion at position x in gene g in cell type ct as follows:

$$p\left(x,g\, |\,{ct}\right)=p\left(g \, | \, {ct}\right)p\left(x \, | \, g,{ct}\right).$$

(2)

${{{\rm{p}}}}\left({{{\rm{g}}}},|,{{{\rm{ct}}}}\right)\sim {\mbox{Poisson}}\left({{{\rm{\beta }}}}\left({{{\rm{g}}}},c\right)\right)$ captures the total increase or decrease in number of fragments between the cell types and genes. To parameterize this distribution, we first calculated

$$\hat{{{{\rm{\beta }}}}}\left(g,{ct}\right)={d}_{g,{ct}}+{c}_{g},$$

(3)

Where ${{{{\rm{d}}}}}_{{{{\rm{g}}}},{ct}}\,{\mathbb{\in }}\,{\mathbb{R}}$ was optimized as a free parameter initialized at 0. c_g was fixed to the average number of fragments present in a gene region over all cells. This is used to parameterize the Poisson distribution using the total number of fragments in a cell ${{lib}}_{c}:$

$${{{\rm{\beta }}}}\left({{{\rm{g}}}},c\right)={{{lib}}_{c}e}^{\hat{{{{\rm{\beta }}}}}\left(g,{ct}\right)}.$$

(4)

$p\left(x,|,g,{ct}\right)$ captures the position- and cell-type-specific change in cut-site density within g. This requires a multimodal density function, with numerous local minima and local maxima pertaining to broad or narrow areas of TF or nucleosome positioning (Fig. 1c). This distribution is defined using a series of bijective transformations that transforms a discrete uniform distribution over the whole window $\left\{{{{\rm{l}}}},{{{\rm{l}}}}+1,..,{{{\rm{r}}}}\right\}$ into a multimodal one^32,33. We define a set of resolutions

$$k=\left\{25,50,100,250,500,1000,2500,5000\right\},$$

(5)

and calculate for a given cut site within a gene g and cell type ct:

$${{{\rm{\alpha }}}}\left(x,{ct}\right)={\sum}_{k\in k}^{n}{b}_{k,{i}_{k}\left(x\right)}+{a}_{k,{i}_{k}\left(x\right),{ct}},$$

(6)

where i_k(x) is the i-th bin index for resolution k:

$${{{{\rm{i}}}}}_{{{{\rm{k}}}}}\left({{{\rm{x}}}}\right)=\left\lfloor \frac{{{{\rm{x}}}}}{{{{\rm{k}}}}}\right\rfloor$$

(7)

Both ${{{{\rm{b}}}}}_{{{{\rm{k}}}},{{{{\rm{i}}}}}_{{{{\rm{k}}}}}\left({{{\rm{x}}}}\right)}$ and ${{{{\rm{a}}}}}_{{{{\rm{k}}}},{{{{\rm{i}}}}}_{{{{\rm{k}}}}}\left({{{\rm{x}}}}\right),{ct}}$ are free parameters that are optimized by the model. b represents the baseline accessibility within a bin, while a represents the change in accessibility in a bin and cell type. Because both a and b are defined at multiple resolutions, the model can freely choose to make the baseline accessibility broad, while making the change in accessibility narrow (e.g., Fig. 3h) or vice-versa (e.g., Fig. 3i). To ensure that the model selects the widest appropriate resolution available that is supported by the data, a is regularized:

$$a\sim {\mbox{Normal}}\left(0,{{{{\rm{\sigma }}}}}_{a}\right),$$

(8)

with ${{{{\rm{\sigma }}}}}_{{{{\rm{a}}}}}=1.5$ a hyperparameter that was optimized using test data (Supplementary Fig. 4h).

A final soft-max transform is used to normalize α over the whole domain $\left\{{{{\rm{l}}}},{{{\rm{l}}}}+1,..,{{{\rm{r}}}}\right\}$:

$$p\left(x \,|\, g,{ct}\right)=\frac{{e}^{{{{\rm{\alpha }}}}\left(x,{ct}\right)}}{{\sum }_{x\in \left\{l,l+1,..,r\right\}}{e}^{{{{\rm{\alpha }}}}\left(x,{ct}\right)}}$$

(9)

To reduce memory consumption, this normalization can be performed at the smallest resolution together with a scaling factor:

$$p\left(x \,|\, g,{ct}\right)=\frac{{e}^{w\left(x\right)}}{{\sum }_{x\in {K}_{0}}{e}^{w\left(x\right)}}\frac{1}{{k}_{0}}$$

(10)

where K₀ are the knots at lowest dimension, i.e. ${{{{\rm{K}}}}}_{0}=\{{{{{\rm{w}}}}}_{0},{{{{\rm{w}}}}}_{0}+{{{{\rm{k}}}}}_{0},{{{{\rm{w}}}}}_{0}+2{{{{\rm{k}}}}}_{0},\ldots,{{{{\rm{w}}}}}_{1}\}$.

The goal of training is to approximate the posterior ${{{\rm{P}}}}\left({{{\rm{a}}}},{{{\rm{b}}}},{{{\rm{c}}}},{{{\rm{d}}}},|,{{{\rm{x}}}}\right)$. We use maximum a posteriori estimation, optimized using gradient descent with as loss function the evidence lower-bound:

$${{\mbox{ELBO}}}=-\log p\left({{\mbox{x}}} \, | \, {{\mbox{g }}},{{\mbox{ct}}}\right)-\log p\left({{\mbox{g }}}\, | \, {{\mbox{ct}}}\right)+\log p\left({{\mbox{a}}}\right).$$

(11)

To train the model, we split the data into train, validation and test cells according to a 3:1:1 split. We trained using minibatches of cells (n = 5000) for 150 epochs and with a learning rate of 10⁻³.

Interpretation of ChromatinHD-pred

To interpret ChromatinHD-pred models, we compared the test-set on the full data with that obtained from censored data. For positional predictivity in particular, we censored fragments for which a fragment was removed if one Tn5 insertion site was overlapping with a window. We performed this censoring using a scanning window approach of window sizes 50, 100, 200, 500, 1000 and 2000 base pairs, with a stride length of half of the window’s size. We calculated the robustness of a window’s Δ cor using a one-sided t-test across the different folds and set the Δ cor to 0 if the adjusted p-values (Benjamini Hochberg correction) were higher than 0.1. We then extracted a base-pair position importance by linearly interpolating the Δ cor for a given window size, and summing up these interpolated values divided by the window size.

For interpretation of fragment size importance, we removed fragments of a particular size window (20 bp) ranging from 10 to 770 and compared the fragment size mean Δ cor across genes with the mean number of fragments of that particular size to a relative Δ cor. To split into different types of fragments, e.g. TF footprints and Mono − , we calculated the local minima and maxima of relative Δ cor, and split the fragment sizes by taking the midpoint between these minima and maxima.

Interpretation of ChromatinHD-diff

To interpret ChromatinHD-diff models, we use the trained model to extract $P\left(x,g,|,{\mbox{ct}}\right)$ for all genes g, cell types ct and positions (with step size 25 bp). This probability is subsequently averaged across all 5 folds. From this, we obtain a position-specific fold-change by calculating

$${{\mbox{lfc}}}\left(x,g,{\mbox{ct}}\right)=\log p\left(x,g \, | \, {\mbox{ct}}\right)-\frac{1}{{n}_{{{\rm{ct}}}}}{\sum }_{{{\rm{ct}}}}P\left(x,g \, | \, {\mbox{ct}}\right),$$

(12)

and linearly interpolating across positions. Differentially accessible regions (DARs) can then be called by determining consecutive positions where lfc remains above a particular cutoff, by default log 2. We only retained regions where baseline accessibility was higher than a specified cutoff, i.e. ${{{\rm{p}}}}\left({{{\rm{x}}}},{{{\rm{g}}}},|,{\mbox{ct}}\right)\ge 0.25$.

Benchmark

CRE methods

MACS2 peaks are frequently post-processed in different ways depending on the study^72,73, and we included several variants to make the comparison fair. For “MACS2 all cells”, we used MACS2 v2.2.7.1⁷², with fragments and the –no-model and –BEDPE parameter, as suggested by the authors. For “MACS2 per cell type” we split the fragments based on the cell type, called peaks, and kept all peaks even if they overlap as separate features for downstream analyses. For “MACS2 per cell type merged”, the recommended pipeline in signac¹¹, we merged all peaks from “MACS2 per cell type” using the bedtools merge⁷⁴. For “MACS2 summits 200 bp“⁷⁵, we called peaks as before with the –call-summits, and defined peaks by padding each summit 100 bp up- and downstream. For Cellranger⁷⁶, we used the peaks as provided by Cellranger 3.0.2 multiome pipeline. We used Genrich v0.6.1⁷⁷ with ATAC-seq mode -j. For window approaches, we simply divided the region around a gene’s TSS in non-overlapping windows. We also included SCREEN regions (v3)¹³ as these have been proposed to be a good substitute for dataset-specific peak calling^4,13 (https://screen.encodeproject.org/). Cell by CRE counts were obtained by determining whether one or two cut sites of a fragment overlapped with the CRE.

For detecting DARs using CRE-based methods, we provided the CRE counts for those CREs overlapping with at least one gene window to scanpy v1.9.1 and SnapATAC 1.0. For all scanpy functions, we first normalized using sc.pp.normalize_total and sc.pp.log1p. We calculated differentially accessible CREs using (1) scanpy’s rank_genes_groups for t-test and t-test-foldchange, (2) rank_genes_groups with method wilcoxon for wilcoxon test, (3) SnapATAC’s findDAR for snapatac and (4) rank_genes_groups with method logreg for Logistic regression. The DARs were ranked according to the relevant scoring metrics: fold-change for t-test-foldchange and snapatac, z-score p-value for t-test and wilcoxon, and logistic regression coefficient for logreg.

Comparing gene expression prediction

To make the comparison fair for all methods, we included all CREs that overlap at least partially with a given window around a TSS, in this case -100kb and +100 kb. Peak-based approaches are typically linked to target gene expression on an individual basis using correlation analyses^11,19, and to best replicate this we included both linear, regularized linear, and nonlinear boosted trees regression. For window-based approaches both single-window correlational analysis at about 50-100 bp¹⁵ as well as multiple window regularized regression using 500 bp¹⁶ have been described, and as such both were included within the benchmark. Finally, several papers have linked accessibility with gene expression using a single large window encompassing upstream regions, the TSS and/or the gene body^11,19, sometimes combined with a distance-dependent weighting scheme¹⁹. We included these approaches as a baseline, given that we would expect that any other approach (both CRE-centric or ChromatinHD) should at the very least be able to isolate the predictive from the non-predictive regions within this larger window.

We used the CRE counts overlapping with (part of) a gene’s window to perform linear and lasso regression using scikit-learn’s (v1.5.2) LinearRegression and LassoCV respectively. For LassoCV, we provided the same set of validation cells as provided to ChromatinHD-pred, and n_alphas=10, which will automatically determine the optimal penalization parameter on a per-gene basis. For boosted trees regression, we used XGBoost’s (v2.1.1) XGBRegressor with 100 estimators and 50 early stopping rounds. To perform this early stopping, we provided the same validation cells as provided to ChromatinHD-pred. Final correlation values were then obtained for test cells. If no CREs were found within the gene region, the correlation was set to 0.

To compare the methods we used the Pearson correlation and out-of-sample R² between predicted and observed MAGIC-imputed gene expression. For the out-of-sample R²⁷⁸, we calculated

$${{{{\rm{R}}}}}_{{{{\rm{oos}}}}}^{2}= 1{{{\rm{\hbox{-}}}}}{{\mbox{MSE}}}_{{{{\rm{m}}}}}/{{{\rm{MS}}}}{{{{\rm{E}}}}}_{{{{\rm{bmk}}}}}\\ {{\mbox{MSE}}}_{{{{\rm{m}}}}}= \frac{1}{{{{\rm{n}}}}}{\sum}_{{{{\rm{i}}}}=1}^{{{{\rm{n}}}}}{\left({{{{\rm{Y}}}}}_{{{{\rm{i}}}}}-\widehat{{{{{\rm{Y}}}}}_{{{{\rm{i}}}}}}\right)}^{2}\\ {{\mbox{MSE}}}_{{bmk}}= \frac{1}{n}{\sum}_{i=1}^{n}{\left({Y}_{i}-\overline{{Y}_{{\mbox{train}}}}\right)}^{2},$$

(13)

where Y_i the observed expression and $\widehat{{{{{\rm{Y}}}}}_{{{{\rm{i}}}}}}$ the predicted expression.

All methods were run using 5-fold cross validation across the cells, with a 3:1:1 split for train, validation and test cells. For training and testing on different datasets, we applied training and testing on respectively the full train and test dataset only once. Methods that ran longer then 72 h, primarily window-based methods on the -100kb – TSS – +100 kb region, were excluded from the benchmarking.

Comparing to CRISPRi

We obtained the raw guide counts³⁴ (https://osf.io/uhnb4/), and performed a simple linear regression modeling the library-size normalized log1p counts of a gRNA as a function of the bin representing an expression level (A to F). The slope of this function, divided by the number of bins (6), represents the fold-change in bin counts from the highest to the lowest expressing bin, denoted as the CRISPRi fold enrichment. Because the CRISPRi results tend to be highly guide-specific, we calculated the average CRISPRi fold enrichment per 50 bp windows.

To compare CRISPRi results with ChromatinHD-pred or alternative methods, we first calculated a region importance score either by calculating the correlation between MAGIC-imputed gene expression (CRE-based methods) or the Δcor (ChromatinHD-pred). Because many guides do not directly overlap with their respective accessible regions (e.g., Fig. 2f), we calculated for each 50 bp window the smooth region importance score as the maximal region importance score within the 500 bp up- or downstream of the window. The Pearson correlation between the smooth region importance and the CRISPRi fold enrichment was then used for benchmarking.

For comparing the ChromatinHD-pred with CRE-based region importance in Fig. 2f, we calculated the difference in z-scored region importance for a CRE-method with the z-scores region importance for ChromatinHD-pred. If this difference is positive, it indicates that the region is ranked higher using CREs, indicating a false-positive compared to ChromatinHD-pred.

Comparing motif enrichment

We scanned for motifs within regions using position weight matrices and precalculated thresholds from HOCOMOCO v12⁷⁹. We first defined DARs using the ChromatinHD-diff result as consecutive positions having a ${\mbox{lfc}} > \log 3$. For benchmarking, we then extracted for each cell type and alternative method a set of top DARs, ranked by their score, to best match the number of ChromatinHD-diff differential positions as close as possible.

To calculate enrichment of motifs within DARs of a particular cell type, we compared the motif counts from DARs from cell type A with all DARs from other cell types. In this way, we automatically controlled for GC content and bias towards particular regions (gene body, promoter), as these are likely equally present between DARs from different cell types. A Fisher exact test was used to determine motif enrichment and p-values, which were corrected using the Benjamini-Hochberg procedure. To compare different methods according to their motif enrichment, we first determined a set of differentially expressed set of TFs in each cell type by comparing expression of cell type A with that of all other cell types using scanpy’s rank_genes_groups function (scanpy z-score > 10 or <-10). We then calculated the average log-odds ratio for all differentially expressed TFs, where the log-odds ratio was inverted if the TF was downregulated.

For the comparison between cluster/TF features and the ratio of differentially bound TFs (Supplementary Fig. 4b), we defined transient cell states as Granulocyte precursors, multipotent progenitors (MPP), granulocyte-monocyte progenitors (GMP) and megakaryocyte-erythroid progenitors (MEP), while potential stripe factors were obtained from³⁷.

Comparing eQTL and GWAS enrichment

We obtained GWAS SNPs linked to immunological disorders (pbmc10k, hspc, lymphoma, pbmc10k_gran, pbmc10kx), liver disorders (liver), lymphoma (lymphoma), hematopoiesis (hspc), and brain (e18brain, alzheimer), from the GWAS catalog⁸⁰ Supplementary Data 1. We obtained eQTLs linked to whole blood (pbmc10k, hspc, lymphoma, pbmc10kx, pbmc10k_gran), liver (liver) and cerebellum (e18brain, alzheimer) from GTEX v8⁸¹. For the same tissues, we obtained fine-mapped CAVIAR⁸² and CaVEMaN⁸³ eQTLs from GTEX v8. Fine-mapped GWAS SNPs were obtained from CAUSALdb v2.0⁸⁴. For mouse datasets, we used liftover from GRCh38 to GRCm38. For both GWAS SNPs and eQTLs, we created a separate dataset by including those variants in linkage disequilibrium r² ≥ 0.9 using Ensembl’s REST API⁸⁵ with the GBR population from phase 3 of the 1000 genomes project⁸⁶. Differential genes were defined as those genes having a normalized dispersion higher than 1 (according to scanpy’s highly_variable_genes function and were used to subset the eQTLs into separate differential and non-differential eQTL datasets.

We first defined DARs using the ChromatinHD-diff result as consecutive positions having a maximal fold change between any pairwise comparison (cluster vs rest) higher than 1.5. For benchmarking, we then extract for each cell type and alternative method a set of top DARs, ranked by their maximal score for any pairwise comparison, to best match the number of ChromatinHD-diff differential positions as close as possible. Within these DARs, we calculated enrichment scores as before.

Enrichment across region sizes

Enrichment of GWAS variants and eQTLs across different region sizes was calculated by utilizing any non-differential position as background, and comparing these positions with those part of a differential region within a specific size range. For TFBSs, we used significant cell type – motif links in the comparison with all region lengths (q-value < 0.1, odds-ratio > 1.5), and performed enrichment by comparing those positions part of a differential region of a particular size that are differential in a cell type of interest, against those that are differential in any other cell type while also being part of a differential region of that particular size.

Baseline versus differential accessibility comparison

We binned every genomic position based on their baseline (mean) accessibility across clusters, and differential accessibility defined as either the standard deviation of the accessibility across clusters (CRISPRi, GWAS, eQTL) or fold change for a particular cluster compared with the mean (TFBS). For TFBSs enrichment, we focused on TF-cluster combinations with an enrichment in ChromatinHD-diff DARs (FDR corrected p-value < 0.05, odds-ratio > 1.5) in the hspc dataset. For CRISPRi enrichment, we used the hspc dataset, calculated the average CRISPRi fold enrichment for each 50 bp bin, defined significant enrichment as being lower than 0.8 fold-change, and compared this through an odds ratio with the 50 bp window being (partially) part of a DAR.

Timing

Both timing comparisons (Supplementary Fig. 2g, h, Supplementary Fig. 4f) were performed using a 24GB Nvidia RTX3090 GPU and AMD Ryzen Threadripper 3960×24-core processor. All methods were allowed to use all 48 threads available.

Overlap between CRE and ChromatinHD methods

We calculated the overlap between differential accessibility in two ways. The Jaccard positions score was calculated using the Jaccard similarity J between whether a position was part of a DAR. The F1 regions score⁸⁷ between method a and method b was calculated by first determining the Jaccard similarity between all pairs of DARs ${{{{\rm{J}}}}}_{{{{\rm{g}}}},{{{\rm{i}}}},{{{\rm{j}}}}}$, and then calculating:

$${{\mbox{Recovery}}}= \frac{1}{{{{{\rm{n}}}}}_{{{{\rm{a}}}}}}{\sum}_{{{{\rm{i}}}}\in {{{{\rm{n}}}}}_{{{{\rm{a}}}}}}{\max}_{j\in {n}_{b}}{J}_{i,j},\\ {{\mbox{Relevance}}}= \frac{1}{{{{{\rm{n}}}}}_{{{{\rm{b}}}}}}{\sum}_{{{{\rm{i}}}}\in {{{{\rm{n}}}}}_{{{{\rm{b}}}}}}{\max}_{j\in {n}_{a}}{J}_{i,j},\\ {F}_{1}= \frac{2}{\frac{1}{{{\rm{Recovery}}}}+\frac{1}{{{\rm{Relevance}}}}}.$$

(14)

Here, na and n_b is defined as the number of DARs in method a and b respectively.

Co-predictivity

To compare a model where information cannot be shared non-additively between fragments, we first trained a baseline model in which only one linear layer is used to predict gene expression from the cell embedding, without any blocks.

To determine co-predictivity between pairs of windows, we used the censoring approach to calculate the predictivity of a particular window in a gene on a per-cell basis $\Delta {{{\rm{co}}}}{{{{\rm{r}}}}}_{{{{\rm{c}}}},{{{\rm{g}}}},{{{\rm{w}}}}}$. Specifically, we first z-scored the actual gene expression ${{{{\rm{y}}}}}_{{{{\rm{norm}}}},{{{\rm{g}}}}}$, predicted gene expression ${\hat{{{{\rm{y}}}}}}_{{{{\rm{norm}}}},{{{\rm{g}}}}}$ and perturbed gene expression for a particular window (w) ${\widetilde{{{{\rm{y}}}}}}_{{{{\rm{norm}}}},{{{\rm{g}}}},{{{\rm{w}}}}}$ as:

$$\begin{array}{c}{{{{\rm{y}}}}}_{{{{\rm{norm}}}}}=\frac{{{{\rm{y}}}}-{{{\rm{mean}}}}_{{{{\rm{c}}}}}{{{\rm{y}}}}}{{{{\rm{std}}}}_{{{{\rm{c}}}}}{{{\rm{y}}}}},\\ {\hat{y}}_{{norm}}=\frac{\hat{y}-{{{\rm{mean}}}}_{c}\hat{y}}{{{{\rm{std}}}}_{c}\hat{y}}\\ {\widetilde{{{{\rm{y}}}}}}_{{{{\rm{norm}}}},{{{\rm{w}}}}}=\frac{{\tilde{{{{\rm{y}}}}}}_{{{{\rm{w}}}}}-{{{\rm{mean}}}}_{{{{\rm{c}}}}}\hat{{{{\rm{y}}}}}}{{{{\rm{std}}}}_{{{{\rm{c}}}}}\hat{{{{\rm{y}}}}}}.\end{array}$$

(15)

We then calculated the cell-specific predictivity for a window w as:

$$\Delta {z}_{w}=\left|{y}_{{norm},w}-{\hat{y}}_{{norm},w}\right|-\left|{y}_{{norm},w}-{\widetilde{y}}_{{norm},g,w}\right|.$$

(16)

The absolute value is taken in this formula because it indicates whether the removal of fragments from a window worsens the predictive accuracy of the model irrespective of the direction.

Co-predictivity was then determined by calculating the Pearson correlation between all pairs of windows:

$${\mbox{Co}}{\mbox{-}}{\mbox{predictivity}}\left({w}_{1},{w}_{2}\right)={cor}\Delta {z}_{{w}_{1},{w}_{2}}={cor}\left(\Delta {z}_{{w}_{1}},\Delta {z}_{{w}_{2}}\right).$$

(17)

To determine the average co-predictivity for different positions relative to the TSS or different distances, we binned the distances in 2 kb bins and calculated the average co-predictivity per bin across all genes.

Linking DNA contact with co-predicitivity

We obtained Hi-C contact matrices for Rao et al.²⁶ from https://data.4dnucleome.org/files-processed/4DNFIXP4QG5B/ and for Harris et al.⁴³ from https://www.encodeproject.org/files/ENCFF555ISR. For the Rao et al.²⁶ data, we mapped each 1 kb bin to co-predictivity windows (100 bp) based on the largest overlap in individual positions, and subsequently extracted the maximal absolute co-predictivity value for each 1 kb bin. For the Harris et al. 2023 data, we applied a similar procedure but using 500 bp bins.

To determine the correspondence between Hi-C data and co-predictivity, we first stratified all pairs of regions in different distance bins of size 10 kb up to a maximum of 150 kb, which corrected the analysis both for the distance-dependency of both Hi-C scores and co-predictivity (Supplementary Fig. 6d). Per gene and per distance bin, we then calculated an odds score based on whether co-predictivity and/or the normalized Hi-C contact score were higher than their respective mean scores. Log odds-ratios were then averaged across genes and distance bins. Max-pooling on the Hi-C data was performed by taking the maximal Hi-C contact score for all region pairs within a specified genomic distance.

We calculated pileups of Hi-C signal around co-predictive 100 bp regions by first selecting only those pairs with cor Δz > 0.05 and within a specific distance bin, i.e. 5–10 kb, 10-15 kb, 20-25 kb, 30-35 kb and 40-45 kb. Only regions away from the TSS (<-1k or >+1 kb) were used for this analysis. For each such pair, we picked a random pair of regions with the same genomic distance within the gene’s window (-100kb to +100 kb) and calculated the ratio between the co-predictive pair and random pair. These log-ratios were averaged to retrieve the final pileups as in Fig. 5d. Individual examples, as shown in Supplementary Fig. 6f, were created by normalizing against 100 random pairs from the same gene. For enhancer-promoter interactions, only pairs of regions were included where one 100 bp region was close to the TSS (>-1k and <+1 kb).

To determine how the contact frequency changes when genes are upregulated, we calculated the difference in log-ratio between co-predictive regions coming from genes that were significantly upregulated in B-cells (naive, memory and plasma cells, fold-change ≥1.5, FDR-corrected p-value < 0.05, 728 genes) to those that are downregulated (fold-change ≤1.5, FDR-corrected p-value < 0.05, 1892 genes).

To determine the enrichment of looping factors (YY1, CTCF, RAD21, ZNF143), B-cell TFs (SPI1, EBF1, IRF4, PAX5) or the transcription machinery (POLR2A), we obtained ChIP-seq data from GM12878 cells from ENCODE⁹ (Supplementary Data 2). We ranked all 100 bp regions for a gene according to their predictivity (Δcor) subsetting on those with Δcor ≤−0.01, and iteratively selected those regions if they were further away than 1 kb from any previously selected region. With these regions as the center, we calculated the mean log-ratio between highly co-predictive enhancers (those where the average co-predictivity was larger than the mean within a gene) versus lowly co-predictive enhancers (all other enhancers) for various up and down-stream distances.

Fragment sizes

To compare the enrichment of motifs depending on predictivity or Mono − /TF footprint ratios, we calculated the GC-content corrected motif counts by first creating a spline model (quadratic spline, 8 knots, implemented in R’s smooth.spline function) that calculates the relationship between motif counts and GC content in 100 bp windows. From this model, we extracted the residuals to get the corrected counts. Next, we used linear models (using R’s lm function) for each motif to determine the relationship between either predictivity or Mono − /TF footprint ratio with these GC-corrected counts. The slope and its associated p-value (corrected using Benjamini-Hochberg correction) were used for downstream analysis.

For footprinting, we used Hint-ATAC⁵⁵, using the Regulatory Analysis Toolbox (RGT) toolkit v1.0.0 (https://reg-gen.readthedocs.io/en/latest/), in ATAC-seq and paired-end mode. We obtained footprints using DNase I hypersensitivity footprinting from different immune cell types from⁸⁸.

As reference ChIP-seq data, we downloaded all ChIP-seq peaks from ENCODE using the GM12878 cell line and excluding CTCF, RAD21, POL2RA, and EP300 (Supplementary Data 2). To count the number of TFs binding within a window, we determined if at least part of a peak, as identified by ENCODE’s narrowPeaks output, overlapped with the window.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.