Space debris and satellite laser ranging combined using a megahertz system

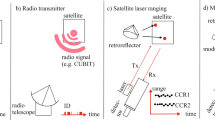
Abstract

Satellite laser ranging and space debris laser ranging are two closely related range measurement techniques with slightly different setups relying on different lasers. Satellite laser ranging measures light reflections of corner cube retro reflectors at mm-level range precision. Space debris laser ranging gathers diffuse reflections from the whole space debris object and offers a precision down to the sub meter-level. Within this work we show the usage of Megahertz lasers to combine the strengths of both systems within one setup. During the regular tracking schedule to scientific satellite laser ranging targets, specific space debris objects of interest can then be tracked without the need of making adaptions to the system. Megahertz satellite laser ranging measurements to the defunct Jason-2 satellite lead to a measurement precision down to a few μm when ranging to retro reflectors. Space debris laser ranging data reveals reflections from individual surfaces of the target and allows to draw conclusions on the rotational behavior.

Introduction

The International Laser Ranging Service^1,2 (ILRS) is a well working example of an international cooperation crossing national boundaries. Approximately 40 satellite laser ranging (SLR) stations worldwide are providing their range measurements to different data centers which then calculate high-precision orbits and predictions. Scientific usage covers various different regimes such as terrestrial coordinate frames, Earth topography, Earth magnetic field to relativistic effects^3,4. On the other hand, space debris laser ranging (SDLR) still lacks the stations necessary for a coordinated improvement of predictions. Only a few stations worldwide are capable of doing SDLR^{5,6,7,8,9,10,11}. Instead of using cooperative targets—satellites with corner cube retro reflectors (CCRs)—SDLR uses the diffuse laser reflection coming from the whole target, which is distributed over a large area on ground. The diffuse reflection can hence also be detected by other stations, even without having a laser^11,12. Such bistaic or multistatic space debris laser ranging has the advantage of allowing to improve predictions with a lower amount of SDLR stations¹³. By contrast, in monostatic SDLR setups, a single station sends the laser beam and detects the reflected photons. The laser is either sent using the receive telescope or, as for Graz SLR station, piggyback mounted. SDLR was demonstrated to work during daylight conditions as well¹⁴. The utilization of the laser ranging technique allows for measurement precision even below the current mm-level^15,16. Attitude and spin analysis possibilities^17,18,19,20 arise from the measured target signature of space debris. The target signature seen in SLR and SDLR measurements can be defined as depth information within range data resulting from the shape of the target itself or the positioning of the CCRs. Due to the mm-precision of modern SLR systems even individual CCRs are identifiable for Low Earth Orbit (LEO) satellites. With respect to future developments of SLR technology, papers about high repetition rate laser ranging (100 kHz–1 MHz)²¹ showed that return rates of up a peak of 250,000 measurements per second can be achieved. Using a pulse duration of only 10 ps and if the return rate is kept at single photon level, the normal point precision can be reduced well below current SLR systems. MHz capable detectors currently provide a Full Width Half Maximum (FWHM) jitter as low as 50 ps which is slightly larger than the one of tailored kHz capable systems like the Compensated Single Photon Avalanche Diode (C-SPAD)^22,23. However, this difference can be compensated by the number of returns²⁴. Due to the large data yield, the normal point precision²⁵ will even be better with respect to e.g., 2 kHz operation. Using high repetition rates in monostatic laser ranging configurations, the backscatter from atmosphere will always limit the effective power which can be utilized for space debris laser ranging to 50%. To avoid an overflow of the detector with atmospheric backscatter reflections a burst mode is implemented, switching between a sending and a receiving phase.

In this work we utilize a single setup allowing for both tasks: 1) High-precision satellite laser ranging and 2) space debris laser ranging. The higher power of MHz-based systems combined with the high precision due to the picosecond pulse duration offers unique flexibility, fulfilling tasks on both ends of the spectrum: geodetic applications and SDLR. Using lasers with ns pulse duration leads to single shot precisions just below 1 m. Such a precision is sufficient for improving Two Line Element-based space debris predictions (given by a set of orbital elements), but rendering it unusable for mm-level precision geodetic applications. Considering the costs and impact of collision avoidance maneuvers, an on-demand availability and improvement of space debris predictions would be of importance to satellite operators. The impact on the geodetic community will be low as space debris targets will amount to only a few out of more than 100 targets. For future space debris removal missions, e.g., of the VEga Secondary Payload Adapter (VESPA) profound attitude information is essential²⁶. The upgrade of existing SLR systems to MHz systems would boost SDLR capabilities immediately. We demonstrate the usage of a bistatic setup directly at Graz SLR station, which directly avoids backscatter using the full power of the laser. The main SLR station sends laser pulses up to a repetition rate of a true 1 MHz. A second 80 cm telescope located on the roof of the observatory building ~10 m away from the main SLR station receives the reflected photons (Fig. 1). It is theoretically shown that even with such short baselines the field of view of the receiving part is outside the atmospheric backscatter. By using the bistatic approach we present results to space debris and cooperative targets for repetition rates up to a true 1 MHz without the need to use a burst mode for backscatter avoidance.

Fig. 1: Bistatic MHz space debris laser ranging at Graz SLR station.

The main SLR station (background) consists of a 0.5 m receive telescope with a 0.07 m laser transmit telescope attached to the main tube. The 0.8 m Ritchey Chretien telescope (foreground) is mounted in a narrow dome of approximately 2 m height and acts as the receiving station in the bistatic measurement setup. Due to the separation of ~10 m between transmit and receive optics, the receive telescope is outside of the field of view of the atmospheric backscatter of the laser beam.

Results

Based on the Space Track catalog, more than 300 uncooperative space debris objects with large radar cross-section (RCS) were selected for MHz laser ranging. Uncooperative targets are space objects without retro reflectors which hence reflect light based on diffuse or specular reflection. An observation session is given by the terminator period, the time during which it is already sufficiently dark at the SLR station, while space debris is still illuminated by sunlight and not in Earth’s shadow.

The MHz laser operates at repetition rates between 0.05 and 10 MHz, with a central wavelength of 532.15 nm and 10 ps pulse duration. For all of the monostatic and bistatic measurements shown on the following pages, the same laser was used only varying the repetition rate at green wavelength. The single-shot precision is limited by the components on the transmit and receive parts. On the transmit side: start pulse diode, pulse distribution unit, event timer. On the receive side: SPAD detector, pulse distribution, event timer. The laser pulse width adds to the precision of the detector. The calibration RMS of the MHz system is determined as 16–20 ps. This is close to the 12–14 ps which can be reached under perfect conditions in the kHz system. The first laser beam expansion to ~2 cm is realized in the laser room on an optical bench. After that the laser beam is redirected to the observatory dome using a mirror system (Coude path). The second beam expansion telescope (expanding to ~7 cm) is coupled to the azimuth and elevation axis of the main receive telescope.

During each observation, the observer follows the following routine: A CMOS camera image of the reflected sunlight from the satellite is used to pre-center the target in the field of view of the receiving system. Along track offsets are then corrected by changing the time bias (the time reference of the predictions). Across-track biases are corrected by adapting the pointing direction of the telescope. During monostatic tracking, the axes of transmit and receive have to be aligned using a piezo-controlled mirror before laser exit. In bistatic mode on transmit side the laser has to be locked on the target. On the receiving side only the target is kept in the center utilizing a camera image. The displayed residuals and the histogram give the observer feedback on the tracking success.

100 kHz monostatic SDLR

In the first observation scenario, the monostatic configuration is used at 100 kHz repetition rate. Except using the MHz capable laser and detector, the setup is identical to the system used for standard geodetic observations. The transmit telescope is piggyback-mounted on the 0.5 m receive telescope. Repetition rates up to 100 kHz are used, corresponding to an average output power of 11 W at 532 nm. The time difference between consecutive pulses (e.g., 1 μs for 1 MHz) is much lower than the backscatter timespan (e.g., 50 μs oneway for 15 km atmosphere). Hence, in monostatic high repeptition rate systems the laser needs to operate in a burst mode: 1) the laser is fired with switched off detector until the first reflected photons are expected back, 2) the system stays idle for ~100 μs until the atmospheric backscatter from the last sent photon arrives back, 3) the system receives photons reflected from the target which are not spoiled by backscatter. This however halves the effective laser power which can be utilized to 5.5 W.

After three unsuccessful sessions, modifications on the second harmonic generation were done to improve the output power. Furthermore, using ray tracing simulations, a new beam expander was defined allowing to adapt the diameter of the laser beam after the first stage of the expansion. The first successful returns showed a very large background noise, which was found be correlated to sunlight reflections from the target itself. This was counteracted by introducing a narrower filter with a width of only 0.19 nm, instead of the previously used 1.0 nm filter. The wavelength shift due to the Doppler effect of light resulting from the relative movement between the satellite and observer is in the order of 0.01 nm and can hence be neglected.

The Observed-Minus-Calculated residuals (Fig. 2) show the difference of the true (measured) ranges to the predicted (calculated) ones in dependency of the time (seconds of day) and satellite elevation. Time and range biases are removed from the data set during post-processing, hence the displayed data is the offset relative to an improved orbital arc. A radar plot shows the pass over Graz SLR station relative to the cardinal coordinates. The histogram counts the overall number of photons within a given range bin. For comparability, the histogram is normalized to photon counts per time and range interval. All histogram data is plotted in higher resolution in Supplementary Information and the data is available in Supplementary Data 1. Azimuth and elevation prediction data of all satellite or space debris passes over Graz SLR station is plotted in Supplementary Information and is available in Supplementary Data 2. General Information on all targets is also summarized in Supplementary Information.

Fig. 2: Space debris laser ranging, 100 kHz, monostatic, burst mode.

Observed minus calculated (O-C) residuals vs. seconds of day and satellite elevation to four different rocket bodies: a SL-14 R/B, b ARIANE 40+ R/B, c SL-14 R/B, d H-2A R/B. The panel in the lower left of each plot shows a radar plot of the full pass over Graz SLR station (red) and the displayed segment (green). The center of the radar plot corresponds to 90° elevation, upwards direction to 0° azimuth or Northern direction.

Three different types of rocket bodies were measured, two passes of an SL-14 rocket body, one pass each of an Ariane 40 and H-2A rocket body. The denser regions in front of the noise background correspond to valid reflections (returns) coming from the target. The reduction of overall noise level due to the 0.19 nm filter is clearly visible in the histogram data. The first pass to the SL-14 R/B was measured using the 1.0 nm filter (Fig. 2a) and showed significantly larger background noise. An indication of the target signature is visible in all cases, however, due to the low effective laser power, only the largest object (Fig. 2d) clearly shows returns from a depth of 7 m. The other targets include depth information from ~2 m (Fig. 2a–c). We conclude that due to the low laser power only the more direct part of the scattered photons is identifiable. We hence proceeded with the implementation of a bistatic setup directly at Graz SLR station.

1 MHz bistatic SLR to Jason 2

The main downside of monostatic approaches is the power reduction due to the burst operation mode. Hence a bistatic approach was followed utilizing a 80 cm Ritchey Chretien telescope as a receiver ~10 m away from Graz’ main SLR station. From geometrical considerations it was found that a baseline of 10 m between transmit and receive path is sufficient to effectively avoid backscatter down to low elevations (see “Methods”, subsection: “Backscatter in bistatic configurations”). A separate complete laser ranging detection package was built and mounted on one of the Nazmyth foci of the 80 cm telescope assembly. The detector on the receiving side is in free-running operation mode. However, for an optional gating mode, the start epoch from the sending station is also directed to the receiving station via a BNC cable. The stop pulses from the receiver are directed to the event timer which is located in the main station dome. A network connection is ensuring communication between the two stations. When working in high count rate conditions (noise + reflected sunlight + signal) the previously used event timer has overflow issues for the realization of true 1 MHz, as high precision and not repetition rate was their main design intention. The availability of only one channel with a certain deadtime can lead to the situation that a start pulse might not be registered if a stop pulse triggered the system. Hence a different event timer from Swabian Instruments is used with multiple separate channels. Furthermore, post-processing of MHz data increases the computational demands e.g., in terms of data loading time or Lagrange interpolation. This is counteracted by developing a new software tool in Python utilizing GPU programming and different file formats (see “Methods”, subsection: “MHz post-processing”).

The first target measured in bistatic configuration was the defunct satellite Jason 2, a satellite with a CCR pyramid mounted on one side. The system laser operates with a true 1 MHz repetition rate at ~17 W power. Jason 2 is not stabilized or nadir pointing and started spinning soon after decommission. The raw return signal clearly demonstrates the behavior of the SPAD detector in the presence of strong signals (Fig. 3a). Besides the clear track from the CCRs of the target at ~−10 m, a gap is visible before noise increases significantly. In the literature, this effect is referred to as after pulse²⁷. The gap of 16.7 m is correlated to the dead time of the detector. Incoming photons lead to an electron-hole pair, which triggers an avalanche in the active layer of the SPAD. During the deadtime, the system is not sensitve to any incoming photons and hence the signal is zero. A very strong signal—as in the case of Jason 2—leads to charge carriers being trapped in the system. However, after the deadtime a new avalanche can be triggered in the detector by the trapped charge carriers. The probability of such an event is dependent on the number of trapped carriers and is decreasing exponentially after the deadtime²⁸. The reason for remaining signal during the deadtime is that the return signal from the satellite is not 100%.

Fig. 3: Satellite laser ranging, 1 MHz, Jason 2.

Observed minus calculated (O-C) residuals vs. seconds of day and satellite elevation to Jason 2 (NORAD ID: 33105) observed on day 135 of 2024: a After the main track from the target’s CCRs, the raw data shows increased noise after a gap of 16.7 m, which results from detector after pulsing due to the strong signal. b The final 2.2 sigma cleaned residuals include a total of 8.7 million valid returns (up to 2.1 million points per normal point). The histogram clearly shows two tracks from the visible pyramid CCRs. The location of the two CCRs is determined for time intervals of 2 s (red dots). The separation of the two CCRs slightly decreases over time, related to the tilt angle of the satellite. In the histogram of the final data, the count rate is larger than the true one which results from an overrepresentation of large return rates due to the small histogram step size.

Taking a closer look at the signal from Jason 2 reveals a very large number of valid returns (Fig. 3b). After orbital cleaning with 2.2 sigma acceptance criterion within 110 seconds overall 8.7 million valid data points contribute to the measurement. The largest number of points within a 15 s normal point is 2.15 million data points, equivalent to a return rate of 14.3%. The normal point RMS varies between 14.3 mm and 15.3 mm. Dividing the standard deviation of the result points by the square root of the number of points²⁹ leads to a normal point precision between 5 μm and 27 μm. The normal point Consolidated Laser Ranging Data Format (CRD) file is available in Supplementary information and in Supplementary Data 3.

In the residuals and histogram, tracks of two CCRs are clearly visible. Based on a 2D-histogram (time interval: 2 s) the position of both CCR peaks was determined over time. The CCRs are separated by ~8 mm at the start of the pass, decreasing to 6 mm towards the end. The identification of individual CCRs in data with high temporal resolution allows for alternative approaches regarding normal point formation or attitude determination³⁰. The measurement was peaking at more than 250,000 returns per second. Using our standard 2 kHz system using 0.8 W allows up to 1000 returns per second to Jason-2 at optimal conditions. The factor of 250 can not simply be explained by the difference in power (17 W vs. 0.8 W), which would yield a factor of 21. The optimal case for an SLR station is to operate in the single photon regime. At 2 kHz the pulse energy is 400 μJ which is under normal conditions returning multiple photons from the satellite. Hence, effectively too many photons have been sent out per pulse. Increasing the repetition rate (lowering the pulse energy) then directly increases the number of returns per second. The energy per pulse should be lowered to a level that always only single photons reach the detector after reflection. Ideally, the repetition rate should be adapted to the satellite, orbit, and weather conditions.

1 MHz bistatic SDLR

The major advantage of the used system is its versatility, allowing it to switch between cooperative and debris targets without setup changes. In the bistatic system at 1 MHz, a variety of different upper stage rocket bodies were measured (Fig. 4). The targets clearly show range variations indicating reflections from the whole body. With 10 m the largest target signature is visible for an SL-16 rocket body (Fig. 4a). An Ariane 40 rocket body (Fig. 4b) shows a signal depth of up to 6 m. In the data three different regions are visible. Two highly reflecting parts, separated by ~1 m and a faint region extending up to +5 m. The two narrow peaks can be interpreted to come either from the rocket booster or the payload adapter, the fainter region from the cylindrical rocket body itself. The data of an H-2A rocket body (Fig. 4c) consists of two regions, a dense band with a depth of 2 m and a very narrow reflection region. The narrow region is expected to come from a material with a more specular reflection. The correlation between brightness of the target (sunlight reflections) and background noise level is clearly visible if a target enters the Earth shadow (Fig. 4d). Similar to solar eclipses a core shadow (umbra) and half shadow (penumbra) region exists. For a bistatic pass at 1 MHz to an SL-14 rocket body the transition from illumination to shadow gradually decreases the overall noise level (cyan). The target decreases its brightness after second 75,175 when entering the penumbra (Fig. 4d, dashed green) and the noise level reaches a minimum 12 s later entering the umbra (Fig. 4d, dashed red). This also underlines the importance of accurate predictions. Without visual feedback, it is not possible to roughly center the target in the field of view of the receiving telescope before starting the searching routine. The only feedback is SLR returns, and hence a larger region in the sky needs to be searched. Assuming high-quality predictions optical centering would not be necessary. Due to the lower noise level identification of returns will be easier.

Fig. 4: Space debris laser ranging, 1 MHz, bistatic.

Observed minus calculated (O-C) residuals vs. seconds of day and satellite elevation to four different rocket bodies: a SL-16 R/B, b ARIANE 40 R/B, c H-2A R/B, d SL-14 R/B. The noise variation within the data to SL-16 corresponds to the target entering the penumbra of Earth’s shadow at second 75175 (vertical green line). The overall noise level is represented by the cyan curve. Denser regions of data correspond to reflected photons from the target in front of the uniformly distributed noise. Range residuals represent the deviation of the data from the reference orbit. The panel in the lower left of each plot shows a radar plot of the full pass over Graz SLR station (red) and the displayed segment (green). The center of the radar plot corresponds to 90° elevation, upwards direction to 0° azimuth or Northern direction.

As seen for Jason-2 at 1 MHz, in strong signal conditions, signal-to-noise and also the return rate reaches levels which allow for reducing the normal point precision significantly. However, looking at space debris passes, comparing monostatic at 100 kHz to bistatic at 1 MHz indicate a decrease in signal-to-noise ratio. The signal to noise level depends on the repetition rate and laser power (see “Methods”, subsection: “Signal-to-noise at different repetition rates”). The noise level increases with the repetition rate, the signal strength with the power. Comparing the signal-to-noise ratio of two repetition rates to each other it found that for strong signal conditions the following approximation holds: The larger the power, the larger the signal-to-noise ratio, independent of repetition rate (Eq. (4)). In low signal conditions (as for space debris) the increase in noise limits the identification of the signal: The change in signal to noise ratio when increasing the repetition rate is (besides the power) also dependent on the repetition rate. The benefits from power increase will be compensated by noise due to the larger repetition rate (Eq. (3)). To prove these considerations, a bistatic session was conducted at 100 kHz.

100 kHz bistatic SDLR

The reason for the faint 1 MHz return track results from the fact that in free-running SLR systems the recorded noise scales with the repetition rate, whereas the signal scales with the power. The advantage gained due the larger power when avoiding the burst mode in bistatic mode is counteracted by the noise which is by a factor of 10 larger for 1 MHz when compared to 100 kHz. Furthermore, the receiving aperture is not the same in bistatic and monostatic mode (0.8 m vs 0.5 m). To verify the expected advantage using lower repetition rates, a bistatic session with 100 kHz was performed.

The shown passes cover two different rocket bodies (SL-8 and SL-14), and two COSMOS satellites, launched 1987 and 1990. The signal-to-noise ratio as compared to 1 MHz is improved and the target signature clearly identifiable. During real-time tracking, returns are easier to identify allowing to optimize the tracking progress. The SL-8 rocket body launched in 1971 (Fig. 5a) reduces its RMS to reach a minimum at approximately second 77670. Due to the relatively short duration of the pass it is not clearly possible to state that this effect comes from an intrinsic slow rotation. It could also be connected to an apparent rotation effect resulting from the pass geometry over Graz SLR station. For COSMOS 1867 the situation is clear (Fig. 5b). Minimal range residuals can be found at second 79,225, 79,305, and 79,385. Assuming that the debris is cylindrically shaped, a rotation period of ~160 s can be estimated. The minimal residuals occur if the symmetry axis is aligned orthogonally to the observer. As the target rotates further, the symmetry axis turns away from the observing station and the RMS of the range residuals increases. The denser data regions alternate between being closer and further and further away from the observer, which could be connected to an extended structure at one side of the object. The background noise also shows variations which are correlated to the range residuals. Shortly after each of the minimum residuals the noise level increases. COSMOS 2082 shows multiple regions of variable reflection behavior (Fig. 5c). A minimum is reached at second 77,360 which could again point towards a rotation of the target. Several features extend outward from this point towards larger and lower ranges, which are an indication of a complex shape. Multiple parallel fainter tracks occur at constant ranges (e.g., at −2 m and −3.5 m). This could be an indication of parallel reflective surfaces. The signal-to-noise level of this target is better than for all previous targets. Finally, the results of the SL-14 R/B highlight the dependence of the detectability on the noise level (Fig. 5d). The pass was started at 100 kHz repetition rate until returns from the target were found. After second 81,953 the repetition rate was increased to 1 MHz. Clearly the noise level increases and no returns from the target can be identified anymore. The variation of the noise within both repetition rates comes from a change of the brightness of the target or a change in atmospheric conditions.

Fig. 5: Space debris laser ranging, 100 kHz, bistatic.

Observed minus calculated (O-C) residuals vs. seconds of day and satellite elevation to four different space debris targets: a SL-8 R/B, b COSMOS 1867, c COSMOS 2082, d SL-14 R/B. Denser regions of data correspond to reflected photons from the target in front of the uniformly distributed noise. Range residuals represent the deviation of the data from the reference orbit. The panel in the lower left of each plot shows a radar plot of the full pass over Graz SLR station (red) and the displayed segment (green). The center of the radar plot corresponds to 90° elevation, upwards direction to 0° azimuth or Northern direction.

Discussion

It is shown that MHz laser ranging is possible both for cooperative satellites and diffusely reflecting space debris. Bistatic laser ranging allows for an increase of the power by a factor of 2, avoiding the burst mode backscatter avoidance. Even a baseline separation of 10 m places the receiving telescope outside of the backscatter resulting from transmission side (see “Methods”, subsection: “backscatter in bistatic configurations”). The presented bistatic Jason-2 pass measured at 1 MHz repetition rate shows that the normal point precision can be reduced to the μm-level. Tracks of individual CCRs in the data are resolvable to a high temporal resolution. The precision and the dependency on $\sqrt{{{{\rm{N}}}}}$ at such repetition rates should be considered by orbit analysts selecting tailored normal point lengths depending on the repetition rate of the station. In bistatic mode, even for a repetition rate of 1 MHz, space debris laser ranging is possible, however with relatively low signal-to-noise ratios. For low return rates (e.g., smaller, diffusely reflecting debris targets), an increase of the repetition rate to the MHz level is not beneficial. However, existing MHz lasers allow for fast switching of repetition rates based on the requirements of the target. As expected by theoretical considerations (see methods, subsection: signal to noise at different repetition rates) at 100 kHz the signal to noise rate was significantly improved. The combination of the optimal precision due to the picosecond pulse width of the laser together with large repetition rates, reveals fine depth information of space debris objects. Conclusions on the rotational behavior and attitude can be drawn from the variations in the residuals. Within the sessions, switching between cooperative targets and space debris targets is easily possible without necessary changes to the system. This way, future SLR systems equipped with MHz laser can follow their regular schedule, while still contributing to space safety for selected high-risk targets.

Further improving the system, especially for space debris targets mainly allows for two strategies. Increasing the signal strength or decreasing the noise: As noise is mainly dominated by sunlight reflected from the target itself, using narrower filters can potentially also reduce noise. However, this also demands more precise adjustment of the tilt of the filter while guaranteeing temperature stability to avoid drifts of the central filter wavelength. Using the primary wavelength of the laser in infrared (1064 nm) instead of green (532 nm) can reduce atmospheric absorption while also lowering the noise from sunlight reflections. Indium gallium arsenide-based SPAD detectors currently are only available with a limited size, increasing the requirements on pointing stability. Superconducting nanowire detectors¹⁰ could be a future solution offering large wavelength flexibility. However, due to cooling requirements, it significantly increases the space requirements and operational effort of an SLR station. On the other hand, increasing the signal is mainly connected to increasing the effectively used laser power. We demonstrated that a bistatic arrangement, splitting transmit and receive telescopes, doubles the available laser power. The backscatter avoidance burst mode in monostatic systems is not needed as long as there is sufficient distance between transmit and receive. Further improvements can be gained by mounting the MHz laser directly on the main telescope assembly. Graz’ Coude mirrors (the mirrors directing the laser beam from the laser room to the receiving telescope) amount to ~30% additional loss. Larger laser output diameters up to 15 cm can reduce the divergence and hence the energy arriving at the target in space. In infrared systems doubling the larger output diameter allows for divergences equal to green and the advantages gained by lower atmospheric losses will dominate to improve signal-to-noise. A further reduction of the noise level can be reached by using a detector with a lower dark count rate. The detector used for the presented measurements has a specified dark count rate of 500 cps. A higher-grade sensor can reduce the remaining noise even further. This will be especially beneficial in situations where the object is not illuminated.

The strengths and weaknesses of the MHz-capable setup are summarized in comparison to the current standard: 2 kHz SLR and 200 Hz SDLR (Table 1). All the methods are compared based on the currently used setups at Graz SLR station. The system configurations at 2 kHz and 200 Hz are very close to the ones modern stations are using for SLR and SDLR. Twelve categories are defined and the suitability of each method is graded between A (very good, large benefit) and F (not possible) and given at the beginning of each cell.

Table 1 Comparison of SLR and SDLR for different repetition rates

• 1. Use case: A particular strength of the MHz approach is that a measurement setup allows to measure in both regimes, SLR and SDLR, without the need to apply changes. SLR systems at 2 kHz lack the power to detect diffuse reflections from space debris. SDLR at 200 Hz suffers from reduced precision due to the laser pulse width to allow for SLR measurements.

• 2. Measurement setup: The implementation of a MHz-capable system requires an initial effort to adapt the station with respect to detector, event timer and laser. However, as presented in the paper, all technical issues can be solved.

• 3. Repetition rate: The repetition rate of MHz systems can be flexibly adapted according to the target or environment, whereas in the other two systems the repetition rate is fixed.

• 4. Laser pulse width: In terms of precision, related to the laser pulse width, 2 kHz and 1 MHz lasers are to be favored. A laser with nanosecond pulse width suffers from a larger RMS.

• 5. Laser power: The power of the MHz-capable system is comparable to 200 Hz SDLR setup. The lower power of 2 kHz SLR systems laser limits the use case to cooperative targets only.

• 6. Computational effort: At low repetition rates the computational effort is reduced due to the low amount of data which needs to be processed, both in real-time observations and post-processing. MHz laser ranging needs specific software approaches to handle such amounts of data.

• 7. Photon regime: To increase the number of returns per time interval, an operation in the single photon regime is beneficial. At kHz repetition rates the energy per pulse is large and leads—especially for low-flying satellites—to multiple photons arriving at the detector per pulse. Hence, some of the overall laser power is lost. Stations have different strategies to reach optimal precision at 2 kHz: 1) detectors can be compensated (C-SPAD) to decrease time-walk effects from multi-photon detections, 2) the return rate can be reduced by changing the divergence of the laser beam or by applying offset pointing. MHz-capable systems naturally have very low pulse energy to ensure single-photon operation even for LEO satellites. For space debris targets, due to the low return-signal, all systems operate in the single photon regime.

• 8. NP precision: Due to the extremely large number of returns per second the normal point (NP) precision of the MHz system outperforms 2  Hz systems when ranging to cooperative targets. For space debris targets, an increase in precision can be expected due to 1) the ps pulse width of the laser, 2) signature effects allowing to potentially identify specific parts of the target.

• 9. Signal/noise: MHz systems operate with a pulse energy low enough to allow for single photon operation. This utilizes the available laser power in the most efficient way, which clearly becomes visible for LEO targets. For SDLR, signal-to-noise at 200 Hz is better than for the available passes at 1 MHz. A more detailed comparison between 100 kHz and 200 Hz needs to rely on a larger subset of passes, while considering the different boundary conditions (detector, filter, telescope aperture, event timer).

• 10. Noise: The noise of 2 kHz and 200 Hz systems is related to the gating of the C-SPAD detector: the lower the repetition rate, the lower the noise. Using a MHz-capable detector in low signal conditions the noise can be lowered by reducing the repetition rate from 1 MHz to e.g., 100 kHz.

• 11. Backscatter avoidance: Backscatter avoidance is needed in all systems except for the presented bistatic approach. In kHz systems, if backscatter from the atmosphere is detected, the laser fire epoch shifted adapted accordingly. MHz systems in monostatic setups require a burst mode operation, which reduces the effective laser power, or a separation of the transmit and receive system.

• 12. Range gating: Range gating of the detector is needed when using the C-SPAD at 2 kHz or 200 Hz. For MHz-systems the detector is only gated in SLR daytime operation to avoid an overflow of the event timer or to reduce computational effort.

The larger pulse width of conventional SDLR systems severely affects the precision, not allowing to see details in ranging data to space debris. The low power of current SLR systems does not allow for SDLR. It was found that SDLR at very large repetition rates can suffer from noise, which can be counteracted by reducing the repetition rate to 100 kHz. Dedicated SDLR systems, utilizing high-power lasers, larger receiving optics at high-elevation locations can outperform MHz system, especially in terms of the minimal observable size of space debris targets. The presented approach shows the potential how to integrate SDLR in the standard operation of future high-performance SLR stations, simultaneously improving the precision for geodetic and scientific targets. The bistatic configuration combined with free running detectors has the potential for the astronomical observatories to participate in SDLR.

Methods

Hardware and software

The following list summarizes the key hard- and software components used for acquiring the results.

• Laser: neoLASE neoMOS, 50 kHz–20 MHz, M² = 1.15, 10 ps

• Laser power infrared: P = 41.3 W@1MHz, P = 28.1W@100kHz, green: P = 17W@1MHz, P = 11W@100kHz

• Receive telescope 1: Contraves, Cassegrain, d = 0.5 m, for monostatic setup

• Receive telescope 2: ASA, Ritchey-Chretien, d = 0.8 m, for bistatic setup

• Transmit telescope: Contraves, d₁ = 0.07 m, monostatic and bistatic setup

• Detector: Micro Photon Devices Photon Counter d = 100 μm, Grade A 500 cps

• Filter 1: Thorlabs, TL FLH532-1, FWHM = 1.0 nm

• Filter 2: Alluxa, optical density 6, FWHM = 0.19 nm

• Range gate generator: Altera Cyclone V GX FPGA

• Event timer 1: Eventech A033-ET/USB, monostatic setup

• Event timer 2: Swabian Instruments Time Tagger Ultra, bistatic setup

• Timing: Brandywine NFS220 plus, 10 MHz/1 pps clock

• Post-processing software: Python, self-developed

• SLR ranging software: C++, self-developed

Noise level comparison: 100 kHz vs. 1 MHz

For all successful passes at 100 kHz monostatic and 1 MHz bistatic, the noise level was analyzed. By selecting only successful debris passes (passes with clear returns) it can be ensured that the sunlight reflection of the target is contributing to the noise. The overall number of photon counts per meter and second (cpms), including noise and signal, is evaluated and the occurrence calculated and displayed by means of a histogram plot (Fig. 6, blue). For 100 kHz (monostatic) the noise level peaks at approximately 1 cpms. Depending on the brightness of the target the noise level increases up to 2.5 cpms. At 1 MHz (bistatic) the average noise level is larger, with multiple distinguishable peaks between ~50 and 120 cpms. As the overall number and variety of targets was larger (17 successful passes for 1 MHz), the individual peaks are expected to belong to different object sizes. At ~20 cpms an additional small peak is visible, connected to low noise conditions. To investigate the reason for this behavior, at 1 MHz for a full pass just background sky noise was recorded. A LEO space debris target was tracked with a large offset to ensure that the object was well outside of the field of view of the receiving path. During the whole pass, the laser was on and the laser energy was periodically varied to see if backscatter has any effect on the noise. The recorded noise data showed no periodic variation, which proves that the receiving telescope is outside the backscatter region. Adding the sky noise measurement data to the histogram (Fig. 6b, red) shows that the noise level due to the sky is exactly at the same location as the first peak in the dataset based on analyzing illuminated debris objects. We conclude that this peak corresponds to observation conditions where the target is invisible or outside the field of visible. This marks the minimum noise condition for the current bistatic observation settings.

Fig. 6: Noise distribution.

Histogram distribution of the background noise level of all successful space debris laser ranging passes at a 100 kHz monostatic and b 1 MHz bistatic. The noise counts per meter and second (cpms) are plotted with respect to the normalized occurrence. The noise connected to illuminated space debris (blue) for 1 MHz is by a factor of 50-100 larger as compared with 100 kHz. A noise measurement of the sky background (red) reveals the minimal noise level which is present in both distributions. During the sky measurement the laser power was varied periodically without any influence on the noise level, verifying that the receiving station does not detect laser backscatter in bistatic configuration.

Compared to 100 kHz in monostatic mode (50 kHz effectively due to burst mode), the noise level at 1 MHz is by a factor of ~50–100 larger. A factor of 20 can be explained by the difference in repetition rate. The rest is expected to come from the larger aperture of the bistatic receiving telescope (80 cm vs. 50 cm).

Signal to noise at different repetition rates

The bistatic results of Jason-2 reveal that MHz repetition rate plays out its true strength when operating in the single photon regime at large return rates. Ideally each laser pulse should just carry enough energy to deliver single photons to the detector. Once operating in the multi-photon level, excessive pulse energy will reduce the overall returns per second, which is limited by the power of the laser. This intuitive explanation holds if the signal is much bigger than the underlying noise level. As seen before (Figs. 6, 4d), the main source of noise in space debris observation is resulting from photons of reflected sunlight. The following discussion will analyze the dependency of signal, noise and signal to noise. A comparison between 100 kHz and 1 MHz will be done to explain the previous results in further detail. Similar to the dark count rate of the SPAD^27,31, sunlight reflections are assumed to follow a Poisson statistic. The SNR can then be explained by the following basic equation.

$${{{\rm{SNR}}}}=\frac{{{{\rm{S}}}}}{\sqrt{{{{\rm{S}}}}+{{{\rm{N}}}}}}$$

(1)

Working in the single photon detection regime, the signal S (reflected laser photons reaching the detector) is limited by the laser power, while the noise N is limited by the repetition rate ν. For 100 kHz each pulse has nominally 6.8 times the pulse energy as for 1 MHz, which increases the probability of detecting a photon accordingly. However, the number of signal photons received per second is proportional to the laser power P, which favors 1 MHz in terms of signal having 1.5 times the power of 100 kHz.

In free running detector mode, the noise rate reaching the detector is constant. For each laser pulse, only photons returning within a time-frame of 1 μs - corresponding to a range difference of 300 m - are stored. Hence, the recorded noise is dependent on the repetition rate of the system. When compared to 1 MHz, for 100 kHz the effective noise is then reduced by a factor of 10. Comparing the SNR for two repetition rates leads to the following equation for the signal to noise rate ratio (SNRR), where in the second part of the equation the discussed dependencies for signal and noise are introduced: S₂ = P₂/P₁ ⋅ S₁ and N₂ = ν₂/ν₁ ⋅ N₁.

$${{{\rm{SNRR}}}}=\frac{{{{{\rm{SNR}}}}}_{1}}{{{{{\rm{SNR}}}}}_{2}}=\frac{{{{{\rm{S}}}}}_{1}\sqrt{{{{{\rm{S}}}}}_{2}+{{{{\rm{N}}}}}_{2}}}{{{{{\rm{S}}}}}_{2}\sqrt{{{{{\rm{S}}}}}_{1}+{{{{\rm{N}}}}}_{1}}}=\frac{{{{{\rm{P}}}}}_{1}}{{{{{\rm{P}}}}}_{2}}\sqrt{\frac{\frac{{{{{\rm{P}}}}}_{2}}{{{{{\rm{P}}}}}_{1}}{{{{\rm{S}}}}}_{1}+\frac{{\nu }_{2}}{{\nu }_{1}}{{{{\rm{N}}}}}_{1}}{{{{{\rm{S}}}}}_{1}+{{{{\rm{N}}}}}_{1}}}$$

(2)

In the limits of a very weak (S₁ → 0) and very strong signal (S₁ → ∞) the equation can be transformed to

$${{{{\rm{SNRR}}}}}_{{{{{\rm{S}}}}}_{1}\to 0}={{{{\rm{SNRR}}}}}_{{{{{\rm{N}}}}}_{1}\to \infty }=\frac{{{{{\rm{P}}}}}_{1}}{{{{{\rm{P}}}}}_{2}}\sqrt{\frac{{\nu }_{2}}{{\nu }_{1}}}$$

(3)

$${{{{\rm{SNRR}}}}}_{{{{{\rm{S}}}}}_{1}\to \infty }={{{{\rm{SNRR}}}}}_{{{{{\rm{N}}}}}_{1}\to 0}=\sqrt{\frac{{{{{\rm{P}}}}}_{1}}{{{{{\rm{P}}}}}_{2}}}$$

(4)

The same equations also hold for strong (N₁ → ∞) and weak noise (N₁ → 0) conditions. For strong signals or low noise, the SNRR only scales with power of the laser. For weak signals the repetition rate, which is directly connected to the noise level, gets important. For a diminishing signal, increasing the repetition rate by a factor k, can be compensated by increasing the power by a factor $\sqrt{{{{\rm{k}}}}}$. It will be shown that this factor will be reduced the larger the signal and the lower the noise gets, finally favoring larger repetition rates at some point.

In the following, the formula is evaluated for repetition rates of 100 kHz and 1 MHz. The factory parameters of our laser at 1064 nm are: P₁ = 41.3 W at ν₁ = 1 MHz and P₂ = 28.1 W at ν₂ = 100 kHz. The dependencies are the same for 532 nm but we rely here on the more precise parameter of the laser company. For strong signal strengths, large repetition rates are favored: the SNR of 1 MHz is increased by a factor of 1.21. At very low signal strengths lower repetition rates should be selected: 1 MHz is by a factor of 0.46 less efficient. The extreme values of the SNRR of two repetition rates are only dependent on the repetition rates and laser power. The shape of the curve in between however strongly depends on the noise level (Fig. 7a, b). A value of SNRR = 1.0 is reached if the SNR is equal for both repetition rates. Above SNRR = 1.0 1 MHz is performing better in terms of signal-to-noise. At lower noise, larger repetitions rate will be favorable. Vice versa, the stronger the noise level, the longer lower repetition rates will stay more effective.

Fig. 7: Signal-to-noise comparison at 100 kHz and 1 MHz.

a Computed signal-to-noise rate (SNR) in dependency of the signal S in kilo counts per second (kcps) for three different noise levels: N = 50 cpms (blue), N = 100 cpms (green), N = 300 cpms (red). b Signal-to-noise rate ratio (SNRR) comparing 1 MHz to 100 kHz at different signal strengths. For strong signals, SNRR reaches a threshold which is dependent on the power. For weak signals, SNRR is dependent on the power and repetition rate. c SNRR evaluated for different noise and signal strengths. Blue color indicates that 100 kHz is favored, red color that 1 MHz is favored. White color corresponds to the equality of both repetition rates.

Based on the measurements at 1 MHz (Fig. 6) the SNR and SNRR were evaluated for noise levels of 50 (blue), 100 (green) and 300 cpms (red). The signal strength was varied between 0 and 20,000 cps (counts per second). The dashed red line corresponds to the SNR at 100 kHz (Fig. 7a). For N = 300 cpms equal noise ratios at both repetition rates are reached at a S = 10 cps. A contour plot shows the dependency of SNRR on the signal and noise. White color corresponds to equal SNR at both repetition rates, red color means 1 MHz is favored, blue color 100 kHz favored (Fig. 7c).

The relationship between noise, signal and signal to noise also has implications on real time tracking. The detection probability will depend on the selected range binning and on the integration time during ranging. The range bin size should be just large enough to cover all potential returns. A larger bin size would only increase the noise while the signal remains the same. On the other hand, reducing the bin size would decrease both signal and noise equally. Assuming equally distributed signal and noise in the bin, a bin size reduction by a factor of k would lead to a decrease of the SNR by $\sqrt{{{{\rm{k}}}}}$ and hence lowers detection chances of valid signal. In the optimal case, the range bin size needs to be adapted to the expected target signature (small for single CCRs, medium for CCR arrays, large for space debris). Increasing integration time in principal improves the detectability of a weak signal. However, at large integration times changes made aiming for an increase in return rate (e.g., due to mount offsets) might get lost.

Backscatter in bistatic configurations

Utilizing a MHz laser for laser ranging with piggyback-mounted transmit telescopes, one needs to overcome a few technical and software challenges. Due to the high repetition rate, leading to temporal separations of only 1 μs between the individual pulses, atmospheric backscatter would overflow the detector in regular operation, making it impossible to detect any returns. Backscatter is assumed to be reflected from the first 15 km of the atmosphere, which means that scattered photons from a single laser pulse can be detected within the timespan corresponding to 100 μs, equal to 30 km maximum two-way range. The pulse separation of 1 μs makes clear why a burst mode approach needs to be used: Backscatter would arrive continuously and the detector is saturated with noise. The solution for systems with piggyback-mounted transmit telescopes is to fire laser pulses until the first photons reflected from the satellite are expected to arrive back at the station. Then the laser fire is stopped (3 ms for LEOs up to 0.25 s for geostationary satellites) and the system stays idle until the backscatter of the last pulse which was sent out arrives back. After that, the remaining time is used for detecting the incoming (backscatter-free) photons. The detection phase is then followed by the next sending phase and so on.

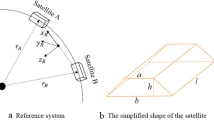
In this paper, we demonstrate the utilization of a bistatic system, separating transmit and receive path, to avoid backscatter photons in the receiving path. This way the burst mode can be avoided, effectively doubling the utilized power of the system. Furthermore, the repetition rate can be increased to a true 1 MHz. For bistatic laser ranging, using two observatories close to each other, the distance d₀ between the transmitting and receiving unit is a limiting factor (Fig. 8). The critical factor is the intersection of the field of views of the transmit path α_t (limited by the laser beam divergence) and the receive path α_r (limited by the field of view of the detector). From simple geometry considering both telescopes pointing upwards the intersection height h₀ can be calculated as

$${{{{\rm{h}}}}}_{0}=\frac{{{{{\rm{d}}}}}_{0}}{\tan {\alpha }_{{{{\rm{r}}}}}+\tan {\alpha }_{{{{\rm{t}}}}}}$$

(5)

As long as h₀ is further away than the atmospheric backscatter h_a, no backscatter can enter the field of view of the receive telescope. At low elevations, ϵ the effective atmosphere is increasing due to the larger distance covered in the atmosphere. The following equation is considering the radius of Earth r_e and the backscatter-relevant zenith atmosphere h_z = 15 km assumed to be in the upper troposphere³².

$${{{{\rm{h}}}}}_{{{{\rm{a}}}}}=\sqrt{{{{{\rm{h}}}}}_{{{{\rm{z}}}}}^{2}+2{{{{\rm{h}}}}}_{{{{\rm{z}}}}}\cdot {{{{\rm{r}}}}}_{{{{\rm{e}}}}}+{{{{\rm{r}}}}}_{{{{\rm{e}}}}}^{2}-{{{{\rm{r}}}}}_{{{{\rm{e}}}}}^{2}\cdot {\cos }^{2}\epsilon }-{{{{\rm{r}}}}}_{{{{\rm{e}}}}}\cdot \sin \epsilon$$

(6)

In addition to that, the effective distance d_e between transmit and receive depends on the elevation ϵ, but also on the azimuth ϕ of the two stations. At ϕ = 0° and ϕ = 180° both systems point towards the connection line between the two telescopes. Hence d_e is reduced by the factor $\sin \epsilon$. Orthogonally to the connection line for ϕ = 90° and ϕ = 270°, the effective distance is constant at d_e = d₀. For arbitrary azimuth angles, d_e can be expressed by calculating the projection of a vector with the length d₀ pointing at azimuth ϕ, and elevation ϵ onto the (y,z)-plane. Expressing the Cartesian coordinates (x,y,z) in with respect to (ϵ, ϕ, d₀) and setting x = 0 leads to the following expression for d_e.

$${{{{\rm{d}}}}}_{{{{\rm{e}}}}}={{{{\rm{d}}}}}_{0}\sqrt{{{\cos }^{2}\epsilon \cdot {\sin }^{2}\phi+{\sin }^{2}\epsilon }}$$

(7)

Summarizing, for successful bistatic operation the following equation should hold the condition that the field of view intersection h₀ is larger than the effective contributing atmosphere h_a.

$${{{{\rm{h}}}}}_{0}=\frac{{{{{\rm{d}}}}}_{0}\sqrt{{{\cos }^{2}\epsilon \cdot {\sin }^{2}\phi+{\sin }^{2}\epsilon }}}{\tan {\alpha }_{{{{\rm{r}}}}}+\tan {\alpha }_{{{{\rm{t}}}}}} \, > \, \sqrt{{{{{\rm{h}}}}}_{{{{\rm{z}}}}}^{2}+2{{{{\rm{h}}}}}_{{{{\rm{z}}}}}\cdot {{{{\rm{r}}}}}_{{{{\rm{e}}}}}+{{{{\rm{r}}}}}_{{{{\rm{e}}}}}^{2}-{{{{\rm{r}}}}}_{{{{\rm{e}}}}}^{2}\cdot {\cos }^{2}\epsilon }-{{{{\rm{r}}}}}_{{{{\rm{e}}}}}\cdot \sin \epsilon={{{{\rm{h}}}}}_{{{{\rm{a}}}}}$$

(8)

For Graz SLR station, the main SLR station (transmitter) is separated by ~d₀ = 10 m from 80 cm astronomical telescope (receiver), which is located on the roof of the main building at Lustbühel observatory. The connection line is approximately pointing towards North-West (ϕ = 310°) as seen from the receiving system. The transmit telescope output diameter of ~7 cm together with an M² = 1.15 of the laser leads to α_t = 10.7 μrad. The half-angle field of view of the 100 μm SPAD detector is ~α_r = 70 μrad. For different station separations d₀ between 0.5 m and 10.0 m the field of view intersection h₀ was calculated and compared to the atmospheric backscatter length (Fig. 9). The case for observations in the direction of the connection between the two telescopes ϕ = 0° leads to a minimal observation elevation of ~ϵ = 20° for our observation geometry (Fig. 9a). Considering observation azimuth ϕ and elevation ϵ, the limiting elevation (dashed blue line) below which backscatter will become dominant, is given by a curve similar to an ellipse (Fig. 9b, c). The field of view intersection is highlighted within a polar contour plot for d₀ = 4.0 m and d₀ = 10 m. Both graphs demonstrate that for avoiding backscatter in bistatic observation configuration, a narrow transmit and receive field of view, a large separation between both systems, and an observation direction orthogonally to the connection line favors the observations.

Fig. 8: Field of view intersection: transmit, receive.

The field of view intersection of the transmit (observatory 1) and receive path (observatory 2) in bistatic configuration occurs at the height h₀. The output diameter of the laser transmit telescope leads to a divergence angle α_t. Separated by a distance d₀, the field of view of the receive optics and the correlated angle α_r is given by the focal length of the receive telescope and the size of the detector. If the intersection height of the field of views is higher than the region the atmospheric laser backscatter is originating from, no backscatter from the laser from observatory 1 can reach the received optics from observatory 2.

Fig. 9: Theoretical analysis of the expected backscatter for a bistatic system.

a Field of view intersection height h₀ of transmit and receive system (separated by the distance d₀) in dependence of the elevation ϵ. The telescopes point into the direction connecting both systems (azimuth ϕ = 0° or phi = 180°) which is the scenario with largest backscatter. The dashed blue line corresponds to the effective atmospheric backscatter height h_e, marking the estimate observation threshold. b, c Field of view intersection h₀ in dependence of the azimuth ϕ and elevation ϵ for d₀ = 4 m and d₀ = 10 m. If at a given elevation h₀ is lower than h_e, backscatter from the laser can enter the receiving system. The dashed blue line marks this threshold.

Noise filtering

To reduce the noise during SLR measurements usually narrow-band filters are used. This is especially important during daytime operation to reduce the sky noise background at wavelengths different from the laser wavelength. For the reduction of noise from the sunlight reflected by the satellite or the sky background two different filters with varying FWHM were tested: 1) Thorlabs, FWHM = 1.0 nm and 2) Alluxa, FWHM = 0.19 nm. For the Alluxa filter, a central filter wavelength above the nominal wavelength of the laser is chosen, as tilting the filter decreases the central wavelength. By gradually tilting the filter mounted in a COTS high-precision kinematic mount it is then possible to optimize the system to the nominal laser wavelength of 532.15 nm. The filter was also temperature-stabilized to within 0.5 °C to avoid any necessary re-adjustment of the filter, by connecting an oven via a proportional integral-derivative (PID) controller. Directly comparing the noise level for 22 recorded passes at 100 kHz showed a reduction of noise level by a factor of 4 when using the narrow-band filter.

MHz post-processing

Post-processing MHz laser ranging data can be a computationally demanding process if millions of data points are involved. For LEO satellites, data has to be read from files with sizes up to 1 GB. To accelerate read in times, Graz data format was converted to Apache Parquet. The column-based file format accelerated read in times by a factor of 20. For the calculation of Observed-Minus-Calculated (O-C) residuals, for each of the measured ranges data, a predicted range has to be calculated based on the reference orbit. This involves Lagrange interpolation and a conversion from X, Y, Z coordinates to local azimuth, elevation, and range. These two routines, though intrinsically simple, were found to be the main bottleneck during data analysis of large datasets. Speed issues were circumvented by using GPU-based programming, CUDA, and C++ code within the core Python-based cleaning program. With a single RTX3060 graphics card, when compared to Python (using vectorized functions) the GPU-based routines lead to an acceleration by a factor up to 25. The interpolation of x, y and z coordinates of 50 million points took 13.1 s with vectorized Python and only 0.5 s with GPU acceleration. As each variation of the reference orbit during post-processing involves the above mentioned transformation this step was crucial for efficiently reducing the data.