Statistical analysis of spatial patterns in tumor microenvironment images

Abstract

Advances in tissue labeling, imaging, and automated cell identification now enable the visualization of immune cell types in human tumors. However, a framework for analyzing spatial patterns within the tumor microenvironment (TME) is still lacking. To address this, we develop Spatiopath, a null-hypothesis framework that distinguishes statistically significant immune cell associations from random distributions. Using embedding functions to map cell contours and tumor regions, Spatiopath extends Ripley’s K function to analyze both cell-cell and cell-tumor interactions. We validate the method with synthetic simulations and apply it to multi-color images of lung tumor sections, revealing significant spatial patterns such as mast cells accumulating near T cells and the tumor epithelium. These patterns highlight differences in spatial organization, with mast cells clustering near the epithelium and T cells positioned farther away. Spatiopath enables a better understanding of immune responses and may help identify biomarkers for patient outcomes.

Introduction

Immunotherapy has become a mainstream cancer treatment, thanks to positive and unprecedented clinical outcomes against many types of cancers. Recent research in cancer biology has highlighted the importance of studying the (micro-)environment of the tumor (TME), which includes immune cells, stromal cells, blood vessels, and extracellular matrix¹. The TME has a dual ambivalent role: it is crucial for cancer progression and metastasis, but it also contains immune cells that fight against the cancer cells. Interestingly, the spatial distribution of immune cells within the TME seems to be critical to predict patient outcome^2,3,4,5 or evaluate the response to immunotherapy⁶. For example, the infiltration of T cells is commonly associated with good prognosis⁷, and Li et al. recently studied the spatial distribution of CD8⁺ T cells in triple negative breast cancer². Similar studies have been conducted for other kinds of cancers as well- Zwing et al. analyzed the density and association distance of myeloid cells and T cells in colorectal cancer tissue samples, and observed a correlation between the spatial distribution of the cells and the functioning of cytotoxic T cells⁸. Similar findings based on the spatial organization of immune cells within the TME are discussed in the review paper by Heindl et al.⁹. Recent advances in tissue staining complemented with state-of-the-art imaging¹⁰ have made possible the in situ mapping of the TME of several types of cancer. However, a recurrent image analysis problem is then to reconstruct key structures within the TME as spatial objects either by segmenting structures of interests (such as tumor epithelium, stroma, etc.) or via automatic localization of the different immune cell types using advanced object detection techniques. While such tasks have dominated research in image analysis, it may be said that they only serve as the hors d’oeuvre in the grand scheme of gaining a system-level understanding of the immune response during therapy. Equipped with state-of-the-art algorithms which can digitally reconstruct and localize different biological structures at scale, the next generation challenge is to extract robust information to analyze the spatial data and extract biologically relevant information.

From a mathematical perspective, it is first necessary to describe the association between two different populations of already detected immune cells. Such cell-cell interactions may be appropriately tackled using spatial statistics tools for point processes^{11,12,13,14,15}. Since its inception in the field of geographical information sciences¹⁶ in the mid-70’s, spatial statistics have been adopted by the imaging community to solve problems in bioimage informatics^17,18,19,20, super-resolution microscopy^14,15,21, and in computer vision^13,22. In the context of immunotherapy, Bull et al.³ used a combination of spatial statistics to describe immune cell localizations, and recently Mi et al. have published their findings on characterizing the distributions of five different immune markers on whole slide histopathological images²³.

The case for analyzing the association of immune cells to the large, and complex-in-shape tumor epithelium (i.e., the regions within a tumor that contain the cancer cells²⁴) is more complex. Unlike the cell-cell case where the relatively small immune cell’s spatial position can be approximated to its center-of-mass, the cell-region spatial analysis cannot be performed within a point-process framework, as existing spatial analysis models are typically not equipped to handle large structures with complex-geometry. While the method described in ref. ¹⁵ exports point coordinates to cluster regions, the association metric is computed via an area overlap measure. In contrast, the immune cells are not always contained within the tumor epithelium, but can be physically apposed to the tumor epithelium boundary at some distance, in the so-called tumor stroma²⁴. Of the many approaches mentioned here, only the SODA technique in ref. ¹⁴ can be used to recover the distance of spatial association, albeit only for the cell-cell case.

Broadly, two crucial design aspects are fundamental to develop a generic spatial analysis framework for histopathology. The first is to generalize the theory of spatial point processes to accommodate interactions between point patterns and closed shapes. The second aspect is to be able to distinguish between real associations that are statistically significant from fortuitous accumulation of cells to shapes. Measuring interaction between two spatial sets is a challenging problem in itself. Existing methods, that include some commercially available software for histopathological data analysis often describe this in terms of the density of accumulating cells with respect to a second set of objects^2,25,26,27. However, research in spatial pattern analysis have established that such counting-based measures are not robust enough to describe interactions within the TME²⁸. Consider a hypothetical situation where a group of immune cells are randomly distributed in the domain of analysis. These spatially random cells could still accumulate at some distances from a second set of spatial objects (say tumor epithelium), and the accumulation would be more prominent when the cells are densely packed. However, this observation does not imply real interaction between the two spatial sets which are statistically independent due to the randomness in localizations. Indeed, the task of describing spatial interaction goes beyond simply counting the accumulation of points to another set of objects. To this end, we make a distinction between fortuitous spatial accumulation and spatial association (i.e., a significant spatial accumulation)- a statistical definition that describes spatial interaction within a robust, statistical framework.

Our proposed method, namely SPATIOPATH, is a mathematical framework to extract the spatial patterns within the TME that are statistically relevant. The core contributions of our work are summarized as follows:

Generalized theory: We establish a mathematical theory for spatial analysis in histopathology which can deal with point-point interactions (cell-cell) as well as point-object associations (cell-tumor epithelium). The proposed method generalizes theoretically Ripley’s method for any arbitrarily shaped object.

Robust informatics: Based on a null hypothesis paradigm, Spatiopath is equipped to distinguish statistically significant associations of immune cells from fortuitous accumulations when the cells are randomly distributed.

Computational efficacy: the model hyperparameters of Spatiopath are analytically computed, unlike many statistical techniques that rely on computationally extensive Monte Carlo simulations for parameter estimation.

We present hereafter the theory of object-based spatial analysis, introduce the proposed Spatiopath technique, and define quantitative features for object-based association. The method is then validated through extensive stochastic simulations, demonstrating Spatiopath’s ability to quantify cell-to-cell and cell-to-region associations in large, complex tissue regions. We further showcase Spatiopath’s versatility by applying it to an open-access multiplex dataset of pancreatic islet cells from patients at various diabetes stages, identifying spatial association patterns between endocrine and immune cells that align with or extend findings from other methods. Finally, by analyzing multiplex chromogenic immunohistochemically stained tumor sections from non-small cell lung cancer patients, we assess immune cell associations and their enrichment or depletion around tumor epithelium. This detailed spatial mapping of immune cells and their environment offers new insights into anti-cancer immune responses at the patient level, with potential as predictive markers for disease outcomes and immunotherapy responses.

Results

Spatiopath theory

Generalizing Ripley’s K function

Let A and B be two sets of spatial objects and $\Omega \subset {{\mathbb{R}}}^{2}$ the domain of analysis. The elements of set A are spatial objects (typically the boundaries of the segmented tumor epithelium) which are represented as closed 2-D contours. This representation also admits 2-D point coordinates by representing them as infinitesimally small circular contours. Accordingly, set A can represent both segmented tumor epithelium, or the spatial coordinates of detected immune cells. The elements of set $B=\{{u}_{1},\ldots,{u}_{j},\ldots,{u}_{| B| }\}({u}_{j}\in {{\mathbb{R}}}^{2})$ are restricted to 2-D immune cell coordinates. Therefore, a mapping from B ↦ A can sufficiently describe both cell-cell and cell-tumor epithelium spatial associations. Designing a quantitative methodology to describe this spatial interaction is a two stage pipeline. First, we seek a generic mathematical formulation to count the accumulation of points in B to the shapes in A, and introduce a notion of generalized accumulation function. Second, a statistical null hypothesis model is described to distinguish fortuitous accumulations from associations that are statistically significant.

In the special case of cell-cell interaction where the set A elements are strictly restricted to point coordinates $\{{v}_{1},\ldots,{v}_{i},\ldots,{v}_{| A| }\}({v}_{i}\in {{\mathbb{R}}}^{2})$, Ripley’s function^16,29 can be used for spatial analysis of marked point processes^30,31,32 as follows:

$${{{\mathcal{R}}}}(r)=\frac{| \Omega | }{| A| | B| }{\sum }_{i=1}^{| A| }{\sum }_{j=1}^{| B| }{\mathbb{1}}\left(| | {v}_{i}-{u}_{j}| | -r\right)b\left({v}_{i},{u}_{j},r\right)$$

(1)

Here ∣∣.∣∣ is the Euclidean norm, ∣A∣ and ∣B∣ are the number of points in sets A and B, ∣Ω∣ is the volume of the domain of analysis and ${\mathbb{1}}(x)=1$ if x ≤ 0, and it is zero for x > 0. Typically, the Ripley’s function ${{{\mathcal{R}}}}(r)$ first counts the average number of points in B from any point v_i ∈ A within a circular zone of radius $r\in {{\mathbb{R}}}^{+}$, which is then averaged over all the points in set A. The term b(·) is a boundary correction function that takes into account the effect of any boundary artifacts in computing spatial accumulation²⁹. For monotonically increasing radii r = r₀, …, r_N, the m-th element ${{{{\mathcal{R}}}}}_{m+1,m}={{{\mathcal{R}}}}({r}_{m+1})-{{{\mathcal{R}}}}({r}_{m})$ of the N-dimensional vector ${{{\bf{R}}}}={\left[\cdots,{{{{\mathcal{R}}}}}_{m+1,m},\cdots \right]}^{T}$ for m = 0, …, N − 1, would provide information about the average accumulation of B cells within a distance comprised between r_m and r_m+1 from the points in A. In addition to spatial accumulation, the vector R also describes the physical distance at which the points are spatially apposed. The Statistical Object Distance Analysis (or SODA) technique by Lagache et al.^14,33 would be useful in understanding the spatial orchestration between two immune cell populations. However, this theory needs to be extended and generalized in order to analyze the spatial association of points to closed shapes (cell-tumor epithelium interactions) within a consolidated mathematical framework.

We now consider the generic case when A contains closed parametric shapes {S_i}, ∀ i = 1, …, ∣A∣. By this definition, S_i can represent the contour of a segmented tumor epithelium, or reduce to a point ${v}_{i}\in {{\mathbb{R}}}^{2}$ in the case of a cell coordinate. From the theory of geometric active contours³⁴, a shape S_i can be implicitly represented as the zero levelset of a signed distance function ${\phi }_{i}:\Omega \,\, \mapsto \, {\mathbb{R}}$. The embedding is performed such that for (x, y) ∈ Ω, ϕ_i(x, y) = 0 if (x, y) ∈ S_i. Additionally, ϕ_i(x, y) is negative for all points that are inside S_i, and its is positive for points outside the closed contour. Accordingly, A can now be expressed as a set of levelset functions A = {ϕ₁, …, ϕ_∣A∣}. Using this generic representation for shapes and points, we now describe the generalized statistic to compute accumulation of B cells to A. Given a set of scalar level values L = {l₀, …, l_N}, let us define the annular region between two successive levelsets l_m and l_n(l_n > l_m ∈ L) of ϕ_i as ${\omega }_{mn}^{i}=\{(x,y)| {l}_{m}\le {\phi }_{i}(x,y) \, < \, {l}_{n}\}$. We now describe the generalized Ripley’s function as

$${{{{\mathcal{R}}}}}_{g}({l}_{m},{l}_{n})=\frac{| \Omega | }{| A| | B| }{\sum }_{i=1}^{| A| }\underbrace{{\left({\sum }_{j=1}^{| B| }{\chi }_{mn}^{i}\left({u}_{j}\right)\right)}}_{{{K}_{i}(m,n)}}$$

(2)

Here, ${\chi }_{mn}^{i}\left({u}_{j}\right)=1$ if l_m≤ ϕ_i(u_j) < l_n, and it is zero otherwise. The entity K_i(m, n) counts the number of points in B that are accumulated inside the region ${\omega }_{mn}^{i}$, and for m = 0, …, N − 1, we define a N-dimensional vector ${{{{\bf{R}}}}}_{g}={\left[\cdots,{{{{\mathcal{R}}}}}_{g}({l}_{m},{l}_{m+1}),\cdots \right]}^{{\prime} }$. Comparing this to the Ripley’s vector R, the vector R_g can be described as the generalization of the Ripley’s spatial statistic when A contains either points or closed parametric shapes. Comments on Boundary Correction The boundary correction term is absent in Eq. (2). Correcting for boundary artifacts is necessary when using Ripley’s function because the circular arcs may extend beyond the boundary of Ω (illustrated in Fig. 1), and the possible accumulations outside the domain needs to be accounted for. However ϕ_i is a mapping from Ω to ${\mathbb{R}}$, and by definition the levelsets of ϕ_i are always embedded within the domain boundary, thereby eliminating the need for additional corrections. This is a favorable by-product of implicit shape embedding. When the domain boundary is complex and irregular, designing the correction is mathematically tricky and computationally intensive¹⁴.

Fig. 1: Comparing different shape embedding.

Two set A points (in green), and three set B points (in red) are distributed over the domain Ω. Distribution of red points are analyzed within a distance of r units from A objects (in gray). a For Ripley-based spatial analysis, boundary correction is necessary because the circles can extend beyond Ω. b When shapes are individually embedded via levelsets ϕ₁ and ϕ₂, boundary correction is no more necessary. However, the point lying in the intersection zone is still counted twice. c This is eliminated in the ensemble representation using a single levelset function ϕ to represent the shapes as an ensemble. Moreover, standard Ripley-based analysis (a) is restricted to point objects for the set A, while (b) and (c) can embed any closed form.

Distinguishing spatial association from accumulation via null-hypothesis testing

The generalized function ${{{{\mathcal{R}}}}}_{g}$ in Eq. (2) essentially counts the number of points that are accumulated between l_m and l_n units (of distance) from the objects’ boundary in A. If we model A and B to be stochastic sets of spatial objects²⁰, such counting-based measures would compute accumulation (at some distance) even if the sets are statistically independent. This is clearly misleading from a biological perspective. For example, a set of immune cells could be randomly distributed with respect to another population and still report non-zero accumulation via Eq. (2). However, such fortuitous accumulations do not convey any reliable information vis-à-vis their collaborative behavior during therapy. Indeed, to make a reliable hypothesis it is necessary to distinguish such fortuitous accumulations from statistically significant spatial associations.

Naturally, the above discussion spawns a pertinent question: how can we determine if an observed accumulation is significant? We provide a solution by performing this spatial analysis within a statistical null hypothesis framework. The idea is to define a null hypothesis that would describe the spatial interactions when A and B are spatially independent. Therefore, an observed accumulation (via Eq. (2)) would qualify as a statistical association only if it is statistically above the expected value computed under the null hypothesis. Spatial independence between A and B cannot be easily assessed without extensive bootstrapping of the positions of the object sets observed in the tissue. Such stochastic simulations are computationally intensive for the large tissue images acquired by slide scanners. Therefore, we simplified the null hypothesis of object set independence by assuming a random distribution for the B cell set. Under this hypothesis, the set of points B = {u₁, …, u_∣B∣} are distributed according to the homogeneous Poisson law with constant intensity $\lambda :\Omega \, \mapsto {{\mathbb{R}}}^{+}$. The probability of finding k < ∣B∣ points inside any closed region ω ⊂ Ω is then given as follows:

$${\mathbb{P}}\left({N}_{\omega }=k\right)=\frac{{e}^{-\lambda | \omega | }{\lambda | \omega | }^{k}}{k!}$$

(3)

The random variable N_ω represents the number of points inside ω, and the maximum likelihood estimate of the density λ can be computed as $\hat{\lambda }=| B| /| \Omega |$. We write the area enclosed by ω as ∣ω∣. Under this law, the point process B is characterized by a property called complete spatial randomness or CSR, where any two realizations of the point process are spatially independent and random samples {u_j} drawn from this spatial process follow an uniform distribution described by ${u}_{j} \sim {{{\mathcal{U}}}}\left[\Omega \right]$. Due to this CSR property the objects in A and the points in B are spatially independent. In line with the arguments made by Lagache et al. in ref. ¹⁴ it can be further proved that under the CSR assumption, ${{{{\mathcal{R}}}}}_{g}$ is a Gaussian random variable, and its expected value and variance are derived (see “Methods”) to be:

$${\mathbb{E}}\left[{{{{\mathcal{R}}}}}_{g}\right]=\frac{1}{| A| }{\sum }_{i=1}^{| A| }| {\omega }_{mn}^{i}|$$

(4)

$${{{\rm{Var}}}}\left[{{{{\mathcal{R}}}}}_{g}\right]=\frac{| \Omega {| }^{2}}{| A{| }^{2}| B| }{\sum }_{i=1}^{| A| }{\sum }_{j=1}^{| A| }\left(\frac{| {\omega }_{mn}^{i}\cap {\omega }_{mn}^{\,j}| }{| \Omega | }-\frac{| {\omega }_{mn}^{i}| | {\omega }_{mn}^{\,j}| }{| \Omega {| }^{2}}\right)$$

(5)

Comparing the results in Eq. (4) and (5) to the derived mean and variance terms in SODA¹⁴, we infer that the generalized statistic defined in Eq. (2) is behaviorally similar to the Ripley’s function when objects in A are restricted to point coordinates. This proves that the proposed theory indeed provides a theoretical generalization for the Ripley’s function (and consequentially the SODA method) for arbitrary closed shapes. We can leverage the generalized statistic ${{{{\mathcal{R}}}}}_{g}$ to describe both cell-cell and cell-tumor epithelium spatial associations, and therefore this method provides a consolidated structure to analyze the spatial information extracted from histopathological images.

While this theoretical generalization achieves one of our goals, the method described so far still remains sub-optimal from a computational perspective. In the following section we discuss a mathematical procedure to enable faster and more precise spatial statistics.

Ensemble shape representation for Spatiopath

The function ${{{{\mathcal{R}}}}}_{g}$ in Eq. (2) treats each object in A individually via the embedding functions {ϕ_i} for i = 1, …, ∣A∣. This individual representation is sub-optimal for histopathological applications where regions of tumor epithelium within the tumor border should be considered as members of the same histopathological category. Isolated islets of tumor epithelium often belong to the same physical object and the disjoint appearance is merely an artifact of projecting a 3-D structure onto a 2-D image plane. It is therefore important from a biological perspective that the objects in set A should be treated as an ensemble, and not in isolation. Ensemble representation is mathematically more convenient and it requires significantly fewer computations compared to the individual shape embedding approach described earlier. Statistical properties of the Spatiopath ensemble statistic are derived next, followed by discussion on the merits of this particular representation.

$${\tilde{{{{\mathcal{R}}}}}}_{g}({l}_{m},{l}_{n})=\frac{| \Omega | }{| B| }{\sum }_{j=1}^{| B| }{\chi }_{mn}({u}_{j})$$

(6)

$${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}={\left[{\tilde{{{{\mathcal{R}}}}}}_{g}({l}_{0},{l}_{1}),\cdots,{\tilde{{{{\mathcal{R}}}}}}_{g}({l}_{N-1},{l}_{N})\right]}^{{\prime} }$$

(7)

The indicator function χ_mn(u_j) = 1 if u_j ∈ ω_mn, and it is zero otherwise. The vector ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}\in {{\mathbb{R}}}^{N}$ is constructed for N discrete intervals of the scalar level values $\left[{l}_{0},\ldots,{l}_{N}\right]$. This ensemble representation is a special case of the generic shape embedding via multiple levelsets, and Eq. (6) can be derived from Eq. (2) by substituting ∣A∣ = 1. The ${\tilde{{{{\mathcal{R}}}}}}_{g}$-function in Eq. (6) is therefore proportional to the number of points in B that are accumulated within a distance of l_m and l_n units from the zero levelset of ϕ, and each element of the vector ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}$ describes spatial accumulation within given range of distances.

From Eq. (6), we note that the binary indicator function χ_mn(u) = 1 only if u ∈ B and u ∈ ω_mn, ∀ u ∈ Ω. Therefore, χ_mn is a Bernoulli random variable, formally written as χ_mn ~ Ber(p_mn). Under the null hypothesis, when the points u_j ∈ B are uniformly distributed over Ω, this parameter which indicates the probability of finding a point within ω_mn is proportional to its area. Mathematically, we derive the following relationships:

$${\chi }_{mn} \sim {{{\rm{Ber}}}}\left({p}_{mn}\right),\quad {p}_{mn}=| {\omega }_{mn}| /| \Omega |$$

(8)

$$\chi :=\left({\sum}_{u\in B}{\chi }_{mn}(u)\right) \sim {{{\rm{Binomial}}}}\left(| B|,{p}_{mn}\right)$$

(9)

Eq. (9) follows from the fact that the summation of ∣B∣ Bernoulli random variables produces a Binomial random variable with a mean of ∣B∣p_mn and variance ∣B∣p_mn(1 − p_mn). From this derivation, it follows naturally that ${\tilde{{{{\mathcal{R}}}}}}_{g}({l}_{m},{l}_{n})$ is Binomially distributed as well, and it asymptotically converges to a Gaussian distribution that is characterized by a mean μ_mn and variance ${\sigma }_{mn}^{2}$ which are derived analytically as:

$${\mu }_{mn}=\frac{| \Omega | }{| B| }{\mathbb{E}}\left[\chi \right]=| {\omega }_{mn}|$$

(10)

$${\sigma }_{mn}^{2}=\frac{| \Omega {| }^{2}}{| B{| }^{2}}{{{\rm{Var}}}}\left[\,\chi \right]=\frac{| {\omega }_{mn}| }{| B| }\left(| \Omega | -| {\omega }_{mn}| \right)$$

(11)

We generalize these expressions for N successive intervals of level values, and the random Normal vector ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}\in {{\mathbb{R}}}^{N}$ (Eq. (7)) is characterized as follows:

$${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}} \sim {{{\mathcal{N}}}}\left({{{\bf{M}}}},{\mathbf{\Sigma}} \right)$$

(12)

$${{{\bf{M}}}}={\left[\cdots {\mu }_{mn}\cdots \right]}^{{\prime} }\,{{{\rm{and}}}}\,{{{\mathbf{\Sigma }}}}={{{\rm{diag}}}}\left[\cdots {\sigma }_{mn}^{2}\cdots \,\right]$$

(13)

From Eq. (12), under the null hypothesis, the association vector ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}$ follows the Normal distribution, which is fully characterized by its mean M and covariance matrix Σ, as shown in Eq. (13). Additionally, both M and Σ are computed analytically, which enables us to perform spatial analysis without resorting to computationally intensive Monte Carlo experiments for parameter estimation of a distribution.

Advantages of Spatiopath’s ensemble shape representation

The ensemble representation is a subcategory of the generalized Ripley’s function (Eq. (2)), and it is trivial to verify that Eq. (10) and Eq. (11) can also be derived by substituting ∣A∣ = 1 in Eq. (4) and Eq. (5) respectively. In addition to this generalization property and the biological motivation stated earlier, ensemble analysis is desirable from the computational aspect as well. From Eq. (2), the computational cost for computing ${{{{\mathcal{R}}}}}_{g}$ is ${{{\mathcal{O}}}}(| A| | B| )$, which is reduced to ${{{\mathcal{O}}}}(| B| )$ computations for the ensemble case in Eq. (6). Second, while both these formulations do not require boundary correction (unlike Ripley’s function ${{{\mathcal{R}}}}$), using a single function ϕ to embed all the shapes ensures that the level lines are always non-intersecting. This is not the case for the generalized Ripley’s function where two (or more) level lines of distinct embedding functions ϕ_i and ϕ_j could be intersecting. This has an implication for accurately reconstructing the number of statistical accumulations in a prescribed region. From the example shown in Fig. 1b, the number of accumulations of red points to the green objects could be overestimated because of the fact that the point inside the intersection zone is counted twice. This issue is well known, and these are typically compensated using approximations via unmixing. We refer the reader to¹⁴ for more details. In contrast, from Eq. (6), we can reconstruct the exact number of accumulations of the red points (3), because the level lines of ϕ are non-intersecting. Third, this non-intersection property also provides significant performance benefit while estimating the statistical properties of the accumulation function. We will revisit this property following the theory of statistical analysis of spatial accumulation. Finally, we compare the mean and variance expressions for ${\tilde{{{{\mathcal{R}}}}}}_{g}$ (in Eq. (10) and Eq. (11)) to Eq. (4) and Eq. (5) respectively. From these comparisons it is evident that the ensemble computations are faster by at least a factor of ∣A∣ for the mean, and by a factor of ∣A∣² for the variance. This further attests to the benefits of adopting the ensemble shape representation for the spatial analysis problems relevant to this paper.

Spatial attributes derived via Spatiopath

Based on the aforementioned theory of spatial association, we now extract quantitative features to describe the association of the immune cells to the set A objects. Let ${{\mathbb{1}}}_{N}$ denote a N-dimensional vector whose entries are one. We also define $\Theta :{{\mathbb{R}}}^{N}\mapsto {\{0,1\}}^{N}$ which maps each element v_i of a vector ${{{\bf{v}}}}\in {{\mathbb{R}}}^{N}$ to one if v_i> 0, or to zero if v_i≤ 0. First, we compute the total accumulation of points within the levelsets (corresponding to the level values {l₀, …, l_N}) of ϕ as:

$${\eta }_{t}=\frac{| B| }{| \Omega | }{{\mathbb{1}}}_{N}^{T}{\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}$$

(14)

From our previous discussion, a non-zero η_t does not necessarily mean that these points are statistically associated to set A. Only the points that are statistically above the expected accumulations under the null hypothesis of B set random distribution are deemed to be spatially associated. Let’s consider that a proportion 0 ≤ α ≤ 1 of ∣B∣ are statistically associated to set A, and that the remaining 1 − α proportion of ∣B∣ points are randomly distributed. The total number of spatial associations (η_a = α ∣B∣) can be computed as follows:

$${\eta }_{a}=\frac{| B| }{| \Omega | }{\left[\Theta \left({{{{\mathbf{\Sigma }}}}}^{{{\bf{-1}}}}({\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}-{{{\bf{M}}}})-\tau (N){{\mathbb{1}}}_{N}\right)\odot \left({\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}-(1-\alpha ){{{\bf{M}}}}\right)\right]}^{T}{{\mathbb{1}}}_{N}$$

(15)

Here the symbol ⊙ represents element-wise vector multiplication and τ(N) a statistical threshold to determine the levelsets with a significant accumulation of points (cells). The second term $\left({\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}-(1-\alpha ){{{\bf{M}}}}\right)$ is an estimate of the number of associated points within these levelsets, that is the total number of accumulated points minus the expected number under the null hypothesis of random distribution. To determine the total number of B points that are statistically associated to A, we need to estimate the two parameters, τ(N) and α in Eq. (15).

To determine the value of α, we use that η_a = α∣B∣, and after rearranging Eq. (15), we obtain that:

$${\eta }_{a}=\frac{1}{1-{p}_{\omega }}\frac{| B| }{| \Omega | }{\left[\Theta \left({{{{\mathbf{\Sigma }}}}}^{-{{{\bf{1}}}}}({\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}-{{{\bf{M}}}})-\tau (N){{\mathbb{1}}}_{N}\right)\odot \left({\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}-{{{\bf{M}}}}\right)\right]}^{T}{{\mathbb{1}}}_{N}$$

(16)

where

$${p}_{\omega }=\frac{1}{| \Omega | }{\left[\Theta \left({{{{\mathbf{\Sigma }}}}}^{-{{{\bf{1}}}}}({\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}-{{{\bf{M}}}})-\tau (N){{\mathbb{1}}}_{N}\right)\odot {{{\bf{M}}}}\right]}^{T}{{\mathbb{1}}}_{N}$$

(17)

is the proportion of Ω that is covered by the levelsets with a significant accumulation of B points. We highlight that we neglected the corrective factor $\frac{1}{1-{p}_{\omega }}$ in our previous Ripley-based analysis of spatial association^14,35, as the area ∣ω∣ of the region(s) with points’ accumulation corresponded to a subset of annular regions around A points and was small compared to the region of analysis ∣ω∣ ≪ ∣∣Ω. Yet, it cannot be ignored here as the surface of levelsets around tumor epithelium regions (TER) is not necessarily small compared to the region of analysis Ω.

To determine the threshold τ(N), we note that:

$${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}:={{{{\mathbf{\Sigma }}}}}^{-{{{\bf{1}}}}}({\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}-{{{\bf{M}}}}) \sim {{{\mathcal{N}}}}({{{\bf{0}}}},{{{\bf{1}}}})$$

(18)

which follows directly from Eq.(12). We then leveraged the work of Donoho and Johnstone³⁶, and used the universal threshold $\tau (N)=\sqrt{2\log N}$. Indeed, such threshold has been shown to be optimal to determine the statistically significant entries in a N − dimensional random Normal vector, such as ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}$.

We can interpret Eq. (16) as follows: If we consider a specific region ω_mn which is enclosed by the m and n levelsets of ϕ, the number of spatially associated points$\,{\eta }_{a}^{mn}$ within this region is non-zero only if the total accumulation ${\eta }_{t}^{mn} > \frac{| B| }{| \Omega | }\left({\mu }_{mn}+\tau (N){\sigma }_{mn}\right)$ with ${\tau }_{N}=\sqrt{2\log N}$. The number of spatially associated points ${\eta }_{a}^{mn}$ within ω_mn is then given by:

$${\eta }_{a}^{mn}=\left\{\begin{array}{cc}\frac{1}{1-{p}_{\omega }}\left({\eta }_{t}^{mn}-\frac{| B| | {\omega }_{mn}| }{| \Omega | }\right) & {{{\rm{if}}}}\,{\tilde{{{{\mathcal{R}}}}}}_{g}({l}_{m},{l}_{n}) \, > \, {\mu }_{mn}+{\sigma }_{mn}\tau (N),\\ 0 \hfill & {{{\rm{otherwise}}}}\hfill\end{array}\right.$$

(19)

From Eq. (16), the number of spatially associated points in a levelset region ω_mn is zero when the accumulation is not statistically significant, i.e., less than the threshold τ(N). When the accumulation is significant, this association measure eliminates the false accumulations (computed as the fraction ∣ω_mn∣/∣Ω∣ of ∣B∣) that represent fortuitous accumulations due to spatial randomness of the points.

The statistical significance of the spatial association can be measured by computing the

$$\, {{\mbox{p}}} - {{\mbox{value}}} \,=1-{\psi }^{N}\left({\sup }_{N}{\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}\right),$$

(20)

where ψ(·) is the cumulative distribution function of a normalized Gaussian density³⁵.

In parallel to statistical association, it is worth noting that our framework can also detect the statistical depletion of points of the set B in the different regions ω_mn. Here, depletion refers to an amount of points B that would be significantly lower than expected with a random Poisson distribution. As reduced statistic ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}$ tends to a symmetric normal law ${{{\mathcal{N}}}}({{{\bf{0}}}},{{{\bf{1}}}})$, we can test for depletion in ω_mn with the lower threshold ${\sigma }_{mn}^{-1}\left({\tilde{{{{\mathcal{R}}}}}}_{g}({l}_{m},{l}_{n})-{\mu }_{mn}\right) < -\tau (N)$. We use the mathematical framework established so far to extract the following attributes to describe spatial interaction between the sets:

Association-Index or ASI: the association index α, or ASI $\in \left[0,1\right]$ is a global indicator of statistically significant spatial association of B elements, expressed as the fraction of the total points that are spatially associated to A. Mathematically,

$${{{\rm{ASI}}}}={\eta }_{a}/| B|$$

(21)

We later explain via statistical simulations that ASI is indeed a robust marker to determine spatial association of immune cells to tumor epithelium or another group of cells.

Association-Distance (δ_a): In addition to a global index of spatial association, it is also interesting in immunotherapy to identify the distance at which the cells are statistically associated to the second category of objects.

Accordingly, our framework allows for the reconstruction of an average distance of association. The embedding function ϕ is implemented via Euclidean distance transform, and therefore the distance of a point u ∈ B to boundary of the objects in A is given by ∣ϕ(u)∣₊ (in pixels), where ∣·∣₊ is the absolute value. Also, if u ∈ ω_mn, we define the probability of the point being associated to set A to be $\theta (u)={\eta }_{a}^{mn}/{\eta }_{t}^{mn}$. The average distance of spatially associated points is reconstructed as the following weighted average:

$${\delta }_{a}=\frac{{\sum }_{u\in B}\theta \, (u)| \phi (u){| }_{+}}{{\sum }_{u\in B}\theta (u)}$$

(22)

From Eq. (19) and Eq. (22), δ_a is non-zero only for statistically significant spatial associations, and δ_a > 0 is the average distance at which the immune cells are significantly localized with respect to the islet’s periphery. In the next section we design a set of experiments through statistical simulations, and analyze the characteristics of the spatial attributes under different spatial configurations.

Statistical simulations and performance analysis

Stochastic simulation environment for spatial analysis

A robust stochastic simulation platform is essential to objectively analyze the efficacy of a mathematical algorithm. Here we describe a model-based approach to simulate spatial association between sets A and B, which extends Thomas point processes¹⁴ for closed shapes. The simulator is characterized by the set of parameters $\left(\alpha,{\delta }_{0},s\right)$. Here $\alpha \in \left[0,1\right]$ is the fraction of the B points that are statistically associated to the set A at a distance of δ₀ units. The parameter s is the standard deviation of a Gaussian white noise that is applied to the computed position of each associated B point. Therefore, the spatial distribution of the B elements are simulated as follows: For a given association level α, (1 − α)∣B∣ points are chosen at random from the set B, and they are uniformly distributed over the domain Ω⧹A, where Ω which is implemented here as a rectangle. Then, for each of the remaining α∣B∣ points the following steps are repeated: 1-Compute the levelset ${\omega }_{{\delta }_{0}}=\left\{(x,y)\in \Omega \setminus A| \phi (x,y)={\delta }_{0}\right\}$ at distance δ₀ from the contour of A, 2- Select a random point ${{{{\bf{x}}}}}_{{\delta }_{0}}^{(j)}$ of the discretized levelset ${\omega }_{{\delta }_{0}}$, and 3- The associated point of the set B is finally located at position ${{{{\bf{x}}}}}_{{\delta }_{0}}^{{\,(j)}^{{\prime} }} \sim {{{\mathcal{N}}}} ({{{{\bf{x}}}}}_{{\delta }_{0}}^{(j)},s )$, which corresponds to a spatial perturbation of the the point coordinate ${{{{\bf{x}}}}}_{{\delta }_{0}}^{(j)}$ localized at a distance of δ₀ units from the contour of A.

The algorithm described above therefore simulates a spatial distribution of ∣B∣ points over Ω such that only the fraction α of these points are spatially associated to A (at an average distance of δ₀ units). The remaining (1 − α) fraction of the points are spatially random over Ω. Therefore, when α = 0, the points in B are distributed according to the homogeneous Poisson distribution which corresponds to the CSR hypothesis. Accordingly, with increasing α, one can simulate a spatial point distribution which is increasingly associated to the A objects at the specified distance. The procedure to simulate each statistically associated point ${{{{\bf{x}}}}}_{{\delta }_{0}}^{{(\,j)}^{{\prime} }}$, for 1 ≤ j≤ α ∣B∣ is illustrated in Fig. 2. In Fig. 3, we simulated three scenarios that involve a single large object in set A (shown by orange mask), and a set B containing 2000 points with an increasing level of association α = 0, 0.1 and 0.3 respectively, at a specified distance of δ₀ = 80 μm and a Gaussian position noise s = 10 μm (1 pixel = 0.65 μm). Increasing α results in a denser cluster of points at the specified distance as shown in Fig. 3b, c, whereas Fig. 3a describes the CSR case. The spatial association of the points is analyzed within different level sets around the set A of objects, which are shown by the orange contours. The corresponding Ripley statistics ${\tilde{R}}_{g}^{0}$ (Eq. (18)) for each levelset are plotted in Fig. 3d–f. Statistical accumulations of B points are clearly detected in levelsets 60–80 and 80–100 where ${\tilde{R}}_{g}^{0} > \, \tau (N)$. When statistical association is detected, we computed the related ASI (Eq. (21)) and estimated the distance of association (Eq. (22)) which are close to the simulated values (ASI = 0.10 and δ_a = 81.54 μm for α = 0.1 and a simulated distance of association equal to δ₀ = 80 μm, and ASI = 0.31 and δ_a = 79.39 for the α = 0.3 example). In the next section, we perform additional simulations to measure the robustness and accuracy of our method across a large range of parameters.

Fig. 2: Simulating spatial association between the A set of regions and B set of points.

A proportion (1 − α) of B points is randomly distributed within the domain Ω⧹A (yellow dots). The other α∣B∣ points (red dots) are spatially associated to set A (orange mask) following the following iterative method: the levelset at coupling distance δ₀ from the contour of the A set is computed (white line) and a point ${{{{\bf{x}}}}}_{{\delta }_{0}}^{(j)}$ is randomly selected on this contour (blue cross). The position of the associated point ${{{{\bf{x}}}}}_{{\delta }_{0}}^{{(j)}^{{\prime} }}$ (red point) is then obtained with a Gaussian draw centered at ${{{{\bf{x}}}}}_{{\delta }_{0}}^{(j)}$ with variance s²: ${{{{\bf{x}}}}}_{{\delta }_{0}}^{{(j)}^{{\prime} }} \sim {{{\mathcal{N}}}}({{{{\bf{x}}}}}_{{\delta }_{0}}^{(j)},s)$. Square with a dotted blue contour is zoomed. In this figure, α = 0.1, μ = 80, σ = 20, and for a sake of clarity of the figure, we decreased the number of B points to 150.

Fig. 3: Simulation of spatial association.

a, b, c Three snapshots of ∣B∣ = 2000 points that are spatially associated with objects in set A (shown in orange) with simulated association levels α = 0, 0.1 and 0.3 respectively, and association distance parameters (δ₀, s) = (80 μm, 10 μm). d, e, f Corresponding Ripley’s vectors ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}$ (Eq. (18)) for increasing levelset regions are plotted. Significant accumulations (respectively depletions) are highlighted with green (respectively red) rectangles. Horizontal dotted lines correspond to statistical thresholds  ± τ(N). The coupling distance δ₀ is highlighted with a vertical dotted line. The coupling estimates (ASI, δ_a) of the simulated association parameters (α, δ₀) for the shown snapshots are indicated. Source data are provided as a Source Data file.

Measuring the performances of Spatiopath with synthetic simulations

The following experiments are designed to evaluate the suitability of ASI defined in Eq. (21) to capture the level of spatial association in interacting processes for a large range of parameters. We compared the characteristics of ASI with the following indices: the Accumulation-Index or ACI = η_t/∣B∣, and the Significant Accumulation Index or SAI = η_s/∣B∣, where ${\eta }_{s}=\frac{| B| }{| \Omega | }\Theta {\left({\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}-\tau (N){{\mathbb{1}}}_{N}\right)}^{T}{\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}$

The Accumulation-Index ACI essentially counts the fraction of points η_t that are accumulated within the regions described by the levelsets of ϕ. Such counting-based measures are predominantly used in spatial analysis, and especially in histopathology to describe interaction between spatial objects, and therefore it is interesting to evaluate its robustness and suitability as an effective metric of spatial association. The index SAI is somewhat similar to ACI, but it only counts the fraction of statistically associated points η_s and does not discount for the accumulations due to randomness. In the following sets of experiments, we seek to reconstruct the Thomas process association parameter α using simulations, and the robustness of the three spatial indices are analyzed quantitatively.

In our simulation framework, set A of objects is initially generated using a TER mask extracted from experimental data. Then the set B (2000 points) is created according to a Thomas process, i.e., with a proportion α of points that are spatially associated to set A at a distance $\sim {{{\mathcal{N}}}}({\delta }_{0},s)$ and the remaining proportion (1 − α) randomly distributed with a homogeneous Poisson distribution across the entire domain Ω. We report the three association indices, ASI, SAI, and ACI for increasing simulated association 0 ≤ α ≤ 0.5 in Fig. 4a–c. Other parameters of the simulation are fixed to δ₀ = 80 and s = 10. Each simulation is repeated for M = 40 independent random trials, and the average value of the indices are plotted. To validate the robustness of Spatiopath to user-defined parameters, we plotted results for four different zone width, i.e., distance between successive levelsets ∣l_m − l_n∣, 0 ≤ l_n ≤ l_m ≤ l_N around the contours of A objects. Selected zone width are equal to 5, 10, 20, and 50.

Fig. 4: Measuring the performances of Spatiopath with synthetic simulations.

When not specified, default values for simulation parameters are (α, δ₀, s) = (0.1, 80, 10). a The Accumulation Index (ACI) corresponds to the total proportion of B points that accumulate within levelsets around A. ACI is plotted for increasing levels of simulated association α. We performed simulations for 4 different zone width, i.e., the distance between successive levelset values 0 ≤ l_m < l_n≤ l_N (zone width 5 μm in green, zone width 10 μm in red, zone width 20 μm in blue, and finally zone width 50 μm in purple). The light-colored envelope around each curve corresponds to the 10^th and 90^th percentiles of the M = 40 simulations. b The Statistical Association Index (SAI) corresponds to the proportion of B points within levelset regions where statistical accumulation is detected. c The Association-Index (ASI) corresponds to the measured percentage of B points that are spatially associated to set A (Eq. (21)). Dotted line (black) corresponds to the ideal ASI = α curve. d Measured association ASI for increasing simulated distance of association δ₀ and constant α = 0.1 (black dotted line). e Measured association ASI for increasing simulated variance of association distance s and constant α = 0.1 (black dotted line). f Measured association ASI for increasing maximum distance of analysis l_N. Vertical dotted line (gray) indicates simulated distance of association δ₀ = 80. Horizontal dotted line (black) corresponds to simulated level of association α = 0.1. g Measured association distance δ_a (Eq. (22)) for increasing simulated association distance δ₀. Dotted line (gray) corresponds to the ideal δ₀ = δ_a. h Measured association distance δ_a for increasing simulated association α. Dotted line (gray) corresponds to the simulated distance δ₀. i Measured association distance δ_a for increasing simulated variance of association distance s. Dotted line (gray) corresponds to the simulated distance δ₀. Source data are provided as a Source Data file.

Ideally, the optimal index should be close to the simulated association level α (plotted via dotted line y = x in Fig. 4a–c). The results clearly suggest that ACI is significantly biased, and hence it is not suitable for assessing spatial association. This supports our theoretical hypothesis that a counting-based accumulation measure is less robust, compared to a statistical measure. In comparison, both ASI and SAI are better suited to report spatial association, although SAI consistently overestimates the association level. This overestimation is more pronounced for lower values of α which mimics a realistic spatial configuration in real examples. To compare the accuracy of different indices for estimating spatial association between B points and set A, we computed the root mean squared error (RMSE) between simulated α values and computed ACI, SAI and ASI (Supplementary Table I). We found that, for each zone width used in the computations, the ASI index is significantly more accurate (0.12 ≤ RMSE ≤ 0.39) than SAI (0.64 ≤ RMSE ≤ 2.22) and ACI (6.69 ≤ RMSE ≤ 6.81). These statistical studies strongly suggest that ASI is indeed a robust indicator of spatial association between points and objects.

To further assess the accuracy and robustness of Spatiopath, we evaluated how well the ASI retrieved the simulated association level α under various simulation parameters: the mean δ₀ and variance s of the association distance (Fig. 4d–e), and the maximum level set l_N for defining the analysis domain Ω⧹A (Fig. 4f). ASI demonstrated robustness with respect to the simulated association distance, with only a slight underestimation due to a few associated B points that fall into level sets far from the mean simulated distance δ₀ because of the Gaussian perturbation with variance s (where s = 10 here). This is confirmed by analyzing the sensitivity of ASI to s (Fig. 4e), where we observe that the underestimation of α by ASI increases with s due to the dispersion of associated B points across multiple level sets. We also note that this underestimation is less pronounced when the zone width is large, as it limits the spread of associated points across multiple level sets.

Finally, we assess the sensitivity of ASI to the maximum level set distance of analysis l_N. As expected, we observe that ASI cannot capture the simulated association α when l_N < δ₀ = 80 μm. For l_N ≳ δ₀ + s, ASI reaches a stable plateau that closely approximates α. We, therefore, emphasize that, when applying Spatiopath to experimental data, it is crucial to ensure that the maximum analysis distance is sufficiently large for ASI to reach this plateau, indicating that all associated spatial points have been included in the analysis. This sensitivity analysis demonstrates that Spatiopath can robustly estimate the spatial association of points with set A, effectively quantifying the accumulation of immune cells around TER or another cell set.

In a last set of experiments we evaluate the efficiency of Spatiopath to reconstruct the distance of spatial association, and as earlier the results are established via stochastic simulations. In Fig. 4g–i, we plot the reconstructed association distance δ_a (from Eq. (22)) With respect to three varying parameters: the level of simulated association, α, and the mean δ₀ and variance s of the simulated distance of association, we find that the mean association distance δ₀ is accurately estimated by δ_a for a large range of simulated distances (Fig. 4g). A staircase effect is observed for the very large zone width of 50 μm. This occurs because the association distance is estimated by averaging the distance of all B points contained in the level sets where statistical accumulation is detected (Eq. (22)). Consequently, when the interval between level sets (zone width) is large, many B points within zones of statistical accumulation are not necessarily associated with A, which introduces a bias in the estimation of the association distance.

Next, we plot the estimated distance of association for an increasing level of simulated spatial association α. We observe that estimation accuracy (and variance) increases (and decreases, respectively) with α. This is again linked to the method for computing the distance estimate δ_a, where all B points in level set zones with statistical accumulation are considered. Indeed, as α increases, more of the considered B points are truly associated with A, improving the accuracy of the estimation. We also observe that accuracy improves with smaller zone width. A third sensitivity test measures the accuracy of δ₀ estimation for an increasing variance s (Fig. 4i). We observe that the estimation δ_a of the association distance remains accurate for increased variance s, but the variability of the estimation increases. This is due to the degraded estimation of the level of association α for large variance s (Fig. 4e).

This set of statistical simulations strongly support our hypothesis that Spatiopath is an efficient tool to identify the distance of spatial association, and accordingly that it may be used to robustly quantify the apposition of immune cells to the tumor epithelium’s boundary.

Computational analysis

The following set of experiments are performed to highlight the gain in accuracy obtained with levelset embedding of complex shapes compared to reducing objects to points in SODA¹⁴, and experimentally justify our claim that the ensemble shape embedding described in Eq. (6) provides significant computational benefits.

SODA quantifies point-to-point spatial associations by reducing cells to their positional center-of-mass, making it particularly suitable for single-molecule localization microscopy techniques (e.g., PALM³⁷, STORM³⁸) and a reasonable approximation for fluorescence microscopy of molecules, which often appear as small round spots due to the diffraction limit of the microscope. To measure the accumulation of points (set B) around other points (set A), SODA computes Ripley’s K function^11,29 by evaluating expanding concentric rings around each point in set A (Supplementary Fig. 1). After identifying rings where a significant accumulation of B points occurs (determined by statistical thresholding of the K function), SODA calculates the total number of associated (or coupled) B points. When the coupling distance is within the typical inter-point spacing of set A, a final unmixing correction is applied to prevent overestimation due to shared associations of B points among closely spaced A points.

To assess the performance of SODA and Spatiopath across various cell shapes and quantities, we designed a simulation framework that generates A cells with complex shapes, varying sizes, and varying quantities (see “Methods”). For each cell size, we measured the performance of SODA and Spatiopath in retrieving the simulated level of spatial association α and distance of association δ₀ (Fig. 5).

Fig. 5: Comparing the performances of Spatiopath and SODA for different cell sizes.

a–d A cells (white masks) are randomly distributed in Ω = 1024 × 1024 pixels (1 pixel = 1 μm). Four increasing cell sizes are simulated (from left to right, μ = 1, 5, 10, and 20 μm). The positional centers of mass of the cells are represented by red dots. The spatial accumulation of points (set B) around A cells is simulated according to a Thomas process as previously described: a subset of B points is randomly distributed in Ω (blue dots), while the remaining B points are coupled to A cells (yellow dots). e–h Comparison of the association level ASI obtained from Spatiopath (blue curves, solid line = mean, shaded envelope = ±standard error, n = 10 simulations per condition) and SODA (red curves) in relation to simulated values (α, δ₀). Dotted lines represent the ideal value of ASI = α. i–l Comparison of the estimated association distance (δ_a obtained from Spatiopath (blue curves, solid line = mean, shaded envelope = ±standard error, n = 10 simulations per condition) and SODA (red curves) in relation to simulated value δ₀. Dotted lines represent the ideal value of δ_a = δ₀. Source data are provided as a Source Data file.

Recovering the level of spatial association

We observed that the association level (ASI) and distance (δ_a) calculated by Spatiopath were highly accurate, closely matching the simulated values (α, δ₀) across various cell sizes and corresponding numbers. However, the accuracy of SODA significantly decreased as cell size increased. While SODA provided relatively good estimates of the association level α (with a relative error of  < 20%) for smaller cells (μ = 1 and 5 pixels), it tended to overestimate α for μ = 10 or failed to detect the simulated spatial association for larger cells (μ = 20). The initial overestimation is likely due to the partial coverage (~10%) of the domain Ω by cell A, which reduces the effective area where B points are distributed. This leads to an underestimation of the expected density of B points, as SODA assumes an expected density of n_B/∣Ω∣ instead of the effective n_B/∣Ω\A∣. Consequently, B points become over-accumulated in certain regions. SODA’s ability to detect the spatial association of B points declines sharply for larger cells (μ = 20 pixels). This is likely due to the size and irregular shape of the cells. The association of B points is simulated at a mean distance δ₀ from the cell contour, but for large and complex-shaped A cells, the accumulation of B points occurs at a greater and more variable distance (δ₀ + μ) from the centers of mass of A cells. This increased spread makes it more difficult to accurately characterize the association.

Recovering the distance of spatial association

Spatiopath almost perfectly recovers the simulated association distance, in contrast to SODA, which tends to overestimate it. We hypothesize that this overestimation is due to the high association distance (δ₀ = 50 pixels from the contours of A cells), which is on the same order as the distance between A cells. As a result, SODA may falsely detect an association of B points in larger rings around the centers of A cells, even after applying the unmixing correction for overlapping rings.

Computational impact

In contrast to Spatiopath, which embeds the contours of all A cells within a single level-set function, SODA computes the accumulation of B points around each A cell (reduced to the coordinates of its center of mass). In our simulations, we kept the coverage of Ω nearly constant by adjusting the number of A cells, except for smaller cells (μ = 1 and 5) where we fixed n_A = 200 to limit the computational load of SODA. We compared the computational load of SODA and Spatiopath for decreasing A cell sizes (and increasing numbers) from n_A = 30 (μ = 20) to n_A = 200 (μ = 1 and 5) (Supplementary Fig. 2). We observed that Spatiopath maintained a nearly constant runtime (≤10 s) regardless of the number of cells, whereas the computational load of SODA increased supra-linearly from 10 s for n_A = 30 to 90 s for n_A = 200. The majority of the time savings comes from the variance computation, which operates in O(n_B) compared to O(n_An_B). This efficiency explains why Spatiopath remains consistent as n_A changes and, unlike SODA, is well-suited for analyzing large-field images containing several thousand cells.

Previous simulation results confirm that Spatiopath is better equipped than SODA to quantify the association of points to cells in large-field tissue imaging. Specifically, Spatiopath is more robust when handling large and complex-shaped cells, such as those typically labeled in tissue sections, and in cases of high coupling distances, i.e., when the distance is of the same order of magnitude as the spacing between A cells. Additionally, embedding all the cells within a single level-set function ensures that the computational load remains manageable for large images containing several thousand cells.

Analyzing an open-source dataset of multiplex images

To show the versatility and robustness of Spatiopath, we used an open-source multiplex dataset and compared the results with those obtained using other statistical methods. We applied Spatiopath to the diabetes multiplex dataset from³⁹ (https://data.mendeley.com/datasets/cydmwsfztj/2) and compared our findings with those reported using SpicyR, another second-order Ripley-based statistical method⁴⁰. The study by Damond et al.³⁹ aimed to characterize the spatial distribution of markers and cells within pancreatic islets. They examined three different stages of Type 1 Diabetes Mellitus (T1DM) progression: non-diabetic, onset diabetes, and long-duration diabetes (n = 4 patients per group). The open-access dataset consists of images of pancreatic islet cells across these three stages, acquired through Imaging Mass Cytometry (IMC)⁴¹ using 37 markers. The number of images per subject ranged from 64 to 81, with a total of 845 images (non-diabetic = 274, onset = 290, long-duration = 281). Similar to the SpicyR study, we focused our analysis on subsets of endocrine cells (alpha, beta, and delta) and immune cells (T helper (Th), T cytotoxic (Tc), neutrophils, and macrophages) and compared the spatial associations between pairs of cells in non-diabetic patients and those with diabetes onset.

For each patient in the different stages of type 1 diabetes, we computed the association index (ASI) between various cell types (Fig. 6). We observed that the association patterns were generally conserved among patients within the same diabetes stage but differed across stages. We highlight that the association matrices reported in Fig. 6 are asymmetrical, unlike those in SpicyR. The association of cell type j to type i computed with Spatiopath corresponds to the spatial accumulation of cell type j around type i. This does not imply the accumulation of cell type i around type j, particularly when the densities of the two cell types are very different. Here, image patches for each patient are centered around endocrine islets, making endocrine cells much more abundant than immune cells (Supplementary Fig. 3).

Fig. 6: Association index (ASI) between endocrine and immune cells in non-diabetic patients and those with onset diabetes.

For each patient of each diabetes stage (Onset diabetes (a–d) and non-diabetic (e–h)) we measured the spatial association (ASI) between the different endocrine cell subsets (alpha, beta, and delta) and the immune cell subsets (T helper (Th), T cytotoxic (Tc), neutrophils and macrophages). The element (i, j) of each table is equal to the association index of cell type j to cell type i, i.e., the statistical accumulation of cell type j in level sets around cell type i. Source data are provided as a Source Data file.

In agreement with the results obtained from SpicyR analysis, we observed a global increase in the association of endocrine cells (alpha, beta, and delta) to immune Th and Tc cells in patients with onset diabetes compared to non-diabetic patients. The mean association distance (Supplementary Fig. 4) between endocrine and immune cells is approximately equal to 80 μm for different patients. This suggests that the cells are not closely apposed and instead reflects the infiltration of immune cells into the endocrine islets of patients (Supplementary Fig. 5).

When pooling the results and comparing the ASI differences across all patients in the different stages (ΔASI(p_i(onset diabetes) − p_j (non diabetic)) for 1 ≤ i, j ≤ 4, a total of n = 16 values) (Fig. 7), we observed that the increase in the accumulation of endocrine cells around Th cells is significant, whereas the association with Tc cells is not, except in the case of beta cells (Fig. 7a). This difference is due to the more heterogeneous distribution of cell-to-cell associations among patients. For instance, patient number 6362 with onset diabetes exhibits a low ASI ( < 0.04) for endocrine to Tc cells, while non-diabetic patient number 6278 shows a particularly high association (ASI > 0.2) across all endocrine cells. Spatiopath analysis also measured a significant decrease in the association of delta to beta cells from non-diabetic to onset-diabetes patients (Fig. 7b), consistent with the SpicyR analysis. The low association distance between these two endocrine cell types (< 20 μm, Supplementary Fig. 4) suggests direct cell apposition, which appears to be disrupted during the rearrangement of islets at the onset of diabetes (Supplementary Fig. 5).

Fig. 7: Differences in cell-to-cell associations (ASI) between onset- and non-diabetes patients.

For each pair of cell types, the boxplots (n = 16) display the differences in association index (ASI) calculated for each patient between the diabetes onset and non-diabetic stages. Each boxplot illustrates the distribution- First quartile - median - third quartile of the metrics for each configuration. Whiskers indicate the range of the data, and outliers are represented as individual points. A global increase in ASI from non-diabetic to onset-diabetes patients is shown in green, while a decrease is shown in red. When the increase or decrease in association is statistically significant (Wilcoxon rank-sum test, p < 0.05), dark green or dark red is used, respectively, instead of lighter shades. a Immune-Endocrine cells. b Endocrine-Endocrine cells. c Endocrine-Immune cells and d Immune-Immune cells. All p values are reported in the Source Data file. Source data are provided as a Source Data file.

Spatiopath also revealed spatial patterns that had not been previously reported, such as a significant decrease in the spatial association of Th to beta cells in patients with onset diabetes (Fig. 7c). The average distance of association is particularly small (< 10 microns, Supplementary Fig. 4), suggesting direct cell-to-cell apposition (Supplementary Fig. 5). The reduction in cellular apposition among patients with onset diabetes is likely due to beta cell depletion and the subsequent dismantling of islets. We also measured a significant increase of Th-Tc cells apposition (Fig. 7d, with distance  < 20 μm, Supplementary Fig. 4) in patients with onset diabetes, a pattern that remains unexplained.

In summary, the quantitative results obtained using Spatiopath on multiplex imaging of endocrine and immune cells in patients at different stages of diabetes reveal spatial patterns consistent with those identified by other statistical methods. These include the increased association of endocrine cells to Th and Tc cells due to immune cell infiltration in islets, and the reduced association between delta and beta cells in patients with onset diabetes. Spatiopath, with its ability to asymmetrically compute cell associations (i.e., analyzing the accumulation of A cells around B, and vice versa) and measure association distances, also provided new insights. It identified previously unreported patterns, such as the close association of Th cells to beta cells in non-diabetic patients, or the significant increase in Th-Tc apposition in patients with onset diabetes. This highlights Spatiopath’s versatility and its capability to identify significant spatial patterns across various multiplex imaging modalities.

Data analysis and results

Experimental background

The spatial organization of immune cells within the TME in non-small cell lung cancer (NSCLC) has arisen as an important predictive parameter for patient survival and response to immunotherapy^42,43,44. A NSCLC tumor consists of several micro-anatomical regions and contains at least 13 different types of immune cells⁴⁵. However the lack of tools for studying the TME in whole tumor sections has hindered its in-depth understanding. To help deciphering the role of immune cells related to their spatial distribution in whole tumor sections we tested our method on multiplex chromogenic immunohistochemically stained tumor section images using a protocol established in²⁴. These stained slides were imaged by a slide scanner at a resolution of 243 nm resulting in a whole slide image (WSI) of gigapixel size. In the following, we consider two putative key players of the immune response in the tumor landscape: CD3+ T cells in brown color stain and tryptase+ mast cells in cyan color stain (see Fig. 8) within the tumor. The pan-cytokeratin+ cancer cells stained in yellow, form tumor islet regions that are difficult to detect at the single-cell level. We therefore consider a group of cancer cells in close contact as a TER. To illustrate the versatility of Spatiopath compared to the more traditional Ripley-based approach, we analyzed the spatial accumulation of the two types of immune cells around the TER (cell-region association), as well as the spatial association between the immune cells themselves (cell-cell association). The immune cells are usually small and roundish and were therefore reduced to points through the computation of their centers of mass. Conversely, the contour of the complex-shape TER was mapped with a levelset function.

Fig. 8: Pipeline.

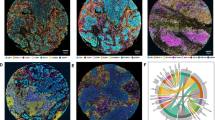
a–d The tumor area is delineated manually by an expert on a WSI. Within that tumor border, tiles are created and processed to obtain spatial object detection, i.e., positions of immune cells and border of TER. e DA detection of tryptase-positive mast cells (cyan stain), f DB detection of CD3-positive T cells (brown stain), g DC detection of pan-cytokeratin-positive TER (yellow stain). h–k We then extract spatial patterns within the relations between these different cells and regions with Spatiopath; set A, from which the levelsets are computed, is denoted by solid arrow and set B, which corresponds to the set of associated points, is denoted by dotted arrow.

Pipeline

The proposed pipeline (Fig. 8) is composed of 3 main steps: (i) selection of regions of interest (ROIs), (ii) detection of spatial objects (TER and immune cells) composing the TME, and (iii) extraction of significant spatial patterns with Spatiopath.

The histological tumor border is first manually delineated on each whole slide image (WSI) by a biologist expert. The tumor area contains imaging artifacts due to tissue preparation (fixation and cutting) as well as necrotic sub-regions. For each patient, these artifacts and necrotic regions are manually removed from the analysis. The cleaned tumor region, i.e., the domain of analysis Ω, is then divided into patches of size 2048 × 2048 pixels. To reduce the computational load without compromising the accuracy of the analysis (Fig. 9, Supplementary Fig. 6), 10% of the patches are automatically and uniformly selected for further spatial analysis, resulting in n = 17 ± 6 ROIs per patient. We then mapped the union of the selected ROIs within Ω using level-set functions around the different objects of interest (TER or immune cells) and performed spatial analysis.

Fig. 9: Quantitative analysis of spatial associations between immune cells (mast cells and T cells) and TER across eight patients.

The figure organizes data by patient (columns) into four rows for the following configurations: (1) T cells to mast cells, (2) mast cells to T cells, (3) TER to T cells, and (4) TER to mast cells. Each panel displays ${\tilde{R}}_{g}^{0}$ values within level sets (zone width = 10 μm, N = 15 level sets). Green bars indicate an excess of cells relative to a uniform distribution, suggesting cell accumulation, and red bars indicate a significant depletion of cells. Dotted lines mark thresholds for statistically significant deviations from expected values,  ±τ(N). Source data are provided as a Source Data file.

Key structures within the TME are then detected as spatial objects either by segmenting regions (such as tumor epithelium, stroma, etc) or detecting the different immune cells²⁸. The image is initially quantized to three colors using color clustering to isolate the yellow stain of the pan-cytokeratin-positive TER. The extracted contours of these regions are then polygonized and smoothed⁴⁶, resulting in the TER contours.

To detect the immune cells, we use a deep learning (DL) approach based on a U-Net architecture (Supplementary Fig. 7). To generate ground truth for the positions of immune cells, we perform a preliminary coarse detection of cells with a wavelet-based algorithm⁴⁷. These detections are then refined and corrected by expert biologists using the Icytomine plugin⁴⁸ for data annotation in Icy (https://icy.bioimageanalysis.org/)⁴⁹. The analysis shows good performance for both cell types, with CD3+ T cells generally having higher detection accuracy (Supplementary Fig. 8 and Supplementary Fig. 9) and a more robust F1 score across thresholds (F1 score > 0.8 for T_p ∈ [0.1; 0.9]) compared to tryptase+ mast cells (F1 score ≃ 0.8 for T_p ∈ [0.2; 0.8]). The missed detections often occur in cases where the cell nucleus is not visible or due to image artifacts. Given that the accuracy of cell detection remains stable for a large range of probability thresholds T_p, we choose T_p = 0.5 for further experimental analysis.

Once regions and cells are extracted, Spatiopath analysis is performed. We designed Spatiopath to be robust to cellular context and especially to varying cell densities within tissue or between patients. Indeed, Spatiopath characterizes second-order properties of spatial processes (i.e., distances between objects), and thanks to the null-hypothesis testing statistical framework, it can handle changes of cell densities. Among the n = 8 patients that were analyzed, we computed the density of CD3+ T cells and tryptase+ mast cells (Supplementary Fig. 10). We observe that the mast cell density (~10–100 cells per mm²) is typically more than one order of magnitude lower than the T-cell density (~100–1000 cells per mm²), except for the 8^th patient A08, where cell densities are similar and close to 100 cells per mm². Moreover, the density of cells is very variable from one patient to another. For example, the density of mast cells in patients A01, A02, A03, and A06 is ≤40 cells per mm², whereas it is close to 100 cells per mm² for patients A05 and A08. The same discrepancy appears for T cells, with densities close to 500 cells per mm² for patients A02, A03, and A08, and densities almost twice as large for patients A01, A05, and A06. Finally, the high (resp. low) density of one type of cell does not imply that the density of the other type of cell will also be high (resp. low) in a given patient. The use of normalized, second-order statistics is therefore necessary for the unbiased comparison of the coordinated immune response within the different patients.

We then extracted significant spatial patterns in the TME for all the 8 NSCLC patients with different cell density profiles. We analyzed two types of cell-cell associations (accumulation of T cells around mast cells, and vice versa) and two cell-region associations (T cells and mast cells around the TER). For all these cases, we set the number of levelsets to N = 15, and the level width to 10 μm, that approximates the size (diameter) of the observed immune cells (T cells and mast cells), resulting in a 150 μm observation zone around each object (cell or region).

Spatiopath analysis is performed on the Icy platform⁴⁹. For our collaborative work, that includes the delineation of tumor regions by experts in biology, we use Cytomine server⁵⁰ jointly with Icytomine⁴⁸ plugin to handle WSIs for processing and storing the gigapixel images and their relevant structures. These structures are either regions, encoded by polygons (tumor epithelium or stroma) or points (immune cells). To efficiently compute levelsets even in very large images, we leveraged the vector based morphological operators that have been proposed in⁴⁶ to process polygons dilatation at sub-pixel level using a vectorial representation. In addition to computational efficiency, this sub-pixel vectorial approach provides better precision for counting the number of cells within each level-set.

Results

For each patient, and each configuration (mast cells to T cells, TER to T cells, T cells to mast cells and TER to mast cells, see Fig. 8), we compute the reduced statistics ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}$ (Eq. (18), Fig. 9) by pooling results obtained within selected patches in tumor region, involving several hundreds to thousand cells for each cell type (740 ± 407 mast cells and 12546 ± 11846 T cells per patient, Supplementary Table II). In Fig. 9, the green rectangles highlight the different levelsets where a significant accumulation of cells is observed (i.e., where the values of ${\tilde{R}}_{g}^{0}$ exceeds the universal threshold $\tau (N)=\sqrt{2\log N}$³⁶). Red rectangles indicate levelsets with a significant depletion of cells (${\tilde{R}}_{g}^{0} < -\tau (N)$.

Previous ${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}$ plots show conserved patterns of spatial associations with some variability between individuals. To obtain more concise and readable indicators of the spatial association between different cell types and tumor regions in patients, we estimate the spatial association index ASI (Eq. (21)) and the mean distance of association δ_a (Eq. (22)) for each configuration and each patient (Fig. 10, Supplementary Table III).

Fig. 10: Summary statistics for the n = 8 patients investigated.

a Association Index (ASI) for the four different configurations: T cells to mast cells (green), mast cells to T cells (orange), TER to T cells (blue) and TER to mast cells (purple). Each boxplot illustrates the distribution—First quartile—median—third quartile of the metrics for each configuration. Whiskers indicate the range of the data, and outliers are represented as individual points. Parameters of Spatiopath analysis are Zone width = 10 μm, number of levelsets = 15, analysis neighborhood = 150 μm. b Estimated association distance δ_a. c log (p value) (log scale). To effectively represent the broad range of computed p values, we used log(p value). Lower values indicate that p value are closer to 0, and that detected spatial associations are more significant. Source data are provided as a Source Data file.

We first observe that immune mast cells and T cells are spatially associated in the TME. In particular, mast cells are strongly and closely associated with T cells (median ASI = 0.43, interquartile range IQ = 0.22, for n = 8 patients), median $\log (\, {{p}}\! - \!{{\mbox{value}}})=-17.6$ (lower value indicating more significant association), and median distance δ_a = 9.9 μm with IQ = 2.8 μm. Conversely, the proportion of T cells that are significantly associated with mast cells is lower (median ASI = 0.22, IQ = 0.13, median $\log (\,{\mbox{p-value}})=-79.0$), and the associated T cells are spread over more level sets, leading to a higher mean association distance (median δ_a = 31.9 μm, IQ = 6.7 μm).

This difference in association patterns when measuring either the association of mast cells around T cells (higher ASI and lower association distance δ_a) or the association of T cells around mast cells (lower ASI and higher, more variable association distance δ_a) can be explained by the fact that mast cells are  ~ 10 times less abundant than T cells (Supplementary Fig. 10 and Supplementary Tables II and IV). Therefore, while some of the fewer mast cells are closely apposed to selected T cells, the distribution of the more numerous T cells appears more spread (Fig. 9 (${\tilde{{{{\bf{R}}}}}}_{{{{\bf{g}}}}}^{{{{\bf{0}}}}}$)). Moreover, the more abundant T cells lead to lower p-values, as the significance of spatial accumulation is more obvious, even if the measured association index ASI is lower.

Around the tumor epithelium, our statistical framework detects a significant depletion of T cells near the border of the TER (first one to four levelsets, Fig. 9) corresponding to a depletion zone of  ~20–40 μm. This depletion is balanced by a significant accumulation of T cells in further distant levelsets, leading to a distant association (median ASI = 0.19, IQ = 0.19 and median $\log (p-value)=-10.4$) of T cells around TER, with a median association distance δ_a = 76.1 μm (IQ = 13.5 μm). Conversely, the mast cells slightly accumulate close to the TER boundary for most patients (A01, A03, A04, A05, A07, and A08) with median ASI = 0.12 (IQ = 0.19, median $\log (p-value)=-3.6$) and median distance δ_a = 12.0 μm with IQ = 9.72 μm. For two patients (A02 and A06), no significant spatial pattern is detected (neither accumulation nor depletion).

Sensitivity analysis

Spatiopath requires two user-defined parameters: the zone width, which is the distance between successive level sets, l_k+1 − l_k, with 0 ≤ k ≤ N − 1, and the maximum distance of analysis, l_N. To assess the robustness of the Spatiopath analysis with respect to these two parameters, we performed a sensitivity analysis where we computed, for the different cell-to-cell and cell-to-region configurations, the spatial association index ASI, distance δ_a, and p-value for increasing zone width = 5, 10, 20, and 50 μm, and maximum distance l_N = 50, 100, 150, and 200 μm (Supplementary Fig. 11).

We find that ASI and distance δ_a do not vary much with increasing zone width (panels (a) and (b)), except for a slight increase in ASI. This trend is also observed in synthetic simulations (Fig. 3), and is due to the potential missing of significant accumulations of cells in a subset of level sets for smaller zone width. Panel (c) shows that the p-values decrease (i.e., statistical significance increases) with larger zone width. This results from the increased number of spatially associated cells in larger level sets.

When varying the maximum distance of analysis (panels (d–f)), we find that ASI and the estimated distance δ_a increase with l_N, before reaching a plateau at l_N≤ 150 μm for all configurations. This means that all spatially associated cells are taken into account, and there is no need to increase the analysis field further (the p-values remain relatively constant).

Sensitivity analysis demonstrates that the results obtained with Spatiopath do not vary much with user-defined parameters, except for the maximum distance of analysis l_N, which needs to be high enough to account for all spatially associated cells (we chose l_N = 150 μm in our analysis). This demonstrates that Spatiopath is a robust statistical framework for the characterization of the spatial relations between immune cells and tumor regions.

Biological interpretation

We observe significant spatial patterns that are conserved between all the patients investigated such as the spatial association of mast cells and T cells. These findings strongly suggest that T cells and mast cells make physical contacts in the TME. Conversely, our statistical framework highlighted the depletion of T cells from the tumor epithelium border, which was more pronounced in some patients (A01, A03, and A05) compared to others. Pronounced depletions of T cells in some patients might be due to an increased stiffness of extracellular matrix along the TER, preventing an easy infiltration of immune cells. Local depletion of T cells near the tumor border might appear contradictory with the slight accumulation, or absence of patterns, of mast cells around TER, as mast and T cells are spatially associated. This apparent contradiction can be explained by the fact that Spatiopath analyses spatial patterns at the cell’s population level. Therefore, an increased association between T and mast cells outside the TER border region could reconcile all these measured spatial patterns.

Discussion

The imaging of the TME with various modalities, ranging from the historical labeling with hematoxylin and eosin (H&E)⁵¹, to immunohistochemistry⁵², or recent multiplexed imaging^53,54 allows the detailed mapping of the immune response to cancer in patient tissues. While the automatic analysis of these images has largely benefited from the development of deep-learning methods for the segmentation and classification of cells and cellular neighborhoods such as tumor epithelium⁵⁵, the in-depth understanding of the immune response also requires the robust analysis of the spatial relations between immune cells and their environment. Spatiopath is based on a null hypothesis paradigm that can distinguish statistically significant spatial associations of immune cells from fortuitous accumulations when the cells are randomly distributed. This approach is particularly relevant when immune cells are abundant as Spatiopath can discriminate the actual associations from fortuitous ones due to the high cell density.

Spatiopath identified two spatial patterns associated with the localization of mast cells in the tumor stroma. First, a statistically significant coupling of mast cells with T cells was found at a distance of one levelset, which corresponds to the diameter of a cell (~10 μm) and thereby strongly suggest that these two immune cell types make physical contacts (Supplementary Fig. 12a). The frequent colocalization of mast cells and T cells was confirmed using high-magnification IHC images. Second, an accumulation of mast cells along TERs, at a distance of two levelsets (~20 μm), was detected. These findings are intriguing and unexpected because, in contrast to T cells which have been much investigated, the potential roles of mast cells in cancer remain poorly understood⁵⁶. During the antitumor immune attack, it is well established that T cells detect mutated proteins of cancer cells (tumor antigens) by interacting closely with professional antigen-presenting immune cells such as dendritic cells, macrophages, and B cells, and that cytotoxic CD8 T cells kill cancer cells via physical contacts. In contrast, T cells are currently not known to functionally interact with mast cells in tumors. Interestingly, mast cells have been reported to be able to present antigens to T cells^57,58, and may therefore potentially present tumor antigens to T cells in NSCLC tumors. Our findings suggest that mast cells may play an important, yet uncharacterized role in cancer via close collaboration with T cells.

Spatiopath revealed a significant depletion of T cells at the proximity of TERs and an accumulation of T cells at a distance of 3–4 levelsets (~30–40 μm) from the border of the TERs (Supplementary Fig. 12b, c). This apparent depletion of T cells from the TERs is of biological importance because cytotoxic CD8 T cells need to make physical contacts with the cancer cells to kill them. Variations in the density of the extracellular matrix (ECM) of the tumor stroma may provide an explanation for the observed T cell localization. Previous in vitro studies using viable slices of human NSCLC tumors showed that T cells preferably reside in stromal regions with a loose network of collagen and fibronectin fibers, whereas stromal regions with a dense ECM were nearly devoid of T cells⁵⁹. Importantly, it was reported that TERs are surrounded by dense and parallel fibers of ECM that extend approximately 50 μm from the TER border, and these regions with a dense ECM around TERs contain few T cells. Experimental matrix reduction with collagenase resulted in T cells becoming uniformly localized in the tumor stroma and being able to come in contact with the TERs⁵⁹. Thus, the observed depletion of T cells at the proximity of TERs may be due to a physical barrier consisting of a dense ECM.

Using immunohistochemistry labeling of several immune cells in non-small cell lung cancer patients, we could measure the spatial associations between different immune cells and their significant accumulation (or depletion) around the tumor epithelium. These observations, albeit preliminary, open the way to new investigations. It is now well-established that each patient responds differently to immunotherapy, and that personalized treatment is much more efficient. Therefore, we predict that statistical analysis of the individual differences regarding the spatial organization of immune cells within tumors using tools such as Spatiopath will pave the way to a better understanding of the state of the anti-cancer immune response for each patient, and could serve as robust predictive markers of disease outcome and response to immunotherapy.

Methods

Derivation of the mean and variance of generalized Ripley function ${{{{\mathcal{R}}}}}_{g}$ under CSR

We use the integers i, j ∈ {1, …, ∣A∣} to denote the objects in A that are implicitly represented via level-set functions ϕ_i and ϕ_j. Also, we define the scalars 0 < l₁ < … < l_m < l_n < …l_N to indicate the increasing levelsets of an embedding function ϕ_j. The following terms are also defined.

• ${\omega }_{mn}^{i}:=\{(x,y)\in {{\mathbb{R}}}^{2}| {l}_{m} < {\phi }_{i}(x,y)\le {l}_{n}\}$,

• ${\omega }_{0}^{i}:=\{(x,y)\in {{\mathbb{R}}}^{2}| {\phi }_{i}(x,y)\le 0\}$.

• ${\omega }_{mn}^{ij}:={\omega }_{mn}^{i}\cap {\omega }_{mn}^{\,j}$.

Computing expectation

We first note that when the spatial elements in B exhibit the CSR property discussed above, we can write from Eq. (2) that the indicator function χ_mn is a Bernoulli random variable. Accordingly, the term K_i(m, n) (which is the sum of ∣B∣ Bernoulli random variables) follows the Binomial law. Mathematically, we write ${K}_{i}(m,n) \sim {\mathsf{Bin}}\left(| B|,{p}_{mn}^{i}\right)$, where ${p}_{mn}^{i}$ is the probability of a point u ∈ B to be localized within ${\omega }_{mn}^{i}$. Under CSR, the points in set B are uniformly distributed over Ω, and this term is calculated as

$${p}_{mn}^{i}:={\mathbb{P}}\left(u\in {\omega }_{mn}^{i}\right)=| {\omega }_{mn}^{i}| /| \Omega |$$

(23)

The expected value of ${{{{\mathcal{R}}}}}_{g}({l}_{m},{l}_{n})$ under the null hypothesis is calculated from Eq. (2) as follows:

$$\begin{array}{l}{\mathbb{E}}\left[{{{{\mathcal{R}}}}}_{g}({l}_{m},{l}_{n})\right]=\frac{| \Omega | }{| A| | B| }{\sum }_{i=1}^{| A| }{\mathbb{E}}\left[{K}_{i}(m,n)\right]\\=\frac{| \Omega | }{| A| | B| }{\sum }_{i=1}^{| A| }| B| \,{p}_{mn}^{i},\,{as}\,{K}_{i}(m,n) \sim {\mathsf{Bin}}\left(| B|,{p}_{mn}^{i}\right).\\=\frac{| \Omega | }{| A| | B| }{\sum }_{i=1}^{| A| }| B| \frac{| {\omega }_{mn}^{i}| }{| \Omega | }=\frac{1}{| A| }{\sum }_{i=1}^{| A| }| {\omega }_{mn}^{i}| \end{array}$$

(24)

Computing variance

To simplify the mathematical notations, for this section of the proof we will drop the notation (m, n) from the symbols. It is implied that the analysis is performed for the sets of regions ${\omega }^{i} :={\omega }_{mn}^{i}$, and the symbol (m, n) is omitted for brevity. In order to compute the variance, we observe the following from Eq. (2):

$${\mathbb{E}}\left[{K}_{i}\right]={\mu }^{i}=| B| {p}^{i}\quad \quad {{{\rm{where}}}}\,\,{p}^{i}=\frac{| {\omega }^{i}| }{| \Omega | }$$

(25)

Note that the statistic in Eq. (2) could be re-arranged as ${{{{\mathcal{R}}}}}_{g}=\frac{| \Omega | }{| A| | B| }{\sum }_{i=1}^{| A| }{K}_{i}$, where ${K}_{i}={\sum }_{j=1}^{| B| }{\chi }^{i}({u}_{j})$ and we define the indicator function χⁱ(u) as follows:

$${\chi }^{i}(u)=\left\{\begin{array}{l}1\,\,{\mbox{if}}\,\,\,u\in {\omega }^{i}\quad \hfill \\ 0\,\,{\mbox{otherwise}}\,\quad \end{array}\right.$$

(26)

It is easy to verify that ${\mathbb{E}}\left[{\chi }^{i}(u)\right]=\Pr \{u\in {\omega }^{i}\}={p}^{i}$. With this definition, we can compute the variance in the following manner.

$${{{\rm{Var}}}}\left[{{{{\mathcal{R}}}}}_{g}\right]=\frac{| \Omega {| }^{2}}{| A{| }^{2}| B{| }^{2}}{\sum }_{i=1}^{| A| }{\sum }_{j=1}^{| A| }{\mathbb{E}}\left[\left({K}_{i}-{\mu }^{i}\right)\left({K}_{j}-{\mu }^{\,j}\right)\right]$$

(27)

It is easy to show that ${\mathbb{E}}\left[\left({K}_{i}-{\mu }^{i}\right)\left({K}_{j}-{\mu }^{j}\right)\right]={\mathbb{E}}\left[{K}_{i}{K}_{j}\right]-{\mu }^{i}{\mu }^{j}$. Let us analyze K_iK_j.

$$\begin{array}{rcl}{K}_{i}{K}_{j}&=&\left({\chi }^{i}\left({u}_{1}\right)+\ldots+{\chi }^{i}\left({u}_{| B| }\right)\right)\left({\chi }^{j}\left({u}_{1}\right)+\ldots+{\chi }^{j}\left({u}_{| B| }\right)\right)\\ &=&{\sum }_{m=1}^{| B| }{\chi }^{i}({u}_{m}){\chi }^{j}({u}_{m})+{\sum }_{m=1}^{| B| }{\sum }_{n\ne m=1}^{| B| }{\chi }^{i}({u}_{m}){\chi }^{j}({u}_{n})\hfill\end{array}$$

(28)

Now, we know that for ∀ m ≠ n, ${\mathbb{E}}\left[{\chi }^{i}({u}_{m}){\chi }^{j}({u}_{n})\right]={\mathbb{E}}\left[{\chi }^{i}({u}_{m})\right]{\mathbb{E}}\left[{\chi }^{j}({u}_{m})\right]$. This is due to the CSR assumption, any point u is equally likely to be contained in any bounded subset of Ω. Additionally, ${\mathbb{E}}\left[{\chi }^{i}({u}_{m}){\chi }^{j}({u}_{m})\right]=\Pr \{{u}_{m}\in {\omega }^{i}\cap {\omega }^{j}\}$, which is defined as p^ij = ∣ωⁱ ∩ ω^j∣/∣Ω∣. It could be noted that when i = j, p^ij = pⁱ = p^j. Therefore, we could write the expectation of (28) in the following manner.

$$\begin{array}{rcl}{\mathbb{E}}\left[{K}_{i}{K}_{j}\right]&=&{\sum }_{m=1}^{| B| }{\mathbb{E}}\left[{\chi }^{i}({u}_{m}){\chi }^{j}({u}_{m})\right]+{\sum }_{m=1}^{| B| }{\sum }_{n\ne m=1}^{| B| }{\mathbb{E}}\left[{\chi }^{i}({u}_{m})\right]{\mathbb{E}}\left[{\chi }^{j}({u}_{n})\right]\\ &=&\left({\sum }_{m=1}^{| B| }{p}^{ij}+{\sum }_{m=1}^{| B| }{\sum }_{n\ne m=1}^{| B| }{p}^{i}{p}^{\,j}\right)=| B| {p}^{ij}+(| B{| }^{2}-| B| ){p}^{i}{p}^{\,j}\end{array}$$

(29)

Therefore, substituting the values in Eq. (27), we obtain:

$${{{\rm{Var}}}}\left[{{{{\mathcal{R}}}}}_{g}\right]= \frac{| \Omega {| }^{2}}{| A{| }^{2}| B{| }^{2}}{\sum }_{i=1}^{| A| }{\sum }_{j=1}^{| A| }\left({\mathbb{E}}\left[{K}_{i}{K}_{j}\right]-{\mu }^{i}{\mu }^{\,j}\right)\\= \frac{| \Omega {| }^{2}}{| A{| }^{2}| B{| }^{2}}{\sum }_{i=1}^{| A| }{\sum }_{j=1}^{| A| }\left(| B| {p}^{ij}+(| B{| }^{2}-| B| ){p}^{i}{p}^{\,j}-| B{| }^{2}{p}^{i}{p}^{\,j}\right)\\= \frac{| \Omega {| }^{2}}{| A{| }^{2}| B| }{\sum }_{i=1}^{| A| }{\sum }_{j=1}^{| A| }\left({p}^{ij}-{p}^{i}{p}^{\,j}\right)$$

(30)

Finally, we can write the expression of variance as

$${{{\rm{Var}}}}\left[{{{{\mathcal{R}}}}}_{g}\right]=\frac{| \Omega {| }^{2}}{| A{| }^{2}| B| }{\sum }_{i=1}^{| A| }{\sum }_{j=1}^{| A| }\left(\frac{| {\omega }_{mn}^{\,i}\cap {\omega }_{mn}^{\,j}| }{| \Omega | }-\frac{| {\omega }_{mn}^{i}| | {\omega }_{mn}^{\,j}| }{| \Omega {| }^{2}}\right)$$

(31)

Simulation design for comparing the performance of Spatiopath and SODA

We begin by generating n_A points located at coordinates ${x}_{i}^{A}$, representing the centers of cells, distributed uniformly at random across a 1024 × 1024 pixel square domain Ω. To assess the performance of SODA and Spatiopath across various cell shapes, we model cell contours using star-convex polygons, which have demonstrated strong ability to represent and identify complex cellular shapes⁶⁰. Cell size is adjusted by varying the mean axis length μ of the star shape, starting from μ = 1 pixel (producing pointillistic cells) up to μ = 20 pixels for the largest cells.

For each cell center ${x}_{i}^{A}$ and a given size μ, the points of each cell’s contour polygon are determined iteratively: the first point ${x}_{i}^{A}(1)$ of the contour is determined by selecting a uniformly distributed angle ${\theta }_{i}^{A}(1) \sim U(0,2\pi )$ and a distance ${r}_{i}^{A}(1)=\parallel {x}_{i}^{A}(1)-{x}_{i}^{A}\parallel \sim N(\mu,\sigma )$. The other points ${x}_{i}^{A}(j)$, for 2 ≤ j ≤ m, are then generated by selecting the angle

$${\theta }_{i}^{A}(j)={\theta }_{i}^{A}(1)+\frac{(j-1)}{m}\times 2\pi$$

and by drawing the distance

$${r}_{i}^{A}(j-1)+N(0,\sigma ).$$

We performed simulations for increasing cell sizes with μ = 1, 5, 10, and 20 pixels. The standard deviation σ of axis length and the number m of contour points are adjusted to cell size: σ = μ/4 and m = μ ⋅ pixel⁻¹. For each size, the number of cells n_A is chosen so that the surface occupied by all the A cells covers 10% of the field of view Ω. Therefore, the number of A cells decreases as their size (μ) increases. To avoid a too large computational load for SODA, we limited the number of smaller A cells (for μ = 1 and 5) to n_A = 200.

The simulation of B points’ coupling to set A was then performed as previously described. For each simulation, the number of B points is equal to n_B = 1000.

Tumor section images

Patients and lung tumor samples

Tumor specimens were obtained from non-small cell lung cancer (NSCLC) patients (n = 8) diagnosed with squamous cell carcinoma TNM stage 1a/1b and who underwent tumor resection at the Department of Cardiothoracic Surgery at Oslo University Hospital, Ulleval hospital, Oslo, Norway, during the period 01.01.2000-31.12.2008. These patients had not received neoadjuvant chemotherapy, preoperative radiotherapy, or immunosuppressive therapy. The pathological TNM stage and tumor subtype was determined by two lung pathologists based on histopathologic criteria according to the 8th edition of Union for International Cancer Control TNM staging system and the 2015 World Health Organization guidelines. The study was reviewed and approved by the Norwegian Regional Ethical Committee (ref: 2019/352). Written informed consent was obtained from all included patients who were alive when the study was initiated. Exemption from obtaining written informed consent from patients who were dead at the start of the study was granted by the Norwegian Regional Ethical Committee (ref: 2019/352).

Multiplex immunohistochemistry (IHC)

Multiplex chromogenic IHC staining was performed on 3 μm sections of formalin-fixed, paraffin-embedded NSCLC tumors. The multiplex staining was performed using a Ventana Discovery Ultra automated slide stainer (Ventana Medical System, Roche, Cat. No. 750-601). In brief, after deparaffinization of the sections, heat-induced antigen retrieval was performed by using cell conditioning 1 buffer (CC1, Ventana Medical System, Cat. No. 950-500). Next, the tumor sections were incubated with the primary monoclonal antibodies (mAbs), followed by the secondary antibodies conjugated with peroxidase or alkaline phosphatase. The primary and secondary antibodies are listed in Supplementary Tables V and VI, respectively. Visualization of the bound antibodies was achieved as follows: bound anti-CD3 was visualized using the ChromoMap DAB kit (Ventana Medical System, Cat. No. 760-159), and tryptase with the DISCOVERY Teal HRP kit (Ventana Medical System, Cat. No. 760-247). IHC was performed sequentially, completing the staining of one cellular marker, before continuing with staining of another in the same section. Thus, to block for potential binding of subsequently added antibodies to the already applied primary and secondary antibodies, the tissue sections were treated with Ribo CC solution (CC2, Cat. No. 760-107, Ventana Medical System) at 100 °C for 24 min. A mixture of primary mAbs specific for cytokeratins (mAb clones AE1, AE3, and PCK26) in epithelial cells (normal and cancerous) visualized with the Discovery Yellow AP detection kit (Ventana Medical System, Cat. No. 760-239) was included in the staining panel to visualize the tumor epithelium. In the end, the tissue sections were counterstained manually with hematoxylin. Isotype- and concentration-matched irrelevant antibodies were used as negative controls.

Imaging

For image analysis of immune cells in tumors, whole tumor sections were scanned with a Pannoramic MIDI II scanner (3DHISTECH, Budapest, Hungary) at 20× magnification and digitized with high resolution, at a pixel size of 0.243094 μm × 0.243094 μm. Microscopy images of the stained tumor sections shown in figures were captured by an Olympus BX51 microscope, model BX51TF (Olympus, Tokyo, Japan) using a Colorview digital camera (Olympus) at a magnification of ×400.

Annotation of regions of interest in scanned images

The Icy open-source software platform⁴⁹ was used for annotation of regions in the scanned images of the tumor tissue sections. The tumor area was delimited manually by drawing a line at the border of the tumor in the scanned images. The tumor border line was drawn in such a way that all cancer cells were localized within the tumor border. The next step was to identify and annotate manually microanatomical regions of tumors such as tumor epithelium, tumor stroma, fibrotic regions, necrotic regions, mucinous regions, blood vessels, and empty areas, in order to develop the algorithm by deep learning. The tumor epithelium was visualized using pan-cytokeratin mAbs and was defined as areas of yellow cells with blue nuclei within the tumor border. The tumor stroma was defined as non-yellow areas within the tumor border.

Algorithmic details for DL-based detection of immune cells

In this section, we detail the different steps of the DL-based pipeline that we developed for the accurate detection of immune cells.

Preprocessing of ground-truth cells’ localizations

The ground truth data consist of a series of coordinates corresponding to the positions of cell centers. Fully convolutional networks, such as U-Net⁶¹, have proven their effectiveness in object detection in biological imaging. The main output of such networks is a probability map for each pixel indicating the likelihood of it belonging to an object. The required ground truth, therefore, is a cell density map rather than a series of discrete coordinates. To accurately represent cell positions, we pre-process the ground truth data by generating masks from the provided cell coordinates (x, y). For each cell located at (x_i, y_i), we place a Gaussian function defined by:

$${G}_{i}(x,y)=\exp \left(-\frac{{(x-{x}_{i})}^{2}+{(\,y-{y}_{i})}^{2}}{2{\sigma }^{2}}\right)$$

(32)

where σ is the standard deviation of the Gaussian. To preserve distinct Gaussian peaks associated with individual cell positions and provide an accurate representation of cell density, the final intensity value I(x, y) at each pixel (x, y) of the input ground truth image is computed as the maximum value of all Gaussian functions evaluated at that position (Supplementary Fig. 13):

$$I(x,y)={\max }_{i}{G}_{i}(x,y)$$

(33)

To standardize the intensity values, the image is normalized by scaling the highest intensity value to 1:

$${I}_{{{{\rm{normalized}}}}}(x,y)=\frac{I(x,y)}{{\max }_{(x,y)}I(x,y)}$$

(34)

This preprocessing ensures the preservation of distinct peaks associated with individual cell positions, providing an accurate representation of cell density.

Model architecture and training

We employed a UNet architecture for cell detection, starting with 32 initial filters. The model consists of an encoder-decoder structure with several convolutional layers, max-pooling layers in the encoder, and upsampling layers in the decoder. ReLU activation is used in all layers except the output layer, where a sigmoid activation function is applied to ensure the prediction values are between 0 and 1. The UNet model outputs two channels: one for T cells and one for mast cells. The model is optimized using the Adam optimizer with a learning rate α of 10⁻⁴. We use the Binary Cross-Entropy (BCE) loss function, defined as:

$$\, {{\mbox{BCE}}}\,=-\frac{1}{N}{\sum }_{i=1}^{N}\left[{y}_{i}\log ({\hat{y}}_{i})+(1-{y}_{i})\log (1-{\hat{y}}_{i})\right]$$

(35)

where y_i is the ground truth value, ${\hat{y}}_{i}$ is the predicted value, and N is the total number of pixels. While the preprocessed masks are continuous and the output is fed through a sigmoid activation function, we prefer BCE over Mean Squared Error (MSE) because BCE is more suitable for binary classification tasks, even when the targets are continuous probabilities. It provides better gradients for learning when the predicted values are close to 0 or 1, which aids in faster and more stable convergence.

Training and dataset information

The model was trained for 400 epochs on a dataset consisting of 700 patches. These patches were split into 80% for training, 10% for validation, and 10% for inference. The patches come from different patients, exhibiting varying textures, cell densities, and stain intensities. This variability ensures that the model is robust across diverse conditions, allowing it to generalize well to new, unseen data. Inference and Post-Processing After training, inference is performed by applying a sigmoid activation to obtain raw output probabilities. Local peaks are identified using a 5-pixel window. A threshold of 0.5 is used to filter out uncertain detections, ensuring that only confident predictions are considered.

Evaluation

For evaluation, we compute a distance matrix between the peaks of the ground truth and the predicted peaks. The distance matrix D is computed where each element D_ij represents the Euclidean distance between the i-th ground truth peak and the j-th predicted peak. The optimal matching is found by solving the following linear assignment problem:

$${\min }_{\pi }{\sum }_{i=1}^{n}{D}_{i,\pi (i)}$$

(36)

where π is a permutation of the prediction indices. From the assignment, true positives are pairs of matched peaks, false negatives are ground truth peaks without a matched prediction, and false positives are predicted peaks without a matched ground truth.

The precision, recall, and F1-score are calculated as follows:

$${{{\rm{Precision}}}}=\frac{TP}{TP+FP}$$

(37)

$${{{\rm{Recall}}}}=\frac{TP}{TP+FN}$$

(38)

$$F1\,{\mbox{-score}}\,=2\times \frac{{{{\rm{Precision}}}}\times {{{\rm{Recall}}}}}{{{{\rm{Precision}}}}+{{{\rm{Recall}}}}}$$

(39)

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.