Sensing flow gradients is necessary for learning autonomous underwater navigation

Abstract

Aquatic animals are much better at underwater navigation than robotic vehicles. Robots face major challenges in deep water because of their limited access to global positioning signals and flow maps. These limitations, and the changing nature of water currents, support the use of reinforcement learning approaches, where the navigator learns through trial-and-error interactions with the flow environment. But is it feasible to learn underwater navigation in the agent’s Umwelt, without any land references? Here, we tasked an artificial swimmer with learning to reach a specific destination in unsteady flows by relying solely on egocentric observations, collected through on-board flow sensors in the agent’s body frame, with no reference to a geocentric inertial frame. We found that while sensing local flow velocities is sufficient for geocentric navigation, successful egocentric navigation requires additional information of local flow gradients. Importantly, egocentric navigation strategies obey rotational symmetry and are more robust in unfamiliar conditions and flows not experienced during training. Our work expands underwater robot-centric learning, helps explain why aquatic organisms have arrays of flow sensors that detect gradients, and provides physics-based guidelines for transfer learning of learned policies to unfamiliar and diverse flow environments.

Introduction

Ocean monitoring is essential for understanding ecosystem functioning¹, marine biodiversity², and the ocean’s carbon cycle³, particularly in the face of our rapidly changing climate^4,5. To expand the current capabilities of underwater robots for long-term ocean surveillance and monitoring^4,6,7,8, we need effective control strategies that enable robotic swimmers to seamlessly navigate through shifting currents, much like biological swimmers^9,10,11, using only on-board sensors. But is it feasible for robots to learn underwater navigation autonomously from an egocentric perspective without any land references?

Navigating underwater environments presents unique challenges because of the dynamic nature of flow currents and the absence of global positioning signals. The naive intuition that to reach a destination, it suffices to turn towards that destination and move in a straight line to reach it, may not be optimal or even feasible when the navigator experiences strong flow currents¹². Planning trajectories using optimal control theory such as in Zermelo’s navigation problem requires detailed prior knowledge of the entire flow field and its time evolution^13,14,15,16, information not readily available to an autonomous underwater navigator. Methods like adaptive control^17,18 and model predictive control^19,20 exist for motion planning in partially known flow fields, but fall short under limited flow information.

Reinforcement learning (RL) approaches—a suite of artificial intelligence algorithms that solve problems through trial and error^{21,22,23,24,25,26,27,28,29,30,31}—are particularly suited to learning optimal navigation strategies by interacting directly with the flow environment. RL is already driving the next innovations in aerial and underwater locomotion^{32,33,34,35,36,37}, navigation^38,39, and trajectory tracking^8,40,41. In RL, the agent, in either a simulated^38,39,42 or physical^{8,33,43,44,45} flow environment, acts according to a control policy. The policy processes inputs, observations of the agent’s environment, to generate an action. This observation-to-action mapping is continuously refined through repeated interactions with the surrounding environment, guided by a predefined reward function to optimize the agent’s performance²¹.

But what environmental cues should the agent detect, or observe, to learn efficient underwater navigation? For inspiration and to explore potential solutions, it is reasonable to turn to aquatic organisms. Fish, for example, are thought to orient themselves using both geocentric and egocentric visual maps⁴⁶, similar in their neural basis to those used by mammals and birds for spatial navigation⁴⁷. Fish also possess an elaborate lateral line system that allows them to determine the direction and rate of water movement^48,49. This flow sensing ability is important for evading predators⁵⁰, homing⁵¹, and rheotaxis^11,52,53. However, despite extensive laboratory and field studies, the sensory cues available and employed by fish for navigation remain an open problem^53,54. This knowledge gap motivates us to explore the minimal sensory cues necessary for autonomous underwater navigation in fish and fish-like robots at the meter scale⁵⁵. At this scale, the flow environment is characterized by long-lived coherent vortex structures^56,57,58, distinct from the uniform turbulence experienced at smaller scales^59,60.

We consider underwater swimmers characterized by two unique features: (1) the swimmer only senses instantaneous and local flow information, with no immediate, past, or future knowledge of spatial flow variations beyond its sensing range, and (2) the swimmer senses the flow in an egocentric frame, with no knowledge of a global flow direction or inertial frame of reference. Egocentrism here is more nuanced compared to its interpretation in studying how animals build visual maps of the physical space⁴⁶: it implies that the agent has no awareness of an external frame of reference, and no information of its own position and orientation or the flow direction in such frame. The agent operates independently of a geocentric land-based coordinate system. This underwater navigator is different from existing studies where the agent knows the full velocity field^12,42,61,62, or where the agent relies on inertial information, such as knowledge of the direction of gravity^32,60, the agent’s location and orientation in a geocentric frame of reference^{8,38,42,61,62}, or the global direction of an oncoming flow³⁹.

The incorporation of these two features—egocentrism and locality of flow sensing—is quintessential for establishing a paradigm of underwater robotic learning grounded in the robot’s own sensory world, similar to the “Umwelt" concept in animal behavior⁶³. This approach would allow robots to perceive, interact with, and learn from their environment based on their unique sensory inputs. This, in turn, would lead to more adaptive and autonomous behaviors and help overcome current limitations in learning that rely on geocentric observations^8,38. Geocentric policies are not invariant to rotations and translations of the flow field and not suitable for autonomous deployment in the open ocean without continuous support from and communication with a terrestrial control center⁸.

In this study, we first investigate if an artificial agent interacting with a simulated flow environment can learn autonomously using egocentric flow observations without the extra support of a geocentric inertial reference. We find that, while sensing local flow speeds is sufficient for geocentric navigation, successful egocentric navigation requires additional information about local flow gradients. Then, we compare the adaptability of geocentric and egocentric navigators to unfamiliar flow environments. We find that, with the additional observation of local flow gradients, egocentric navigators are as successful in familiar environments and could be more robust under unfamiliar conditions. To elucidate the sensory cues the agent uses for decision-making, we map the agent’s trajectories from the physical space to the space of flow observations, and we employ tools from dynamical systems theory to explain the behavior of the trained RL policy in comparison to heuristic policies.

Our work paves the way towards truly autonomous underwater learning from a robot-centric perspective⁶⁴, provides fresh insights into why aquatic animals possess a network of flow sensors (e.g., lateral line system of fish^49,65 and array of whiskers of the harbor seal⁹) to detect local flow gradients, informs the design of optimal sensing and control strategies for future underwater robots^53,66, and offers a gateway for transfer learning in new flow environments⁶⁷. It also opens new avenues for future exploration of hybrid strategies that integrate egocentric and geocentric representations of the environment^68,69,70,71.

Results

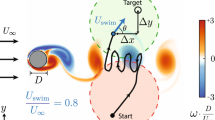
Consider the problem of an artificial swimmer tasked with navigating to a destination located across an unsteady wake (Fig. 1A). The wake consists of a trail of alternating-sign vortices generated by a freestream flow of speed U past a fixed cylinder of diameter D, which we simulated numerically using a computational fluid dynamics (CFD) solver (Methods, Supplementary Fig. 1,^72,73,74). The swimmer, modeled as a self-propelled agent, is constrained to move at a constant speed V = 0.8U weaker than the freestream speed U.

Fig. 1: Autonomous underwater navigation in unsteady flows.

A Unsteady flow generated by a uniform freestream flow U past a cylinder of diameter D at Re  = 400. A swimmer moving at constant speed V = 0.8U must navigate the wake to reach the target (black star). Motion planning using time-optimal control (black trajectory) requires prior knowledge of the entire flow field and its time evolution. Flow and visual sensory cues in (B) a terrestrial geocentric frame (e_x, e_y) or (C) a body-fixed egocentric frame (t, n). D To navigate across unsteady flows, we train, using Deep RL, a swimmer that senses the ambient flow and target location locally.

This problem is challenging because when positioned outside the wake, the swimmer cannot overcome the flow; it drifts downstream. In Zermelo’s classic optimization problem, a swimmer in an overpowering uniform stream with control only over its heading direction can, at best, optimize its motion either to minimize the time it takes to travel a given distance across the stream or to minimize its downstream drift distance (Methods, Supplementary Fig. 2). To navigate to a target across an unsteady wake, the swimmer must follow three stages: enter the wake, slalom between vortices to exploit the weaker flows in the wake to swim upstream, and exit upstream of the target to ensure reaching it despite the stronger downstream current. These three stages—entering, zigzagging inside, and exiting the wake—universally characterize navigation across an unsteady wake; they arise in trajectories based on time-optimal control given full knowledge of the spatiotemporal evolution of the flow field, when the swimmer has direct control over its heading direction³⁸ and when it has control only over the rotational rate at which it changes its heading direction (Fig. 1A). Slaloming inside the wake was reported in live fish negotiating unsteady wakes⁷⁵ and is thought to endow fish with energetic benefits when swimming alone⁷⁵ and in groups^76,77; slaloming also emerges robustly in inanimate swimmers interacting with unsteady flows^78,79,80,81.

Because full knowledge of the spatiotemporal evolution of the flow field is often unavailable for robotic or biological underwater navigators, it was demonstrated in ref. ³⁸ that an optimal strategy for entering, zigzagging in, and exiting the wake can be learned using RL with only local and instantaneous observations of the flow velocity and relative position of the target—the agent has no memory of past states and makes no prediction of future states. The problem of navigating across unsteady wakes in strong currents is thus controllable and solvable with either full or partial observations of the flow field, as long as observations are provided in an inertial frame of reference. But is learning feasible in the agent’s Umwelt, from an egocentric perspective?

Distinguishing between egocentric and geocentric observations

To illustrate the difference between egocentric and geocentric sensing, consider the geocentric learning in ref. ³⁸ where, to reach a target located across the unsteady wake, the policy relied on geocentric observations taken in an inertial frame of reference (e_x, e_y). In this inertial frame, the target is located at x^⋆ ≡ (x^⋆, y^⋆). Geocentric observations consisted of (i) the local flow velocity u ≡ (u, v) measured at the location x ≡ (x, y) of the agent and (ii) the relative position Δx = x^⋆ − x ≡ (Δx, Δy) of the target to the agent (Fig. 1B). Practically, to obtain these observations, the swimmer must first measure these quantities using on-board sensors in its own body-frame, say, (t, n) chosen to coincide with the swimmer’s heading t and transverse n directions (Fig. 1C). Basically, the agent must first observe, at its location, the longitudinal and transverse components (u_b, v_b) ≡ (u ⋅ t, u ⋅ n) of the fluid velocity u and the relative position (Δx_b, Δy_b) ≡ (Δx ⋅ t, Δx ⋅ n) of the target (Fig. 1C). Then, to transform these measurements into an inertial frame, the agent needs to know its own orientation θ, i.e., heading direction ${{\bf{t}}}\equiv (\cos \theta,\sin \theta )$, relative to the inertial frame (e_x, e_y), which usually means the assistance of a satellite, compass, or inertial measurement unit (Table 1). Additionally, to properly align the inertial frame relative to the freestream direction as done in ref. ³⁸, the swimmer must know the freestream direction in advance, which is typically unavailable in underwater environments^11,49,53,82.

Table 1 Minimal observations for successful learning

In an equivalent egocentric set-up, the agent collects sensory observations directly in its body frame (t, n), with no prior knowledge of freestream direction and no dependence on terrestrial coordinates or inertial frame. Basically, the agent observes, at its location, the longitudinal and transverse flow components (u_b, v_b) and the relative position (Δx_b, Δy_b) of the target (Fig. 1C). It has no knowledge of its own orientation θ, which eliminates potential time delays and computations inherent to assessing inertial signals^8,83. Thus, if amenable to learning in underwater environments, egocentric observations would at once be less demanding in terms of sensory requirements and offer greater flexibility in underwater environments where obtaining and communicating external sensory data to the agent is unfeasible.

We formulated the learning problem such that, given a set of observations o, the policy π(a∣o) outputs an action a aimed to guide the artificial agent to a target location across the wake (Fig. 1D, Methods). To reflect practical limitations on motion steering in biological and robotic systems^39,84,85, we considered the agent’s action a to control the rate of change $\dot{\theta }$ of its heading direction; the agent has no direct control over its heading angle θ. The policy $\pi (\dot{\theta }| o)$ is learned by maximizing, through repeated interactions with the environment, a cumulative reward composed of a sparse reward given once the swimmer reaches the target and a dense reward given at every timestep equal to the negative change in distance to the target. Each training episode is initiated by randomly positioning the target (x*, y*) inside a circular region at one side of the wake and the agent (x_o, y_o) inside an equally-sized circular region at the opposite side of the wake and pointing in a random orientation θ_o (Fig. 1A). Training is initialized at a random time, i.e., phase, t_o relative to the wake evolution.

Egocentric learning requires sensing flow gradients

To assess the advantages and limitations of geocentric versus egocentric sensing, we asked, in the same fluid environment, which set of observations facilitates learning the task of navigating across the unsteady wake with no prior knowledge of the fluid environment.

Starting from the same set of geocentric observations o = (Δx, Δy, u, v) employed in ref. ³⁸, the swimmer failed to learn the navigation task. In ref. ³⁸, the swimmer learned successfully because it had direct control over its heading angle θ. To remedy this, and because these geocentric observations require implicit knowledge of the swimmer’s heading angle θ in inertial frame, we allowed the swimmer to explicitly observe θ, thus augmenting the geocentric observations to o = (Δx, Δy, θ, u, v) (Table 1). The policy converged in each of the 17 training sessions we conducted, with some variation in reward (Fig. 2A, Supplementary Table 1). To highlight the importance of flow sensing, we trained a flow-blind swimmer that observed only its own orientation and relative position to the target (Δx, Δy, θ). The flow-blind swimmer failed to reach the target (Fig. 2A), performing worse than the flow-blind swimmer in³⁸ because of the different actions ($\dot{\theta }$ versus θ) taken by the agents.

Fig. 2: Learning underwater navigation using egocentric observations requires sensing flow gradients.

We trained RL policies with geocentric and egocentric observations in two flow environments: high-fidelity CFD simulations and a von Kármán vortex street (VS) model. All policies underwent training of equal length (2 × 10⁷ timesteps for CFD and 0.5 × 10⁷ timesteps for VS). Learning curves represent the moving mean of cumulative rewards per episode, calculated over a window of 500 episodes. A Geocentric observations: sensing (Δx, Δy, θ) only, the flow-blind agent failed to learn in six instances of learning. Adding flow sensing abilities (u, v), the agent learned to navigate in CFD wake in all 17 instances of learning. Training in VS wake with the same observations succeeded in all four instances, with faster convergence. B Egocentric observations: sensing (Δx_b, Δy_b, u_b, v_b) only, the agent failed in CFD wake in all 10 instances of learning. Adding local flow gradients (n ⋅ ∇ u_b, n ⋅ ∇ v_b) resulted in successful learning in all 16 instances of learning in the CFD wake and 4 instances of learning in the VS wake. Success rate of (C) geocentric and (D) egocentric agents for each of the trained policies are evaluated over a distribution of 1000 randomly generated test conditions (Supplementary Fig. 4). The larger variance of success rates in CFD compared to VS wakes reflects that CFD flows are more challenging to navigate. Additional training with entire domain for initialization and training in CFD wake at Re = 1000 is provided in Supplementary Fig. 3.

We next trained the swimmer using the same set of observations taken in body frame o = (Δx_b, Δy_b, u_b, v_b). This flow-limited swimmer failed to learn (Fig. 2B). When, in addition, we provided the swimmer with the ability to sense the transverse flow gradient (n ⋅ ∇ u_b, n ⋅ ∇ v_b), that is, when considering an augmented set of six egocentric observations o = (Δx_b, Δy_b, u_b, v_b, n ⋅ ∇ u_b, n ⋅ ∇ v_b), the policy converged in each of the 16 training sessions, reaching equally high reward as the geocentric policy (Fig. 2B). Egocentric learning is also possible when augmenting the local observations to sense the longitudinal flow gradients t ⋅ ∇ u_b and t ⋅ ∇ v_b in the direction of motion of the agent (Supplementary Table 1). Sensing flow gradients is thus essential for autonomous underwater navigation in unsteady environments.

To further substantiate our conclusion that sensing flow gradients at the swimmer’s scale is necessary for egocentric point-to-point navigation in coherent flows, we repeated our reinforcement learning methodology using a different model of the fluid environment. Namely, we emulated the CFD wake using a well-known inviscid vortex street (VS) model consisting of two infinite rows of equal-strength, opposite-sign point vortices^79,81,86 (Methods, Supplementary Fig. 1). Training in this reduced order representation of the flow field, we arrived at the same result: egocentric learning is not possible without the additional observations of either longitudinal or transverse flow gradients.

Training sessions in the VS environment converged faster than in the CFD environment (Fig. 2A, B), with similar convergence trends across multiple training sessions: the geocentric policy learned faster while the egocentric policy was capable of reaching equally high rewards but with slightly larger training variance and longer convergence time.

The trained agent, whether using geocentric or egocentric observations and whether trained in CFD or VS wake, followed the three stereotypical stages of navigation across an unsteady wake in strong currents: entering the wake, slaloming between vortices to swim upstream, and exiting the wake upstream of the target (Fig. 3, Supplementary Movie 1,³⁸). In Fig. 3, we also plotted the corresponding trajectories in the flow observation sub-spaces (u, v) for the geocentric agent and (u_b, v_b) and (n ⋅ ∇ u_b, n ⋅ ∇ v_b) for the egocentric agent. To distinguish the flow sensing cues in each of the three stages of navigation, we highlighted the wake entry, zigzag within, and exit stages.

Fig. 3: Trajectories of trained agents in physical and flow observation spaces.

Trajectories are shown in black (geocentric) and blue (egocentric) for the same initial conditions and target location. A Geocentric and (B) egocentric agents, trained in CFD wake at Re = 400, learn to enter, slalom inside, and exit the wake. Agents trained in the reduced VS flow representation succeed when tested in (C, D) VS wake and (E, F) CFD wake (Supplementary Movies 1 and 2). Corresponding trajectories in the spaces of flow observations are shown in the right panels of (A, C, E) and (B, D, F) for the geocentric and egocentric agents, respectively. The three stages of navigation are marked using dark red for wake entry, dark blue for wake exit, black (geocentric), and light blue (egocentric) for slaloming inside the wake.

Upstream motions require the agent’s velocity in the upstream direction $\dot{{{\bf{x}}}}\cdot {{{\bf{e}}}}_{x}={{{\bf{e}}}}_{x}\cdot ({{\bf{u}}}+V{{\bf{t}}})$ to be positive. This streamwise velocity can only be positive when the agent is within the wake. For the geocentric agent with direct access to u = e_x ⋅ u, it suffices that u + V ≥ 0 be non-negative for the agent to unambiguously determine that it is inside the wake. Indeed, as the geocentric agent slalomed between vortices in the physical space, its motion followed periodic oscillations in the observation space for which u + V ≥ 0, reflecting that the geocentric agent learned the sensory cues u + V ≥ 0 to stay inside the wake and move upstream (Fig. 3A, C).

The egocentric agent also learned to enter the wake and change direction to stay in the wake to satisfy $\dot{{{\bf{x}}}}\cdot {{\bf{t}}}={u}_{b}+V\ge 0$ (Fig. 3B, D), but this condition alone does not guarantee upstream motion nor that the agent is located within the wake. For example, the agent’s initial location outside the wake and pointing downstream also satisfies this condition. Therefore, the agent needs additional observations of flow gradients to determine when it is inside the wake. To further support this claim, we repeated the egocentric training with the agent tasked to swim in the upstream direction, with no specific target position, starting from initial locations inside the wake. The agent failed to learn by observing only fluid velocities (u_b, v_b) without additional observations of flow gradients such as (n ⋅ ∇ u_b, n ⋅ ∇ v_b) or (t ⋅ ∇ u_b, t ⋅ ∇ v_b) or both.

Next, in Fig. 4, we considered the same 1000 test cases that we employed in Fig. 2, counted the cases that reached each target, and interpolated the success rate over a regular grid spanning the target training domain. The policies trained and tested in the same wake, whether in CFD or VS, achieved nearly 100% success, consistent with Fig. 2C, D. In Fig. 4, we plotted, for all 1000 test cases, the probability density function (p.d.f.) of encountering a set of flow observations as colormaps on observation subspace (u, v) for the geocentric agent and subspaces (u_b, v_b) and (n ⋅ ∇ u_b, n ⋅ ∇ v_b) for the egocentric agent. The biggest difference appeared in the egocentric observations of velocity gradient—the CFD wake offered much richer signals of transverse flow gradients, while the gradients in the VS wake were more concentrated. These flow gradients are essential for an egocentric navigator to differentiate its location within or outside the wake.

Fig. 4: Flow observations and transfer from low- to high-fidelity flow representations.

Geocentric and egocentric agents trained and tested in (A, B) CFD wake at Re = 400, (C, D) VS wake, and (E, F) trained in VS and tested in CFD wake. Green colormap shows the success in reaching a target based on the 1000 random test cases (Supplementary Fig. 4); sample trajectories from Fig. 3 are superimposed; red (flow velocity) and gray (velocity gradient) colormaps show the probability density function (p.d.f.) of flow observations for all 1000 test cases. P.d.f. plots of observations of relative target locations are provided in Supplementary Fig. 6.

To further highlight the complexity of the navigation task that the RL policies are trained to learn, we compared the RL policies to two naive policies: an optimal control policy arrived at by assuming a uniform flow everywhere (Supplementary Fig. 2C) and a flow-blind strategy where the agent turns towards the target with no knowledge at all of the flow (Supplementary Fig. 2D). These naive policies fail everywhere in reaching the target across the unsteady flow. They experience limited success in reaching the target from upstream locations, where the background flow facilitates the agent’s motion toward a downstream target.

Lastly, we compared the geocentric and egocentric RL policies, and total time they take to reach the target, to those obtained using optimal control theory (Fig. 1A). The RL agents, following only instantaneous and local observations, take similar amount of time to reach the target, tracing nearly identical trajectories to the time-optimal trajectory obtained with knowledge of the spatiotemporal evolution of the entire flow field (Methods, Supplementary Fig. 4). In addition to limited sensory requirements, a major advantage of the RL agents over the classic optimal control is their robustness to initial and target locations; the optimal trajectory fails at the slightest perturbations to agent or target, requiring to restart the optimization process. The RL agents succeed everywhere in the training domain and are generalizable beyond the training conditions as discussed next.

Transfer of RL policies to unfamiliar flow environments

We tested the geocentric and egocentric policies under superimposed rotations to the entire flow field, thus introducing a misalignment between the wake direction and the inertial frame. Specifically, we gradually rotated the CFD wake relative to the inertial frame (e_x, e_y), and at each degree of misalignment between the wake and the inertial frame, we tested the performance of the trained agent considering initial conditions and target locations in the same domains relative to the wake as those explored during training (Fig. 5A, B, Supplementary Movie 1). The performance of the geocentric policy degraded rapidly with increasing misalignment between the wake and the reference frame, while the egocentric policy, by construction, maintained its high performance at any degree of misalignment. These results demonstrate that the egocentric policy is rotationally symmetric—that is, invariant to the absolute orientation of the wake—while the geocentric policy requires a priori knowledge of the alignment between the wake and the inertial frame. Invariance to rotations and successfully reaching the target irrespective of the direction of the unsteady currents is a major advantage of egocentric learning; in geocentric learning, an incorrect estimate or a change in flow direction would require a re-training of the policy.

Fig. 5: Transfer to unfamiliar flows and Reynolds numbers.

A Agents trained at Re = 400 and tested in the same wake under -30^∘ misalignment between the wake and inertial frame: geocentric agent fails where the egocentric agent succeeds (Supplementary Movies 1). B With increasing misalignment, the success rate of the geocentric agent quickly drops to nearly zero; whereas the performance of the egocentric agent is invariant to such rotations. Geocentric and egocentric agents trained at Re = 400 succeed when tested at (C) Re = 200 and (D) Re = 1000 (Supplementary Movies 2). E Success rates of geocentric and egocentric agents trained in CFD wake at Re = 400 and tested across a range of Reynolds numbers are summarized using box plots, where the median, lower, and upper quartiles are indicated with horizontal bars, and outliers are marked by “×”. All 17 geocentric and 16 egocentric policies are included, each tested over 1000 test cases. P.d.f. plots of visual and flow observations collected at Re = 200, 400, and 1000 are provided in Supplementary Fig. 7. Agents trained at Re = 1000 succeed when tested at (F) Re = 1000 and (G) Re  = 600. H Success rates of geocentric and egocentric agents trained in CFD wake at Re = 1000 and tested across a range of Reynolds numbers are summarized using the same box plot convention as in (C). All 5 geocentric and 5 egocentric policies are included, each tested over 1000 test cases. In (E, H) to evaluate the difference in performance between the egocentric and geocentric policies, a two-sample t-test is used^119,120. The null hypothesis states that there is no significant difference in success rates. A smaller p-value indicates stronger evidence against the null hypothesis, suggesting a more significant difference in performance. * p < 0.05, ** p < 0.01, *** p < 0.001.

We next probed the limitations of transfer learning across distinct flow fields. We performed these tests with the reference frame properly aligned with the wake. In Fig. 3C, we tested the RL policies trained in VS wake when placed in the CFD wake. Remarkably, both geocentric and egocentric policies succeeded in entering the wake, zigzagging between vortices to swim upstream, and even exiting the wake at an appropriate time and location. With the egocentric policy, after the swimmer missed the target by a small distance on its first attempt, it swam back into the wake, and continued to navigate upstream (Supplementary Movie 2). This remarkable adaptive behavior shows that egocentric policies are resilient and robust to perturbations and has two important implications for applying transfer learning techniques in underwater environments⁶⁷. First, it shows that the agent continues to perform reliably in unseen environments and avoids actions that put it at risk^87,88. Importantly, it allows the agent to continue to collect and update its observations, which is a key factor in the success of transfer learning⁸⁹. These findings will open new opportunities for bridging the gap between simulations and real environments^44,67 using lifelong learning algorithms⁹⁰.

To investigate the broader applicability of these results, we tested the VS-trained policy in the CFD wake using all 1000 test cases (Fig. 4C). The geocentric policy outperformed the egocentric policy because the latter had difficulties reaching targets further away from the wake of the first approach. This difficulty is due to inaccuracy in the exit conditions. But even when the agent missed the target, it re-entered the wake and tried again (Fig. 3C, Supplementary Movie 2). The analysis in observation space (Fig. 4C) emphasizes that aspects of the task, such as entering and zigzagging between vortices, are more robust to transfer from low to high-fidelity flows while exiting the wake is more sensitive to flow gradients. Therefore, a divide-and-conquer approach, say using curriculum learning^91,92, may optimize transfer learning in underwater navigation by breaking up the policy into sub-tasks and focusing on improving the most challenging aspect (here accurate exit conditions) in higher-fidelity flow environments⁹³.

We next tested the policies learned in CFD at Re = 400 in CFD wakes, ranging from Re  = 200 to 1000 not seen during training. In Fig. 5C, D, we show sample trajectories at Re = 200 and 1000. Both geocentric and egocentric policies succeeded, albeit with some struggle at higher Re where the vortex wake became unstable. In Fig. 5E, we report the performance of all policies trained in CFD (Re = 400) as Re number varied. Namely, we tested each of the 17 geocentric and 16 egocentric policies on the 1000 random cases at each of the six values of Re, a total of 198,000 tests. We found that at lower Reynolds numbers (Re = 200, 300), egocentric policies generalized better in a statistically-significant manner. At higher Reynolds numbers, the performance of both geocentric and geocentric policies declined, and the difference in success rate between the two became less significant statistically. The inability of both egocentric and geocentric policies to keep up with flows at higher Re is caused by the changing nature of the wake: at lower Re, the downstream wake is stable, but at higher Re, the wake loses stability⁹⁴, as evident by the cross-stream motion of the vortices in Fig. 5D, introducing novel physical challenges to deal with. Notwithstanding the changing flow physics, the gradual degradation of performance with Re (Fig. 5E) suggests ample opportunity for updating the learned policy as Re increases using lifelong learning⁹⁰.

The likelihood of flow observations based on all tests at Re = 200, Re = 400, and Re = 1000 exhibited similar features, with periodic oscillations in the space of flow observations reflecting the zigzagging motion of the agent inside the wake (Fig. 4). However, the magnitude of flow signals differed with Re number. Transfer from Re = 400 to Re = 200, although the flow character remains unchanged, means transfer to weaker flows and requires interpolation of flow observations acquired during training. Transfer to higher Re means stronger flows, with distinct character, and requires extrapolation of flow observations, which is notoriously difficult for learning-based models⁹⁵. Consideration of the physics of the flow environment is thus of paramount importance in assessing the limitations of transfer learning to unfamiliar flows.

To further assess the effects of the flow field in which the agents are trained on transfer to novel flows, we next trained both geocentric and egocentric policies at Re = 1000. For each set of observations, we repeated the training five times. Both policies successfully converged in all instances of training, demonstrating that RL training is possible in diverse flow regimes (Fig. 5F and Supplementary Fig. 3). Interestingly, trajectories of the policies trained and tested at Re = 1000 are similar to the trajectory of the egocentric policy trained at Re = 400 and tested at Re = 1000, indicating that, when successful, the trajectory of the transferred egocentric policy was time-optimal in the new environment (Fig. 5). For each of the 10 training instances at Re = 1000, we systematically tested the resulting policy on the 1000 random cases at each of the six values of Re, a total of 60,000 tests (Fig. 5H). At Re = 1000, geocentric and egocentric policies succeeded almost surely. As Re decreased, success rates declined gently at first, and more steeply below Re = 600. At Re = 600, egocentric policies outperformed geocentric policies; see Fig. 5G for sample trajectories at Re = 600 illustrating failure of the geocentric policy in reaching the target, where the egocentric policy succeeds under the same conditions. At even lower Re, both policies failed (Fig. 5H). Taken together, the results in Fig. 5E, H show that both egocentric and geocentric policies successfully transfer to new flows at Re values close to those used during training, but struggle to adapt when the change in Re induces substantial changes in the nature of the wake. In particular, transfer from higher to lower Re favors egocentric policies, and success of transfer to novel flows is asymmetric: it depends on the nature of the training flow.

Transfer of RL policies to conditions unseen during training

We probed the performance of both egocentric and geocentric navigators when subjected to novel conditions unexplored during training. In Fig. 6A, B, we tested the behavior of both policies starting at locations upstream of the target. The agent with geocentric observations failed immediately and headed outside the wake. The egocentric agent performed better; it initially turned toward the target, and when it missed, it went back into the wake, zigzagged through the vortices, and exited the wake to locate the target. This remarkable robustness to new conditions is a hallmark of egocentric policies; it emphasizes that the policy itself acts as a resilient feedback controller with built-in redundancy that ensures functionality even in the event of failure. When placed downstream of the target (Fig. 3C), both egocentric and geocentric policies performed well at moderate downstream locations, but further downstream, the egocentric policy failed first. The failure occurred despite the agent’s attempt to enter the wake and engage with the vortices (Supplementary Movie 3).

Fig. 6: Transfer to locations outside the training domain and interpretation of RL policies.

A Geocentric and (B) egocentric agents starting from initial conditions unseen during training: geocentric agents fail upstream of the target location but outperform egocentric agents downstream of the target (Supplementary Movie 3). Success rates and consumed time of (C, E) geocentric and (D, F) egocentric agents reaching a fixed target (*) starting anywhere in the wake (Green colormap) with 100% success of both policies within the training domain (black circle), 58% and 66% in favor of egocentric policy outside the training domain, and overall 60% and 68% success across the entire domain. Both policies fail downstream: solid lines marking failure of the geocentric policy align with the direction of the “time-optimal” strategy (Supplementary Fig. 2A) and those of the egocentric policy align with the direction of the “drift-optimal” strategy (Supplementary Fig. 2B). The field of “preferred orientations” defined by the stable fixed points of the average policy for (G) geocentric and (H) egocentric agents explains the behavior of the trained agent inside and outside the training domain. Preferred orientations that align with time-optimal and drift-optimal strategies are highlighted in green and orange, respectively.

We systematically challenged the swimmer to reach a fixed target located at the center of the training domain starting from any initial position in the flow field, including at locations unexplored during training (Fig. 6). To standardize these tests, we initialized the agent’s position on a regular grid over the entire fluid domain and, at each grid point, we initialized the agent orientation using 36 distinct initial orientations evenly distributed from 0 to 360^∘. We fixed the initial phase t_o of the flow. In total, we performed 34,020 test cases per policy. As expected, both geocentric and egocentric policies almost surely succeeded when starting within the training domain (Fig. 6C, D). The egocentric policy generalized better upstream of the training domain (90% success of egocentric policy versus 55% success of geocentric policy). The geocentric policy performed better at downstream locations (63% success of geocentric policy versus 47% success of egocentric policy), but both policies reached a limit beyond which they failed (straight gray lines in Fig. 6C, D). Failure downstream of the training domain occurred before physical limitations due to viscous decay of the vortex structures were reached, reflecting the limitations of the policies themselves. We return to this point later.

In addition to the success rate, we systematically evaluated the average time that successful trajectories spent to reach the target (Fig. 6E, F). On average, the geocentric navigator spent slightly less time than the egocentric navigator; namely, the geocentric agent was on average 8% faster than the egocentric agent when starting inside the training domain, but the difference was negligible, less than 1.5%, outside the training domain; the average total time to reach the target being nearly 23 (geocentric) and 25 (egocentric) in units of D/U inside the training domain versus 35 (geocentric) and 35.4 (egocentric) outside the training domain.

Interpretation of underwater RL policies

Intuitively, when placed directly upstream of the target, we expect even a naive navigator that orients toward the target, ignoring entirely the flow field, to reach the target simply by drifting downstream (Supplementary Fig. 2D, Methods). A slightly savvier navigator, aware of only the background uniform flow U could exploit this flow to reach the target from a broader range of upstream locations (Supplementary Fig. 2C, Methods). But the geocentric policy has no such “intuition” of the flow. Its failure at upstream locations is due to policy limitations. When collecting observations in an inertial frame, upstream situations are novel to the policy. The egocentric agent performs better because the self-centric view of the flow and target provides a richer set of observations.

Far downstream, we expect flow physics to impose limits on what is achievable by even the savviest agent. Vortices decay downstream. This viscous diffusion is best illustrated in flow physics using the Oseen solution where an initially concentrated vortex decays spatially due to viscosity (Supplementary Fig. 5). Far downstream, the wake’s streamwise velocity u approaches the freestream velocity U and the flow exhibits weaker gradients, prohibiting the swimmer from exploiting the wake to move upstream. We thus expect the performance of both policies to deteriorate as the vortex intensity decreases (Supplementary Fig. 5), with a faster drop in the performance of the egocentric policy because it relies on flow gradients to navigate and is thus more disadvantaged in flows with weaker gradients.

To elucidate the reasons for the disparity in performance between geocentric and egocentric policies, we analyzed these policies using tools from dynamical systems theory^35,96,97,98. From the dynamical systems perspective, the average policy defines a deterministic function $\dot{\theta }=\pi (o)$, and this averaged rotational dynamics forms a “dynamical flow field” over the phase space of action and observations. This is a high-dimensional space that prohibits direct visualization of the policy and complicates the analysis of its stability and convergence to the target position^35,98. Luckily, at a given location (x, y) and phase t, the observations depend on the agent’s heading direction, and the average policy can be viewed as a dynamical system $\dot{\theta }=\pi (o(\theta ))$ over the phase space $(\theta,\dot{\theta })$. We thus defined the field of preferred direction θ_p as follows: of all potential orientations θ at a given location (x, y) and phase t, the preferred direction is a stable equilibrium of the dynamical system $\dot{\theta }=\pi (o(\theta ))$ for which the average policy $\dot{\theta }=\pi (o(\theta ))=0$ vanishes and its derivative with respect to θ is negative $\partial \dot{\theta }/\partial \theta \, < \, 0$ (Fig. 6G, inset).

In Fig. 6G, H, we plotted the preferred directions over the entire domain for the geocentric and egocentric policies. Locations with multiple arrows imply multiple preferred directions. The generalizability of the egocentric policy upstream of the target (Fig. 6D) correlates with its tendency to have multiple preferred directions at these locations, increasing the chance of taking a correct action. In contrast, at these locations, the geocentric policy instructs the agent to confidently take action towards a single preferred direction that does not lead to the target (Fig. 6C, E), exhibiting a worst-case scenario in decision-making. This explains why the geocentric policy behaves much worse than the naive policy at upstream locations.

Downstream and outside the wake, the geocentric policy tries to minimize either the downstream drift (Fig. 6G, orange arrows), the time to reach the wake (Fig. 6G, green arrows), or a trade-off between both. The egocentric policy mostly instructs the agent to move into the wake while minimizing downstream drift (Fig. 6H). Downstream and inside the wake, however, preferred directions of the geocentric policy clearly favor upstream motion (Fig. 6G), while the egocentric policy exhibits multiple preferred directions that confuse the agent and lead to failure (Fig. 6H). This explains why the performance of the egocentric policy deteriorates faster than that of the geocentric policy at downstream locations. The ability of the geocentric policy to unambiguously favor upstream directions inside the wake can be attributed to the fact that it has knowledge of the agent’s orientation relative to the orientation of the wake (through the a priori knowledge of the wake alignment with the inertial frame (e_x, e_y) and the agent’s observation θ), whereas the egocentric policy doesn’t. In a direct comparison of the trajectories in Fig. 6A, B to the vector field of preferred directions in Fig. 6G, H, it is clear even when the egocentric agent is initially placed at a location with an unambiguous preferred direction and tries to enter and engage with the wake, failure occurs as the agent moves into locations with multiple preferred directions.

This analysis has several important implications. It shows that ambiguity in the preferred direction is favorable when flow physics acts in concert with the desired task (upstream locations), but ambiguity is detrimental when flow physics challenges the desired task (downstream locations). It also shows that the application of tools rooted in dynamical systems theory unveils promising paths for evaluating and interpreting the behavior of machine-learned policies.

Expanding the training conditions: when more is less

Could the agent perform better when trained over the entire flow domain? To address this question, we trained both geocentric and egocentric navigators by sampling initial conditions over the entire flow domain while keeping the target location within the same circular domain as before and systematically analyzed the converged policies using the tools presented in Fig. 6 (Supplementary Figs. 3 and 8). Surprisingly, compared to the policies trained by sampling over the limited set of initial conditions, both geocentric and egocentric agents performed worse when trained over the entire domain. Although trained by sampling over the entire domain, the policies hardly learned to navigate across the vortical wake and were successful only over a limited set of initial locations upstream of the target, with the egocentric policy exhibiting marginally better success rates, and both policies requiring, on average, the same overall time to reach the target. These results underscore that more is not always better. They point to an important fact that hinders learning when expanding the training domain: because when starting upstream from the target, it is relatively easy to reach the target even for a naive agent, the agent quickly learns this policy and gets trapped in a local optimum, which prevents it from continuing to improve itself when exposed to more challenging initial conditions. This pitfall affects both geocentric and egocentric navigators equally. The training domain employed in Fig. 1 represents one of the most difficult, yet physically achievable, scenarios for crossing an unsteady wake.

Lastly, we returned to the egocentric policy trained over the smaller domains of initial and target locations introduced in Fig. 1. We asked how would the RL policy be affected when limiting the observations of the target location to only the angular position of the target relative to the agent, without giving the agent any information about its actual distance to the target. Visually, it is easier to perceive the angular location of an object than its distance, because smaller objects that are close are indistinguishable from larger objects that are far^99,100,101. Thus, instead of (Δx_b, Δy_b), we trained an egocentric RL policy using a single angular observation $\arctan (\Delta {y}_{b}/\Delta {x}_{b})$. We tested the performance of the so-trained policy both inside and outside the training domain (Supplementary Fig. 9). Compared to the egocentric policy with full knowledge of the target position, the policy with only partial knowledge of the target heading performed worse when tested inside the training domain, but, surprisingly, it generalized better when tested starting at novel locations not observed during training. Outside the training domain, the success rate of the egocentric policy with full knowledge of the target position was 56.54%, while that of the egocentric policy with only knowledge of the angular position of the target succeeded at 79.30% rate. These results emphasize that failure farther downstream from the training domain is a persistent feature of the RL egocentric policy, independent of the wake representation, CFD simulations (Fig. 6D) or vortex street (Supplementary Fig. 9A), reflecting an inherent difficulty in the task itself. But, more importantly, these results demonstrate that the ability of the agent to transfer its experience during training to novel challenging situations depends on the nature of the observations: a choice that ensures a wider variety of observations are encountered during training generalizes better to unseen situations. These surprising results underscore the importance of the choice of the training domain and observations in designing generalizable and robust underwater navigation policies.

Discussion

We investigated a fundamental problem of underwater navigation within a flow regime of direct relevance to medium-scale robotic underwater vehicles⁵⁵. At these scales, underwater navigation often involves interactions with unsteady wakes of persistent and coherent vortex structures at intermediate Reynolds number, presenting unique challenges distinct from those faced by millimeter-scale organisms navigating turbulent flows^39,60,102. Learning to enter, slalom within, or exit such coherent flows is thus essential for any underwater robotic mission involved in ocean exploration and surveillance^8,38,44,103. We analyzed, using a combination of physics-based simulations and reinforcement learning methods, the feasibility of robot-centric learning in such flow environments. Unlike existing learning studies that require inertial observations^8,38, say with the help of a satellite, or continuous measurements of a global direction of gravity⁶⁰ or wind³⁹, in robot-centric learning, observations are collected in the robot’s own world, through on-board sensors, without a priori or acquired knowledge of a global flow direction or inertial frame of reference.

Our study demonstrated that (1) learning underwater navigation from a robot-centric perspective is feasible provided that the robotic agent senses local flow velocities and local flow gradients; (2) robot-centric policies respect physical symmetries and are invariant to flow rotations; (3) robot-centric policies exhibit adaptive behavior in unknown environments, allowing the robot to re-enter the wake and try again when missing the target, and (4) robot-centric policies facilitate transfer learning from reduced to high-fidelity flow environments and between different Reynolds number flows.

Our analysis of the sensory requirements for autonomous underwater navigation (Table 1) indicates that egocentric sensing in the agent’s own world eliminates potential time delays and computations inherent to assessing inertial signals^8,83 at the expense of requiring more sensors to observe spatial variations in the flow field at the scale of the navigator. We envision that, to learn more complex and diverse navigation tasks in future underwater^8,44 and aerial^33,104 robotic applications, flow gradients measured at multiple locations and directions^53,105, using a distributed array of flow sensors⁵⁷ along the swimmer, and supplemented by the ability to remember and update a history of flow observations^39,57,58,102 might be necessary. These directions will be investigated in future work.

In addition to its implications for robotic systems, our study opens avenues for understanding the link between flow sensing and behavior in biological systems^39,106. To connect with biological solutions, it is crucial to recognize that flow and spatial representations are inherently shaped by the ecological system and the organism’s morphology and brain structure¹⁰⁷. For example, in plankton—millimeter scale organisms that drift in water currents—many can swim, detect flow velocity gradients, and sense light or gravity to move upward to nutrient-rich surface waters at night and downward to avoid visual predators during the day^108,109,110. The environmental cues and navigation mechanisms that enable planktonic vertical migration in turbulent waters⁶⁰ are inherently distinct from those employed by a fish-inspired robotic agent navigating a coherent flow field created by a conspecific or predator^38,44,77,111. Aquatic organisms that interact with coherent vortex structures have bilateral arrays of flow sensors suited for computing flow gradients^49,53, e.g., fish lateral line system^65,112,113 and harbor seal whiskers⁹. The methods we propose here offer an exciting opportunity for future studies that unravel how flow-sensing abilities in aquatic organisms have been shaped, not only by the size and morphology of the organism, but also by the flow environment it navigates.

Taken together, our work establishes promising directions for learning, from a robot-centric perspective, in dynamically changing physical environments, provides systematic analyses particularly suited for bridging the gap between simulations and real-world environments, and opens avenues for future investigation of the mapping between environmental conditions and sensory requirements in biological and robotic systems.

Methods

Flow field models

We considered a cylinder of diameter D fixed in a background flow of uniform velocity U, traveling from right to left. The cylinder diameter D and the freestream speed U are used as characteristic length and speed, respectively. The spatial-temporal evolution of the flow field is governed by the incompressible Navier-Stokes equations, given in dimensionless form as

$$\frac{\partial {{\boldsymbol{u}}}}{\partial t}+{{\boldsymbol{u}}}\cdot \nabla {{\boldsymbol{u}}}=-\nabla p+\frac{1}{{{\rm{Re}}}}\Delta {{\boldsymbol{u}}},\qquad \nabla \cdot {{\boldsymbol{u}}}=0,$$

(1)

where u(x, y, t) = (u(x, y, t), v(x, y, t)) denotes the flow velocity field as a function of space and time, and p(x, y, t) is the pressure field. Here, Re = DU/ν is the Reynolds number, where ν denotes the kinematics viscosity of the fluid. We impose a uniform-velocity inlet on the right boundary and no-slip boundary conditions on the surface of the cylinder. The flow field is solved with IBAMR, an open-source implementation of the immersed boundary method^{73,74,114,115}. We chose a [−24, 8] × [−8, 8] rectangular computational domain, with the cylinder centered at the origin (0, 0). The coarsest Eulerian is a uniform 128 × 64 Cartesian grid, with three layers of adaptive Eulerian mesh refining it; the refinement ratio between two layers is 4; the refinement region is based on both the solid boundary and vorticity. The simulation time step is Δt = 2 × 10⁻⁴. In Supplemantary Fig. S1A is a depiction of the wake at Re = 400, where the resultant Strouhal number St = fD/U = 0.22 is consistent with past experimental measurements¹¹⁶. We additionally simulated a series of cylinder flows at Reynolds numbers ranging from 200 to 1000.

To simplify the simulation environment, we used a reduced-order inviscid model of the von Kármán vortex street, consisting of two infinite rows of equal-strength Γ, but opposite-sign, point vortices, at lateral offset 2A and wavelength λ⁸⁶. The flow field u(x, y, t) ≡ (u, v) can be analytically described by in complex notation z = x + iy and w = u − iv,

$$w(z,t)=\frac{i\Gamma }{2\lambda }\left[\cot \frac{\pi (z+iA-{U}_{s}t)}{\lambda }-\cot \frac{\pi (z-\lambda /2-iA-{U}_{s}t)}{\lambda }\right]-U,$$

(2)

Here, U_s is the moving velocity of the vortex street as the superposition of its self-induced constant velocity (to the right) and the freestream flow velocity U (to the left),

$${U}_{s}=\frac{\Gamma }{2\lambda }\tanh \frac{2\pi A}{\lambda }-U$$

(3)

In Supplemantary Fig. S.1B, we chose λ = 4D, A = 0.2D, Γ = 3UD to emulate the high-fidelity wake at Re = 400. We regularized the flow near the point vortex singularities to avoid unreasonably large velocities at the vortex location.

Optimization problem

Zermelo problem considers a swimmer moving at constant velocity V crossing a river of uniform speed U of width H¹². Here, we considered V < U and let ${{\bf{t}}}=(\cos \theta,\sin \theta )$ be the swimmer’s heading direction, with θ the angle between the heading of the swimmer and the flow direction. Given this setup, the course velocity of the swimmer is $(-U+V\cos \theta,V\sin \theta )$. Thus, the time required for crossing the river is $H/(V\sin \theta )$, and the streamwise drift distance is $H(U-V\cos \theta )/(V\sin \theta )$. The orientation θ can be optimized to minimize either the time or the streamwise drift (Supplementary Fig. 2A, B),

$$\,{\mbox{Time}}\; {\mbox{optimal:}}\,\quad {\theta }_{{{\rm{opt}}}}=\frac{\pi }{2},\qquad \,{\mbox{Drift}}\; {\mbox{optimal:}}\,\quad {\theta }_{{{\rm{opt}}}}={\cos }^{-1}\frac{V}{U}.$$

(4)

Consider now point-to-point navigation in the same uniform flow u ≡ (−U, 0) such that the swimmer with velocity V and heading ${{\bf{t}}}=(\cos \theta,\sin \theta )$ needs to navigate to a target located at Δx = (Δx, Δy) relative its own position. An optimal strategy for minimizing the total time to reach the target consists of choosing a constant heading direction,

$${\theta }_{{{\rm{opt}}}}=-\arcsin \frac{U\Delta y}{V\sqrt{\Delta {x}^{2}+\Delta {y}^{2}}}+\arctan \frac{\Delta y}{\Delta x}.$$

(5)

This equation has no solution when $\left\vert \frac{U\Delta y}{V\sqrt{\Delta {x}^{2}+\Delta {y}^{2}}}\right\vert > 1$.

For navigating across an unsteady wake with associated velocity field u(x, y, t), we formulated a constraint optimization problem, given full knowledge of the vector field u. The optimization problem is to find the optimal rate of change $\Omega=\dot{\theta }$ that minimizes the overall time of travel ${{\mathcal{J}}}$

$$\arg {\min }_{\dot{\theta }(t)}{{\mathcal{J}}}=\arg {\min }_{\dot{\theta }(t)}\int_{0}^{T}dt$$

(6)

subject to the equality constraints

$$\begin{array}{ll}\,{{\rm{Boundary}}} \, {{\rm{conditions}}}: \hfill & {x}{(0)}={x}_{0},\,{y}{(0)}={y}_{0},\,\theta {(0)}={\theta }_{0},\,\left[{x}{(T)}-{x}^{*}\right]^2+\left[{y}{(T)}-{y}^{*}\right]^2\leq(0.15D)^2. \hfill \\ \,{{\rm{Equations}}} \, {{\rm{of}}} \, {{\rm{motion}}}: \hfill & \dot{x}{(t)}={u}{({x},{y},{t})}+{V}\cos \theta,\quad \dot{y}{(t)}={v}{(x,y,t)}+{V}\sin \theta .\hfill\end{array}$$

(7)

We discretized this problem and used collocation methods to numerically solve for optimal rate of change of heading directions ${\dot{\theta }}_{{{\rm{opt}}}}(t)$ that guide the swimmer to the desired destination across the unsteady wake; this is in contrast to ref. ³⁸, where they directly optimized the heading direction θ(t). The optimization problem is solved using the function fmincon in MATLAB.

Model-free deep reinforcement learning

For navigating across an unsteady wake, we trained the artificial agent using Deep RL to maximize a cumulative reward through repeated experiences with the surrounding environment. The reward was composed of two parts: a sparse reward of 200D given as a completion bonus once the swimmer reached within 0.15D from the target, and a dense reward offered at every timestep equal to the change in distance between the swimmer and the target. Swimmers that exited the simulation domain, collided with the cylinder, or exceeded a maximum completion time were treated as unsuccessful. The RL algorithm maximized the return, which is the cumulative discounted reward with discount factor γ = 0.995.

$${R}_{t}={\sum }_{{t}^{{\prime} }=t}^{{t}_{f}}{\gamma }^{{t}^{{\prime} }-t}{r}_{{t}^{{\prime} }}$$

(8)

Here, time is implicitly minimized during training because of the structure of the return R_t, or objective function as the discounted reward at the initial state. Given γ < 1, later rewards are discounted more. The sparse component of the reward—the success bonus—is significantly larger than the dense reward, but it is given to the agent at the last timestep only if the target is reached, thus the overall value of R_t highly depends on the weight before the sparse reward component. Given that the incremental reward is the increase or decrease in relative distance at each time step, and because rewards received at later time steps contribute less to R_t, the RL training implicitly converges to a time-optimal strategy, as opposed to the optimal control approach where time is explicitly minimized (6). In cases when the trained RL policy does not reach the minimal time derived from optimal control, it occurs primarily because of the limitations in available sensory information, which hinders the RL agent’s ability to make perfectly informed decisions at every step (see Supplementary Fig. 4).

At the beginning of each training episode, we chose the target location (x^⋆, y^⋆) randomly inside a circular area of radius 2D on one side of the wake and the swimmer’s initial position (x_o, y_o) randomly inside a circular area of the same size on the other side of the wake. We choose the swimmer’s initial orientation θ_o randomly between 0 and 2π; we set a random initial time t_o for the start of the training relative to the wake evolution, which we denote from hereon as the initial phase.

We used V-RACER, a model-free deep RL algorithm, implemented in Smarties¹¹⁷ to train the agent. The V-RACER algorithm has proven suitable for control problems in complex flow fields^34,118. The policy and value function together are approximated by a 128 × 128 feedforward deep neural network with an additional residual layer that bypasses the second regular layer and additional weight as the standard deviation for action sampling. We set the decision time interval to 0.1 unit time in units of D/V, and we constrained the angular velocity to lie in the interval $\dot{\theta }\in [-4,4]$ in units of V/D.

To consistently evaluate the performance of the RL policies obtained from distinct training and observations, we prepared 1000 test cases by randomly sampling the swimmer’s initial position (x_o, y_o) and orientation θ_o, initial phase t_o, and target position (x^⋆, y^⋆), all taken within the same ranges used during training (Supplementary Fig. 4). We tested each of the 105 policies on these 1000 cases (a total of 105,000 tests). Success rates are summarized in Supplementary Table 1.