Introduction

Viruses protect their genome in a protein shell called a capsid, which must remain stable in the environment to allow a virus to infect a new host and continue its viral life cycle1. One of the most abundant capsids in the virosphere are the ones associated with tailed bacteriophages (or tailed phages). These capsids have adapted to infect bacterial hosts across all environmental conditions2 while storing the double-stranded DNA viral genome at the highest density known among biological entities3. This condensed viral genome generates 30–50 atmospheres of internal pressure pushing out onto the capsid, and this pressure helps initiate the translocation of the DNA to infect the host4,5.Despite this internal pressure, tailed phage capsids have evolved in size to accommodate from 10 kilo base pairs (kb) to some of the largest genomes found in the virosphere, around 750 kb6. A key factor that has allowed tailed phages to achieve this feat is the sophisticated maturation process that stabilizes their capsids.

The assembly of tailed phage capsids starts with scaffolding proteins and major capsid proteins (MCPs) nucleating around a protein portal complex, forming an empty shell called the procapsid. The DNA is then packaged through the portal, causing the scaffolding proteins to be either ejected or degraded and the MCPs to undergo conformational changes, leading to the final mature polyhedral capsid7. This maturation process is possible thanks to the plasticity of the HK97-fold present in the MCPs across tailed phages and other evolutionary-related viruses that store their genome at high densities, like tailed archaeal viruses and herpes-like viruses8,9,10. The HK97-fold is characterized by three structurally conserved domains: the axial domain (A-domain), the peripheral domain (P-domain), and the extended domain (E-loop)7. The HK97-fold MCPs organize in clusters (capsomers) of five proteins (pentamers) at the vertices of the polyhedral capsid and clusters of six proteins (hexamers) connecting the vertexes. In the maturation process, the MCP hexamers experience the most dramatic conformational changes of any element in the capsid, often transitioning from smaller and skewed hexamers in the procapsid to larger, highly symmetrical hexamers in the mature capsid. This transition introduces stabilization mechanisms like covalent and non-covalent cross-linking of the MCPs11,12. It also helps accommodate accessory proteins (also known as cement, reinforcement, and decoration proteins) that can further stabilize the capsid, especially at the local three-fold axes of the icosahedral capsids13. It is likely that these stabilization mechanisms have facilitated the evolution of larger viral genomes and capsids. However, the cross-linking and accessory protein stabilization mechanisms characterized in different model systems are too evolutionarily distant to reveal the underlying molecular mechanisms able to accommodate an incremental increase in the genome size of the capsid.

To explore this gap, we concentrated on phages infecting the Actinobacteria phylum. These so-called actinobacteriophages represent the largest curated collection of viruses, with 4,000 annotated phage genomes (as of April 2023)14. We recently used a cryo-EM multiplex method to obtain medium-resolution maps (about 6 Å) of multiple capsids15. Combining the actinobacteriophages genome nucleotide similarity16 and the folded structure of major capsid proteins, we built a structural dendrogram of the actinobacteriophage major capsid proteins17 to facilitate navigating evolutionarily related capsids. One of the most remarkable findings from the medium-resolution maps was Patience, which was clustered in the Structural Group 11 (or Patience-like). Phage Patience displayed a supersized T = 7 icosahedral capsid containing 415 HK97-fold MCPs and 420 minor proteins organized in trimers15 distributed following the trihexagonal lattice18. The internal diameter (63 nm) is more than 10% larger than classic T = 7 capsids like phage lambda, 56 nm in internal diameter19, and a 48.4 kb genome. The 40% increase in internal volume facilitates the accommodation of Patience’s larger genome (70.5 kb). The increase in genome capacity is consistent with the (4/3)3/2 ≈ 1.5 increase predicted in trihexagonal lattices due to the 4/3 times more surface associated with the trimeric minor protein18. The volume and genome capacity are about 15% smaller than for two recent Thermus phages, P74-26 (83.3 kb) and P23-45 (84.2), also described to form supersized T = 7 capsids reinforced by trimers20,21. However, an intriguing feature of Patience was that its hexamers seem to display a large chasm along their pseudo 2-fold local symmetry line, effectively separating the hexamer into two halves. These split hexamers were also observed when analyzing computationally the quasi-rigid domains of Patience’s capsid22. Split or skewed hexamers are common in procapsids but were not previously observed in mature capsids, which usually contain near-6-fold symmetry hexamers. Additionally, the chasm had an apparent density within it that could not be resolved. This density represented a candidate for a reinforcement mechanism that could change the established paradigm of mature capsids.

In this work, we followed up that preliminary observation to obtain a high-resolution cryo-EM map of Patience to 2.4 Å as well as the map for an evolutionary-related phage, Adjutor, which displays structural protein homology while storing a different genome length. The reconstruction of the high-resolution cryo-EM maps for Patience and Adjutor confirms the existence of split hexamers containing an accessory protein that stabilizes the hexamers and has adapted its length to accommodate the change in genome length without having to increase the size of the capsid. The derivation of a mathematical theorem allows us to predict what other capsid architectures could use an analogous stabilization mechanism that could adapt to increments of genome length.

Results

An accessory protein interacting with skewed mature hexamers

The high-resolution cryo-EM map of Patience to 2.4 Å confirmed the presence of split hexamers (Figs. 1a, Supporting Fig. 1 and Supplementary Table 1 for final resolution and collection parameters) and revealed that the chasm’s density was associated with a different protein from the major capsid protein (Figs. 2, 3). De novo model building of the density identified the protein as gp4. Our annotation was further supported by previous mass spectrometry analysis of the Patience capsid, which had identified gp423 within the mature viral capsid. Gp4 (Supplementary Fig. 2) is a small 102 amino acid long protein of 10.7 kDa that forms a dimer within the hexamer and is only observed in the hexamer (the pentamer did not show any evidence of a density that could be gp4). We note that there was some density we could not model under the local 3-fold axes (Supplementary Fig. 3) that showed a small helix but at too low a resolution to model. Three gp4 dimers organized around the global 3-fold axis form a three-point star complex (trimer of dimers) that does not interact with other three-point stars gp4 complexes, nearby pentamer major capsid proteins, or the nearby minor capsid proteins, which sit on top of the major capsid proteins at the local 3-fold axes (Fig. 1a). Thus, gp4 only interacts with the major capsid proteins of the hexamer. Circular dichroism analysis (Supplementary Fig. 4) of unbound Patience gp4 showed that the secondary structure of the protein is a random coil, while in the capsid, it forms a helix.

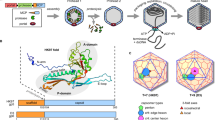
Fig. 1: Capsids of the Patience-like major capsid protein family.
figure 1

The icosahedrally averaged cryo-EM maps of Patience (A) and Adjutor (B) capsids. Both use the related Patience-like family major capsid protein and are supersized T = 7 architectures. Different parts of the capsid have been removed to highlight the important constituents of the capsids. Major capsid protein hexamers are colored blue while the pentamers are colored pink. The minor capsid proteins are colored green and the gp4 accessory protein is colored light red. On the far right, a single gp4 dimer shown in the cryo-EM density has been enlarged and displayed in the inset.

Full size image
Fig. 2: Hexamers of the Patience-like major capsid protein family.
figure 2

The hexamers of both Patience (A) and Adjutor (B) with the gp4 molecules running through the center. The pseudo 2-fold symmetry is highlighted by a dashed line in the Patience hexamer with the pseudo 2-fold chasm labeled.

Full size image
Fig. 3: Gp4 interaction with major capsid proteins.
figure 3

The left-hand side shows the underside of a single hexamer capsomer from the Patience and Adjutor bacteriophages. The right-hand side shows a single copy of gp4 and how it interacts with the different major capsid proteins of the hexamer. The major capsid proteins are numbered for comparison with Supplementary Table 3 and Supplementary Table 4, which show the number of interactions and buried surface area.

Full size image

Patience-like phages show a conserved stabilization mechanism

The search of gp4 homologs among actinobacteriophages yielded candidates in the AC, D, H, and R clusters (Supplementary Table 2). The predicted protein structure with Alphafold revealed that the candidate proteins in the D and H clusters adopted a similar structure to Patience gp4 (Supplementary Fig. 5). We decided to focus on Adjutor (D cluster, gp4 homolog to Patience gp4) to carry out cryo-EM to confirm the Alphafold prediction (Fig. 1b) because it had the smallest gp4 homolog. The cryo-EM map showed that Adjutor has a similar capsid morphology to Patience. We note that the curve corresponding to the tight mask exhibits a pronounced sharpness (Supplementary Fig. 1), which may indicate potential inaccuracies in the mask generation process. We also note the FSC curve for Adjutor does not go to high enough resolution so that the correlation can be judged; this is likely due to issues with box size arising from memory limitation on the GPUs used for the reconstruction, meaning that the Nyquist limit reached. minor capsid protein lacks the peanut-like protein domain found in Patience (Supplementary Fig. 6). However, the rest of the minor capsid protein of Adjutor is structurally very similar to Patience’s (Supplementary Fig. 6) and is part of the same protein family (Supplementary Fig. 2). The cryo-EM map was at a high enough resolution (2.7 Å, Supplementary Table 1 for collection parameters) to once again identify the protein density found between the two halves of the major capsid protein hexamer as gp4 of Adjutor. Gp4 of Adjutor is half the size of Patience gp4 at just 54 amino acids and a molecular weight of 6.2 kDa. Once again, it exists as dimers within the hexamer and as trimers of dimers around the global 3-fold axes. (Fig. 1b). As observed in Patience, Adjutor-gp4 only contacts the major capsid protein hexamer capsomer and makes no contact with the pentamer or minor capsid protein. Likewise, no density for Adjutor-gp4 was observed in the pentamer capsomer.

Gp4 bridging of split hexamers allows an increased size of the genome to be packaged

The smaller size of the Adjutor-gp4 proteins suggests that it is a simpler version of the Patience-gp4. A single Adjutor-gp4 protein (Fig. 3) makes hydrogen bonds and salt bridges (Supplementary Table 3, Fig. 3) to four of the chains of the hexamer (A, B, E, and F). Most of the buried surface area in a single Adjutor-gp4 is between chains A and F, i.e., the two major capsid proteins on either side of the pseudo 2-fold chasm. The second Adjutor-gp4 protein (Fig. 3) performs the same function but for the opposite end of the hexamer pseudo 2-fold chasm, whereby it makes the most contacts with chains C and D. The two adjutor-gp4 chains fill all the space of the chasm, with the weaker contacts presumably stabilizing the position of the gp4 molecules.

The Patience-gp4 makes far more contacts than the Adjutor-gp4, and a single Patience-gp4 (Fig. 3) makes interactions (both hydrogen bonds/salt bridges and buried surface area) with every copy of the major capsid protein in the hexamer (Supplementary Table 4). Like with Adjutor-gp4, most interactions are with the A and F chains of the hexamer (with the second Patience-gp4 molecule having the most interactions with chains C and D). In contrast to Adjutor-gp4, Patience-gp4 is far longer and threads its way between the spaces of the major capsid proteins at its N and C termini. At the C-terminal end, this results in a peg-in-hole interaction, with the thirty-five residues between Patience-gp4 60 and 93 forming a loop structure (the hole) around residues 335–345 of chain A major capsid protein, with a small helix turn (339–341) acting as the peg (Supplementary Fig. 7). Several salt bridges and hydrogen bonds stabilize the interaction. At the N-terminal end of Patience-gp4, it continues to thread between Chain E and Chain F of the major capsid proteins, making several stabilizing interactions with those proteins. The major capsid proteins of Adjutor have similar pockets that could accommodate a longer gp4, and Adjutor-gp4 follows the same path as Patience-gp4 but lacks the length to thread between the other major capsid proteins.

Patience and Adjutor display the same internal capsid diameter (63 nm), but Patience packs a larger genome (70.5 kb) than Adjutor (64.5 kb). This constitutes a 10% increase in genome density, which in tailed phages implies an increase of internal pressure24,25. The concomitant increase of the gp4 length and number of interactions in Patience with respect to Adjutor was attributed to this increase in internal pressure. This suggests that gradual changes in gp4 length would help accommodate slight genome length increases in the evolution (or engineering) of tailed phages. This mechanism, however, requires the formation of split hexamers, which had not been observed in mature capsids previously. To show that all split hexamers (and, therefore, analogous stability mechanisms) are potentially relevant to other capsids, we investigated mathematically the different icosahedral capsid architectures that can contain all-split hexamers. This mathematical prediction is shared in the last section of the results. Before presenting those results, it is worth completing the experimental characterization of the structure of Patience and Adjutor.

The E-loop is over-extended in the major capsid proteins that bridge the pseudo 2-fold chasm

The two chains in Patience and Adjutor (A and D) have E-loops (Supplementary Fig. 8) that bridge the pseudo 2-fold chasm (Fig. 3). This is achieved by straightening and elongating the E-loop starting at Val73 (Supplementary Fig. 8). In the other four chains (B, C, E, and F), the E-loop folds into a U-shape before forming the two beta strands starting at Val58. In the A and D chains, the two beta strands are abolished, and the U-shape is straightened out, leading to the elongation of the E-loop. The elongated E-loops are stabilized by an intramolecular salt bridge between Glu78 and Arg370, with the arginine and glutamic acid repositioning to make the interaction. In the other four chains, these amino acids are pointed away from one another, and Glu78 is part of the two beta strands of the E-loop. We used the distance measurement tool in ChimeraX to measure the distance between the C-alpha of Glu93 (the residue at the tip of the E-loop) and Thr70 (a residue within the core of the HK97-fold) and found that the distance within Chain A, with an elongated E-loop, and Chain B, without an elongated E-loop. We observed a difference of 4 angstroms between the two (Chain A: 64.4 angstroms and Chain B: 60.4 angstroms).

The straightening is also supported by the gp4 molecule with five hydrogen bonds between gp4 and the E-loop of chains A and D. In Patience, the E-loop is further constrained by the C-terminus of gp4 that folds over the top of the E-loop at the straightened position. This straightening of the E-loop allows the loop region to make the same contacts in A and D with the adjacent major capsid proteins as B, C, E, and F do, despite the increased distance the E-loop must cover. Thus, the first salt bridge between Glu85 (E-loop) and Arg148 of the spine helix and the final salt bridge between Arg98 (E-loop) and Glu26 of the N-arm are spatially equivalent in all chains, with the N-arm folding over the E-loop and locking it into position above the spine helix of an adjacent chain. The same overall mechanism for E-loop extension is observed for Adjutor. The amino acids making hydrogen bonds are different, and Adjutor shows more hydrogen bond/salt bridge interactions than Patience (37 intermolecular bonds of Adjutor E-loop and 21 in Patience E-loop). Despite the decrease in length of gp4 in Adjutor, the C-terminus still folds over the straightened E-loop at the same position as in Patience to lock in the structure.

The major capsid protein of the Patience-like actinobacteriophages shows variation from the canonical HK97-fold and forms a putative metalloprotein

The major capsid protein of Patience and Adjutor shows major differences to the canonical HK97 phage HK97-fold8. The Patience-like major capsid proteins have a seven-strand beta-sheet in the A-domain with an alpha helix (211–225) that lies across it and an extended G-loop, forming a small beta-hairpin. Following the G-loop is a loop that we have previously described in other actinobacteriophages (and others have described in phage T726). This loop makes no inter or intra-molecular interactions aside from a possible hydrogen bond between Arg188 and Thr20 of two different chains (but only in chains C and F where the N-arm is pointed up). Unlike most previously characterized HK97-folds in tailed phages, the N-arm does not make long-range interactions with other major capsid proteins. Instead, the N-arm forms a helix that runs almost parallel to the P-domain spine helix below it (Supplementary Fig. 9) before turning back on itself. At the turn, it makes a single salt bridge with the G-loop of a neighboring major capsid protein (Asp 40 of the N-arm and Gln171 of the G-loop). This interaction only occurs between major capsid proteins located within each half. The interaction is lost for the chains that bridge the pseudo 2-fold chasm (Chains C and D or E and F). In these chains (C, D, E, F), Gln171 of the G-loop makes no interaction, while Asp40 interacts with Asn100 of the gp4 chain. After the N-arm turns back on itself, it makes several intramolecular contacts with the P domain before crossing over the E-loop of an adjacent major capsid protein. It ends in between the spine helix and the N-arm helix, pointing down between those two helices (Supplementary Fig. 9). In chains C and F, the two N-terminal amino acids sit up compared to the other chains; the N-termini of these chains appear to be displaced by the presence of the gp4 molecules that lie adjacent to the N-arm helix.

His198, His200, Glu223, and His224 in the A domain form a putative metal binding domain. There is clear density in the cryo-EM derived map for a metal ion (Supplementary Fig. 10). We have not modeled a metal ion into that position since it is not practical to definitively identify the metal ion. Bioinformatic analysis using the Metal-Ion Binding27 site online server (Supplementary Table 5) suggested Cobalt and Zinc for Patience and Adjutor, respectively (Supplementary Fig. 10), although Zinc yielded a higher score for Adjutor and the related Candle bacteriophage. Other viral proteins evolutionarily distinct from the HK97-fold, for example, Hepatitis B virus28, are known to use Zinc in its capsid proteins, and this is the most common metal that interacts with viral proteins29. We therefore speculate that Zinc is the most likely metal ion to be present in all the Patience-like bacteriophages. The position of the metal binding domain at the bottom of the helix that crosses the beta-sheet in the A-domain suggests that it would be involved in locking the bottom of the helix into the correct position. This is likely to be especially important in chains A and D where the pseudo 2-fold chasm’s presence implies that there is no neighboring major capsid protein A domain to stabilize the A-domain helix. The metal binding domain is conserved across the Patience-like actinobacteriophages. We picked a representative major capsid protein from each cluster that uses the Patience-like major capsid protein and predicted their structure using Alphafold. All the major capsid proteins were structurally near identical despite relatively low amino acid sequence identity (Supplementary Fig. 11). All have a putative metal binding domain at the same position in the major capsid protein and use at least three histidine residues but show varying amino acids that are also part of the putative metal binding site (Supplementary Fig. 12). For example, Adjutor has an additional histidine and glutamic acid, while Candle (cluster R) has five histidine residues.

Icosahedral capsids that can be built with split or skew hexamers

To determine if a pseudo 2-fold-like chasm mechanism could be relevant in other capsids, we investigated mathematically what icosahedral capsids can contain all-split hexamers. A key property of icosahedral capsids is that they display three types of axes of symmetry: 5-fold, 3-fold, and 2-fold. MCPs sitting on the 5-fold axes form 5-fold symmetric pentamers that generate the topological curvature necessary to close the quasi-spherical capsid18,30,31. However, the 3-fold and 2-fold axes of the capsid do not necessarily pass through the center of a hexamer because the distribution of hexamers, as shown in Fig. 4a, changes depending on the icosahedral T-number, which is defined by Eq. 1.

$$T(h,k)={h}^{2}+{hk}+{k}^{2}.$$
(Eq. 1)
Fig. 4: Required 3-fold hexamers in icosahedral capsids.
figure 4

a Capsids with hexamers not centered on the 3-fold axis (top) and a hexamer centered on the 3-fold axis (bottom). The triangulation number, T(h,k), is displayed for each capsid. Patience and Adjutor are both T = 7 capsids. The semi-transparent triangle indicates the true 3-fold axis in each capsid. b Icosahedral capsid with a hexamer on the 3-fold axis illustrating the hexagonal coordinates (top). The locations of the nearest pentamer (h,k) and central hexamer (hH,kH) are displayed. The dotted lines connect the nearby pentamers (h = 2, k = 2). (Bottom) The same capsid highlighting triangular areas defined by the pentamers, T(h,k) (in blue), and the central hexamer, T(hH,kH) (in orange). c Reconstruction of SIO-2 phage procapsid displaying the full T(2,2) = 12 architecture displaying the path connecting pentamers with black dashed lines (top), and the region around the 3-fold axis displaying the symmetrical hexamer surrounded by split hexamers (bottom). The white polygons highlight the symmetric and split hexamers. The procapsid was rendered from the map EMD-5383 using ChimeraX.

Full size image

Here, h and k are the steps necessary on the hexagonal lattice to join two nearby pentamers, and the icosahedral capsid is formed by 60 T MCPs distributed in 10(T-1) hexamers and 12 pentamers. Hexamers with 6-fold symmetry guarantee the formation of any icosahedral capsid because they are compatible with both 3-fold and 2-fold symmetry axes, which might explain why near 6-fold symmetric hexamers are so common in mature capsids. However, the split hexamers observed in Adjutor and Patience only have 2-fold symmetry, which relates instead to the common skew hexamers of tailed phages’ procapsids, Supplementary Fig. 13. Since the 2-fold hexamer configuration would cause a symmetry mismatch in capsids that use T-numbers where the center of a hexamer sits on a global 3-fold axis, this reduces the problem of finding capsids with all-split (or skew) hexamers to determine mathematically the T-numbers that do not contain a hexamer on the center of a global 3-fold axis.

We initially investigated the range of icosahedral capsids associated with the HK97-fold, that is, from T = 1 to T = 52, computationally. The generated icosahedral capsids showed eight capsids containing a hexamer sitting on a global 3-fold axis: T = 3, 9, 12, 21, 27, 36, 39, and 48 (Supplementary Table 6) as illustrated by T = 9 and T = 12 in Figs. 4a and 4b. The remaining twelve capsids could contain all split/skew hexamers: T = 4, 7, 13, 16, 19, 25, 28, 31, 37, 43, 49, 52, as illustrated by the T = 7 capsid in Fig. 4a. The capsids displaying hexamers on the 3-fold axes shared a mathematical pattern: Their T-numbers were multiple of 3, e.g., T = 21 = 3 × 7 (Supplementary Table 6). Interestingly, the remaining factor in those capsids recovered the sequence of classic T-numbers, that is, T/3 = 1, 3, 4, 7, 9, 12, 13, and 16. These observations from the computational analysis let us formulate the following general theorem: “An icosahedral capsid display a hexamer centered on each global 3-fold axis if and only if the T-number is multiple of three.”

We proved the theorem as follows. In capsids with hexamers centered on a true 3-fold axis, one can define hH and kH as the hexagonal lattice steps joining a pentamer with the hexamer sitting on a global 3-fold axis, as illustrated for T = 12 in Fig. 4b. By symmetry, the triangle formed by three pentamers is three times larger than the triangle formed by one pentamer and the two vertices placed on nearby 3-fold axes. The normalized area of the small triangle formed by the central hexamer follows the same expression as the classical T-number sequence given by Eq. (1), except that the steps used are hH and kH instead of h and k. The final triangulation number is three times this small triangle, leading to the T-number, TH, for capsids with hexamers centered on global 3-fold axes:

$${T}_{H}\left({h}_{H},{k}_{H}\right)=3\left({h}_{H}^{2}+{h}_{H}{k}_{H}+{k}_{H}^{2}\right)=3T\left({h}_{H},{k}_{H}\right)$$
(Eq. 2)

The associated steps h and k can be expressed as a function of hH and kH by h = 2hH + kH and k = kH − hH (Fig. 4b). Introducing these expressions in Eq. (1) offers an alternative way to derive TH:

$$T({h=2h}_{H}+{k}_{H},\,k={k}_{H}-{h}_{H})=\,{T}_{H}\left({h}_{H},{k}_{H}\right)=3T\left({h}_{H},{k}_{H}\right).$$
(Eq. 3)

Equations (2) and (3) imply that any T-number multiple of three is associated with a capsid with centered hexamers on the global 3-fold axes. This is equivalent to say that any T-number multiplied by three leads to another T-number with hexamers centered on the 3-fold axes. For example, T = 1 leads to T = 3, T = 3 to T = 9, T = 4 to T = 12, etc. This theorem predicts that capsids and procapsids (immature capsids) of tailed phages forming, e.g., T = 3, 9, or 12, will display at least 20 hexamers with 3-fold (or 6-fold) symmetry on the global 3-fold icosahedral axes. This prediction was supported empirically by the published reconstruction of the procapsid of SIO-2 tailed phage, which adopts a T = 12 capsid with non-split hexamers at the true 3-fold axes32 (Fig. 4c).

The theorem derived above can be also stated as follows: “An icosahedral capsid can be formed with all-skew (split or 2-fold) hexamers if and only if the T-number is not multiple of three.” This captures all the capsids that could display an analogous stability mechanism as Patience and Adjutor. Notice that since the T-numbers for centered hexamers are generated as three times a classic T-number, these capsids are less frequent than those with all skey/split hexamers. In particular, on average one expects that 1 of every 3 capsids will require a centered hexamer, while 2 of every 3 can accommodate all skew hexamers. This is consistent with the observation made computationally where about 2/3 of the capsids explored (12 out of the 20) could accommodate all skew/split hexamers while only about 1/3 (8 out of 20) displayed a 3-fold centered hexamer. The volume of a capsid with non-split hexamers compared to the same capsid with split hexamers is expected to be the same. However, the chasm-reinforcing mechanism offers a molecular strategy to increase the genome length while conserving the capsid size, adding an evolutionary degree of freedom that could favor these capsids. In fact, a recent study identified that the distribution of genome lengths among isolated tailed phages had prominent peaks associated with genomes inferred to fit in T = 4, T = 7, and T = 16 capsids, and when including metagenome-assembled genomes it included a peak in T = 13 capsids33. These T-numbers coincide with the first group of capsids compatible with all skew/split hexamers (Supplementary Table 6), in favor of the evolutionary advantage in selecting capsids compatible with the chasm-reinforcing mechanism.

Discussion

The extension of the decoration protein in the chasm-reinforcement mechanism described here can accommodate a 10% genome length equivalent to 5 kb between Adjutor (64.5 kb) and Patience (70.5 kb) without altering the capsid size. This mechanism supports the hypothesis of the gradual evolution of capsids and genome lengths21. This gradual evolution was recently discussed, associated with the expansion of the hexamers in Thermus phages P74-26 and P23-45, thanks to the reinforcement by the trimeric decoration proteins20,21. These thermophilic phages adopt, like Adjutor and Patience, supersized T = 7 capsids with a packaging capacity that nearly doubles the capacity of canonical T = 7 capsids like lambda phage. In both cases, this increase in volume is due to the longer E-loops allowing larger hexamers and pentamers than for classic HK97-fold capsids. The trimeric minor proteins reinforcing the capsids, present in P74-26, P23-45, Adjutor, and Patience, were hypothesized to offer a molecular mechanism facilitating a gradual expansion of the hexamers and the internal capsid volume. However, in the case of P74-26 and P23-45, it was not possible to appreciate the specific molecular variations adding the gradual change in genome between them; the differences in genome length between phages P74-26 (84.2 kb) and P23-45 (83.3 kb) were only about 1% (a difference of 900 bp), their major capsid proteins were identical, and their minor proteins were 79% similar but had the same length and adopted similar structures. However, the chasm-reinforcing mechanism observed in Patience and Adjutor offers direct evidence of how the increase in the chasm-decoration protein facilitates the accommodation of a larger genome length, supporting the gradual evolution hypothesis.

Nonetheless, the existence of mechanisms favoring the gradual evolution of genome and capsids like the trimeric reinforcement associated with supersized T-numbers and the chasm reinforcement mechanisms described here does not deny the existence of mechanisms capable of capsid evolutionary leaps (leap hypothesis)20,21. The experimental observation of single point mutations responsible for changes in the T-number of viral capsids34,35,36 suggests that it is plausible for viruses to produce larger capsids in one infection. However, given the need of tailed phages to store the genome at a density ~0.5 bp/nm3 to accumulate the pressure required to initiate the host infection process33,37,38, an increase in capsid size due to a single point mutation would require a headful packaging mechanism that can fill up the capsid with additional DNA besides the virus genome39. Thus, we propose that phages relying on headful packaging could benefit from both gradual and leap capsid transitions, while phages relying on pac site packaging39 would rely on gradual capsid transitions. We speculate that the use of pac site packaging might be a strategy to slow down capsid size evolution and select a preferential genome length that may have advantages for example during replication. Investigating the relationship of packaging strategies and evolution capsid strategies is an important task to be pursued in future studies. Such investigation would also benefit from including the way the E-loop stabilizes intra-capsomer and inter-capsomer connections, which is highly diverse and seems a key factor in the HK97-fold regulating capsid architecture7. In the case of Adjutor and Patience, the E-loop displays a conformational change that bridges and contributes to the stabilization the pseudo 2-fold chasm in the split hexamers (Fig. 3). The evolution of the alternative extended E-loop conformation was probably a key factor in increasing the genome length, and it could be argued that the alternative stabilization strategies of the E-loop observed in other capsids may have played a key role in both gradual and leap capsid evolution scenarios, including the topological lasso in the P74-26 and P23-45 supersized capsids20,21 (19,20), the non-covalent chainmail in BPP-1’s head40, the covalent chainmail of HK9741 and the destabilization effect of single point mutations in the E-loop of P22 capsids42.

An approach to investigate the possible scenarios of capsid evolution is to consider the capsids predicted by our mathematical analysis to allow all-skew hexamers, that is, those capsids with T-numbers that are not multiple of three. It is important to compare this prediction with a previous mathematical approach that investigated the different shapes of hexamers in icosahedral capsids based on the endo angle propagation from proteins forming the pentamers43,44. That framework identified four shapes: flat (F), ruffled (R), wing (W), inverted wing (I), and single pucker (S). In our split hexamer framework, the F and R shapes would be incompatible with being skewed or split, while the W, I, S shapes would be compatible with skewed or split hexamers. For the capsid range analyzed in the endo angle framework, T = 1 to 243, only two had hexamer shapes compatible with all skewed hexamers, T = 4 (W), and T = 7 (S), which is consistent with our framework. The reason the endo angle propagation framework differs from our theorem for T > 7 capsids is due to their more restrictive assumptions: The propagation of the pentameric endo angle and the use of rhomboid shape tiles, which impact on the direction of the angles being propagated. In fact, in the endo angle propagation framework, the T = 12 capsid (Fig. 2 in Mannige and Brooks 201044) is predicted to use hexamers with R, W, and I shape. The R shape coincides with our prediction of the 3-fold hexamer at the 3-fold axes, but the orientation of the R and W hexamers is incompatible with the orientation of the split hexamers in the 3D reconstruction of the SIO-2 procapsid (Fig. 4c). One explanation for this discrepancy is that the orientation and rhomboid shape of the capsid tiles in the endo angle propagation framework was inspired by the single jelly-roll fold, while the SIO-2 procapsid is built from the HK97-fold which is oriented and shaped differently. Additionally, the interpretation of the T = 12 procapsid of SIO-2 implies two types of hexamers (split and near six-fold), as predicted by our split hexamer framework, while the endo propagation framework predicts three types of hexamers for a T = 12. We hypothesize that the lower number of hexamer types is because the constrain imposed by the pentamers may not propagate much further that near capsomers in large capsids. Thus, the less restrictive skew framework proposed here is compatible with the capsids studied, while the endo propagation angle framework shows inconsistencies. However, a more thorough analysis with other capsids and protein folds would be necessary to determine if our predictions are as general as our current study suggests.

In conclusion, we have structurally characterized two actinobacteriophages that use a previously uncharacterized capsid organization which involves split hexamers that are stabilized by an accessory protein. Bacteriophages are ancient and have had a long time to explore the multiple solutions to create an icosahedral capsid; these two phages reveal one such solution. The capsid organization allows the phage to package larger genomes without having to change the T-number. We predict that capsid architectures that can accommodate all skew/split hexamers and benefit from the chasm-stabilization mechanism described here are characterized by T-numbers that are not a multiple of three due to symmetry constraints.

Methods

Production and purification of bacteriophages for cryo-electron microscopy

Phages were made as previously described17. Each bacteriophage was mixed with its respective host (Supplementary Table 2), plated in top agar on Luria agar plates, and incubated overnight at the temperatures shown in Supplementary Table 1 to produce twenty webbed plates. Webbed plates were flooded with 5 mL of Phage Buffer (10 mM Tris-HCl pH 7.5, 10 mM MgSO4, 68 mM NaCl, 1 mM CaCl2) and incubated overnight at room temperature to allow diffusion of the phages into the Phage Buffer. This solution was aspirated from the plates and centrifuged at 15,000 × g for 15 min at 4 °C to remove cell debris. Phage particles were initially pelleted using an SW41Ti swinging bucket rotor (Beckman Colter, Brea, CA) at 111,132 × g (30,000 rpm) for 3 h using 12.5 mL open-top polyclear tubes (Seton Scientific, Petaluma, CA). The phages in the pellet were resuspended in 4 mL of Phage Buffer by rocking overnight at 4 °C. To further purify the phage particles in this solution, isopycnic centrifugation was performed by adding 5.25 g of CsCl to the 7 mL of phage lysate. The CsCl/phage solutions were centrifuged at 137,000 × g (40,000 rpm) in an S50-ST swinging bucket rotor (Thermofisher Scientific, Waltham, MA) for 16 h, and the phage particle band (that appeared roughly halfway down the tube) was removed with a syringe and needle (around 1 mL removed per band). The phage particles were then dialyzed three times against the Phage Buffer to remove CsCl. This was accomplished by placing the CsCl/phage solution in dialysis tubing with a 50 kDa MWCO. The phages were pelleted at 250,000 × g (75000 rpm) in an S120-AT2 fixed angle rotor (Beckman Colter, Brea, CA) to allow for concentration. The phage particles were resuspended in 20 µL of Phage Buffer with gentle pipetting.

Preparation of cryo-electron microscopy grids

Three microliters of concentrated phage particles (around 10 mg/mL) were added to plasma-cleaned Au-flat 2/2 (2 µm hole, 2 µm space) cryo-electron microscopy grids (Protochips, Morrisville, NC, USA) using a Vitrobot mk IV (FEI, Hillsboro, OR, USA). Grids were blotted for 5 s with a force of 5 (a setting on the Vitrobot) before being plunged into liquid ethane.

Cryo-electron microscopy

Data were collected on a 300 keV Titan Krios (FEI, Hillsboro, OR, USA) at the Pacific Northwest Center for Cryo-EM with a K3 direct electron detector (Gatan, Pleasanton, CA, USA). Supplementary Table 1 provides the collection parameters for each phage.

Cryo-electron microscopy data analysis

Relion 3.1.145 was used for phage capsid map reconstructions using the standard workflow. Micrographs were motion-corrected using Relion’s own implementation with the default parameters, and the gain file was flipped 180 degrees in Y. The contrast transfer function (CTF) was estimated using CTFFIND 4.146 with default settings. Bacteriophage capsids were picked with the Relion LoG-based auto-picking with a minimum diameter for loG filter of 500 Å and Max diameter for loG filter of 800 Å. Particles were extracted with a box size of 2400 Å and Fourier cropped (binned) to 800 Å due to GPU memory limitations. Extracted particles were subjected to two rounds of 2D classification. Particles in the first two classes (Patience) and the single first class (Adjutor) (Supplementary Fig. 1) were used for de novo 3D model generation using C1 symmetry in Relion. This de novo 3D model was used as the initial model with the selected particles in a 3D classification job with default parameters and C1 symmetry to further select a homogenous population of particles. A single class of particles was selected for high resolution 3D refinement, applying I1 symmetry to the particles and using the de novo 3D model as the initial model. I2, I3, I4, and C1 reconstructions were also performed, but we observed no difference in the final maps apart from the resolution achieved. A mask was then created in Relion using the default parameters, and the mask was used for post-processing. The modular transfer function (MTF) was determined for the F3 detector at 300 kV. The high-resolution map was further refined using the CTF and aberration refinement job in Relion to correct for various aberrations and to re-estimate the per-particle defocus values. Default parameters were used for this job. Bayesian polishing was not carried out because, based on prior experience in bacteriophages, the computation time is not worth the small improvement in resolution. Finally, Ewald sphere correction was performed for each refined map using the relion_image_handler command included with Relion. The mask_diameter value used in the Ewald sphere correction is reported in Supplementary Table 1. The Ewald corrected map was sharpened by Phenix version 1.19.2–415847 using the “Autosharpen map or map coefficients” method with default parameters; this map was used for the model building, but the model was checked against the unsharpened map as well.

Model building

The amino acid sequence of the major and minor capsid proteins was folded by AlphaFold version 2.048 using the default settings on a local device. The highest-ranked prediction model was evaluated and fitted into the cryo-EM map using the “Fit in Map” command in ChimeraX version 1.349. To further fit the density, Coot version 0.9.250 was used to fit the models using the “Stepped sphere refine active chain” option provided by the Python script developed by Oliver Clarke51. Following this, any outlying parts of the protein chain were manually moved to density. The protein chains were trimmed for amino acids that had no corresponding density. Patience major capsid protein was trimmed to threonine-20, removing the first 19 amino acids of the N-terminus, while Adjutor major capsid protein was trimmed to asparagine-28, removing the first 27 amino acids of the N-terminus. The minor capsid proteins of both bacteriophages had the N-terminal methionine. Gp4 for both bacteriophages was built in by hand using Coot. All the amino acids apart from the N-terminal methionine could be fitted into the map density.

After the initial fitting of the model to the map, the model had a final manual fit using the ChimeraX plugin, Isolde version 1.352. The whole model simulation temperature in Isolde was set to 20 degrees Kelvin, and default parameters were used. After manual fitting, the real-space refinement tool of Phenix version 1.19.2–415847 with global energy minimization and geometry restraints was used to iteratively refine the model, followed by manual corrections for Ramachandran and geometric outliers in Coot. The model quality evaluation was carried out using MolProbity53.

Purification and circular dichroism of recombinant gp4

The Patience gp4 construct was designed with an N-terminal maltose-binding protein (MBP) tag separated from the sequence with a factor Xa protease cleavage site, and a C-terminal Hexa-His tag separated from the sequence by a tobacco etch virus (TEV) protease cleavage site. The DNA fragment encoding the protein was codon optimized for E. coli protein expression and synthesized by GenScript, USA, before being cloned into the pETDuet-1 vector. The protein was produced in NEBExpress Competent E. coli High Efficiency cells (New England BioLabs, USA). The cells were grown in Luria broth media containing 3% glucose and 100 μg/mL or ampicillin at 30 °C until the optical density (O.D.) reached 0.6 and then were induced with 1 mM IPTG and grown for 3 h at 30 °C. The cells were pelleted by centrifugation at 15,000 x g for 15 min and frozen at -80 °C. The frozen cell pellets were resuspended in lysis buffer (50 mM TRIS pH 7, 150 mM NaCl, 1 mM EDTA, Roche’s complete Protease inhibitors, 1% Triton X-100, 1 mM BME, and small quantities of DNase and RNase). The resuspended cells were ruptured by the One-Shot Cell Disruptor (Constant Systems, UK), and the lysate was incubated for 1 hour, shaking at room temperature. The lysate was centrifuged at 30,000 x g for 30 min at 4 °C to remove cell debris. The lysate was run over a MBP column (MBPTrap HP Cytiva, USA), dialyzed into Ni buffer A, run over a Ni-NTA affinity column (HisTrap Cytiva, USA), and dialyzed back into MBP buffer A. MBP buffer A is 50 mM TRIS pH 7, 150 mM NaCl, 1 mM EDTA, and 0.1% Triton X-100 and MBP buffer B has 10 mM maltose added. Ni buffer A is 50 mM TRIS pH 7, 150 mM NaCl, and 0.1% Triton X-100, and Ni buffer B has 200 mM imidazole added. The fraction containing protein was then cut for 48 h at 4 °C with 1 mg of TEV protease per 100 mg gp4 and 1 mg of factor Xa protease per 100 mg gp4. The cut fraction was run on a Superdex 75 Increase 10/300 GL using 1/3x PBS buffer (Cytiva, USA). The protein-containing fraction was concentrated in a 3 kDa MWCO Amicon until 3 mg/mL. The CD spectra were measured from 180 nm to 280 nm at 4 °C.

Computationally generated icosahedral capsids

Icosahedral architectures were rendered by forming T-numbers from T = 1 to T = 52. This range of structures has been observed in shells assembled from HK97-fold capsid proteins11. The T-number or triangulation number follows the Diophantine equation18,30 shown in Eq. (1). The equation was implemented on a Python script. The T-numbers were generated using h and k values, satisfying T(h,k) ≤ 52. These capsids were rendered in 3D using the hkcage tool from ChimeraX33,49,54. Images centered on a 3-fold axis were saved for analysis (see Supplementary Table 6). The process was automated by developing a ChimeraX script in cxc file format.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.