Metavalent alloying and vacancy engineering enable state-of-the-art cubic GeSe thermoelectrics

Abstract

Conventional alloying strategies often require high alloying concentrations, leading to impurity phases and additional phase transition that limit the figure of merit of thermoelectric materials. Here, we introduce metavalent alloying and vacancy engineering as transformative strategies to facilitate the orthorhombic-to-cubic phase transition, in which we stabilize pure cubic GeSe under ambient conditions with just 10% alloying concentration using Sb₂Te₃ as an effective alloying agent. Compared to the covalently bonded orthorhombic phase, the metavalently bonded cubic GeSe features lower cation vacancy formation energy, reduced bandgap, enhanced band degeneracy, weaker chemical bonding, stronger lattice anharmonicity, and multiple phonon scattering centers. These properties synergistically improve the power factor and suppress the lattice thermal conductivity. Subsequent trace Pb doping further reduces the lattice thermal conductivity, achieving an unprecedented ZT of 1.38 at 723 K in cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1, along with a remarkable energy conversion efficiency of 6.13% under a 430 K temperature difference. These results advance the practical application of GeSe-based alloys for medium-temperature power generation and provide critical insights into the orthorhombic-to-cubic phase transition mechanism in chalcogenides.

Introduction

Thermoelectric energy conversion technology is crucial for addressing the global energy crisis by efficiently converting low-grade thermal energy into valuable electrical energy^1,2,3,4,5. The energy conversion efficiency (η) of thermoelectric devices is governed by the dimensionless figure of merit, ZT = S²σT/κ, where σ, S, κ, and T represent the electrical conductivity, Seebeck coefficient, thermal conductivity (comprising both carrier κ_e and lattice κ_L contributions), and absolute temperature, respectively^6,7,8. Enhancing thermoelectric performance typically involves band engineering^9,10 and phonon engineering^11,12,13. Band engineering focuses on optimizing the electronic band structure, such as through band convergence¹⁴, band anisotropy¹⁵, or the introduction of resonant energy levels^16,17, to improve the power factor (S²σ). In contrast, phonon engineering aims to reduce the κ_L by lowering the sound velocity (v_m) or introducing multi-scale defects to shorten the phonon mean free path^18,19.

Recent advancements have brought layered orthorhombic SnSe into the spotlight due to its unparalleled ZT values^20,21. Similarly, GeSe, another IV-VI group semiconductor, has emerged as a promising candidate for medium-temperature thermoelectric applications^22,23. Density functional theory (DFT) calculations predict that optimally doped orthorhombic GeSe could achieve a peak ZT of 2.5 along the b-axis at 800 K²². However, the limited solubility of dopants in orthorhombic GeSe restricts the effective carrier concentration (n_H), leading to a low ZT of approximately 0.2²⁴. In contrast, transitioning to rhombohedral or cubic GeSe has demonstrated significantly enhanced ZT, driven by its unique metavalent bonding (MVB) mechanism^25,26,27. Unlike the conventional covalent bonding (CVB) in orthorhombic GeSe where two electrons are shared^28,29, resulting in a bond order of 1, MVB involves the sharing of approximately one electron between neighboring atoms, yielding a bond order of ~1/2. This bonding type, distinct from covalent, ionic, and metallic bonds, endows MVB solids with exceptional properties for carrier and phonon transport^28,30. Electrically, compared to its covalently bonded orthorhombic counterpart, metavalently bonded rhombohedral or cubic GeSe exhibits a reduced bandgap (E_g), lower Ge vacancy formation energy, narrower band edges, and greater band degeneracy (N_V). Thermally, it demonstrates a lower v_m and stronger lattice anharmonicity. These factors collectively contribute to the enhanced ZT value observed in metavalently bonded GeSe³¹.

Current research on high-performance p-type GeSe primarily focuses on its rhombohedral phase³². Significant advancements, such as Sb-Cd co-doping³³ and alloying with compounds like InTe³⁴, CdTe²⁷, MnCdTe₂³⁵, AgInTe₂³⁶, LiBiTe₂³⁷, and Ag(Sb, Bi)(Se, Te)₂^{26,38,39,40,41}, have successfully transformed orthorhombic GeSe into the rhombohedral structure, achieving ZT values ranging from 0.90 to 1.36^{26,27,33,34,35,36,37,38,39,40,41}. However, cubic GeSe, which is unaffected by Peierls distortion, offers larger band degeneracy, lower v_m and greater lattice anharmonicity²⁵, theoretically surpassing thermoelectric performance of the rhombohedral phase. Additionally, the phase transition from orthorhombic (or rhombohedral) to cubic at elevated temperatures causes a significant change in the coefficient of thermal expansion, leading to internal stresses that can damage the materials or disrupt the material-electrode interfaces. This, in turn, compromises the long-term reliability of thermoelectric devices. Therefore, facilitating the orthorhombic-to-cubic phase transition and stabilizing the cubic phase across the entire temperature range hold both theoretical and practical importance.

Understanding the mechanisms driving the orthorhombic-to-cubic phase transition in chalcogenides is therefore critical. In these materials, the orthorhombic structure exhibits strong Peierls distortion, characterized by high electron sharing (ES) between neighboring atoms, while the cubic structure, free from such distortion, displays minimal ES due to the absence of s- and p-band hybridization²⁸. By chemically or physically suppressing Peierls distortion (effectively reducing the ES capacity between neighboring atoms), the bonding can be transitioned from CVB to MVB, enabling the progression of GeSe from the orthorhombic to the rhombohedral, and ultimately, to the cubic phase^28,29. Strategic alloying of GeSe with compounds such as InSnTe₂ and AgSnTe₂ has been explored to facilitate this phase transition^42,43. However, limited solubility in these alloys has hindered the complete elimination of residual orthorhombic phases and the prevention of secondary phase precipitation, presenting challenges to achieving fully cubic GeSe.

Previous studies have investigated the critical role of chemical bonding mechanism in governing dopant solubility. High miscibility is achieved when both the host material and the dopant share the same MVB mechanism, as demonstrated in systems like SnTe-AgSbTe₂⁴⁴ and GeTe-PbSe-PbS⁴⁵. In contrast, mixing metavalent compounds with covalent solids often leads to phase separation, as observed in the GeTe-GeSe-GeS system⁴⁶. Consequently, MVB compounds, such as IV-VI, V₂VI₃, and I-V-VI₂, exhibit excellent solubility in GeSe, minimizing residual orthorhombic or precipitated phases (Fig. 1a). However, alloying cubic GeSe with IV-VI or I-V-VI₂ compounds typically requires extremely high alloying concentrations, which can negatively impact μ_H and, consequently, the ZT value. For example, stabilizing cubic GeSe through I-V-VI₂ alloying necessitates at a minimum of 30% content, significantly lowering the ZT compared to rhombohedral GeSe^38,43,47. Quantum chemical calculations and enthalpy of formation analyzes reveal that cation vacancies destabilize covalently bonded orthorhombic GeSe⁴⁸, but are essential for mitigating unfavorable anti-bonding Ge-Se interactions in metavalently bonded rhombohedral or cubic GeSe⁴⁹. This suggests that the introduction of cation vacancies is critical for stabilizing high-symmetry phases (Fig. 1a). Furthermore, DFT calculations and X-ray diffraction (XRD) studies indicate that the concentration of Ge vacancies in cubic GeTe is significantly higher than in its rhombohedral counterpart⁵⁰. These findings imply that alloying with V₂VI₃ compounds, which offer high solubility and additional cation vacancies, can accelerate the orthorhombic-to-cubic phase transition in chalcogenides, potentially bypassing the intermediate rhombohedral phase.

Fig. 1: Design strategy and high physical properties of the cubic GeSe-based TE materials and devices.

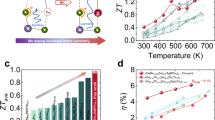
a Illustration of design strategy for cubic GeSe: metavalent V₂VI₃ alloying with high solid solubility and additional cation vacancy⁴⁹. Here Orth. refers to the orthorhombic structure, while Rhom. represents the rhombohedral structure. b Alloying content (x) and configurational entropy (ΔS) required for obtaining cubic GeSe studied herein in comparison with literature data^26,38,43,47 (the bar chart corresponds to x and the red line represents ΔS). c Comparison of peak ZT of this work and reported works^{24,26,33,34,35,36,37,38,40,41,42,43,64}. d Energy conversion efficiency (η) of single-leg GeSe-based device under various temperature differences (∆T) in comparison with literature data³⁶.

Results and discussion

According to the Hume-Rothery rules⁵¹, the atomic size mismatch between Ge and Bi is significantly larger compared to that between Ge and Sb, resulting in a higher solubility of Sb₂Te₃ in GeSe than Bi₂Te₃ (Supplementary Fig. 1). Based on this principle, we introduced a small amount (> 7.5%) of metavalent Sb₂Te₃ as an alloying agent to accelerate the stabilization of cubic GeSe (Fig. 1b). Compared to orthorhombic GeSe, cubic GeSe exhibits optimized n_H, enhanced μ_H, and a higher density-of-states effective mass (m^*), leading to a significant improvement in the S²σ. Additionally, the weakened chemical bonding and enhanced lattice anharmonicity in cubic (GeSe)_1−x(Sb₂Te₃)_x, combined with multiple phonon scattering mechanisms, effectively reduce the κ_L. To further minimize κ_L, trace amounts of Pb was doped into (GeSe)_0.9(Sb₂Te₃)_0.1, achieving a record-breaking ZT = 1.38 at 723 K in cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1. The single-leg device demonstrated an impressive η of 6.13% under a ΔT of 430 K (Fig. 1c, d). These results not only represent a significant breakthrough in the ZT of cubic GeSe but also provide valuable insights into the key factors driving the orthorhombic-to-cubic phase transition in chalcogenides.

To determine whether the integration of non-stoichiometric metavalent Sb₂Te₃ can accelerate the stabilization of cubic GeSe, powder X-ray diffraction (XRD) was performed on the full series of (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples (x = 0 ~ 15%, y = 3 ~ 7%). As shown in Fig. 2a, the room-temperature XRD patterns reveal significant structural changes in GeSe with increasing Sb₂Te₃ content (x). The initial sample with x = 0 exhibited diffraction peaks characteristic of the typical orthorhombic structure (Pnma). After alloying with Sb₂Te₃, the intensity of the orthorhombic phase peaks between 30° and 33° decreased significantly, while the intensity at 31.3° increased, indicating the formation of a cubic phase (Fm-3m). This suggests the coexistence of cubic and orthorhombic phases in the sample with x = 0.05. When the Sb₂Te₃ content increased to x ≥ 0.075, a predominantly cubic structure was consistently observed in all samples at room temperature. Notably, further addition of trace Pb to the x = 0.10 sample had minimal impact on the phase structure, as shown in Supplementary Fig. 2.

Fig. 2: Characterizations of the phases of as-prepared (GeSe)_1−x(Sb₂Te₃)_x samples.

a Room-temperature powder X-ray diffraction (XRD) patterns. Calculated b lattice parameters a, b, c and c bond distances. Here, 0.1% error bar is employed. Variable-temperature XRD patterns for d x = 0.075 and e x = 0.01 samples. f Calculated formation energy of Ge vacancy for orthorhombic GeSe, cubic GeSe, and cubic (GeSe)_0.9(Sb₂Te₃)_0.1. g Phase structure and vacancy concentration evolution upon Sb₂Te₃ alloying according to the XRD Rietveld refinement results.

To quantify the impact of Sb₂Te₃ alloying on the crystal structure of GeSe, structural refinement was conducted using the Fullprof Suite⁵², allowing precise determination of the lattice parameters for the (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples (Supplementary Table 1 and Supplementary Figs. 3 and 4). Specifically, the x = 0 sample exhibited a purely orthorhombic phase. As x increased, the proportion of the orthorhombic phase decreased significantly, while the fraction of the cubic phase correspondingly increased. For instance, in the x = 0.05 sample, the ratio of cubic to orthorhombic phases was quantified as 55.84% to 44.16%. Interestingly, while the room-temperature XRD pattern of the x = 0.075 sample suggested no detectable orthorhombic phase, structural refinement revealed a residual orthorhombic fraction of 6.36%. Complete transformation to a 100% cubic phase was achieved at x = 0.10, emphasizing the critical requirement for Sb₂Te₃ content to exceed 7.5% to stabilize cubic GeSe at ambient conditions.

As shown in Fig. 2b and Supplementary Fig. 5, the lattice parameters (a, b, and c) of both orthorhombic and cubic GeSe increase significantly with the rising values of x or y. This lattice expansion is attributed to the larger ionic radii of Sb (145 pm), Pb (175 pm), and Te (221 pm) compared to those of Ge (73 pm) and Se (198 pm), respectively⁵³. More importantly, as shown in Fig. 2c and Supplementary Fig. 6, the bond lengths in orthorhombic GeSe generally range from 2.52 to 2.61 Å, whereas those in cubic GeSe extend from 2.84 to 2.89 Å. Based on the phenomenological bond length-bond strength relationship, shorter bonds typically correspond to stronger interactions, while longer bonds tend to indicate weaker interactions. Thus, the elongation of bond lengths in the cubic structure signifies a weakening of chemical bonding. This reduction in bond strength leads to weaker atomic interactions, which in turn reduces the v_m and significantly lowers the κ_L.

To assess the effect of Sb₂Te₃ alloying on phase stability at high temperatures, temperature-dependent XRD measurements were conducted on the x = 0.075 and x = 0.10 samples (Fig. 2d, e). Upon heating, trace orthorhombic phases were observed in both samples, consistent with thermodynamic predictions that the metastable cubic phase transitions to the more stable orthorhombic structure under thermal stress. Notably, the orthorhombic phase appears above 623 K in the x = 0.075 sample and above 673 K in the x = 0.10 sample. Furthermore, the intensity of the orthorhombic peaks is significantly weaker in the x = 0.10 sample, indicating better retention of the cubic structure at higher temperatures. While increasing the Sb₂Te₃ content could potentially suppress the formation of the orthorhombic phase at elevated temperatures, it would likely compromise the ZT value.

To validate whether metavalent Sb₂Te₃ alloying with additional cation vacancies can accelerate the formation of cubic GeSe, we compared the required alloying concentrations with conventional approaches (Fig. 1b). Traditional alloying to achieve a fully cubic structure typically demands a high alloying content, such as over 40% for AgSnTe₂⁴³ and at least 30% for AgBiTe₂²⁶, AgSbTe₂³⁸, and AgBiSe₂⁴⁷. In contrast, our study demonstrates that orthorhombic GeSe can successfully transition to a pure cubic phase with Sb₂Te₃ alloying concentrations as low as 10% or less. To further clarify the influence of different alloying types, we quantitatively evaluated the configurational entropy (ΔS) required for various cubic GeSe-based alloys using Boltzmann theory⁵⁴: $\Delta S=-R{\sum }_{i=1}^{n}{x}_{i}\,{{\mathrm{ln}}}\,{x}_{i}$, where R represents the gas constant, n denotes the number of element types, and x_i specifies the mole fraction of the i-th element (Fig. 1b). Notably, alloying with AgSnTe₂, AgBiTe₂, and AgSbTe₂ requires ΔS values exceeding the typical threshold for high-entropy alloys (ΔS = 1.50 R)⁵⁵. In the case of Sb₂Te₃ alloying, the cubic structure becomes mostly stable at ΔS = 0.98 R and fully stable at ΔS = 1.21 R. Compared to existing literature, the observed alloying content and ΔS in this study are significantly reduced, highlighting the importance of understanding the key factors governing the orthorhombic-to-cubic phase transition in chalcogenides. This reduced requirement underscores the efficiency and practicality of using Sb₂Te₃ as an alloying agent to stabilize cubic GeSe.

The driving force for the formation of cubic (GeSe)_1−x(Sb₂Te₃)_x alloys was investigated through the theoretical calculations of Ge vacancy formation energy (E_V). As shown in Fig. 2f, we simulated three different crystal structures, namely Ge₃₁Se₃₂ (Pnma), Ge₂₆Se₂₇ (Fm-3m), and Ge₂₂Sb₄Se₂₁Te₆ (Fm-3m), and calculated E_V using DFT. Notably, E_V decreased significantly from 0.99 eV for binary orthorhombic Ge₃₁Se₃₂ to 0.35 eV for binary cubic Ge₂₆Se₂₇. For cubic Ge₂₂Sb₄Se₂₁Te₆, E_V was further reduced to 0.07 eV. Given that cubic GeSe typically requires extreme conditions, such as high temperatures (> 900 K) or high pressures (> 8 GPa)^56,57, our results confirm that metavalent Sb₂Te₃ alloying can accelerate the formation of the cubic phase under ambient conditions by intentionally introducing cation vacancies. This highlights the role of Sb₂Te₃ in reducing vacancy formation energy, enabling the stabilization of cubic GeSe without the need for extreme synthesis conditions.

In addition to theoretical calculations, cation vacancy concentration can be quantitatively evaluated through XRD refinement by analyzing the atomic occupancy of cation sites⁵² (Fig. 2g). Ideally, the atomic occupancy of cation sites should be 100%; however, with increasing Sb₂Te₃ content (x), this occupancy gradually deviates from 100%, indicating a significant increase in cation vacancy concentration. For instance, the cation site occupancy decreased sharply from 100% in the x = 0 sample to 96.8% in the x = 0.10 sample and further dropped to 93.2% in the x = 0.15 sample. This trend demonstrates a direct correlation between the increasing Sb₂Te₃ alloying content and the generation of cation vacancies. In contrast, the addition of Pb to the x = 0.10 sample increases the cation site occupancy, thereby reducing the concentration of cation vacancies, as shown in Supplementary Table 2.

The solubility of dopants, in addition to the cation vacancy, plays a pivotal role in facilitating the rapid formation of cubic GeSe-based materials. The powder XRD patterns of the (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x series (Fig. 2a and Supplementary Fig. 2), alongside scanning electron microscopy (SEM) combined with energy-dispersive X-ray spectroscopy (EDS) (Supplementary Figs. 7–12), confirmed the absence of any impurity phases. Additionally, X-ray photoelectron spectroscopy (XPS) measurements confirmed the valence states of Ge, Pb, Sb, Se, and Te as 2⁺, 2⁺, 3⁺, 2⁻, and 2⁻, respectively (Supplementary Fig. 13). To further investigate the chemical composition and distribution in the (GeSe)_0.9(Sb₂Te₃)_0.1 sample, transmission electron microscopy (TEM), known for its high chemical sensitivity and spatial resolution, was employed. Figure 3a, obtained by high-angle annular dark-field (HAADF) imaging, reveals a smooth surface with no evidence of secondary phases. EDS mapping further supports this observation, showing a uniform distribution of the matrix elements Ge and Se, as well as the dopants Sb and Te, throughout the sample. These findings, combined with XRD and SEM results, confirm the effective incorporation of metavalent Sb₂Te₃ into the GeSe matrix. A similar absence of impurity phases was observed in other metavalent Ag-V-VI₂ alloyed GeSe systems^38,39. In contrast, when GeSe was alloyed with compounds possessing different bonding types (e.g., covalent, ionic, or metallic bonding), such as InSe⁵⁸, InTe³⁴, CdTe²⁷, MnCdTe₂³⁵, AgInTe₂³⁶, and AgSnTe₂⁴³, secondary phases like In₂Se₃, Ge₂In₂Se₆, MnCdSe₂, CdSe, and Ag₂Te were formed. This highlights the superior solubility of MVB compounds, such as Sb₂Te₃, in GeSe, which promotes the full stabilization of the cubic phase while effectively preventing the formation of undesired secondary phases. Thus, alloying with high-solubility, non-stoichiometric MVB compounds, combined with the deliberate introduction of cation vacancies, is identified as a critical factor in accelerating the orthorhombic-to-cubic phase transition in chalcogenide materials. This approach highlights the synergy between chemical design and defect engineering in stabilizing the cubic phase under ambient conditions.

Fig. 3: Structural characterization by transmission electron microscope (TEM) for (GeSe)_0.9(Sb₂Te₃)_0.1 sample.

a Low-resolution TEM images of (GeSe)_0.9(Sb₂Te₃)_0.1, including energy dispersive spectroscopy (EDS) mapping of elements Ge, Sb, Se, and Te. b High-resolution imaging reveals nanoscale or atomic-scale defects. c A close-up of b, showing atomic arrays compared with the corresponding atomic model of the cubic phase. d The fast Fourier transform (FFT) of b reveals the diffraction pattern of cubic GeSe along the $[0\overline{1}0]$ direction. e High-intensity Ge vacancies in (GeSe)_0.9(Sb₂Te₃)_0.1. f A close-up image collected from the white box in (e). g Corresponding intensity profile marked in f.

The high-resolution TEM (HRTEM) image in Fig. 3b further confirms the cubic structure of (GeSe)_0.9(Sb₂Te₃)_0.1. A magnified view of the white boxed region in Fig. 3b reveals a well-defined atomic arrangement, where alternating Ge and Se atoms occupy the lattice positions. Due to the higher atomic number of Se (34) compared to Ge (32)⁵³, Se anions appear with brighter contrast, as illustrated in Fig. 3c. The observed atomic structure aligns perfectly with the atomic-level crystal structure model of cubic GeSe. To further verify the crystal structure, a fast Fourier transform (FFT) analysis was performed to identify the diffraction pattern. As shown in Fig. 3d, the FFT pattern corresponds to a cubic GeSe phase projected along the $[0\overline{1}0]$ direction. This analysis confirms that Sb₂Te₃ alloying successfully induces the formation of cubic GeSe.

Typically, rhombohedral and cubic GeSe exhibit lower Ge vacancy formation energy compared to the orthorhombic phase, creating a more favorable environment for Ge precipitation and resulting in Ge vacancy defects^35,48. Specifically, in rhombohedral GeSe systems, Ge vacancy planes are frequently observed, primarily due to larger atoms substituting smaller Ge atoms, leading to a pinning effect on the cation vacancy migration process³⁴. In this work, HRTEM analysis was conducted to explore structural defects in cubic GeSe. As shown in Fig. 3e, a high density of stripe-like defects was observed in (GeSe)_0.9(Sb₂Te₃)_0.1, consistent with previously reported characteristics of Ge vacancy planes³⁴. Figure 3f provides a magnified view of the boxed region in Fig. 3e, clearly showing weaker contrast for vacancy planes compared to lattice positions occupied by atoms. To further characterize these defects, Fig. 3g illustrates the line intensity distribution corresponding to Se layers, Ge layers, and Ge vacancy stripe layers. A significant intensity reduction (~35 ~ 40%) is observed for the vacancy layers, directly visualizing the presence of Ge vacancy defects. These Ge vacancy defects effectively scatter mid-frequency phonons, thereby suppressing the κ_L, contributing to the improved thermoelectric performance of the material.

To investigate the effect of Sb₂Te₃ alloying on the electrical transport properties, we used DFT to calculate the electronic band structures of orthorhombic GeSe, cubic GeSe, and Sb₂Te₃-alloyed cubic GeSe. Figure 4a–c show band structures of the orthorhombic GeSe, cubic GeSe, and cubic (GeSe)_0.9(Sb₂Te₃)_0.1, and Fig. 4d-f show corresponding partial density-of-states (PDOS). Orthorhombic GeSe exhibits an indirect E_g of 0.79 eV (Fig. 4a), where the relatively large E_g leads to low n_H and limits the potential for achieving a high S²σ (Fig. 4d). In contrast, pure cubic GeSe shows a direct E_g of 0.05 eV along the L-symmetry direction (Fig. 4b), making it highly susceptible to minority carrier excitation and, consequently, to bipolar conduction effects (Fig. 4e). Upon Sb₂Te₃ alloying, the E_g widens significantly to 0.33 eV (Fig. 4c), effectively mitigating the detrimental impact of bipolar conduction (Fig. 4f). This E_g optimization highlights the critical role of Sb₂Te₃ alloying in improving the electronic properties of cubic GeSe and enhancing its thermoelectric performance.

Fig. 4: Calculation results based on first-principles density functional theory.

a–c Band structures and d–f corresponding partial density-of-states (PDOS) for the orthorhombic GeSe, cubic GeSe, and cubic (GeSe)_0.9(Sb₂Te₃)_0.1.

Additionally, in orthorhombic GeSe, the valence band maximum (VBM) is located along the Γ-Y direction, exhibiting a valley degeneracy (N_V) of 2 (Supplementary Fig. 14a). By increasing the doping level and shifting the Fermi level deeper into the valence band, a second maximum can emerge at the Γ point, increasing N_V to 3. However, due to the inherently low solubility of dopants in covalently bonded GeSe, achieving such high n_H experimentally remains challenging²⁴. In contrast, cubic GeSe, with its higher symmetry Brillouin zone, has its VBM located at the L point, resulting in a high N_V of 4 (Supplementary Fig. 14b). At higher doping levels, the Σ band, which exhibits an N_V of 12, can also contribute to conduction, leading to a total N_V of 16 in cubic GeSe. This behavior is similar to that observed in cubic PbTe and GeTe^59,60. However, in binary cubic GeSe, the significant energy separation (ΔE = 0.39 eV) between the first and second valence band maxima limits the contribution of deeper valence bands to electrical transport. In this context, Sb₂Te₃ alloying plays a crucial role in reducing ΔE, facilitating the convergence of multiple valence bands. This promotes substantial orbital convergence and enhances the m^*, thereby improving the thermoelectric performance of cubic GeSe.

To elucidate the impact of non-stoichiometric metavalent Sb₂Te₃ alloying on the electrical transport properties of all (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples, Fig. 5a presents the room-temperature n_H and μ_H. Initially, pure orthorhombic GeSe exhibited an extremely low n_H of 1.2 × 10¹⁶cm⁻³, attributed to its relatively wide E_g and sparse Ge vacancies. Furthermore, the limited solubility of dopants in orthorhombic GeSe hindered the effective tuning of the Fermi level required to optimize n_H. Metavalent Sb₂Te₃ alloying rapidly converted the CVB-dominated orthorhombic GeSe into MVB-connected cubic GeSe by deliberately introducing additional cation vacancies. This structural transition led to a dramatic increase in room-temperature n_H, skyrocketing from 1.2 × 10¹⁶cm⁻³ in binary orthorhombic GeSe to 2.7 × 10²⁰cm⁻³ and 5.6 × 10²⁰cm⁻³ in the x = 0.075 and x = 0.15 samples, respectively. This significant increase arose from the phase transition from the orthorhombic to the cubic structure, which considerably narrowed the E_g. Moreover, unlike materials dominated by strong CVB interactions with few cation vacancies, MVB materials inherently generate cation vacancies to eliminate energetically unfavorable anti-bonding interactions³¹, leading to a four-order-of-magnitude increase in n_H. Additionally, the larger atomic radius of Pb compared to Ge suppresses the formation of Ge vacancies, resulting in a slight reduction in n_H in Pb-containing samples.

Fig. 5: Electrical transport properties of (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples.

a Room-temperature carrier concentration (n_H) and carrier mobility (μ_H). Temperature-dependent (b) electrical conductivity (σ) and c Seebeck coefficient (S). d Calculated Pisarenko curves at room temperature based on the single parabolic band (SPB) model. e The effective mass (m^*) in comparison with literature data^{27,34,35,38,39,42,43,58}. f Temperature-dependent weighted mobility (μ_W). g The power factor (S²σ) vs. n_H relationship calculated using SPB model at room temperature. h Temperature-dependent S²σ. i Temperature-dependent S²σ derived in the present work and other high-performance GeSe-based materials^{26,27,33,34,35,36,37,38,39,40,41,42,43,58,64}.

According to the Kane band model⁶¹, the effective mass of the band edge carriers (m_b^*), which is inversely proportional to the E_g, plays a critical role in determining electrical transport properties. In orthorhombic GeSe, the larger E_g results in flatter valence band edges, which are associated with a higher m_b^*. This leads to a significantly lower μ_H at room temperature, measured at 1.2 cm²V⁻¹ s^{−1 35}. Alloying with Sb₂Te₃ induces a dual transformation effect. For one thing, Sb₂Te₃ alloying enhances the crystal symmetry and significantly reduces E_g, leading to a lower m_b^* and a rapid increase in μ_H. For another, the introduction of Sb₂Te₃ and Pb introduces a substantial number of substitutional point defects and cation vacancies, which enhance the point defect scattering on the carriers. These opposing effects resulted in an initial sharp increase in room-temperature μ_H for the cubic x = 0.10 sample, reaching 7.8 cm²V⁻¹ s⁻¹, followed by a gradual decline to 2.3 cm²V⁻¹ s⁻¹ in the cubic x = 0.15 sample. This trend reflects the balance between improved band structure and increased point defect scattering in the alloyed system. Figure 5b presents the temperature-dependent σ of the (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples. Initially, σ increases significantly with the addition of Sb₂Te₃, followed by a gradual decrease as the Sb₂Te₃ content continues to rise. The initial increase in σ is directly linked to the substantial enhancements in both n_H and μ_H. However, despite the continued rise in n_H, the subsequent decrease in σ is primarily attributed to the reduction in μ_H. For example, at room temperature, σ increases sharply from 0.3 S m⁻¹ for the orthorhombic x = 0 sample to an impressive 3.3 × 10⁴ S m⁻¹ for the cubic x = 0.075 sample, before slightly decreasing to 2.0 × 10⁴ S m⁻¹ for the cubic x = 0.15 sample. Additionally, pristine orthorhombic GeSe and low Sb₂Te₃-alloyed samples (0 ≤ x < 0.10) show an increase in σ with temperature, indicative of semiconductor-like transport dominated by carrier grain boundary scattering. In high Sb₂Te₃-alloyed samples (x ≥ 0.10), the high n_H reduces grain boundary scattering, leading to a decrease in σ near room temperature, reflecting metal-like behavior. However, the introduction of Pb slightly lowers n_H, reinstating thermally activated σ and semiconductor-like behavior.

In contrast to the σ, the S initially undergoes a significant decrease, followed by an increase with increasing Sb₂Te₃ and Pb content, as shown in Fig. 5c. Specifically, at room temperature, S drops sharply from 775 μV K⁻¹ in pristine GeSe to 130 μV K⁻¹ for the x = 0.05 sample, before increasing to 232 μV K⁻¹ for the x = 0.10, y = 0.07 sample. The initial decrease in S for the Sb₂Te₃-alloyed samples is primarily attributed to the dramatic increase in n_H, which rises by four orders of magnitude compared to the original orthorhombic GeSe. This significant increase in n_H reduces the thermoelectric voltage generated per unit temperature gradient, leading to the observed reduction in S. Moreover, the S of pristine orthorhombic GeSe reaches its peak around 473 K before decreasing at higher temperatures, indicating the onset of a bipolar effect. This effect is intensified by its ultra-low n_H, despite the large E_g, and severely diminishes S and consequently the ZT at elevated temperatures. However, Sb₂Te₃ and Pb alloying facilitate the formation of cubic GeSe, which significantly increases n_H and shifts the onset temperature of the bipolar effect to higher values.

In addition to the n_H, the S is closely tied to the m^*, a key parameter influencing thermoelectric performance. Using the single parabolic band (SPB) model⁶², we calculated the relationship between S and n_H at room temperature, highlighting the significant impact of Sb₂Te₃ alloying on m^* (Fig. 5d). As shown in Supplementary Fig. 14, orthorhombic GeSe exhibits a relatively low m^* of 0.72 m₀, attributed to its limited N_V = 2. However, the incorporation of non-stoichiometric metavalent Sb₂Te₃ effectively mitigates Peierls distortion, facilitating the transition of GeSe to the cubic structure. This structural evolution leads to a substantial increase in N_V = 4. Moreover, electronic band structure calculations reveal that Sb₂Te₃ alloying promotes multivalley band convergence, further enhancing m^*. As a result, cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 achieves an exceptional m^* of 4.82 m₀, the highest reported value for rhombohedral and cubic GeSe-based alloys (Fig. 5e)^{27,34,35,38,39,42,43,58}. This significant increase in m^* explains the observed improvements in thermoelectric performance in the Sb₂Te₃-alloyed samples.

Weighted mobility (μ_W) analysis provides deeper insights into the electronic band structure and scattering mechanisms within the material, offering a clearer evaluation of electron transport properties by considering the interplay between μ_H and m^{* 63}. Figure 5f illustrates the variation of μ_W over the entire temperature range, calculated using the method described in the literature. Notably, the cubic (GeSe)_0.9(Sb₂Te₃)_0.1 sample exhibits the highest μ_W across the entire temperature range. Compared to pristine orthorhombic GeSe, the significant increase in μ_W highlights the effective manipulation of the electronic band structure facilitated by Sb₂Te₃ alloying. While Pb substitution leads to a slight reduction in μ_W, attributed to enhanced alloy scattering, particularly at ambient temperatures. The μ_W of cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 consistently remains above 40 cm²V⁻¹ s⁻¹ at all temperatures. This robust performance underscores the tremendous potential of the material for further enhancing its ZT, demonstrating its viability for high-performance thermoelectric applications.

Figure 5g elucidates the relationship between S²σ and n_H. The addition of Sb₂Te₃ causes a rapid increase in n_H, bringing it closer to the optimal threshold. Notably, the actual n_H of the x = 0.10 sample aligns closely with the ideal value. This synergistic optimization of n_H and μ_W significantly enhances S²σ across the entire temperature range, as depicted in Fig. 5h. Specifically, the cubic x = 0.10 sample achieves a peak S²σ of 15.12 μW cm⁻¹ K⁻² at 723 K, which is approximately 32 times higher than that of pristine orthorhombic GeSe (0.46 μW cm⁻¹ K⁻²). Although the introduction of trace Pb slightly reduces n_H and μ_W, the cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 sample still demonstrates a highly competitive maximum S²σ of 13.52 μW cm⁻¹ K⁻². This exceptional performance makes it one of the most efficient GeSe-based thermoelectric materials reported to date^{26,27,33,34,35,36,37,38,39,40,41,42,43,58,64}, as illustrated in Fig. 5i, underscoring its significant potential for high-performance thermoelectric applications.

Non-stoichiometric metavalent Sb₂Te₃ alloying has a profound impact on the thermal transport properties, as shown in Fig. 6. Evidently, the κ decreases rapidly with increasing Sb₂Te₃ content near room temperature, and this trend becomes even more pronounced with subsequent Pb alloying (Fig. 6a). Although Pb alloying slightly reduces S²σ, it intensifies phonon scattering through point defects, further lowering κ_L, and also reduces κ_e due to a decrease in σ. Together, these effects result in a significant reduction in total κ. Specifically, the room-temperature κ gradually decreases from 1.76 W m⁻¹ K⁻¹ in pristine orthorhombic GeSe to 0.86 W m⁻¹ K⁻¹ for the cubic x = 0.10 sample and further to 0.65 W m⁻¹ K⁻¹ for the cubic x = 0.10, y = 0.05 sample. This substantial reduction in κ demonstrates the effectiveness of Sb₂Te₃ and Pb alloying in suppressing thermal transport, which is crucial for enhancing the thermoelectric performance of GeSe-based materials.

Fig. 6: Thermal transport properties of (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples.

Temperature-dependent of a total thermal conductivity (κ) and b lattice thermal conductivity (κ_L). c Temperature-dependent and d room-temperature κ_L derived in the present work and other GeSe-based materials^{26,27,33,34,35,36,37,38,39,40,41,42,43,58,64}. Room-temperature (e) sound velocity (v_m) and f Grüneisen constants (γ) as a function of Sb₂Te₃ and Pb content. g Room-temperature κ_L as a function of Sb₂Te₃ content for (GeSe)_1−x(Sb₂Te₃)_x series. The red dotted line and bule dotted line represent the fitted κ_L considering the mass and strain contrast between Ge-Sb and Se-Te, and mass and strain contrast between Ge-Sb, Se-Te, and Ge vacancy, respectively. h Calculated spectral lattice thermal conductivity (κ_s) using the Debye-Callaway model. i Relationship between μ_W and 1/κ_L at 300 K in comparison with literature data^27,35,42.

The κ_L was calculated by subtracting the electronic contribution (κ_e) from the κ. κ_e was determined using the Wiedemann-Franz law⁶⁵, κ_e = LσT, where L is the Lorenz number estimated using the formula L = 1.5 + exp(−|S | /116) (Supplementary Fig. 15). Figure 6b visually illustrates the effect of Sb₂Te₃ and Pb alloying on κ_L. Notably, near room temperature, κ_L decreases progressively with increasing Sb₂Te₃ and Pb content. Specifically, room-temperature κ_L significantly decreases from 1.71 W m⁻¹ K⁻¹ for pristine orthorhombic GeSe to 0.72 W m⁻¹ K⁻¹ for cubic x = 0.10 sample, and further to 0.61 W m⁻¹ K⁻¹ for cubic x = 0.10, y = 0.05 sample. Remarkably, for the (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 sample, the κ_L reaches a minimum of 0.42 W m⁻¹ K⁻¹ at 723 K, approaching the amorphous limit of GeSe²⁴. Figures 6c, d compare the κ_L values obtained in this study with literature-reported data, revealing that the current κ_L values are among the lowest for GeSe-based thermoelectric materials. These findings highlight the exceptional ability of Sb₂Te₃ and Pb alloying to suppress κ_L and improve thermoelectric performance^{26,27,33,34,35,36,37,38,39,40,41,42,43,58,64}. Furthermore, pristine orthorhombic GeSe exhibits a κ_L ~ T^−1.21 trend, aligning with acoustic phonon scattering (κ_L ~ T^−1.0). Alloying with Sb₂Te₃ and Pb reduces the power law exponent. Specifically, the cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 sample demonstrates a κ_L ~ T^−0.45 trend, consistent with dominant alloy scattering (κ_L ~ T^−0.5).

To explore the mechanisms contributing to the reduction in κ_L toward the theoretical minimum for GeSe, the following factors can be identified. Firstly, according to the phonon transport model, v_m is a critical determinant of κ_L. v_m is influenced by the interatomic force constant (F), which reflects the chemical bond strength, and the atomic mass (M) according to ${v}_{{{{\rm{m}}}}}\propto \sqrt{F/M}$ ³¹. In orthorhombic GeSe, the strong CVB, where a pair of electrons is shared between neighboring atoms, results in rigid bonds and a higher v_m. In contrast, cubic GeSe with MVB, characterized by single-electron sharing between neighboring atoms, exhibits weaker chemical bonds, leading to a lower v_m. This reduction in bond strength is corroborated by the elongated bond lengths observed in XRD refinements (Fig. 2c) and the reduced bulk/Young’s modulus and Debye temperature listed in Supplementary Table 3, all indicating weaker bonds in cubic GeSe. Secondly, the replacement of Ge with heavier atoms like Sb and Pb, and Se with Te, further reduces v_m. For example, the room-temperature v_m decreases significantly from 2242 m s⁻¹ in pristine orthorhombic GeSe to 2139 m s⁻¹ in the cubic x = 0.10 sample and further to 2073 m s⁻¹ in the cubic x = 0.10, y = 0.05 sample (Fig. 6e). These mechanisms demonstrate how Sb₂Te₃ and Pb alloying effectively weaken the bonds and reduce the v_m, thereby suppressing κ_L and enhancing thermoelectric performance.

Additionally, lattice anharmonicity plays a critical role in controlling intrinsic phonon scattering by the Umklapp process (U-process), which significantly affects κ_L³¹. U-process scattering has been identified as the dominant phonon scattering mechanism in most thermoelectric materials⁶⁶. In contrast to the behavior of covalently bonded orthorhombic GeSe, the highly delocalized p-electrons in metavalently bonded cubic GeSe exhibit long-range interactions along the <100> direction. These interactions induce significant electron-transverse optical phonon coupling, which softens optical phonon modes and enhances lattice anharmonicity. The softened optical phonons strongly couple with heat-carrying acoustic phonons through anharmonic scattering, reducing the group velocity of acoustic phonons and expanding the phase space for Umklapp scattering processes⁶⁶. To quantify this effect, we calculated the Grüneisen parameter (γ), an indicator of lattice anharmonicity³¹. Higher γ values indicate greater anharmonicity, which, in turn, results in lower κ_L. As shown in Fig. 6f, at room temperature, γ increases from 1.36 in orthorhombic GeSe to 1.67 in the cubic x = 0.10 sample, and then gradually rises to 1.71 in the cubic x = 0.10, y = 0.07 sample. Additionally, we observed a slight decrease in γ (and a corresponding increase in v_m) with higher Sb₂Te₃ contents (x > 0.05), likely due to the influence of Sb₂Te₃ alloying on the phonon dispersion relationship. In summary, this increase in anharmonicity, driven by MVB and the softening of optical phonons, is a key factor in the further reduction of κ_L.

Additionally, Sb₂Te₃ and Pb co-alloying introduces substitution and vacancy point defects, disrupting the lattice periodicity and inducing mass and strain field fluctuations, which enhance phonon scattering. Therefore, a point defect scattering model was employed to simulate the impact of mass and strain contrast on κ_L^67,68, as illustrated in Fig. 6g. Specifically, we considered three types of point defects: Sb/Ge substitution, Te/Se substitution, and Ge vacancies. The simulation revealed that even with these combined scattering mechanisms, the experimentally observed κ_L in (GeSe)_1−x(Sb₂Te₃)_x is significantly lower than the theoretical predictions. This discrepancy suggests the presence of additional phonon scattering mechanisms beyond those considered in the point defect model. To further investigate the impact of multiscale microstructures on heat transport in the (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 sample, the Debye-Callaway model was applied to calculate the spectral lattice thermal conductivity (κ_s)⁶⁹ (Fig. 6h). This model accounted for various phonon scattering mechanisms, including Umklapp and normal processes (U + N), grain boundaries, substitutions, Ge vacancies, and Ge vacancy layers (detailed calculation parameters are provided in Supplementary Table 4 of the Supporting Information). The area between the two κ_s curves corresponds to the reduction in κ_L caused by each specific phonon scattering mechanism: grain boundaries primarily scatter low-frequency phonons, substitutions and Ge vacancies primarily impede high-frequency phonon transport, and planar defects significantly reduce κ_L by scattering mid-frequency phonons. In summary, the combination of weakened chemical bonding, strong lattice anharmonicity, and the presence of multiple phonon-scattering centers collectively reduces κ_L, bringing it closer to the theoretical minimum. These factors highlight the synergy between material design and multiscale defect engineering in optimizing thermoelectric performance. Besides, stabilizing cubic GeSe through non-stoichiometric metavalent Sb₂Te₃ alloying enables a synergistic optimization of electrical and thermal transport properties. This is clearly demonstrated by the correlation between the μ_W and the reciprocal of the κ_L (1/ κ_L) at 300 K (Fig. 6i)^27,35,42 and the temperature-dependent quality factor (β_B) (Supplementary Fig. 16) for (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples.

As shown in Fig. 7a and Supplementary Table 5, the cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 sample exhibits an optimized n_H, enhanced μ_H, increased m^*, and reduced κ_L, collectively leading to a maximum ZT (ZT_max) of 1.38 at 723 K, representing a remarkable 27-fold improvement compared to pristine orthorhombic GeSe, which shows a ZT_max of 0.05 at 673 K. This ZT_max is the highest reported to date for GeSe-based alloys, spanning orthorhombic, rhombohedral, and cubic structures (Figs. 1c, 7b)^{24,26,33,34,35,36,37,38,40,41,42,43,64}. Moreover, as illustrated in Fig. 7c, the ZT_ave values for samples with x = 0.10 across the y series consistently exceed 0.60, highlighting their excellent thermoelectric performance over a wide temperature range. These results underscore the significant potential of Sb₂Te₃-alloyed cubic GeSe for high-performance thermoelectric applications. Although trace amounts of Pb are incorporated in this work, its usage is reduced by an order of magnitude compared to traditional PbTe-based alloys. Moreover, there is an inherent trade-off between material toxicity and achieving high ZT values, as superior performance is essential for thermoelectric applications.

Fig. 7: Figure of merit, mechanical properties, and performance evaluation of device.

a Temperature-dependent ZT values for (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples. b Temperature-dependent ZT for cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1, comparing with those of other high-ZT cubic GeSe-based materials^38,42,43,47. c The average ZT (ZT_ave) values for the (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples. d Fracture toughness (K_IC), e Vickers hardness (HV), and f compression strength (σ_bc) at 300 K for the (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples. Current (I)-dependent (g) output voltage (V), h output power (P), and i η of a single-leg (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 device under various ∆T.

The mechanical properties of thermoelectric materials have become increasingly important as they determine their processability, operational stability, and cost-effectiveness in thermoelectric devices. Sb₂Te₃ and Pb alloying significantly enhance critical mechanical parameters, such as fracture toughness (K_IC), Vickers hardness (HV), and compressive strength (σ_bc). Pristine orthorhombic GeSe exhibits moderate mechanical properties, with K_IC of 0.36 MPa m^1/2, HV of 1.1 GPa, and σ_bc of 255 MPa (Fig. 7d–f). The introduction of Sb₂Te₃ leads to substantial improvements: for the cubic x = 0.10 sample, K_IC increases to 0.88 MPa m^1/2, HV rises to 1.8 GPa, and σ_bc reaches a peak of 495 MPa. Further substitution with Pb results in slight additional enhancements, with K_IC reaching 0.90 MPa m^1/2, HV improving to 2.1 GPa, and σ_bc climbing to 555 MPa. Since metavalent bonding is inherently weaker and associated with a high concentration of cation vacancies, cubic GeSe is expected to exhibit lower HV and σ_bc than orthorhombic GeSe. However, alloying with Sb₂Te₃ and Pb introduces significant solid-solution strengthening, enhancing HV and σ_bc beyond those of the original orthorhombic GeSe. Although solid-solution strengthening can sometimes reduce toughness, MVB acts as an intermediate state between localized covalent and delocalized metallic bonding, enabling materials to absorb and distribute strain more effectively under stress. This mechanism mitigates brittle fracture and enhances toughness, explaining the superior K_IC of Sb₂Te₃ and Pb co-alloyed cubic GeSe compared to its orthorhombic counterpart. This enhanced mechanical performance makes Sb₂Te₃- and Pb-alloyed cubic GeSe more suitable for practical thermoelectric applications, offering both improved durability and processability.

After achieving enhanced thermoelectric and mechanical performance, we fabricated a single-leg thermoelectric device using the optimized cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 sample and evaluated its performance with a custom-designed system. Figure 7g illustrates the current (I) and output voltage (V) characteristics of the single-leg device under various ΔT, with the cold-side temperature (T_c) maintained at 285 K. The internal resistance (R_in) of the device was calculated from the slope of the V-I curves, and the open-circuit voltage (V_OC) increased significantly as the hot-side temperature (T_h) rose from 523 to 723 K. Specifically, the V_OC increased from 49.6 to 98.9 V, while R_in decreased from 1.71 to 1.39 Ω. Concurrently, the V decreased linearly with increasing I. Figures 7h, i show the output power (P) and η as functions of I under different ΔT. Both P and η initially increased with I, reaching their maximum values when the external load resistance matched R_in, and then decreased. Ultimately, the single-leg device achieved a maximum power density of 0.21 W cm⁻² and a peak η of 6.13% under a ΔT of 430 K. The experimentally measured η remains significantly lower than the theoretical value of 8.36%, which can be attributed to several factors, including inconsistencies in the soldering process, heat losses within the testing apparatus, non-ideal characteristics of the thermoelectric model, dimensional inaccuracies, and measurement errors in the module⁷⁰. These factors highlight the need for further optimization of device fabrication and measurement techniques to fully realize the theoretical performance potential of the materials. Furthermore, the development of high-performance n-type GeSe-based alloys to complement their p-type counterparts is critical for fabricating efficient p-n legs in thermoelectric devices. This advancement represents a key area for future research and is essential for facilitating the industrial-scale application of GeSe-based materials.

In conclusion, we synthesized a series of (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x samples to explore the strategies for accelerating the orthorhombic-to-cubic phase transition in chalcogenides. Our findings reveal that only 10% metavalent Sb₂Te₃ alloying is sufficient to stabilize cubic GeSe under ambient conditions without the formation of detectable impurity phases. This stabilization is attributed to the high solubility of Sb₂Te₃ and its role in introducing additional cation vacancies. Compared to its covalently bonded orthorhombic counterpart, the metavalently bonded cubic GeSe exhibits a lower Ge vacancy formation energy, a narrower E_g, and higher valley degeneracy. The Sb₂Te₃ alloying further facilitates multivalley band convergence, enhancing orbital degeneracy, and optimizing n_H, improve μ_H, and increase m^*. These improvements lead to a significant enhancement in S²σ. Moreover, the weak chemical bonding, strong lattice anharmonicity, and multiple phonon-scattering centers in the cubic (Ge_1−yPb_ySe)_1−x(Sb₂Te₃)_x effectively suppress κ_L to 0.42 W m⁻¹ K⁻¹ at 723 K, approaching the amorphous limit of GeSe. As a result, cubic (Ge_0.95Pb_0.05Se)_0.9(Sb₂Te₃)_0.1 achieves an impressive ZT of 1.38 at 723 K and a peak η of 6.13% under a ∆T of 430 K in a single-leg thermoelectric device. These findings highlight the critical role of chemical bonding and vacancy engineering in facilitating the orthorhombic-to-cubic phase transition in chalcogenides and provide valuable insights for designing next-generation thermoelectric materials.

Methods

Synthesis procedure

All the GeSe-based samples were prepared using a systematic process involving melting, quenching, ball milling, and spark plasma sintering (SPS). High-purity element chunks of Ge, Se, Sb, Te, and Pb (≥ 99.999%, Beijing Yipin Chuancheng Technology Co., Ltd.) were weighed according to the stoichiometric compositions (GeSe)_1−x(Sb₂Te₃)_x (x = 0.05, 0.075, 0.10, 0.125, 0.15) and (Ge_1−yPb_ySe)_0.9(Sb₂Te₃)_0.1 (y = 0.03, 0.05, 0.07). The weighted materials were placed into quartz tubes with a 20 mm diameter and sealed under a vacuum of 10⁻³ Pa. The encapsulated mixtures were heated in a muffle furnace to 1323 K for 8 hours, held at this temperature for 10 hours, and then cooled to 1123 K, followed by rapid quenching in water. The resulting ingots were pulverized using a ball mill (MSK-SFM-3, MTI Corporation) at 1000 rpm for 25 minutes under vacuum. The resulting fine powders were then consolidated using SPS at 723 K for 5 minutes under a uniaxial pressure of 50 MPa, producing high-density cylindrical samples with a 20 mm diameter, suitable for microstructural analysis and thermoelectric performance evaluation.

Phase and microstructure characterization

The phase purities and crystal structures of the samples were analyzed at room temperature using XRD (Cu-Kα radiation, SmartLab, Rigaku®, Japan). Lattice parameters for the various crystal structures were determined via Rietveld refinement using the Fullprof Suite software⁵². The uncertainty in the XRD structural refinement was quantified as ± 0.002 Å. The chemical valence states were confirmed using XPS (Thermo ESCALAB 250, Japan) with monochromatic Al Kα radiation. Microstructural characterizations were conducted using SEM (Hitachi® SU-70, Japan) equipped with EDS, along with high-resolution TEM (HRTEM, FEI Titan Themis G2 300).

Thermoelectric performance measurement

The temperature-dependent σ and S were simultaneously measured using a ZEM-3 (Ulvac-Riko®, Japan) under a protective helium atmosphere, with the measuring error of 10% for σ and 7% for S. In this vein, the σ was measured using four-probe method and the S was measured by static direct-current methods. Thermal diffusivity (D) was determined by the laser flash method (LFA 467, Netzsch®, Germany), with the measure error of 3%. The sample density (d) was evaluated using the Archimedes method⁷¹, while the specific heat capacity (C_p) was estimated using the Dulong-Petit law⁷². The κ was then calculated using the formula κ = DdC_p. The κ_e was computed using the Wiedemann-Franz law⁷³, κ_e = LσT, where the Lorenz number (L) was estimated using the formula L = 1.5 + exp(−|S | /116)⁷⁴. Subsequently, the κ_L was derived by subtracting κ_e from the κ. The maximum measurement temperature for all samples was 723 K. The Hall coefficient (R_H) was measured at room temperature using the physical properties measurement system (PPMS-9, Quantum Design®, America). The uncertainty of R_H measurements was ± 5%. n_H and μ_H were calculated via the equation n_H = 1/e R_H and μ_H = σR_H, respectively. The longitudinal (v_l) and transverse (v_t) components of sound velocity were measured using an ultrasonic pulse receiver (MS-100, Ritec Laboratories, France).