Introduction

One of the ultimate goals of computational materials science is to rapidly identify promising material structures and compositions with specific properties to guide experimental scientists and automated laboratories1. This is particularly true in the time-critical fields of pharmacy and materials for energy and sustainability where a number of large scale autonomous experimentation initiatives are underway2,3. In the past decades, computational materials discovery has been achieved by going through large databases of existing materials and computing properties from first principles using methods such as density functional theory (DFT) and molecular dynamics4,5. These methods have proven to be successful in many cases6,7,8,9, but suffer from two main limitations: (1) they are computationally expensive and (2) they cover a small subspace of all possible materials.

In an effort to alleviate the first problem, machine learning (ML) based property prediction methods have become an integral part of materials science10,11. Various models exploit different materials representations (e.g., graphs, fingerprints)12,13, model architectures (e.g., neural networks, random forests)14 and datasets (experimental or computed) and their accuracy has been steadily increasing, often competing with that of DFT10. The success and adoption of these models is due largely to the powerful tools developed by the ML and data science communities (such as Pytorch15, Tensorflow16, Pandas17, etc.). However, despite their promising performance on benchmark datasets, ML property predictors still suffer from poor generalizability18, exhibiting much lower performance on out-of-distribution data, i.e., materials that are different from what they have been trained on.

Materials and molecule generation can alleviate the second limitation: it can theoretically explore the full space of all possible materials. Traditionally this has been done using minima hopping19, metadynamics20 and evolutionary approaches21,22,23, but machines can also learn to generate realistic materials4. The goal is no longer to predict properties but to predict realistic structures24. Materials and molecular generation using ML is a rapidly evolving field with a large body of recent methods including variational autoencoders25,26,27, flow-based models28,29, diffusion models30,31, models based on reinforcement learning (RL)32,33 and many others34,35.

In this paper, we exploit one of the most important and fundamental features of neural networks, their differentiability, to directly optimize a target property with respect to the graph representation itself starting from a pre-trained predictive model. This concept sometimes termed gradient ascent, or input optimization, has been used extensively in other fields36,37 and a similar idea has been applied to molecular generation with SELFIES38. Here we apply input optimization to molecular GNNs. We describe how carefully constraining the molecular representation makes this “naive” approach possible and show that it can generate molecules with requested properties as verified with density functional theory and empirical models. It does so with comparable or better performance than existing methods while consistently generating the most diverse set of molecules.

Results

Rationale and workflow overview

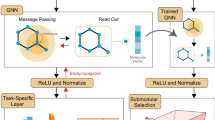
Our method can technically be applied to any GNN architecture that uses molecular graphs. To train our GNN we use (1) an explicit representation of the adjacency matrix, A, where non-zero elements are the bond orders and (2) a feature matrix, F, often referred to as a feature vector, that contains a one-hot representation of the atoms. These two matrices fully describe the graph and contain exactly the same information as a SMILES string. Since all functions in the GNN have well-defined gradients (allowing it to be trained in the first place), the adjacency matrix and the feature vector can be optimized through a gradient descent with respect to a target property as illustrated in Fig. 1. This is termed gradient ascent–although it does not change the direction of the gradients but rather, the variable with respect to which they are taken. This approach could be seen as a “naive” way to tackle the problem of conditional molecular and materials generation; unconstrained, it would lead to meaningless results that do not follow the basic structures of the adjacency matrix (e.g., its symmetry) and the feature matrix (e.g., one non-zero element per line). The major contribution of this paper is to enforce structural and chemical rules such that optimized inputs can only be valid molecules allowing for direct optimization into graph space.

Fig. 1: Key concepts of the generative framework.
figure 1

a Molecular representation for this work using an HCN molecule as an example. b A visual representation of a typical training process for a neural network in comparison to an input optimization scheme.

Full size image

The adjacency matrix is constructed from a weight vector wadj containing \(\frac{{N}^{2}-N}{2}\) elements. These elements are squared and populated in an upper triangular matrix with zeros on the main diagonal. The resulting matrix is then added to its transpose to obtain a positive symmetric matrix with zero trace. Elements of the matrix are then rounded to the nearest integer to obtain the adjacency matrix. The key element here is that the adjacency matrix needs to have non-zero gradients with respect to wadj, which is not the case when using a conventional rounding half-up function. To alleviate this problem we used a sloped rounding function,

$${[x]}_{{{{\rm{sloped}}}}}=[x]+a(x-[x])$$
(1)

where [x] is the conventional rounding half-up function and a is an adjustable hyper-parameter. These steps guarantee that only valid near-integer filled adjacency matrices are constructed. However, it does not take into account any chemistry: atoms are allowed to form as many bonds as there are rows in the adjacency matrix. To avoid that, we use two strategies: (1) we penalize valence (sum of bond orders) of more than 4 through the loss function and (2) we do not allow gradients in the direction of higher number of bonds when the valence is already 4.

The feature vector, on the other hand, is constructed directly from the adjacency matrix. The idea is to define the atoms from their valence, i.e., the sum of their bond orders. For example, a node with four edges of value one, or, in other words, an atom forming four single bonds, would be defined as a carbon atom, a node forming one double bond would be defined as an oxygen atom, a node forming a double bond and a single bond would be defined as a nitrogen atom, etc. In terms of matrices, this means that the sum of a row (or column) of the adjacency matrix defines the element associated with that row (or column).

To deal with an arbitrary number of elements that may have the same valence, an additional weight matrix wfea is used to differentiate between these elements. If the valence of an atom is 1, the weights of the corresponding row in wfea specify if this atom is H, F or Cl for example.

More details on how constraints on the adjacency matrix and feature vectors are implemented can be found in the supplementary information.

Energy gap targeting

The first task is to generate molecules with a specific energy gap μ between their highest occupied molecular orbital (HOMO) and their lowest unoccupied molecular orbital (LUMO). The HOMO-LUMO gap is a particularly interesting property because it is relevant to a number of applications, it is relatively expensive to compute and it is available in many databases39,40,41,42. Furthermore, the ability to generate molecules with a specific emission wavelength is of special interest to our own research on the discovery of efficient blue organic light emitting diodes (OLED) materials.

We trained a simple GNN proxy model on the QM9 dataset39 and used our direct inverse design procedure to generate 100 molecules with HOMO-LUMO gaps within 10 meV of 3 different target values: the first percentile of QM9 energy gaps, 4.1 eV, the median, 6.8 eV, and the 99th percentile, 9.3 eV. As an additional soft target, we aimed for atomic fractions (the relative number of each elements in the molecule) close to the average atomic fractions in QM9. This helps guide the generation towards molecules that the proxy can predict better.

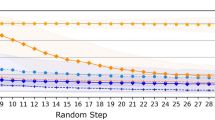
The results are illustrated in Fig. 2. Note that all generated molecules are within the requested range according to the proxy model by construction: generation stops when that criterion is met. The DFT-calculated energy gap, on the other hand, is distributed around the requested property with relatively small overlap between different targets.

Fig. 2: Generated molecules energy gap, density functional theory (DFT) and proxy predictions.
figure 2

Generated molecules are overlaid on the proxy model performance on the QM9 dataset (test + train) in grey. The shape and filling of the dots highlight different aspects of the generated molecule that may affect predictive performance. Open dots indicate a trait that can be detected before the calculation. Source data are provided as a Source Data file.

Full size image

The generated molecules predictions are overlaid on the predictions for the QM9 dataset. It is apparent that the proxy model’s performance is significantly worse on generated molecules than on the test set. If the model was generalizing perfectly, we should expect the performance to be similar to that of the test set, MAE=0.12eV, rather than the observed performance of about 0.8 eV. This highlights the importance of benchmarking generating schemes on DFT-confirmed properties, not solely on ML predicted properties.

We compared our method to JANUS35 an ML enhanced state-of-the-art genetic algorithm that was recently tested against several materials generations schemes on various benchmarks43. We chose to compare our method to a genetic algorithm, because of their prevalence, their performance44 and because, like our method they do not require any training other than that of the proxy model. We ran the algorithm directly with DFT as an evaluation function and with our proxy model; the results are presented in Table 1 and in Figure S6. Details of the calculations and JANUS model parameters can be found in the SI.

Table 1 Comparison of generated molecules from our procedure (DIDgen) with those generated with a state-of-the-art genetic algorithm (JANUS)35
Full size table

As a measure of performance, for each target, we counted the number of molecules within 0.5 eV of the target, the mean absolute distance from the target value and the average Tanimoto distance between Morgan fingerprints of each pair molecules within 0.5 eV of the target. In Table 1 we refer to our method as DIDgen, direct inverse design generator. DIDgen and JANUS are both able to significantly increase the proportion of molecules within the target range compared to a random draw of QM9 molecules. Our approach nearly matches or outperforms the genetic algorithm for all 9 metrics in Table 1.

DIDgen takes on average 12.0 s to generate an in-target molecule for 4.1 eV, 2.1 s for 6.8 eV and 10.4 s for 9.3 eV whereas JANUS takes about 100 s to generate 100 in-target molecules (1 s per molecule) for all targets using the same computer (4-CPU, 3.40 GHz). Timing varies significantly depending on the task and parameters used for both methods. DIDgen generates all molecules completely independently; all 100 molecules could be generated simultaneously. We did not implement batch generation with the use of a GPU, but it might significantly enhance performance in future versions.

logP targeting

The second task is to target a specific range of octanol-water partition coefficient (logP) values. It is relevant for drug discovery where logP can be used as a measure of cell permeability45,46. Most commercial drugs have a value between 0 and 5. In more recent studies in the field of ML, logP and penalized logP have been used extensively as a benchmark for generative models due to the existence of a cheap empirical model for logP developed by Wildman and Crippen45 sometimes called “Crippen logP” that is readily available in the RDkit47. Here we will use the same target range as33 which were used in several recent papers on molecular generation.

We trained “CrippenNet” a GNN developed specifically for this task on a subset of the ZINC dataset26,48 and QM939. More details about CrippenNet can be found in the Methods and in the supplementary information. For each of the two target ranges ([-2.5, -2], [5, 5.5]) we generated 1000 molecules and evaluated their diversity using the average pairwise Tanimoto distance–we evaluated the diversity of all generated molecules, not only the ones in the target range to be consistent with ref. 33. We limited the molecule size to 85 atoms (including hydrogens), again to be consistent with ref. 33. For this task generated molecules can contain the same element types as in the ZINC250 dataset: C, O, N, F, H, S, Cl, Br, I, and P. We initialized the generation with random molecules from QM9 because CrippenNet performed significantly better on these molecules.

The results are presented in Table 2 in comparison with refs. 25,27,32,33,34. DIDgen generates the most diverse molecules of all methods for both target ranges. When compared to other methods that use a trained proxy model as a predictor for logP, as opposed to the ground truth empirical model which we termed “oracle” in Table 2, DIDgen shows the highest performance by a factor of x4 and x2 respectively. However, it does not have a higher success rate then GCPN and SGDS which both use the oracle directly. This is not surprising since the success rate relies heavily on the proxy model performance and generalizability. All methods except JT-VAE could technically use CrippenNet which would offer a way to compare the generation schemes themselves separately of the proxy model’s performance (like we did for the energy gap task).

Table 2 LogP targeting to a certain range. Data from Ref. 34
Full size table

DIDgen takes on average 5.6 s to generate a molecule in the −2.5 to −2 range and it takes on average 3.4 s to generate a molecule in the 5 to 5.5 range on a local machine (4-CPU, 3.40GHz). The authors of LIMO report generating 33 molecules per second within the target range on 2 GTX 1080 Ti GPUs. Other authors did not report their compute times. Again, the performance of DIDgen could be improved with trivial parallelization and batch generation on GPUs.

Discussion

Generative methods like ours that use a learned proxy rely heavily on its performance, especially its ability to generalize in order to hit target properties. Models that can directly use an oracle do not always suffer from this limitation. For example, in the logP targeting task, the oracle was not computationally limiting and thus the number of evaluations was not taken into account. In that case, oracle-based methods had superior success rates. But since oracle evaluations are not costly, as pointed out by other groups of authors27, it would be easy to generate more molecules and filter out molecules that do not meet the criteria.

For instance, when targeting logP between −2.5 and −2, since the rate of success of DIDgen is about half of that of SGDS, we could simply generate twice as many molecules to obtain the same number of in-target molecules. Since the oracle is inexpensive, this would be easy to verify. In fact, the success rate metric makes little sense outside the context of budgeted (expensive) evaluations: in principle one can always make an algorithm that “generates” a molecule only if it reaches the target. For example, a genetic algorithm that would iterate until the entire population is inside the target range would achieve exactly that. The success rate becomes useful when one has a budget of x oracle evaluations and wants to obtain the highest number of true positives within that budget.

Furthermore, application-relevant properties are often computationally expensive and directly optimizing them is not an option, this is actually the case with the water-octanol partition (logP) which is difficult to evaluate precisely beyond Wildman and Crippen’s model49. The energy gap task is another example of that. In that case, we have seen that JANUS was able to find significantly more molecules in the target range when using a proxy than when using DFT directly because it could not go through enough generations within a reasonable time limit. So, even though JANUS does not require the use of a proxy, it clearly benefits from its use. This means that for a lot of applications, methods that can use an oracle will also end up being dependant on the performance and generalizability of an ML proxy.

In that same vein, inverting a predictive ML model with our method can be a good way to identify its weaknesses. For example, in the energy gap task, many of the generated molecules for which the proxy model was least accurate contained an O-O bond. The presence of that bond is particularly important for the large gaps (9.3 eV). As illustrated in Fig. 2, there is a group of generated molecules containing O-O bonds around a DFT gap of 8 eV which are all predicted to have a gap of around 9.3 eV. This explains, in part, the poor performance of the model on generated data. In the future, our method could be used as part of an active learning loop to iteratively improve the model generalizability, in this case, by retraining on a set of molecules containing O-O bonds, for example.

This drop in model performance is observed across all generated molecules including molecules generated with JANUS using DFT and with DIDgen using the Graph Isomorphism Network (GIN)50. To verify if this drop in performance would also affect more complex models, we trained, PaiNN51, an equivariant message passing network on QM9 and tested its performance on generated molecules. Despite having a much lower MAE on QM9 data (0.048 eV vs. 0.12 eV), PaiNN performed worse than our model on generated molecules with an MAE of 1.16 eV versus 0.96 eV for our model (see Figure S7 and Table S2). This suggests that generating molecules might be a good way to obtain out of distribution data that could be used for benchmarking and fine-tuning ML models. As a first step in that direction, we provide on our public repository a dataset of 1617 unique generated molecules with their corresponding DFT relaxed 3D coordinates as well as their dipole moments, HOMO energy, LUMO energy and energy gap. This data was generated to obtain Table 1 and Table S1.

Another way to evaluate the performance of generative models that is independent of the evaluation method is to measure their ability to generate diverse molecules. On that metric, our method performed better than all other methods we have tested it against. This is important because for any application, new materials must simultaneously meet multiple criteria that cannot all be modeled and optimized for. For example, molecules for display applications must emit light of a certain color, but they must also be synthesizable, bright, stable, cheap, safe, soluble, etc. Generating a more diverse set of molecules simply increases the chances that one of the generated molecules will meet multiple of these criteria.

The inversion procedure presented here can be used on any GNN architecture that uses molecular 2D graphs (like SMILES), but it requires modifying them so that they use an explicit representation of the adjacency matrix which may require retraining. This can be a limiting factor for the adoption of our procedure. To help ease this process, in addition to the implementations of our simple energy gap GNN and CrippenNet, we implemented and tested 5 commonly used GNNs: Graph Isomorphism Network (GIN)50, Graph Attentions Networks (GATs)52, GraphSAGE (SAmple and aggreGatE)53, Graph Convolutional Network (GCN)54 and Crystal Graph Convolutional Neural Networks (CGCNN)55. For GIN, GAT, GraphSAGE and GCN, we started from the implementations found in ref. 56. These models can either be used directly to train and generate, or as a starting point to implement other models. For example, we performed the energy gap targeting task with GIN and compared the properties of the generated molecule with DFT. The model predictive performance matched the literature without any hyper-parameter tuning and the generation performance was slightly worse than when using our GNN. Detailed results are presented in the SI.

In conclusion, we demonstrated that by carefully constraining the representation of molecules, a property predicting GNN can be turned into a diverse conditional generator without any additional training. Our method is a literal implementation of the inverse design paradigm: properties are put in and materials are obtained going backwards through a pipeline that is built to do the opposite. Although it is a “naive” way to approach this problem, we showed that it rivals with complex state-of-the-art models. Ultimately, we hope that will help accelerate the design and discovery of functional materials.

Methods

Training of the property predictors

Since optimizing the inputs (generating molecules) will require an explicit representation of the adjacency matrix, sparse matrices and lists of edge indices cannot be used during training of the property predictor GNN. Mini-batching using a single adjacency matrix per batch thus uses a large amount of memory that scales quadratically with the total number of atoms in a batch. To avoid that issue, we use a fixed graph size (N) instead which allows us to store the adjacency matrices as a B × N × N array where B is the batch size. Empty rows of the adjacency matrix are associated with atoms of type “no-atom” in the feature vector one-hot encoding. This allows for molecules of any size smaller than N.

Although sloped rounding and maximum functions guarantee that the adjacency matrix and the feature vector are populated with near-integer values, these values are not exactly integers and these variations around integer values can have a significant impact on the property predicated by the GNN. To make the GNN less sensitive to these variations, we add a small amount of random noise around integer values of A and F during training.

For the energy gap task, we used a simple graph convolutional network (GCN) with an adjustable number of convolutions, a pooling layer and an adjustable number of linear layers. We trained this model on the QM9 dataset containing approximately 130000 small molecules for which the energy gap was calculated with density functional theory (DFT). With manual hyperparameter tuning, we obtain a mean absolute error of about 0.12 eV on the test set which is on par with other models using the same amount of information (2D graphs, no coordinates)39. More details on this model can be found in the SI.

For the LogP task, we use CrippenNet a graph neural network that we developed based on the structure of Crippen’s empirical model. CrippenNet classifies atoms inside molecules as one of 69 classes associated with a logP value and then sums the individual contributions of each atom to obtain the total logP of the molecules. In the empirical model, each of these classes is defined by certain properties described by SMARTS string. For example, class #18 is an aromatic carbon atom and its associated logP is 0.158145. In CrippenNet the classes are learned from the graph of the molecule by training on a subset of the ZINC dataset48 containing 250,000 molecules (the same subset used in Ref. 26) and QM9. More details on CrippenNet can be found in the supplemental information. Our goal was to get a model that resembles the ground truth model as much as possible in order to be as close as possible to directly inverting it. Note that it may be possible to obtain a perfect classification from the graph representation of the molecule in which case DIDgen’s success rate would be 100%. This would require a careful analysis of the SMARTS classes and their resulting convolutions.

DFT validation of the energy gap

For each generated molecule, we obtained the conformation (3D atomic positions) using the RDKit. In some cases no conformation could be obtained from the generated molecule. In those cases, the molecule was discarded and a new molecule was generated until a total of 100 molecules with conformation were obtained for each target. About 19% of initially generated molecules were discarded when targeting 4.1 ev, 2% when targeting 6.8 eV and 1% when targeting 9.3 eV.

For all 300 molecules, we performed density functional theory calculations to obtain the “true” HOMO-LUMO gap. For consistency, we used DFT parameters as close as possible to Ramakrishnan et al.39. We fully relaxed the molecules and obtained the HOMO-LUMO gap with B3LYP/6-31G(2df,2p) as implemented in ORCA57.

Loss function for the inversion procedure

In order to improve generative performance, we added a simple additional term (Lc) to the loss function: the average atomic fraction, Ci, in QM9 for each element i, i.e. the fraction of all atoms that are of type i. The total loss for this task was the following:

$$L=\frac{{\lambda }_{l}{L}_{l}^{2}+{\lambda }_{s}{L}_{s}^{2}+{\lambda }_{c}{L}_{c}^{2}}{{\lambda }_{l}+{\lambda }_{s}+{\lambda }_{c}},$$
(2)

where

$${L}_{c}={\sum}_{i}\frac{{\sum }_{j}{F}_{ij}}{{\sum }_{ij}{F}_{ij}}-{C}_{i},$$
(3)

Ll is the root mean square error with respect to the target p, Ls is the loss associated with the maximum valence defined in equation S1 of the supplementary informatio, F is the feature vector and λl,s,c are adjustable hyperparameters. Generated molecules with balanced valence could include molecules with disproportional amounts of certain elements (by replacing all H with F, for instance). The idea of this loss is to steer the generation away from these cases for which the proxy model would underperform and where there would likely be no valid conformation. It is a very simple example of how the loss can be used to guide generation towards molecules with desirable properties. More complex co-objectives such as accessibility scores could be used in the future.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.