A self-conformation-aware pre-training framework for molecular property prediction with substructure interpretability

Abstract

The major challenges in drug development stem from frequent structure-activity cliffs and unknown drug properties, which are expensive and time-consuming to estimate, contributing to a high rate of failures and substantial unavoidable costs in the clinical phases. Herein, we propose the self-conformation-aware graph transformer (SCAGE), an innovative deep learning architecture pretrained with approximately 5 million drug-like compounds for molecular property prediction. Notably, we develop a multitask pretraining framework, which incorporates four supervised and unsupervised tasks: molecular fingerprint prediction, functional group prediction using chemical prior information, 2D atomic distance prediction, and 3D bond angle prediction, covering aspects from molecular structures to functions. It enables learning comprehensive conformation-aware prior knowledge, thereby enhancing its generalization across various molecular property tasks. Moreover, we design a data-driven multiscale conformational learning strategy that effectively guides the model in understanding and representing atomic relationships at the molecular conformational scale. SCAGE achieves significant performance improvements across 9 molecular properties and 30 structure-activity cliff benchmarks. Case studies demonstrate that SCAGE accurately captures crucial functional groups at the atomic level, which are closely associated with molecular activity, providing valuable insights into quantitative structure-activity relationships.

Introduction

Despite recent advances in medicinal chemistry and pharmacology, the discovery and development of new drugs continues to be constrained by a multidimensional challenge that requires a comprehensive balance of various drug properties^1,2. Drug development is a costly and risky process, with 90% of drug candidates failing during clinical phases due to the high cost of experimental trials and inadequate biomedical properties^3,4. Thus, conducting full-scale experimental evaluations on millions of drug-like candidates in high-throughput scenarios is not advisable. To address this issue, various computer-aided methods^5,6, especially the artificial intelligence-based methods^7,8, have been developed, offering promising prospects for accelerating drug discovery and development.

As a burgeoning field of artificial intelligence, deep learning for drug discovery has attracted interdisciplinary attention and has been applied to a variety of biomedical challenges, including protein-ligand design^9,10, drug response^11,12, bio-sequence binding site predictions^13,14. Leveraging large-scale molecular data to guide the above biomolecule-related tasks is beneficial. To this end, Molecular Pretrained Models (MPMs) have emerged^15,16,17,18. From the perspective of molecular representations, recent molecular pretraining frameworks can be categorized into sequence-based, 2D graph-based, 3D graph-based and image-based approaches. Sequence-based approaches focus on understanding chemical rules using natural language processing (NLP) architectures. In this approach, molecules are typically represented as 1D strings (e.g., SMILES, etc.). For instance, Irwin et al.¹⁹ proposed Chemformer, a sequence-based BART²⁰ model pretrained on 0.47 million reactions and 100 million molecules, in which the molecules are represented with SMILES. Chithrananda et al.²¹ and Ahmad et al.²² developed ChemBERTa and ChemBERTa-2, respectively, pretrained on 77 million PubChem²³ data through a predictive multitask approach. However, the intrinsic limitation of the sequence-based approaches lies in ignoring the structural information representation. To address this issue, 2D graph-based approaches transform molecules into 2D molecular graph and utilize graph neural network to pretrain and learn the molecular structural representations. In this approach, molecules are represented as 2D molecular graphs, where atoms are depicted as nodes and chemical bonds as edges. Rong et al. proposed GROVER¹⁷, a self-supervised graph transformer framework pretrained on 10 million molecules, which addresses challenges such as insufficient labeled molecules and poor generalization to newly synthesized molecules. Wang et al.²⁴ introduced three contrastive-based tasks, utilizing 10 million unlabeled graph molecules for model pretraining. Fang et al. also proposed KANO²⁵, a contrastive learning method enhanced by knowledge graphs, incorporating functional group information as a priori knowledge. Although 2D molecular graphs can represent molecular structures to some extent, they cannot capture the 3D spatial structural information of molecules. To overcome this limitation, 3D graphs are introduced to enhance molecular representation. Fang et al.²⁶ introduced conformation and bond-angle graphs, pretrained on a 20-million scale, and implemented a geometric-level self-supervised learning task by constructing 3D molecular maps. Zhou et al. proposed Uni-Mol²⁷, which extends the representation capability and application of molecular representation learning schemes by rationally integrating 3D information. More recently, Yang et al.²⁸ introduced MolAE, which uses an a priori training dataset of 19 million molecules and 209 million conformations, employing positional coding as atomic identifiers to learn spatial relationships between atoms from real molecular substructures.

Unlike the molecular representation methods mentioned above, image-based approaches represent molecules at the pixel level with the aid of computer vision techniques. Zeng et. al²⁹. proposed ImageMol, employing five independent learning strategies on 10 million unlabeled images of drug-like compounds. These strategies include Multi-Granularity Chemical Clusters Classification (MG3C), molecular image reconstruction, image mask contrastive learning, molecular rationality discrimination, and jigsaw puzzle prediction. Together, they address multiple aspects of pretraining, focusing on consistency and chemical plausibility.

The performance of the pretraining approaches for molecular property prediction discussed above is still limited due to several key challenges in molecular representation learning. (1) Most of existing methods mainly focus on the representation learning from molecular structures (e.g., 2D and 3D structures)^26,27. However, existing methods typically employ pretraining tasks leveraging 3D structures to facilitate learning 3D molecular representations. In contrast, few approaches integrate 3D information directly into the model architecture to guide molecular representation learning. (2) Functional groups, defined as specific atoms or groups of atoms with distinct chemical properties, play a crucial role in determining molecular characteristics. However, previous methods involving functional groups are limited either by the small number of recognized functional groups³⁰ or by their inability to model functional groups accurately at the atomic level²⁵. It easily leads to the insufficient capture of the molecular functional characteristics. (3) Incorporating the learning of molecular spatial structure information into pretraining tasks has proven effective^27,31,32. However, when multiple pretraining tasks are involved, their contributions to model learning vary. Existing methods struggle to achieve an effective dynamic balance among these tasks.

To address the challenges, we propose self-conformation-aware graph transformer (SCAGE), an innovative deep learning architecture pretrained with conformational knowledge from ~5 million drug-like compounds. This architecture is designed to adaptively learn generalized representations for a wide range of downstream tasks. To achieve expressive and robust molecular representations, we developed a multitask pretraining paradigm called M4, which integrates both supervised and unsupervised tasks. The M4 framework guides molecular representation learning through four key tasks: molecular fingerprint prediction, functional group prediction with chemical prior information, 2D atomic distance prediction, and 3D bond angle prediction. These enable the capture of comprehensive molecular semantics, from structures to functions. We demonstrate that the proposed multitask pretraining strategy adaptively balances the loss across these tasks, outperforming existing pretraining approaches. Moreover, we designed an innovative functional group annotation algorithm that assigns a unique functional group to each atom, enhancing the understanding of molecular activity at the atomic level. Additionally, we innovatively introduce a data-driven Multiscale Conformational Learning (MCL) module, which effectively and directly guides our model in understanding and representing atomic relationships across different molecular conformation scales, eliminating the need for manually designed inductive biases present in existing methods. Through attention-based and representation-based interpretability analyses, we demonstrate that SCAGE can identify sensitive substructures (i.e., functional groups) closely related to specific properties, effectively avoiding activity cliffs. Case studies on the BACE target further validate that SCAGE accurately identifies sensitive regions of query drugs, with results highly consistent with molecular docking outcomes. This underscores SCAGE’s potential in uncovering quantitative structure-activity relationships (QSAR) and accelerating drug discovery.

Results

Framework of proposed SCAGE

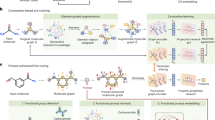
The framework of our SCAGE is illustrated in Fig. 1. It follows a pretraining-finetuning paradigm, comprising two parts: a pretraining module for molecular representation learning and a finetuning module for the prediction of downstream molecular property tasks (Fig. 1a). The two modules of SCAGE are described below.

Fig. 1: The overview of our SCAGE framework.

a Workflow of SCAGE. It follows the pretraining-finetuning paradigm. The pretraining phase involves four tasks: molecular fingerprint (FG) prediction, functional group prediction, 2D atom-atom distance prediction, and 3D bond angle prediction. Subsequently, finetuning is performed for molecular property prediction and activity cliff tasks. Finally, the molecular properties are predicted and analytically explained. b Model architecture. We represent chemical molecules as 2D molecular graphs, where nodes represent atoms and edges represent chemical bonds. Stable molecular conformations are generated using the Merck Molecular Force Field (MMFF). Molecular representations are extracted from the 2D graphs using a Graph Transformer, while the Multiscale Conformational Learning Module to mask attention scores based on interatomic distances. The resulting atomic-level representations and graph-level representations are processed through a Multi-Layer Perceptron (MLP) to obtain molecular embeddings. c Pretraining module and Dynamic Adaptive Multitask Learning algorithm. The atom or molecule embeddings generated by the model are used to compute losses for the four pretraining tasks. These tasks include: predicting Morgan fingerprints, identifying each atom’s functional group, learning the 2D atomic distance matrix, and predicting 3D bond angles between chemical bonds. The weights of these losses are then dynamically optimized to balance the contributions of each task. ${{\mathcal{l}}}_{i}^{t}$ denotes the $i$ th kind of loss score in the $t$ th iteration. The ${{\mathcal{l}}}_{i}^{{avg}}$ represents the average of $i$ th type of loss value over the loss queue from ${{\mathcal{l}}}_{i}^{t}$ to ${{\mathcal{l}}}_{i}^{t-n}$, where $n$ is the length of queue we take into consideration. ${{\rm{X}}}_{i}^{t}$ is the obtained weight of the $i$ th kind of loss score at the $t$ th iteration.$\tau$ is a temperature coefficient. $W$ is the weight of each loss when finetuning the task. The algorithm derives weights from loss decline rates and value ranges to balance the optimization of the four tasks. d Functional group annotation algorithm. We first obtain functional group species information from Wikipedia, Daylight, and other motif databases. Each atom in a molecule is annotated with functional group information. In the molecular diagram, different colors represent distinct functional groups.

In the pretraining module, the given molecules are initially transformed into molecular graph data. To effectively explore the spatial structural information, we utilize the Merck Molecular Force Field (MMFF) to obtain stable conformations of the molecules (Fig. 1b). Among these conformations, we select the lowest-energy conformation, as it represents the most stable state of the molecule under the given conditions. To ensure the robustness of our approach, we conduct additional experiments using conformations with varying energy levels. While the local minimum conformation does not always yield the highest prediction accuracy, it produces optimal results in most cases (Supplementary Table S1). Consequently, we choose the local minimum conformation for our experiments to balance stability and predictive performance. Next, the molecular graph data is input into a modified version of a graph transformer, which incorporates an MCL module (Fig. 1b) designed to learn and extract multiscale conformational molecular representations. This enables us to capture both the global and local structural semantics of the molecules. Afterwards, SCAGE is pretrained using a multitask learning architecture on ~5 million molecular graph data along with their conformations. For convenience, the architecture is referred to as M4, as it includes four pretraining tasks: molecular fingerprint prediction, functional group prediction, 2D atomic distance prediction, and 3D bond angle prediction (Fig. 1c). To adaptively optimize and balance these tasks, we introduce a Dynamic Adaptive Multitask Learning strategy (Fig. 1c), which learns comprehensive semantics from molecular structures to functions and improves the generalization of the model. Notably, we propose a functional group annotation algorithm that assigns a unique functional group to each atom, thereby enhancing the understanding of molecular activity at the atomic level (Fig. 1d).

After model pretraining, in the finetuning module, the well-pretrained SCAGE is finetuned on molecular property and activity cliff tasks. For instance, in the context of molecular toxicity prediction, the pretrained SCAGE model is first finetuned on the toxicity dataset. It then quantitatively predicts whether the query molecules are toxic or not.

Performance comparison of SCAGE and state-of-the-art approaches on benchmark datasets

Performance comparison for molecular property prediction

To comprehensively evaluate SCAGE for molecular property prediction, we conducted experiments on nine widely used benchmark datasets encompassing diverse attributes, such as target binding, drug absorption, and drug safety (Supplementary Table S2). We compared SCAGE’s performance with state-of-the-art baseline approaches: MolCLR²⁴, KANO²⁵, GEM²⁶, ImageMol²⁹, GROVER¹⁷, Uni-Mol²⁷, and molAE²⁸. To ensure fairly evaluate these methods on the datasets, we did the following experimental setting. First, we employed scaffold split³³ and random scaffold split³⁴ strategies for dataset split. The difference between the two strategies is that dividing the dataset into disjoint training, validation, and test sets is based on different molecular substructures. The scaffold split is a method based on the skeleton structure, ensuring that the difference in skeletons between the training and test sets is maximized. The random scaffold split introduces randomness to the data segmentation. Thus, the performance evaluation under scaffold split is generally more stringent than that under random scaffold split. It is worth to note that for random scaffold split, we used the results of the baseline methods reported in previous study²⁹, which ensures the same evaluation setting. We also followed the same setting to evaluate our SCAGE for fair comparison. Second, all the methods were performed for 10 trials with 10 random seeds, and the mean and standard deviation are calculated for each method. Third, the same evaluation metrics are used. Since the datasets include two task types: classification and regression tasks, the area under the receiver operating characteristic curve (AUC-ROC) is often used as the evaluation metric for classification tasks while the root mean square error (RMSE) is applied to regression tasks. To this end, Tables 1 and 2 summarize the comparison between SCAGE and other state-of-the-art (SOTA) approaches on the molecular property benchmarks with scaffold split and random scaffold split, respectively.

Table 1 Overall performance of our SCAGE and state-of-the-art methods on nine molecular property benchmarks with scaffold split

Table 2 Overall performance of our SCAGE and state-of-the-art methods on nine molecular property benchmarks with random scaffold split

We observed the following: (1) For the scaffold split, no single method achieves optimal performance across all nine datasets. However, SCAGE outperforms other methods on eight datasets, while the other methods only achieve optimal performance on at most two datasets. For random scaffold split, SCAGE achieve optimal performance on all methods. (2) Notably, in the scaffold split evaluation, SCAGE surpasses ImageMol with a 10.8% relative improvement in AUC and MolAE with a 2.2% relative improvement in AUC on the BACE dataset. On the ClinTox dataset, SCAGE surpasses Uni-Mol and MolAE by 6.2% and 16.3%, respectively, highlighting SCAGE’s effectiveness in tasks with limited labeling information and its significant performance improvement on small datasets. In the random scaffold split evaluation, SCAGE achieves a 3.7% relative improvement in AUC over the suboptimal method, ImageMol, on the SIDER dataset. (3) As for the regression tasks, SCAGE achieves a 3.4% improvement on the lipophilicity dataset and 2.1% on the FreeSolv dataset in scaffold split. Although SCAGE does not achieve the best performance on the ESOL dataset, it achieves an average improvement of 42.5% compared to ImageMol and Uni-Mol. Notably, SCAGE achieves SOTA performance across all regression tasks using random scaffold split, with an average improvement of 12.8%. Specifically, it demonstrates a 29.7% gain on the FreeSolv dataset and a 4.9% gain on the ESOL dataset. These improvements suggest that SCAGE may adopt a more effective strategy for capturing lipophilic or hydrophilic groups, which are highly related to solubility. In general, our SCAGE outperforms existing methods in molecular property prediction tasks. Moreover, it is worth noting that as compared to other pretraining approaches, our SCAGE used far less pretraining data—only one-quarter of the data used by the runner-up method, Uni-Mol (see details in Supplementary Table S3). Although our method and Uni-mol use different pretraining data sources, our approach uses PubChem²³, which offers comprehensive chemical and bioactivity information. In contrast, Uni-mol employs ZINC³⁵, a dataset more rigorously curated for specific tasks such as drug development and virtual screening. This further demonstrates the superiority of our method.

Performance comparison for activity cliff prediction

We further evaluated SCAGE’s performance on the activity cliff prediction task using a total of 30 activity cliff datasets derived from Tilborg et al.³⁶. Several baseline methods, including AFP³⁷, CNN³⁸, GAT³⁹, GCN⁴⁰, MPNN⁴¹, ImageMol²⁹, and GEM²⁶, were chosen and evaluated on the same datasets. The ability of each method to predict biological activity, measured as pEC50 or pKi, in the presence of activity cliffs was assessed. Note that all the compared methods followed a consistent evaluation protocol across the datasets³⁶. The predictive performance was quantified using the root mean square error (RMSE) and RMSE_cliff. RMSE reflects the quantification of the model’s performance with respect to the bioactivity values, whereas the RMSE_cliff calculations are performed so that compounds belonging to at least one activity cliff pair can be considered, thus reflecting the quantification of the activity cliff compounds. The calculation details of the metrics are provided in the section “Evaluation Metrics.”

Figure 2 illustrates the predictive results across the 30 activity cliff datasets. Detailed results are presented in Supplementary Tables S4 and S5. Our observations are as follows: (1) Compared to baseline models, our model demonstrates superior performance across all 30 datasets in terms of RMSE. Specifically, it achieves SOTA on 23 datasets and ranks second on another six datasets in terms of RMSE_cliff (see Supplementary Tables S4 and S5). (2) As shown in Fig. 2a, b, our method yields lower error values, with RMSE values ranging from 0.405 to 0.881. In contrast, RMSE values range from 0.468 to 1.003 for ImageMol and from 0.466 to 0.926 for GEM. (3) To further investigate the importance of considering activity cliffs in model evaluation, we compared RMSE_cliff to the overall error for the test set molecules. Regardless of the method, compounds associated with activity cliffs tended to exhibit higher prediction errors. This highlights that overall error alone is insufficient for evaluating models on activity cliff compounds. SCAGE balances performance on RMSE_cliff while achieving excellent results on the RMSE metric (Fig. 2b, c).

Fig. 2: Performance of methods on the active cliff dataset.

RMSE represents the root mean square error for the entire dataset. RMSE_cliff represents the root mean square error for the subset of molecules with active cliffs. SCAGE is our proposed method. AFP³⁷, CNN³⁸, GAT³⁹, GCN⁴⁰, MPNN⁴¹, ImageMol²⁹, and GEM²⁶ are our compared methods. a RMSE and RMSE_cliff results across $n$=30 datasets using various methods. Each result is the average of 10 replicate experiments using different random seeds. Center line shows the median; box limits represent the 25th (Q1) and 75th (Q3) percentiles; whiskers extend to 1.5× interquartile range (IQR); points are outliers beyond whiskers. b Each violin plot RMSE and RMSE_cliff use the distribution of results across $n$=30 datasets for various methods. Each result is the mean deviation of n = 30 methods in (a). The left and right sides indicate the probability density distribution of the data. The central bold line indicates the interquartile range (25th to 75th percentile), while the black dot indicates the median (50th percentile). c Errors for all methods for active cliff compounds (RMSE_cliff) compared to errors for all compounds (RMSE). Colored dots indicate the predicted results of the method. Gray dots indicate the results of all other methods. The black dashed line indicates RMSE = RMSE_cliff, while the gray dashed line indicates a difference of ±0.25 between RMSE_cliff and RMSE.

MCL is effective for capturing spatial structural information of molecules

To investigate the impact of the Multiscale Conformational Learning (MCL) module on model performance, we conducted a comparative study using molecular conformations of varying scales on the MoleculeNet⁴² and Active Cliffs³⁶ datasets. We introduce the concept of a receptive field, which defines a distance threshold. For a given atom, information from other atoms is excluded if their distance from the atom exceeds this threshold, ensuring that only local interactions within the specified range are considered. The receptive field can be defined either as a single value or as a combination of values, with each value referred to as a threshold. These thresholds represent specific distance limits that determine the extent to which atomic information is considered for a given atom within a molecule. When multiple values are utilized, the receptive field is established by the combination that best corresponds to the atomic information, enabling the model to adaptively capture interactions at varying spatial scales.

First, we employ a percentage-based threshold to define the receptive field. In this approach, the threshold is expressed as a percentage of the maximum distance between atoms within a molecule. This percentage is then used to calculate a corresponding absolute distance threshold for each molecule, allowing the receptive field to adapt dynamically based on the molecular structure. We compared the use of 2D topological distance (Shortest paths between atoms on a 2D graph) and 3D conformational distance (atomic distances in 3D graph). As shown in Fig. 3a, b, the use of 3D conformational distance led to better predictive performance. Next, we explored the combination of two thresholds, based on the 3D conformational distance, to identify which scale combinations enhance model learning. The multiscale information can be adaptively adjusted according to molecular conformations (see the “Multiscale Conformational Learning Module” section). Figure 3c illustrates that, for most datasets, the model demonstrates the best learning ability when the combination of thresholds falls within the 20% to 60% range. This suggests that focusing too narrowly on small scales captures only local information, neglecting global features, while large scales emphasize global features at the expense of local details. In the task involving three thresholds (Fig. 3d), the optimal values also cluster around the 50% scale, indicating that the performance distribution is similar to that observed with two-threshold combinations, further validating our previous conclusions. Finally, we compare the model’s performance with a fixed receptive field threshold (Fig. 3e). In this case, the model underperforms compared to our multiscale module, which adapts according to molecular conformation. For small molecules, a fixed threshold of 3 might approximate global coverage, leading to homogeneity in the neighborhood information captured by each atom, making them indistinguishable. In contrast, MCL, based on conformationally adaptive scales, effectively resolves this issue by aggregating information from different scales, enabling each atom to adaptively focus on key information.

Fig. 3: The impact of multiscale conformational learning module.

Each statistic in the figure is the average of the results of ten runs using different random seeds. a Using one atom as a benchmark, we select 30% and 60% of its 2D distance to calculate the receptive field. b Results for eight of the datasets (BACE, BBBP, ClinTox, Tox21, CHEMBL1862_Ki, CHEMBL204_Ki, CHEMBL231_Ki and CHEMBL233_Ki)^36,42 using a single threshold. For each dataset, the experiment was repeated with $n$=10 different seeds, and the resulting figures were plotted. Blue and red colors represent the selection of receptive field based on 2D and 3D distance, respectively. The colored area represents the data distribution. For the four curves on the left, the x-axis represents the AUC value, with higher values indicating better performance. For the four curves on the right, the x-axis represents the RMSE value, with lower values indicating better performance. c Results using two thresholds on eight datasets (BACE, BBBP, ClinTox, Tox21, CHEMBL231_Ki, CHEMBL233_Ki, CHEMBL244_Ki and CHEMBL287_Ki)^36,42. Each subplot shows the effect of combining distance bars across different datasets. Darker colors represent higher values. The horizontal axis represents thresholds ranging from 20% to 100%, while the vertical axis represents thresholds from 10% to 90%. The receptive field corresponding to the point with the best value is labeled by diamonds. The mean value of the results for each row and column are given by the bar plots. d Results using three thresholds on four datasets (BACE, ClinTox, CHEMBL231_Ki and CHEMBL233_Ki)^36,42. Each plot contains $n$=120 sample points, ensuring the condition receptive field 1 <receptive field 2 <receptive field 3. Each point represents the mean result over ten seeds. Red-labeled points indicate optimal values, with their projected coordinates marked by dashed lines. e A comparison of using fixed thresholds versus percentage-based thresholds on four datasets (BACE, ClinTox, CHEMBL231_Ki and CHEMBL233_Ki)^36,42.1, 2, and 3 represent visual distances as spatial distances 1, 2, 3. Percent represents thresholds calculated from our percentages. Data are presented as mean ± standard deviation. Source data are provided as a Source Data file.

Proper pretraining tasks learn generic molecular representations to improve molecular property prediction

Firstly, we investigated how different pretraining tasks influence the performance of SCAGE for molecular property prediction. Figure 4a, b illustrate the performance of various pretraining tasks across four datasets from MoleculeNet and Active Cliffs, respectively. As observed, combining all four tasks simultaneously for model pretraining yields the best performance. In contrast, using any single pretraining task alone results in performance degradation. This indicates that different pretraining tasks may complement each other, contributing to improved performance.

Fig. 4: A study of pretraining tasks.

The AUC represents the area under the receiver operating characteristic curve and the RMSE represents root mean square error. The results of the ablation experiments are established at the default parameter settings. a Finetuning results of various pretraining tasks on the MoleculeNet dataset. Each pretraining task was repeated $n$=10 repetitions using different random seeds. The metric displayed in the graph is the AUC value or RMSE. The top and bottom edges of the graph represent the maximum and minimum values, respectively, while the left and right sides illustrate the probability density distribution of the data. The red dot in the center indicates the median. The w/o pretrain represents not loading the pretrained model. “FG” represents functional group prediction task. “Finger” represents molecular fingerprint prediction task. “SP” represents 2D atomic distance prediction task. “Angle” represents 3D bond angle prediction task. The red dashed line indicates the average performance in the case of using all pretrained tasks. b Finetuning results of different pretraining tasks on the Active Cliffs dataset. Each pretraining task was repeated $n$=10 repetitions using different random seeds. The metrics in these graphs are RMSE values. The top and bottom edges of the graphs represent the maximum and minimum values, respectively, while the left and right sides depict the probability density distribution of the data. The red dot in the center indicates the median. The red dashed line indicates the average performance in the case of using all pretrained tasks. c Analysis of pre-training representation capacity. We evaluate the representations learned by different pre-training tasks using t-Distributed Stochastic Neighbor Embedding (t-SNE) visualization (coloring points by label) and Davies-Bouldin Index (DBI) scores calculated on both the original high-dimensional representations (‘DBI original’, indicating intrinsic feature separability) and the 2D t-SNE projections (‘DBI t-SNE’, reflecting clustering quality in the visualization). Samples with the same label have the same color. Red circles indicate areas of sample confusion. The red dashed line divides the sample into two parts that do not overlap. Source data are provided as a Source Data file.

We evaluated the model’s molecular representation learning capabilities across different pretraining tasks. We began by analyzing its performance on downstream tasks, examining the representations learned from various pretraining tasks. Using the BACE dataset as an example, we extracted the final layer of SCAGE’s representation and mapped it to a 2D space using t-Distributed Stochastic Neighbor Embedding (t-SNE)⁴³. The proximity of the data points was evaluated using the Davies-Bouldin Index (DB Index). A lower DB Index indicates more centralized data after t-SNE clustering, reflecting the model’s enhanced ability to distinguish between different data groups. As shown in Fig. 4c, SCAGE was trained with six different combinations of pretraining tasks, and the resulting molecular representations were assessed. We observed that although various pretraining methods improved the model’s ability to distinguish between positive and negative samples, performance varied depending on whether functional groups, molecular fingerprints, bond angles, or their combinations were used. When the model was randomly initialized, the different types of samples were completely mixed. However, the model’s ability to distinguish between samples improved with the application of different pretraining strategies, as evidenced by a corresponding decrease in the DB Index. Notably, the model achieves its highest discriminative power and the lowest DB Index when all four pretraining tasks are employed.

We conducted a homogeneity analysis of the molecular representations to investigate why combining different pretraining tasks leads to improved performance. We mapped the learned molecular representations onto 2D space and visualize their distribution on a unit circle (Supplementary Fig. S1). Notably, the model exhibited the strongest discriminative ability when all four pretraining tasks were used. These results indicate that the molecular representations learned by our model, through comprehensive pretraining tasks, exhibit a non-uniform distribution. In contrast, representations generated by other learning strategies tend to be more uniform. This indicates that our pretrained model effectively captures global intrinsic molecular features.

Attention-based explainability analysis explains the relationship between structure and property for quantitative structure-activity

To quantitatively explore the relationship between molecular structures and properties, we present substructures considered necessary by SCAGE through the calculation of atomic-level attention scores. SCAGE offers a natural approach that leverages attention scores to establish connections between structure and activity for a given molecule. To capture the sensitive structures of the demand property, we employed global attention scores within the Graph Transformer layer to calculate aggregated atomic sensitivity scores. Additionally, the edgewise sensitivity score is defined as the average of the two end atoms. In this way, the sensitive scores reflect the contribution of each node to the target property. Furthermore, each atomic sensitivity score aggregates neighborhood information, indicating that it incorporates contextual information. As shown in Fig. 5a, the sensitive substructures are color-coded according to different gradations, highlighting the potential to quantify structure-activity connections. For example, in the case of properties such as water solubility, the sensitivity score is concentrated around polar groups, which aligns closely with the “like dissolves like” principle⁴⁴. In addition, for properties related to drug safety, the sensitivity scores help identify the source of toxicity, providing valuable guidance for the structural optimization of lead compounds.

Fig. 5: Attention-based explainable analysis.

a Cases of attention-based explainability analysis on eight benchmark datasets⁴². The calculated sensitivity score determines the color gradation. Darker colors denote a higher level of importance assigned to the atom or edge. b Explainability analysis of active cliff molecules³⁶. A set of active cliff molecules are presented in the figure. The red labels indicate the significance of each atom, while the blue areas highlight the positions of the active cliffs. K_i represents the inhibition constant. Darker colors denote a higher level of importance assigned to the atom or edge. c Visual comparison of functional group tasks. The left panel shows the finetuning results after applying our atomic-level functional group pretraining task, while the right panel displays the finetuning results after pretraining the task using the number of molecular-level functional groups. Darker colors correspond to higher attention scores. Each subfigure separately presents attention visualizations and attention score matrices on the molecular graph. The axes of the attention score matrix represent the atomic numbers. Key functional groups (FG) are highlighted with blue boxes on the molecular diagram and labeled with their corresponding positions on the Attention Score Matrix plot.

Activity cliffs refer to pairs or groups of structurally similar compounds that are active against the same target but exhibit significant differences in their properties⁴⁵. We selected a set of active cliff molecules with similar structures but differing functional groups. As shown in Fig. 5b, we identified groups of activity cliff molecules. Within each group, the molecules exhibit only minor differences in their motifs, yet these variations result in significant variations in Ki, which in turn affect biological activity. We applied an attention mechanism to provide a scientific explanation for the activity cliff predictions. Atoms are color-coded based on their attention weights, with blue regions highlighting the areas of activity cliffs. The results from both sets of experiments demonstrate that our model effectively identifies regions of difference between molecules, going beyond their common structural features. These regions of difference are often associated with changes in the functional groups. This suggests that functional groups play a crucial role in activity cliffs. Our functional group-assisted model accurately distinguishes these differences, offering valuable insights for drug and target docking.

To further explore the impact of the functional group task on model learning, we examined two distinct pretraining approaches: (1) a functional group identification task at the atomic level and (2) a task predicting the number of functional groups at the molecular level. As shown in Fig. 5c and Supplementary Fig. S2, we visualized the learned attention weights for both tasks. After training with the atomic-level approach, the model was able to identify functional group positions with greater granularity. We also annotated the functional groups with their corresponding positions in the attention matrix, providing a plausible explanation: by leveraging the atomic-level task, attention scores for key substructures were higher, enabling the model to more accurately analyze molecular properties.

Case study on drug-target binding prediction with SCAGE

To evaluate the expressiveness of SCAGE for drug-target binding, we conducted experiments using the BACE dataset as an example. The BACE dataset contains both quantitative (IC50) and qualitative (binary label) binding results for a set of inhibitors of human β-secretase 1 (BACE-1). All the data are experimental values, reported in the scientific literature over the past decade. Since the value of the BACE label represents the docking affinity between the target and the protein, the calculated atomic weight can reflect the docking scores of the input molecule, as determined by AutoDock Vina⁴⁶. Therefore, we calculated contribution scores by applying substructure-level masks to the given molecule. These atomic weights further elucidate drug-target predictions, offering insights into the underlying mechanisms of protein-based drug discovery. For weight visualization, we selected the 2QP8 structure from the Protein Data Bank (PDB) database⁴⁷. We performed molecular docking experiments on these molecules using Discovery Studio⁴⁸ or ProteinsPlus^49,50,51. Figure 6 presents a visualization of the molecular docking results. Protein-ligand interaction binding patterns, obtained after molecular docking using Discovery Studio and ProteinsPlus, are shown on the right side of each subplot in Fig. 6. Important sites are labeled in the figure for reference. For example, the Thr292A mutation refers to the substitution of threonine with alanine at amino acid position 292 of the protein, which alters the ligand binding mode. The corresponding position within the molecule shows a higher importance score in the values obtained by SCAGE. The highlighted substructures of the sampled molecules closely match those identified in the molecular docking experiment, demonstrating that SCAGE can effectively identify molecular structures sensitive to the target protein from a statistical perspective.

Fig. 6: Explanation of SCAGE on BACE datasets.

A case study of SCAGE based on the BACE⁶³ dataset with 2QP8 complexes^71,72. The binding surfaces for proteins and ligands are depicted on the left, showcasing the visualization of protein binding patterns to 3D molecules and their corresponding atomic importance scores in the middle. On the right, 2D protein-ligand interaction binding patterns are illustrated, generated via docking using either Discovery Studio⁴⁸ (a, b) or ProteinsPlus^49,50,51 (c, d). The protein-target pairs names are given in Figure. ΔG represents the absolute binding free energy of interaction. The binding sites of the amino acids are labeled in the figure on the right.

Discussion

In this work, we present SCAGE, a molecular property architecture that leverages both molecular conformation and spatial information. Specifically, SCAGE incorporates a multitask learning pretraining method and two main strategies: (1) Multitask-Guided Pretraining Algorithm (M4): This approach integrates chemical prior knowledge with both 2D and 3D molecular representations to enable the learning of comprehensive, conformation-aware features. (2) MCL Module: This module leverages spatial distances between atoms to adaptively mitigate the issue of gradual homogenization in node characterization. (3) Atomic-Level Functional Group Annotation Algorithm: This algorithm enhances functional group knowledge from the molecular level to the atomic level, thereby facilitating the interpretation of drug properties and activity cliffs. Extensive experiments demonstrate SCAGE’s superiority across various benchmark biomedical datasets and drug discovery tasks compared to multiple competitive baselines. Ablation studies further validate the effectiveness of our three key modules. Additionally, case studies on activity cliffs and drug-target interactions highlight SCAGE’s potential in revealing QSAR rules.

As a pretraining model, SCAGE highlights the critical importance of selecting pretraining tasks. A well-chosen combination of pretraining tasks can significantly enhance the model’s generalization capabilities. Our experiments, which involved varying the number of datasets used during pretraining, demonstrate that simply increasing the dataset size yields only limited improvements in model performance. Additionally, our investigation into the MCL module addresses the manually introduced generalization biases inherent in existing methods and offers further insights into the development of graph transformers.

Despite its promising performance, SCAGE has some limitations. First, while the MCL module enhances molecular characterization, molecules exhibit diverse spatial conformations, and a uniform metric may not apply universally. Investigating the interpretability of different scales in molecular characterization may yield valuable insights for molecular design and optimization. Second, conformations calculated using the MMFF force field are not always the most accurate. Further investigations into more precise conformational calculation methods could significantly enhance molecular characterization. Finally, although functional groups were employed to explain activity cliffs, integrating functional group-assisted techniques with other research areas presents an intriguing avenue for future exploration.

Methods

Topological-level molecular representation

In topological molecular graphs, atoms are represented as nodes and chemical bonds as edges, defined as ${{\mathcal{G}}}^{2d}=\left({v}^{2d},\,{\varepsilon }^{2d}\right)$, where ${v}^{2d}$ denotes the set of nodes and ${\varepsilon }^{2d}$ denotes the set of edges. Detailed descriptions of atomic features are provided in Supplementary Table S6. The backbone architecture employed in this study is the Transformer model, which is composed of stacked Transformer blocks. Each Transformer block comprises two layers: a self-attention layer and a feedforward layer, both of which incorporate normalization.

For the molecule $i$, the input at layer $l$ is denoted as ${h}_{i}^{(l)}$, and the multihead self-attention is computed as follows:

$${Q}^{(l)}={h}_{i}^{(l)}{W}_{Q}^{(l)},\,{K}^{(l)}={h}_{i}^{(l)}{W}_{K}^{(l)},{V}^{(l)}={h}_{i}^{(l)}{W}_{V}^{(l)}$$

(1)

$${{attn}}_{j}^{(l)}={softmax}\left(\frac{{Q}^{\left(l\right)}{({K}^{\left(l\right)})}^{T}}{\sqrt{d}}\right){V}^{(l)}$$

(2)

$${\rm{MultiHead}}\left({Q}^{\left(l\right)},\,{K}^{\left(l\right)},{V}^{\left(l\right)}\right)={Concat}\left({{attn}}_{1}^{\left(l\right)},\,\cdots,\,{{attn}}_{k}^{\left(l\right)}\right){W}^{\left(l\right)}$$

(3)

where ${W}_{Q}^{(l)}\in {{\mathbb{R}}}^{d\times d}$, ${W}_{K}^{(l)}\in {{\mathbb{R}}}^{d\times d}$, and ${W}_{V}^{(l)}\in {{\mathbb{R}}}^{d\times d}$ are trainable weight matrices. $d$ is the dimension of the ${K}^{(l)}$. ${W}^{(l)}\in {{\mathbb{R}}}^{d\times d}$ are trainable weight matrices. The molecular representation is then computed using a feed-forward network as follows:

$${h}_{i}^{{\left(l\right)}^{{\prime} }}={h}_{i}^{\left(l\right)}+{\rm{MultiHead}}\left({Q}^{\left(l\right)},\,{K}^{\left(l\right)},{V}^{\left(l\right)}\right)$$

(4)

$${h}_{i}^{\left(l+1\right)}={h}_{i}^{{\left(l\right)}^{{\prime} }}+{GELU}\left({h}_{i}^{{\left(l\right)}^{{\prime} }}{W}_{1}\right){W}_{2}$$

(5)

where ${GELU}(\cdot )$ stands for the GELU activation function⁵², ${W}_{1}\in {{\mathbb{R}}}^{d\times d},$ and ${W}_{2}\in {{\mathbb{R}}}^{d\times d}$ stand for the trainable projection matrices.

Multiscale conformational learning module

Although the multihead self-attention mechanism enables each subgraph node to gain a global perspective, an excessive number of transformer layers can lead to the gradual homogenization of subgraph nodes, which is not conducive to node-level feature representation. To address this issue, we propose an Multiscale Conformational Learning (MCL) mechanism. Specifically, we first generated molecular conformations and then used these to calculate distances. The 2D-based MCL module leverages distances within the molecular graph. For each atom in the molecular graph, the shortest path distances from other atoms are computed, and attention scores are proportionally masked based on these distances. In contrast, the 3D-based MCL module is derived from the 3D conformational distances between atoms.

To achieve an optimal balance between local and global perspectives, we concatenate the attention scores computed across multiple n-threshold limits. We concatenated multiple n-threshold-restricted attention scores and defined this n-threshold for limiting as a ${receptive\; field}$, which consists of several thresholds stitched together as follows:

$${receptive}\; {field}={Concat}\left({{threshold}}_{1},{{threshold}}_{2},\cdots,{{threshold}}_{n}\,\right)$$

(6)

where, ${threshold}\in N$ represents the percentage number given to calculate the ${AtomDistBar}$. The ${Concatenate}(\cdot )$ is used to merge thresholds to form a ${distance\; bar}$. ${AtomDistBar}$ is calculated as follows:

$${{AtomDistBar}}_{n}={percentile}\left({AtomDist},{{threshold}}_{n}\right)$$

(7)

$${AtomDistBar}={Concat}\left({{AtomDistBar}}_{1},{{AtomDistBar}}_{2},\cdots,{{AtomDistBar}}_{n}\right)$$

(8)

where ${AtomDist}\in {R}^{m\times m}$ is a matrix consisting of the distances between the atoms in a molecule, and $m$ is the number of atoms in the molecule. The ${percentile}(\cdot )$ is used to calculate the distance ${threshold}$ based on the distance matrix and threshold. First, ${AtomDist}$ is expanded into a one-dimensional array and sorted in ascending order, denoted as ${{AtomDist}}_{{flatten}}$, and then the rank of the number corresponding to threshold is calculated as follows:

$${Rank}=\,\frac{{threshold}\,}{100}\times \left(n-1\right)$$

(9)

If the calculated position is an integer, the value corresponding to that position is the requested value. If the position is a decimal, linear interpolation is performed. Assuming the position is $k$ between the ${floor}(k)$ and ${ceil}(k)$ positions, the interpolation formula is:

$${{AtomDistBar}}_{n}= {{AtomDist}}_{{flatten}}\left[{floor}\left(k\right)\right] \\ +f \times \left({{AtomDist}}_{{flatten}}\,\left[{ceil}\left(k\right)\right]-{{AtomDist}}_{{flatten}}\left[{floor}\left(k\right)\right]\right)$$

(10)

where$\,f$ is the fractional part of $k$, ${floor}(\cdot )$ is the upward rounding function, and ${ceil}(\cdot )$ is the downward rounding function.

Then, we employ a linear transformation layer as follows:

$${{Attn}}_{{ij}}^{{maske}{d}_{n}}={Softmax}({{AttnScore}}_{{ij}}\, \cdot \,{{Mask}}_{{d}_{{ij}} < {{AtomDistBar}}_{n}}) \, \cdot \, V$$

(11)

$${{Attn}}_{{ij}}^{{masked}}={Concatenate}\left({{Attn}}_{{ij}}^{{maske}{d}_{1}},{{Attn}}_{{ij}}^{{maske}{d}_{2}},\cdots,{{Attn}}_{{ij}}^{{maske}{d}_{n}}\right)$$

(12)

where ${{AttnScore}}_{{ij}}$ is the attention score of atom ${v}_{i}$ and atom ${v}_{j}$. $V$ is the ${V}^{(l)}$ of a layer in Eq. (1). ${\rm{Mask}}$ is an indicator function that indicates where the mask needs to be performed. The ${d}_{{ij}}$ is the distances between atom ${v}_{i}$ and ${v}_{j}$. The ${Concatenate}(\cdot )$ is commonly used to integrate or merge features to form a multiscale representation.

Functional group annotation algorithm

We developed an algorithm to classify each atom within a molecule into a specific functional group category, enabling functional group annotations at the atomic level. In this algorithm, each atom is matched to all functional groups that are compatible with it. Then, the algorithm evaluates whether any of the matched functional groups exhibit an inclusion relationship. If such a relationship exists, the contained functional groups are eliminated. The algorithm is described below:

Algorithm 1

Finding Functional Group for atom v

Input: Atom v, functional group set P

1.  ${G}_{v}\,=\,\varnothing \,$

2. for $i$ in $1\ldots {P}$ do

3.   if ${p}_{i}$ matches v

4.     ${G}_{v}={G}_{v}\cup \{ {p}_{i}\,\}$

5. for ${p}_{i}\; {\bf{in}}\; {G}_{v}$ do

6.   for ${p}_{j}\; {\bf{in}}\; \{ {G}_{v}\mbox{--}{p}_{i}\,\}\,$ do

7.     if ${p}_{j}$ dominates ${p}_{i}$

8.       ${G}_{v}={G}_{v}-{p}_{i}$

9. return ${G}_{v}$

Multitask pretraining framework - M4

The M4 framework facilitates molecular representation learning through four key tasks: (1) molecular fingerprint prediction, (2) functional group prediction, (3) 2D atomic distance prediction, and (4) 3D bond angle prediction. To enhance the extraction of generic molecular representations, a dynamic adaptive multitask learning strategy is employed across these tasks. Below, we provide the details of the four pretraining tasks and the dynamic adaptive multitask learning strategy, respectively.

Molecular fingerprint prediction. A molecular fingerprint is a compact encoding that represents the structure of molecules, widely applied in cheminformatics, drug discovery, and molecular modeling⁵³. By learning to predict fingerprints, the model implicitly integrates this information into its characterization process, enhancing its understanding of chemical structures. The molecular fingerprint prediction task focuses on learning 2048-bit-long Morgan molecular fingerprints. For each molecule, its molecular fingerprint is computed, and the model leverages its learned molecular representations to predict this fingerprint. The loss function for this task is defined as follows:

$${\mathcal{L}}_{fingerprint}=\frac{1}{\left|{\mathcal{M}}\right|}\sum _{{m{\in }} {\mathcal{M}}} [{\mathcal{F}}_{m} \, \cdot \, \log {h}_{G}+(1-{\mathcal{F}}_{m}) \, \cdot \, \log ({1-h}_{G})]$$

(13)

where ${\mathcal{M}}$ represents the set of all molecules, $m$ represents one of the molecules, ${{\mathcal{F}}}_{m}$ denotes the molecular fingerprint of molecule $m$, and ${h}_{G}$ represents the global feature predicted by the model.

Functional group prediction. The structure of functional groups within a molecule is a crucial aspect often closely related to the molecule’s properties⁵⁴. The task of functional group prediction aims to identify the specific functional group to which each atom belongs. We compiled a total of 190 functional group types from KANO²⁵, GROVER¹⁷, and DayLight⁵⁵. Moreover, the impact of varying numbers of functional groups on performance can be seen in Supplementary fig. S3a. Then, we employed a functional group annotation algorithm that assigns one of the 190 functional group types to each atom, ensuring that every atom is classified into only one functional group. The loss function for the functional group prediction task is defined as follows:

$${{\mathcal{L}}}_{{functiongroup}}=\frac{1}{\left|{\mathcal{V}}\right|}\sum _{v{\mathscr{\in }}{\mathcal{V}}}\left[{{\mathcal{F}}{\mathcal{G}}}_{v}\, \cdot \, \log {h}_{v}+\left(1-{{\mathcal{F}}{\mathcal{G}}}_{v}\right)\, \cdot \, \log ({1-h}_{v})\right]$$

(14)

where ${\mathcal{V}}$ represents the set of atoms, $v$ is one of the atoms, ${{\mathcal{F}}{\mathcal{G}}}_{v}$ denotes the functional group type to which atom $v$ belongs, and ${h}_{v}$ is the node feature output by the model.

2D atomic distance prediction. The 2D atomic distance prediction task aims to learn the distance matrix for all atom pairs, which enables the model to better understand and represent the global connectivity of molecules, thereby capturing their overall structural features at a higher level. Each element of this matrix represents the shortest path distance between two atoms in the molecular graph. We denote the shortest path distance between atoms $u$ and $v$ as ${{SP}}_{{uv}}$, capping all distances >20 at 20. The loss function for this unsupervised task is defined as follows:

$${{\mathcal{L}}}_{{sp}}=\frac{1}{{\left|{\mathcal{V}}\right|}^{2}}\sum _{u,\,v{\mathscr{\in }}{\mathcal{V}}}{Focal\; Loss}\left({h}_{v},\,{{SP}}_{{uv}}\right)$$

(15)

where ${\mathcal{V}}$ represents the set of atoms, $v$ is one of the atoms, ${{SP}}_{{uv}}$ is the shortest path between atoms $u$ and $v$, and ${h}_{v}$ is the node feature output by the model. ${Focal\; Loss}$ is the loss function used to solve the imbalance problem⁵⁶.

3D bond angle prediction. The 3D bond angle prediction task aims to learn the bond angles between any two chemical bonds, which allows the model to reason about the 3D structure based on a given 2D graph, allowing it to learn information not presented in the original input graph. For this task, bond angles calculated from the generated conformations are discretized into 20 intervals, ranging from 0 to π in equal steps. The loss function for this self-supervised task is defined as follows:

$${{\mathcal{L}}}_{{angle}}=\frac{1}{\left|{\mathcal{A}}\right|}\sum _{\left(u,\,v,w\right){\mathscr{\in }}{\mathcal{V}}}{Focal\; Loss}\left({h}_{{\mathcal{A}}},{\rm{bin}}(\phi )\right)$$

(16)

where ${\mathcal{A}}$ represents the set of key angles, $\left(u,{v},w\right)$ denotes a key angle in this set, ${h}_{{\mathcal{A}}}$ is the predicted angle output by the model, $\phi$ is the true key angle value, and ${bin}(\cdot )$ is used to map the angle values to one-hot vectors.

Dynamic adaptive multitask learning. The four tasks mentioned above exhibit varying loss function scales and differing levels of complexity, which makes balancing the weights across them a challenging task. To address this, we employ Dynamic adaptive multitask learning⁵⁷, a method that adaptively adjusts the loss weighting for each task, ensuring a balanced optimization process. Specifically, we introduce a descent rate for the ${i}$-th loss ${r}_{i}^{(t)}$ at the $t$-th training step to measure the complexity of the $i$-th task, and a normalizing coefficient ${\alpha }_{i}$ to standardize the magnitude of the $i$-th loss. By combining these, the total loss at the $t$-th step, ${{\mathcal{L}}}_{T}^{(t)}$, is defined as follows:

$${{\mathcal{L}}}_{T}^{\left(t\right)}=\mathop{\sum }\limits_{i=1}^{{K}_{t}}\left(\frac{\exp \left(\frac{{r}_{i}^{\left(t\right)}}{\tau }\right)}{{\sum }_{j=1}^{{K}_{t}}\exp \left(\frac{{r}_{j}^{\left(t\right)}}{\tau }\right)}{\alpha }_{i}^{t}{{\mathcal{L}}}_{i}^{\left(t\right)}\right),\,{r}_{i}^{\left(t\right)}=\frac{{{\mathcal{L}}}_{i}^{\left(t-1\right)}}{{{\mathcal{L}}}_{i}^{\left( {t-2} \right)}},\,{\alpha }_{i}^{t}=\frac{n}{{\sum }_{j=t-1}^{t-n}{\mathcal{L}}_{i}^{\left(j\right)}}$$

(17)

where $n$ is the capacity of the queue that we take into consideration to obtain $\alpha$.

Datasets and splitting method

For model pretraining, we pretrained SCAGE using ~5 million unlabeled molecules sampled by ChemBERTa²¹ from PubChem²³, an open-access repository of drug-like chemicals. The selection of 5 million data points for model pretraining is based on findings regarding the impact of different pretraining data sizes on model performance, as shown in Supplementary fig. S3b. Moreover, we examined the impact of data sources and found that molecular data derived from PubChem²³ is the most suitable for this study, compared to other data sources including QM9 (see detailed results in Supplementary Fig. S3c).

For molecular property prediction tasks, we conducted experiments on nine benchmark datasets, which include physiology (i.e., BBBP⁵⁸, Tox21⁵⁹, SIDER⁶⁰, ClinTox⁶¹, and ToxCast⁶²), biophysics (i.e., BACE⁶³), physical chemistry (i.e., FreeSolv⁶⁴, Lipophilicity⁶⁵, ESOL⁶⁶). A description of these datasets is provided in Supplementary Table S2. To better evaluate the generalization ability of the models, we employed a scaffold split and random scaffold split for the train/validation/test sets, with a ratio of 8:1:1. Information regarding the pretraining and finetuning hyper-parameters is presented in Supplementary Table S7. For the active cliff analysis, we used a total of 30 datasets provided by Tilborg et al.³⁶, adhering to their split for model training and evaluation.

Evaluation metrics

According to MoleculeNet⁴², the area under the receiver operating characteristic curve (AUC-ROC)⁶⁷ is employed to evaluate the performance of classification tasks, while the RMSE⁶⁸ is employed to evaluate the performance of regression tasks. In the activity cliff task, performance was quantified using RMSE, with lower values indicating better performance. This was calculated both for the entire test set (RMSE) and for the subset of molecules with an activity cliff (RMSE_cliff).

The overall model performance was quantified using the RMSE calculated from the bioactivity values, as follows.

$${RMSE}=\sqrt{\frac{{\sum }_{i=1}^{n}{\left(\hat{{y}_{i}}-{y}_{i}\right)}^{2}}{n}}$$

(18)

where $\widehat{{y}_{i}}$ is the predicted bioactivity of the ith compound, ${y}_{i}$ is the corresponding experimental value, and $n$ represents the number of considered molecules. The performance on activity cliffs compounds was quantified by computing the RMSE_cliff only on compounds that belonged to at least one activity cliff pair, as follows:

$${{RMSE}}_{{cliff}}=\sqrt{\frac{{\sum }_{j=1}^{{n}_{c}}{\left(\hat{{y}_{j}}-{y}_{j}\right)}^{2}}{{n}_{c}}}$$

(19)

where $\hat{{y}_{j}}$ is the predicted bioactivity of the jth activity cliff compound, ${y}_{j}$ is the corresponding experimental value, and ${n}_{c}$ represents the total number of activity cliff compounds considered.

Baselines

To evaluate the performance of the proposed SCAGE model, we compared it with several competitive baselines. For the molecular property prediction tasks, we selected the following: MolCLR²⁴, KANO²⁵, GEM²⁶, ImageMol²⁹, GROVER¹⁷, Uni-Mol²⁷, and molAE²⁸. To ensure a fair comparison, we used the same dataset split and reproduced each method across all datasets by running 10 random seeds. For the active cliff analysis tasks, we chose a baseline of AFP³⁷, CNN³⁸, GAT³⁹, GCN⁴⁰, MPNN⁴¹, ImageMol, and GEM for comparison with our proposed SCAGE. We used the data derived from Tilborg et al.³⁶ and their data split for model training and evaluation.