Introduction

Atomic-scale superconducting Josephson junctions are highly susceptible to phase fluctuations due to their small size. For small typical junctions in Al or Pb (with critical temperature Tc of 1.2 K and 7.2 K respectively), the critical current Ic is often small, in the nA range, and the Josephson coupling energy \({E}_{{{\rm{J}}}}=\frac{{\Phi }_{0}}{2\pi }{I}_{{{\rm{c}}}}\) (Φ0 being the flux quantum) can fall down to the mK range. Thus, even at temperatures well below Tc, there are significant thermal fluctuations of the superconducting phase, which suppress the Josephson current.

To address the behavior of small sized Josephson junctions we start by discussing the standard resistively and capacitively shunted junction (RCSJ) model, shown in Fig. 1a (black lines)1. The bias current Ib can be separated through Kirchoff’s law into the sum of the supercurrent through the junction \({I}_{{{\rm{c}}}}\sin (\varphi )\) (from the first Josephson relation, φ is the phase difference across the junction), the current through a resistance \(\frac{{\Phi }_{0}}{2\pi {R}_{S}}\frac{d\varphi }{dt}\) (RS is the resistance and the second Josephson relation is \(V=\frac{{\Phi }_{0}}{2\pi }\frac{d\varphi }{dt}\)), and the current through a capacitance \({C}_{{{\rm{J}}}}\frac{dV}{dt}\) (given by \(\frac{{\Phi }_{0}}{2\pi }{C}_{{{\rm{J}}}}\frac{{d}^{2}\varphi }{d{t}^{2}}\)). Thermal phase fluctuations induce phase difference runaway φ(t), whose influence in the circuit can be reduced by designing the electromagnetic environment to obtain large damping, for instance through a large RC impedance engineered at very small distances to the junction2,3,4,5. However, it is not always feasible to modify the local environment of a junction, for instance in Josephson junctions made with a Scanning Tunneling Microscope (STM) using a superconducting tip probing a superconducting sample.

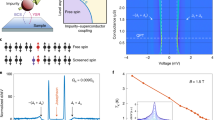
Fig. 1: Feedback-driven resistively and capacitively shunted junction (RCSJ) model.
figure 1

a Schematic representation of the RCSJ model with feedback. The resistance RS, capacitance CJ and the Josephson junction J are enclosed within the gray dashed rectangle. The feedback subtracts the voltage after a delay from the actual voltage and the result is added to the circuit. b The RCSJ model is often compared to the motion of a particle (black dots) in a periodic potential U (lines) along a coordinate which represents the phase difference across the Josephson junction φ. At low bias (salmon), thermal excitation induces phase fluctuations (gray dashed arrow, the black dots schematically represents the value of φ at a certain time). By applying a bias to the junction, the periodic potential U is tilted downwards, as illustrated by the blue and magenta lines, causing the particle to slip along the potential. Incorporating a feedback mechanism with a time constant τD periodically modifies the tilt in U (violet dashed line). c Time-averaged current 〈I〉 vs time-averaged voltage 〈V〉 measured in a STM junction between a Pb tip and a Pb sample at different temperatures: T = 0.15 K (solid blue), T = 1 K (cyan), T = 2 K (orange) and T = 3 K (red). Tunneling conductance is G ≈ 0.4 G0, being G0 the conductance quantum. Further details of the experiment are given in Methods Section “Measurement of the Josephson current with STM”. These curves are a zoom around zero voltage of the 〈I〉 − 〈V〉 curve shown in the upper left inset. Dashed blue line are data taken without a feedback (see also Methods Section “Measurement of the Josephson current with STM”), at T ≈ 0.15 K and G ≈ 0.4G0. The upper right inset shows the time-dependent trace of the voltage at the point in the current-voltage curve marked by a blue point in the main panel. We show, for clarity, only curves obtained by ramping up the bias.

Full size image

Scanning Josephson spectroscopy (SJS) consists in obtaining maps of the near-zero voltage current with atomic precision on the surface of a superconductor. This requires a vacuum atomic size junction, which essentially fixes RS to the vacuum impedance shunting the circuit at high frequency, and CJ to the capacitance between tip and sample. SJS has contributed to the understanding of photon assisted Cooper pair tunneling6, tunneling at the quantum limit7, thermal properties of small junctions8 or a diode effect9. It has also been of help to map pair density waves (PDW) in cuprates and chalcogenides10,11, or unveil inhomogeneous superconductivity in pnictides12.

A route often taken to operate systems with large thermal fluctuations is to use a delayed and time dependent feedback which couples close to the characteristic time scale of the system13,14,15. However, for ultrasmall Josephson junctions, it has been recently shown that coupling to a system much slower than the Josephson time scale leads to conversion of a high frequency signal into a measurable near DC signal, and to novel dynamical behavior in between the zero voltage Josephson and the high voltage (quasiparticle) resistive regime16,17,18. Here, we show that a delayed feedback element, given by the current-voltage converter typically used in STM experiments, leads to a regime with a spontaneous oscillatory behavior, i.e. an oscillation without an external AC drive, providing a new method for SJS with minimal adjustments in the STM set-up.

Results and discussion

Feedback driven Josephson junction

To understand the effect of a feedback coupling on a Josephson junction, we recall that the phase φ behaves as the position of a particle in a one dimensional potential U. We can write \(U(\varphi )=\int\,d\varphi \left({I}_{{{\rm{b}}}}-{I}_{{{\rm{c}}}}\sin (\varphi )\right)\). U has the form of a tilted washboard potential as shown in Fig. 1b19. With a small Ib (orange curve in Fig. 1b), the phase difference φ remains around a potential minimum, resulting in zero voltage across the junction. As the bias is increased (blue and magenta curves), the phase rolls down the potential, leading to a non-zero voltage (often at this point Cooper pair tunneling ceases and the junction jumps into quasiparticle tunneling). A feedback adds a time delayed current to the actual Josephson current and periodically inhibits the evolution of the phase with time by reducing the tilt, as schematically shown in Fig. 1a, b. As we show below, this periodic behavior induced by the feedback leads to a regime which presents spontaneous oscillations at the time constant τD of the circuit and a time averaged current which is almost independent of temperature.

In Fig. 1c, we compare the time-averaged current vs the time-averaged voltage, 〈I〉 − 〈V〉, for a Josephson junction formed between a Pb STM tip and a Pb sample (blue line) when a feedback element is integrated into the circuit, to the result obtained without a feedback element (dashed blue line, the experiment is described below and in Methods Section “Measurement of the Josephson current with STM”). We observe a regime with a sustained current in the circuit with a feedback over a bias range that is considerably larger than in the circuit without a feedback. Whereas the behavior close to zero bias is highly temperature dependent (following approximately the same behavior as in the circuit without a feedback), the current in the regime induced by the feedback is almost independent of temperature (see Fig. 1c). Importantly (upper right inset of Fig. 1c), in this regime there are temporal oscillations which can be used as a new probe for microscopy, as we show below.

To gain a deeper understanding, let us start by establishing the feedback RCSJ model at zero temperature. We can write

$$\frac{d{x}_{2}}{d\tau }=\frac{{i}_{{{\rm{b}}}}-\sin ({x}_{1})-{x}_{2}}{\beta }+F(\tau,{\tau }_{{{\rm{D}}}}),$$
(1)

where the feedback F(τ, τD) is given by

$$F(\tau,{\tau }_{{{\rm{D}}}})=-\frac{1}{2\beta } \int _{\tau }^{\tau+\Delta \tau }\frac{1}{\Delta \tau }\left[{x}_{2}(\tau ^{\prime} -{\tau }_{{{\rm{D}}}})-{x}_{2}(\tau ^{\prime} )\right]d\tau ^{\prime} .$$
(2)

Here, x1 ≡ φ and \({x}_{2}\equiv \frac{d\varphi }{d\tau }\) are the dimensionless variables, the reduced time is \(\tau=\frac{t}{{\tau }_{{{\rm{J}}}}}\), with \({\tau }_{{{\rm{J}}}}=\frac{{\Phi }_{0}}{2\pi {I}_{{{\rm{c}}}}{R}_{{{\rm{S}}}}}\) the characteristic Josephson time (and \({\omega }_{{{\rm{J}}}}=\frac{2\pi }{{\tau }_{{{\rm{J}}}}}\) the Josephson frequency), the reduced bias current is ib ≡ Ib/Ic, and \(\beta=\frac{2\pi {I}_{{{\rm{c}}}}{R}_{{{\rm{S}}}}^{2}{C}_{{{\rm{J}}}}}{{\Phi }_{0}}\) is the McCumber parameter. Eq. (1) corresponds to the conventional RCSJ model plus the feedback term F(τ, τD). Δτ is the bandwidth of the measurement circuit. The behavior of the solutions to the new coupled equations \(\frac{d{x}_{1}}{d\tau }={x}_{2}\) and Eq. (1) is shown in Fig. 2.

Fig. 2: Feedback driven RCSJ regimes.
figure 2

a The minimum and maximum values of x2 (proportional to the junction voltage) as a function of the reduced bias current ib = Ib/Ic. We identify three different regimes, shadowed with orange, blue, and purple backgrounds. b-d Evolution of the current [\(i=\sin ({x}_{1})\)] and the voltage (x2) through the junction at different times. The color in each panel represents schematically the regime, following the color of the dots in (a). In (b) the junction quickly reaches a stable state with a time-independent finite current and zero voltage (stable regime). In (c) the junction leaves the zero voltage state and oscillates between a zero and a finite voltage state (bistable regime). Oscillations are spontaneous, i.e. without the action of an external AC drive. In (d) both the current and the voltage oscillate at frequency \(\frac{2\pi }{{\tau }_{{{\rm{J}}}}}\) (periodic regime), but the current averages to zero while the voltage averages to a finite value. e x2 vs time (blue line) together with the feedback term multiplied by 2β (black line), see Eq. (1). Parameters in these simulations are T = 0 K, β = 2, τD = 105 and Δτ = 6 ⋅ 103 (both τD and Δτ in units of τJ).

Full size image

In Fig. 2a–d we show the evolution of the voltage x2 as function of ib. We identify three distinct regimes. For ib ≤  1 (orange in Fig. 2a, b) we find zero voltage, x2 = 0, and a finite Josephson current i = ib. In this regime, Eq. (1) is the usual DC Josephson junction equation ib = sin(x1). The most interesting regime is the bistable regime, which sets in when ib ≃ 1. Then, x2(τ) ≠ 0. The current through the junction i (current through the middle branch within the dashed rectangle in Fig. 1a) first increases and then oscillates at a time scale which is of order of τJ, as shown in Fig. 2c, leading to a finite voltage x2(τ) ≠ 0. However, just when ib is increased above one, x2(τ − τD) is still zero, which leads to a non-zero feedback term F(τ, τD). As x2(τ) increases with time (blue line in Fig. 2e), the feedback F(τ, τD) increases (black line in Fig. 2e). But x2(τ − τD) increases too and thus at some point the feedback F(τ, τD) decreases again. Then, x2(τ) decreases until x2(τ) = 0 again. x2(τ − τD) decreases and in this process the feedback changes sign. Having now a negative feedback leads to increasing x2(τ) ≠ 0, and the process starts again.

When ib ≃ 1, the feedback exactly compensates the additional current above the critical value in Eq. (1) within a short amount of time and the oscillations in x2(τ) and F(τ, τD) have essentially a square shape. But when ib increases, the compensation sets in only gradually. For example, in Fig. 2c we are approximately in the middle of the bistable regime. The time interval where the feedback and x2 vary occupies approximately half a cycle (0.5τD). This interval increases with ib, until the feedback no longer compensates the appearance of a finite voltage and the oscillations in x2(τ) and F(τ, τD) are triangular like. Then, we enter another regime. The third regime is similar to the conventional AC periodic Josephson regime, characterized by a finite time-averaged voltage x2 = ib and a zero time-averaged current (purple in Fig. 2a and Fig. 2d).

The bistable regime is characterized by an oscillating behavior which appears without a drive, at the feedback time constant τD, and is independent of the Josephson frequency τJ. Furthermore, the current and voltage are determined by the time dependent behavior, rather than by their sensitivity to temperature.

We now compare theory and experiment at a finite temperature. In Fig. 3a, we show a time-averaged current-voltage characteristic taken on an atomic size tunnel junction between a tip and a sample of Pb (\({T}_{{{\rm{c}}}}^{{{\rm{(Pb)}}}}=7.2\) K, and ΔPb = 1.37 meV, τJ ≈ 10−9 s). Starting from zero bias, we observe that the average current increases, reaches a peak, and then decreases and saturates at a plateau, eventually dropping to zero at higher bias. The time dependence of the voltage for different bias (colored points in Fig. 3a) is shown in Fig. 3b and the minimum and maximum values in the inset of Fig. 3a (we use Δτ ~ 10−5 s for the temporal range or bandwidth of the experimental set-up, see also Methods Section “Measurement of the Josephson current with STM”). We observe a bistable regime (orange to blue curves) where the junction oscillates periodically, approximately every 0.15 ms, between zero and a finite voltage. We note that the oscillation appears spontaneously, without the action of any AC drive. In Fig. 3c we show the time-averaged current vs the time-averaged voltage resulting from our simulations. The voltage vs time is shown in Fig. 3d and the minimum and maximum values in the inset of Fig. 3c. We see that experiment and calculations are mostly identical. The shape of the time-averaged current vs time-averaged voltage curve is similar, the hysteresis has a similar shape and, most importantly, the oscillatory behavior in the bistable regime occurs in experiment as well as in simulations.

Fig. 3: Feedback driven Josephson effect.
figure 3

a Time-averaged tunneling current vs time-averaged voltage, 〈I〉 − 〈V〉, near zero bias (solid blue lines) for a STM atomic size Josephson junction made between two Pb electrodes. The blue arrows indicate the direction of the ramp. Colored dots represent the locations at which we stop the ramp and make time-dependent measurements, shown in (b). The junction conductance G is ~ 0.4G0, being \({G}_{0}=\frac{2{e}^{2}}{h}\) the conductance quantum and T = 150 mK. The bottom right inset shows the maximum and minimum of the voltage vs Ib. b Voltage vs time at the colored dots marked in the main panel of (a). The curves are vertically shifted by 0.25 mV for clarity. c Time-averaged current vs time-averaged voltage, 〈I〉 − 〈V〉, obtained from the model described in the text. The arrows provide the direction of the ramp. The bottom right inset shows the maximum and minimum of the voltage vs Ib. d Voltage as a function of time for the colored dots marked in (c) Curves are shifted for clarity by 0.5 mV. Note that τ is in units of τJ ≈ 10−9 s, see text and Methods (Sections 2,3) for further details. Parameters in the simulations are T = 1.2 K, β = 2, τD = 105 and Δτ = 6 ⋅ 103 (both τD and Δτ in units of τJ).

Full size image

The occurrence of the bistable regime depends on the direction for ramping the bias (light and dark blue lines in Fig. 3a, c show the different ramping directions). The model shows that, when decreasing ib, x2(τ − τD) ≠ 0 and the feedback F(τ, τD) (Eq. (2)) remains at a small value. Thus, a smaller ib is needed to reach the bistable regime.

This behavior is completely different from the known behavior of hysteretic Josephson junctions1. Instead of switching out of the Josephson Cooper pair tunneling regime into a quasiparticle branch, entry in and exit out of the bistable regime is between two different regimes of Cooper pair tunneling. It occurs between states that are similar to the DC (finite current and zero voltage at the junction) and AC (finite voltage and a rapidly oscillating current at the junction) Josephson effects of an isolated Josephson junction.

Increasing the temperature reduces both the bistable regime as well as the size of the hysteretic behavior (Methods Section “Temperature dependence in the feedback-driven RCSJ model” and “Feedback driven RCSJ model and experiment as a function of temperature”), but leads, as shown in Supplementary Fig. 1, to a temperature independent value of the time-averaged current in the bistable regime.

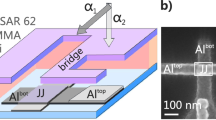
A detailed analysis of the different parameters governing the feedback RCSJ model (Supplementary Fig. 2 and Methods Section “Parameters of the feedback-driven RCSJ model”) shows that the appearance of the bistable regime for different time constants τD goes all the way down to τD being one or two orders of magnitude larger than τJ. Furthermore, there is a large range of β > 1 where the bistable regime can be observed. On the other hand, Δτ should be smaller than τD but below Δτ ≈ 0.1τD, the integration does no longer provide a sufficiently large feedback term. In the experiment, we have observed the bistable regime in Pb-NbSe2 and Al-Al atomic size junctions (Supplementary Figs. 3, 4 and Supplementary Information Section 1). We note that τD is controlled by an RC filter in the amplifying circuit and discuss the detailed dependence on the circuit parameters in Methods (Section “Measurement of the Josephson current with STM” and Supplementary Fig. 5).

Note that there is a discrepancy between the symmetric peaks obtained in the voltage as a function of time in the bistable regime of our simulations, and the asymmetric peaks observed in the experiment (yellow and green curves in Fig. 3b and Fig. 3d). We also note that the oscillations in the model are always periodic, whereas we observe a stochastic instability to enter the bistable regime in the experiment (see Supplementary Information Section 2). We do not have a clear explanation for these discrepancies. The asymmetry might be related to asymmetries in the circuit. For instance, different resistance and capacitance values in the two branches connecting the junction (Fig. 1a), which are not included in our feedback RCSJ model. The stochastic peaks could be related to excitations, as photons, driving the junction into the bistable regime. The other essential features, such as the existence of a bistable regime and its accompanying hysteretic behavior, are accurately captured by the feedback RCSJ model.

Critical current from the bistable regime in feedback driven ultra small Josephson junctions

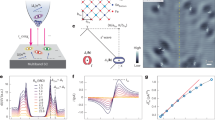
From the feedback RCSJ model at a finite temperature, we find that \(\langle I \rangle={I}_{{{\rm{c}}}}\frac{\Delta \tau }{4{\tau }_{{{\rm{D}}}}}\) in the bistable regime, just before the transition to the periodic regime. This is in sharp contrast to the value of the current close to zero voltage, for ib ≈ 1, which inversely proportional to temperature,  ~ T −1, or with the derivative of the current near zero voltage, which decreases with temperature as  ~ T −2 (see Supplementary Information Section 3). For the experiment shown in Fig. 3a, we find Ic ~ 50 nA, which is very similar to the estimation provided by the Ambegaokar-Baratoff equation \({I}_{{{\rm{c}}}}=\frac{G}{{G}_{0}}\frac{e}{2\hslash }\Delta\) for symmetric junctions at zero temperature20 (G being the conductance and G0 the quantum of conductance, and Δ the superconducting gap, we use G ≈ 0.4G0 and ΔPb = 1.37 meV). By taking Δτ = 0.06τD and Ic ~ 50 nA we can follow closely the dependence of Ic on G, as shown in Fig. 4, finding that the experiment (dots) follows the detailed calculations of Ic vs G of ref. 21 (line). Thus, the bistable regime provides a quantitative measurement of the critical current Ic of the junction.

Fig. 4: Current in the bistable regime vs conductance.
figure 4

Time-averaged tunneling current 〈I〉bistable just before the loss of the bistable regime as a function of the conductance G normalized to the conductance quantum G0, for STM Josephson junctions made with tip and sample of Pb. The colored circles correspond to the experimental results whereas the line corresponds to the expression \({I}_{{{\rm{c}}}}\frac{\Delta \tau }{4{\tau }_{{{\rm{D}}}}}\). Ic is determined as a function of G following ref. 21. In the upper left inset we show the time-averaged tunneling current \(\langle I \rangle\) vs the time-averaged voltage \(\langle V \rangle\). Each line corresponds to a different tunneling conductance, following the color code of the circles in the main panel (G = 0.61G0 (violet), 0.50G0 (blue), 0.43G0 (light blue), 0.37G0 (cyan), 0.31G0 (light cyan), 0.27G0 (green), 0.22G0 (light green), and 0.18G0 (yellow)). Dashed lines in the inset are for decreasing bias. In the lower right inset we show a map of the amplitude of the oscillatory signal in the bistable regime showing atomic resolution in 2H-NbSe2. The amplitude of the oscillatory signal improves significantly the signal to noise ratio and increases with Ic. White scale bar is 1 nm long. In the upper left corner of the inset we show the Fourier transform, where we can identify the Bragg peaks of the hexagonal Se lattice (white circles) and the Bragg peaks due to the PDW (red circles, more details in Supplementary Fig. 6 and in the Supplementary Information Section 4).

Full size image

Pair density wave in 2H-NbSe2 observed on atomic resolution maps of the oscillatory component

We have observed the bistable regime in a Josephson junction with a Pb tip and a superconducting 2H-NbSe2 sample, and used the bistable regime to obtain a considerably improved measurement of the atomic scale variation of the Josephson critical current in 2H-NbSe2, as compared to the measurement of the current or the tunneling conductance close to zero bias used in previous SJS experiments (details in Methods Section “Measurement of the time dependent signal in the bistable regime with STM” and in the Supplementary Information Sections 4 and 5). We have followed the amplitude of the spontaneous oscillatory signal as a function of the position. The amplitude of the oscillation increases with bias, as shown in the insets of Fig. 3a, c, until the system leaves the bistable regime. It is proportional to the bias range in which the bistable regime is found and to the critical current Ic, as shown in the inset of Fig. 4. Measuring the amplitude of the oscillation in the bistable regime, we benefit from the improved detection of an oscillatory signal at a well-defined frequency and achieve a considerable improvement of the signal to noise ratio. 2H-NbSe2 has a charge density wave (CDW) below TCDW = 33 K which coexists with superconductivity below Tc = 7.2 K. 2H-NbSe2 presents atomic size modulations of the superconducting order parameter22. These modulations are linked to the charge modulations of the CDW through a pair density wave (PDW) 11. The PDW consists of spatial modulations of a coherent pair density 23. The PDW has been observed in cuprates, pnictides and heavy fermions, and is believed to cover the link between charge order and Cooper pair formation that prevails on the phase diagram of high Tc superconductors 10,24,25,26,27,28,29. As shown in the lower right inset of Fig. 4, we observe the PDW by mapping the oscillatory signal in the bistable regime.

The newly uncovered bistable regime is a considerable addition on Josephson probes, of particular interest in Josephson junctions including a topological superconductor28,29,30,31,32,33,34,35,36,37,38,39 or a chain of magnetic adatoms40,41. In those cases, Cooper pair tunneling between the s-wave state of the tip and p-wave state of the sample is expected to occur through higher-order processes with a significant reduction of the usual I = Icsin(φ) current phase relation38. Mapping the bistable regime with atomic registry in these systems should provide radically new information from the measurement of an oscillating signal that arises without an AC drive, and the new phenomena arising from the Josephson relation modified by the feedback. The bistable regime opens thus new avenues to study unconventional superconductivity.

In conclusion, we have unveiled a bistable regime of Josephson junctions governed by a feedback action and providing Josephson characteristics in a frequency range six orders of magnitude below the Josephson frequency. The oscillating behavior is a defining feature of ultra small size feedback driven Josephson junctions and can be used to map the Josephson effect down to atomic scale through a Josephson dynamic behavior which is very different from dynamics of usual tunnel junctions.

Method

Measurement of the Josephson current with STM

We use a STM set-up in a dilution refrigerator with superconducting tip and sample. The tips are always prepared and cleaned through repeated indentation inside a pad of the same material as the tip. We indent the tip in a controlled way and follow the conductance steps characteristic of atomic-size junctions42,43. The same preparation method is used for tip and sample when measuring Pb-Pb, Pb-2H-NbSe2, and Al-Al junctions. The STM set-up, the software used and aspects of the cryogenics are described in refs. 43,44,45,46,47,48. The 2H-NbSe2 sample has been cleaved in-situ at low temperatures.

In our setup (Supplementary Fig. 5), we employ a circuit featuring an operational amplifier for the feedback element, which is commonly utilized for SJS measurements6,7,9,10,11,12,24,25,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64. There is nevertheless an important difference between our circuit and similar ones. Often, the resistor R is chosen within the range of 1−10 MΩ (amplification between 106 to 107) and an additional filtered amplification stage is employed to achieve current-to-voltage conversions in the 108, 109 or higher ranges. We do not use the latter filter in the amplification stage, because it can eliminate or reduce any oscillatory behavior present in the junction like the bistable regime discussed in this work.

In absence of such an additional filtering stage, the current flowing through the atomic-size tunnel junction is directly measured through the operational amplifier in a current-to-voltage configuration. In principle, the junction is voltage biased. But, in our setup we use a voltage source with a 10 kΩ resistor connected in series. The voltage drop on this resistor is subtracted from the applied voltage to obtain the time-averaged \(\langle I \rangle - \langle V \rangle\) curves. We determine the voltage as a function of time by multiplying the output of the operational amplifier by the resistor in parallel to the amplifier R and subtracting an offset.

The role of the feedback of the operational amplifier is to make sure that the current flows through the resistor R and reaches ground, thereby simultaneously nullifying the voltage difference at the amplifier’s two inputs. However, the feedback’s action is not immediate but rather delayed by a certain time constant τD, limited by the junction’s resistance and the capacitance C. This delay leads to the spontaneous oscillatory behavior discussed here.

The capacitance C in our circuit is mainly due to the capacitance in parallel to the resistor in Supplementary Fig. 5, which mostly consists of the wiring to ground. This can be significant due to the typical long wiring in a dilution refrigerator setup44,48. We observe the oscillatory behavior when \({C}_{{{\rm{wire}}}}\simeq 0.3\) nF. In the Al-Al experiment (discussed in the Supplementary Information Section 1), we use a capacitor of C ≈ 2 nF and get an approximately ten times larger τD. When the setup has a capacitance of  ~ 10 nF, τD further increases and the bistable regime is lost, resulting in the Josephson behavior reported in previous works, discussed in more detail in the Supplementary Information Section 3 and shown in Fig. 1b of the main text (blue dashed line).

In our experiment, taking \(\beta=\frac{2\pi }{{\Phi }_{0}}{I}_{{{\rm{c}}}}{R}_{{{\rm{S}}}}^{2}{C}_{{{\rm{J}}}}=4\), we estimate that CJ is on the order of, or below, a few fF. The capacitance of tunnel junctions made with STM have been measured and calculated for typical tip shapes and sample-tip distances, yielding values in the range of tens of fF8,65. These capacitance values indicate that the tip can be modeled by a sphere with an effective radius close to 1 μm. This suggests that the junction capacitance CJ is primarily determined by the geometry of the tip at a distance slightly below that value, typically in the range of a few tens to hundreds of nm.

We use the OPA 111 amplifier in our setup, featuring a low bias current66. In the operational amplifier, two field effect transistors (FET) are connected to the input and to the power supply. The inputs ( + and  − in Supplementary Fig. 5) are connected to the gate of each FET while the power supply is connected to the source and the output to the drain of each FET. Before reaching the output, the signal is amplified through a low-noise cascode. As the gain is very large in the used circuit, we expect the settling time to be of order of the RC time of the circuit.

Temperature dependence in the feedback-driven RCSJ model

The entry and exit behavior between different regimes is thermally driven, as shown in the Supplementary Fig. 7 and discussed in the Supplementary Information Section 2. SJS in the bistable regime provides an exit behavior that can be traced as a function of the position. The full loss of Cooper pair transport between tip and sample occurs when leaving the bistable regime by increasing the bias. Entering and leaving the bistable regime occurs at a bias which is far above the usual bias at which a thermally smeared Josephson current is observed (Fig. 3). As shown in the Supplementary Information Section 2, this eventually allows identifying and studying non-reciprocal (diode) Josephson behavior. Furthermore, the value of the current in the bistable regime is given by the critical current, but the exit point depends on the shape of the current phase relation. As we show in Supplementary Fig. 8 and discuss in the Supplementary Information Section 5, the exit out of and entry into the bistable regime is different when taking a current phase relation deviating from I = Icsin(φ). In the bistable regime we can make atomic size maps of the exit behavior by tracing directly the oscillatory signal as a function of the position. We observe (Supplementary Fig. 9) spatial modulations at the PDW wavevector.

We follow the feedback-driven RCSJ model, see refs. 67,68. By using the Kirchhoff equations on the circuit of Fig. 1a and introducing the feedback term and thermal noise, we obtain the set of differential equations

$$V=\frac{{\Phi }_{0}}{2\pi }\frac{d\varphi }{dt},$$
(3)
$${I}_{{{\rm{b}}}}- k\frac{1}{\Delta t}\int_{t}^{t+\Delta t}\left[V({t}^{{\prime} }-{t}_{{{\rm{D}}}})-V({t}^{{\prime} })\right]d{t}^{{\prime} }=\\ {I}_{{{\rm{c}}}}\sin \varphi+\frac{V}{{R}_{{{\rm{S}}}}}+{C}_{{{\rm{J}}}}\frac{dV}{dt}-\sqrt{\frac{2{k}_{{{\rm{B}}}}T}{{R}_{{{\rm{S}}}}{h}_{t}}}{f}_{{{\rm{RND}}}}(t).$$
(4)

The first equation corresponds to the voltage drop through the circuit while the second one accounts for the total current. The first term in the second equation is the current bias Ib and the second one is the feedback term. This term compares the voltage at two different times, t and t − tD, and adds to the circuit, multiplied by a coupling constant k that has units of inverse resistance. Since the feedback element may not allow for a full resolution of τJ, we introduce an average for time-scales Δt > τJ. The third term gives the current through the Josephson junction, with Ic the critical current and φ the phase difference. The fourth and fifth terms provide the currents through the resistance RS and the capacitor CJ, respectively. The last term simulates the current fluctuations in the junction as a result of thermal noise, with T the temperature and fRND(t) a time-dependent function that provides normally distributed random values that average to zero with standard deviation of one. This term is modeled following ref. 68, which offers an expression especially suitable for Runge-Kutta solvers (ht is the time discretization).

We can now rewrite the set of first-order differential equations of Eqs. (3) and (4) as a (dimensionless) second-order differential equation

$$\frac{{d}^{2}\varphi }{d{\tau }^{2}}= \frac{{i}_{{{\rm{b}}}}-\sin (\varphi )-\frac{d\varphi }{d\tau }}{\beta }\\ -\frac{k{R}_{{{\rm{S}}}}}{\beta }\frac{1}{\Delta \tau }\int_{\tau }^{\tau+\Delta \tau }\left(\frac{d\varphi }{d\tau }({\tau }^{{\prime} }-{\tau }_{{{\rm{D}}}})-\frac{d\varphi }{d\tau }({\tau }^{{\prime} })\right)d{\tau }^{{\prime} }\\ +\frac{1}{\beta }\sqrt{{\frac{2\pi }{{I}_{{{\rm{c}}}}\Phi }}_{0}}\sqrt{\frac{2{k}_{{{\rm{B}}}}T}{{h}_{\tau }}}{f}_{{{\rm{RND}}}}(\tau ),$$
(5)

where τ = t/τJ is the reduced time (with \({\tau }_{{{\rm{J}}}}=\frac{{\Phi }_{0}}{2\pi {I}_{{{\rm{c}}}}{R}_{{{\rm{S}}}}}\) the inverse of the characteristic Josephson frequency), \(\beta=\frac{2\pi {I}_{{{\rm{c}}}}{R}_{{{\rm{S}}}}^{2}{C}_{{{\rm{J}}}}}{{\Phi }_{0}}\) the McCumber parameter, and ib ≡ Ib/Ic the reduced bias current. Notice that τD = tD/τJ and Δτ = Δt/τJ are also written in units of τJ.

Defining x1 = φ and \({x}_{2}=\frac{d\varphi }{dt}\), we can write

$$\frac{d{x}_{2}}{d\tau }= \frac{{i}_{{{\rm{b}}}}-\sin ({x}_{1})-{x}_{2}}{\beta }\\ -\frac{k{R}_{{{\rm{S}}}}}{\beta }\frac{1}{\Delta \tau }\int_{\tau }^{\tau+\Delta \tau }\left[{x}_{2}({t}^{{\prime} }-{\tau }_{{{\rm{D}}}})-{x}_{2}({t}^{{\prime} })\right]d{t}^{{\prime} }\\ +\frac{1}{\beta }\sqrt{{\frac{2\pi }{{I}_{{{\rm{c}}}}\Phi }}_{0}}\sqrt{\frac{2{k}_{{{\rm{B}}}}T}{{h}_{\tau }}}{f}_{{{\rm{RND}}}}(\tau ).$$
(6)

This equation is equivalent to Eq. (1) of the main text but including the effect of a finite temperature through a white noise term. Moreover, we assume in the main text perfect coupling between the feedback element and the circuit, provided by kRS = 0.5, in which the feedback perfectly compensates the voltage drop through the circuit (at Δτ → 0).

We solve this non-linear delayed differential equation using a fourth-order Runge-Kutta method as a function of time and sweeping for different bias current ib. For each current bias ib, we impose as initial condition the values of (x1, x2) found for the previous value of ib. In this way we obtain a hysteretic behavior as also found in the experiments. We employ a small time discretization step hτ so that the time scale τJ is well-resolved (hτ = 0.1τJ) and we compute the solution for very large time scales so that one can account for the phenomena happening at scales of τD. Notice that there are five orders of magnitude between τJ and τD, which makes these simulations computationally challenging.

Once x1(τ) and x2(τ) are found we compute the current and voltage through the Josephson junction as

$$I(\tau )={I}_{{{\rm{c}}}}\sin \left({x}_{1}(\tau )\right),\ \ \ V(\tau )={R}_{{{\rm{S}}}}{I}_{{{\rm{c}}}}{x}_{2}(\tau ),$$
(7)

and find their time average \(\langle I \rangle\) and \(\langle V \rangle\). We remove the initial solutions to the differential equation in the time average (a few τD intervals) as the simulations may take some time to reach a possible different regime when changing ib. We also run several times (10 times) the same simulation using the same ib and initial condition, and average among the solutions to remove the dependence on a particular realization of thermal noise.

Feedback driven RCSJ model and experiment as a function of temperature

We show the dependence of the current-voltage \(\langle I \rangle - \langle V \rangle\) characteristic for different temperatures in Supplementary Fig. 1. We observe that temperature fluctuations suppress the value of the current at the peak (the peak reaches  ~ 50 nA at T → 0). To a lesser degree, the extension of the bistable regime is also decreased with temperature and may actually disappear for too high temperatures. On the contrary, the time-averaged current \(\langle I \rangle\) in the bistable regime is barely affected by temperature. To understand this behavior, we note that at T → 0 the entire stable regime happens just at \(\langle V \rangle=0\), while the bistable regime happens for a wide range of \(\langle V \rangle\). Temperature mixes the regimes close to their transitions, thus suppressing the peak at \(\langle V \rangle \to 0\) (and moving it to larger \(\langle V \rangle\) values) as it hybridizes with the bistable regime. On the other hand, \(\langle I \rangle\) in the central part of the bistable regime is barely affected by temperature, as it hybridizes with other \(\langle V \rangle\) values inside the same bistable regime. This also implies that whenever the thermal energy is comparable to or larger than the voltage range of the bistable regime, no bistability is possible. Analytically, we find that the time-averaged current within the bistable regime, just prior to transitioning to the AC Josephson regime, is roughly given by

$${ \langle I \rangle }_{{{\rm{bistable}}}}\simeq {I}_{{{\rm{c}}}}\left(\frac{1-2k{R}_{{{\rm{S}}}}}{1-k{R}_{{{\rm{S}}}}}+\frac{\Delta \tau }{2{\tau }_{{{\rm{D}}}}}\frac{{\left(k{R}_{{{\rm{S}}}}\right)}^{2}}{1-k{R}_{{{\rm{S}}}}}\right).$$
(8)

We have checked that this analytical expression agrees with our numerical data either when Δτ is negligible, and thus the first term dominates, or when Δτ is comparable to τD so that the second one does. For intermediate values, the behavior of the system is more complex than the one this analytical equation can predict. Notably, this equation aligns well with the experimental data, as in our experimental setup Δτ is comparable to τD. Particularly, assuming perfect coupling kRS = 0.5 and Δτ ≃ 0.05τD, this equation allows us to estimate a critical current Ic of 50 nA for the junction discussed in the Fig. 3a of the main text, in agreement with Ambegaokar-Baratoff theory. Further support for this expression is demonstrated in Fig. 4 of the main text, where the current within the bistable regime obtained through experimental measurements closely follows the theoretical prediction of ref. 21 across a wide range of tunneling conductances.

Parameters of the feedback-driven RCSJ model

To explore the impact of different parameters of the feedback on the results of the model we calculate the time-averaged current \(\langle I \rangle\) for different bias currents ib and parameters: kRS (shown in Supplementary Fig. 2a, \(\langle I \rangle\) is given by the color scale), Δτ (Supplementary Fig. 2b), β (Supplementary Fig. 2c) and τD (Supplementary Fig. 2d) at zero temperature. In the stable regime, ib ≤ 1 (Supplementary Fig. 2a), the coupling constant has no significant influence since the feedback does not play a significant role. However, for ib > 1 we observe a substantial bistable regime that appears within the range of kRS ≃ 0.4 to kRS ≃0.5, as indicated by the red area in Supplementary Fig. 2a (red indicates a finite \(\langle I \rangle\), see color scale on the right). The saddle points of the differential equation determine the bistablility regime, which follows in this case \({i}_{{{\rm{b}}}}^{{{\rm{(max)}}}}\propto \left(\frac{1-k{R}_{{{\rm{S}}}}}{1-2k{R}_{{{\rm{S}}}}}\right)\). There is a divergence at kRS = 0.5, which serves as the upper boundary for the bistablility range. Conversely, the lower boundary for kRS is when \({i}_{{{\rm{b}}}}^{{{\rm{(max)}}}}=1\). Below this value the range for the bistable regime is infinitesimally close to the stable regime. In the present simulation this occurs at kRS ≃ 0.4.

The effect of the integration interval Δτ is very similar to that of kRS as it ultimately modifies the coupling between x2(τ) and an average near x2(τ − τD). Thus, even at perfect coupling kRS = 0.5, see Supplementary Fig. 2b, the bistability is possible when Δτ is smaller than the characteristic delay time τD, as x2(τ − τD) is averaged to a very different quantity. Notice, nevertheless, that the bistable regime disappears when Δτ ~ τD, as the feedback element averages to a time-independent constant.

The relationship between the bistable regime and the McCumber constant β (Supplementary Fig. 2c) is more intricate. In principle, one might argue that the saddle points of the differential equation are independent of β, suggesting that the bistablility range should remain unaffected by it. However, the value of β does influence the rate at which the differential equation converges to the saddle points, which in turn influences the extension in parameter space of the bistable regime.

To better understand this, let us explain in more detail the evolution of the system with time (for Δτ → 0). As discussed in the main text, the system undergoes a periodic evolution (with period 2τD) in the bistable regime, oscillating between two distinct saddle points. Initially, the system reaches a periodic fixed point that persists for a time τD. This fixed point can be linked to an AC Josephson regime but with an average voltage that is renormalized to \(\langle {x}_{2} \rangle={i}_{{{\rm{b}}}}/(1-k{R}_{{{\rm{S}}}})\) instead of the conventional ib. After this time τD, the action of the feedback element changes, leading the system to transition towards a different fixed point for an additional period τD. This latter saddle point is stable and exhibits similarities to a DC Josephson regime albeit with a renormalized current given by \({x}_{1}={i}_{{{\rm{b}}}}\left(\frac{1-k{R}_{{{\rm{S}}}}}{1-2k{R}_{{{\rm{S}}}}}\right)\). Notably, the transition between these two saddle points occurs continuously in time. The system passes through an intermediary saddle point during this evolution. This intermediate point corresponds to the conventional AC Josephson regime (i.e., with \(\langle {x}_{2} \rangle={i}_{{{\rm{b}}}}\)), but it only serves as a fixed point for a (brief) period of time when the condition x2(t − τD) ≃ x2(t) is (approximately) satisfied. As the bias current ib is increased the transition between the two primary fixed points is slower until reaching a critical value \({i}_{{{\rm{b}}}}^{{{\rm{(max)}}}}\) beyond which the evolution becomes so sluggish that the system remains solely in the conventional AC regime.

The value \({i}_{{{\rm{b}}}}^{{{\rm{(max)}}}}\) is also influenced by k, Δτ and β since the rate of the transition is dependent on these parameters as well. In fact, one can analytically show that the eigenvalues of the Jacobian of the linearized differential equations near the saddle points exhibit a dependence on β, and specifically the real part scales as ~1/β. This implies an exponential decay of the eigenstates towards the saddle points with a rate of ~ 1/β, and so does \({i}_{{{\rm{b}}}}^{{{\rm{(max)}}}}\). Our numerical simulations, see Supplementary Fig. 2c, confirm this intuition by showing that the extent of the bistable regime (red area) decreases approximately like  ~1/β. Note however that β = 0 is a case in which there is no bistable regime.

We finally explore the dependence of the bistable regime with the delay time τD in Supplementary Fig. 2d. We observe that the value of τD does not influence the bistable regime except when τD is comparable to τJ, i.e., τD ≲ 102, where the behavior is more complex. This is because the evolution between the stable points becomes slower than τD itself, thereby disrupting the bistablility regime.

Measurement of the time dependent signal in the bistable regime with STM

To obtain spatial maps in the bistable range, we have used a lock-in amplifier at the frequency of the bistable modulation signal (7.4 kHz here). We measure the output of the current-voltage converter with the lock-in without any further amplification, and obtain the magnitude of the oscillatory signal. As seen in Fig. 3b, d, the voltage oscillates spontaneously in the bistable regime (i.e. without the action of an external drive). This leads to a current oscillation read by the current-voltage converter (Supplementary Fig. 5). The amplitude of the oscillation is proportional to the magnitude of the range in bias where the bistable regime appears (Fig. 3a, c). To make spatial maps of the Josephson critical current, it is particularly convenient to just trace the amplitude of the oscillatory signal using a lock-in amplifier measuring at the frequency of the oscillation, 2π/τD, as a function of the position at atomic scale.

We show in Supplementary Fig. 10a the tunneling conductance as a function of the time-averaged voltage for different tunneling conductances, using tip and sample of Pb. We observe the peak at zero bias, due to the Josephson effect. In previous work (refs. 6,7,9,10,11,12,24,25,49,50,51,52,53,54,55,56,57,58,59,60,62,63,64) this peak is used to follow the magnitude of the (strongly smeared by thermal fluctuations) Josephson current as a function of the position and obtain atomic scale Josephson current maps. Note the presence of two negative resistance peaks at finite bias. The peak at low bias occurs on entering the bistable regime and the second one at larger bias when leaving the bistable regime. In Supplementary Fig. 10b we show the finite frequency signal simultaneously observed in the lock-in amplifier as a function of the time-averaged voltage. We clearly see that the time dependent modulation only occurs in the bistable range and that its magnitude is large, making it easy to follow as a function of the position. The peak in the bistable regime is due to the time dependent oscillation shown in Fig. 3b, and the oscillatory signal is zero elsewhere. The amplitude of this peak is traced as a function of the position to make the maps shown in Supplementary Figs. 6, 9.

We find that the spontaneous oscillatory signal obtained after the amplifier is as large as a fraction of a V (Supplementary Fig. 10b). We can estimate the signal to noise ratio as the current at zero bias minus the current at large bias in the usual Scanning Josephson microscope (Supplementary Fig. 10a), and compare it with the signal to noise ratio of the feedback driven atomic scale Josephson microscope, which is the oscillatory signal at the peak minus the signal outside the bistable range. We find that the signal to noise ratio is at least an order of magnitude larger in the Feedback driven atomic scale Josephson microscope. This also allowed us to observe the PDW in a small field of view, as shown in Supplementary Fig. 6.