Introduction

Topological spin textures such as magnetic skyrmions1,2,3,4,5,6,7 are promising candidates as information carriers for next-generation memory-in-logic devices8. Antiferromagnetic spin textures9,10,11,12,13, compared to their ferromagnetic counterparts, innately possess high stability with respect to external disturbance14,15 and high-frequency dynamics16,17,18,19 compatible with ultrafast information processing. Collective spin dynamics in a magnetically ordered system known as spin waves (or magnons)20, are promising for low-power information processing due to its inherent advantage of charge-free transport. Nonlinear dynamic systems have been studied to a wide variety of scientific disciplines in physics, biology and engineering, including turbulent fluids, neural networks and Josephson arrays, etc21. Nonlinear spin waves are spin waves with large amplitudes that exhibit various nonlinear effects, such as the frequency multiplication22 and the foldover effect23. Driving nonlinear spin-wave excitations in a non-uniform spin texture (k0 ≠ 0) using uniform microwave perturbation (\({k}_{1}\approx 0\), namely, \({k}_{1}\ll 1\) rad μm-1) is inefficient4,5,6,7. Likewise, the excitation of short-wavelength magnons24,25 (\({k}_{1}\ne 0\), specifically, \({k}_{1} > 1\) rad μm-1) in uniform spin alignment (\({k}_{0}=0\)), is again proved to be highly challenging and usually inefficient. One would need to exert non-uniform excitation field (\({k}_{1}\ne 0\)) on a static spin texture (\({k}_{0}\ne 0\)) in the condition \({k}_{1}\approx {k}_{0}\ne 0\) in order to increase the excitation efficiency and reduce the threshold for nonlinear behaviors. In view of other prerequisites for deeply nonlinear behaviors in noncollinear textures, it is extremely hard to find a ferromagnetic system that simultaneously hosts spin textures8 and possesses low damping26,27, particularly at room temperature1,2. However, a recently revisited antiferromagnet (AFM), α-Fe2O3, also known as hematite, may provide an exceptional opportunity to study nonlinear magnons, since it has been proved to exhibit ultralow magnetic damping28,29,30 of \({10}^{-5}\) and to host noncollinear AFM textures such as half-skyrmions and bimerons at room temperature in thin films12.

In this work, we excite AFM spin textures in a single-crystalline α-Fe2O3 using a coplanar waveguide (CPW)31 with a 150 nm-wide signal line32 (inset of Fig. 1a) providing a sufficiently large dynamic wavevector \({k}_{1}\ne 0\) that approaches the wavevector of the static spin texture \({k}_{1}\approx {k}_{0}\ne 0\) (Fig. 1b). Above a threshold microwave power (~ 10 dBm), nonlinear magnons are excited in an AFM domain wall (DW) as evidenced by BLS microscopy33,34,35,36. Owing to this excitation, the initial AFM domain wall state is switched into a new noncollinear state (M1) with a different frequency by simply applying one 100 ns long pulse at the DW resonance. The system can be repeatedly initialized to the same DW state by applying an in-plane magnetic field (~ 150 mT) along the CPW direction. The switching between different AFM spin textures by nonlinear magnons is demonstrated to be fully deterministic by a multiple-cycle experiment. By repeated microwave pulses at the M1 resonance, we observe an unexpected switching from M1 to another state, M2. Finally, we experimentally demonstrate a tri-state full switching among the DW, M1, and M2 states with 1000 cycles at room temperature. Switching between the two domain wall configurations known to exist in hematite33,36 does not explain our observations. By spatially resolved BLS, we observe the formation and growth of circular and elliptical excitation regions, which are stable and exhibit lower eigenfrequencies than the one attributed to domain walls.

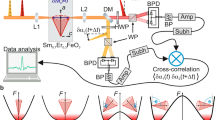
Fig. 1: Excitation of magnons in antiferromagnetic spin textures.
figure 1

a Illustration of dynamic excitation on spin textures using a nanoscale CPW antenna with its signal (S) and ground (G) line widths being 150 nm as shown in the SEM image. The wavevectors for the dynamic spin excitation and static spin texture are denoted as \({k}_{1}\) and \({k}_{0}\), respectively. b Schematic diagram of four categories of ferromagnetic spin dynamics with different conditions for \({k}_{1}\) and \({k}_{0}\). At \({k}_{1}\approx {k}_{0}\ne 0\) (yellowish area), nonlinear magnons may be excited with high microwave power in a material with low magnetic damping. c Reflection spectra measured with a millimetric (left, \({k}_{1}=0\)) and nanometric (right, \({k}_{1}\ne 0\)) CPW antenna as a function of magnetic field with a microwave excitation power of 0 dBm. The insets illustrate the antiferromagnetic resonance (AFMR) and the domain-wall (DW) resonance modes. d Single spectra extracted from the measurement with a nanoscale antenna at 20 mT (red) and 100 mT (blue). e Magnetization characterization by vibrating sample magnetometry on a single-crystal hematite (α-Fe2O3) with its crystal structure.

Full size image

Results

Fig. 1c shows spin-wave reflection spectra measured by all-electrical spin-wave spectroscopy (see “Methods”) using mm-scale (left) and nanoscale (right) CPWs. The results with mm-scale CPW (\({k}_{1}=0\)) measure the low-frequency antiferromagnetic resonance (AFMR)28,29,30 of the single-crystal hematite in association with the DMI-induced canted moment, by the vector network analyzer (VNA). Above the Morin temperature37 (\({T}_{{{{\rm{M}}}}}\simeq 262\)K), α-Fe2O3 is an easy-plane antiferromagnet with its Néel vector constrained in the (0001) basal plane, being also the sample surface plane (Supplementary Fig. S1). With a nanoscale CPW (\({k}_{1}\ne 0\)), apart from the conventional AFMR mode, an emergent mode is observed unexpectedly below the AFMR frequency (Fig. 1d). We attribute this mode to the resonance of a domain walls33,34,36 (between a pair of domains with swapped sub-lattices) stabilized by the competition between the AFM exchange and magnetoelastic interaction33,36. With a higher applied field, the DW mode becomes weaker, whereas the AFMR mode becomes stronger. The magnetization measurement up to 12 T in Fig. 1e (“Methods”) confirms a small canted moment (∼ 2.2 emu/cm3) induced by the DMI33. In view of the weak in-plane anisotropy, the canted moment is supposed to be fully saturated with a small in-plane field (\( < 5\) mT)29. However, it is reported that AFM domain walls can persist up to 500 mT36,38,39,40. In our case of the α-Fe2O3 single crystal, the local strain-induced anisotropy due to the deposition of the CPW could also contribute to the formation of the DW state because of hematite’s large magneto-elastic coupling30,33,41,42,43. Importantly, the magnetoelasticity enhances the stability of the switched AFM spin textures by a back-action on the local Néel vector via a local magnetic anisotropy41,42, which stabilizes its orientation and thereby enables the functionality of a non-volatile magnon memory44. A surface-sensitive spin-Hall magnetoresistance probe showed excellent agreement between bulk and surface measurements in an α-Fe2O3 single crystal45, which suggests that the possible surface magnetic layer46,47 may not be significant for our inductive measurements, as their electromagnetic field generated by the antenna extends considerably into the bulk of the magnetic crystal compared to its surface layer. When the sample is cooled below the Morin temperature48,49 to 250 K, the DW mode39 is shifted to lower frequency due to a change in the anisotropies (Supplementary Fig. S2). At the resonance, the domain wall starts to oscillate about its equilibrium position. When the excitation power (or rf excitation field)50 is increased further, the DW oscillation turns nonlinear22 and eventually enters the deeply nonlinear regime, in which the DW spin texture becomes strongly disordered.

In this experiment, we demonstrate the switching from the DW state to a new noncollinear state (M1) with a single microwave pulse at the DW resonance at zero field (Fig. 2a). With a microwave power below 5 dBm, the system remains in the equilibrium DW state after the pulse. However, when the microwave power exceeds the first threshold power \({{{{\rm{\vartheta }}}}}_{1}=5\) dBm (Fig. 2a), the system enters the nonlinear regime (Fig.Supplementary Fig. S3) and does not fully return to its equilibrium DW state after the pulse, leading to a decrease of the DW signal and the emergence of the M1 resonance at a lower frequency (7.4 GHz). When the pulse power reaches a secondary threshold \({{{{\rm{\vartheta }}}}}_{2}=10\) dBm, the system switches fully into the M1 state after one single pulse, where the DW signal vanishes and the M1 signal is at its maximum (Fig. 2b). In the M1 state, we measure the field-dependent reflection spectra (Fig. 2c), where two salient modes are observed. The upper one is the low-frequency AFMR mode (\(k=0\)). Fitting of its field dependence yields an effective DMI field of about 2.3 T, close to previously reported values28,29,30. The M1 mode (7.4 GHz) is almost independent of the magnetic field. If the applied field increases to 150 mT, the system is reset to the initial DW state. In Fig. 2d, we demonstrate the deterministic switching from the DW state to the M1 state by repeating 100 times a cycle comprising one microwave pulse (100 ns) of 10 dBm (DW→M1) and a field sweep to 150 mT (M1→DW). The pulse requires only 1 nJ of energy. One indispensable ingredient in the switching recipe is to excite the DW resonance (10.8 GHz). Excitations at other frequencies (7.4 GHz, 10.0 GHz and 12.0 GHz) with the same power were ineffective (Supplementary Fig. S4).

Fig. 2: Switching from the AFM domain wall state to M1 state.
figure 2

a Spin-wave reflection spectra measured after a microwave pulse (100 ns) of different power from -5 dBm to 18 dBm applied at zero external field. The frequency of the pulse is set at the resonance frequency of the DW state at zero external field. After each pulse, a reflection spectrum is measured at − 20 mT with a probing power of − 5 dBm. b Resonance amplitude extracted from the reflection spectra at − 20 mT for the M1 state (7.4 GHz). The yellow shaded area: intermediate power region with partial switching. The bottom panel shows the pulse function applied to the system, where two threshold powers are marked. \({{{{\rm{\vartheta }}}}}_{1}=5\) dBm represents the activation power for the nucleation of the M1 state whereas \({{{{\rm{\vartheta }}}}}_{2}=10\) dBm is the threshold power above which the system is fully switched to the M1 state. c Field-dependent reflection spectra measured after the sample is prepared in the M1 state. The black dashed line is a fitting of the low-frequency AFMR. The resonance frequency of the M1 state is independent of the applied field (white dashed line). d Repeated switching between the DW and M1 states with the external field of − 20 mT for 100 cycles (DW→M1→DW). The bottom panel records the resonance frequency read from low-power (− 5 dBm) microwave spectra, demonstrating switching between the DW and the M1 states.

Full size image

The switching from the DW state to the M1 state was shown to be deterministic, as it can be reproduced over many cycles. It appears to be irreversible, in the sense that a microwave pulse cannot switch the system back from M1 to DW state. If one excites the M1 resonance (7.4 GHz) with a high microwave power, the system is transformed into another state (M2). In contrast to the sharp switching from DW to M1 state, the switching from M1 to M2 state cannot be accomplished by one pulse, but rather occurs progressively using several pulses, in a process during which an intermediate (Mx) state emerges (Fig. 3a). After one pulse of 13 dBm at the M1 resonance, the M1 signal drops abruptly. With more pulses, the M1 signal decreases further while the M2 signal builds up in a regular staircase manner (Fig. 3b), which can be controlled by the switching pulse power (Supplementary Fig. S5). This tunable increment resembles a controllable weighted sum operation of synapses in artificial neural networks51. The signal of the intermediate Mx state vanishes progressively while the intensity of the M2 state substantially increases. Also, the Mx state can be easily converted into M2 state using a field sweep from − 20 mT to 20 mT as shown in Fig. 3c, where we also show that the M2 state exhibits a field dependence completely different from the M1 state (Fig. 2c). The M2 state was stable against microwave irradiation, even at a power level as high as 18 dBm. We reset the system every time from the M2 state to the initial DW state by applying an in-plane magnetic field of 150 mT. This reconfigurability, combined with the previously demonstrated switching from DW to M1 and from M1 to M2, completes the switching cycle (DW→M1→M2→DW) as illustrated in Fig. 3d. Finally, in order to demonstrate the deterministic switching and high stability of each state, we conducted a 100-cycle switching measurement (Fig. 3e), and also a 1000-cycle switching experiment (Supplementary Fig. S6).

Fig. 3: Progressive switching from M1 state to M2 state.
figure 3

a Reflection spectra \({S}_{11}\) measured during the progressive switching induced by multiple microwave pulses at 7.4 GHz with a power of 13 dBm. Two distinguishable states at about 8.6 GHz (Mx) and 9.2 GHz (M2) appear. b Reflection magnitude \({S}_{11}\) for M1 and M2 states probed at low power after several switching pulses (blue arrows) at 7.4 GHz and 13 dBm. After one pulse, the M1 intensity significantly drops, and the M2 state appears. Then the magnitude of M1 gradually decreases while that of the M2 state increases concurrently. c Field-dependent spectra showing the transformation from the Mx state to the M2 state by sweeping the external magnetic field from − 20 mT to 20 mT. d Schematic diagram for various spin texture states and the switching protocols among them. e Switching between the DW and M1 and M2 states repeated in 100 cycles (DW→M1→M2→DW) with resonance frequencies recorded for the three AFM spin textures. At each state, 10 data counts are measured before the system is switched to the next state.

Full size image

To analyze the magnetic textures, we performed two-dimensional spatial imaging of the magnon modes using spatially resolved BLS measurements. The schematic of the experiment is depicted in Fig. 4a. The location of the CPW region and a reference BLS measurement with an off-resonance frequency are shown in Supplementary Fig. S7. After applying a large field of 180 mT parallel to the CPW, we directly measured the spatial distribution of microwave excited (5 dBm) magnon modes at the frequencies corresponding to DW (10.8 GHz, Fig. 4b), Mx (8.8 GHz, Fig. 4c) and M2 (9.4 GHz, Fig. 4d) states at an applied field of 20 mT. The BLS intensity corresponds to the square of the out-of-plane component of the dynamic local net magnetization in our measurement52. As it is shown in Fig. 4b, the DW state is more uniformly spread in a large area. Still, clear irregular domain wall patterns can be identified. Interestingly, the Mx (Fig. 4c) and M2 (Fig. 4d) states coexist with the DW state in the BLS images; however, the spatial distribution of the DW mode is dominant, which can explain the high signal intensity of the DW mode in VNA measurements. After applying a 1-second-long microwave pulse with a power of 24 dBm at the DW resonance frequency (10.8 GHz), a partial disappearance of the DW texture is evidenced (Fig. 4e). As it is clear from Fig. 4f, the Mx state gains importance, and two pronounced circular textures appear. At the same time, a change in the spatial distribution of the M2 mode and a slight increase in its intensity are observed in Fig. 4g. The microwave pulse switches the DW state only partially due to the low power efficiency in the BLS microscope, which is caused by the large impedance mismatch from the wire-bonding that delivers the microwave from the signal generator to the CPW. We mention that the microscopy data of Fig. 4 indicate that direct switching of DW mode to other modes than M1 is also possible. The switching behavior imaged by the BLS microscope qualitatively corresponds to the switching of the AFM spin textures observed by the VNA. The domain wall patterns are mainly located under the nano-CPW, and the domain walls have a spatial distribution in the order of a micrometer, which is comparable to the dimension of the CPW. It is noted that the DW alignment is not along the x or y-directions, so the wavevector provided by the CPW (in the y-direction) can effectively excite the spin precession. As a result, the direct 2D mapping of the domain structures demonstrates that the requirement of \({k}_{1}\approx {k}_{0}\) is expected to be satisfied in the experiment.

Fig. 4: Spatially resolved magnon distribution in the α-Fe2O3 sample before and after a microwave pulse.
figure 4

a Sketch of microwave(MW)-assisted Brillouin light scattering microscopy on a α-Fe2O3 crystal (blue) with an integrated CPW (yellow). The CPW is made of three 120 nm thick gold wires, 150 nm in width and separated by 250 nm-wide gaps. The laser spot has a diameter of about 355 nm according to the Abbe diffraction limit and is scanned over an area of 3 by 9 μm2 (marked with a semi-transparent trapezoid) in the xy plane. The step size is 100 nm in both x and y-direction. The field is applied along the x-axis. Spatial mapping of three different modes of DW, Mx and M2 excited by the CPW at (b), 10.8 GHz and (c), 8.8 GHz and (d), 9.4 GHz, respectively, with a microwave power of 5 dBm in a field of 20 mT after applying a large field of 180 mT. After applying a microwave signal at 10.8 GHz with a high power (24 dBm) for 1 sec, the magnon distributions of the same sample area are irreversibly modified when probed with (d), a 10.8 GHz and (e), a 8.8 GHz and (f), a 9.4 GHz microwave signal of 5 dBm applied to the CPW.

Full size image

The BLS images contain circular and elliptical regions with low excitation frequencies. They suggest the existence of noncollinear spin structures whose spins deviate from an easy axis (point along a hard axis)53. The key distinction between the VNA and BLS techniques lies in their detection focus. The VNA primarily measures the global response of the system, while the BLS microscope provides spatially resolved measurements of local spin-wave excitations. One possible reason the M1 state is not obvious in the BLS measurements could be due to its spatial distribution. The M1 state might occupy only a limited region, making it challenging for the BLS microscope, which detects localized spin-wave signals. In addition, the stability of the M1 state under the specific excitation and measurement conditions of the BLS experiment may differ from those in the VNA experiment, where the signal is globally averaged across the entire sample. Another factor to consider is the sensitivity of the BLS microscope to magnon modes in different AFM spin textures. Due to its small size and circular spin structures, the BLS microscope may be less sensitive to the resonance modes associated with the M1 state. Furthermore, we point out that the lower resonance mode, observed below the AFMR mode, may be influenced by a phase change to Fe3O4 at the hematite surface upon deposition or a possible surface magnetism on the α-Fe2O3/Au Interface54,55. AFM bimerons were observed by the XMLD and NV magnetometry measurement on an α-Fe2O3 film12,56. Hence, future studies with spatially resolved techniques such as NV magnetometry56,57 are desired to image directly the stable magnetic states reached by the experimentally observed switching processes under microwave irradiation. Using advanced time-domain techniques57 may provide insights on the temporal dynamics of the real inhomogeneous spin systems. Moreover, comprehensive numerical characterization of the AFM spin textures and their dynamic switching behaviors requires further development of the microspin simulations for AFM systems, including magnetoelasticity, which is beyond the scope of the current work.

In order to understand the switching process, we performed a time-dependent micromagnetic simulation (Fig. 5). We model α-Fe2O3 as an A-type antiferromagnet to capture its primary magnetic characteristics, despite its complex up-down-down-up spin arrangement along the c-axis deviating from the conventional A-type antiferromagnet58. More accurate simulations for such complex AFM crystal structures may require atomic-scale calculations59. Initially, the magnetic ground state was determined by minimizing the total energy. Considering contributions from exchange energy, anisotropy energy, and DMI energy, a periodic stripe domain state was obtained, characterized by opposite magnetization in adjacent antiferromagnetically coupled layers (see “Methods”). The stripe domain period is approximately 250 nm, and we designate as the DW state in the simulation (Supplementary Fig. S8). To determine the resonance frequencies of different states, a sinc pulse was applied, followed by a fast Fourier transformation of the dynamic magnetizations (Supplementary Fig. S9). A microwave pulse \({H}_{{{{\rm{ex}}}}}={H}_{{{{\rm{CPW}}}}}\sin \left(2{{{\rm{\pi }}}}{ft}\right){e}_{x}\) was then applied at the DW resonance frequency for 1 ns within a field pattern resembling that of a CPW antenna. Under low-power excitation (\({H}_{{{{\rm{CPW}}}}}=0.05\) T) at the resonance frequency of the DW state, the spin dynamics remain in the linear regime, exhibiting harmonic oscillations around equilibrium (Fig. 5a). When a high-power microwave pulse (\({H}_{{{{\rm{CPW}}}}}=0.1\) T) is introduced, AFM half-skyrmions are nucleated by nonlinear magnons (Fig. 5b). Once the excitation is turned off, the half-skyrmions (Bloch merons and anti-merons) with the same topological charge Q pair into Bloch bimerons, thereby stabilizing into the M1 state. Furthermore, when a microwave pulse is introduced at the resonance frequency of the M1 state, nonlinear magnons drive the motion of half-skyrmions. When Bloch merons and anti-merons with opposite topological charges meet, they form a topologically trivial meron pair, losing their topological protection and subsequently annihilating. After the microwave pulse is turned off, the spin texture switches to the stripe domain state within the CPW-covered region, with the orientation of the stripe domains differing from the initial DW state (Supplementary Fig. S10). While we acknowledge that simulations alone cannot fully confirm the exact nature of the experimentally observed states, the qualitative agreement in excitation conditions, simulated dynamics, and the switching behavior of different AFM spin textures offer one possible switching mechanism.

Fig. 5: Linear and nonlinear excitation for the deterministic switching revealed by micromagnetic simulations.
figure 5

a Snapshots showing the linear excitation of the stripe domain state by the nano-CPW. The images depict the mz magnetization component of the bottom layer. The excitation field is applied during the first nanosecond, with the yellow squares indicating the excitation regions. b Snapshots showing the nonlinear excitation for the switching from the DW state to the M1 state. The red square marks one representative Bloch bimeron.

Full size image

Further challenges are currently hindering the performance of micromagnetic simulations for antiferromagnetic materials with micron-scale thicknesses. The substantial computational resources needed to model these thick structures, especially with respect to accurate meshing and long-range interactions, add to the difficulty. In addition, the role of inhomogeneities in thicker antiferromagnetic materials is crucial for obtaining reliable simulation results. Overcoming these challenges will be essential for advancing our understanding of spin dynamics in bulk-like antiferromagnetic systems.

Discussion

In summary, we have demonstrated experimentally the deterministic switching among three characteristic types of non-collinear AFM spin textures. When the wavevector (\({k}_{1}\)) excited by a nanoscale antenna matches the wavevecor (\({k}_{0}\)) of spin textures, the excitation of spin dynamics becomes highly efficient, owing to the strong coupling between evanescent microwave photons60 and solitonic magnons4,5,6,7 when \({k}_{1}\approx {k}_{0}\ne 0\) in analogy to the magnon-photon coupling studied in a cavity61 with \({k}_{1}={k}_{0}\approx 0\). In view of the ultralow damping of hematite, nonlinear magnons are triggered above a threshold microwave power and, as a result, the system is switched from one stable spin texture state to another. The underlying switching mechanism may be understood as magnon-induced spin torque62,63 that drives the system into the nonlinear regime. This switching process is significantly faster and less energy demanding (1 nJ) than using current-induced spin torque (which also has a chaotic nature64) in AFM semimetals65. The transformation from M1 state to M2 state occurs progressively. The M1 and M2 states can be switched back reproducibly to a domain-wall state35 with a magnetic field. Finally, we demonstrate the remarkably high controllability of the switching with 1’000 cycles and its extraordinarily high stability in a 7(day)\(\times\)24(hour) experiment (Supplementary Fig. S11). Our results on AFM spin texture dynamics and switching behaviors are reminiscent of neuronal nonlinear activation function66 (Fig. 2b) and synaptic weighted sum operation51 (Fig. 3b), and therefore open up opportunities for AFM-based neuromorphic computing with low-power consumption and ultrafast information processing based on AFM topological charges67.

Methods

Sample information and device fabrication

The α-Fe2O3 single-crystalline film with the dimensions of 5 mm ×5 mm × 0.5 mm was grown by the commercial company SurfaceNet. The Morin transition temperature is around 262 K. Above the Morin transition temperature, α-Fe2O3 is an easy-plane antiferromagnet with a canted magnetic moment in (0001) film plane due to the Dzyaloshinskii-Moriya interaction. Below the Morin transition temperature, the anisotropy field is along the [0001] axis, and α-Fe2O3 is a uniaxial antiferromagnet with the Néel vector along the [0001] crystalline orientation. Magnetization characterization was conducted by the vibrating sample magnetometer (VSM) mounted on a PPMS (Quantum Design). A nanoscale coplanar waveguide (CPW) is integrated on top of the α-Fe2O3 film by electron beam lithography. The width of the signal line and ground line is 150 nm wide, and the gap in-between is 250 nm.

All-electrical spin-wave spectroscopy

All-electrical broadband spectroscopy is used to detect the AFM spin excitations in three states at room temperature. A vector network analyzer (Keysight PNA-X N5247B) is used to generate microwave pulses with the width down to 100 ns and detect the spin dynamic states of different AFM spin textures. The impedance of the CPW is measured as \({Z}_{0}=\)1.24 Ω, indicated by the Smith chart. An in-plane external field is applied perpendicular to the CPW. The film was initially applied an in-plane external magnetic field of 300 mT parallel to the CPW, and the field was then turned off. The reflection spectra \({{{\rm{S}}}}\)11 of three AFM spin texture states are measured at the in-plane field of − 20 mT, with the detection power of − 5 dBm. The upper limit of the microwave pulse power is 18 dBm. The low-temperature measurements are conducted in a temperature-controlled probe station (Lakeshore CRX-EM-HF) with low-loss microwave cables.

Microwave-assisted Brillouin light scattering microscopy

Spin-wave modes were probed via Brillouin light scattering (BLS) microscopy at room temperature with a microwave (MW) signal applied to the CPW (Fig. 4a). The same device as being studied with VNA was used in the BLS experiment. For BLS, the integrated CPW was connected to the MW signal generator via bonding wires. They allowed for the short working distance of the objective lens. We used a 100x objective lens with a numerical aperture of 0.75 and focused a green laser (532 nm in wavelength, 0.3 mW in power) on the sample surface. Energy shifts of the inelastically scattered photons were detected by a Sandercock-type six-pass tandem Fabry-Pérot interferometer. The sample was mounted on a piezo-positioning system with high precision for movements along the x, y and z-axes. The spatially resolved BLS signals (magnon distributions) were collected by moving the sample in the xy-plane with 100 nm steps while a fixed frequency microwave current was applied to the CPW. The 2D maps of BLS signals presented in Fig. 4b–g were collected during nominally the same acquisition time with a continuous-wave microwave current applied at 5 dBm. Note that the CPW was connected to the signal generator via Al wires with a diameter of 30 micrometers and unknown impedance instead of the impedance-matched microwave probe used in the VNA measurements. We hence assumed that the actual microwave power level at the CPW was much lower under the BLS microscopy than in the VNA probe station. The 150 nm-wide Au leads were smaller than the laser focus diameter of about 355 nm according to the Abbe diffraction limit and did not induce a significant signal intensity modulation when scanning over the CPW. Figures 4b–d show the spatial mapping of magnons excited by the CPW at 10.8 GHz, 8.8 GHz and 9.4 GHz with a power of 5 dBm. Fig. 4e–g shows the BLS signals taken on the same sample area excited at 10.8 GHz, 8.8 GHz and 9.4 GHz with a power of 5 dBm after applying for 1 s a 10.8 GHz microwave signal at a power level of 24 dBm. The distinct differences between the BLS signals observed before and after applying a high-power microwave signal evidence the microwave-induced modifications of the spin textures in α-Fe2O3 close to the CPW and are consistent with the conclusions drawn from the VNA data. The spatially resolved BLS data provide a microscopic picture of the modified sample regions.

Micromagnetic simulations

The GPU-accelerated micromagnetic simulation program MuMax3 was utilized. We consider an A-type antiferromagnet, setting the AFM interlayer exchange coupling and the ferromagnetic intralayer exchange coupling. The simulated antiferromagnet structure with the dimensions of \(2{{{\rm{\mu }}}}{{{\rm{m}}}}\times 2{{{\rm{\mu }}}}{{{\rm{m}}}}\times 4\,{{{\rm{n}}}}{{{\rm{m}}}}\) (x y z) is investigated, with the mesh sizes of \(10{{{\rm{nm}}}}\times 10{{{\rm{nm}}}}\times 2{{{\rm{nm}}}}\). The magnetization of a single sublattice is set as \({M}_{{{{\rm{S}}}}}=920{{{\rm{kA}}}}{{{{\rm{m}}}}}^{-1}\). The antiferromagnetic exchange constant, hard-axis anisotropy energy and easy-axis anisotropy energy are set as A = \(-460\times {10}^{-12}\) J m-1, \({K}_{A}=400\times {10}^{3}\,\)J/m3 and \({K}_{a}=27.6\,\)J/m3 respectively. Here, we consider a three-fold magnetocrystalline anisotropy, with one field along the x-axis and the other two at \(\pm\)120 degrees relative to the x-axis, in order to accurately model the real case of hematite. The intralayer FM exchange coupling is set as AFM = 17 pJ/m. The damping coefficient is set as α = 0.001. The bulk DMI is included in the simulation with the value Dbulk = 1.84 × 10−3 J m−2. An external bias field of 20 mT is applied in the y-direction. In order to determine the resonance frequencies of different states, a uniform field is applied according to Hex = H0sin(2πf0t)/(2πf0t), with H0 = 10 mT and f0 = 50 GHz. The ground state is first obtained by minimizing the total energy, and then the time-dependent simulations are conducted with 600 equidistant times in the step of 10 ps. The fast Fourier transformation is then performed with dynamic magnetizations for obtaining the resonance frequency of different states. For the simulation of deterministic switching different AFM states, an oscillating magnetic field \({H}_{{{{\rm{ex}}}}}={H}_{{{{\rm{CPW}}}}}\sin \left(2{{{\rm{\pi }}}}{ft}\right){e}_{x}\) is applied for the signal line and \({H}_{{{{\rm{ex}}}}}={-\frac{1}{2}H}_{{{{\rm{CPW}}}}}\sin \left(2{{{\rm{\pi }}}}{ft}\right){e}_{x}\) for the ground line with the duration of 1 ns.