Abstract
Thin-film composite membranes are integral to the reverse osmosis (RO) process, effectively converting seawater and brackish water into potable water. While significant strides have been made in improving water permeability and salt rejection, there has been a corresponding lag in enhancing chlorine resistance and boron rejection. This study presents a suprasmolecular nanocrystalline membrane (SNM) with abundant subnanometer channels created through precisely assembled and well-oriented tetra-oligomer chains, enhanced by interfacial hydrogen bonding under nanoconfined space. The 6 nm-thick SNM exhibits highly aligned nanocrystalline domains and a Young’s modulus of 4 ± 0.5 GPa. Benefiting from its ultrathin thickness and well-oriented subnanoscale channels, the SNM functions effectively as a permeation and selective layer, achieving 99.6% NaCl rejection at 55 bar with a 3.5 wt% NaCl feed and delivering 2-4 times higher water permeance than commercial seawater RO membranes. Molecular dynamics simulations reveal that the abundant, well-aligned subnanochannels facilitate rapid water transport while raising the energy barrier for sodium ion transport. Furthermore, the SNM shows superior boron rejection (exceeding 92.5% at pH 7), remarkable chlorine resistance (200 ppm NaClO exposure for 300 hours), and sustained operational stability under extreme pH conditions (1 and 13) for over 168 hours. These findings establish that space-confined interfacial hydrogen bonding governs the precision self-assembly of robust subnanochannels, offering a new paradigm for high-resilience desalination membranes.
Similar content being viewed by others
Introduction
The escalation of water scarcity around the world has amplified the urgency for efficient and sustainable water purification solutions1,2,3,4. Desalination—removing salts and impurities from seawater or brackish water—has become a vital technology that is applied in various fields, including drinking water supply, agriculture, and industrial operations5,6,7,8,9,10. Membrane-based desalination processes, particularly reverse osmosis (RO) and nanofiltration (NF), employ semipermeable polymeric membranes as their core separation elements. These advanced polymer membranes have become the industry standard due to their superior performance, scalability, and cost-effectiveness9,11,12,13,14. While research has increased membrane permeability through various modifications, these efforts have yielded only marginal improvements in energy efficiency12,15,16,17,18. More critically, their desalination selectivity and structural stability tend to deteriorate under harsh mechanical and chemical stresses, including high-pressure conditions, hypersaline feeds, and oxidative environments15,19. These limitations are most evident in two aspects of conventional RO membranes: (1) poor boron rejection (typically <60% at neutral pH, where boron exists as uncharged B(OH)3)15,20,21, and (2) susceptibility to chlorine-induced degradation via N-chlorination of amide bonds or aromatic ring substitution22,23,24. These persistent shortcomings have driven the development of next-generation desalination membranes that simultaneously achieve enhanced selectivity, chlorine resistance, and long-term stability for sustainable water purification.
Crystalline polymer membranes have emerged as a promising alternative for their unique attributes of selective transport and mechanical stability12,25. The ordered crystalline regions within these membranes enhance structural integrity and facilitate the diffusion of water while impeding the passage of salts26,27,28,29. Despite notable advancements, these membranes still face limitations in performance and stability under high-salinity conditions (e.g., seawater with 30000-40000 ppm NaCl). Recent advances have opened a promising window by leveraging multiscale engineering and self-assembly techniques to craft precisely structured polymers with superior properties30,31,32,33,34,35,36. Through the meticulous assembly and orientation of polymer chains, the crystallinity of polymer nanofilms is enhanced at a nanoscale level37,38. This, in turn, leads to a substantial improvement in both desalination selectivity and durability when treating brackish water and seawater.
To boost chain alignment and polymer crystals at a nano-confined space, e.g., when the microdroplets spread at the interface of two phases, two essential factors need to be considered: (1) the spreading coefficient should be greater than 0 for fast and extensive spreading with a large-area and ultrathin membrane, and (2) abundant interfacial binding motifs are required to facilitate the accumulation of polymer chains through the interaction with the interface30,39,40. Ensuring these two factors greatly promotes sufficient packing and orientation of polymer chains within a short period, leading to enhanced crystallinity at a nano-confined space41,42,43. In addition, the assembly at air/liquid and liquid/liquid interfaces has offered a reliable way for the fabrication of 2D polymer membranes44,45,46,47. These assembly processes typically employ surfactants or macromolecules as intermediate layers that mediate interfacial interactions39,48,49,50. The considerable progress in this area provides inspiration for designing functional nanocrystalline membranes via molecular engineering and interface chemistry51.
Here we report supramolecular nanocrystalline membranes (SNMs) through the precise assembly and orientation of tetra-oligomer chains under nanoconfinement. Using polyethylene glycol (PEG)-mediated interfacial hydrogen bonding, we guide the organization of polycaprolactone (PCL) chains at the interface, enabling a highly selective and permeable nanofilm layer. The optimized 6 nm SNM exhibits large crystalline domain sizes of 100–150 nm and a threefold increase in Young’s modulus. Moreover, by varying the PEG aqueous solution concentration, we directly modulate the density and strength of interfacial hydrogen bonds, enabling precise tuning of membrane spreading area, thickness, crystallinity, and zeta potential. The SNM demonstrates impressive desalination capacities for both brackish water and seawater, achieving over 99.6% rejection of NaCl, and exhibits a water flux of 69.9 L m−2 h−1 at 15.5 bar for a 0.58 wt% NaCl feed solution and an even higher flux of 117 L m−2 h−1 at 55 bar for a 3.5 wt% NaCl feed solution. Additionally, the SNM demonstrates high boron rejection ( > 92.5% at pH 7), excellent chlorine resistance (200 ppm NaClO exposure for 300 hours), and sustained operational stability in harsh conditions (pH 1 and pH 13) over 168 hours. The superior transport properties of the SNM are primarily attributed to its abundant, well-aligned subnanochannels within the nanocrystalline domains. Molecular dynamics simulations reveal that this unique configuration offers dual benefits: it promotes the formation of continuous water channels and ensures an ordered arrangement of water molecules, thereby enhancing water flux while increasing the energy barrier for sodium ion transport. Combining experimental and theoretical insights, this work advances the fundamental understanding of space-confined, hydrogen bond-assisted formation of well-oriented subnanochannels, enhancing the resilience and desalination performance of reverse osmosis membranes for both brackish water and seawater applications.
Results
Preparation and characterizations
In designing high performance deslination membranes, aligned PCL chains that form robust subnanochannels within nanocrystalline domains simultaneously enable rapid water transport and efficient solute rejection. The strategic incorporation of tetraphenol—a rigid, bulky building block—further enhances the membrane’s mechanical strength and chemical resilience. This dual optimization addresses two key challenges in membrane desalination: the permeability-selectivity trade-off and long-term operational stability under harsh conditions. Tetra-oligomer was synthesized via the ring-opening polymerization of ε-Caprolactone (ε-CL), as confirmed by proton nuclear magnetic resonance (1H NMR) (Figs. S2–2). The gel permeation chromatography (GPC) profile indicated an average molecular weight of ~ 8000, with a polydispersity index (PDI) of 1.37 (Fig. S3). The nanofilms were prepared by depositing a microdroplet (2 mg mL−1) of tetra-oligomer PCL in chloroform (CHCl3) onto PEG aqueous solutions (0-4 wt%). Rapid solvent evaporation and favorable spreading conditions (spreading parameters >0, Fig. S4) enabled the formation of large-area, ultrathin membranes at the interface within seconds (Fig. 1a, b). This process was driven by abundant hydrogen bonding between PEG and PCL oligomers, which directed the organization and alignment of hydrophobic alkyl chains under nanoconfinement. The resultant supramolecular nanocrystalline membranes were denoted as SNM-x, where x is the percentage concentration of the PEG aqueous solution.
a Schematic illustration of the preparation of highly crystalline PCL nanofilm at the air/PEG aqueous solution interface. Interfacial hydrogen bonding facilitates the ordered assembly and orientation of PCL chains, resulting in highly crystalline membranes. PEG refers to polyethylene glycol, while PCL represents polycaprolactone. b An optical image of SNM-2 transferred on the polyethersulfone (PES) support. c An optical microscopy image of SNM-2 on the SiO2/Si wafer, accompanied by the corresponding water contact angle of 43 ± 2°. d The SEM image of SNM-2 transferred on the SiO2/Si wafer. e The height image of SNM-2 dertermined by AFM. f The 3D surface morphology of SNM-2 with a scan area of 10 × 10 μm. Free volume in Tetra-PCL/PEG (g) and Tetra-PCL/H2O (h) (see the space occupied by green volume) detected by a theoretical probe with a radius of 1.2 Å. Simulated pore diameter distributions (i) and fractional free volume (j) of Tetra-PCL/PEG and Tetra-PCL/H2O.
SNM-2, when transferred onto 300 nm SiO2/Si wafers, showed a uniform surface as confirmed by the optical microscopy (Fig. 1c) and scanning electron microscopy (SEM) images (Fig. 1d). SNM-2 displayed a hydrophilic nature with a water contact angle of 43 ± 2°, which is lower than that of SNM-0 (Figs. 1e and S5). This observation suggests an increased presence of hydrophilic units such as hydroxyl and carboxyl motifs on the surface of SNM-2. The thickness profile of SNM-2 on the silicon wafer was determined to be ~ 6 nm using atomic force microscopy (AFM) (Fig. 1e). The AFM 3D topological measurement (Fig. 1f) showed a low root mean square roughness (Rq) of 1.46 nm over a 10 × 10 μm area, indicating SNM-2’s smooth surface. The presence of the 2 wt% PEG aqueous solution did not bring significant changes in the thickness and roughness of SNM-2, in contrast to the counterpart SNM-0 (Fig. S6 and 7).
The concentration of the underlying PEG aqueous solution directly modulates the density and strength of interfacial hydrogen bonds during microdroplet spreading, consequently controlling the resulting SNM’s spreading area and thickness. The spreading area of SNM-1 and SNM-2 remained over 100 cm2, slightly lower than that of SNM-0, and then underwent a drastic reduction as the PEG concentration was higher than 2 wt% (Fig. S8). Surprisingly, even at the concentration of 4 wt% PEG, the spreading area of SNM-4 achieved nearly 40 cm2. The membrane thickness did not show any distinct changes up to 2 wt% PEG concentration, maintaining approximately 6 nm, and then increased to around 3 times that of the pristine as the PEG concentration reached 4 wt% (Fig. S9). The underlying reasons for the variations in spreading area and thickness with increased PEG concentrations were elucidated by calculating the spreading parameters. As shown in Fig. S4, the spreading coefficient followed a downward trend as PEG concentrations increased. Remarkably, the spreading coefficient exhibited a gradual reduction up to 2 wt% PEG concentration, followed by a sharp decrease within the 2-4 wt% range. The reduced spreading coefficient decreased the microdroplet spreading rate at the solution interface, yielding membranes with greater thickness and smaller surface area.
The pore sizes and fractional free volume of the membranes were simulated. Two structural models, Tetra-PCL/PEG and Tetra-PCL/H2O, were constructed to analyse the free volume, represented by the green volume, using a theoretical probe with a radius of 1.2 Å (Fig. 1g, h). The Tetra-PCL/PEG system exhibited a more homogeneous distribution of pore diameters (Fig. 1i) and a comparable fractional free volume to the Tetra-PCL/H2O system (Fig. 1j).
Improved and tuneable crystallization
The crystalline behaviour of the resultant nanofilms was analysed using various techniques. Dark-field transmission electron microscopy (TEM) analysis, providing a colour contrast image where the bright regions are associated with crystalline domains and the dark zones typically represent amorphous phases, revealed a substantial increase in the size of crystalline domains (100–150 nm) in SNM-2 (Fig. 2a), approximately 3 times larger than that of SNM-0 (Fig. S10). High-resolution TEM (HRTEM) imaging displayed SNM-2’s highly oriented morphology, with lattice fringes corresponding to the plane (110) (Fig. 2b, c), and the patterns acquired through selected area electron diffraction (SAED) verified SNM-2’s high crystallinity (Fig. 2d). Grazing incidence X-ray diffraction (GIXD) investigating the arrangement of tetra-oligomer chains (Fig. 2e) exhibited pronounced Bragg reflection at (110), verifying the crystalline nature and the edge-on orientation of tetra-oligomer chains. We noted that the diffraction intensities of the nanofilms significantly rose from SNM-0 to SNM-2 (Fig. 2f). The relative degree of crystallinity (rDoC) of the nanofilms (Fig. S11) was calculated based on (110) diffraction peak intensity (Fig. 2f), which showed that the rDoC increased as the PEG concentration reached 2 wt% but did not greatly vary with PEG concentrations above 2 wt%. Differential scanning calorimetry (DSC) showed that the transition temperature of the nanofilms was around 59 °C. In comparison to SNM-0 and SNM-1, SNM-2 had a higher melting enthalpy, suggesting that crystallinity enhances with an increase in the concentration of the PEG aqueous solution (Fig. 2g). Improved PEG concentrations directed a significant increase in both the quantity and strength of interfacial hydrogen bonds, promoting the assembly and alignment of PCL chains, thereby enhancing the crystallinity of the nanofilm. The peak force quantitative nanomechanical mapping (PFQNM) AFM revealed distinct modulus distributions of SNM-2 and SNM-0 (Fig. 2h and j), where higher modulus values represented crystalline domains and lower modulus values corresponded to amorphous phases. SNM-2 displayed a modulus of 4 ± 0.5 GPa, approximately threefold greater than SNM-0 (Fig. 2i and k).
a Dark-field TEM imaging of SNM-2 reveals crystalline domains (bright regions) dispersed within an amorphous matrix. b Bright-field TEM of SNM-2 shows large, well-defined crystalline domain. c HRTEM imaging of SNM-2 shows the highly oriented lattice fringes, corresponding to the (110) planes of the PCL lattice. d The SAED pattern from SNM-2’s crystalline domain identified in the HRTEM image. e The GIXD pattern of SNM-2 on 300 nm SiO2/Si wafer. f Diffraction intensity along Qxy direction from GIXD analysis. g The second heating DSC curves of SNM-0, SNM-1, and SNM-2. h, i AFM modulus and profile of SNM-2. j, k AFM modulus and profile of SNM-0.
Experimental and computational verification of interfacial hydrogen bonds
To verify the existence of interfacial hydrogen bonds, we conducted surface chemical analysis and zeta potential measurements. Raman spectroscopy and angle-resolved X-ray photoelectron spectroscopy (XPS) were performed on the bottom surfaces that were in contact with the PEG aqueous solution. Compared to SNM-0, the Raman spectra of the SNM-2 surface showed increased intensities for the carbonyl peak at 1680 cm−1 and the hydroxyl group at 3500 cm−1 (Figs. 3a, b and S12). Similarly, surface XPS fine spectra showed more distinct signals of C = O (8.8%) and C-O (36.3%) on the bottom layer of SNM-2 than those of SNM-0 (Fig. 3c, d and Table S1). The surface zeta potential was measured at pH 8 (mimicking seawater conditions) in 0.01 M KCl solution (ambient temperature, Fig. S13). The nanofilms exhibited progressively stronger negative zeta potentials with increasing PEG concentration. This trend suggests that PEG-derived interfacial hydrogen bonds enabled dynamic reorganization of hydrophilic groups (carbonyl and hydroxyl), increasing their surface density and consequently enhancing negative charge.
Raman spectra of carbonyl (a) and hydroxyl group (b) of SNM-0 and SNM-2. XPS fine spectra of SNM-0 (c) and SNM-2 (d). The geometry structures of the PCL/H2O system (e) and the PCL/PEG/H2O system (f). g Binding energies of the PCL/H2O system and the PCL/PEG/H2O system. h Surface electrostatic potential of H2O, PEG, and PCL, respectively, from left to right. Charge density difference maps of the PCL/H2O system (i) and the PCL/PEG/H2O system (j). Reduced density gradient maps of the PCL/H2O system (k) and the PCL/PEG/H2O system (l).
To investigate how PEG influences hydrogen bonding interactions with PCL at the atomic level, we performed Density functional theory (DFT) simulations by calculating binding energy, electrostatic potential, charge density difference, and reduced density gradient. Figure 3e and f reveal that the number of hydrogen bonds increases dramatically within the PCL/PEG/H2O system compared to the PCL/H2O system alone. As shown in Fig. 3g, the interactions in the PCL/PEG/H2O system exhibit a binding energy of −0.665 eV, compared to −0.386 eV in the PCL/H2O system. This substantial rise in binding energy suggests that the PEG incorporation promotes the formation of hydrogen bonds, which can be attributed to the PCL/PEG/H2O system’s more favourable configuration facilitating closer and more effective packing of molecules. Electrostatic potential calculations (Fig. 3h) further supported these findings, where the surface electrostatic potential of PCL and PEG had multiple sites of negative electrostatic potential, with PEG displaying the most negative value at −1.73 eV. This feature implies that PEG molecules can act as an efficient mediator in enhancing physical interactions in a nano-confined space, thus further stabilizing the PCL/PEG/H2O system.
Charge density difference maps provided a more pronounced and intricate pattern of electron transfer within both PCL/H2O and PCL/PEG/H2O systems (Fig. 3i, j), suggesting a stronger and more dynamic interaction at the molecular level, driven by the presence of PEG molecules. The polar interaction zones could be enhanced, thus increasing the overall stability of the PCL/PEG/H2O system. Reduced density gradient (RDG) maps were also employed to compare the two systems (Fig. 3k, l). The RDG maps showed intensified green and blue regions, which indicate stronger hydrogen bonding, in the PCL/PEG/H2O system relative to the PCL/H2O system, further validating the synergistic effect of PEG molecules in enhancing the molecular interactions.
The DFT calculations elucidate two valuable atomic-scale insights: (1) the nature and strength of interfacial hydrogen bonding interactions, and (2) the changes in electron distribution and binding energy induced by PEG incorporation.
Desalination performance
Our study revealed a concentration-dependent relationship between PEG content and membrane performance. Higher PEG concentrations in the fabrication process yielded SNMs with reduced water permeance (A), as shown in Fig. S14. At a pressure of 15.5 bar, the peak water permeance of SNM-0 reached approximately 18.3 L m−2 h−1 bar−1, while SNM-2 showed a water permeance of 8.4 ± 0.3 L m−2 h−1 bar−1. Meanwhile, the pure water flux increased nearly proportionally as the applied pressure rose from 5 to 100 bar, suggesting SNM-2’s mechanical robustness and structural integrity (Fig. S15).
The desalination performance of SNMs was evaluated using NaCl feed solutions at two representative salinities: 0.58 wt% (brackish water conditions) and 3.5 wt% (seawater conditions). The brackish water desalination was conducted under an applied pressure of 15.5 bar (Fig. 4a and Table S2). The water fluxes of SNM-0 to SNM-4 decreased from 191.65 ± 2.1 L m−2 h−1 to 33.93 ± 0.79 L m−2 h−1, and rejection rates increased from 70.6 ± 1.13% to 99.72 ± 0.03%. Similarly, for the desalination of 3.5 wt% NaCl solution at 55 bar, the water flux witnessed a reduction from 312.78 ± 4.41 L m−2 h−1 to 52.59 ± 2.28 L m−2 h−1 from SNM-0 to SNM-4. Conversely, the rejection rates rose rapidly to 99.62 ± 0.04% from SNM-0 to SNM-2 and then gradually grew to 99.78 ± 0.03% for SNM-4 (Fig. 4b and Table S2). It is worth mentioning that SNM-2 showed around 99.6% rejection for both 0.58 wt% and 3.5 wt% NaCl solutions, surpassing the benchmark of commercial brackish water reverse osmosis (BWRO) membranes and commercial seawater reverse osmosis (SWRO) membranes52,53,54.
The water flux and rejection rates of SNMs when desalinating 0.58 wt% (a) and 3.5 wt% (b) NaCl feed solutions at pH = 8 and 0% recovery with 15.5 bar and 55 bar, respectively. c The boron rejection of SNMs using a 5-ppm feed solution at 15.5 bar. d The desalination performance of SNM-2 after continuous treatment for 168 hours at 15.5 bar and pH = 8 with 0.58 wt% NaCl solution. e The desalination performance of SNM-2 after immersion in acidic (pH = 1), basic (pH = 13), and urea (1 wt%) solutions for 24 hours, followed by thorough cleaning with deionized water. Desalination tests were performed at 55 bar using a 3.5 wt% NaCl feed solution. The water flux and salt rejection of SNM-2 that was exposed to a 200 ppm NaClO aqueous solution for 300 hours at pH = 5 (f) and pH = 9 (g). The total chlorine exposure amount was 60,000 ppm h (200 ppm NaClO solution for 300 hours). SNM-2 was soaked in the NaClO solution under continuous stirring at 25 °C, and the solution pH was adjusted to the set values. The chlorine solution was replaced with a fresh solution every 24 hours. At certain times, the membranes were removed from the solution, rinsed thoroughly with deionized water, and tested for their desalination performance under the following experimental conditions: an effective membrane area of 12.5 cm2, 35000 ppm NaCl feed solution, crossflow rate of 4 L min−1, constant pressure of 55 bar. h Comparison with commercial BWRO and SWRO membranes in terms of water permeance and NaCl rejection ratios at the same filtration conditions: 55 bar applied pressure with 35,000 ppm NaCl feed solution at pH 8 at a recovery of 8% for SWRO membranes, and 15.5 bar applied pressure with 5800 ppm NaCl feed solution at pH 8 at a recovery of 15% for BWRO membranes. i Water permeance and NaCl rejection of this study and literature reported BWRO and SWRO membranes. The error bars represent the standard deviation of data obtained from three duplicate measurements.
In addition, the SNMs showed effective boron removal capabilities when evaluated with a feed solution containing 5 ppm boric acid (H3BO3) at 15.5 bar and pH = 7. The boron rejection rate rose rapidly to 92.6% for SNM-0 to SNM-2, then gradually increased to 94.8% for SNM-4 (Fig. 4c and Table S3). When tested under basic conditions, the boron rejection rates significantly increased at higher pH values. For example, at pH 8, SNM-2 showed a boron rejection rate of 93.5% (Fig. S16), comparable to or higher than commercial RO membranes (Table S3)15,52,55, while the rejection rate of anionic B(OH)4- exceeded 98% at pH = 10 (Fig. S16).
The desalination robustness and structural integrity were thoroughly examined under diverse mechanical and chemical conditions. During extended periods of operation, no notable alterations were detected in water flux and rejection rates for the 0.58 wt% NaCl feed solution even after 168 hours (Fig. 4d). In the case of the 3.5 wt% NaCl solution at 55 bar, after continuous operation of 168 hours, SNM-2 displayed a slight decrease of 7% in water flux while maintaining a rejection rate above 99.6% (Fig. S17). Furthermore, SNM-2 retained a defect-free surface morphology and crystalline structure after prolonged operation, as confirmed by SEM, AFM, and XRD characterizations (Figs. S18–20).
Chemical resistance to extreme pH and hydrogen bond-disrupting agents is critical for wastewater treatment membranes. We systematically evaluated SNM-2’s stability by immersing samples in acidic (pH = 1), basic (pH = 13), and urea (1 wt%) solutions for up to 168 hours. At specific times, SNM-2 was taken out from the solution and thoroughly cleaned with deionized water, and the desalination performance was subsequently measured under standard conditions of 55 bar pressure and a 3.5 wt% NaCl feed solution. For all the tested solutions, 24-h immersion did not affect the SNM’s desalination performance, verified by the unchanged water flux and rejection rates above 99.6% for NaCl solution (Fig. 4e); nor were there noticeable changes in water flux and rejection rates even after 168-h immersion (Figs. S21–23). Notably, urea—known to disrupt hydrogen bonds—failed to compromise membrane integrity and desalination performance, confirming the remarkable resilience of the supramolecular network.
Chlorine resistance measurements were also conducted (Figs. 4f, g and S24). SNM-2 was immersed in 200 ppm NaClO solutions at varying pH levels (5, 7, and 9) while continuously stirring at 25 °C for 300 hours (totaling exposure to 60000 ppm h of free chlorine). The solutions were refreshed with every 24 hours. At certain times, the membranes were removed, rinsed with deionized water, and evaluated for desalination performance. SNM-2 maintained stable water flux consistent NaCl rejection across all tested pH levels, indicating remarkable resistance to oxidative degradation. This outstanding performance can be attributed to three key factors: (1) Our SNM membranes lack reactive amine group vulnerable to N-Cl bond formation; (2) Tight crystalline packing physically excludes ClO- ions; (3) High surface modulus effectively limits oxidative penetration.
We compared our membranes with commercial BWRO and SWRO membranes in terms of water permeance and NaCl rejection under two identical filtration conditions: (1) an applied pressure of 55 bar with a NaCl feed solution of 35000 ppm at pH 8 and an 8% recovery, and (2) an applied pressure of 15.5 bar with a NaCl feed solution of 5800 ppm at pH 8 and a 15% recovery. As indicated in Fig. 4h and Table S4, our membranes showed significant advantages over the commercial BWRO and SWRO membranes, achieving 2-4 times higher water permeance, compared to commercial SWRO membranes. Furthermore, SNM-2 membranes surpassed the existing upper-bound water/NaCl selectivity of state-of-the-art lab-prepared RO membranes (Fig. 4i and Table S2)18,52,53. For BWRO preformed at 15.5 bar with a 0.58 wt% NaCl feed solution, SNM-2 showed a water permeance of 8.4 LMH/bar with the maximum water/NaCl selectivity of 60 bar−1; while for SWRO at 55 bar with a 3.5 wt% NaCl feed solution, SNM-2 exhibited a water permeance of 7.2 LMH/bar and a water/NaCl selectivity of 49.7 bar−1.
Mechanisms of solutes transport through the membrane
The equilibrium structure of each system revealed that the specific orientation of oligomer chains in the crystalline domains facilitates the formation of continuous water channels (Fig. 5a–d), enabling uninterrupted water transport. In contrast, the random distribution of oligomer chains in the amorphous regions results in irregular and discontinuous water pathways (Fig. 5e–h), indicative of a wetting-dewetting transition that slows down water transport56. This difference in water channel organization explains the higher water flux observed in the crystalline regions. We also calculated the number of water molecules transferred across the membranes during the final 15 ns of the desalination process (Fig. 5i). The water flux in the crystalline domains (2.86 molecules/ns) was approximately 1.8 times greater than that in the amorphous regions (1.56 molecules/ns). To further explore this difference, we calculated the mean square displacement (MSD) of water molecules in both regions, with results showing faster water diffusion in the crystalline structures (Fig. 5j). Additionally, the distribution of water dipole angles (Fig. 5k) indicated that water molecules in the crystalline domains align with the orientation of PCL chains, contributing to enhanced water diffusion and, consequently, higher water permeability.
Equilibrium membrane structure with crystalline (aligned) regions (a) and the continuous water channel formed (b–d). Equilibrium membrane structure with amorphous (disordered) regions (e) and discontinuous water pathways constructed (f–h). During desalination, continuous water channel in crystalline regions results in continuous water transport; while the wetting-dewetting process occurs in amorphous phases due to the discontinuous water pathways, as shown in green dashed circles. Water molecules are depicted as transparent surfaces for clarity in (a) and (e), while the membranes are shown with transparent surfaces to highlight the water channel features in (b–d) and (f–h). i Number profiles of water molecules transferred across membranes with crystalline and amorphous structures during desalination. j Mean square displacement of water molecules in the crystalline and amorphous regions. k Distribution probability for water dipole angles in the crystalline and amorphous zones. l Potential of mean force profiles for sodium ion transporting from membrane centre to the membrane’s entrance. m Pore size distribution of equilibrium solvation structures in crystalline and amorphous regions. n Evolution of sodium ion solvation structures during transport across the crystalline and amorphous regions, respectively.
Experimental results also indicated improved ion rejection performance in the crystalline areas of SNM; however, we did not observe ion transport across the membrane due to time scale limitations. To explain the experimental observations, we calculated the potential of mean force profiles (PMF) for sodium ion transport from the centre to the edge of the membrane (Fig. 5l). The PMF profiles showed that the sodium ion transport needs to overcome a higher energy barrier in the crystalline regions, leading to better ion rejection performance. Furthermore, we profiled the pore size distributions of the crystalline and amorphous regions, as indicated in Fig. 5m. The amorphous regions featured a larger size distribution, allowing sodium ions to transport more freely, thereby resulting in a lower ion rejection rate. We noted that the consistent trend in pore size distribution is shown between Figs. 1i and 5m. While both analyses employed the same geometric pore detection algorithm, Fig. 1i reflects dynamic formation during the interfacial assembly, whereas Fig. 5m characterizes the equilibrium solvation structure in crystalline domains. This difference in temporal regimes accounts for the minor quantitative variations while maintaining the same qualitative trend of pore size refinement. To further investigate the ion transport mechanisms, we captured the ion solvation structures during sodium ion transport across the membrane (Fig. 5n). The evolution of the ion solvation structure during transport revealed that more oxygen groups replace the water solvation with sodium at both the ends and the middle of the crystalline domains because of the structural features of the units. The transport of sodium ions requires the disruption of the solvation structure between the polymer chains and sodium ions, while the chains in the crystalline regions should be of less mobility. As a result, sodium ions need to overcome a higher energy barrier in the oriented channels within crystalline regions compared to amorphous structures.
We also elucidated the mechanisms behind the effective rejection performance of B(OH)3 at pH 7. Radial distribution functions (RDFs) were calculated to assess the solvation properties of B(OH)3 and water. As shown in Fig. S25a, the RDF peak between boron atoms in B(OH)3 (B) and oxygen atoms from water (Ow) is lower than that for Ow-Ow, indicating weak solvation of B(OH)3 in water. The RDF peaks suggest a solvation radius of 5.6 Å for B(OH)3, while water has a smaller solvation radius of 3.4 Å, allowing easier absorption of water into the membrane channels. Once these channels are occupied by water, B(OH)3 struggles to displace the surrounding water due to weak solvation. Figure S25b shows hydrogen bonds (HB) formed by bulk water are stronger than those between B(OH)3 and water. The nanoconfinement in membrane channels further strengthens the HB network of water, making them much stronger than those involving B(OH)3. Consequently, transporting B(OH)3 through the membranes disrupts stable HB networks of water clusters, thus requiring significant energy to overcome barriers, which contributes to the effective rejection of B(OH)3. This mechanism is supported by potential of the mean force (PMF) profiles in Fig. S25c, showing higher energy barrier for B(OH)3 transport through membranes compared to water.
Discussion
Our integrated experimental-computational approach reveals the fundamental mechanisms underlying the exceptional performance of SNMs. The strong correlation between simulations and experimental results explains the simultaneous enhancement in water permeability and solute rejection. Well-oriented polymer chains in crystalline regions creat continuous water channels, enabling rapid, uninterrupted water transport. This configuration leads to higher water flux compared to the amorphous regions. Notably, SNM-2 demonstrates outstanding water permeability, surpassing both reported and commercial membranes under both brackish water and seawater conditions. Sodium ion transport, on the other hand, requires overcoming a high energy barrier due to the disruption of solvation shells within the subnanochannels, achieving excellent sodium ion rejection. Furthermore, the superior boron rejection versus conventional RO systems comes from the following key factors: (1) B(OH)3 has weaker hydration with a solvation radius of 5.6 Å, higher than water (3.4 Å), enabling preferential adsorption of water into the channels; (2) Bulk water H-bonds are stronger than B(OH)3-water interactions, and nanoconfinement further enhances water hydrogen-bonding networks in channels, which creats a higher energy barrier for B(OH)3 penetration.
Our multiscale computational effort demonstrates the detailed mechanisms behind the improved membrane performance: DFT calculations quantify how PEG incorporation strengthens interfacial hydrogen bonding with PCL at the atomic level. MD simulations elucidate how these optimized interactions facilitate rapid water transport through aligned sub-nanochannels, showing excellent agreement with experimental permeance data. The synergy between atomic-scale bonding and macroscopic transport properties confirms PEG’s dual role as both a molecular binder and subnanometer channel regulator.
To further elucidate the channel formation mechanisms, future investigations will target: (1) pressure-dependent nucleation kinetics, (2) chain chemistries (length, functional groups) for pore uniformity, and (3) dynamic channel stability in long-timescale simulations. Besides, MD studies can capture the coexistence of crystalline and amorphous structures within the SNM. For example, hybrid models with controlled crystallinity ratios can be created.
In summary, this work, both experimentally and theoretically, establishes the critical role of nano-confined interfacial hydrogen bonding in designing ultra-permeable, selective desalination membranes. Compared to the counterpart, 6 nm-thick SNM-2 showcases a larger crystalline domain size and an improved Young’s modulus of roughly 4 GPa. Moreover, performance breakthroughs such as high rejection of NaCl ( > 99.6%) and boron ( > 93.5%) at pH = 8 as well as excellent chlorine resistance (totaling 60000 ppm h of free chlorine) are demonstrated, with an 8.4 LMH bar−1 water permeance at a 0.58 wt% NaCl solution and over 7.2 LMH bar−1 at a 3.5 wt% NaCl solution, greatly outperforming both reported and commercial RO membranes. In addition, the membrane maintains functionality under extreme conditions (pH =1, pH = 13, and 1 wt% urea) for 168 hours. Theoretical simulations reveal these achievements stem from well-aligned subnanochannels that simultaneously enable fast water transport and strong ion rejection. By bridging molecular-scale interfacial chemistry with macroscopic membrane performance, this work provides both fundamental insights and practical solutions for addressing global water scarcity through next-generation desalination technologies.
Building on these findings, we envision three critical pathways to advance SNM technology toward practical implementation: (1) scalable manufacturing development; (2) system integration and performance validation; and (3) advanced materials engineering. To bridge the lab-to-industry gap, developing a continuous roll-to-roll fabrication system enables both in situ membrane formation and automated substrate transfer. Besides, implementing a precision microfluidic deposition system will ensure uniform oligomer solution application. Future efforts should also focus on innovative module designs that maintain membrane integrity and operational stability in pilot-scale testing. Furthermore, material optimization will pursue molecular-level designs to enhance target functionalities, alongside developing cost-effective oligomer alternatives to meet industry price targets. Together, these strategic initiatives in manufacturing, engineering, and materials science will advance both fundamental science and practical implementation, positioning SNMs as a transformative solution for applications ranging from municipal desalination plants to modular emergency water systems.
Methods
Materials
ε-Caprolactone (ε-CL), stannous isooctanoate, and NaCl ( ≥ 99%) were obtained from J&K Scientific. Methanetetrayltetraphenol ( ≥ 98%) was purchased from Alfa Chemical. Polyethylene glycol (PEG, Mn 380-420) and boric acid B(OH)3 (analytical grade) were sourced from Sigma-Aldrich and utilized without further modification. Single crystal silicon wafers, acquired from Si-Mat Germany, were employed as the substrate for AFM measurements.
Synthesis of tetra-oligomers PCL
The tetra-oligomer PCL was synthesized through the ring-opening polymerization of ε-CL. In a 50-mL flask, 0.3844 g of methanetetrayltetraphenol (the initiator), 8 g of ε-CL, and 0.3 wt% stannous isooctanoate (the catalyst) were mixed. The reaction took place at 150 °C for 10 hours under an argon atmosphere. The resulting product was dissolved in toluene, purified, precipitated in cold methanol, and vacuum-dried overnight.
Preparation of supramolecular nanocrystalline membranes
Tetra-oligomer PCL product was dissolved in chloroform to achieve a polymer solution with a concentration of 2 mg/mL. Next, 5 µL of this solution was carefully placed onto the surface of a PEG aqueous solution of varying concentrations from 0 to 4 wt%. The microdroplet quickly spread, forming an ultrathin membrane in the confined space within seconds. After rinsing the nanofilms with distilled water, they were transferred onto various substrates, including polyethersulfone (PES) and silicon wafers, for further measurements.
General characterizations
1H NMR (400 MHz) spectra were recorded using a Bruker DRX 400 spectrometer in chloroform-d. DSC measurements were conducted under a nitrogen atmosphere with an MDSC 2910 system, employing a heating and cooling rate of 10 °C/min over the range of -40 to 110 °C. Data from the second heating cycle are reported unless noted otherwise. The melting temperature and heat of fusion for the samples were determined through heat flow analysis. The surface contact angle of the samples and the surface tension of the microdroplets were assessed with OCA20 equipment (Data Physics, Germany). A digital camera monitored the droplet shape immediately after deposition, with each measurement repeated independently three times. The surface zeta potential of the membranes was measured using an Anton Paar SurPASS solid surface analyser with a 0.01 M KCl solution at room temperature and pH 8. GIXD was performed using Malvern Panalytical’s X’Pert3, with X-ray exposure lasting 5 minutes at an incidence angle of 0.12°. The surface roughness and thickness of the nanofilms were evaluated by AFM (Bruker Dimension Icon with ScanAsyst). After cleaning with distilled water, the nanofilms were placed on silicon wafers and air-dried. Surface roughness is reported as root-mean-square roughness (Rrms), while thickness was measured from the silicon surface to the nanofilm. Chemical composition and elemental analysis were performed using XPS on a PHI Model 5802 with an angle-resolved technique. TEM was conducted on a FEI/Philips Tecnai 12 BioTWIN to assess the crystallization of the nanofilms placed on copper grids for imaging. Surface morphology was obtained through a high-resolution SEM (FEI Quanta 450) at an accelerating voltage of 5 kV. Raman analysis was conducted on a WITec alpha300 access system with a 532-nm wavelength.
Young’s modulus determination by peak force quantitative nanomechanical mapping (PFQNM) analysis
Young’s modulus tests were carried out in PFQNM mode57 with a Bruker Dimension Icon AFM system with ScanAsyst technology. Images were captured using Si3N4 tips (DNP-B, Bruker) at a 1.0 Hz scan rate, and the tips’ spring constant was calibrated using a thermal tune method. In PFQNM mode, a rapid force curve was executed at each pixel by modulating the Z piezo at approximately 1 kHz with a 200 nm amplitude. The peak force from each curve acted as the feedback signal for imaging. Real-time analysis of the force curve data generated a map of various mechanical properties, including modulus and adhesion, with a resolution comparable to that of the height image. This mode allowed for precise control of the tip/sample interaction, minimizing sample deformation and contact area, thereby mitigating potential damage to either the probe or the sample while achieving higher resolution.
Structural model construction and pore size calculations
The tetra-PCL-OH and PEG were drawn by ChemDraw. The interactions between atoms in above structures were described by GROMOCS 54A7 force field58, and force field parameters were further corrected via the Automated force field Topology Builder (ATB)59. The equilibrium configurations of tetra-PCL-OH and PEG produced by ATB were used for subsequent simulations. Considering the computational efficiency and accuracy, a classical water molecule model SPC/E was adopted here.
To evaluate the void characteristics of tetra-PCL-OH on the surfaces of bulk water and the PEG aqueous solution (PEG−water mixtures with 2 wt% PEG content), we built sandwich models, where tetra-oligomer layer was distributed between two layers of bulk water or PEG solution. Then, sandwich models were relaxed at ambient conditions (1 atm and 300 K) until reaching equilibrium state. Subsequently, another 5 ns simulations are performed to collect the configurations of models to identify the void characteristics of tetra-PCL-OH. Void analysis was performed using PoreBlazer60, during which the probe size was fixed at 1.2 Å. In this work, we analysed two critical void characteristics: fractional free volume and pore size distributions.
All molecular dynamics simulations conducted in this work utilized the NPT ensemble, maintaining a temperature of 300 K and a pressure of 1 atm. The Nosé-Hoover method was employed to control both temperature and pressure61. Atomic positions and velocities were updated using the velocity-Verlet algorithm with a time step of 2 fs62. Additionally, periodic boundary conditions were applied in all directions. The simulations were executed on the LAMMPS classical platform63, and the resulting trajectories were visualized using OVITO, an open-source visualization tool64.
Interfacial hydrogen bonds calculation by Density Functional Theory
All spin-polarized DFT calculations for periodic materials were conducted using the Vienna Ab initio Simulation Package (VASP)65, employing the projector-augmented wave (PAW) method66. The exchange-correlation interactions were addressed using generalized gradient approximation (GGA) as defined by the Perdew-Burke-Ernzerhof (PBE) formulation67. Van der Waals (vdW) interactions were incorporated using the DFT-D3 method according to Grimme’s scheme68,69. The PAW method was employed to describe the interaction between atomic cores and electrons, with the plane-wave basis energy cutoff set at 500 eV70. Geometry relaxation utilized a Brillouin zone sampling of a 1 × 1 × 1 grid centred at the gamma (Γ) point. The charge density difference was plotted at a threshold of 0.001 e/bohr³. Structures with a dynamic magnetic moment were fully relaxed until their total energies converged to less than 1×10-6 eV71, and the average residual forces were below 0.02 eV/Å72.
The charge density difference maps are calculated as the electron density difference between the combined interacting systems (PCL/H2O or PCL/PEG/H2O) and the sum of electron densities of their individual isolated constituents. Specifically, the “difference” refers to:
for Fig. 3i (PCL/H2O system), and similarly,
for Fig. 3j (PCL/PEG/H2O system).
Thus, these maps clearly illustrate the electron redistribution resulting from intermolecular interactions, notably highlighting regions of electron accumulation (negative charge difference) and depletion (positive charge difference), which serve as explicit indicators of hydrogen-bond formation and interaction strength between components.
The binding energy (\({{{{\rm{E}}}}}_{{{{\rm{binding}}}}}\)) is defined as:
where \({{{{\rm{E}}}}}_{{{{\rm{total}}}}}\) is the total energy of the combined system (e.g., PCL/PEG fragment interacting with water), \({{{{\rm{E}}}}}_{{{{\rm{PCL}}}}/{{{\rm{PEG}}}}}\) is the energy of the isolated polymer fragment, and \({{{{\rm{E}}}}}_{{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}}\) is the energy of the isolated water molecule. A more negative binding energy indicates stronger intermolecular interactions, primarily arising from hydrogen bonding between the polymer chains and water molecules.
Transport mechanism elucidated by molecular dynamics simulations
Molecular dynamics simulations were conducted to investigate the transport mechanisms underlying the experimental findings. The initial configuration contained no predefined channels; all nanochannels emerged spontaneously during equilibration through thermodynamically driven chain rearrangement under applied pressure. Partial z-constraints enabled spontaneous channel formation by allowing x/y relaxation while preventing crystal collapse. Some representative equilibrium structures are shown in Fig. 5a. To assess the impact of crystalline structures on desalination performance, two systems were modelled: one representing an amorphous structure and the other a crystalline one. As shown in Fig. 5a and and e, each system featured a membrane positioned centrally, flanked by a saline water reservoir (feed side) and a pure water reservoir (permeate side). Two pistons, labelled P1 and P2, were applied at either end of the system to maintain external pressure. The saline reservoir contained 1806 water molecules and 19 sodium/chloride ions, achieving a concentration of 35000 ppm, while the pure water reservoir had 903 water molecules. The crystalline structures were generated by directly replicating the unit cell73, while additional annealing procedures proposed by Jiang et al. were employed to create the amorphous structure74. As indicated in Fig. 5b–d, the simulation snapshot showed one representative channel for clarity, while multiple such channels formed periodically in the full system.
Ions were represented using the Lennard-Jones (LJ) potential, with parameters sourced from Merz Jr.’s work75. A cutoff distance of 12 Å was set for vdW interactions, and long-range electrostatics were calculated using the Particle-Particle-Particle Mesh (PPPM) method with a precision of 10-4 76. A timestep of 1 fs was adopted for all simulations, with data recorded every 10,000 timesteps for subsequent analysis.
Each system underwent an initial energy minimization, followed by a 5 ns equilibration phase. Based on the equilibrated structures, a 20 ns desalination simulation was conducted to mimic the experimental pressure-driven desalination process, characterized by a significant pressure difference between the feed and permeate sides. During both the equilibration and desalination phases, the system temperature was maintained at 300 K using a Nosé-Hoover thermostat, with a coupling time constant of 1 ps77. An environmental pressure of 0.1 MPa was applied to both pistons during equilibrium. To enhance the desalination process and improve the signal-to-noise ratio at the nanoscale, a high pressure difference was implemented, with P1 set at 600 MPa and P2 at 0.1 MPa78.
The umbrella sampling method was utilized to determine the potential of mean force for sodium ions crossing the membranes. An additional force of 50 kcal/mol/Å was applied to selected sodium ions to facilitate exploration of the membrane’s inner regions. The reaction axis (z-axis) was divided into 25 windows, each measuring 1 Å in length, from the entrance to the centre of the membrane. Biased MD simulations were conducted for 2 ns per window, and the results were analysed using the weighted histogram analysis method (WHAM)79 to eliminate bias and produce an unbiased free energy profile.
All MD simulations were executed on the LAMMPS platform63, with snapshots visualized via Visual Molecular Dynamics (VMD) software80.
Desalination performance
The performance of the nanofilms in desalination was evaluated using a filtration setup configured for crossflow filtration. The housing cell included a 7.6 cm long, 2.8 cm wide, and 0.3 cm high rectangular channel. The crossflow rate was 4 L min−1, corresponding to a velocity of 0.8 m s−1. The active area of the nanofilm was 12.5 cm2. The temperature was maintained at 25 ( ± 1) °C. A high-pressure diaphragm pump was utilized to supply the feed solution from a feed tank into the membrane cell. Before conducting tests with brackish or seawater, the samples were conditioned for a minimum of 8 hours under pressures of 20 bar or 70 bar using pure water to establish steady-state conditions. Subsequently, filtration tests were performed at pH 8 and at lower pressures: 15.5 bar for brackish water (0.58 wt% NaCl solution) and 55 bar for seawater (3.5 wt% NaCl solution). For boron rejection testing, the feed solution contained 5 ppm, with NaOH used to adjust the pH. Solute concentrations in both the feed and permeate were monitored using a conductivity meter or inductively coupled plasma optical emission spectrometry (ICP-OES). At least four membrane samples were assessed to determine an average value and standard deviation.
Water flux, Jw (L m−2 h−1), was calculated using the following equation:
where ΔV is the permeate water volume (L) collected over the time period t (h), and A (L m−2 h−1 bar−1) is the effective membrane area (m2). Water permeance or the water permeability coefficient, A, was determined using the following equation:
where Jw,0 is the pure water flux, and ΔP is the applied pressure. Salt rejection was determined with the following equation:
where R is salt rejection rate (%), and Cp and Cf are the salt concentrations (mg L−1) of the permeate and the feed solution, respectively. To account for the concentration polarization, the salt permeability coefficient, B (L m−2 h−1), was calculated by the following equation:
where k is the mass transfer coefficient in the feed channel, estimated based on the cell geometry and crossflow rate.
Acid/Base/Urea-resistance testing
The SNM membranes were immersed in aqueous solutions with pH levels of 1, 13, and a 1 wt% urea concentration for 168 hours. After specific time intervals, the membranes were removed, thoroughly rinsed with DI water, and evaluated for desalination efficiency under the following conditions: 12.5 cm² effective membrane area, 35,000 ppm NaCl feed solution, 4 L/min crossflow rate, and 55 bar pressure.
Chlorine-resistance testing
The SNM membranes were submerged in a 200 ppm NaClO solution, which was continuously stirred for 300 hours. The solution pH was controlled at 5.0, 7.0, and 9.0 by HCl or NaOH. The container was covered with tin foil and kept in a dark environment. The chlorine solution was refreshed every 24 hours. At designated intervals, the membranes were taken out, cleaned thoroughly with deionized water, and tested for desalination efficiency under the same conditions as mentioned above: 12.5 cm² effective membrane area, 35,000 ppm NaCl feed solution, 4 L/min crossflow rate, and 55 bar pressure.
Data availability
The data supporting the findings of this study are available within the Article and its Supplementary Information. All data are available from the corresponding author upon request.
Code availability
The simulation codes used in this study are available from the corresponding authors on request.
References
Morelos-Gomez, A. et al. Effective NaCl and dye rejection of hybrid graphene oxide/graphene layered membranes. Nat. Nanotechnol. 12, 1083–1088 (2017).
Lu, X. & Elimelech, M. Fabrication of desalination membranes by interfacial polymerization: history, current efforts, and future directions. Chem. Soc. Rev. 50, 6290–6307 (2021).
Farid, M. U. et al. Advancements in nano-enabled membrane distillation for a sustainable water-energy-environment nexus. Adv. Mater. 36, 2307950 (2023).
Dai, R. et al. Nanovehicle-assisted monomer shuttling enables highly permeable and selective nanofiltration membranes for water purification. Nat. Water 1, 281–290 (2023).
Werber, J. R., Osuji, C. O. & Elimelech, M. Materials for next-generation desalination and water purification membranes. Nat. Rev. Mater. 1, 1–15 (2016).
Park, H. B., Kamcev, J., Robeson, L. M., Elimelech, M. & Freeman, B. D. Maximizing the right stuff: The trade-off between membrane permeability and selectivity. Science 356, eaab0530 (2017).
Wang, W. et al. High-surface-area functionalized nanolaminated membranes for energy-efficient nanofiltration and desalination in forward osmosis. Nat. Water 1, 187–197 (2023).
Jia, M. et al. Advanced nanobubble flotation for enhanced removal of sub-10 µm microplastics from wastewater. Nat. Commun. 15, 9079 (2024).
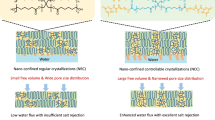
Lu, G. et al. Nano-confined controllable crystallization in supramolecular polymeric membranes for ultra-selective desalination. Nat. Commun. 16, 2284 (2025).
Sun, J. et al. Hydrogel-Based Photothermal-Catalytic Membrane for Efficient Cogeneration of Freshwater and Hydrogen in Membrane Distillation System. Adv. Funct. Mater. 2416768 (2025).
Yuan, B., Zhao, S., Hu, P., Cui, J. & Niu, Q. J. Asymmetric polyamide nanofilms with highly ordered nanovoids for water purification. Nat. Commun. 11, 6102 (2020).
Lu, G. et al. Nano-confined supramolecular assembly of ultrathin crystalline polymer membranes for high-performance nanofiltration. Adv. Funct. Mater. 34, 2309913 (2023).
Huang, J. et al. Polymeric membranes with highly homogenized nanopores for ultrafast water purification. Nat. Sustain. 7, 901–909 (2024).
Huang, J. et al. Thermostable nanofiltration membranes enabling superior hot wastewater purification. J. Membr. Sci. 711, 123216 (2024).
Wen, Y. et al. Metal-organic framework enables ultraselective polyamide membrane for desalination and water reuse. Sci. Adv. 8, eabm4149 (2022).
Tiwari, K. et al. Large area self-assembled ultrathin polyimine nanofilms formed at the liquid–liquid interface used for molecular separation. Adv. Mater. 32, 1905621 (2020).
Jiang, Z., Karan, S. & Livingston, A. G. Water transport through ultrathin polyamide nanofilms used for reverse osmosis. Adv. Mater. 30, 1705973 (2018).
Di Vincenzo, M. et al. Tunable membranes incorporating artificial water channels for high-performance brackish/low-salinity water reverse osmosis desalination. Proc. Natl Acad. Sci. USA. 118, e2022200118 (2021).
Li, Z. et al. Covalent organic framework membrane with sub-nano pores for efficient desalination. J. Membr. Sci. 675, 121551 (2023).
Tu, K. L., Nghiem, L. D. & Chivas, A. R. Boron removal by reverse osmosis membranes in seawater desalination applications. Sep. Purif. Technol. 75, 87–101 (2010).
Shultz, S., Bass, M., Semiat, R. & Freger, V. Modification of polyamide membranes by hydrophobic molecular plugs for improved boron rejection. J. Membr. Sci. 546, 165–172 (2018).
Yao, Y. et al. More resilient polyester membranes for high-performance reverse osmosis desalination. Science 384, 333–338 (2024).
Do, V. T., Tang, C. Y., Reinhard, M. & Leckie, J. O. Effects of chlorine exposure conditions on physiochemical properties and performance of a polyamide membrane) Mechanisms and implications. Environ. Sci. Technol. 46, 13184–13192 (2012).
Stolov, M. & Freger, V. Degradation of polyamide membranes exposed to chlorine: an impedance spectroscopy study. Environ. Sci. Technol. 53, 2618–2625 (2019).
Shen, J. et al. Fast water transport and molecular sieving through ultrathin ordered conjugated-polymer-framework membranes. Nat. Mater. 21, 1183–1190 (2022).
Ding, L. et al. Effective ion sieving with Ti3C2T x MXene membranes for production of drinking water from seawater. Nat. Sustain. 3, 296–302 (2020).
Zhang, Y. et al. Molecularly soldered covalent organic frameworks for ultrafast precision sieving. Sci. Adv. 7, eabe8706 (2021).
Yang, C. et al. Ultrathin nanofiltration membrane assembled by polyethyleneimine-grafted graphene quantum dots. J. Membr. Sci. 642, 119944 (2022).
Wang, M. et al. Ultrafast seawater desalination with covalent organic framework membranes. Nat. Sustain. 5, 518–526 (2022).
Liu, K. et al. On-water surface synthesis of crystalline, few-layer two-dimensional polymers assisted by surfactant monolayers. Nat. Chem. 11, 994–1000 (2019).
Lu, G., Zhu, Q., Ma, R., He, W. & Wu, J. Tough yet reversible hydrogel adhesives with cooperative energy dissipation for multifunctional wearable sensors. Adv. Funct. Mater. 33, 2306914 (2023).
Lu, G. et al. High-Performance Supramolecular Organogel Adhesives for Antimicrobial Applications in Diverse Conditions. ACS Appl. Mater. Interfaces 15, 44194–44204 (2023).
Qiu, Z.-L. et al. Ionic dendrimer based polyamide membranes for ion separation. ACS Nano 15, 7522–7535 (2021).
Zhao, Y. et al. Diurnal humidity cycle driven selective ion transport across clustered polycation membrane. Nat. Commun. 15, 7161 (2024).
Liu, M., Liu, P., Lu, G., Xu, Z. & Yao, X. Multiphase-assembly of siloxane oligomers with improved mechanical strength and water-enhanced healing. Angew. Chem. 130, 11412–11416 (2018).
Cao, C. et al. Sprayable superhydrophobic coating with high processibility and rapid damage-healing nature. Chem. Eng. J. 392, 124834 (2020).
Michell, R. M. & Müller, A. J. Confined crystallization of polymeric materials. Prog. Polym. Sci. 54, 183–213 (2016).
Wang, H. et al. Confined crystallization of polyethylene oxide in nanolayer assemblies. Science 323, 757–760 (2009).
Tan, Z., Chen, S., Peng, X., Zhang, L. & Gao, C. Polyamide membranes with nanoscale Turing structures for water purification. Science 360, 518–521 (2018).
Noh, J., Jeong, S. & Lee, J.-Y. Ultrafast formation of air-processable and high-quality polymer films on an aqueous substrate. Nat. Commun. 7, 12374 (2016).
Vanroy, B., Wubbenhorst, M. & Napolitano, S. Crystallization of thin polymer layers confined between two adsorbing walls. ACS Macro Lett. 2, 168–172 (2013).
Ren, W. et al. Structure of the Poly (methyl methacrylate) adsorbed layer determined by the surface chemistry of the substrate. Macromolecules 56, 1410–1418 (2023).
Yang, Y., Xing, Z., Xie, Z. & Wang, X. Polymer adsorbed layer promotes dipole ordering in gate dielectrics for organic field-effect transistors. J. Phys. Chem. C. 125, 17271–17279 (2021).
Murray, D. J. et al. Large area synthesis of a nanoporous two-dimensional polymer at the air/water interface. J. Am. Chem. Soc. 137, 3450–3453 (2015).
Qi, H., Wang, W. & Li, C. Y. Janus polymer single crystal nanosheet via evaporative crystallization. ACS Macro Lett. 3, 675–678 (2014).
Joncheray, T. J., Denoncourt, K. M., Meier, M. A., Schubert, U. S. & Duran, R. S. Two-Dimensional Self-Assembly of Linear Poly (ethylene oxide)-b-poly (ε-caprolactone) Copolymers at the Air− Water Interface. Langmuir 23, 2423–2429 (2007).
Zhang, F., Fan, J. B. & Wang, S. Interfacial polymerization: from chemistry to functional materials. Angew. Chem. Int. Ed. 59, 21840–21856 (2020).
Liang, Y. et al. Polyamide nanofiltration membrane with highly uniform sub-nanometre pores for sub-1 Å precision separation. Nat. Commun. 11, 2015 (2020).
Sarkar, P., Modak, S. & Karan, S. Ultraselective and highly permeable polyamide nanofilms for ionic and molecular nanofiltration. Adv. Funct. Mater. 31, 2007054 (2020).
Tang, S., Gong, J., Shi, Y., Wen, S. & Zhao, Q. Spontaneous water-on-water spreading of polyelectrolyte membranes inspired by skin formation. Nat. Commun. 13, 3227 (2022).
Zuo, B., Zhou, H., Davis, M. J., Wang, X. & Priestley, R. D. Effect of local chain conformation in adsorbed nanolayers on confined polymer molecular mobility. Phys. Rev. Lett. 122, 217801 (2019).
Di Vincenzo, M. et al. Biomimetic artificial water channel membranes for enhanced desalination. Nat. Nanotechnol. 16, 190–196 (2021).
Zhao, Q., Zhao, D. L., Ee, L. Y., Chung, T.-S. & Chen, S. B. In-situ coating of Fe-TA complex on thin-film composite membranes for improved water permeance in reverse osmosis desalination. Desalination 554, 116515 (2023).
Gai, W., Zhang, Y., Zhao, Q. & Chung, T.-S. Highly permeable thin film composite hollow fiber membranes for brackish water desalination by incorporating amino functionalized carbon quantum dots and hypochlorite treatment. J. Membr. Sci. 620, 118952 (2021).
Han, S. et al. Microporous organic nanotube assisted design of high performance nanofiltration membranes. Nat. Commun. 13, 7954 (2022).
Zhao, D., Liu, J. & Jiang, J. Porous organic cages embedded in a lipid membrane for water desalination: A molecular simulation study. J. Membr. Sci. 573, 177–183 (2019).
Liang, B. et al. Microporous membranes comprising conjugated polymers with rigid backbones enable ultrafast organic-solvent nanofiltration. Nat. Chem. 10, 961–967 (2018).
Schmid, N. et al. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J. 40, 843–856 (2011).
Malde, A. K. et al. An automated force field topology builder (ATB) and repository: version 1.0. J. Chem. Theory Comput. 7, 4026–4037 (2011).
Sarkisov, L. & Harrison, A. Computational structure characterisation tools in application to ordered and disordered porous materials. Mol. Simul. 37, 1248–1257 (2011).
Liu, L. et al. A superstrong and reversible ionic crystal-based adhesive inspired by ice adhesion. Angew. Chem. 133, 9030–9041 (2021).
Hubao, A., Yang, Z., Hu, R. & Chen, Y.-F. Roles of energy dissipation and asymmetric wettability in spontaneous imbibition dynamics in a nanochannel. J. Colloid Interface Sci. 607, 1023–1035 (2022).
Thompson, A. P. et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022).
Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18, 015012 (2009).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Ernzerhof, M. & Scuseria, G. E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 110, 5029–5036 (1999).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Guan, D. et al. Identifying A Universal Activity Descriptor and a Unifying Mechanism Concept on Perovskite Oxides for Green Hydrogen Production. Adv. Mater. 35, 2305074 (2023).
Xiao, W., Kiran, G. K., Yoo, K., Kim, J. H. & Xu, H. The dual-site adsorption and high redox activity enabled by hybrid organic-inorganic vanadyl ethylene glycolate for high-rate and long-durability lithium–sulfur batteries. Small 19, 2206750 (2023).
Li, W. et al. Tuning electron delocalization of hydrogen-bonded organic framework cathode for high-performance zinc-organic batteries. Nat. Commun. 14, 5235 (2023).
Lv, Z. et al. Quasi-topological intercalation mechanism of Bi0.67NbS2 enabling 100 C fast-charging for sodium-ion batteries. Adv. Energy Mater. 13, 2300790 (2023).
Bittiger, H., Marchessault, R. & Niegisch, W. Crystal structure of poly-ε-caprolactone. Acta Crystallogr. B. 26, 1923–1927 (1970).
Liu, J., Xu, Q. & Jiang, J. A molecular simulation protocol for swelling and organic solvent nanofiltration of polymer membranes. J. Membr. Sci. 573, 639–646 (2019).
Li, P., Song, L. F. & Merz, K. M. Jr. Systematic parameterization of monovalent ions employing the nonbonded model. J. Chem. Theory Comput. 11, 1645–1657 (2015).
Luty, B. A. & van Gunsteren, W. F. Calculating electrostatic interactions using the particle− particle particle− mesh method with nonperiodic long-range interactions. J. Phys. Chem. 100, 2581–2587 (1996).
Evans, D. J. & Holian, B. L. The nose–hoover thermostat. J. Chem. Phys. 83, 4069–4074 (1985).
Chen, Q. & Yang, X. Pyridinic nitrogen doped nanoporous graphene as desalination membrane: molecular simulation study. J. Membr. Sci. 496, 108–117 (2015).
Kumar, S., Rosenberg, J. M., Bouzida, D., Swendsen, R. H. & Kollman, P. A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 13, 1011–1021 (1992).
Humphrey, W., Dalke, A. & Schulten, K. V. M. D. visual molecular dynamics. J. Mol. Graph. 14, 33–38 (1996).
Acknowledgements
This work was supported by the Research Grants Council (RGC) of Hong Kong through the General Research Fund (11218122 and 11209421) (A.K.A.), Theme-based Research Scheme (T21-604/19-R). (A.K.A.), Research Fellow Scheme (RFS2223-1S04) (A.K.A.), Hong Kong Innovation and Technology Commission (PRP/077/22FX and ITC-CNERC14EG03) (A.K.A.), and Global Ocean Negative Carbon Emissions (Global ONCE) Program (J.W.).
Author information
Authors and Affiliations
Contributions
G.L. conceived the idea, designed and conducted experiments, and drafted the manuscript. G.L. and W.S. discussed and analysed the results. X.M. and J.F. conducted MD simulation. H.X. performed DFT calculations. H.A. analysed pore size distributions. J.S., X.L., M.J., S.L., and J.W. assisted in the discussion. G.L., A.K.A., X.M., X.C., and S.C. revised the manuscript. G.L., W.S., and X.M. contributed equally. A.K.A., G.L., and J.F. supervised the study. All coauthors read and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
A.K.A. and G.L. declare the following competing interest: A patent application related to this work has been filed in the U.S. (Application No. 63/739,136). All other authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Lu, G., Shang, W., Ma, X. et al. Supramolecular nanocrystalline membranes with well-aligned subnanochannels for enhanced reverse osmosis desalination. Nat Commun 16, 6289 (2025). https://doi.org/10.1038/s41467-025-61352-6
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41467-025-61352-6
This article is cited by
-
Solution-sheared supramolecular oligomers with enhanced thermal resistance in interfacial adhesion and bulk cohesion
Nature Communications (2025)