High-resolution mapping of single cells in spatial context

Ke, Jincan; Xu, Jian; Liu, Jia; Yang, Yumeng; Guo, Chenkai; Xie, Bingbing; Cui, Guizhong; Peng, Guangdun; Suo, Shengbao

doi:10.1038/s41467-025-61667-4

Download PDF

Article
Open access
Published: 15 July 2025

High-resolution mapping of single cells in spatial context

Nature Communications volume 16, Article number: 6533 (2025) Cite this article

16k Accesses
3 Citations
4 Altmetric
Metrics details

Subjects

Abstract

Spatially resolved transcriptomic technologies have emerged as pivotal tools for elucidating molecular regulation and cellular interplay within the intricate tissue microenvironment, but hampered by insufficient gene recovery or challenges in achieving intact single-cell resolution. Here, we develop Cellular Mapping of Attributes with Position (CMAP), a method that efficiently maps large-scale individual cells to their precise spatial locations by integrating single-cell and spatial data through a divide-and-conquer strategy. Analysis of both simulated and real datasets shows that CMAP performs effectively and is adaptable across diverse data types and sequencing platforms. Particularly, CMAP handles scenarios well where discrepancies exist between single-cell and spatial transcriptomics data. Our findings underscore CMAP’s capacity to endow single-cells with exact spatial coordinates, facilitating the dissection of nuanced spatial-organ-specific endothelial cell heterogeneity, as well as the intricate cancer immune microenvironments that elude conventional single-cell or spatial data analysis.

Screening cell–cell communication in spatial transcriptomics via collective optimal transport

Article Open access 23 January 2023

Knowledge-graph-based cell-cell communication inference for spatially resolved transcriptomic data with SpaTalk

Article Open access 30 July 2022

Inference of cell-type composition and single-cell spatial maps from spatial transcriptomics data with SWOT

Article Open access 19 November 2025

Introduction

Single-cell RNA sequencing (scRNA-seq) has become an indispensable tool across diverse fields including developmental biology, neuroscience, pathology, and immunology, furnishing a wealth of data ripe for computational exploration and analysis, for its ability to delve into the heterogeneity of individual cells that comprise the fundamental unit of organism. However, scRNA-seq inherently sacrifices spatial information, overlooking the pivotal role of extracellular and intracellular interplays in shaping cell fates and function within a tissue context. To amend these caveats, a diverse suite of spatial transcriptomics (ST) technologies with varied resolution and scalability has emerged^1,2,3,4,5,6 and poised to revolutionize many fields of biology and pathology. However, due to the general low capturing rate or incomplete transcriptome coverage, and difficulties in accurate cell segmentation and achieving intact 3D, all available ST methods are fraught with suboptimal representation of true single-cell content. Therefore, the downstream applications of spatial profiling that require authentic single-cell resolution and sensitivity in situ tissues—e.g., ligand-receptor interaction, signaling and transcription factor pathways, and cellular trajectory inference—are expected to improve significantly. One approach to tackle this question is to map single-cell modality with spatial data, taking full advantages of both methodologies. Given enormous atlas-level single-cell data available, the computational spatial mapping would be useful to empower the cellular resolution of molecular annotation of tissue organization and cell interaction in the spatial context.

The challenge of integrating scRNA-seq and spatial data to map cells onto spatial tissue has recently attracted substantial attention from computational biologists, giving rise to several innovative tools. For example, CellTrek⁷ trains multivariate random forests model to predict 2D embeddings of cells, subsequently constructing a cell-spot distance matrix using co-embeddings. Mutual nearest neighbor is then applied to extract cell-spot correspondences, facilitating cell-to-spot spatial assignments. CytoSPACE⁸ leverages deconvolution results to estimate spot-wise cell-type proportions, followed by either linear regression of reads and cell numbers or segmentation count-based estimation to quantify cell numbers per spots. Cells are sampled from single-cell datasets accordingly and assigned to optimized spots. While both methods just provide spot-level locations for cells, they randomly distribute cells within a certain spot range, failing to capture the precise positions and intercellular relationships crucial for understanding single-cell communication and interaction. Additionally, the potential for assigning the same single cell to multiple spots introduces significant bias in downstream analysis.

Here, we present Cellular Mapping of Attributes with Position (CMAP), an algorithm designed to precisely predict single-cell locations by integrating spatial and single-cell transcriptome datasets. This approach enables the reconstruction of genome-wide spatial gene expression profiles at single-cell resolution, unlocking the potential to explore tissue microenvironments with enhanced resolution. CMAP facilitates scrutiny beyond the conventional spot-level analysis, allowing the identification of tumor boundaries, shifts in immune and tumor cell spatial distributions relative to normal tissue, and other fine-scale spatial attributes. Through diverse simulations and real-world datasets, we demonstrate the robust capacity of CMAP to map cells to their native locations across various single-cell (e.g., Smart-seq2, 10x Genomics Chromium, et al.) and spatial technology platforms (such as sequential fluorescence in situ hybridization (seqFISH), 10x Genomics Xenium, Slide-seq, 10x Genomics Visium, and geographical position sequencing (Geo-seq)). Notably, CMAP performs well in scenarios where mismatch exists between scRNA-seq and ST data, enabling more reliable integration and interpretation. The accuracy and adaptability of CMAP in allocating the spatial positions of single cells offers valuable insights into the spatial architecture of complex biology systems.

Results

Overview of CMAP

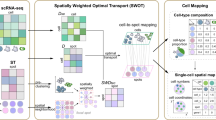
We outlined the CMAP workflow using Visium data as an example. CMAP systematically maps cells through a stepwise progression from the spatial domain to the measured spatial spots/voxels, ultimately arriving at precise spatial locations (Fig. 1a, “Methods”). It consists of three main processes: CMAP-DomainDivision (Level 1 mapping) partitions cells unto spatial domains, CMAP-OptimalSpot (Level 2 mapping) aligns cells to optimal spots/voxels, and CMAP-PreciseLocation (Level 3 mapping) determines the exact cellular coordinates (Supplementary Fig. 1).

**Fig. 1: Schematic and performance assessment of CMAP.**

In CMAP-DomainDivision (Supplementary Fig. 1a), we utilized expression profiles and spatial coordinates from ST data to identify spatially specific genes and cluster spatial domains using hidden Markov random field (HMRF)⁹. The Silhouette score¹⁰, which measures the consistency within clusters, was evaluated to help determine the optimal number of domains. Higher silhouette values indicate better intra-cluster and poorer inter-cluster matching. Alternatively, CMAP can incorporate pre-defined spatial clusters of other methods along with their corresponding domain-specific genes. These spatial domains are designed to delineate broad spatial structures rather than fine-grained subtypes, offering a foundational framework for subsequent analysis. We then trained a classification model—specifically, a support vector machine (SVM) model¹¹ in this study, though other models could be used—to assign spatial domain labels with the highest prediction probability to individual cells, with a tunable probability threshold facilitating the removal of unmatched cells with spatial tissue and enabling a priori assessment of plausibility based on cell type distribution within spatial domains. This step reveals spatial heterogeneity and intra-cell type variation that are not discernible through single-cell RNA expression alone. By pre-selecting and allocating cells to specific spatial domains, the search space for cell mapping is largely reduced, thereby enhancing computation efficiency.

In CMAP-OptimalSpot (Supplementary Fig. 1b), spatially variable genes are identified within each spatial domain, followed by the generation of a random alignment matrix between cells and spots. Cells linked to each spot are aggregated and a cost function is constructed to measure the discrepancy between actual and aggregated spatial expression patterns. To enhance spatial feature capture and structural similarity assessment, we applied an image-based metric, Structural Similarity Index (SSIM)¹², for pattern comparison, and further leveraged information entropy to assess the density of cell distribution in space. SSIM is particularly effective due to its ability to account for structural inter-dependencies, making it superior to absolute error metrics for capturing spatial dependencies and contrast characteristics of expression patterns. Through iterative refinement by deep learning-based optimization, CMAP arrives at the optimal mapping matrix linking cells to their respective spots.

In CMAP-PreciseLocation (Supplementary Fig. 1c), we first built a nearest neighbor graph to represent the relationship among all spots. Given the cellular interactions with their surroundings, we calculated the associations between cells and their neighboring optimal spots. Subsequently, the Spring Steady-State Model learned from physical field is employed to assign each cell an exact location within this spatial context (“Methods”). Remarkably, the predicted cell locations by CMAP attain refined (x, y) coordinates that exceed the mere spot level, effectively bridging the gaps between adjacent spots and offering enhanced spatial resolution.

In subsequent sections, we thoroughly evaluated the performance of CMAP across a variety of simulated and real datasets to demonstrate its efficacy and utility in spatially resolving single cells, and benchmarked it with state-of-the-art methodologies including CellTrek, CytoSPACE and several deconvolution algorithms.

Benchmarking CMAP on sequencing-based simulation data

Evaluating the performance of CMAP necessitates the use of benchmark datasets with well-defined cell distributions and locations. Therefore, we generated simulated mouse olfactory bulb (MOB) spatial data at the spot level, incorporating three predefined spatial domains derived from scRNA-seq datasets using the CARD¹³ framework (Supplementary Fig. 2a, “Methods”). This approach ensures that each cell appears only once, simplifying the evaluation of location prediction accuracy. Theoretically, every cell in this simulated space occupies a unique and fixed position, allowing for the recovery of their spatial relationships upon successful mapping. Consistently, the number of spatial domains corresponding to the highest silhouette score for the MOB simulation data was determined to be three, matching the predefined number of domains (Supplementary Fig. 2b). This result confirms the utility of the silhouette score in identifying the optimal number of spatial domains.

CMAP showed considerable capability in accurately mapping cells to their designated locations and reconstructing the spatial organizations of cells. It achieved a 99% cell usage ratio, successfully mapping 2215 out of 2242 cells. Additionally, 1629 of these cells (74%) were correctly mapped to the corresponding spots, translating to a weighted accuracy of 73% (accounting for both accuracy and usage). Whereas CellTrek and CytoSPACE showed relatively poor performance in terms of accuracy and cell retaining rate. Specifically, CellTrek mapped 999 unique cells to spots, leaving 1243 cells unmapped, resulting in a cell loss ratio of 55%. CytoSPACE mapped 1164 unique cells to spots, leaving 1078 cells unmapped, resulting in a cell lost ratio of 48% (Fig. 1b, c). To further assess mapping fidelity, we compared the number of predicted cells per spot with the ground truth and calculated the entropy of cell count per spot to quantify the heterogeneity of cell distribution. Additionally, we assessed spot-level mapping accuracy by calculating the proportion of correctly recovered cells within each spot (Supplementary Fig. 2c–e). Although the accuracy was not highly satisfactory, CMAP demonstrated higher accuracy compared to CellTrek and CytoSPACE. Of note, we also observed that the number of cells per spot does not show a clear linear correlation (r = 0.38) with the spot’s RNA counts in the MOB data (Supplementary Fig. 2f). Similar poor relationship was observed between the number of cells and UMI counts per spot in real pancreatic ductal adenocarcinoma ST data¹⁴, where the number of cells captured by spots was estimated by counting the nuclei in labeled spots (Supplementary Fig. 2g). This lack of correlation leads to difficulties in estimating cell numbers per spot for certain dataset, which is a primary function applied by CytoSPACE in cell mapping.

In addition to the cell mapping, we also computed the cell-type compositions for each spot based on the mapped cells and compared the results with 12 established deconvolution methods (CARD¹³, cell2location¹⁵, CIBERSORTx¹⁶, DestVI¹⁷, GraphST¹⁸, RCTD¹⁹, Redeconve²⁰, Seurat²¹, SONAR²², SPADE²³, SpatialDWLS²⁴, and SPOTlight²⁵) (Fig. 1d). To provide an intuitive and quantitative assessment, we presented the Root Mean Square Error (RMSE), Relative Dimensionless Global Error in Synthesis (ERGAS)²⁶, SSIM and Universal Image Quality Index (UQI)²⁷ between the predicted and the predefined true cell-type compositions (“Methods”). CMAP almost exhibited the lower RMSE/ERGAS and the higher SSIM/UQI among mapping-based methods. It also performed comparably to deconvolution-based methods (Fig. 1e). Importantly, unlike deconvolution-based methods, which are limited to estimating cell proportions within spatial spots, CMAP takes a step further by providing precise spatial locations of individual cells, enabling downstream spatial transcriptomic analyses at the intact single-cell level. Beyond mapping accuracy, the reconstruction of spatial gene expression patterns serves as a vital evaluation criterion. CMAP consistently outperformed other methods in terms of overall gene pattern similarity and the preservation of domain markers compared to CellTrek and CytoSPACE (Fig. 1f and Supplementary Fig. 2h), revealing its strong performance across multiple assessment metrics.

Benchmarking CMAP on imaging-based simulation data

Although synthetic data generation is a commonly used strategy, it is inherently unable to fully replicate the intricacies of cellular distribution in real sample. To further assess the performance of CMAP and its adaptability to imaging-based spatial data, we obtained published seqFISH data of embryonic day (E)8.5 mouse embryos²⁸, and specifically focused on the first stack slice that closely mimicked the section thickness characteristic of Visium (~ 10 μm). Being an imaging-based, single-cell resolution spatial technology, seqFISH inherently offers precise information on both cellular expression and spatial coordinates of cells.

To facilitate a comparative analysis, we spatially divided the cells into squared grids with a width of approximately 50 μm within each FOV and aggregated transcript counts within these grid-defined “pseudo-spots” (Supplementary Fig. 3a). This dataset includes 10,150 individually resolved cells, representing 23 distinct cell types, and is organized into 669 pseudo-spots, averaging 15 cells per spot (Supplementary Fig. 3b). This gridding strategy effectively emulates the heterogenous cell densities observed across diverse tissue regions in vivo.

CMAP consistently showed improved performance in both mapping accuracy and the fidelity of reconstructed spatial gene expression patterns, as evaluated by the aforementioned metrics when applied to this more physiologically relevant, imaging-based seqFISH dataset. Specifically, CMAP’s mapping results showed a relatively high degree of consistency in terms of cell distribution and cell recovery (24% cell loss) (Fig. 2a, b and Supplementary Fig. 3c–f). In contrast, CellTrek and CytoSPACE displayed much sparser and more homogenized spatial cell distributions, which deviated from the ground truth. CellTrek recorded a significant proportion of unmapped cells (79% cell loss), while CytoSPACE similarly failed to map a substantial number of cells (70% cell loss), despite this synthetic dataset featuring a moderate correlation (r = 0.75) between the number of cells per spot and the corresponding spot’s RNA counts (Supplementary Fig. 3g).

**Fig. 2: Evaluation of CMAP on imaging-based simulation data.**

Given the precise cell locations inherent in seqFISH data, it provided a unique platform to evaluate the effectiveness of CMAP processes in detail. We first assessed the utility of CMAP-DomainDivision function by comparing mapping accuracy with and without the implementation of domain-level assignment. We showed that this preliminary step improved performance (Supplementary Fig. 3h). A key strength of the CMAP’s framework is its ability to accurately predict the precise spatial locations of mapped cells. Through a comparative analysis with random assignment strategies employed by CellTrek and CytoSPACE, the CMAP-PreciseLocation module demonstrated remarkable superiority (Fig. 2c). It transcended mere spot-level resolution and precisely located the cells to the refined positions, even within the gap of individual spots.

Upon recalibrating cell-type composition based on computed locations, CMAP consistently showed improved performance among mapping-based methods and achieved comparable performance to deconvolution-based methods (Fig. 2d–f). Moreover, the high efficiency of CMAP in cell mapping was underscored by its effective performance against alternative spatial mapping methods in reconstructing the spatial expression patterns of all tested genes from seqFISH data (Fig. 2g and Supplementary Fig. 3i). These findings from simulated datasets convincingly demonstrate the proficiency of our approach in predicting cell locations across a wide range of intricate spatial configurations.

Benchmarking CMAP on high-resolution Xenium data

To further evaluate the performance of CMAP, we utilized adjacent serial sections from a cancer tissue block, analyzed separately using scFFPE-seq, Visium, and Xenium⁶. Specifically, we focused on the overlapping region shared between the Visium and Xenium data, which covered 78% of the full Visium area (Supplementary Fig. 4a, b). Given the high similarity in cell-type composition and the number of captured cells across these adjacent sections, we aligned the Xenium image data and coordinates with Visium data. By binning Xenium-detected cells and their associated transcripts into the Visium-level spots, we established a ground truth for cell-type proportions and gene expression at these locations. This alignment provided a robust benchmark for evaluating the Visium mapping results against the high-resolution Xenium data.

We began by projecting the segmented cells detected by Xenium onto the Visium data. Despite the lower resolution of the Visium spatial reference, CMAP demonstrated better performance in reconstructing the cell spatial distributions (Fig. 3a and Supplementary Fig. 4c, d). Unlike CellTrek and CytoSPACE, which randomly disrupted cells within spots and remained limited to the spot-level resolution, CMAP was able to intuitively restore fine spatial structure features. Zooming in on regions with complex cellular compositions. CMAP more accurately revealed the spatial context of in-situ tumor cells (distinct types of ductal carcinoma in situ, DCIS) and surrounding myoepithelial cells, while other methods produced fuzzy reconstructions (Fig. 3b). Despite low mapping accuracy observed across methods (Supplementary Fig. 4e), distance-based analysis showed that most predicted cells localized near true same-type neighbors, with CMAP performing relatively better compared with other methods (Supplementary Fig. 4f). This discrepancy may be due to the limited gene coverage (~300 genes) of Xenium-segmented cells, which might be insufficient to effectively recognize intra-cell-type heterogeneity. Furthermore, when comparing the cell-type compositions of registered cell-bin spots (Fig. 3c), CMAP outperformed other mapping-based methods and showed comparable performance to deconvolution-based methods (Fig. 3d, e). CMAP’s reconstructed spatial gene expression patterns also exhibited higher similarity to the real spatial expression patterns across the entire Xenium-detected gene set (Fig. 3f).

**Fig. 3: Evaluation of CMAP on real high-resolution Xenium data (Xenium data integrated with Visium data).**

Given the comprehensive nature of this dataset, which encompasses spatial technologies across different resolutions, we systematically evaluated the impact of various parameters on the performance of CMAP to ensure robust and reliable mapping results. We focused on four key factors: the number of spatial domains, the necessity of batch removal, classifier selection, and SVM parameter optimization (Supplementary Fig. 4g–n). To determine the optimal number of spatial domains, we first considered the anatomical features of the tissue, followed by the evaluation of silhouette scores. Quantitatively evaluation of cell-type compositions revealed that the number of domains determined around the top silhouette scores (k = 6, 8, and 10) performed consistently well (Supplementary Fig. 4h, i, l). Batch effect removal was found to be crucial for reducing technical variation and improving the correspondence between cells and spots, leading to more accurate mapping results (Supplementary Fig. 4h, j, m). In terms of classifier selection, we compared the embedded SVM classifier with two commonly used algorithms: eXtreme Gradient Boosting (XGBoost)²⁹ and Random Forest (RF)³⁰. SVM performed comparably to XGBoost and RF in this dataset (Supplementary Fig. 4h, k, n). Notably, in this dataset, default settings of SVM classifier achieved comparable results compared to fine-tuned parameters, indicating the robustness of CMAP’s configuration for the task handling.

To further validate the compatibility of CMAP, we mapped scFFPE-seq data onto Visium data (Supplementary Fig. 5a). Unlike the segmented cells detected by Xenium, which accurately reflect the true distribution of cell types in the tissue section, scFFPE-seq data is faulted by the underrepresentation of cells (Supplementary Fig. 4b). CMAP consistently performed better than other mapping-based methods in estimating cell-type composition and exhibited comparable performance to deconvolution-based methods (Supplementary Fig. 5b–d). While CMAP and other methods produced similar reconstructed gene expression patterns (Supplementary Fig. 5e), CMAP showed better overall performance. In summary, CMAP’s performance on real high-resolution Xenium data highlights its capability in handling complex data types.

To assess the computational needs of CMAP, we compared it with other mapping-based and deconvolution-based methods using the above-applied benchmarking datasets. CMAP’s runtime ranges from approximately 5 min (for datasets containing 2242 single cells with 16,975 genes, and 260 spatial spots with 17,073 genes) to 4 h (for datasets containing 159,226 single cells with 313 genes, and 4982 spatial spots with 18,056 genes), and its memory usage ranges from about 1500 MB (for datasets containing 10,150 single cells with 351 genes, and 669 spatial spots with 351 genes) to 30 GB (for datasets containing 27,460 single cells with 17,679 genes, and 4982 spatial spots with 18,056 genes), depending on the dataset size (Supplementary Fig. 5f, g). Although CMAP’s runtime and memory usage are slightly higher than some of the benchmarked counterparts, these demands remain within acceptable limits, particularly considering its improved prediction performance.

Performance of CMAP on real semi-supervised data

Subsequently, we assessed the performance of CMAP on more real tissue datasets. We first conducted spatial mapping by projecting Smart-seq2 mouse cortical single-cell data^7,31, known for its deep gene detection ability through full-length RNA sequencing, onto the cortical Visium data. The unique feature of this single-cell dataset lies in the detailed spatial layer origins of the collected cells (Fig. 4a and Supplementary Fig. 6a), providing a semi-ground-truth for evaluating the efficacy of various cell mapping methods. We found that while all methods managed to replicate the overall layer structure of the cortex, CellTrek and CytoSPACE showed slightly blurred boundaries and high repetition rates (42% and 46%, respectively). In contrast, CMAP effectively localized cells to their corresponding layers with higher accuracy (Fig. 4b, c and Supplementary Fig. 6b, c). To further assess CMAP’s mapping accuracy, we cross-referenced single molecule fluorescence in situ hybridization (smFISH) data³², a well-established reference for quantifying mRNA abundances of single cells, from the primary visual cortex (VISp), a subregion of the cerebral context (Supplementary Fig. 6d, e). By displaying the enrichment score of each cell type across different layers for the smFISH data, we were able to highlight the specific enrichment of various cell types in distinct cortical layers. For direct comparison, we included only those cell types that were present in both the single-cell and smFISH datasets. When compared to the spatial distribution of cell types derived from the smFISH data, CMAP showed a generally high level of consistency in the distribution of major cell types (Fig. 4d, e), though some less abundant cell types, such as Pvalb and Sst, exhibited more specific layer distributions. While CellTrek also performed well overall, it exhibited less precision for certain cell types, such as Lamp5. Conversely, CytoSPACE preferentially positioned excitatory neurons and non-neurons, but failed to incorporate inhibitory neurons, such as Vip, NP, Pvalb, and Sst, resulting in a skewed representation of the cortical spatial architecture (Fig. 4e). Moreover, considering the inherent biases and stochastic nature associated with single-cell techniques (Supplementary Fig. 4b), we investigated the potential mismatch between designated layers and actual spatial origins. Cells collected from specific layers might not precisely reflect the true spatial distribution of cell types (Supplementary Fig. 6a, and Fig. 4d), leading to biases in downstream analysis relied solely on single-cell data. CMAP’s mapping results, however, exhibited better alignment with the spatial distributions of cell types, helping to mitigate this discrepancy (Fig. 4d, e).

**Fig. 4: CMAP performance across diverse real-world scenarios.**

We next evaluated the confidence of spatial mapping-based methods on reconstructed gene expression. The scarcity of perfectly matched single-cell and spatial datasets, in terms of cell numbers and compositions, presents a challenge for direct comparisons. This disparity often results in insufficient single cells for accurate reconstruction, yielding noisy spatial spots with numerous zero values. To address this limitation, we proposed a more generalized spatial entropy-based method (named SSGE, see “Methods”) to identify layer-specific genes, whose spatial patterns can be reliably reconstructed even with limited cell counts, and subsequently evaluated spatial consistency based on these genes. Specifically, we first recognized layer-specific genes through this method from smoothed expression profiles. The distinct specificity patterns of these genes for different layers demonstrated the power of this entropy-based method (Supplementary Fig. 6f). Subsequently, we compared the reconstructed spatial gene expression patterns of the top 25 specific genes for each layer with the Visium data. CMAP exhibited slightly better reconstruction patterns for layers 5 and 6 and performed comparably for layers 2/3 and 4 when compared to other methods in reconstructing the expression patterns of these genes (Supplementary Fig. 6g).

The performance of CMAP on limited and unmatched single cells

This spatial mapping on the semi-supervised real cortical data demonstrated the capability of CMAP to allocate the single cells to their most accurate locations. However, the practicality of any spatial mapping method needs to be evaluated under conditions of limited and unmatched single-cell data, a common scenario due to varied sampling strategies in scRNA-seq or practical constraints like experimental costs. This often results in an imbalanced representation of the true cell-type distribution within tissues. Therefore, assessing whether spatial mapping tools can effectively select and accurately position smaller cell populations within their native spatial context becomes imperative.

To this end, we tested on our previously published single-cell dataset, in which 37 cells were manually collected by micropipette aspiration from the proximal primitive streak (PS) of E7.0 mouse embryos and sequenced using Smart-seq2³³ (Fig. 4f). These cells were characterized by high expression of Fn1, Mixl1, and T—three canonical PS markers—whose expression agreed with the PS regions in published E7.0 spatial Geo-seq data³⁴, confirming their posterior regional identity (Supplementary Fig. 7a, b). When these 37 cells were projected to the corresponding spatial Geo-seq data, CMAP showed its effectiveness by initially localizing them to the proximal region of the PS domain and subsequently refining their exact locations by considering the global optimal relationship between the cells and the Geo-seq samples (Fig. 4g). Despite only a fraction of spots being mappable with single cells, aggregating the expression of mapped single cells and the corresponding spatial spots yielded a significant correlation (r = 0.87), affirming the accuracy of the mapping results (Supplementary Fig. 7c). In contrast, CellTrek and CytoSPACE that relied on the inputs of paired single-cell data, failed to accurately localize these cells, dispersing them across almost the entire embryonic regions (Fig. 4g). Both methods generated a substantial number of repetitive assignments for the same set of 37 unique cells, with CellTrek assigning 353 cell locations (90% of repetition rate), and CytoSPACE assigning 323 cell locations (89% of repetition rate). This high degree of redundancy highlights the limitations of these algorithms in mapping limited number of cells.

To further test the scenarios where the composition of cells in the scRNA-seq data exceeded that of the target spatial tissues dataset, we applied CMAP on Slide-seq³⁵ and scRNA-seq data³⁶ derived from mouse embryos, where the datasets differed in the sampled tissues. This single-cell dataset comprised 21,825 cells, covering all cell types throughout the entire embryo, whereas the Slide-seq data captured 8425 spatial beads, focusing solely on the intraembryonic proper. This disparity resulted in the absence of spatial locations for certain extraembryonic cell types, such as differentiated trophoblasts (Troph) and extraembryonic ectoderm 1/2 (ExE 1 and ExE 2), in the Slide-seq tissue section (Fig. 4h). The identities of these three extraembryonic cell types were confirmed by the high expression scores of their cell-type-specific genes (Supplementary Fig. 7d). This scenario offered an opportunity to assess the capability of spatial mapping methods to identify and exclude unmatched cells. We showed that CMAP demonstrated its effectiveness in filtering out the majority of extraembryonic cells, ensuring that only appropriate cell populations were mapped, whereas CellTrek encountered with substantial cell loss during the filtration process, and CytoSPACE repeatedly mapped ExE 1 cells many times (Fig. 4i, j and Supplementary Fig. 7e, f).

Given that Slide-seq technology extends spatial resolution from the spot level to nearly single-cell resolution, previous spot-based evaluation metrics were not suitable for comparing reconstructed spatial gene expression patterns across different algorithms. The single-cell resolution and precision of spatial localization facilitated the validation of the specificity of reconstructed spatial expression patterns using Moran’s I³⁷, a measure of spatial autocorrelation. We identified spatially variable genes (SVGs) from the original Slide-seq data using SpaGCN³⁸ (Supplementary Data 1) and then calculated Moran’s I for those SVGs from spatially mapped single-cells by CMAP and other cell mapping methods. Under the assumption that a well-performing method would reconstruct SVGs with clearer spatial patterns, reflected by higher Moran’s I value, CMAP significantly outperformed CellTrek, CytoSPACE and even the original spatial data (Fig. 4k and Supplementary Fig. 7g), indicating that the reconstructed patterns generated by CMAP displayed an enhanced spatial specificity.

Altogether, through extensive assessments and comparative analyses, we have substantiated the performance of CMAP across diverse datasets and scenarios. CMAP’s adaptability to a wide range of data types generated by both single-cell and spatial techniques, along with its low reliance on prior knowledge and manual intervention, makes it a suitable tool for various spatial mapping applications.

CMAP dissects the organ specificity of endothelial cells

With CMAP’s accuracy in positioning individual single-cells, we sought to explore how this will change our view of location-dependent attributes of particular single cells, which are usually linked to functions hidden in common single-cell analysis. As a ubiquitous presence of cell type, epithelial cells have been shown to exhibit organ-specific identities discernible from their gene expression profiles³⁹ and spatial projection⁴⁰. Similarly, mature endothelial cells (ECs) are heterogeneous and acquire diverse organ specific function in adult mice⁴¹, which is determined during organogenesis and morphogenesis^42,43. However, the establishment of spatial specificity of embryonic ECs is not readily manifested in single-cell data.

As early as E13.5, all major organs have been formed and the spatial profiles have been characterized in detail⁴⁰. Recently, the brain- and liver-specific ECs from mixed populations during embryo development have been characterized. Nevertheless, a finer resolution for ECs distribution on organs that are closely contacted remains unclassified⁴⁴. To this end, we utilized CMAP to spatially map these embryonic ECs, derived from the TOME dataset⁴⁴, to visceral organs (Fig. 5a). Initially, we selected all the ECs at E13.5 stage and calculated the canonical endothelium features for these cells to confirm their endothelial identity (Fig. 5b). Next, we chose the Visium data that contains visceral organs including Bladder, Gonad, Gut, Pancreas, Stomach and Metanephros as spatial coordinates⁴⁰ (Fig. 5a). Albeit seemingly homogenous, we predicted the previously unclassified ECs by CMAP to their respective delineated organ identities (Fig. 5c and Supplementary Fig. 8a). Although CellTrek and CytoSPACE also established the regional identity of ECs, these cells were evenly dispersed in each spot, losing the typical endothelial feature^45,46. Moreover, CellTrek mapped the same cells to multiple organs (376 cells, 28% of 1341 unique cells), hindering discrete comparative analysis among different organs. In contrast, CMAP-mapped ECs were found to be predominantly distributed around the periphery of spatial spots, as showcased in metanephros related ECs (Fig. 5c)⁴⁷.

**Fig. 5: Organ specificity of endothelial cells dissected by CMAP.**

Next, we identified the genes for delineating visceral organ specific EC cells. With these spatial-directed classification, we revealed organ-specific genes derived from CMAP results (Fig. 5d and Supplementary Data 2). Spatial expression patterns of these genes were visualized in the Visium data, revealing that despite the small voxel size of blood vessels, several identified genes exhibited clear spatial specificity. For instance, Dut was specifically expressed in metanephros (Fig. 5e, f). Galnt18 and Ctsl was exclusively expressed in the stomach and gonads, respectively (Supplementary Fig. 8b–e). To validate these findings, we performed RNA in situ hybridization for Dut, Galnt18, and Ctsl, together with classic endothelial marker Pecam1. We found that these gene expression were indeed organ-specific and in proximity with Pecam1, therefore supporting our analytical conclusions (Fig. 5g and Supplementary Fig. 8f, g). Conversely, the organ-specific ECs genes identified from CellTrek and CytoSPACE lacked evident organ-specific characteristics (Supplementary Fig. 8h, i and Supplementary Data 3 and 4). Accordingly, the markers identified by CMAP did not exhibit tissue specificity under the spatial labels attained by CellTrek and CytoSPACE, possibly due to the mixed assignment of individual single cells (Supplementary Fig. 8j).

Additionally, we observed disparities in the molecular signatures of ECs between adult and embryonic mice. Adult EC marker genes are classified into various organ-specific groups, for example, Igfbp5 and Lcn2, which were reported to be uniquely expressed in the kidney and testis, respectively⁴¹. We found that these genes exhibited organ specificity in adults but did not show a preference for specific organs at E13.5. In contrast, Dut and Ctsl, identified as potential early kidney and testis-specific genes at the E13.5 stage of mouse embryonic development, displayed different trends in their expression (Supplementary Fig. 8k–p). This finding underscores the dynamic nature of endothelial cell identity and gene expression patterns across developmental stages, emphasizing the importance of unleashing the full potential of both the single-cell and spatial data.

CMAP reveals spatial heterogeneity of cells in tumor

The tumor microenvironment (TME) is exemplified by its high degree of heterogeneity and therefore often lacks an ordered spatial pattern. To evaluate the precision of our approach in dissecting the cellular composition of sophisticated TME, we employed CMAP on spatial and single-cell data from a lung cancer patient, with both datasets obtained from adjacent regions of the same tumor⁴⁸. CMAP mapping results achieved a resolution beyond the spot level, revealing the intricate spatial organization of immune and tumor cells. Particularly, infiltrating T and B lymphocytes, which are crucial for antitumor immunity, were found to exhibit high co-localization and intermingling within the tumor cell milieu. In contrast, CellTrek and CytoSPACE, confined to spot level mapping, resulted in a random scattering of cells within each spot, compromising the resolution required for discerning fine-grained spatial insights and obscuring the co-localization patterns of T and B cells (Fig. 6a).

**Fig. 6: Spatial heterogeneity of cells in tumor.**

During clonal expansion, immune cells originating from a common precursor exhibit identical T-cell receptor (TCR) or B-cell receptor (BCR) sequence. Therefore, we further validated the accuracy of CMAP’s cell location prediction from an immunological perspective (“Methods”). Our analysis recovered 2% of cells and 1% of spots harboring BCR heavy chains (Supplementary Fig. 9a–c and Supplementary Data 5–7). Despite the inherent limitations imposed by the 3′-end sequencing protocols, which restrict the assembly of full-length TCR/BCR sequences, CMAP successfully matched one mapped cell to spot bearing identical BCR heavy chains, providing evidence for the accuracy of our model in the context of immune repertoires (Supplementary Data 8). This phenomenon was not replicated in the outcomes from CellTrek and CytoSPACE, indicating better performance of CMAP (Supplementary Fig. 9d and Supplementary Data 9 and 10).

We further explored cell-cell interactions mediated by direct cell contact or proximity (“Methods”)⁴⁹. Given the mixed cellular composition within each spot in the original Visium dataset, directly evaluating cell co-localization between diverse cell types is challenging. Thus, we generated spatial expression profiles based on canonical marker gene sets for different cell types and then assessed the potential for cell co-localization through SSGE method. Our results indicated that T cells and B cells showed the highest co-localization potentiality (Supplementary Fig. 9e, f). Having refined the Visium dataset to single-cell resolution using cell mapping methods, we directly assessed cell co-localization in space, applying a permutation test to statistically evaluate the co-localization potentiality of cell types. CMAP’s results confirmed the most frequent co-localization of T cells and B cells within tumor regions, surpassing CytoSPACE and CellTrek (Fig. 6b and Supplementary Fig. 9g–i). The co-localization of T cell and B cells suggested the presence of Tertiary Lymphoid Structure (TLS). To confirm this hypothesis, we utilized TLS related gene signatures⁵⁰ to compute TLS scores on both the original and reconstructed spatial data. Notably, there is a high accordance of TLS score in T/B cell enriched regions across conditions (Fig. 6c).

With the cellular distribution of B and T cells, we sought to explore potential differences between T cells in close proximity to B cells versus those distant from B cells, as T or B cells in TLS structure are prone to generate localized immune responses against tumors. To this end, we defined T cells within 10 μm of B cells as “Near”, those beyond 200 μm as “Far”, and the intermediate group as “Median”. Similar categorizations were applied to B cells (Fig. 6d). TLS scores calculated for each group revealed a decrease in score with increasing distance between T and B cells in both CMAP and CytoSPACE results, with CMAP generating a more pronounced difference in TLS scores between “Near” and “Far” T/B cells. Conversely, CellTrek results displayed opposing patterns (Fig. 6e). This finding suggests a correlation between cell proximity of T and B cells and their contribution to TLS formation. Meanwhile, T_Near cells displayed a stronger T follicular helper (Tfh)-like gene expression signature⁵¹, including BHLHE40, TOX, TOX2, ICOS, TIGIT, and CTLA4, compared to T cells located far away from B cells, suggesting a direct influence of B cell proximity on T cell differentiation, supporting the notion that the interaction between T and B cells promotes the differentiation of naïve CD4 + T cells into Tfh cells during the formation of TLS. Furthermore, B_Near cells were more likely to express mature B cell markers, such as MS4A1 and CD22, which are involved in the regulation of B cell activation and antigen receptor signaling. In contrast, B_Far cells highly expressed SDC1, a plasma cell marker, indicating these cells are in a terminally differentiated state and primarily function to produce antibodies (Fig. 6f).

To further elucidate the intercellular communications within TME in single-cell level, we analyzed putative interactions between spatially mapped T and B cells (Supplementary Fig. 9j, k). Physically proximal T and B cells (T_Near-B_Near) exhibited pronounced upregulation of ligand-receptor pairs in the CD40 and LIGHT signaling pathways, with ligands CD40LG and TNFSF14 expressed on T cell (source) exhibiting a gradient expression pattern correlating with the distance from B cells. The corresponding receptors, CD40 and TNFRSF14, were expressed on B cell (target), especially on B_Near cells, indicating strong cell-cell communication between T_Near and B_Near cells within this localized region of the TME (Fig. 6g, h and Supplementary Fig. 9l, m). CD40LG binding to CD40 plays a pivotal role in T-dependent immune response, triggering B cell activation and rapid proliferation, leading to the formation of germinal centers⁵². Meanwhile, LIGHT was the cooperative signaling with the CD40 system for T cell co-stimulation⁵³. In the pronounced upregulated ligand-receptor pairs between B cells co-localized with T cells (B_Near-T_Near), we found that the ligands TNFSF9 and CD70 were expressed on B cell (source), particularly on B_Near cells. Correspondingly, the receptors TNFRSF9 and CD27, known as T cell costimulatory molecules, were predominantly expressed on T_Near cell (target), which promoted T cell survival, activation and expansion^54,55,56 (Fig. 6i, j and Supplementary Fig. 9n, o). These observations suggested that B_Near cells sustain T cell activation through antigen presentation, priming for Tfh cell differentiation and promoting TLS generation⁵⁷.

To gain deeper insights into the interactions within TLS-like regions, we performed the subcluster analysis focusing on immune cells, particularly lymphoid cells, which are predominantly enriched in these regions (Fig. 6a). Our primary focus was on CD4⁺ T cells and B cells, as only a few CD8⁺ T cells were detected. Sub-clustering analysis identified four subclusters of CD4⁺ T cells and two subclusters of B cells (Supplementary Fig. 9p–s). Notably, we observed significant colocalization of B and CD4⁺ Tfh subclusters within TLS-like regions (Fig. 6k, l). We then selected spatially proximate B and CD4⁺ Tfh cells within these TLS-like regions and categorized them as the “TLS-Near” group. Interestingly, our analysis revealed that the interaction strength between CD4⁺ Tfh cell (source) and B cell (target) gradually increased with decreasing spatial distance between Tfh-B cell pairs. Specifically, we found that CD40LG-CD40 and TNFSF14-TNFRSF14 mediated Tfh-B cell interactions were stronger in TLS-Near group compared to those within the whole TLS-like region and the entire tissue section (Fig. 6m and Supplementary Fig. 9t). Upon receiving CD40 signaling from CD4⁺ Tfh cells, B cells upregulated ICOSL, triggering a positive feedback loop that further facilitated Tfh cell differentiation via ICOSL-ICOS signaling^58,59 (Supplementary Fig. 9u). Similarly, TNFSF9-TNFRSF9 mediated interaction between B cell (source) and CD4⁺ Tfh cell (target) in TLS-Near group demonstrated higher interaction strength compared with those within the whole TLS-like region and the entire tissue section (Fig. 6n).

In summary, these findings underscore the importance of single-cell ST in unraveling the complexities of the TME and provide novel insights into the mechanisms underlying localized immune responses against tumors. The precision of cell mapping by CMAP in delineating cell-cell interactions and their functional implications offers a useful tool for advancing our understanding of cancer immunology and guiding the development of targeted therapeutic strategies.

Discussion

The study of biological events at the cellular level necessitates an understanding of their spatial organization. While traditional bulk tissue analysis and single-cell investigations provide valuable information, they fail to capture the intricate spatial dynamics that govern cellular behavior. To address this limitation, we introduce CMAP, an innovative method for reconstructing spatial cellular profiles from ST data. CMAP leverages the location information inherent in spatial data to map individual cells to their precise positions within a tissue, increasing the spatial resolution to the intact single-cell level while expanding the number of expressed genes that can be analyzed. The flexibility of CMAP allows for its application in various scenarios, including unmatched cell filtering, small cell population localization, and TME analysis.

Recent high-precision spatial omics technologies, such as Stereo-seq and Visium HD, capture detailed transcriptional information but face challenges in defining cell boundaries, especially for complex cells like neurons, and in high-density tissues. This leads to the use of binned regions rather than true single-cell resolution. Imaging-based methods like Xenium, while distinguishing single cells through membrane staining, are limited by partial transcriptomic coverage and potential biases from cell segmentation. Moreover, finite tissue section thickness can result in fragmented cells, compromising cellular integrity. CMAP addresses these limitations by integrating scRNA-seq and ST to predict precise single-cell locations with comprehensive transcriptomic coverage. This approach achieves true single-cell resolution, ensuring accurate reconstruction of the entire transcriptome’s spatial organization, thus providing deeper insights into cell function within complex tissues.

We extensively evaluated the performance of CMAP through simulations, high-resolution Xenium data, semi-supervised data and real-world biological samples. Simulated datasets served as a controlled environment to systematically assess CMAP’s resilience against noise, bias, and variations in input data quality. The simulation-benchmarking results revealed that CMAP performed better than CellTrek and CytoSPACE, two top-tiers in the field (Figs. 1 and 2). The relatively high concordance between CMAP’s mapped cells and Xenium data underscores its capability to capture the intricate spatial organization of tissues (Fig. 3). Systematically investigating the effect of key parameters on the mapping results, based on this comprehensive Xenium data, further highlights the consistency and adaptability of CMAP (Supplementary Fig. 4g–n). Through carefully evaluating the impact of critical factors such as the number of spatial domains, batch effect removal and classifier selection, we demonstrated that CMAP could deliver more reliable mappings across different experimental settings. The use of silhouette scores aids in determining the optimal number of broad spatial domains. This approach helps to accurately reflect the underlying tissue architecture, enhancing the biological relevance of the mappings. The importance of batch effect removal is particularly evident, as it significantly reduces technical variability, thereby enhancing the integrity of the data. The robustness of the SVM configuration was assessed. Other classifiers, such as RF and XGBoost, also perform comparably well and can be applied based on users’ preferences. These elements collectively contribute to CMAP’s usability to provide high-fidelity integration analysis of single-cell and spatial data.

Evaluation on semi-supervised datasets, such as the mouse cortical data integrated with Visium spatial data, provided a semi-reference for validating CMAP’s mapping efficacy. Here, CMAP showed good accuracy in localizing cells to their correct anatomical layers (Fig. 4a–e). Real-world biological data presented a challenge of mapping under conditions of limited and unmatched single-cell data, reflecting the complexities encountered in experimental settings. When applied to manually curated single-cell data from E7.0 mouse embryos, CMAP more accurately localized cells to their native spatial context, showcasing its capability to handle small cell populations with high precision (Fig. 4f–g). Furthermore, in scenarios involving mismatched datasets, CMAP distinguished and excluded unmatched cells, ensuring that only relevant cell populations were mapped, thereby enhancing the reliability of spatial mapping (Fig. 4h–k).

In endothelium application, CMAP not only delineated their spatial distribution but also identified organ-specific genes, such as Dut for metanephros and Ctsl for gonads, which were validated through RNA in situ hybridization. This demonstrated CMAP’s utility in unraveling the spatial heterogeneity of cell types, even in closely contacted organs (Fig. 5). Furthermore, CMAP’s application to lung cancer spatial and single-cell data unveiled the intricate spatial organization of immune and tumor cells, revealing the high co-localization of T and B lymphocytes within the TME. This level of resolution went beyond what conventional methods could achieve, offering insights into the spatial heterogeneity and potential for localized immune responses (Fig. 6).

While CMAP represents a significant advancement in spatial cellular profiling, several limitations warrant further investigation: (1) an ideal scenario involves the pairing of single-cell and spatial datasets from the same tissue source to minimize non-biological noise. However, technical biases in cell capture and the intrinsic preferences of single-cell technologies often lead to skewed representations of cell types, diverging from the authentic cell-type distribution found in tissues. CMAP’s effectiveness is contingent upon the careful selection and alignment of cells that accurately reflect the spatial data, necessitating strategies to mitigate these discrepancies and ensure a faithful representation of the tissue’s cellular landscape; (2) CMAP adopts a divide-and-conquer approach, which is advantageous for managing computational resources and tackling unmatched problems between single-cell and spatial datasets. Yet, this strategy may introduce biases, especially in the prediction of domain labels. Each step of CMAP’s algorithmic process can potentially skew the final results, highlighting the potential benefit of integrating CMAP with other algorithms to refine predictions and reduce biases; (3) achieving precise predictions of cell numbers within each spatial spot is a formidable challenge due to variations in tissue density and the integrity of sampled cells. Current datasets, either simulations or real ST data with cell counts, often lack a strong correlation between RNA counts and actual cell numbers. This discrepancy complicates the interpretation of cell locations inferred from CMAP’s outputs. It underscores the necessity for cautious analysis, ideally complemented by insights from previous studies or established biological knowledge. Experimental validation serves as the ultimate standard for confirming the accuracy of CMAP’s predictions; (4) although CMAP demonstrates superior performance across various datasets, its generalizability and robustness against diverse biological contexts and data types remain to be thoroughly tested. Further investigations are warranted to ascertain CMAP’s effectiveness in handling a broader range of tissues, developmental stages, and disease states, ensuring that its capabilities are not confined to specific experimental setups or conditions.

CMAP was primarily designed to provide a high-performance tool for researchers to precisely explore single-cell level spatially transcriptome associated discoveries. Our analyses using two simulated datasets (Figs. 1 and 2), one high-resolution Xenium dataset (Fig. 3), and five additional real-world datasets (Figs. 4–6) illustrated the high performance of CMAP. In the future, we envision that CMAP could be further enhanced by integrating multi-omics data of single-cell and spatial dimensions. By combining transcriptomic, proteomic and epigenomic data, CMAP would offer a more comprehensive understanding of spatial cellular heterogeneity and uncover important regulatory mechanisms governing cell function and organization. Furthermore, CMAP’s capabilities would be expanded to investigate the spatial interactions between cells and the role of secretory molecular signals within tissues. The integration of spatially resolved cellular communication with multi-omics data would further enable a deeper understanding of how cells’ functions are precisely regulated, how cells interact, and how these regulatory processes are influenced by local microenvironments. Overall, CMAP provides a powerful, compatible and scalable approach to reconstructing spatial cellular profiles at single-cell resolution, offering invaluable insights into the characteristics of intricate organization of complex biological systems.

Methods

Ethics statement

All experimental procedures involving animals adhered to protocols approved by the Institutional Animal Care and Use Committee of Guangzhou Institutes of Biomedicine and Health (GIBH) (N2019056 and N2024045).

Data preprocessing

The application of CMAP requires single-cell and ST data. The spatial attributes embedded within the spatial data serve as the foundational spatial reference coordinates for cell mapping. For 5′ or 3′ enrichment data, such as those generated by 10x Genomics, we initially use LogNormalized to mitigate the confounding effects of library size and sequencing depth. When dealing with full-length sequencing data, including Geo-seq and Smart-seq2, we use the log(TPM + 1)⁶⁰ transformation to adjust for the biases of gene length. For image-based spatial data, exemplified by seqFISH, we follow the procedures outlined in the original paper, employing the scran package⁶¹ for normalization. Subsequently, we adapt a quantile normalization approach to harmonize the scaling and distribution discrepancies between scRNA-seq and spatial datasets. Given the potential batch effects arising from different experimental platforms and sources, we applied the harmony⁶² method to align single-cell and spatial datasets to remove potential non-biological biases. This integration step embeds both ST and single-cell RNA-seq data into a shared latent space, ensuring their alignment for downstream analysis. These preprocessed data sets are then poised for subsequent CMAP processing.

The CMAP algorithm

CMAP consists of three core components to progressively refine the spatial localization of cells: (1) CMAP-DomainDivision (Level 1 mapping). This initial step involves the stratification of cells into spatial domains, facilitating a coarse-grained assignment that paves the way for more detailed analyses; (2) CMAP-OptimalSpot (Level 2 mapping). This component identifies the most suitable spatial spots for each cell; (3) CMAP-PreciseLocation (Level 3 mapping). The final phase refines the localization process to determine the precise coordinates of each cell within the tissue.

CMAP-DomainDivision: dividing cells into spatial domains

Firstly, we apply HMRF⁹ to do the spatial domain clustering on ST dataset. HMRF concurrently considers gene expression profiles and spatial coordinates, enabling the identification of spatial coherent regions. During this process, HMRF also identifies spatially specific genes of each domain, which we subsequently utilize as the input features for classification. The optimal number of spatial domains is determined based on the anatomical features of the tissue. In the case where the number of domains is unknown, we assess different possible values and select the number that yields the highest average Silhouette width¹⁰.

Next, using the embedded spatial data, we train domain-specific classifiers in this study with a multiclass SVM formulation, specifically employing the One-vs-One strategy. Other classifiers can also be easily integrated into CMAP, offering flexibility in analysis. The One-vs-One approach is known for its enhanced robustness to class imbalance as each binary classifier is trained on a relatively balanced subset of samples from two classes. By focusing solely on two classes at a time, the One-vs-One classifiers could minimize the interference from noise or outliers in other classes, thereby improving classification accuracy and reliability.

SVM is well-regarded in the field of classification due to their strong predictive performance. It excels at handling complex datasets by mapping input features into a higher-dimensional space using kernel functions, which allows for nonlinear decision boundaries. This makes SVM suitable for ST data, where the feature space is often high-dimensional and the relationships between features can be nonlinear. For each pair of spatial domains $(p,q)$ among all $k$ spatial domains, a binary classifier is constructed. Let ${{{{\bf{x}}}}}_{i},i=1,..,n,$ denote the gene expression vector for the $i-{th}$ spot, and ${{{{\bf{y}}}}}_{i}$ represent its domain label. Utilizing the radial basis function (RBF) kernel, we seek the optimal separating hyperplane that maximally separates two classes. The objective function is as follows:

$$\min \frac{1}{2}{||}{{{\bf{w}}}}|{|}^{2}+C {\sum }_{i=1}^{n}{{{{\boldsymbol{\zeta }}}}}_{i},$$

(1)

$${{{\bf{w}}}}={\sum }_{i=1}^{n}{{{{{\bf{c}}}}}_{i}{{{\bf{y}}}}}_{i}\Phi ({{{{\bf{x}}}}}_{i}),$$

(2)

and ${{{{\bf{c}}}}}_{i}$ is obtained by solving the optimization problem subject to:

$${{{{\bf{y}}}}}_{i}({{{\bf{w}}}}\cdot \Phi ({{{{\bf{x}}}}}_{i})+b)\ge 1-{{{{\boldsymbol{\zeta }}}}}_{i},{{{{\boldsymbol{\zeta }}}}}_{i}\ge 0,i=1,\ldots,n,$$

(3)

with the RBF kernel defined as:

$${{{\rm{K}}}}({{{{\bf{x}}}}}_{i},{{{{\bf{x}}}}}_{j})=\Phi ({{{{\bf{x}}}}}_{i})\cdot \Phi ({{{{\bf{x}}}}}_{j})=\exp (-\gamma {||}{{{{\bf{x}}}}}_{i}-{{{{\bf{x}}}}}_{j}|{|}^{2}),\gamma > 0.$$

(4)

In this equation, ${{{\bf{w}}}}$ is a vector in the transformed high-dimensional space. ${{{{\boldsymbol{\zeta }}}}}_{i}$ is a slack variable to quantify the margin of misclassification error. $C$ is an adjustable parameter balancing the interval and tolerance for misclassification. $\gamma$ is the parameter of the RBF kernel, which governs the influence radius of a single training sample.

We utilize the R package e1071 to implement and specifically modify the default behavior of the e1071::svm function, where the class.weight parameter is originally set to FALSE. In our implementation, we enabled class.weight by default in CMAP to handle class imbalance. This setting automatically calculates class weights inversely proportional to their respective frequencies, ensuring fair treatment of underrepresented classes during model training. Prior to training, we optimize parameters $C$ and $\gamma$ via grid search and cross-validation on spatial data. Once the optimized parameters are determined, we train the spatial domain classifiers and predict the domain labels for each single cell. Alongside the predicted domain, probabilities for each spatial domain are provided for every single cell. By setting a probability threshold, we can filter out low-confidence cells that poorly match their spatial domain.

CMAP-OptimalSpot: assigning cells to optimal spots

Within each spatial domain $k$, we aim to assign single cells to their most appropriate spots by constructing a cost function that encapsulates both gene expression and spatial distribution characteristics. Specially, for domain $k$, encompassing $n$ cells and $m$ spots, we first identify the spatial variable genes $g$ that best represent the domain′s features, and then extract corresponding gene expression profiles from both spatial and single cell dataset, denoted as matrices $S(g\times m)$ and $C(g\times n)$, respectively. Initially, CMAP generates a random mapping matrix $M(n\times m,0 < {M}_{{ij}} < 1)$, to record the correspondence between the $i-th$ cell and the $j-{th}$ spot. To ensure that each cell is assigned to exactly one spot, we apply a softmax transformation to $M$, normalizing the entries such that ${\sum }_{j}^{m}{M}_{{ij}}=1$. Specifically,

$${M}_{{ij}}={{{\rm{softmax}}}}({M}_{{ij}})=\frac{{e}^{{M}_{{ij}}}}{{\sum }_{l}^{m}{e}^{{M}_{{il}}}}.$$

(5)

Using the mapping matrix $M$ and single-cell expression profile $C$, we synthesize a spatial gene expression matrix that approximates the following function: $C\times M \sim S$. To enhance the learning of spatial structure expression characteristics beyond mere gene expression similarity, we incorporate the SSIM.

Additionally, we introduce the concept of cellular spatial density, which is inspired by the number of cells allocated to each spot. To assign each cell to its optimal spot, we select the spot with the highest mapping probability, resulting in a binarized mapping matrix ${M}^{{\prime} }(n\times m,{M}_{{ij}}^{{\prime} }\in \{{{\mathrm{0,1}}}\})$. The cellular spatial density is denoted as $\vec{{{{\bf{d}}}}}=\frac{{\sum }_{l}^{n}{M}_{{lj}}^{{\prime} }}{{\sum }_{i}^{n}{\sum }_{j}^{m}{M}_{{ij}}^{{\prime} }}.$ When cells are uniformly distributed across spots, the entropy of $\vec{{{{\bf{d}}}}}$ reaches its maximum, reflecting an even dispersion.

To optimize the assignment of cells to spots, we minimize the following cost function:

$${\lambda }_{1}(1-{{{\rm{SSIM}}}}\left(C\times M,S\right))-{\lambda }_{2}{{{\rm{H}}}}(\vec{{{{\bf{d}}}}}),$$

(6)

where ${\lambda }_{1}$ and ${\lambda }_{2}$ are the weight parameters for the SSIM and entropy terms. By default, we set equal weights (${\lambda }_{1}={\lambda }_{2}=1$) when assuming a uniform distribution of cells on the tissue. However, in scenarios of extreme cellular density heterogeneity, the entropy term’s influence can be reduced (${\lambda }_{1}=1,{\lambda }_{2}=0$). To expedite the search for the global optimum, CMAP utilizes the gradient descent (Nesterov-accelerated Adaptive Moment Estimation, Nadam⁶³) to solve this optimization problem, supporting GPU-accelerated computation to significantly enhance processing speed.

CMAP-PreciseLocation: determining the precise locations

Despite the assignment of cells to optimal spots, the resolution remains constrained at the spot level, failing to achieve true single-cell spatial resolution. Recognizing the profound impact of the spatial environment and intercellular communications, we propose the Spring Model, inspired by principles of force decomposition, to determine the precise spatial location of each cell. To illustrate, consider a simplified scenario where the spatial data are arranged in a square grid. Let $s$ be the optimal spot for cell $c$. From the nearest neighbor graph of spots, we identify the nearest neighbors of spot $s$, namely the upper, lower, left, and right spots, denoted as ${{Up}}_{s},{{Down}}_{s},{{Left}}_{s}\;{and}\;{{Right}}_{s}$, respectively. We use the Spearman rank Correlation Coefficient (SCC) to quantify the relationships between cell $c$ and these spots, denoted as ${{k}_{s},k}_{{{Up}}_{s}},{k}_{{{Down}}_{s}},{k}_{{{Left}}_{s}}$ ${and}\;{k}_{{{Right}}_{s}}$.

Under the assumption that cells maintain equilibrium within their interactive environment, we consider the collective influence exerted by the nearest spots on cell $c$. By equating the sum of forces acting on cell $c$ to 0, we can decompose these forces along the x and y axes:

$${F}_{{up}\cdot x}+{F}_{{down}\cdot x}+{F}_{{left}\cdot x}+{F}_{{right}\cdot x}+{F}_{s\cdot x}=0,$$

(7)

$${F}_{{up}\cdot y}+{F}_{{down}\cdot y}+{F}_{{left}\cdot y}+{F}_{{right}\cdot y}+{F}_{s\cdot y}=0.$$

(8)

Substituting $F=k\cdot \Delta x$, which $k$ represents the similarity coefficient between spot $s$ and cell $c$, and $\Delta x$ is the distance between them (denoted as $d$), we arrive at:

$$ {k}_{{{Up}}_{s}}\cdot {d}_{{{Up}}_{s}}\cdot \cos {\theta }_{{{Up}}_{s}}+{k}_{{{Down}}_{s}}\cdot {d}_{{{Down}}_{s}}\cdot \cos {\theta }_{{{Down}}_{s}} \\ +{k}_{{{Left}}_{s}}\cdot {d}_{{{Left}}_{s}}\cdot \cos {\theta }_{{{Left}}_{s}}+{k}_{{{Right}}_{s}}\cdot {d}_{{{Right}}_{s}}\cdot \cos {\theta }_{{{Right}}_{s}} \\ +{k}_{s}\cdot {d}_{s}\cdot \cos {\theta }_{s}=0,$$

(9)

$$ {k}_{{{Up}}_{s}}\cdot {d}_{{{Up}}_{s}}\cdot \sin {\theta }_{{{Up}}_{s}}+{k}_{{{Down}}_{s}}\cdot {d}_{{{Down}}_{s}}\cdot \sin {\theta }_{{{Down}}_{s}} \\ +{k}_{{{Left}}_{s}}\cdot {d}_{{{Left}}_{s}}\cdot \sin {\theta }_{{{Left}}_{s}}+{k}_{{{Right}}_{s}}\cdot {d}_{{{Right}}_{s}}\cdot \sin {\theta }_{{{Right}}_{s}} \\ +{k}_{s}\cdot {d}_{s}\cdot \sin {\theta }_{s}=0.$$

(10)

By substituting ${d}_{{{Up}}_{s}}\cdot \cos {\theta }_{{{Up}}_{s}}={x}_{{{Up}}_{s}}-{x}_{c}$, ${d}_{{{Up}}_{s}}\cdot s{{in}\theta }_{{{Up}}_{s}}={y}_{{{Up}}_{s}}-{y}_{c}$, we can solve the coordinate of cell $c$. In practical scenarios, the influence of spots along one axis can overshadow that of spots along the other axis. Therefore, in the computations, we focus exclusively on the effects of left and right spots on the x-axis, and similarly for the y-axis, yielding the coordinates of cell $c$ as:

$${x}_{c}=\frac{{k}_{{{Left}}_{s}}\times {x}_{{{Left}}_{s}}+{k}_{{{Right}}_{s}}\times {x}_{{{Right}}_{s}}+{k}_{s}\times {x}_{s}}{{k}_{{{Left}}_{s}}+{k}_{{{Right}}_{s}}+{k}_{s}},$$

(11)

$${y}_{c}=\frac{{k}_{{{Up}}_{s}}\times {y}_{{{Up}}_{s}}+{k}_{{{Right}}_{s}}\times {y}_{{{Down}}_{s}}+{k}_{s}\times {y}_{s}}{{k}_{{{Up}}_{s}}+{k}_{{{Down}}_{s}}+{k}_{s}}.$$

(12)

Nearest neighbor graph construction

To construct the nearest neighbor graph, we employ the Euclidean distance metric to quantify the spatial proximity between each spot. For dataset with regular, grid-like structures, characteristic of platforms like 10x Genomics Visium and ST, the number of nearest neighbors is typically set to four or six, depending on whether the grid is square or hexagonal. For irregular dataset, exemplified by Geo-seq, the number of neighbors is set to four, with the maximum distance threshold of 1.5. For single-cell-level spatial data, the construction of the nearest neighbor graph is based on a predefined maximum distance cutoff.

Simulating spatial datasets using scRNA-seq datasets

To test the performance of CMAP, we leveraged a publicly available mouse nervous system scRNA-seq dataset, along with the spatial coordinates derived from a mouse olfactory bulb ST dataset (https://github.com/YMa-lab/CARD-Analysis/tree/master/simulations)¹³. This scRNA-seq data contains 20,418 cells spanning six primary cell types. Adhering to the simulation protocol established by CARD, we carefully recorded the cells contributing to each synthesized spot. Specifically, the spatial locations were categorized into three distinct anatomic regions, each predominantly occupied by one main cell type. For each region, the number of co-localized cell types, was sampled from a uniform distribution U (0,5). Spot-specific cell type proportions were determined via a Dirichlet distribution, ensuring the dominant cell type held the highest proportion, with remaining types randomly allocated. Each spot was allocated 10 cells. We then randomly selected cells from the scRNA-seq data to populate each spot, aggregating the counts of all cells assigned to the same spot. To facilitate accurate cell mapping assessment, we controlled that each cell only appeared once in the simulating process. The simulation process required 2561 cells across six cell types to populate 260 spatial locations, including astrocytes (n = 179), ependymal cells (n = 319), immune cells (n = 262), neurons (n = 653), oligodendrocytes (n = 997) and vascular cells (n = 151). Due to the scarcity of ependymal cells (n = 15), which was insufficient to ensure representation in each spot, they were excluded from subsequent mapping and benchmark analyses.

Simulating spot-like data using single-cell level spatial datasets

To simulate spot-like data from single-cell level spatial datasets, we utilized mouse embryo seqFISH data acquired from Lohoff et al.²⁸ (https://content.cruk.cam.ac.uk/jmlab/SpatialMouseAtlas2020/). This dataset measures the expression of 351 target genes in midline sections of mouse embryos at the 8–12 somite stage, with each sample featuring a sagittal thickness of 20 μm, comprising two cellular layers. To get close to the thickness of Visium (10 μm), we confined our analysis to the first cellular layer of embryo 1. Following stringent quality control measures, 10,150 cells remained for the downstream analysis. To mimic spot-like data, we partitioned each field into square regions approximately 50 µm in width, treating each as a spot-like region. The gene counts of all cells within a grid were summed to simulate a spot, with the grid’s center serving as the spot’s spatial location.

Benchmark comparison among different methods

To systematically assess the performance of CMAP against existing methods for cell location prediction, we conducted comprehensive benchmarks using various datasets. Specifically, we compared CMAP with two prominent methods: CellTrek (version 0.0.94)⁷ and CytoSPACE (version 1.0.1)⁸, with default parameters. For CellTrek, we didn’t do the interpolation and adjusted the repelling radius (repel_r) parameter according to the spatial coordinates of each dataset. In the simulation datasets, given that each cell occupies a unique and fixed position, we assigned the nearest spot as the cell’s location and filtered out duplicate cells from CellTrek results. Conversely, in real datasets, we retained all cells without eliminating duplicates. CytoSPACE, due to its equitable weighting of cell localization and the negligible duplications rates in simulated datasets (0.17% for simulated MOB data and 0% for simulated embryo data), we applied directly to all datasets without further adjustments.

Our benchmarks extended to evaluating CMAP’s cell-type proportion reconstructions against 12 deconvolution methods: (1) CARD (version 1.1), (2) cell2location (version 0.1.3), (3) CIBERSORTx (https://cibersortx.stanford.edu/), (4) DestVI (version 1.0.2), (5) GraphST (version 1.0.0), (6) RCTD (version 2.2.0), (7) Redeconve (version 1.1.0), (8) Seurat (version 4.3.0.1), (9) SONAR (version 1.0.0), (10) SPADE (version 0.0.0.9000), (11) SpatialDWLS (version 1.1.2), (12) SPOTlight (version 1.5.2). For consistency, we followed the recommended guidelines and default parameter settings for each method in our comparative analysis. Due to SPOTlight’s limitations in handling large datasets, we sampled 50% of cells from each cell type for deconvolution on the high-resolution Xenium data.

Benchmark metrics

In simulation datasets, we evaluated the methods’ performance through mapping accuracy and the fidelity of reconstructed gene expression patterns. Firstly, we categorized correctly assigned spot matching ground truth as accurate assignments, denoted as ${{Num}}_{{match}}$. Given that each spot consists of specific cells in the simulated datasets, while CytoSPACE and CellTrek may incur cell lose or duplication, we introduced the cell usage ratio as a corrective factor for accuracy assessments:

$${Accuracy} \,\ast\, {Usage\; ratio}=\frac{{{Num}}_{{match}}}{{{Num}}_{{used}}}\times \frac{{{Nu}m}_{{unique}}}{{{Num}}_{{all}}},$$

(13)

where ${{Num}}_{{used}}$ corresponds to the number of mapped cells, ${{Num}}_{{unique}}$ represents the number of unique cells among the mapped cells, and ${{Num}}_{{all}}$ is the number of cells initially invested.

To evaluate the performance of spatial gene expression reconstruction, we employed four metrics to quantify the similarities and disparities between the reconstructed patterns (synthetic spot-level data) and the original patterns of spatial data at the image level. These metrics include RMSE, ERGAS, UQI, and SSIM. Each metric was calculated as follows:

RMSE

$${RMSE}=\sqrt{\frac{1}{M \,\ast\, N}{\sum }_{i}^{M}{\sum }_{j}^{N}{\left({x}_{{ij}}-{y}_{{ij}}\right)}^{2}}$$

(14)

It is a common method for image evaluation, where $x$ and $y\;(M\times {N\; pixels})$ represent the reconstructed gene expression pattern and real spatial data, respectively. RMSE is a nonnegative value, and a lower RMSE signifies a closer match between prediction and ground truth.

SSIM

$${SSIM}(x,y)={\frac{(2{{\mu }_{x}\mu }_{y}+{c}_{1})(2{\sigma }_{{xy}}+{c}_{2})}{({\mu }_{x}^{2}+{\mu }_{y}^{2}+{c}_{1})({\sigma }_{x}^{2}+{\sigma }_{y}^{2}+{c}_{2})}}$$

(15)

It is a metric for measuring the similarity between two images $x$ and $y$, where $({{\mu }_{x},\mu }_{y})$ and $({\sigma }_{x}^{2},{\sigma }_{y}^{2})$ are the means and variances of $x$ and $y$, ${\sigma }_{{xy}}$ is the covariance of $x$ and $y$, ${c}_{1}={({k}_{1}L)}^{2}$ and ${c}_{2}={({k}_{2}L)}^{2}$ are two variables to stabilize the division with weak denominator (default, ${k}_{1}=0.01$ and ${k}_{2}=0.03$), and $L$ is the dynamic range of the pixel-values. The pixels have strong inter-dependencies, especially when they are spatial close, so SSIM can help us better capture the structural information. The range of SSIM is [−1,1], where 1 denotes identical images, 0 signifies no similarity, and negative values indicate inverse correlation, though such negative values are rarely encountered in practice. Typically, SSIM values fall within the range of 0 to 1.

ERGAS

$${ERGAS}=100\frac{h}{l}\sqrt{\frac{1}{N}{\sum }_{i=1}^{N}\frac{{{RMSE}}^{2}({B}_{i})}{{\bar{{y}_{i}}}^{2}}}$$

(16)

It is mainly used to measure spectral distortion between two images, where $h$ and $l$ are the pixel sizes of fused and reference images $x$ and $y$, $N$ is the number of spectral bands, ${RMSE}({B}_{i})$ is the RMSE for $i-{th}$ band between fused and reference images, and $\bar{{y}_{i}}$ is the mean of the $i-{th}$ band of reference image. The lower values suggest better prediction performance.

UQI

$${UQI}=\frac{4{\sigma }_{{xy}}{xy}}{({\sigma }_{x}^{2}+{\sigma }_{y}^{2})({x}^{2}+{y}^{2})}$$

(17)

It takes local spatial properties into account, including luminance, contrast, and correlation information, where ${\sigma }_{{xy}}$ is the covariance of image $x$ and $y$, and $({\sigma }_{x}^{2},{\sigma }_{y}^{2})$ are the variances of $x$ and $y$. Its range is [−1,1]. A higher UQI value indicates better prediction performance.

These four metrics are also used to benchmark the accuracy of predicted versus actual cell type proportions across the evaluated methods.

CMAP and downstream analyses

Simulated mouse olfactory bulb data

For implementation of CMAP method, we first used HMRF to cluster the spatial data into three domains. Then, we trained a domain classifier model utilizing the tuned parameters of cost = 2 and gamma = 0.03125 to predict the spatial domains for each cell. These settings were derived from the results of tune_parameter function, ensuring optimal performance. Cells with prediction probability below 0.5 (the default threshold) were excluded, resulting in 2215 cells being retained. These cells were then assigned to optimal spots through the map_cell_to_spot function. A spatial network was constructed using spatial_relation_all function, with parameters spatial_data_type = square, n_near_spot = 5, and dis_cut = 1.3. To pinpoint the precise location of each cell, we employed calculate_cell_location with radius = 1/6.

For CellTrek, we used the default parameters with top_spot = 10 and spot_n = 10, except for repel_r = 0.05 and intp = F. For CytoSPACE, we implemented the lap_CSPR solver and set the geometry mode as square. Out of a total of 2242 cells, CellTrek generated 2476 cell locations for 999 unique cells (55% of loss rate) and CytoSPACE provided 1166 cell locations for 1164 unique cells (48% of loss rate). Given that each cell within the simulated space occupies a distinct and fixed position, we assigned the nearest spot as the cell location and excluded duplicate cells from the CellTrek results.

For CytoSPACE, due to the equal weighting of cell localization and the minimal duplication observed (0.17% of repetition rate), we directly incorporated all cells across all datasets.

Simulated embryonic seqFISH data

We initially clustered the simulated spot-like data into 16 domains. Due to the limited detection of genes, all genes were utilized for training the domain classifiers, with parameters cost = 8 and gamma = 0.125, as determined by tuning. Cells with prediction probability below 0.5 (the default threshold) were excluded, resulting in 7705 cells being retained. These cells were then assigned to optimal spots using map_cell_to_spot, and a spatial network was built through spatial_relation_all, with spatial_data_type = square, n_near_spot = 8 and dis_cut = 10. The calculate_cell_location function was run with radius = 0 to ascertain each cell’s exact location.

For CellTrek, we set repel_r = 1 and intp = F. For CytoSPACE, we implemented the lap_CSPR solver and set the interval between each adjacent spot as 6.2. Out of a total of 10,150 cells, CellTrek yielded 6247 cell locations for 2150 unique cells (79% of loss rate) and CytoSPACE provided 3017 cell locations for 3017 unique cells (70% of loss rate). The same procedure as outlined previously was applied to designate the nearest spot as the cell location for CellTrek and exclude duplicate cells. We compared the spatial expression patterns of 12 spatially specific genes derived from Lohoff et al. ²⁸ among different methods (Supplementary Fig. 3i), where Ttn and Popdc2 are the cardiomyocyte markers, Hand1 and Gata5 are expressed in heart and posterior lateral plate mesoderm, Six3, Lhx2, Otx2 and Pou3f1 are known brain markers, Sox2 is the neural tube marker, Foxf1 is the mesoderm marker, and Foxa1 and Cldn4 are gut endoderm markers. Furthermore, to eliminate bias in gene selection, we also compared the expression patterns of all genes and calculated the similarity between reconstructed and real data using RMSE, ERGAS, UQI, and SSIM.

High-resolution Xenium data processing

To utilize adjacent serial section from Xenium as ground truth, we followed the registration process to align the Xenium image data and coordinates with Visium data (https://github.com/10XGenomics/janesick_nature_comms_2023_companion) and extracted the common regions for comparison. Cell-type annotations were derived from GSE243275. For Xenium data, we filtered out unlabeled cells in the supervised annotations. For Visium data, spots with fewer than 250 genes were excluded, and the remaining 4982 spots were clustered into 8 spatial domains using HMRF.

Xenium data integrated with Visium data

After dividing the spatial domains, we trained an SVM classifier to predict the domain for each cell, using parameters cost = 8 and gamma = 0.5. Cells with a prediction probability lower than 0.8 were excluded. The functions map_cell_to_spot, spatial_relation_all, and calculate_cell_location were then applied to assign 93,923 cells to the optimal spots and calculate their exact locations, using the parameters spatial_data_type = honeycomb and radius = 0.5. CellTrek was run following its tutorial with default parameters, except for repel_r = 0.5 and intp = F. CytoSPACE used the lap_CSPR solver and set the geometry mode to honeycomb. Out of a total of 159,226 cells (excluding unlabeled cells), stromal cells accounted for 26.01%, CellTrek provided 41,541 cell locations for 23,215 unique cells (44% of repetition rate), while CytoSPACE provided 19,917 cell locations for 19,072 unique cells (4% of repetition rate). For the common region between Visium and Xenium hematoxylin and eosin (H&E) images, CMAP located 78,433 cells, with stromal cells accounting for 26.21%. CellTrek provided 33,711 cell locations for 19,797 unique cells, with stromal cells occupying 32.4%, while CytoSPACE provided 19,835 cell locations for 19,001 unique cells, with stromal cells accounting for 20.89%.

For classifier integration, we replaced the e1071::svm function with randomForest::randomForest() using default parameters to predict the spatial domains. For XGBoost, we utilized the R package caret and employed the xgbLinear method to train the classifier for spatial domain prediction.

scFFPE-seq data integrated with Visium data

The scFFPE-seq data, sourced from GSE243280, contained 27,460 cells, with stromal cells comprising 9.5%. To correct for the distortion in stromal cell ratio during single-cell capture, we repeated stromal cells to achieve a stromal cell ratio comparable to the Xenium data. The process applied to Xenium data was followed, replacing it with scFFPE-seq data and adjusting parameters cost = 128 and gamma = 0.125. For the common region of Visium and Xenium H&E images, CMAP located 20,146 cells, with stromal cells accounting for 21.3%. CellTrek provided 21,915 cell locations, with stromal cells comprising 20.58%, while CytoSPACE provided 19,917 cell locations, with stromal cells occupying 24.87%.

Evaluation of running time and computational resources

To evaluate the computational efficiency of CMAP, we conducted a comprehensive comparison of running time and memory usage across various mapping and deconvolution methods on benchmarked datasets. For each run, we allocated an equal number of CPU cores and provided uniform GPU settings. All computations were performed on a server with the following hardware configuration: Intel Xeon Gold 6342 CPU (2.80 GHz, 24 Cores), 1024GB of RAM, and an NVIDIA A100 GPU with 80GB memory. Since CIBERSORTx is accessed via its online portal, which does not provide memory usage information, we compared only the computational time for this method. Additionally, SONAR requires Matlab (R2019b) installed on a laptop, so this method was excluded for the memory usage comparison.

Mouse brain data

The single-cell and spatial datasets were from the tutorial of CellTrek (https://github.com/navinlabcode/CellTrek). This single-cell data was collected through layer-enriching dissections, which included either single or multiple layers. The layer of each cell was recorded, allowing us to calculate the mapping accuracy at the layer level. We first utilized HMRF to cluster the cortical data into 6 domains and trained a classifier model to predict the domain for each cell with parameters cost = 32 and gamma = 0.125. Cells with prediction probability less than 0.8 were filtered out. The map_cell_to_spot, spatial_relation_all and calculate_cell_location functions were then applied to assign 2798 cells to optimal spots and calculate their exact locations, with parameters spatial_data_type = honeycomb, n_near_spot = 7, dis_cut = 30, and radius = 1. CellTrek was executed following its tutorial with default parameters, except for intp = FALSE. CytoSPACE utilized the lap_CSPR solver and honeycomb geometry mode. Out of a total of 4785 cells, CellTrek produced 3251 cell locations for 1877 unique cells (42% of repetition rate) and CytoSPACE provided 4830 cell locations for 2590 unique cells (46% of repetition rate).

smFISH data

This data was downloaded from https://spacetx.github.io/data.html, which included the expression matrix (cell_by_gene.csv), cell locations and belonged layers (mapped_cell_table.csv)³². Cell type annotations were also obtained from SpaceTx (https://github.com/yunzhang813/SpaceTx-cell-type-calling/blob/master/FR-Match_results/smFISH_filtered_mapping_results.csv).

Mapping isolated proximal primitive streak cells to Geo-seq samples

To evaluate the performance of CMAP when mapping small or rare cell papulation to spatial locations, we utilized scRNA-seq data of 37 specific isolated cells from proximal primitive streak region of E7.0 mouse embryo, obtained from GSE171588 in the Gene Expression Omnibus (GEO) database. Complementarily, we accessed the corresponding E7.0 spatial Geo-seq data from GEO (GSE120963). First, we clustered the Geo-seq data into 7 spatial domains and used 500 spatial genes identified by HMRF to train the domain classifier with the following parameters: batch = FALSE, cost = 2048, and gamma = 3.0517578125e-05. Cells were then mapped to their optimal Geo-seq samples and their precise locations through map_cell_to_spot and calculate_cell_location functions, with parameters spatial_data_type = square, n_near_spot = 5, dis_cut = 1.3, and radius = 0.5. For comparative analysis, CellTrek was executed with default parameters, except for intp = FALSE and repel_r = 0.08. CytoSPACE was applied using the lap_CSPR solver and set the interval between each adjacent Geo-seq samples as 0.5.

Mouse embryo Slide-seq data

The Slide-seq data for mouse embryo was obtained from Kumar et al. ³⁵ (https://cellxgene.cziscience.com/collections/d74b6979-efba-47cd-990a-9d80ccf29055). We selected the E8.5_rep1: 201104_12 embryo section for analysis, which detected 27,651 genes across 8425 beads. Cell-type annotations were acquired from the annotated meta table (column: cell_state). Paired single-cell data was downloaded from GEO (GSE122187, WT_E8.5_1ab) and we extracted cells annotated with one of the 37 cell types (https://oc-molgen.gnz.mpg.de/owncloud/s/F8g3y5F79JZRyof). The spatial data was first classified into 16 domains, and an SVM model was trained to predict the domain for each cell with cost = 2 and gamma = 0.5. After filtering out cells with prediction probability less than 0.8, we ran map_cell_to_spot and calculate_cell_location to assign 13,183 cells to optimal Slide-seq samples and calculate the exact locations with the following parameters: spatial_data_type = singlecell_level, n_near_spot = 9, dis_cut = 20, and radius = 0.5. Given the single-cell resolution of Slide-seq data, CellTrek was executed with the parameters top_spot = 1, spot_n = 1, intp = FALSE, and repel_r = 0. CytoSPACE utilized the single-cell spatial approach with -sc and lap_CSPR solver. CellTrek predicted locations for 1904 unique cells, while CytoSPACE provided 8425 cell locations for 7788 unique cells.

Evaluation of reconstructed expression patterns on single-cell resolution spatial datasets

Due to the uncertainty and differences of predicted cell locations, the previous evaluation metrics based on spot-level are not suitable for single-cell resolution data to compare the reconstructed spatial gene expression patterns across different methods. Here, we utilized Moran’s I³⁷ to quantify the spatial autocorrelation of gene expression. The Moran’s I value ranges from −1 to 1. High positive values close to 1 signify a strong spatial pattern, while values near 0 suggest a random spatial distribution. Conversely, values approaching -1 indicate a chessboard-like pattern. Fairly, we used the SpaGCN³⁸ to identify spatially variable genes and calculate the Moran’s I on these genes.

Mapping endothelial cells to different organs

We downloaded the Visium data of S9 section from GEO (GSE237308) and extracted 397 spots of Domain 5, which was annotated as visceral organs. The paired E13.5 single-cell dataset was downloaded from Qiu et al.⁴⁴ (https://tome.gs.washington.edu), from which we retained 3691 cells annotated as ‘Endothelium’. Spatial data was clustered into 8 domains, and an SVM classifier was trained with cost = 2 and gamma = 0.125. After filtering out cells with a prediction probability less than 0.8 (4 cells mapped to the pancreas and gonad_sub domains were so few that they were filtered out together), we mapped 2389 cells to exact locations through map_cell_to_spot and calculate_cell_location functions. CellTrek was executed with the default parameters except for intp = FALSE and repel_r = 2. CytoSPACE was implemented with lap_CSPR solver and honeycomb geometry mode. Out of a total of 3691 cells, CellTrek provided 3308 cell locations for 1341 unique cells (59% of repetition rate), while CytoSPACE provided locations for 1802 unique cells.

Spatial heterogeneity analysis of endothelial cells

Based on the annotated spatial domains and the mapping between cells and spots, we translocated organ labels onto cells, thereby categorizing them into distinct organs. Subsequently, we used FindAllMarkers to identify organ-specific marker genes, with only.pos = TRUE and p_val_adj < 0.05. For visualization purposes, the top eight genes per organ were selected, ranked by adjusted P-value. This analysis was also executed on the mapping outcomes from CellTrek and CytoSPACE. To address the issue of cell duplication for CellTrek, we retained only one instance of the repeated cells that appeared multiple times within the same domain for marker identification.

Lung cancer data

The single-cell and spatial transcriptome data of lung cancer were downloaded from GEO (GSE200972 and GSE200916), specifically from patient 2 (TM_R_P2), focused on immune infiltration in the tumor tissue of the middle lobe (following the guidance of clinical experts), particularly the enrichment of T and B cells.

For scRNA-seq data, we conducted the following steps to filter the low-quality cells: (1) removed the cells with high mitochondrial read fractions (which fell within the range of P < 0.01, Benjamini–Hochberg-corrected) based on the median-centered median absolute deviation-variance normal distribution⁶⁴; (2) filtered out cells with fewer than 300 measured genes; (3) applied DoubletFinder (version 2.0.3)⁶⁵ to identify and remove the potential doublets with the 5% expected number of doublets. This left 8275 cells for downstream analysis. UMI counts were normalized and scaled using NormalizeData and ScaleData functions in Seurat⁶⁶. Two thousand highly variable genes (HVGs) were identified by FindVariableFeatures with the ‘vst’ methods. To avoid the effect of T and B cell receptor variable genes, all TRAV, TRBV, TRDV, TRGV, and IG[X]V related genes were removed from the highly variable gene list. Based on these HVGs, top 20 principal components were selected to construct the shared nearest neighbors graph, and Louvain clustering was applied to group cells into distinct clusters, which were subsequently annotated based on marker gene expression.

For spatial data, spots measuring fewer than 250 genes were filtered out, and the remaining 2455 spots were clustered into 3 spatial domains by HMRF. SVM classifier model was trained with cost = 32 and gamma = 0.125, after which cells with probability less than 0.8 were removed, leaving 5776 cells. Mapping and location calculation were performed similarly to the mouse brain data. For CellTrek, we set repel_r = 1 and intp = F. For CytoSPACE, we implemented the lap_CSPR solver and geometry mode as honeycomb. Out of a total of 8275 cells, CellTrek provided 12,860 cell locations for 4490 unique cells (65% of repetition rate) and CytoSPACE provided 11,057 cell locations for 7816 unique cells (29% of repetition rate).

Calculation of gene set activity score

The Tertiary Lymphoid Structure (TLS) score was calculated based on a 9-gene signature (CD79B, EIF1AY, PTGDS, RBP5, SKAP1, LAT, CETP, CD1D, CCR6)⁵⁰ using AddModuleScore⁶⁷ function from Seurat. In brief, the signature score for each spot or cell was determined as the average expression of gene sets, offset by the aggregated expression of randomly selected control feature sets.

T cell-B cell interaction analysis

To evaluate cell-cell interactions in lung cancer, we utilized CellChat (version 2.1.2)^68,69 to infer and visualize the intercellular communications based on the gene expression of known ligand and receptor pairs. Concentrating on the interactions between T and B cells, we adhere to CellChat’s single dataset analysis tutorial, executing the analysis with default parameters to uncover the intricate dialogue occurring within the TME.

Reconstruction of immune repertoires from scRNA-seq and spatial transcriptomics data

We used the package TRUST4⁷⁰, a tool designed to reconstruct the immune repertoires in T cells and B cells based on scRNA-seq and bulk RNA-seq data. Given that TRUST4 does not inherently support spatial data, we devised a strategy to transform the ST dataset into a format compatible with TRUST4’s requirements. We initiated the workflow by partitioning the sequencing library into discrete sub-libraries, each corresponding to a single spot. This was achieved using “spaceranger count” function from Space Ranger (v2.1.1 from 10x Genomics), with the human genome GRCh38 as the reference. From the output, we selectively extracted the BAM files and segregated them based on unique barcodes. Subsequently, we sorted the BAM files using samtools⁷¹ and employed subset-bam tool (v1.1.0 from 10x Genomics) to generate individual BAM files, each containing data from a single spot. These single-spot BAM files were then fed into TRUST4. Upon generating multiple report files from TRUST4, we appended a barcode column to each file, merged them into one report file, and filtered out rows containing out_of_frame (indicative of non-productive CDR3 sequences). For scRNA-seq data, the samples were processed directly using TRUST4 with default parameters.

Quantifying the spatial specificity of gene expression

Motivated by the foundational role of entropy in measuring distributional heterogeneity^72,73, we introduced the concept of spatial entropy to evaluate the spatial specificity of gene expression patterns (SSGE) at the whole gene levels. Initially, we generated a binary vector ${{{\bf{M}}}}$ representing a predefined spatial pattern, where ${{{{\bf{M}}}}}_{i}=1$ indicated that the $i-{th}$ spot belonged to interested domain, otherwise ${{{{\bf{M}}}}}_{i}=0$. This vector was normalized so that ${\sum }_{i=1}^{n}{{{{\bf{M}}}}}_{i}=1$, where $n$ was the total number of spots. Given the prevalence of zeros and dropout events inherent to 10x Visium data, we employed a smoothing process on gene expression of spots under the assumption that physically proximate spots exhibit similar or gradient gene expression profiles:

$$S={W}_{{ij}}\times X,$$

(18)

$${W}_{{ij}}={e}^{-\frac{{{A}_{{ij}}}^{2}}{2{\sigma }^{2}}}\left(\sigma=0.5\right),$$

(19)

where $S$ is the smoothed expression matrix and $X$ is the original expression matrix. ${W}_{{ij}}$ is the weight matrix constructed using a Gaussian kernel function based on the Euclidean distance matrix ${A}_{{ij}}$, indicating the influence of the $i-{th}$ spot on the $j-{th}$ spot. Following the normalization of the smoothed matrix $S$ with ${\sum }_{i=1}^{n}{S}_{{ig}}=1$ per gene $g$, we applied the Jensen-Shannon Divergence (JSD), a measure of dissimilarity between two probability distributions, defined as

$${{{\rm{JSD}}}}({{{\bf{M}}}},{S}_{g})={{{\rm{H}}}}\left(\frac{{{{\bf{M}}}}+{S}_{g}}{2}\right)-\frac{{{{\rm{H}}}}({{{\bf{M}}}})+{{{\rm{H}}}}({S}_{g})}{2},$$

(20)

where ${{{\rm{H}}}}\left({{{\bf{M}}}}\right)=-{\sum }_{i=1}^{n}{{{{\bf{M}}}}}_{i}\log ({{{{\bf{M}}}}}_{i})$ represents the Shannon entropy of a distribution ${{{\bf{M}}}}$. Finally, we defined the spatial specificity of gene expression (SSGE) for gene $g$ by transforming JSD into a similarity score:

$${{{\rm{SSGE}}}}({{{\bf{M}}}},{S}_{g})=1-{{{\rm{JSD}}}}({{{\bf{M}}}},{S}_{g}).$$

(21)

For each predefined spatial pattern, genes with the highest SSGE values were identified as the most spatially specific.

Cell type co-localization analysis

With the predicted spatial locations of each cell, we defined two cells as being in contact or proximity if they were within 10 µm of each other, a distance comparable to the soma size of the cells. For each cell-type pair, we initially counted the number of cell pairs that were in contact or proximity and compared this with a null distribution, generated by randomly shifting cell locations within a 100 µm radius from their original positions. We then performed 1000 rounds of randomization to obtain the fold change between the observed contact or proximity frequency and the mean expected frequency from these permutations. By calculating the z-score for the observed contact or proximity frequencies against the null distribution, we determined the P-value to assess the significance of contact or proximity frequency between each cell-type pair. The P-values were subsequently adjusted using the Benjamini–Hochberg (BH) method. We considered cell-type pairs with an adjusted P-value less than 0.05 and a frequency greater than 50 as colocalization pairs⁴⁹.

To establish a comparative standard, we initially used each cell-type gene set to calculate the signature scores in the Visium data by AddModuleScore⁶⁷. Based on these cell-type-specific expression scores, we then applied the ${{{\rm{JSD}}}}$ to measure the spatial similarities ($1-{{{\rm{JSD}}}}$) between each cell-type pair. We ranked these pairs according to their similarities to determine the colocalization rank for each pair.

Subcluster analysis of immune cells

We extracted immune cells from the annotated single-cell data for subcluster analysis. To accurately identify cell features, we performed unsupervised analysis by mapping these immune cells to previously annotated CITE-seq reference datasets using Seurat. CD4⁺ T cells, CD8⁺ T cells, monocytes and dendritic cells were selected based on a prediction score greater than 0.6. These cells were subsequently used for sub-clustering analysis. To calculate the communication probabilities between interacting cell groups, we employed the CellChat package and applied the computeCommunProb() function with the parameters type = “truncatedMean” and trim = 0.1.

Embryo collection and hybridization preparation

Wild-type embryos at embryonic day E13.5 were harvested from C57BL/6JGpt mice aged between 8 and 12 weeks, procured from China GemPharmatech. Embryos images were taken for recording and confirmation of developmental stages.

Collected embryos of C57BL/6JGpt mice were embedded in Tissue freezing medium (Leica Microsystems, cat.no.020108926) and stored at −80 °C. Section 9 (S9) of the whole embryo was cryo-sectioned (Leica CM3050S) along craniocaudal axis at 10 μm as previously reported⁴⁰.

Sex identification of embryos

To ensure consistency with the spatial data, particularly for the gonadal region (S9 sampled from a male mouse), we determined the sex of collected embryos. This was achieved by analyzing the umbilical cord for Sry and IL3 gene expression using PCR, followed by gel electrophoresis imaging. An E13.5 male embryo was then selected for further analyses, including fluorescence in situ hybridization (FISH).

RNA in situ hybridization

Validation experiments were carried out using RNA in situ hybridization on fresh-frozen sections (10 μm thick) of E13.5 C57BL/6J mice. The sections were prepared using a Leica CM3050S cryostat maintained at −18 °C. The PinpoRNA^TM double-channel Fluorescent Reagent Kit (Pinpo PIF2000) was employed with a suite of probes targeting Pecam1 (Pinpo 186131-B1), Ctsl (Pinpo 130391-B2), Dut (Pinpo 1100741-B2), Galnt18 (Pinpo 2337331-B2), Negative Control Probe (Pinpo P0005), and Positive Control Probe (Pinpo P0002), according to the manufacturer’s instructions. High-resolution images were acquired at magnifications of 20×, 40×, and 100× using an Olympus FV3000 microscope.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

This study made use of publicly available datasets. MOB data are available from https://github.com/YMa-lab/CARD-Analysis/tree/master/simulations. Mouse embryo seqFISH data are available from https://content.cruk.cam.ac.uk/jmlab/SpatialMouseAtlas2020/. High-resolution Xenium data are available from https://www.10xgenomics.com/products/xenium-in-situ/preview-dataset-human-breast (In Situ Sample 1, Replicate 1, FRP and Visium Spatial Files). Mouse brain ST data are available from https://www.10xgenomics.com/datasets/mouse-brain-serial-section-1-sagittal-anterior-1-standard-1-0-0. Slide-seq data are available from https://cellxgene.cziscience.com/collections/d74b6979-efba-47cd-990a-9d80ccf29055. Endothelium single-cell data are available from https://tome.gs.washington.edu/. All other data used in this study are available in the Gene Expression Omnibus (GEO) database under accession codes: GSE115746, GSE171588, GSE120963, GSE122187, GSE237308, GSE200972 and GSE200916. Source data are provided with this paper.

Code availability

The CMAP software toolkit is available at GitHub: https://github.com/SuoLab-GZLab/CMAP⁷⁴, and is also archived at Zenodo: https://zenodo.org/records/15645346.

References

Ståhl, P. L. et al. Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science 353, 78–82 (2016).
Article ADS PubMed Google Scholar
Chen, J. et al. Spatial transcriptomic analysis of cryosectioned tissue samples with Geo-seq. Nat. Protoc. 12, 566–580 (2017).
Article CAS PubMed Google Scholar
Eng, C.-H. L. et al. Transcriptome-scale super-resolved imaging in tissues by RNA seqFISH+. Nature 568, 235–239 (2019).
Article ADS CAS PubMed PubMed Central Google Scholar
Rodriques, S. G. et al. Slide-seq: a scalable technology for measuring genome-wide expression at high spatial resolution. Science 363, 1463–1467 (2019).
Article ADS CAS PubMed PubMed Central Google Scholar
Chen, A. et al. Spatiotemporal transcriptomic atlas of mouse organogenesis using DNA nanoball-patterned arrays. Cell 185, 1777–1792.e21 (2022).
Article CAS PubMed Google Scholar
Janesick, A. et al. High resolution mapping of the tumor microenvironment using integrated single-cell, spatial and in situ analysis. Nat. Commun. 14, 8353 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Wei, R. et al. Spatial charting of single-cell transcriptomes in tissues. Nat. Biotechnol. 40, 1190–1199 (2022).
Article CAS PubMed PubMed Central Google Scholar
Vahid, M. R. et al. High-resolution alignment of single-cell and spatial transcriptomes with CytoSPACE. Nat. Biotechnol. 41, 1543–1548 (2023).
Article CAS PubMed PubMed Central Google Scholar
Zhu, Q., Shah, S., Dries, R., Cai, L. & Yuan, G.-C. Identification of spatially associated subpopulations by combining scRNAseq and sequential fluorescence in situ hybridization data. Nat. Biotechnol. 36, 1183–1190 (2018).
Article CAS Google Scholar
Rousseeuw, P. J. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 20, 53–65 (1987).
Article MATH Google Scholar
Chang, C.-C. & Lin, C.-J. LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2, 1–27 (2011).
Article Google Scholar
Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 600–612 (2004).
Article ADS PubMed Google Scholar
Ma, Y. & Zhou, X. Spatially informed cell-type deconvolution for spatial transcriptomics. Nat. Biotechnol. 40, 1349–1359 (2022).
Article CAS PubMed Google Scholar
Moncada, R. et al. Integrating microarray-based spatial transcriptomics and single-cell RNA-seq reveals tissue architecture in pancreatic ductal adenocarcinomas. Nat. Biotechnol. 38, 333–342 (2020).
Article CAS PubMed Google Scholar
Kleshchevnikov, V. et al. Cell2location maps fine-grained cell types in spatial transcriptomics. Nat. Biotechnol. 40, 661–671 (2020).
Article Google Scholar
Newman, A. M. et al. Determining cell type abundance and expression from bulk tissues with digital cytometry. Nat. Biotechnol. 37, 773–782 (2019).
Article CAS PubMed PubMed Central Google Scholar
Lopez, R. et al. DestVI identifies continuums of cell types in spatial transcriptomics data. Nat. Biotechnol. 40, 1360–1369 (2022).
Article CAS PubMed PubMed Central Google Scholar
Long, Y. et al. Spatially informed clustering, integration, and deconvolution of spatial transcriptomics with GraphST. Nat. Commun. 14, 1155 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Cable, D. M. et al. Robust decomposition of cell type mixtures in spatial transcriptomics. Nat. Biotechnol. 40, 517–526 (2022).
Article CAS PubMed Google Scholar
Zhou, Z., Zhong, Y., Zhang, Z. & Ren, X. Spatial transcriptomics deconvolution at single-cell resolution using Redeconve. Nat. Commun. 14, 7930 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Stuart, T. et al. Comprehensive integration of single-cell data. Cell 177, 1888–1902.e21 (2019).
Article CAS PubMed PubMed Central Google Scholar
Liu, Z., Wu, D., Zhai, W. & Ma, L. SONAR enables cell type deconvolution with spatially weighted Poisson-Gamma model for spatial transcriptomics. Nat. Commun. 14, 4727 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Lu, Y., Chen, Q. M. & An, L. SPADE: spatial deconvolution for domain specific cell-type estimation. Commun. Biol. 7, 469 (2024).
Article PubMed PubMed Central Google Scholar
Dong, R. & Yuan, G.-C. SpatialDWLS: accurate deconvolution of spatial transcriptomic data. Genome Biol. 22, 145 (2021).
Article PubMed PubMed Central Google Scholar
Elosua-Bayes, M., Nieto, P., Mereu, E., Gut, I. & Heyn, H. SPOTlight: seeded NMF regression to deconvolute spatial transcriptomics spots with single-cell transcriptomes. Nucleic Acids Res. 49, e50–e50 (2021).
Article CAS PubMed PubMed Central Google Scholar
Wald, L. Quality of high resolution synthesized images: Is there a simple criterion? In: Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images, Sophia Antipolis, France, Edited by Ranchin, T. & Wald, L. pp. 99–103 (SEE/URISCA, Nice, France, 2000).
Wang, Z. & Bovik, A. C. A universal image quality index. IEEE Signal Process. Lett. 9, 81–84 (2002).
Article ADS CAS Google Scholar
Lohoff, T. et al. Integration of spatial and single-cell transcriptomic data elucidates mouse organogenesis. Nat. Biotechnol. 40, 74–85 (2022).
Article CAS PubMed Google Scholar
Krishnapuram, B. et al. XGBoost: a scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference Knowledge Discovery and Data Mining 785–794 https://doi.org/10.1145/2939672.2939785 (2016).
Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).
Article Google Scholar
Tasic, B. et al. Shared and distinct transcriptomic cell types across neocortical areas. Nature 563, 72–78 (2018).
Article ADS CAS PubMed PubMed Central Google Scholar
Zhang, Y. et al. Reference-based cell type matching of in situ image-based spatial transcriptomics data on primary visual cortex of mouse brain. Sci. Rep. 13, 9567 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Wang, R. et al. Time space and single-cell resolved tissue lineage trajectories and laterality of body plan at gastrulation. Nat. Commun. 14, 5675 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Peng, G. et al. Molecular architecture of lineage allocation and tissue organization in early mouse embryo. Nature 572, 528–532 (2019).
Article ADS CAS PubMed Google Scholar
Kumar, A. S. et al. Spatiotemporal transcriptomic maps of whole mouse embryos at the onset of organogenesis. Nat. Genet. 55, 1176–1185 (2023).
Article Google Scholar
Grosswendt, S. et al. Epigenetic regulator function through mouse gastrulation. Nature 584, 102–108 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Li, H., Calder, C. A. & Cressie, N. Beyond Moran’s I: testing for spatial dependence based on the spatial autoregressive model. Geogr. Anal. 39, 357–375 (2007).
Article Google Scholar
Hu, J. et al. SpaGCN: integrating gene expression, spatial location and histology to identify spatial domains and spatially variable genes by graph convolutional network. Nat. Methods 18, 1342–1351 (2021).
Article PubMed Google Scholar
Cao, J. et al. The single-cell transcriptional landscape of mammalian organogenesis. Nature 566, 496–502 (2019).
Article ADS CAS PubMed PubMed Central Google Scholar
Qu, F. et al. Three-dimensional molecular architecture of mouse organogenesis. Nat. Commun. 14, 4599 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Kalucka, J. et al. Single-cell transcriptome atlas of murine endothelial cells. Cell 180, 764–779.e20 (2020).
Article CAS PubMed Google Scholar
Paik, D. T. et al. Single-cell RNA sequencing unveils unique transcriptomic signatures of organ-specific endothelial cells. Circulation 142, 1848–1862 (2020).
Article CAS PubMed PubMed Central Google Scholar
Chen, J. et al. Molecular and spatial signatures of mouse embryonic endothelial cells at single-cell resolution. Circ. Res. 134, 529–546 (2024).
Article CAS PubMed PubMed Central Google Scholar
Qiu, C. et al. Systematic reconstruction of cellular trajectories across mouse embryogenesis. Nat. Genet. 54, 328–341 (2022).
Article CAS PubMed PubMed Central Google Scholar
Aird, W. C. Phenotypic heterogeneity of the endothelium: II. Representative vascular beds. Circ. Res. 100, 174–190 (2007).
Article CAS PubMed Google Scholar
Augustin, H. G. & Koh, G. Y. Organotypic vasculature: from descriptive heterogeneity to functional pathophysiology. Science 357, eaal2379 (2017).
Article PubMed Google Scholar
Daniel, E. et al. Spatiotemporal heterogeneity and patterning of developing renal blood vessels. Angiogenesis 21, 617–634 (2018).
Article PubMed PubMed Central Google Scholar
Wang, Y. et al. Multidirectional characterization of cellular composition and spatial architecture in human multiple primary lung cancers. Cell Death Dis. 14, 462 (2023).
Article CAS PubMed PubMed Central Google Scholar
Zhang, M. et al. Molecularly defined and spatially resolved cell atlas of the whole mouse brain. Nature 624, 343–354 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Cabrita, R. et al. Tertiary lymphoid structures improve immunotherapy and survival in melanoma. Nature 577, 561–565 (2020).
Article ADS CAS PubMed Google Scholar
Liu, W. et al. An immune cell map of human lung adenocarcinoma development reveals an anti-tumoral role of the Tfh-dependent tertiary lymphoid structure. Cell Rep. Med. 5, 101448 (2024).
Article CAS PubMed PubMed Central Google Scholar
Garside, P. et al. Visualization of specific B and T lymphocyte interactions in the lymph node. Science 281, 96–99 (1998).
Article ADS CAS PubMed Google Scholar
Chen, L. & Flies, D. B. Molecular mechanisms of T cell co-stimulation and co-inhibition. Nat. Rev. Immunol. 13, 227–242 (2013).
Article PubMed PubMed Central Google Scholar
Ward-Kavanagh, L. K., Lin, W. W., Šedý, J. R. & Ware, C. F. The TNF receptor superfamily in co-stimulating and co-inhibitory responses. Immunity 44, 1005–1019 (2016).
Article CAS PubMed PubMed Central Google Scholar
Hendriks, J. et al. CD27 is required for generation and long-term maintenance of T cell immunity. Nat. Immunol. 1, 433–440 (2000).
Article CAS PubMed Google Scholar
Arens, R. et al. Constitutive CD27/CD70 interaction induces expansion of effector-type T cells and results in IFNγ-mediated B cell depletion. Immunity 15, 801–812 (2001).
Article CAS PubMed Google Scholar
Chaurio, R. A. et al. TGF-β-mediated silencing of genomic organizer SATB1 promotes Tfh cell differentiation and formation of intra-tumoral tertiary lymphoid structures. Immunity 55, 115–128.e9 (2022).
Article CAS PubMed PubMed Central Google Scholar
Choi, Y. S. et al. ICOS receptor instructs T follicular helper cell versus effector cell differentiation via induction of the transcriptional repressor Bcl6. Immunity 34, 932–946 (2011).
Article CAS PubMed PubMed Central Google Scholar
Mintz, M. A. & Cyster, J. G. T follicular helper cells in germinal center B cell selection and lymphomagenesis. Immunol. Rev. 296, 48–61 (2020).
Article CAS PubMed PubMed Central Google Scholar
Wagner, G. P., Kin, K. & Lynch, V. J. Measurement of mRNA abundance using RNA-seq data: RPKM measure is inconsistent among samples. Theory Biosci 131, 281–285 (2012).
Article CAS PubMed Google Scholar
Lun, A. T. L., McCarthy, D. J. & Marioni, J. C. A step-by-step workflow for low-level analysis of single-cell RNA-seq data with bioconductor. F1000Research 5, 2122 (2016).
PubMed PubMed Central Google Scholar
Korsunsky, I. et al. Fast, sensitive and accurate integration of single-cell data with harmony. Nat. Methods 16, 1289–1296 (2019).
Article CAS PubMed PubMed Central Google Scholar
Dozat, T. Incorporating Nesterov Momentum into Adam. In: Proceedings of the 4th International Conference on Learning Representations (ICLR 2016), pp. 1–4 (Workshop Track, San Juan, Puerto Rico, 2016).
Pijuan-Sala, B. et al. A single-cell molecular map of mouse gastrulation and early organogenesis. Nature 566, 490–495 (2019).
Article ADS CAS PubMed PubMed Central Google Scholar
McGinnis, C. S., Murrow, L. M. & Gartner, Z. J. DoubletFinder: doublet detection in single-cell RNA sequencing data using artificial nearest neighbors. Cell Syst. 8, 329–337.e4 (2019).
Article CAS PubMed PubMed Central Google Scholar
Hao, Y. et al. Integrated analysis of multimodal single-cell data. Cell 184, 3573–3587.e29 (2021).
Article CAS PubMed PubMed Central Google Scholar
Tirosh, I. et al. Dissecting the multicellular ecosystem of metastatic melanoma by single-cell RNA-seq. Science 352, 189–196 (2016).
Article ADS CAS PubMed PubMed Central Google Scholar
Jin, S. et al. Inference and analysis of cell-cell communication using CellChat. Nat. Commun. 12, 1088 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Jin, S., Plikus, M. V. & Nie, Q. CellChat for systematic analysis of cell–cell communication from single-cell transcriptomics. Nat. Protoc. 20, 180–219 (2025).
Song, L. et al. TRUST4: immune repertoire reconstruction from bulk and single-cell RNA-seq data. Nat. Methods 18, 627–630 (2021).
Article CAS PubMed PubMed Central Google Scholar
Danecek, P. et al. Twelve years of SAMtools and BCFtools. GigaScience 10, giab008 (2020).
Article Google Scholar
Cabili, M. N. et al. Integrative annotation of human large intergenic noncoding RNAs reveals global properties and specific subclasses. Genes Dev. 25, 1915–1927 (2011).
Article CAS PubMed PubMed Central Google Scholar
Suo, S. et al. Revealing the critical regulators of cell identity in the mouse cell atlas. Cell Rep. 25, 1436–1445.e3 (2018).
Article CAS PubMed PubMed Central Google Scholar
Ke, J. High-resolution mapping of single cells in spatial context. SuoLab-GZLab/CMAP. https://doi.org/10.5281/zenodo.15645346 (2025).
Aibar, S. et al. SCENIC: single-cell regulatory network inference and clustering. Nat. Methods 14, 1083–1086 (2017).
Article CAS PubMed PubMed Central Google Scholar

Download references

Acknowledgements

We thank Dr. XianFa Yang from Guangzhou National Laboratory and Dr. Zisheng Chen from Qingyuan People’s Hospital for helpful advice about this study. This work was supported in part by Major Project of Guangzhou National Laboratory (GZNL2023A02007 to S.S., GZNL2023A03005 to G.P. and S.S.), National Key R&D Program of China (2024YFF0509000 to S.S., 2024YFC3405600 to G.P.), National Natural Science Foundation of China (32370972 to S.S, 32270854, 32161160322 to G.P.), Guangdong Basic and Applied Basic Research Foundation (2024B1515020052, 2023A1515011783 to S.S., 2024B1515040020, 2019B151502054 to G.P.), Science and Technology Planning Project of Guangdong Province (2023B1212060050, 2023B1212120009 to G.P.), the Union Project from Guangzhou National Laboratory and State Key Laboratory of Respiratory Disease, Guangzhou Medical University (GZNL2024B01004 to S.S.), Basic Research Project of Guangzhou Institutes of Biomedicine and Health, Chinese Academy of Sciences (GIBHBRP23-01 to G.P.).

Author information

Authors and Affiliations

Center for Cell Lineage Technology and Engineering, Guangdong Provincial Key Laboratory of Stem Cell and Regenerative Medicine, Guangdong-Hong Kong Joint Laboratory for Stem Cell and Regenerative Medicine, Guangzhou Institutes of Biomedicine and Health, Chinese Academy of Sciences, Guangzhou, China
Jincan Ke, Chenkai Guo & Guangdun Peng
University of Chinese Academy of Sciences, Beijing, China
Jincan Ke, Chenkai Guo & Guangdun Peng
Guangzhou National Laboratory, Guangzhou, China
Jian Xu, Jia Liu, Yumeng Yang, Bingbing Xie, Guizhong Cui & Shengbao Suo
School of Basic Medical Sciences, Guangzhou Medical University, Guangzhou, China
Jian Xu & Guizhong Cui
State Key Laboratory of Respiratory Disease, The First Affiliated Hospital of Guangzhou Medical University, Guangzhou, China
Shengbao Suo

Authors

Jincan Ke
View author publications
Search author on:PubMed Google Scholar
Jian Xu
View author publications
Search author on:PubMed Google Scholar
Jia Liu
View author publications
Search author on:PubMed Google Scholar
Yumeng Yang
View author publications
Search author on:PubMed Google Scholar
Chenkai Guo
View author publications
Search author on:PubMed Google Scholar
Bingbing Xie
View author publications
Search author on:PubMed Google Scholar
Guizhong Cui
View author publications
Search author on:PubMed Google Scholar
Guangdun Peng
View author publications
Search author on:PubMed Google Scholar
Shengbao Suo
View author publications
Search author on:PubMed Google Scholar

Contributions

S.S., G.P., and J.K. conceived the study. S.S. and G.P. supervised the project. J.K. designed and implemented the computational framework and conducted the analysis with guidance from S.S. and G.P. J.X. performed the experiments. J.L. conducted the BCR and TCR analysis. Y.Y. and C.G. assisted with the benchmarking. B.X. and G.C. provided important reagents and suggestions. S.S., J.K., and G.P. wrote the manuscript with the help of others.

Corresponding authors

Correspondence to Guangdun Peng or Shengbao Suo.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Can Yang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Reporting Summary

Description of Additional Supplementary Files

Supplementary Data 1

Supplementary Data 2

Supplementary Data 3

Supplementary Data 4

Supplementary Data 5

Supplementary Data 6

Supplementary Data 7

Supplementary Data 8

Supplementary Data 9

Supplementary Data 10

Transparent Peer Review file

Source data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Ke, J., Xu, J., Liu, J. et al. High-resolution mapping of single cells in spatial context. Nat Commun 16, 6533 (2025). https://doi.org/10.1038/s41467-025-61667-4

Download citation

Received: 29 August 2024
Accepted: 27 June 2025
Published: 15 July 2025
Version of record: 15 July 2025
DOI: https://doi.org/10.1038/s41467-025-61667-4