Tonic dopamine and biases in value learning linked through a biologically inspired reinforcement learning model

Abstract

A hallmark of various psychiatric disorders is biased future predictions. Here we examined the mechanisms for biased value learning using reinforcement learning models incorporating recent findings on synaptic plasticity and opponent circuit mechanisms in the basal ganglia. We show that variations in tonic dopamine can alter the balance between learning from positive and negative reward prediction errors, leading to biased value predictions. This bias arises from the sigmoidal shapes of the dose-occupancy curves and distinct affinities of D1- and D2-type dopamine receptors: changes in tonic dopamine differentially alters the slope of the dose-occupancy curves of these receptors, thus sensitivities, at baseline dopamine concentrations. We show that this mechanism can explain biased value learning in both mice and humans and may also contribute to symptoms observed in psychiatric disorders. Our model provides a foundation for understanding the basal ganglia circuit and underscores the significance of tonic dopamine in modulating learning processes.

Introduction

Our ability to predict future outcomes is crucial in selecting and motivating appropriate actions. Systematic biases in future predictions, however, can lead to maladaptive behaviors, such as those observed in patients with various psychiatric disorders^1,2,3,4. For example, overly negative or pessimistic predictions can contribute to major depression^1,5, whereas excessively positive or optimistic predictions may be associated with pathological gambling, addiction, and mania^3,4,6,7,8. Despite the importance of understanding the causes of biased future predictions, the biological mechanisms underlying them remain poorly understood.

Our future expectations and decisions are shaped by associative learning of positive and negative outcomes. A key idea in associative learning is that learning is driven by prediction errors^9,10. The process of value learning has been modeled using reinforcement learning (RL) models^11,12,13,14, where value predictions are updated based on reward prediction errors (RPEs), that is the discrepancy between received and expected outcomes. In addition to its role in learning, recent studies have indicated the importance of RPEs in mood; these studies have suggested that mood depends not on the absolute goodness of outcomes, but rather on the recent history of RPEs^15,16.

In the brain, dopamine is thought to be a key regulator of learning from positive and negative RPEs. The dynamics of dopamine are often categorized into two modes: tonic and phasic. Tonic dopamine refers to baseline dopamine that operates on a long timescale, such as tens of seconds or minutes, while phasic activity refers to transient changes that occur at a much shorter, sub-second timescale, often triggered by external stimuli^17,18,19,20. A significant body of evidence has shown that phasic responses of dopamine neurons convey RPEs and drive learning of values and actions^19,20,21,22. On the other hand, changes in tonic dopamine might also modulate value learning, yet whether and how the level of tonic dopamine modulates learning remains poorly understood.

Previous studies have reported that patients with psychiatric disorders exhibit biased learning from positive versus negative outcomes. For one, some studies have shown that patients with major depression have a reduced sensitivity in learning from rewarding events, while their ability to learn from negative events remains relatively intact^1,5,23. Similarly, patients with Parkinson’s disease are better at learning from negative than positive outcomes^24,25. Analysis of these patients using RL models has suggested that biases in learning can be explained by alterations in specific parameters in RL models, such as the learning rate parameters or the sensitivity to positive and negative outcomes. For example, some studies have suggested that anhedonia in major depressive disorder may correspond to a reduced learning rate from positive compared to negative outcomes¹.

Mechanistically, some of these changes in RL parameters can be linked to altered functions of dopamine. First, it has been shown that dopamine synthesis capacity, an approximate indicator of baseline dopamine levels, in the striatum, as measured using positron emission tomography (PET), correlates with learning rate parameters²⁶. Second, dopamine medications can change the balance between learning from positive and negative outcomes^24,26,27. Third, responses to positive outcomes in the nucleus accumbens (NAc), as measured based on blood oxygenation-dependent (BOLD) signals, are reduced in patients with psychiatric disorders such as depression^28,29,30,31. These observations point to important roles of reinforcement learning processes and dopamine in regulating value learning. However, the parameters in RL models remain an abstract entity, and the biological processes underlying changes in these parameters are still largely unknown.

One limitation in most RL models used in previous studies is that they do not reflect key neural circuit architectures in the brain (but see refs. ^32,33,34) nor recent findings on intracellular signaling and plasticity rules that can constrain how dopamine functions in biological circuits^35,36,37. Incorporating these key biological factors may lead to a better understanding of how changes in RL parameters may arise in psychiatric disorders. Furthermore, recent studies have found that the activity of dopamine neurons is consistent with a novel RL algorithm called distributional RL^38,39,40. Distributional RL takes into account the diversity in dopamine signals, and a population of dopamine neurons together encodes the entire distribution of rewards, not just the average. Although distributional RL has shown to be efficient in solving various RL problems in artificial intelligence^39,41, how distributional RL can be implemented in biological neural circuits and how distributional RL relates to biased value learning remain to be examined.

In this study, we sought to identify potential biological processes that cause biased value predictions using biologically inspired RL models. To this goal, we first construct an RL model that incorporates the basic circuit architecture in the brain³⁴. We then sought to identify possible biological mechanisms that modulate key parameters in the model, such as learning rate parameters for learning from positive and negative outcomes. Inspired by recent biological findings, such as intracellular signaling and synaptic plasticity rules^36,37, we propose a new model in which learning rate parameters are modulated by the tonic dopamine level (Mechanism 1). We will then show that this new model can explain our previous results in mice, which exhibited optimistic biases in value learning⁴². We also show that the key results in this data cannot be explained by a model in which biased value learning arises from asymmetric scaling of phasic dopamine responses. Finally, we will show how our model can provide an account of how biases in value predictions arise in psychiatric disorders.

Results

Basic reinforcement learning algorithms

We first formulate basic RL algorithms that will become the basis of our later models. Our primary focus lies in the simplest, yet fundamental problem in RL and animal behavior: value prediction. The goal of an agent is to predict the expected sum of discounted future rewards starting from a given state $({s}_{t})$, the quantity known as value¹³. To consider timing within each trial, we will use a temporal difference (TD) learning algorithm, instead of Rescorla-Wagner model¹⁰, which is trial-based. Previous studies have provided evidence that dopamine signals approximate a form of RPE signal in TD learning, called TD errors^19,43,44. A TD error (${\delta }_{t}$) is defined by:

$${\delta }_{t}={r}_{t}+{\gamma \cdot \hat{V}}({s}_{t+1})-\hat{V}({s}_{t})$$

(1)

where ${r}_{t}$ is the reward received at time $t$, ${s}_{t}$ is the state the agent occupies at time $t,$ and $\gamma$ is a discounting factor ($0 < \gamma \le 1$). In the above equation, $\hat{V}({s}_{t})$ is the value estimated at state ${s}_{t}$ (the hat ^ indicates that it is an estimate). When there is no reward, a TD error reflects the change in values between consecutive time points (from $t$ to $t+1$).

To improve the accuracy of the value prediction, TD errors are utilized to update the value estimate. This is done iteratively by adding a fraction ($\alpha$) of $\delta$ (Eq. 2) where $\alpha$ defines the learning rate.

$$\hat{V}\left({s}_{t}\right)\leftarrow \hat{V}({s}_{t})+\alpha \cdot{\delta }_{t}$$

(2)

The value $V$ learned through this algorithm (Eqs. 1 and 2) converges on the expectation of discounted future rewards.

Risk-sensitive RL

The goal of this work is to explain how animals and humans can develop biases in value predictions using RL models. A natural way this can occur is by allowing learning rates for positive and negative RPEs (denoted by ${\alpha }^{+},{\alpha }^{-}$) to differ asymmetrically. This idea dates back to behavioral studies of learning⁴⁵ and was formalized in the framework called risk-sensitive RL⁴⁶.

$$\hat{V}({s}_{t})\leftarrow \hat{V}({s}_{t})+{\alpha }^{+}\cdot {\delta }_{t}\,...\,{{{\rm{if}}}}\,{\delta }_{t} > 0$$

(3)

$$\hat{V}({s}_{t})\leftarrow \hat{V}({s}_{t})+{\alpha }^{-}\cdot {\delta }_{t}\,...\,{{{\rm{if}}}}\,{\delta }_{t} < 0$$

In the presence of stochastic rewards, the value learned through this algorithm (Eqs. 1 and 3) does not converge on the expectation of the reward distribution, but instead on a value higher or lower than the expectation, depending on the relative magnitude of the learning rates ${\alpha }^{+}$ and ${\alpha }^{-}$. This algorithm, therefore, develops optimistic or pessimistic value predictions, respectively. This learning algorithm is called risk-sensitive because values of probabilistic (risky) rewards are biased compared to deterministic (certain) rewards, and, therefore, the agent develops a preference between risky and certain rewards even when the expected values are the same (Fig. 1b).

Fig. 1: Reinforcement learning models.

a Traditional reinforcement learning with a single learning rate ($\alpha$) for both positive and negative RPEs ($\delta$) for the value updates (left). This update rule makes value estimate $(V)$ converge on the expected value of the reward distribution (middle). When the reward probability is varied (i.e., for Bernoulli distributions), the $V$ at convergence scales linearly with the reward probability (right). b Risk-sensitive reinforcement learning with different learning rates (${\alpha }^{+},{\alpha }^{-}$) for positive and negative RPEs, respectively (left). This update rule makes value estimate $(V)$ converge on the quantities that are higher or lower than the expected value of the reward distribution (middle). As the reward probabilities are varied, the convexity of the convergent value $V$ changes depending on the asymmetry between ${\alpha }^{+}$ and ${\alpha }^{-}$. The level of the bias is determined by the asymmetric learning rate parameter $\tau$ (right). c Distributional reinforcement learning contains a set of value predictors (${V}_{i}$) each with a given learning rate for positive and negative RPEs (${\alpha }_{i}^{+},{\alpha }_{i}^{-}$, respectively) (left). This makes each value predictor converge on the quantity equal to the ${\tau }_{i}$-th expectile of the reward distribution. Thus, each value ${V}_{i}$ represents an expectile, and together the set of ${V}_{i}$ represents the entire distribution (right). Source data provided in ‘source_data/figure_1’.

The extent of asymmetry between ${\alpha }^{+}$ and ${\alpha }^{-}$ determines how optimistic or pessimistic the prediction will be and can be characterized by the asymmetric scaling factor $\tau$ defined by:

$$\tau=\frac{{\alpha }^{+}}{{\alpha }^{-}+{\alpha }^{+}}$$

(4)

where $0 < \tau < 1$. Standard RL can be considered a special case of risk-sensitive RL with ${\alpha }^{+}={\alpha }^{-}$, thus $\tau=0.5$.

Distributional RL

The concept of asymmetric updates has been utilized in a novel RL framework called distributional RL^38,39,47. This algorithm allows an agent to learn the entire probability distribution of rewards, instead of the expected value which is typically the learning target in traditional RL algorithms (Fig. 1c). In distributional RL, an agent is equipped with a set of multiple value predictors (${V}_{i}$), where $i$ corresponds to the index of the value predictor (or value neuron). The value of the $i$-th neuron (${\hat{V}}_{i}$) is updated based on the learning rates (${\alpha }_{i}^{+},{\alpha }_{i}^{-}$) and the RPE (${\delta }_{i}$) for that neuron $i$:

$${\hat{V}}_{i}\left({s}_{t}\right)\leftarrow {\hat{V}}_{i}\left({s}_{t}\right)+{\alpha }_{i}^{+}\cdot {\delta }_{i,t}\,...\,{\rm{if}}\,{\delta }_{i,t} > 0$$

(5)

$${\hat{V}}_{i}\left({s}_{t}\right)\leftarrow {\hat{V}}_{i}\left({s}_{t}\right)+{\alpha }_{i}^{-}\cdot {\delta }_{i,t}\,...\,{\rm{if}}\,{\delta }_{i,t} < 0$$

Similar to risk-sensitive RL, the learned value of each value predictor converges on a value higher or lower than the expected value, determined by the asymmetric scaling factor ${{\tau }_{i}=\alpha }_{i}^{+}/({\alpha }_{i}^{+}+{\alpha }_{i}^{-})$. Mathematically, each ${\hat{V}}_{i}$ converges on the τ_i-th expectile of the distribution (Fig. 1c). Expectiles are the solutions to asymmetric least squares minimization and generalize the mean of a distribution (with the mean being the 0.5^th expectile), as quantiles generalize the median (with the median being the 0.5^th quantile)⁴⁸. Since a set of expectiles can define a distribution, the diversity of ${\tau }_{i}$ across the population enables learning of the entire probability distribution.

In most applications of distributional RL, action selection is still based on the expected value of the reward distribution³⁸. Thus, biased value learning and risk-sensitivities could arise in this algorithm if the average asymmetric scaling factors across the population of neurons, ${\tau }_{{population}}$, is higher or lower than 0.5.

Problem

The learning rules discussed above provide mathematical algorithms through which biased value learning can occur. More specifically, they highlight the importance of imbalance in learning rate parameters (${\alpha }^{+},{\alpha }^{-}$) for positive and negative RPEs, which produces optimistic and pessimistic value learning. Importantly, however, the underlying biological mechanism regulating learning rate parameters (${\alpha }^{+},{\alpha }^{-}$) and asymmetry thereof ($\tau$) remains unclear. The primary goal of the present study is, therefore, to identify biological processes that might instantiate imbalance in learning rate parameters for positive and negative RPEs in the brain.

Toward this goal, we will first formulate an RL model that incorporates the basic circuit organization of the brain’s RL circuit, along with recent findings in plasticity rules. We show that this model naturally gives rise to risk-sensitive RL, while maintaining the stability and convergence properties characteristic of traditional RL models. Next, we propose a previously overlooked biological mechanism that may regulate asymmetric learning rates (${\alpha }^{+},{\alpha }^{-}$) through the impact of tonic dopamine on the sensitivity of dopamine receptors (Mechanism 1). We will then contrast this model with a commonly assumed mechanism based on altered phasic dopamine responses (Mechanism 2). Finally, we show how Mechanism 1, but not Mechanism 2, can account for previous experimental data in animals and humans.

Biological aspects of reinforcement learning in the brain

The above RL models provide algorithmic formulations, yet they do not recapitulate fundamental characteristics of the neural circuits thought to perform RL in the brain^49,50,51,52. We next incorporate some of the important circuit and synaptic properties into RL models.

It is thought that dopamine neurons in the ventral tegmental area (VTA) broadcast RPEs¹⁹ and modulate synaptic plasticity in dopamine-recipient areas. The striatum is the major target of dopaminergic projections, and it has been thought that spiny projection neurons (SPNs) in the striatum represent values, and dopamine modulates plasticity of glutamatergic synapses on SPNs^35,36,53,54 (Fig. 2a). In most RL models, each value predictor is typically updated by both positive and negative RPEs. If the value is computed based on a weighted sum of some inputs (i.e., using linear function approximation)¹³, the update rules described above (Eq. 1) are equivalent to performing a semi-gradient descent that minimizes RPEs¹³ (Supplementary Note 4).

Fig. 2: Biologically inspired reinforcement learning model.

a Schematic of the basal ganglia circuitry. Dopaminergic neurons in the VTA modulate plasticity at the level of the cortico-striatal synapses on SPNs in the NAc. The SPNs are subdivided depending on the dopamine receptor type they express (D1R or D2R). b Schematic of the plasticity rules of VTA-NAc circuitry^1,2,3. Transient increases in dopamine, caused by bursts in firing rate of dopamine neurons, generate increases in PKA activity in D1R-expressing SPNs, leading to cortico-striatal LTP. Transient decreases in dopamine, caused by pauses in the firing rate of dopamine neurons, generate increases in PKA activity in D2R-expressing SPNs, leading to cortico-striatal LTP. c Dose-occupancy curves for the D1R and D2R describing receptor occupancies as a function of dopamine concentrations. The curves are shifted between each other due to the different affinities of the receptors. The arrows represent a 3-fold increase (burst) and decrease (pause) in dopamine concentrations, which causes left-ward or right-ward shifts of the same magnitudes in the log-scale. d Schematic and equations of a biologically inspired reinforcement learning model based on ref. ⁴. VTA, ventral tegmental area; NAc, nucleus accumbens; SPN, spiny projection neurons; D1R, D1-type dopamine receptor; D2R, D2-type dopamine receptor; PKA, protein kinase A; LTP, long-term potentiation. Source data provided in ‘source_data/figure_2’.

The basic architectural assumptions of these RL models are, however, at odds with the RL circuitry in the brain. For one, in the striatum, there are two major classes of SPN characterized based on whether it expresses D1- or D2-type dopamine receptors (D1R and D2R)⁵³. SPNs expressing D1R and D2R constitute the so-called direct and indirect pathways, respectively, and exert opposing effects on downstream output neurons, with each pathway promoting or opposing a certain output, respectively.

In addition to the presence of direct and indirect pathways, there are two additional properties in these opposing populations that are essential³⁴.

The first important property is that D1R and D2R have different affinities to dopamine: D2R has a higher affinity, while D1R has a lower affinity (EC₅₀ affinity constant is 1 µM for D1R and 10 nM for D2R)^55,56. Thus, while the dose-occupancy relationships of D1R and D2R are both sigmoidal, they are shifted with one another with respect to dopamine concentration (Fig. 2c). Importantly, at normal dopamine levels (approx. 50–100 nM)^57,58, D2Rs are mostly occupied while D1Rs are mostly unoccupied (Fig. 2b). Although whether the affinities of D1R and D2R differ at the molecular level has been questioned⁵⁹, a recent study showed that intracellular signaling through PKA in D1- and D2-SPNs is triggered by a phasic increase and a decrease in dopamine, respectively, in behaving animals³⁷. These results are consistent with (apparent) difference in affinities of D1R and D2R observed in previous studies⁵⁵, although the exact reason for the difference remains to be clarified⁵⁹.

The second important property pertains to different plasticity rules in D1- and D2-SPNs. Because of the difference in affinity, D1R and D2R are sensitive to an increase and a decrease in dopamine concentrations. Extending this idea, recent studies have shown that glutamatergic inputs on D1-SPNs are potentiated by a transient increase in dopamine, whereas those on D2-SPNs are potentiated by a transient decrease in dopamine^35,36,37 (Fig. 2b). In addition, the extent of long-term potentiation (LTP)^35,36 as well as intracellular PKA signals³⁷ were shown to scale with the magnitude of dopamine transients.

Incorporating biological mechanisms to reinforcement learning algorithms

There have been previous efforts to incorporate direct and indirect pathways (also called “Go” and “NoGo” pathways, respectively) in RL models such as Opponent Actor Learning (OpAL)³², OpAL*⁶⁰ and Actor learning Uncertainty (AU)³⁴. These previous models were developed as Actor-Critic models, which learns a policy for action selection. Here, we will build on the AU model, extending it to address the problem of biased value learning and incorporating the passage of time by adapting it to TD learning.

To reflect the presence of direct and indirect pathway SPNs (D1- and D2-SPNs, respectively), our model assumes two separate populations of predictors that learn the quantities ${P}_{i}$ and ${N}_{i}$, respectively (Eq. 6; Fig. 2d)³⁴. Mimicking dopamine’s effect on potentiation of glutamatergic inputs to D1- and D2-SPNs, ${P}_{i}$ or ${N}_{i}$ will increase if an RPE is positive or negative, respectively, with the learning rates defined by ${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$, respectively (Eq. 6). Importantly, the value ${V}_{i}$ can be obtained simply by taking the difference between ${P}_{i}$ and ${N}_{i}$. (Eq. 7)³⁴.

$$ {{{\rm{D}}}}1{{{\rm{R}}}}-{{{\rm{SPN}}}}:\\ {P}_{i}({s}_{t})\leftarrow {P}_{i}({s}_{t})+{\alpha }_{i}^{+}\cdot \left|{\delta }_{i,t}\right|-\beta \cdot {P}_{i}({s}_{t})\,...\,{{\rm{if}}}\,{\delta }_{i,t}\ge 0\\ {P}_{i}\left({s}_{t}\right)\leftarrow {P}_{i}\left({s}_{t}\right)-\beta \cdot {P}_{i}\left({s}_{t}\right)\,...\,{{\rm{if}}}\,{\delta }_{i,t} < 0\\ {{{\rm{D}}}}2{{{\rm{R}}}}-{{{\rm{SPN}}}}:\\ {N}_{i}\,\left({s}_{t}\right)\leftarrow {N}_{i}\,\left({s}_{t}\right)+{\alpha }_{i}^{-}\cdot \left|{\delta }_{i,t}\right|-\beta \cdot {N}_{i}\,\left({s}_{t}\right)\,...\,{{\rm{if}}}\,{\delta }_{i,t}\le 0\\ {N}_{i}\,\left({s}_{t}\right)\leftarrow {N}_{i}\,\left({s}_{t}\right)-\beta \cdot {N}_{i}({s}_{t})\,...\,{\rm{if}}\,{\delta }_{i,t} > 0$$

(6)

$$ {{{\rm{Value}}}}:\\ {\hat{V}}_{i}({s}_{t})={P}_{i}({s}_{t})-{N}_{i}({s}_{t})$$

(7)

where β is a decay parameter which represents synaptic decay in the absence of RPEs.

This model (Eqs. 6 and 7) preserves various essential properties of previous RL models: (1) learning in $P$ and $N$ can be combined to provide a simple update rule for value $V$, and (2) this update rule approximates the gradient descent that minimizes RPEs (when β = 0, the update rule is equivalent to the gradient descent, Supplementary Note 4). Importantly, with β > 0, we can show that these simple learning rules guarantee convergence of the ${P}_{i}$ and ${N}_{i}$ predictors in the TD learning framework (avoid infinite increases) (Supplementary Note 6and Supplementary Fig. 1), without the need for additional mechanisms to modulate learning rates over iterations.

In stochastic environments where there is a probability $p$ of receiving a reward of a fixed magnitude $r$ (i.e., rewards follow a Bernoulli distribution), the stochastic fixed point of the learned value ${\hat{V}}_{i}$ (i.e., convergence point) will be defined by Eq. 8 (Supplementary Note 7)

$${\hat{V}}_{i}=\frac{\frac{{\tau }_{i}}{1-{\tau }_{i}}\cdot \frac{p}{1-p}}{\frac{{\tau }_{i}}{1-{\tau }_{i}}\cdot \cdot \frac{p}{1-p}+1+C}\cdot r,{{{\rm{where}}}}\,C \,=\frac{\beta }{\left(1-p\right)\cdot \left(1-{\tau }_{i}\right)}\,{{{\rm{and}}}}\,{\tau }_{i}=\frac{{\alpha }_{i}^{+}}{{\alpha }_{i}^{+}+{\alpha }_{i}^{-}}$$

(8)

Note that Eq. 8 contains a term C which depends on the decay factor $\beta$.

This formulation now provides a mechanistic model suitable for risk-sensitive RL (when there is one value predictor) as well as distributional RL (when there are multiple value predictors), which incorporate the neural circuit architecture and plasticity rules of D1- and D2-SNPs found in the brain.

With this model at hand, we now discuss potential biological processes that produce asymmetry in learning rates (${\alpha }_{i}^{+},{\alpha }_{i}^{-}$), which, in turn, causes biases in value predictions.

Asymmetry in learning can arise, based on Eq. 6, due to two potential mechanisms Mechanism 2: Asymmetry in the scaling of reward prediction errors (RPEs) as they are translated into dopamine responses. This mechanism involves differences in the slope (i.e., scaling factor) of dopamine firing rates or dopamine release as a function of RPEs. Previous studies have focused on this mechanism, particularly on asymmetries in the scaling of phasic dopamine firing rates³⁸. Mechanism 1: Asymmetry in the efficacy of dopamine-dependent synaptic plasticity. This mechanism highlights the role of tonic dopamine levels in modulating (scaling) the effect of phasic dopamine responses on synaptic plasticity. While phasic dopamine is the primary driver of dopamine-dependent synaptic plasticity, tonic dopamine can modulate its impact on learning, as we will demonstrate. In the following, we will first introduce the proposed biological mechanism (Mechanism 1), which will then be compared against Mechanism 2.

Mechanism 1: tonic dopamine can modulate asymmetric learning rates

Using the formalism above, we now explore biological processes that modulate the key parameters for biased value learning, such as ${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$. As discussed above, D1R and D2R have different affinities to dopamine, which leads to different levels of receptor occupancy at a given baseline dopamine level (Fig. 2b). Crucially, due to the sigmoidal shape of the dose-occupancy curves, the slope of the curve changes with baseline dopamine levels. Accordingly, a given dopamine transient leads to a different change in receptor occupancy depending on the starting dopamine level (Fig. 3a, b). Because of this effect, the baseline dopamine level alters the sensitivity of dopamine receptors to trigger synaptic plasticity (Fig. 3c). In addition, a key consequence of distinct affinities is that an increase (or a decrease) in baseline dopamine will cause opposite changes in sensitivities for D1R and D2R. Specifically, an increase in the baseline dopamine will increase D1R sensitivity relative to D2R, whereas a decrease in dopamine will increase D2R sensitivity relative to D1R (Fig. 3c, d). The importance of tonic dopamine levels is supported by a previous study using brain slices, which showed that the level of baseline dopamine indeed altered the effect of dopamine transients on SPN plasticity³⁶.

Fig. 3: Potential mechanisms for asymmetric learning.

a Schematic of the Mechanism 1. Increases or decreases in baseline dopamine modulate the degree to which bursts and pauses in dopamine cause changes in D1R and D2R occupancy. Increases in baseline dopamine make dopamine pauses to cause greater decreases in D2R occupancy than the increases in D1R occupancy caused by dopamine bursts. Conversely, decreases in dopamine make dopamine bursts to cause smaller increases in D1R occupancy than the decreases in D2R occupancy caused by dopamine pauses. b Schematic of the change in receptor occupancies in D1R and D2R, for a given transient increase or decrease in dopamine, caused by a firing rate ‘burst’ or ‘pause’, receptively. The slope is modulated by the baseline dopamine (colormap) and is equivalent to the receptor’s sensitivity to dopamine transients (${f}^{{{{\rm{D}}}}1}$ and ${f}^{{{{\rm{D}}}}2}$ in Eq. 9). Here ${\sigma }^{{{{\rm{D}}}}1}$, ${\sigma }^{{{{\rm{D}}}}2}$ corresponds to the receptors’ dose-occupancy curves. The receptor sensitivities (${f}^{{{{\rm{D}}}}1}$ and ${f}^{{{{\rm{D}}}}2}$), act as asymmetric learning rates in our model (${\alpha }^{+}$ and ${\alpha }^{-}$). c Receptor sensitivity for D1R and D2R as a function of baseline dopamine. d Asymmetric scaling factor ($\tau$) as a function of baseline dopamine. Colors depict how ‘optimistic’ or ‘pessimistic’ the convergent value estimate will be when learning with a given $\tau$. e Schematic of Mechanism 2. Left, the relationship between dopamine reward responses (spikes/s denoted by ${\psi }^{+}$ and ${\psi }^{-}$ for dopamine bursts and pauses, respectively) and RPEs. The slopes of these response functions correspond to the asymmetric learning rates (${\alpha }^{+}$, ${\alpha }^{-}$) for positive and negative RPEs, respectively. Colors depict how optimistic or pessimistic the convergent value estimate will be when learning with a given asymmetric scaling factor. Source data provided in ‘source_data/figure_3’.

Taking these factors into account, we postulate that the learning rate parameters for positive and negative RPEs (${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$) are a function of the baseline dopamine levels. We incorporate such modulation of ${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$ in our model (Mechanism 1)(Fig. 3a–d).

The magnitude of these effects can be formalized as follows. In the learning rules described in Eq. 6, ${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$ are given by the sensitivity of D1R and D2R, respectively, and thus depend on the dopamine baseline concentration at the synaptic input level. Since the receptor sensitivity corresponds to the derivative (i.e., slope) of the receptors dose-occupancy curves, evaluated at a given dopamine baseline level $\left({D}_{i}\right)$, the learning rates can be defined by:

$${\alpha }_{i}^{+}{{{\rm{: = }}}} \, {f}^{D1}\left({D}_{i}\right)=\frac{\partial {\sigma }^{D1}}{\partial D}\left({D}_{i}\right)\approx \frac{\Delta {\sigma }^{D1}}{\Delta {D}_{i}}$$

(9)

$${\alpha }_{i}^{-}{{{\rm{: = }}}} \, {f}^{D2}\left({D}_{i}\right)=\frac{\partial {\sigma }^{D2}}{\partial D}({D}_{i})\approx \frac{\Delta {\sigma }^{D2}}{\Delta {D}_{i}}$$

Here, ${\sigma }^{D1}$ and ${\sigma }^{D2}$ correspond to the sigmoidal dose-occupancy functions of D1R and D2R (“Methods”) which are sensitive to positive and negative dopamine transients, respectively. The terms $\frac{\partial \sigma }{\partial D}$ (noted by the variables ${f}^{D1}$ and ${f}^{D2}$) refer to the derivatives of these functions with respect to dopamine, evaluated at a baseline dopamine level ${D}_{i}$. We approximate these derivatives linearly using the expresions on the right-hand side.

Mechanism 2: scaling of phasic dopamine responses can induce asymmetric learning

In Mechanism 2, asymmetry in learning rates arises from a differential scaling (i.e., slope) of dopamine responses evoked by positive versus negative RPEs. This can occur if the slopes of dopamine response functions differ between positive and negative RPEs (Fig. 3e):

$${\alpha }_{i}^{+}{{{\rm{: = }}}} \, {g}_{i}^{+}\left({\delta }_{i}\right)=\frac{\partial {\psi }^{+}}{\partial \delta }\left({\delta }_{i}\right)\approx \frac{\Delta {\psi }^{+}}{\Delta {\delta }_{i}}$$

(10)

$${\alpha }_{i}^{-}{{{\rm{: = }}}} \, {g}_{i}^{-}\left({\delta }_{i}\right)=\frac{\partial {\psi }^{-}}{\partial \delta }\left({\delta }_{i}\right)\approx \frac{\Delta {\psi }^{-}}{\Delta {\delta }_{i}}$$

where ${\psi }^{+}$ and ${\psi }^{-}$ correspond to the function that translates RPEs (${\delta }_{i}$) into dopamine firing rates in the positive and negative regimes, respectively, and $\frac{\partial \psi }{\partial \delta }$ is their derivative (noted by the variables ${g}^{+}$ and ${g}^{-}$), which we approximate with the terms on the right. Given that we assume ${\psi }^{+}\left({\delta }_{i}\right)$ and ${\psi }^{-}\left({\delta }_{i}\right)$ are linear within the positive and negative regime, we can drop the dependency of the derivative on ${\delta }_{i}$: ${g}_{i}^{+}\left({\delta }_{i}\right)={g}_{i}^{+}$ and ${g}_{i}^{-}\left({\delta }_{i}\right)={g}_{i}^{-}$.

A previous study showed that individual dopamine neurons indeed vary in terms of how the magnitude of reward responses is scaled as a function of positive and negative RPEs (Fig. 3e)³⁸. As mentioned, in the distributional RL framework, individual dopamine neurons vary in terms of their asymmetric scaling factor ${\tau }_{i}$ and each of the multiple value predictors (${V}_{i}$) converges on the τ_i-th expectile of the reward distribution (Eq. 5). However, action selection is still based on the expected value of the reward distribution. Thus, biased value learning could arise if the population-level average ${\tau }_{{population}}$ is different from 0.5. For example, this can occur from the differential loss of optimistic or pessimistic dopamine neurons. Another possibility is an overall upward or downward shift in the distribution of ${\tau }_{i}$ across the population due to, for example, intrinsic factors modulating the gain of dopamine phasic responses.

This mechanism is well-suited for distributional RL, as the diversity in response functions at the single neuron levels enables distributional RL as previously proposed³⁸. However, it may also be relevant to risk-sensitive RL if there is asymmetry in the average dopamine responses to positive and negative RPEs, which can impact the behavioral learning rates for positive and negative RPEs $\left({\alpha }^{+},{\alpha }^{-}\right)$(Fig. 3e).

In summary, here we explore two potential mechanisms: Mechanism 2 postulates that the asymmetric learning rates arise at the level of dopamine firing rates, whereas Mechanism 1 postulates that asymmetric learning rates arise at the level of the downstream targets, i.e., in the striatum, due to changes in the tonic dopamine level. This distinction will become important when analyzing dopaminergic data in the following section.

Testing for evidence of either model in experimental data

Tian and Uchida (2015)

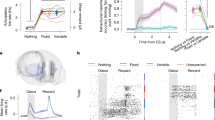
We next examined which proposal can explain the empirical data obtained in experimental animals or humans. We first examined the data obtained in mice in our previous study⁴². In this study, the authors tested the effect of lesioning the habenula, a brain structure which is implicated in depression^61,62,63 and provides disynaptic inhibitory input onto VTA dopamine neurons, modulating the activity of dopamine neurons and reward-seeking behavior. Head-fixed mice were trained in a Pavlovian conditioning task in which odor cues predicted reward with different probabilities (10%, 50%, 90%). After performing habenula (n = 5) or sham (n = 7) lesions, the spiking activity of VTA dopamine neurons was recorded while mice performed the task (Fig. 4a).

Fig. 4: Habenula lesions leads to optimistic reward-seeking behavior and cue-evoked responses in dopamine neurons.

a Experiment by Tian and Uchida (2015)⁵. Animals learned to associate cues with 10%, 50%, 90% reward probabilities (p(r)), or 80% air-puff and underwent habenula (n = 5) or sham (n = 7) lesions. b Lesion group show increased anticipatory licking to the 10% (U = − 3.106, P = 0.001, two-sided M-W test), 50% (U = − 5.820, P < 1 × 10⁻⁹, two-sided M-W test) and 90% (U = − 3.682, P = 0.0002, two-sided M-W test) cues (n = 31 control, n = 30 lesion, sessions, mean ± s.e.m). Licking scaled linearly with p(r) in controls but was concave in the lesion group (U = − 6.444, P < 1 × 10⁻¹⁰, two-sided M-W test on 50% normalized response), consistent with asymmetric learning rates (Supplementary Note 9). c Trial-by-trial fits using a risk-sensitive RL model revealed a significant difference in asymmetric learning rates between groups (U = 3.646, P = 0.0003, two-sided M-W test, pooling sessions). Dots: session (n = 35 control, n = 30 lesion), color: mouse (n = 7 control, n = 5 lesion). d Dopamine responses to 90% cue were reduced after lesions (U = 3.249, P = 0.001, two-sided M-W test, mean ± s.e.m, n = 45 control, n = 44 lesion, neurons). Normalized lesion responses were convex with p(r), with increased 50% cue response (U = − 3.824, P = 0.000131, two-sided M-W test). e T-statistics comparing each neuron’s 50% cue response to the linear interpolation between 90% and 10% responses showed greater variance than chance (M-C test for variance different from zero: P = 0.0222 lesion, P = 0.0217 control, 1000 batches). Lesion distribution was right-shifted from 0 (M-C test for mean larger than zero: P = 1 control, P = 0.022 lesion, 1000 batches) and from control (U = – 2.815, P = 0.0024, single-sided M-W test). f Example t-statistics (mean ± s.e.m, n = 100, trials): t-statistic = 0 indicates linear scaling of cue responses with p(r), t-statistic > 0 indicates convexity (optimism), < 0 indicates concavity (pessimism). M-W test, Mann-Whitney U-test; U,U-statistic; M-C, Monte Carlo. Source data provided in ‘source_data/figure_4’. Slice brain image in Fig. 4a taken from: Claudi, F. (2020). Mouse Brain Sagittal. Zenodo. https://doi.org/10.5281/zenodo.3925911.

After lesions, mice exhibited an elevated reward-seeking behavior (anticipatory licking) in response to cues predictive of probabilistic rewards, consistent with an optimistic bias in reward expectation (Fig. 4b, right). Importantly, anticipatory licking gradually increased over several sessions after lesions, suggesting that the optimistic bias developed through learning (Fig. 4b, left).

Before looking for signatures of Mechanism 1 or 2 in the dopaminergic activity, we first ensured that the behavioral changes observed after lesions could be attributed to asymmetric learning rates rather than other factors, such as changes in reward sensitivity. For this purpose, we fitted alternative reinforcement learning (RL) models to trial-by-trial anticipatory lick responses (Supplementary Fig. 2), assuming a linear relationship between value predictions and anticipatory licking. These models tested three possibilities that could explain the behavioral effects of the lesions: changes in a single learning rate for both positive and negative reward prediction errors (RPEs) (Supplementary Fig. 2a), changes in reward sensitivity (Supplementary Fig. 2b), and asymmetric learning rates (risk-sensitive RL model, Supplementary Fig. 2c). This analysis revealed that reward sensitivity remained consistent between lesion and control groups (Supplementary Fig. 2c). Moreover, attempts to replicate the concave anticipatory-licking response in lesioned animals by increasing reward sensitivity in an RL model failed (Supplementary Fig. 2b, bottom). This shows that reward sensitivity alone cannot explain the observed behavior. Instead, the risk-sensitive RL model revealed an asymmetry in learning rates favoring positive RPEs in the lesion group (Fig. 4c). This was further supported by analytical derivations showing that asymmetric learning rates affect value prediction concavity for probabilistic rewards in line with the data (Supplementary Note 9).

Dopamine neurons’ responses to reward-predictive cues reflect the increases in value expectation predicted by the cue with respect to baseline expectation. The overall magnitudes of cue-evoked responses were not elevated in lesioned animals compared to control animals (Fig. 4d). However, the shape of the response curve pointed to an optimistic bias: while in control animals, cue responses scaled linearly with the expected value (i.e., reward probability), the response function of the lesioned animals was convex. In other words, in control animals, the response to the 50%-reward cue was not significantly different from the quantity that results from the linear interpolation between the responses to 10%- and 90%-reward cues. In lesioned animals, however, the response to the 50%-reward cue was significantly greater than this quantity and near the response to the 90%-reward cue, which is indicative of an optimistic bias in value predictions (Fig. 4d, see Supplementary Note 9 for analysis of value predictions curve convexity). Such a change was observed at the level of the population average. Further analysis using individual neurons showed that when calculating a single-cell level metric that compares the 50%-reward cue to the same linear interpolation point, there was a broad distribution in this metric below and above the interpolated point, both in the control and lesion groups (Fig. 4e, f). The distribution was, however, shifted in its mean to more positive values in the lesion group (Fig. 4e).

These analyses indicated that both anticipatory licking and dopamine cue responses have an optimistic bias as characterized by an overvaluation of probabilistic rewards, without still pointing to the underlying mechanism. We will now look for signatures in dopamine activity that might support either of the proposed mechanisms for this asymmetry.

Mechanism 2 based on phasic dopamine cannot explain the optimistic biases in behavior and cue-evoked dopamine responses after Hb lesions

In this mechanistic explanation of asymmetric learning rates, an optimistic bias in reward expectation can arise if the dopamine response functions with respect to RPEs are steeper for positive than negative RPEs at the population level (i.e., the asymmetric scaling factor, ${\tau }_{{population}}$ becomes greater than 0.5) (Fig. 5a, b).

Fig. 5: Mechanism 2 cannot explain optimistic biases in behavior and cue-evoked dopamine responses of habenula lesioned animals.

a At the population level, Mechanism 2 can cause optimistic biases when the slope of the average dopamine reward responses to positive RPEs $({\alpha }^{+})$ is larger than for negative RPEs $({\alpha }^{-})$ leading to $\tau > 0$ (colormap). Shown are RPEs responses from simulated piece-wise linear functions with varying asymmetries in the slopes keeping ${\alpha }^{+} > {\alpha }^{-}$. b At the single-neuron level, optimistic biases arises if ${\tau }_{i}$ increases across neurons so that ${{{\rm{mean}}}}\left({\tau }_{i}\right) > 0.5$ (colormap). Shown are simulated ${\tau }_{i}$ distributions assuming ${\alpha }_{i}^{+} > {\alpha }_{i}^{-}$ $\forall i$. c Measured reward responses were reduced for the 50% cue (U = 3.726, P = 0.000195, two-sided M-W test), 90% cue (U = 2.987, P = 0.00281, two-sided M-W test), and omission responses to the 90% cue (U = − 4.940, P < 10⁻⁴, two-sided M-W test) in lesioned animals (left, mean ± s.e.m across neurons, n = 45 control, n = 44 lesion). Bootstrapped distributions of $\tau$ values computed from the average responses of the recorded neurons for control and lesion groups (right, 5000 bootstraps) showed no significant shift in lesions (5th percentile of ${\tau }_{{lesion}}-{\tau }_{{control}}$ = – 0.1605). d Distribution of ${\tau }_{i}$ computed for individual neurons (Dots: neurons, n = 45 control, n = 44 lesion) did not significantly differ between groups (t-statistic = 0.3277, P = 0.627, t test). e A risk-sensitive TD model trained with lesion-derived ${\tau }_{i}$ values computed using Mechanism 2 showed no optimistic bias in the value predictions (mean ± s.e.m., n = 10 models). f TD error at cue also lacked signs of an optimistic bias in the model trained with lesion-derived ${\tau }_{i}$ (mean ± s.e.m., n = 10 models). g Value predictions (mean ± s.e.m., n = 20 value predictors) based on risk-sensitive TD learning models using Mechanism 2 and a distribution of asymmetric scaling factors with a mean $\tau > 0.5$. h TD errors at cue (mean ± s.e.m., n = 20 value predictors) from the models in panel (g). The centre of the box plot shows the median; edges are the 25th and 75th percentiles; and whiskers are the most extreme data points not considered as outliers. M-W test, Mann-Whitney U-test; U, U-statistic. Source data provided in ‘source_data/figure_5’.

To test this idea, we obtained the asymmetric scaling factors (${\tau }_{i}$) from dopamine neurons based on their outcome responses: for each neuron, we constructed outcome response functions against the magnitude of RPEs (Fig. 5c and Supplementary Fig. 3a, b); i.e., the function equivalent to ${f}_{i}\left({\delta }_{i}\right)$ in Eq. 10. The response functions were obtained based on (1) whether reward was delivered (positive RPEs) or not (negative RPEs), and on (2) the magnitude of the reward expectation given by the reward probabilities predicted by each cue (0.1, 0.5, 0.9) (Supplementary Fig. 3a, b). We then obtained the point at which the responses are more likely to be below or above baseline (i.e., ‘zero-crossing points’)³⁸ (Supplementary Fig. 3c), and computed ${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$ as the slopes of the responses in the positive and negative domains relative to this zero-crossing point (Supplementary Fig. 3d), respectively. In both control and lesioned animals, the asymmetric scaling factors derived from single neurons tiled a wide range between 0 and 1 and exhibited other signatures consistent with distributional RL³⁸ (Supplementary Fig. 4). Nonetheless, although the variance of the distribution of asymmetric scaling factors was greater in lesioned animals, the mean did not change, indicating a lack of bias between ${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$ at the population level (Fig. 5d). This was also the case when the asymmetric scaling factor was derived directly from the average population response (Fig. 5c). These results indicated that Mechanism 2 does not explain optimistic biases in neither the value predictors nor cue responses (Fig. 5e, f).

To verify the validity of these analyses, we next tested whether Mechanism 2 could explain the data if asymmetric scaling factors (τ) were indeed overall biased (Fig. 5g, h and Supplementary Fig. 5). We trained our model with Mechanism 2 by imposing a shift in the mean of the asymmetric scaling factors (i.e., ${\tau }_{{population}} > 0.5$) both in the distributional RL and the risk-sensitive RL formulations (Fig. 5g, hand Supplementary Fig. 5a, c). As expected from the fixed-point analysis (Supplementary Note 7), the value predictors indeed exhibited optimistic biases (Fig. 5g and Supplementary Fig. 5e, f). However, the model did not reproduce the optimistic bias in cue-induced TD errors observed in the data (Fig. 5hand Supplementary Fig. 5b, d).

The lack of optimism in cue-evoked TD errors is an issue of this mechanism for asymmetric learning rates. This happens because the asymmetric scaling factors $({\alpha }_{i}^{+},{\alpha }_{i}^{-})$ act directly on the TD errors and, thus, scale the cue responses: ${\delta }_{i,{cue}}={\alpha }_{i}^{+}\cdot (\gamma \cdot {V}_{{cue}}-{V}_{{baseline}})$ or ${\delta }_{i,{cue}}={\alpha }_{i}^{-}\cdot (\gamma \cdot {V}_{{cue}}-{V}_{{baseline}})$ in Eq. 2. Importantly, this issue persisted in both distributional or risk-sensitive RL (Supplementary Fig. 5a, b and c, d). The difficulty of explaining biased dopaminergic cue responses further makes this an unlikely mechanism to explain the optimistic biases in the data.

Thus, contrary to the conclusion in our previous study⁴², these analyses indicated that changes in reward responses (and the resulting scaling factor $\tau$) do not explain the optimistic biases in behavior nor cue responses in lesioned animals (Fig. 5e, f).

Mechanism 1 based on tonic dopamine can explain the optimistic biases in behavior and cue-evoked dopamine responses by Hb lesion

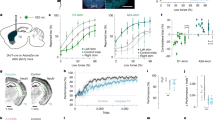
In addition to changes in the magnitude of dopamine RPEs, we observed that baseline firing rates of dopamine neurons were elevated in lesioned animals (Fig. 6b). According to our proposed mechanism, if this increase in firing rates leads to a corresponding rise in baseline dopamine levels in the striatum, it should result in biased value learning $({\alpha }^{+} > {\alpha }^{-})$ and an optimistic bias in value expectations. However, it remains unclear whether the observed elevation in baseline firing rates can result in functionally relevant changes in receptor occupancies.

Fig. 6: Biophysical model based on firing rates of dopamine neurons predicts increases in dopamine concentration and receptor occupancies at baseline.

a Schematic of the analysis. A biophysical model was used to predict dopamine concentrations, receptor occupancies, and value predictions from dopamine neurons firing rates. This figure shows the first three stages. b Population-averaged firing rates (left, n = 45 control, n = 44 lesion) show higher baseline activity in the lesion group (right) (U = − 2.010, P = 0.02, single-sided M-W test). c Dopamine concentrations predictions from the biophysical model of dopamine (90% reward trials are shown). d Receptor occupancies predictions from the biophysical model for rewarded (left) and omission (right) trials for D1R and D2R, respectively (90% reward trials are shown). e Biophysical model predictions of dopamine concentrations at baseline (n = 45 control, n = 44 lesion) show higher levels in the lesion group (U = – 2.109, P = 0.0175, single-sided M-W test). f Biophysical model predictions of receptor occupancies at baseline (n = 45 control, n = 44 lesion). show higher occupancies for D1R and D2R in lesion group (U = – 2.1664, P = 0.0151, U = – 2.1328, P = 0.0165 for D1R and D2R, single-sided M-W test). The centre of the box plot shows the median; edges are the 25th and 75th percentiles; and whiskers are the most extreme data points not considered as outliers. M-W test, Mann-Whitney U-test; U, U-statistic. Source data provided in ‘source_data/figure_6’.

To quantitatively predict dopamine concentrations in the striatum and resulting receptor occupancies of D1R and D2R, we used a biophysical model commonly used in the field⁶⁴ (Fig. 6a). This model has the firing rate of dopamine neurons as its input, and considers dopamine reuptake, and D2-autorreceptor-mediated inhibition of dopamine release to predict the dopamine concentration in the striatum (Fig. 6c). In addition, it considers the affinities of D1R and D2R to estimate their occupancy levels (Fig. 6d). After estimating these two variables (dopamine concentration and receptor occupancy), we derived the receptor sensitivities. The receptor sensitivities were quantified as the slope of the change in receptor occupancy given the observed baseline and phasic responses of dopamine neurons.

The biophysical model indeed supported that the observed change in dopamine neuron firing can cause a significant increase in dopamine concentration (Fig. 6c, e) and in D1 and D2 receptor occupancies at baseline (Figs. 6d, f, 7b). These changes are expected to alter the relative sensitivity of dopamine receptors sufficiently to cause a significant asymmetry between D1R-mediated and D2R-mediated learning (Fig. 7c, d).

Fig. 7: Mechanism 1 can account for optimistic biases in reward-seeking behavior and cue-evoked dopamine responses.

a Schematic of the analysis. This figure shows the last three stages. b Schematic shows model predictions of dopamine concentrations and receptor occupancies for control (black) and lesion (red) groups. The arrows depict the increase or decrease in occupancy for a fixed positive or negative dopamine transient. c Model predicted changes in receptor occupancy as a function of dopamine transients (mean ± s.e.m., n = 45 control, n = 44 lesion). The slope for positive and negative domains corresponds to D1R and D2R sensitivities, respectively. d Asymmetric scaling factors derived from receptors’ sensitivities (n = 45 control, n = 44 lesion) are increased in the lesion group (U = − 7.707, P < 1.0 × 10⁻¹⁵, single-sided M-W test). e Risk-sensitive TD model trained on these receptor sensitivities predicts a higher baseline value for the lesion group’s derived parameters (t-statistic = − 6.484, P < 1.0 × 10⁻⁷, two-sided t test). f The same risk-sensitive TD learning model predicts increases in value predictions for all cues (t = − 5.761, P < 1.0 × 10⁻⁶, t = − 6.433, P < 1.0 × 10⁻⁷, t = − 6.282, P < 1.0 × 10⁻⁶, two-sided t test, for 10%, 50% and 90% cues, mean ± s.e.m, n = 45 control, n = 44 lesion) and an optimistic bias in normalized value prediction to the 50% cue (t-statistic − 6.444, P < 1.0 × 10⁻⁷, two -sided t test). g The same risk-sensitive TD learning model predicts lower cue responses in lesioned animals (mean ± s.e.m. n = 45 control, n = 44 lesion, U = 4.844, P < 1.0 × 10⁻⁵, U = – 3.658, P = 0.00025, U = 4.734, P < 1.0 × 10⁻⁴, two -sided M-W test for 10%, 50% and 90% cues). Normalized TD errors for the 50% cue show an optimistic bias (t = – 6.508, P < 1.0 × 10⁻⁷, two-sided t test). The centre of the box plot shows the median; edges are the 25th and 75th percentiles; whiskers are the most extreme data points not considered as outliers. M-W test, Mann-Whitney U-test; U, U-statistic; t, t-statistic. Source data provided in ‘source_data/figure_7’.

The receptor sensitivities were derived from the biophysical model results (Fig. 7c, “Methods”) and used as the asymmetric learning rates (${\alpha }^{+},{\alpha }^{-}$) to update predictions, P and N (Eq. 6). After training, the model produced optimistic biases in value predictions and in normalized cue responses, similar to those observed in lesioned animals (Fig. 7f, g). The models simulating control animals developed no significant biases.

In addition, the overall decrease in the raw (unnormalized) magnitude of cue responses observed in lesioned animals was reproduced by this mechanism (Fig. 7f, see Supplementary Fig. 5e, f for results with a wider range of value learning biases, see Supplementary Fig. 6a for results using a set of decay factors $\beta$). This occurs because in TD learning, the cue response (${\delta }_{{cue}}$) is based on the change in value prediction induced by the cue relative to the value prediction at baseline, and the latter was also increased by optimistic value learning (Fig. 7f. Importantly, given that in Mechanism 1 the asymmetric scaling factors act on the value predictor updates and not directly on the TD errors, the optimistic biases in ${\delta }_{{cue}}$ could be reproduced, as opposed to the results from the previous section. In fact, if we multiply the ‘optimistic’ cue responses (${\delta }_{{cue}}$) that result from Mechanism 1 with the asymmetric scaling factors used to bias the value updates (as it happens in Mechanism 2), the cue responses do not show the optimistic biases seen in the data (Supplementary Fig. 5g).

These results, together, indicate that this proposed mechanism provides a parsimonious account of the data: a change in baseline firing of dopamine neurons, rather than changes in phasic responses, is the likely mechanism that led to optimistic biases in reward-seeking behavior as well as cue-evoked dopamine responses in habenula lesioned animals.

Mechanisms for asymmetric learning based on phasic and tonic dopamine play complementary roles in distributional RL

We focused the above analysis on the mechanism for asymmetric learning rates underlying the optimistic biases observed in the lesioned group. However, although the scaling of phasic dopamine responses did not explain the optimistic biases in the data in habenula-lesioned mice, this mechanism could still support distributional RL. Indeed, distributional RL explained other features of the data (Supplementary Figs. 3, 4). As mentioned, in both control and lesioned animals, asymmetric scaling factors tiled a wide range between 0 and 1³⁸ (Supplementary Fig. 4a). Furthermore, the non-linearities of the cue-evoked responses of individual neurons showed a wider distribution than what is expected by noise (Fig. 4d). Finally, the core prediction of distributional RL – a positive correlation between the asymmetric scaling factors of the RPE responses and their zero-crossing points of individual neurons (Supplementary Fig. 4c, d)³⁸ – was also present in controls and after Hb lesions. Together, these results support that the basic features of distributional RL are present in a way consistent with Mechanism 2 at the single-neuron level.

Altogether the data supports a model in which the mechanisms implemented by tonic and phasic dopamine play complementary roles in the encoding of asymmetric learning rates (Supplementary Fig. 6b). The mechanism of phasic dopamine explains the variability in single neuron dopamine responses, consistent with the expectile code in distributional RL (Supplementary Fig. 6b bottom), and persisted even in habenula-lesioned animals. On the other hand, the effect of tonic dopamine manifests at the population level, generating asymmetry in learning rates and biases in value expectations (Supplementary Fig. 6b middle).

Taken together, the above results suggest that both mechanisms driving asymmetric learning rates coexist in the brain, but with different functions if one considers the more general framework of distributional RL. This can be formalized by defining the asymmetric learning in our RL model (Eq. 6) as the product of the scaling factors given by Mechanisms 1 and 2:

$${\alpha }_{i}^{+}{{{\rm{: = }}}} \, {f}^{D1}\left({D}_{i}\right)\cdot {g}_{i}^{+}$$

(11)

$${\alpha }_{i}^{-}{{{\rm{: = }}}} \, {f}^{D2}\left({D}_{i}\right)\cdot {g}_{i}^{-}$$

Where the functions ${f}^{D1},{f}^{D2}$, ${g}^{+}$, ${g}^{-}$ are defined in Eqs. 9 and 10. Effectively, Mechanism 1 acts as an additional scaling factor (i.e., the receptor sensitivity) on top of the scaling factor determined by the individual response functions of dopamine neurons of Mechanism 2. Indeed, when we consider both mechanisms in an RL model, the model can more comprehensively explain the data in the habenula lesion experiment (Supplementary Fig. 6h–i).

Linking asymmetric learning and baseline dopamine levels in healthy subjects

Cools et al., (2009)²⁶

The above analyses using the mouse data indicated that optimistic value learning could occur through the proposed mechanism based on tonic dopamine levels. What about in other species, particularly in humans? There have been very few studies that examined the relationship between tonic dopamine levels and asymmetry in learning from positive and negative outcomes. As a rare case for such examinations, Cools et al. (2009)²⁶ provided intriguing human data. They compared the performance in a reversal learning task (Fig. 8a) and the quantity called ‘dopamine synthesis capacity’. Dopamine synthesis capacity is estimated by injecting the positron emission tomography (PET) tracer [¹⁸F]fluorometatyrosine (FMT) and is thought to be correlated with baseline dopamine levels^65,66. This study found that higher dopamine synthesis capacity was correlated with better learning from gains but not with learning from losses (Fig. 8b). As a result, in reversal learning, subjects with higher dopamine synthesis capacity learned at a faster rate from gains than losses, reported as the ‘relative reversal learning (RRL)’ index in their study (Fig. 8e, dots). This result, thus, provides direct evidence supporting our Mechanism 1.

Fig. 8: Mechanism 1 predicts asymmetric learning rates in healthy humans given inter-individual differences in baseline dopamine.

a In the reversal task from Cools et al. (2009)⁶, subjects completed blocks with two switch types: Type I (punished → rewarded: switch of contingencies is signaled by a previously punished stimuli that is then rewarded, probing positive RPE learning) and Type II (rewarded → punished: switch of contingencies is signaled by a previously rewarded stimuli that is then punished, probing negative RPE learning). Relative reversal learning (RRL) was defined as the difference in prediction accuracy on the second trial post-switch. Positive RRL reflects stronger learning from positive RPEs; negative RRL, from negative RPEs. b Schematic of dopaminergic axon terminals (left) showing D2s receptors on presynaptic sites and D2l on postsynaptic sites. Right: effect of bromocriptine on receptor activation curves when acting on D2l only (orange), both D2l and D2s (purple), and accounting for its partial agonism (green). c In Mechanism 1, the RRL is approximately $2\tau -1$, where $\tau$ is derived from the receptors’ sensitivity. This predicts a positive relationship between $2\tau -1$ and baseline dopamine. d Predicted change in $2\tau -1$ under Mechanism 1 after bromocriptine (10^0.8 nM) considering effects on D2l receptors (orange), D2l and D2s (purple), and its partial agonism (green). e RRL under control conditions plotted against striatal dopamine synthesis capacity measured with PET imaging (Cools et al., 2009, black dots, bottom x-axis) and against baseline dopamine (pink line, top axis) –as predicted by a risk-sensitive RL agent performing the task, with $\tau$ derived from receptors’ sensitivity. f Change in RRL under drug administration condition as a function of striatal dopamine synthesis capacity (Cools et al., 2009, black dots, bottom x-axis, mean ± s.e.m.). Model predicted change in RRL (mean ± s.e.m.) under bromocriptine administration (10^0.8 nM) as a function of baseline dopamine (pink line, top axis) predicted by a risk-sensitive RL agent performing the task with $\tau$ derived from the receptors’ sensitivity considering the bromocriptine effects in D2l receptors (orange), D2l and D2s (purple), and partial agonism (green). Source data provided in ‘source_data/figure_8’.

In addition, they found that dopamine synthesis capacity predicts the effectiveness of bromocriptine (D2 partial agonist) in altering learning rate asymmetry: bromocriptine’s ability to bias learning from gains over losses (i.e., positive change in RRL) was negatively correlated with dopamine synthesis capacity (Fig. 8f, dots). We found that this result can also be explained by Mechanism 1. For this, we simulated the effects of bromocriptine with the biophysical model used above (Fig. 8b), and derived the asymmetric learning rates from the slopes of the D2R occupancy (Fig. 8d and Supplementary Fig. 7a, b) or activation curves (Fig. 8dand Supplementary Fig. 7c, d). The RRL parameter reported by Cools et al. (2009) is linearly related to the asymmetric scaling factor $\tau$, and is equivalent to $\left(2\tau -1\right)$ (as described in the Methods). We then computed what would be the change in this parameter $\Delta \left(2\tau -1\right)$ induced by bromocriptine (Fig. 8f and Supplementary Fig. 7e–l).

This analysis revealed that by considering the asymmetries in learning rates induced by changes in the baseline occupancy of the receptors, our model can capture their results. Intuitively, the less dopamine there is at baseline, the lower the occupancy of D2R at placebo conditions. This leads to a larger increase in D2R occupancy induced by D2 agonist in low dopamine baseline conditions (Fig. 8b–d left, Supplementary Fig. 7a) and, thus, a larger increase in asymmetry in learning from gains over losses, if D1R occupancy is kept fixed. These effects still hold even if we consider, in addition to bromocriptine’s effects in postsynaptic receptors (D2 long or D2l), its effect on inhibition of dopamine release via presynaptic (D2 short or D2s) autoreceptors^67,68 (Fig. 8b–d middle, Supplementary Fig. 7b). This can be simulated as a decrease in dopamine level, which leads to a shift in the occupancy curves to the right. Finally, we can consider the effect of the partial agonism of the drug, that leads to a lower activation level of receptors even if the occupancy is maximal (Fig. 8b–d right, Supplementary Fig. 7c, d). Even after considering this last factor, the results remain qualitatively the same as those found in the original study. These results were robust to a relatively wide range of values in the simulation’s parameters (Supplementary Figs. 7, 8). Finally, to further reaffirm these observations, we simulated an RL agent performing the reversal learning task from Cools et al. (2009), using the D1R and D2R sensitivities derived from the placebo and drug administration conditions. We then computed the relative reversal learning (RRL) parameter directly from the task performance (Methods). The results (Fig. 8e, f) are qualitatively similar to those found above. All together, this analysis provides evidence in favor of a role of Mechanism 1 in inducing asymmetric learning rates in humans, and presents predictive power for understanding the effects of dopamine-related drugs in risk-sensitive behavior. This was made possible by developing a detailed biophysical model that incorporates drug affinities for the two main subtypes of D2R dopamine receptors, and integrating this framework into a reinforcement learning model that accounts for the properties of both D1 and D2 receptors. These findings highlight the critical role of dopamine receptor occupancy dynamics in modulating learning, as well as the importance of understanding the mechanisms by which drug manipulations exert their effects in order to accurately interpret results.

Discussion

A hallmark of various psychiatric disorders is overly optimistic or pessimistic predictions about the future. Using RL models, we sought to identify potential biological mechanisms that give rise to biased value predictions, with a particular focus on the roles of phasic versus tonic dopamine. Our results demonstrate that variations in tonic dopamine levels can modulate the efficacy of synaptic plasticity induced by positive versus negative RPEs, thereby resulting in biased value learning (Mechanism 1). This effect arises due to the sigmoidal shape of the dose-occupancy curves and different affinities of dopamine receptors (D1R and D2R); alterations in the tonic dopamine level result in changes in the slope of the dose-occupancy curve (and thus, sensitivity) of dopamine receptors at the baseline dopamine concentration. We show that this mechanism offers a simple explanation for how changes in tonic dopamine levels can result in biased value learning in a few examples of value learning in mice and humans. In addition, we show that this mechanism may underlie symptoms of various psychiatric and neurological disorders. Although altered phasic dopamine responses could have been a natural suspect as a candidate mechanism for biased value learning^39,40, our study provides an overseen mechanism; the interaction between tonic and phasic dopamine can give rise to biased value learning, even when phasic dopamine responses remain relatively unchanged.

The impact of properties of dopamine receptors on reinforcement learning (RL)

Our results highlight the importance of considering properties of dopamine receptors and neural circuit architecture (i.e., direct and indirect pathways) in RL models. Based on the different affinities of dopamine D1 and D2 receptors, it has been proposed that D1- and D2-SPNs play predominant roles in learning from positive and negative dopamine responses^{34,69,70,71,72}. In support of this idea, recent experiments have demonstrated that PKA signaling in D1- and D2-SPNs is primarily driven by a phasic increase and decrease of dopamine, respectively³⁷. Furthermore, LTP-like changes in D1- and D2-SPNs are triggered by a phasic increase and decrease of dopamine, respectively^35,36,73. These recent pieces of evidence suggest that these plasticity rules are a basic principle of the RL circuitry in the brain. Here, we explored the properties of this RL model and found the impact of the shape (slope) of receptor occupancy curves and showed that the tonic dopamine levels can modulate the relative efficacy of learning from positive versus negative RPEs.

One assumption in our model is that after a change in the tonic dopamine level, intracellular signaling reaches a steady inactive state, and it is the change in receptor occupancy that matters for inducing synaptic plasticity, rather than the absolute level of receptor occupancy reached during phasic dopamine responses. We note that absolute level might also contribute, yet it is expected that an increase or decrease in absolute occupancy levels will cause effects in the same direction as the effects of relative change that we explored in this study.

In addition, our model, which incorporates the new plasticity rules, the opponent circuit architecture and properties of D1/D2 dopamine receptors, provides insights into the basic design principle of the brain’s RL circuit. It should be noted that the dose occupancy curves were plotted as a function of the logarithm of dopamine concentration, which makes the occupancy curves into sigmoidal shapes (Fig. 3 and Supplementary Fig. 9). This logarithmic scaling is important in two ways. First, considering two sigmoidal curves for D1R and D2R together, the curves are approximately symmetric around the normal baseline dopamine level (Fig. 3a, Normal). Second, logarithmic scaling means that a fold-change in dopamine concentration will lead to the same leftward or rightward shift in these plots. It has long been argued that signaling of RPEs by dopamine neurons is curtailed by the fact that dopamine neurons have relatively low firing rates (2-8 spikes per second), and inhibitory responses of dopamine neurons tend to be smaller than excitatory responses^74,75. Importantly, if we consider logarithmic scaling of dopamine concentration, the problem of this asymmetry is substantially mitigated (Supplementary Fig. 10). For example, with the baseline firing of 6 spikes per second, a phasic increase to 18 spikes per second and a phasic decrease to 2 spikes per second will cause the identical fold-changes in spiking (i.e., 3-fold changes in both directions), which would lead to a similar fold-changes in dopamine levels (Supplementary Fig. 11) and similar percent increase and decrease in receptor occupancy in D1R and D2R, respectively (Fig. 3a). Consequently, the system achieves symmetry in its response to positive and negative dopamine responses of observed magnitudes.

This may help understand why the basal ganglia circuit employs the opponent circuit architecture in the first place. In the model used in the present study, the value is encoded as the difference between the activity of D1- and D2-SPNs ($V=P-N$)³⁴. We propose that this opponent circuit architecture, together with the logarithmic scaling of dopamine concentration, allows the system to effectively learn and encode both positive and negative values, which are contributed by the increase of firing in D1- and D2-SPNs, respectively. This would allow to expand the dynamic range of value coding, without requiring high baseline firing rates. Thus, at the normal dopamine baseline, learning from positive and negative dopamine responses is well balanced. When the tonic dopamine level deviates from the normal level, however, then the symmetry is broken and value learning becomes biased, as explored in the present study.

The role of tonic dopamine levels in psychiatric disorders

As mentioned above, our modeling results provide an account for biased value predictions observed in various psychiatric and neurological conditions. For one, our model provides a link between findings in depressive-like states in animal models and the value learning biases exhibited by humans.

In a rodent model of depression, it has been reported that the spontaneous activity of dopamine neurons is decreased⁷⁶ (but see refs. ^77,78). In addition, decreased spontaneous firing of dopamine neurons has been observed as a result of chronic pain-induced adaptations that correlate with anhedonia-like behavior⁷⁹. Furthermore, maternal deprivation, which increases susceptibility to anhedonia, led to an upregulation of D2R expression in the VTA⁸⁰, which is expected to decrease the excitability of dopamine neurons via its autoreceptor function. Finally, chronic administration of corticosteroids, a method to mimic anxiety and anhedonia-like states, results in an increase in somatodendritic dopamine concentration, which then decreases dopamine excitability via D2R hyper-activation⁸¹. These results of decreased dopamine excitability correlated with anhedonia-like states are consistent with findings of increased burst firing of lateral habenula (LHb) neurons⁶¹ and potentiation of glutamatergic inputs onto the habenula⁶² in depression models. This is further supported by reports that depressive-like behavioral phenotypes can be ameliorated by optogenetic activation of dopamine neurons⁸² and the anti-depressant effects of ketamine might be mediated by the inhibition of bursting in the LHb⁶³.

The mechanism by which a broad change in dopamine excitability could lead to depressive-like states remains to be revealed. Just by assuming that a decrease in spontaneous firing leads to a decrease in baseline dopamine level in the striatum, our model readily predicts that learning from negative outcomes will be emphasized over learning from positive outcomes (Fig. 3a, b), as has been reported in some studies of patients with major depressive disorder (MDD)¹. In addition, RL agents learning in these conditions exhibit enhanced risk-aversive behavior, pessimistic outcome expectations, and increased sensitivity to losses compared to gains, all of which are signatures of depressive-like conditions^1,5,23,83,84. This contrasts with findings of increased dopamine synthesis capacity in pathological gambling patients⁸⁵, who show the opposite behavioral signatures³.

An additional line of research relevant to our proposal is PD patients and pathological gambling as a comorbidity. Previous work has emphasized the interaction between the degree of dopaminergic loss and the effects of PD medications^86,87,88, which can sometimes result in the development of addictive disorders such as pathological gambling. The loss of dopaminergic axons in PD patients has been reported to happen predominantly in the dorsal regions of the striatum⁸⁹. Thus, at the onset of the motor impairment symptoms, which is when L-DOPA medication tends to be prescribed, the dopamine level is expected to be low in the dorsal striatum, while it might be relatively intact in the ventral striatum. This can lead to ‘overdose’ of dopamine by medication: while L-DOPA might take dopamine levels in the dorsal striatum back to its original set-point, it might cause an ‘overdose’ in the ventral striatum^87,90. Our model predicts that this overdose would lead to decreases in D2R sensitivity relative to D1R. Assuming that the ventral striatal regions have a dominant role in value learning, this would result in excessive optimistic expectations and risk seeking, two key behavioral features of pathological gambling and addictive disorders. We provided indirect evidence for this hypothesis; future work should directly test these predictions.

It should be noted that we did not consider changes in dopamine receptor density, which have also been related to value learning biases⁹¹ and psychiatric conditions⁹². Future studies should explore the influence of this additional factor in the encoding of asymmetric learning rates (i.e., $({\hat{\alpha }}_{i}^{+},{\hat{\alpha }}_{i}^{-})$.

Tonic dopamine as a modulator of ‘mood’

Mood refers to a person’s emotional state as it relates to their overall sense of well-being. Although the exact neural substrate of mood remains unknown, recent studies have indicated that mood reflects not the absolute goodness of outcomes but rather on the discrepancy between actual and expected outcomes in recent history^15,16. That is, mood depends on the cumulative sum of RPEs that occurred recently¹⁵. It has also been proposed that mood, in turn, affects the way we perceive and learn from positive and negative outcomes (RPEs)¹⁵.

Our model provides a unified mechanism for these two aspects of mood; both the subjective feeling of mood and biased learning from positive versus negative outcomes can arise from changes in baseline dopamine levels, which can be modulated by a recent history of phasic dopamine responses. It was proposed that this history-dependent modulation of learning is an adaptive mechanism that allows organisms to adapt quickly to slow changes in environments based on the momentum of whether the situation is changing in a better or worse direction on a slow timescale (e.g., seasonal change)^15,16. The models presented in the present study may provide mechanistic insights into such mood-dependent modulation of learning and perception.

Neural circuits for distributional reinforcement learning (RL)

We examined the possibility that optimistic biases in reward-seeking behavior and dopamine cue responses observed in habenula-lesioned mice can be explained by Mechanism 2, either based on risk-sensitive RL (the average response) or distributional RL (responses of a diverse set of individual dopamine neurons). We did not find evidence supporting this possibility. However, the present study makes two important contributions with respect to distributional RL. First, we can show that our model, which incorporated direct and indirect pathway architecture, can support distributional RL (Supplementary Fig. 6). It would be interesting to examine what additional features and functions could be gained by having this opponent architecture. Second, we largely replicated the previous results³⁸ using an independent data set. That is, the signatures of distributional RL were present in this data set (Supplementary Figs. 3and 4), and dopamine cue-evoked responses did show an optimistic bias. This provides further evidence for a distributional code in dopamine neurons, and shows that there is an mean-shifted distributional representation in dopamine cue responses in habenula-lesioned animals.

Taken together, our biologically inspired RL model provides a foundation to link findings in the brain and formal models of RL. Our work highlights a causal impact of baseline dopamine on biasing future value predictions, which may underlie mood and some abnormalities observed in psychiatric patients and could be used to regulate risk sensitive behavior.

Methods

Overall research trajectory

Our initial motivation of this study was to apply the distributional RL framework³⁸ to reinterpret the data in our previous study⁴²as well as to test the predictions of distributional RL in an independent data set. Our results showed that the dopamine responses in this data set conform to basic predictions of distributional RL both in control and habenula-lesioned animals (Fig. 4 and Supplementary Figs. 3, 4), providing an independent confirmation of the basic results reported in Dabney et al. (2020). However, this investigation also revealed that the key effects of habenula lesions – optimistic biases in licking and dopamine cue responses – cannot be explained by the basic distributional RL model. Furthermore, these analyses also indicated that our previous explanation based on a greater impairment of reward omission dips compared to positive dopamine responses⁴² cannot explain the key effect of habenula lesions, if the data was quantified using the method derived from distributional RL (Mechanism 2). These results prompted us to seek a novel model that can explain the data. Inspired by recent biological findings regarding synaptic plasticity of SPNs and other basic properties of dopamine receptors and the circuit architecture, we conceived a novel model (Mechanism 1). This model uses the basic architecture of a previous model, the Actor learning Uncertainty (AU) model³⁴. Our contribution is to highlight what biological mechanisms may regulate the key parameters in the model, such as the learning rate parameters (${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$), and how they impact value learning at the behavioral level. We then found that Mechanism 1 can explain optimistic biases observed in habenula-lesioned mice⁴², while Mechanism 2 cannot. We then searched for another data that examined the effect of tonic dopamine levels on value learning, leading to the test using the data obtained in humans²⁶. Mechanism 2 is also an extension of the AU model. Mechanism 2 uses the same model architecture as the AU model, but uses multiple value predictors and incorporates asymmetric scaling of dopamine responses in response to positive and negative RPEs, like the way used in a previous study³⁸.

Computational models

TD learning with D1 and D2 populations

In this work, we extend the TD learning algorithm to have separate populations for D1 and D2 SPNs³⁴. For a more extensive introduction to the reinforcement learning (RL) algorithms we build upon, the reader is referred to the Supplementary Note 1–3. In our model, the computation of TD RPE of standard TD learning is still used; yet this model differs in the updates and computation of $\hat{V}\left({s}_{t}\right)$.

As mentioned previously, the updates in the ${P}_{i}$ and ${N}_{i}$ populations using TD errors happen exclusively with positive or negative TD errors, respectively:

$${P}_{i}\left({s}_{t}\right)\leftarrow {P}_{i}\left({s}_{t}\right)+{\alpha }_{i}^{+}\cdot \left|{\delta }_{i,t}\right|-\beta \cdot {P}_{i}({s}_{t})\ldots {{{\rm{if}}}}\,{\delta }_{i,t} > 0$$

$${P}_{i}\left({s}_{t}\right)\leftarrow {P}_{i}\left({s}_{t}\right)-\beta \cdot {P}_{i}\left({s}_{t}\right)\ldots {{{\rm{if}}}}\,{\delta }_{i,t}\le 0$$

$${N}_{i}\left({s}_{t}\right)\leftarrow {N}_{i}\left({s}_{t}\right)+{\alpha }_{i}^{-}\cdot \left|{\delta }_{i,t}\right|-\beta \cdot {N}_{i}\left({s}_{t}\right)\ldots {{{\rm{if}}}}\,{\delta }_{i,t} < 0$$

$${N}_{i}\left({s}_{t}\right)\leftarrow {N}_{i}\left({s}_{t}\right)-\beta \cdot {N}_{i}\left({s}_{t}\right)\ldots {{{\rm{if}}}}\,{\delta }_{i,t}\ge 0$$

Where ${\alpha }^{+}$ and ${\alpha }^{-}$ are the learning rates for the $P$ and $N$ populations. The variable $\beta \in \left({{\mathrm{0,1}}}\right)$ is the decay factor, which we keep constant throughout the simulations and serves to stabilize $P,N$. The computation of the value estimate $\hat{V}\left({s}_{t}\right)$ is given by: ‘

$$\hat{{V}_{i}}\left({s}_{t}\right)={P}_{i}\left({s}_{t}\right)-{N}_{i}\left({s}_{t}\right)$$

Mechanism 1 for asymmetric learning rates

w?>In Mechanism 1, the learning rates ${\alpha }^{+},{\alpha }^{-}$ in the equations correspond to the D1 and D2 receptors’ sensitivities, respectively, and depend on the dopamine baseline level at the SPN level $\left({D}_{i}\right)$. For now, we allow ${D}_{i}$ to depend on each ${i}_{{th}}$ SPN. Given the receptors sigmoidal dose occupancy curves (${\sigma }_{D1R}$ and ${\sigma }_{D2R}$), the receptors’ sensitivity is given by the derivative of this curve:

$${\alpha }_{i}^{+}{{: = }} \, {f}^{D1}\left({D}_{i}\right)={\sigma }^{D1}\left({D}_{i}\right)\cdot \left(1-{\sigma }^{D1}\left({D}_{i}\right)\right)$$

$${\alpha }_{i}^{-}{{: = }} \, {f}^{D2}\left({D}_{i}\right)={\sigma }^{D2}\left({D}_{i}\right)\cdot (1-{\sigma }^{D2}\left({D}_{i}\right))$$

Where ${\sigma }_{D1R}$ and ${\sigma }_{D2R}$ correspond to the sigmoidal function of the D1, D2 receptor’s dose-occupancy curves that can take the following form:

$${\sigma }^{D1}({D}_{i})=\frac{{D}_{i}}{{D}_{i}+{{{\rm{E}}}}{{{{\rm{C}}}}}_{D1R}^{50}}$$

$$\left.{\sigma }^{D2}{D}_{i}\right)=\frac{{D}_{i}}{{D}_{i}+{{{\rm{E}}}}{{{{\rm{C}}}}}_{D2R}^{50}}$$

We can locally approximate this derivative by taking the ratio of the change in receptor occupancy $\Delta \sigma$ for a given change in dopamine levels $\Delta {D}_{i}$ (elicited by a pause or burst in dopamine firing rates)

$${\alpha }_{i}^{+}\approx \frac{\Delta {\sigma }^{D1}}{\Delta {D}_{i}}$$

$${\alpha }_{i}^{-}\approx \frac{\Delta {\sigma }^{D2}}{\Delta {D}_{i}}$$

Note that in Fig. 3${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$ were obtained from the local slopes of the receptor occupancy curve as a function of the logarithmic changes in dopamine concentrations. In Supplementary Note 10 we show that the simulations’ results with this mechanism do not depend on the choice of logarithmic or linear changes in dopamine levels.

Mechanism 2 for asymmetric learning rates

Here, the asymmetric learning rates correspond to the slope of dopamine responses evoked by positive and negative RPEs, separately. Using the equations above this can be implemented by allowing ${f}_{i}\left({\delta }_{i}\right)$ to be a piece-wise linear function:

$${\alpha }_{i}^{+}{{{\rm{: = }}}} \, {g}_{i}^{+}\left({\delta }_{i}\right)=\frac{\partial {\psi }^{+}}{\partial \delta }\left({\delta }_{i}\right)\approx \frac{\Delta {\psi }^{+}}{\Delta {\delta }_{i}}\ldots {{\rm{if}}}\,{\delta }_{i} > 0$$

(12)

$${\alpha }_{i}^{-}{{{\rm{: = }}}} \, {g}_{i}^{-}\left({\delta }_{i}\right)=\frac{\partial {\psi }^{-}}{\partial \delta }\left({\delta }_{i}\right)\approx \frac{\Delta {\psi }^{-}}{\Delta {\delta }_{i}}\ldots {{\rm{if}}}\,{\delta }_{i} < 0$$

Note that here ${\alpha }_{i}^{+}$ and ${\alpha }_{i}^{-}$ are now the slopes of the functions determining the evoked responses of dopamine neurons for a given RPE (${\psi }^{+}$,${\psi }^{-}$), which are assumed to be linear. Given this linearity ${g}^{+}\left({\delta }_{i}\right)$ and ${g}^{-}\left({\delta }_{i}\right)$ do not depend on ${\delta }_{i}$ and thus we can drop the dependency: ${g}_{i}^{+}\left({\delta }_{i}\right)={g}_{i}^{+}$ and ${g}_{i}^{-}\left({\delta }_{i}\right)={g}_{i}^{-}$.

Mechanism 1 and 2 with complementary roles in distributional reinforcement learning

The signatures of distributional RL were preserved in dopamine neurons firing rates after habenula lesions and explained other features of the data. This suggests a model where both mechanisms driving asymmetric learning rates coexist, but with different functions if one considers the more general framework of distributional RL. This can be formalized by defining the updates of the $P$ and $N$ populations in our model, considering both Mechanisms 1 and 2:

$${P}_{i}\left({s}_{t}\right)\leftarrow {P}_{i}\left({s}_{t}\right)+{f}^{D1}\left({D}_{i}\right)\cdot {g}_{i}^{+}\cdot \left|{\delta }_{i,t}\right|-\beta \cdot {P}_{i}\left({s}_{t}\right)\,...\,{{\rm{if}}}\,{\delta }_{i,t} > 0$$

$${P}_{i}\left({s}_{t}\right)\leftarrow {P}_{i}\left({s}_{t}\right)-\beta \cdot {P}_{i}\left({s}_{t}\right)\,...\,{{\rm{if}}}\,{\delta }_{i,t} < 0$$

$${N}_{i}\left({s}_{t}\right)\leftarrow {N}_{i}\left({s}_{t}\right)+{f}^{D1}\left({D}_{i}\right)\cdot {g}_{i}^{-}\cdot \left|{\delta }_{i,t}\right|-\beta \cdot {N}_{i}\left({s}_{t}\right)\,...\,{{\rm{if}}}\,{\delta }_{i,t} < 0$$

$${N}_{i}\left({s}_{t}\right)\leftarrow {N}_{i}\left({s}_{t}\right)-\beta \cdot {N}_{i}\left({s}_{t}\right)\,...\,{{\rm{if}}}\,{\delta }_{i,t} > 0$$

Where the functions ${f}^{D1},{f}^{D2},{g}^{+}$, ${g}^{-}$ are defined above. Effectively, Mechanism 1 acts as an additional scaling factor on top of the scaling factor determined by the individual response functions of dopamine neurons of Mechanism 2. The former allows for risk sensitivities and global optimistic or pessimistic biases and does not depend on individual SPNs; the latter gives rise to a distributional expectile code for value.

The TD errors are computed considering the distributional TD framework (see Supplementary Note 3)

$${\delta }_{i,t}={r}_{t}+\gamma \cdot \widetilde{z}\left({s}_{t+1}\right)-{V}_{i}\left({s}_{t}\right)$$

Where $\widetilde{z}\left({s}_{t+1}\right)$ are samples from the estimated return distribution $\sim Z\left({s}_{t+1}\right)$⁴¹.

These set of update equations are approximately equivalent to a modified version of the update equation of distributional RL. Where, for performing the updates, we average across a set of $M$ updates, each depending on a single sample ${\delta }_{i,t}$.

$$\left[\Delta {V}_{i}\left({s}_{t}\right)\right]\approx \frac{1}{M}{\sum}_{j}^{M}{f}_{D1}\left({D}_{i}\right)\cdot {{g}_{i}^{+}\cdot \delta }_{i,j}\cdot {I}_{{\delta }_{i,j} > 0}+{f}_{D2}\left({D}_{i}\right)\cdot {{g}_{i}^{-}\cdot \delta }_{i,j}\cdot {I}_{{\delta }_{i,j} > 0}$$

$${{{{\rm{V}}}}}_{{{{\rm{i}}}}}\left({s}_{t}\right)\leftarrow {V}_{i}\left({s}_{t}\right)+{{{{\mathbf{E}}}}}\left[\Delta {V}_{i}\left({s}_{t}\right)\right]$$

Computational model of dopamine release and receptor occupancy

To predict changes in dopamine concentrations and receptor occupancies (Fig. 6), we employed a biophysical model developed elsewhere⁶⁴. It presents two interacting dynamical systems. The first system models the change in receptor occupancies, while the second the change in dopamine levels.

In the first system, the occupancy of receptors is modelled as a binding reaction between dopamine $({DA})$ and D1 or D2 receptors $(R)$, using the constants for forward and backward reactions (${k}_{{on}},{k}_{{off}}$).

$${{{\rm{DA}}}}+{R}_{{k}_{{off}}}{\rightleftarrows }^{{k}_{{on}}}\,{{{\rm{DA}}}}:R$$

This formulation results in the following equation for the change in receptor occupancy ${{{\rm{Occ}}}}\left(t\right)$ per unit time:

$$\frac{d{{{\rm{Occ}}}}\left({{{\rm{t}}}}\right)}{{dt}}=\left(1-{{{\rm{Occ}}}}\left(t\right)\right)\times {k}_{{on}}\times {C}_{{DA}}\left(t\right)-{{{{\rm{Occ}}}}\left(t\right)\times k}_{{off}}$$

The values used for the association and dissociation constants for each receptor type (${k}_{{on}}$ and ${k}_{{off}}$, respectively) are detailed in Supplementary Table 1.

In the second system, the change in dopamine concentration (${C}_{{DA}}\left(t\right)$) is a function of both dopamine release and uptake.

$$\frac{{{{{\rm{d}}}}C}_{{DA}}\left(t\right)}{{{{\rm{dt}}}}}={{{{\rm{DA}}}}}_{{{{\rm{release}}}}}\left({{{\rm{t}}}}\right)-{{{{\rm{DA}}}}}_{{{{\rm{uptake}}}}}\left({{{\rm{t}}}}\right)$$

Dopamine release is a product of firing rate $(\nu (t))$ and release capacity $(\gamma (t))$

$${{{{\rm{DA}}}}}_{{{{\rm{release}}}}}\left({{{\rm{t}}}}\right)=\gamma \left(t\right)\cdot \nu \left(t\right)$$

Where:

• 1. $\nu \left(t\right)$ is the firing rate of dopamine neurons, provided by the neural data.

• 2. $\gamma \left(t\right)={\gamma }_{p{r}_{n}}\cdot {P}_{r}\cdot {{{{\rm{G}}}}}_{D2}\left(t\right)$ is defined as the increase in ${C}_{{DA}}\left(t\right)$ by a single synchronized action potential:

  • a. ${P}_{r}=1$ release probability in the absence of presynaptic D2-autoreceptors,

  • b. ${\gamma }_{p{r}_{n}}=2$ release capacity in the absence of presynaptic D2-autoreceptors. This value was set to be deliberately high and anticipates a ~ 50% reduction by terminal feedback.

  • c. ${{{{\rm{G}}}}}_{D2}\left(t\right)$ is a multiplicative gain that represents the modulation of dopamine release by D2-autoreceptors. This is a decaying function of the occupancy of D2-autoreceptors (${{{{{\rm{Occ}}}}}_{D2}}_{a}\left(t\right)$), which is modelled by the same binding reaction explained above. The gain is parametrized by the autoreceptor efficacy, ${{{\rm{\alpha }}}}=3$. The smaller the ${{{\rm{\alpha }}}}$ the less the decay in release with receptor occupancy.

$${G}_{D2}\left(t\right)=\frac{1}{1+{{{\rm{\alpha }}}}\cdot {{{{{\rm{Occ}}}}}_{D2}}_{a}\left(t\right)}$$

Dopamine uptake is a function of the uptake of dopamine by the dopamine transporter (DAT) and other non-DAT sources

$${{{{\rm{DA}}}}}_{{{{\rm{uptake}}}}}\left({{{\rm{t}}}}\right)={dt}\cdot \left(\frac{{V}_{\max }^{{{{\rm{p}}}}{{{{\rm{r}}}}}_{n}}\cdot {C}_{{{{\rm{DA}}}}}\left(t\right)}{{K}_{m}+{C}_{{{{\rm{DA}}}}}\left(t\right)}-{K}_{{{{\rm{nonDAT}}}}}\right)$$

Where:

• ${V}_{\max }^{{{{\rm{p}}}}{{{{\rm{r}}}}}_{n}}=1500\frac{{{{\rm{nM}}}}}{\sec }$ s the maximal uptake capacity assuming approximately 100 terminals in the near surroundings.

• ${K}_{m}=160$ ${{{\rm{nM}}}}$, is the Michaelis-Menten parameter for uptake mediated by DAT

• ${K}_{{{{\rm{nonDAT}}}}}=0.04$ ${{{\rm{nM}}}}$ is a constant for the dopamine removal not mediated by DAT. For example, monoamine oxidase (MAO) and norepinephrine transporter (NET) mediated uptake.

The variables of the model reported in Fig. 6 correspond to: ${{{{\rm{Occ}}}}}_{{{{\rm{D}}}}1{{{\rm{R}}}}}\left(t\right)$, ${{{{\rm{Occ}}}}}_{{{{\rm{D}}}}2{{{\rm{R}}}}}\left(t\right)$,${{{{\rm{C}}}}}_{{{{\rm{DA}}}}}\left(t\right)$. We used as input to the model the firing rates derived from the electrophysiological recording of optogenetically identified dopamine neurons conducted in Tian and Uchida (2015)⁴². This modeling, while considering major processes, does not consider all of the complexity of the biological environment in the brain, yet we used this model to obtain an approximate estimate of the order of changes in dopamine concentrations and receptor occupancies.

Habenula lesion data

Animals, surgery and lesions

The rodent data we re-analyzed here were first reported in Tian and Uchida (2015)⁴². Below, we provide a brief description of the methods. Further methodological details can be found in the original paper. Bilateral habenula lesions were performed in five animals. Seven animals were in the control group, including two with a sham-lesion operation, one with only a small contralateral side lesion of the medial habenula, and four animals without operations in the habenula. During surgery, a head plate was implanted on the skull, and adeno-associated virus (AAV) that expresses channelrhodopsin-2 (ChR2) in a Cre-dependent manner was injected into the VTA (from bregma: 3.1 mm posterior, 0.7 mm lateral, 4–4.2 mm ventral). After recovery from surgery, mice were trained on the conditioning task, after which mice were randomly selected to be in the lesion or sham-lesion group. Electrolytic lesions were made bilaterally using a stainless-steel electrode (15 kU, MicroProbes, MS301G) with a cathodal current of 150 mA. Each side of the brain was lesioned at two locations (from bregma: 1.6 mm/1.9 mm posterior, 1.15 mm lateral, 2.93 mm depth, with a 14 angle). For sham-lesion operations, no current was applied. In the same surgery, a microdrive containing electrodes and an optical fiber was implanted in the VTA (from bregma: 3.1 mm posterior, 0.7 mm lateral, 3.8–4.0 mm ventral)⁹³.

Behavioral task

Twelve mice were trained on a probabilistic Pavlovian task. In each trial, the animal experienced one of four odor cues for 1 s, followed by a 1-s pause, followed by a reward (3.75 μl water), an aversive air puff or nothing. Odor 1 to 3 signaled a 90%, 50% and 10% probability of reward, respectively. Odor 4 signaled a 90% probability of an air puff. Odor identities were randomized across trials and included: isoamyl acetate, eugenol, 1-hexanol, p-cymene, ethyl butyrate, 1-butanol, and carvone (1/10 dilution). Inter-trial intervals were exponentially distributed. An infrared beam was positioned in front of the water delivery spout, and each beam break was recorded as one lick event. We report the average lick rate over the interval 500–2000 ms after cue onset.

Electrophysiology

Recordings were made using a custom-built microdrive equipped with 200 μm-fiber optic-coupled with eight tetrodes. DA neurons were identified optogenetically⁹³. A stimulus-associated spike latency test (SALT) algorithm⁹⁴ was used to determine whether light pulses significantly changed a neuron’s spike timing.

Neural data analysis

Data analyses were performed using Python 3. To measure firing rates, peristimulus time histograms (PSTHs) were constructed using 1-ms bins. These histograms were then smoothed by convolving with the function $f\left(t\right)=\left(1-{e}^{-t}\right)\cdot {e}^{-\frac{t}{\tau }}$ where $\tau$ was a time constant set to 20 ms as in ref. ²⁰. A number 44 dopamine neurons were recorded from lesioned animals (5 animals, 30 sessions), and 45 dopamine neurons were recorded from control animals (7 animals, 35 sessions). We pooled all the cells across animals in each group for analysis. Cue-evoked responses were defined as the average activity from 0 to 400 ms after cue onset. Outcome-evoked responses were defined as the average activity from 2000 to 2600 ms after cue onset.

The normalization of cue response shown in Fig. 4 was carried out following a previous work³⁸ on a per-cell basis as: ${c}_{50}^{{{{\rm{norm}}}}}=\frac{{c}_{50}-\bar{{c}_{10}}}{\bar{{c}_{90}}-\bar{{c}_{10}}}$, where $\bar{{c}_{90}},\bar{{c}_{10}}$ corresponds to the mean across trials within a cell for the 90% and 10% probability cure responses. To derive the t-statistics in Fig. 4e, f, we performed a two-tailed t test of the cell’s normalized responses to the 50% cue against the average midway point between responses to the 10% cue and responses to the 90% cue.

The derivation of asymmetric scaling factors from outcome responses (${\tau }_{i}$), was carried out following³⁸, with some modifications to adapt it to the task. The procedure is illustrated in Supplementary Fig. 3.

• To compute the reversal points, outcome responses were first aligned to the RPE for each trial type, computed with the true expected value of each reward distribution. Assuming a fixed reward value of r = 1 (arbitrary units), the expected value for the 90%, 50%, 10% reward probability trials corresponded to 0.1, 0.5, 0.9, respectively. Given this, omission responses from the 90, 50, and 10% reward probability trials correspond to RPEs of -0.9, -0.5 and -0.1. The rewarded responses from the 90, 50, and 10% reward probability trials correspond to RPEs of 0.1, 0.5 and 0.9. The reward value is arbitrary and doesn’t have an effect in this computation, as it only shifts the RPE axis by a fixed amount. The reversal points for each cell (${Z}_{i}$) was defined as the RPE that maximized the number of positive responses to RPEs greater than ${Z}_{i}$ plus the number of negative responses to RPEs less than ${Z}_{i}$. The distribution of reversal points is reported in Supplementary Fig. 4. To obtain statistics for the reliability of the computed reversal points, we partitioned the data into random halves and estimated the reversal point for each cell separately in each half. We repeated this procedure 1000 times with different random partitions, and we report the distribution of Pearson’s correlation across these 1000 folds (Supplementary Fig. 4).

• After measuring reversal points, we fit linear functions separately to the positive and negative domains. Given that dopamine’s responses are non-linear in the reward space but present a putative utility function⁹⁵, we approximated the underlying utility function from the dopamine responses to RPEs of varying magnitudes. We used these empirical utilities instead of raw RPEs for computing the slopes that correspond to ${\alpha }_{i}^{+},{\alpha }_{i}^{-}$. We then computed the asymmetric scaling factors as ${\tau }_{i}=\frac{{\alpha }_{i}^{+}}{{\alpha }_{i}^{+}+{\alpha }_{i}^{-}}$. We performed the same cross-validation procedure used for the reversal points. The distribution of R value across the 1000 folds are reported in Supplementary Fig. 4.

A key prediction of distributional RL³⁸ is the presence of a correlation (across cells) between reversal points ${Z}_{i}$ and asymmetric scaling factors ${\tau }_{i}$. To elucidate whether signatures of distributional RL were still present after lesions, we followed the procedure given by Dabney et al. (2020)³⁸ to compute this correlation. We first randomly split the data into two disjoint halves of trials. In one half, we first calculated reversal points ${Z}_{i}^{1}$ and used them to calculate ${\alpha }_{i}^{+},$ ${\alpha }_{i}^{-}.$ In the other half, we again calculated the reversal points ${Z}_{i}^{2}$. The correlation we report in Supplementary Fig. 4 is between ${Z}_{i}^{2}$ and ${\tau }_{i}.$

Model fitting to the anticipatory licking responses

We performed fitting of reinforcement learning models to the anticipatory licking responses to elucidate whether the lesion-induced behavioral changes could be captures with asymmetric learning rates. We assumed that the lick rates were related to the value prediction with a linear function ${lick}=\eta \cdot V$ and fit three models: (1) Standard RL model with learning rate and $\eta$ as free parameters; (2) RL model with reward sensitivity and $\eta$ as free parameters; and (3) Risk- sensitive RL model with asymmetric learning rates and $\eta$ as free parameters. For each trial we computed the average lick rate over the interval 0.5–2 s after cue onset. For each model, we fit the free parameters to the lick rates using maximum likelihood estimation. The optimization was performed using the SciPy optimization toolbox (Python 3) that minimized the difference between the predicted lick rates and the ground truth ones, with a uniform prior distribution over the parameters. The models, parameters and bounds used for each of them are detailed in Supplementary Table 2 and Supplementary Fig. 2.

Simulation details

Biophysical model simulations

For each recorded dopamine neuron, the simulations were carried on a trial-by-trial basis that consisted of a time window [− 15, 20] s with respect to cue onset. A relatively large window was used to allow for the relevant variables to stabilize in its baseline, as the simulations were initialized at zero. For each trial, spikes were first binned with 10-ms windows and then smoothed by a Gaussian kernel ($\sigma=0.3\times \left({{{\rm{IS}}}}{{{{\rm{I}}}}}_{{{{\rm{mean}}}}}\right)$). All trials were then averaged across trials to determine the mean single-cell response for dopamine release and D1 and D2 receptor activation. Final average dopamine concentrations and receptor occupancies were obtained from the average of all mean single-cell responses.

Computation of receptors sensitivities from the model results

We computed the receptor sensitivity from the occupancies ${{{{\rm{Occ}}}}}_{D1R}$, ${{{{\rm{Occ}}}}}_{D2R}$ and their theoretical dose-occupancy curves. Starting from the occupancy at baseline, we derived the change in occupancy as a function of the transients in dopamine concentration ${{{{\rm{C}}}}}_{{DA}}$ elicited by RPE-evoked dopamine responses, at the level of the population average. The ratio between these quantities corresponds to the receptors’ sensitives. These are transferred as ${\alpha }^{+}$ and ${\alpha }^{-}$ in our reinforcement learning model:

$${f}_{{{{\rm{D}}}}1{{{\rm{R}}}}}\approx \frac{\Delta {{{{\rm{Occ}}}}}_{{{{\rm{D}}}}1{{{\rm{R}}}}}}{\Delta {C}_{{{{\rm{DA}}}}}}={\alpha }^{+}\ldots {{{\rm{if}}}}\,\Delta {C}_{{{{\rm{DA}}}}} > 0$$

$${f}_{{{{\rm{D}}}}2{{{\rm{R}}}}}\approx \frac{\Delta {{{{\rm{Occ}}}}}_{{{{\rm{D}}}}2{{{\rm{R}}}}}}{\Delta {C}_{{{{\rm{DA}}}}}}={\alpha }^{-}\ldots {{{\rm{if}}}}\,\Delta {C}_{{{{\rm{DA}}}}} < 0$$

Where $\Delta {C}_{{{{\rm{DA}}}}}$, $\Delta {{{{\rm{Occ}}}}}_{{{{\rm{D}}}}1{{{\rm{R}}}}}$, $\Delta {{{{\rm{Occ}}}}}_{{{{\rm{D}}}}2{{{\rm{R}}}}}$ are the changes computed with respect to baseline, as: $\Delta x={\bar{x}}_{{outcome}}{-\bar{x}}_{b}$, for each variable $x=\left\{ {C}_{{{{\rm{DA}}}}},{{{{\rm{Occ}}}}}_{{{{\rm{D}}}}1{{{\rm{R}}}}}\right.$, $\left.{{{{\rm{Occ}}}}}_{{{{\rm{D}}}}2{{{\rm{R}}}}}\right\}$. Where $\bar{x}$ denotes the population average response for each group. The outcome responses were taken as the average from [0,1] sec after outcome onset, while the baseline was taken as the average from [− 1, 0] sec with respect to cue onset.

Simulations of Mechanism 1

The simulations for Mechanism 1 were carried out with our TD learning model with D1 and D2 populations. We ran the simulations using the resultant receptor sensitivities from the biophysical model as the population-level asymmetric learning rates in Mechanism 1 (${\alpha }^{+}={f}_{{{{\rm{D}}}}1{{{\rm{R}}}}},{\alpha }^{-}={f}_{{{{\rm{D}}}}2{{{\rm{R}}}}}$ for $P$ and $N$ updates). The simulations were run for 3000 trials on the Pavlovian conditioning task used in the study⁴². We assumed a uniform distribution of trial types across the session. Each trial consisted of 4 states (baseline, cue, delay, reward), assuming Markovian dynamics between them. All variables were initialized at zero. The model had as hyperparameters a discounting factor of $\gamma=0.99$ and a decay term $\beta=0.002;$ though this model reproduces key signatures of the data irrespective of the choice of the decay factor $\beta$.

Simulations of Mechanism 2

The simulations for Mechanism 2 were carried out with the same TD learning model as above, using the same simulation hyperparameters. Here, the asymmetric learning rates correspond to the single cell asymmetric scaling factors derived from slope of the firing rates of dopamine neurons as a function of RPEs.

Simulations of Mechanism 1 and 2 in the Distributional RL framework

Here, we used the distribution of single cell asymmetric scaling factors (${\alpha }_{i}^{+},{\alpha }_{i}^{-}$) derived from the dopamine neurons firing rates and the receptors sensitivities derived from the biophysical model simulations to perform the $P$ and $N$ updates in Eq. 6. In Supplementary Note 3 we emphasized that in order to accurately compute the TD RPE in distributional TD, we require taking samples from the estimated return distribution ${\widetilde{z}}_{i}\left({s}_{t+1}\right) \sim Z\left({s}_{t+1}\right)$. We did this by running an optimization process where we minimize for the expectile loss between the taken samples ${\widetilde{z}}_{i}\left({s}_{t+1}\right)$, ${V}_{i}\left({s}_{t+1}\right)$ from the model, and ${\tau }_{i}$ as estimated from the data. The problem was defined as ${{{\rm{argmi}}}}{{{{\rm{n}}}}}_{{s}_{i}\ldots {s}_{m}}{{{\mathcal{L}}}}\left(s,V,\tau \right)$ where:

$$ {{{\mathcal{L}}}}\left(s,V,\tau \right) \\ =\frac{1}{M}{\sum}_{m=1}^{M}{\sum}_{i=1}^{N}\left|{\tau }_{i}-{{{{\mathbf{{ I}}}}}}_{{{{{\rm{s}}}}}_{{{{\rm{m}}}}} < {V}_{n}}\right|{\left({\hat{z}}_{{{{\rm{m}}}}}-{V}_{i}\right)}^{2},{{{\rm{for}}}}\,N\,{{{\rm{neurons}}}}\; {{{\rm{and}}}}\,M\,{{{\rm{samples}}}}$$

In the simulations, we took M samples where M equals the number of neurons (N) and performed an update taking the expectation across all samples.

Simulations of Cools et al. (2009)

In the study form Cools et al., they performed a reversal learning task and reported a parameter called ‘relative reversal learning (RRL)’. Briefly, the task consisted of subjects learning to predict reward or punishment from a set of stimuli. On each trial, two stimuli were presented: a face and a scene. After a stimulus was highlighted, the subject had to predict whether the stimulus would lead to a reward or punishment. After a baseline practice block they performed reversal blocks. There were two conditions: (1) the ‘unexpected reward’ condition, where reversals were indicated by unexpected rewards occurring after the previously punished stimulus was highlighted; and (2) the ‘unexpected punishment’ condition, where reversals were signaled by unexpected punishment that followed the previously rewarded stimulus. The stimulus that was highlighted on the first trial of each reversal was always highlighted again on the second trial after the reversal. The RRL performance metric was measured from this second trial, on which the subjects had to implement the reversed contingencies and switch their predictions, by calculating the difference in the prediction accuracy between the unexpected reward condition and the unexpected punishment conditions. The task was performed under control conditions and after the administration of bromocriptine (1.25 mg).

To simulate the control condition, we computed the parameters ${\alpha }^{+},{\alpha }^{-}$ from the slopes of the D2l (postsynaptic D2 receptors) and D1 occupancy curves or activation curves for a set of dopamine baseline levels (from 10¹ to 10^2.5 nM). For analyzing the effect of bromocriptine, we made use of the biophysical model for dopamine release and receptor occupancy and simulated the predicted the receptor’s occupancies for the same set of dopamine baseline levels. In these simulations, we added an additional ligand for D2 receptors to the update equations for occupancy:

$$\frac{{d0{{{\rm{cc}}}}}_{{{{\rm{DA}}}},{r}_{j}}\left({{{\rm{t}}}}\right)}{{dt}}=\left(1-{{{\rm{Oc}}}}{{{{\rm{c}}}}}_{{{{\rm{DA}}}},{r}_{j}}\left({{{\rm{t}}}}\right)\right)\times {k}_{{{{\rm{on}}}}}^{{{{\rm{DA}}}},{r}_{j}}\times {{{{\rm{C}}}}}_{{{{\rm{DA}}}}}\left(t\right)-{k}_{{{{\rm{off}}}}}^{{{{\rm{DA}}}},{r}_{j}}$$

$$\frac{{d0{{{\rm{cc}}}}}_{{{{\rm{Drug}}}},{r}_{j}}\left({{{\rm{t}}}}\right)}{{dt}}=\left(1-{{{\rm{Oc}}}}{{{{\rm{c}}}}}_{{{{\rm{Drug}}}},{r}_{j}}\left({{{\rm{t}}}}\right)\right)\times {k}_{{{{\rm{on}}}}}^{{{{\rm{Drug}}}},{r}_{j}}\times {{{{\rm{C}}}}}_{{{{\rm{Drug}}}}}\left(t\right)-{k}_{{{{\rm{off}}}}}^{{{{\rm{Drug}}}},{r}_{j}}$$

Where ${r}_{j}:\left\{{{{\rm{D}}}}1,{{{\rm{D}}}}2{{{\rm{s}}}},{{{\rm{D}}}}2{{{\rm{l}}}}\right\}$, and ${k}_{{{{\rm{on}}}}}^{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{s}}}}}=$ 0.02083, ${k}_{{{{\rm{off}}}}}^{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{s}}}}}=0.1$, ${k}_{{{{\rm{on}}}}}^{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{l}}}}}=$0.04, ${k}_{{{{\rm{off}}}}}^{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{l}}}}}=0.1$ are reported in Supplementary Table 1⁹⁶.

To calculate the effects of the efficiency of the drug, we calculated the activation of D2l and D2s receptors in the following way:

$${{{\rm{Ac}}}}{{{{\rm{t}}}}}_{{r}_{j}}\left(t\right)={E}_{{{{{\rm{DA}}}},r}_{{{{\rm{j}}}}}}\cdot {{{\rm{Oc}}}}{{{{\rm{c}}}}}_{{{{\rm{DA}}}},{r}_{j}}\left(t\right)+{E}_{{{{{\rm{Drug}}}},r}_{{{{\rm{j}}}}}}\cdot {{{\rm{Oc}}}}{{{{\rm{c}}}}}_{{{{\rm{Drug}}}},{r}_{j}}\left(t\right)$$

Where ${{{{\rm{E}}}}}_{{{{{\rm{DA}}}},r}_{{{{\rm{j}}}}}}=1$ is the efficiency of dopamine on the receptors activation, and ${E}_{{{{{\rm{Drug}}}},r}_{j}} < 1$ the efficiency of the drug, for ${r}_{j}:\left\{{{{\rm{D}}}}1,{{{\rm{D}}}}2{{{\rm{s}}}},{{{\rm{D}}}}2{{{\rm{l}}}}\right\}$. The parameter for D1 receptors was kept at ${E}_{{{{\rm{Drug}}}},{{{\rm{D}}}}1}=0$ for all simulations.

To simulate the effects of D2s activation by the drug in D2l occupancy, we report the effects of ${E}_{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{s}}}}}=0$(Fig. 8d–f, left) and ${E}_{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{s}}}}}=0.6$ (Fig. 8d–f middle). To simulate the effect of the drug in D2s and D2l activation in Fig. 8d–f right, we report the effects of ${E}_{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{s}}}}}=0.6,{E}_{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{l}}}}}=0.6$.

As a first approach we approximated the RRL as the difference between the positive and negative learning rates in our model: ${{{\rm{RRL}}}}={\alpha }^{+}-{\alpha }^{-}\propto \tau -(1-\tau )=2\tau -1$, reported in Fig. 8c, and then computed this metric from the occupancy curves ${\left(2\tau -1\right)}_{{{{\rm{Occ}}}}}$ or activation curves ${\left(2\tau -1\right)}_{{{{\rm{Act}}}}}$. The change in relative reversal learning in Fig. 8d was calculated as taking the difference between the drug and the placebo condition as:

$${\Delta \left(2\tau -1\right)=\left(2\tau -1\right)}_{{{{\rm{Drug}}}}}-{\left(2\tau -1\right)}_{{{{\rm{Control}}}}}$$

We show how the qualitative nature of the effects of the drug in relative reversal learning still holds regardless of whether the parameter $\tau$ is computed from the occupancy curves (Supplementary Fig. 7a, b, e, f, j, Supplementary Fig. 8a and Fig. 7d–f left, middle) or the activation curves (Supplementary Fig. 7c, d, g, h, k, l, Supplementary Fig. 8band Fig. 7d–f right). In addition, we show that the qualitative results still hold regardless of the choice of the efficiency parameters ${E}_{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{s}}}}}$ and ${E}_{{{{\rm{Drug}}}},{{{\rm{D}}}}2{{{\rm{l}}}}}$ (Supplementary Fig. 8).

As a second approach, we deployed the ${\alpha }^{+},{\alpha }^{-}$ obtained from the placebo and bromocriptine conditions, to train an RL agent to perform the task from Cools et al. 2009 using our RL model with P and N populations. The task was run by first allowing the agent to have a block of 50 trials of practice and then performing a set of 20 reversal blocks. Each reversal happened once the number of consecutive correct responses exceeded a randomly sampled number of trials between 5 and 10. The RRL was calculated as in Cools et al. 2008.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.