Introduction

Humanity has always been fascinated by the concept of randomness. Chance decisions are often considered to be of mystical origin, associated with a perception of fairness and divinity. Various types of dice-like objects, dating back thousands of years, have been identified across many cultures, which underpins this fascination and showcases early applications of randomness and chaos1.

One of the first mathematical descriptions of randomness in the context of probability in gambling is credited to Gerolamo Cardano2, with probability theory subsequently originating in the 17th century3. Today, randomness is frequently used as a tool, for example, to test statistical theories by sampling experiments or to find approximative solutions to complex problems. With the arrival of the digital age, the importance of randomness has perhaps found its peak as a fundamental tool for computer science and information theory. Random numbers have become indispensable for modern cryptography4, and the concept of (Shannon-) entropy is essential to today’s understanding and description of information and signal transmission5.

While randomness is, for the abovementioned reasons, frequently used for some types of data analysis and highly sought after in computer science, many experimentalists, in particular within life science, tend to consider it a nuisance in the lab. Randomness interferes with experiments, adds noise, and blurs signals. Considerable time and effort go into performing significance tests of experimental results, mathematically removing and excluding random effects as best as possible. We argue that these difficulties caused by randomness can sometimes blind natural scientists to its other, fascinating side that can valuably contribute to applied science. Therefore, we want to offer a perspective that embraces randomness as something of use, looking for synergies to inspire more interdisciplinary research. We argue there is an increasing incentive to look at experimental science from an information point of view, addressing scientists from all backgrounds. By bringing together these disciplines, we hope to re-instill a fascination for randomness in physical and (bio-)chemical systems and thus address a topic that falls through the gaps of most university curriculums.

As this perspective encompasses a vast and multidisciplinary topic, we cannot hope to cover all relevant aspects in depth. Rather, this work is to be understood as a high-level overview. We abstain from extensive mathematical descriptions and will often use simplifications for a more conceptual understanding of complex theories, additionally drawing on subjective accounts. We use examples from our viewpoint as experimental scientists who have collaborated with information theorists and computer scientists, looking at the molecular world from an information perspective. First, we give a very brief overview of the notion and significance of information in the digital age, leading to a high-level introduction of various entropy terms and their relevance in the physical sciences and information theory, highlighting where they intersect. We further discuss the importance of random numbers sourced from physical systems and give examples where thermodynamic entropy and stochastic processes are directly translated into digital randomness. In particular, we focus on two applications, where information is both physically sourced and encoded, and where random processes translate information to entropy: Physical unclonable functions (PUFs) and molecular information technology (i.e., data storage, computation, and cryptography). Finally, we conclude that an inquisitory look at randomness with a basic understanding of the information theoretic concepts and physical random processes can reveal new synergies and lead to fruitful interdisciplinary collaboration.

Information technology: short history and theoretical concepts

The information age

In a lecture on the concept of information in physics, T. Dittrich6 describes information as a defining cultural leitmotif of our time, a concept marking a scientific revolution in the sense of Kuhn7 with concomitant socioeconomic changes of global significance.

This aligns with the latest paradigm shift within human history as outlined by Hilbert et al.8 (Fig. 1), and is associated with the third industrial revolution and the arrival of the information age. The beginning of this transformation has been associated with the invention of the transistor (1947)9 and the optical amplifier (1957)10 and can be generally characterized as the transition from analog to digital information, going hand in hand with an economic shift from conventional producing industries towards information technology8.

Fig. 1: Technology progress from early human history to the digital information age.
figure 1

Based on Hilbert8.

Full size image

The year 2002 can be considered another important milestone for the digital age, as this was the time when humanity was first able to store more digital than analog information11. In the 2010s, in every 2.5–3 year interval, our capability of information storage exceeded the previously stored information integrated over all of humanity since the dawn of civilization8. This accelerated transition has had far-reaching implications for economics, communication, data and knowledge management, and the fundamental way humankind interacts on both the individual and the societal level. Indeed, information technology has become such a vital part of contemporary society that it permeates almost all aspects of our everyday lives. Information has therefore also become a unifying concept relevant to all research fields with their respective subdisciplines. Molecular science and information are perhaps closer entwined than ever -  for example, in the efforts going towards quantum computing.

However, along the lines of Claude Shannon’s warning in his now famous publication “The Bandwagon”12, willy-nilly applying concepts from information theory to other fields without the necessary scientific rigor and experimental testing can be more harmful than beneficial. This general concern regarding the over-use of certain terms due to their popularity is still as relevant today as it was at the time of Shannon’s letter in 1956. Therefore, a careful dissection of the connections between experimental sciences and information theory is necessary, along with a proper distinction between different meanings and formalisms of similar concepts across disciplines.

Entropy across disciplines

A key concept that arguably marks one of the closest connections between information theory and the physical sciences is entropy. Thermodynamic entropy is cited as a core principle for phenomena as fundamental as the formation of the universe13 and the development of life14, perhaps contributing to the term’s association with the intriguing and the mysterious in popular perception15.

However, there are many definitions of entropy used across different fields. Entropy as a concept is thus of high relevance not only in sub-disciplines of physics (thermodynamics, statistical mechanics, cosmology, etc.) but also holds meaning in other research areas in both the natural and social sciences16,17. In The Entropy Universe17, Ribeiro et al. give an overview of these entropy terms and their relations (Fig. 2). Their comprehensive review not only delves deeper into the history of entropy and how the different terms emerged but also provides mathematical definitions, grouping and relating them to each other. For the purpose of this perspective, we will focus on Gibbs and Shannon entropy, as the two are important nodes within this relational framework and share a very similar mathematical format. Moreover, they were established early on, providing the basis for subsequent research. They remain very frequently cited and are central to various disciplines; Gibbs entropy is known to most experimental scientists as a basic principle from their undergrad thermodynamics course, and Shannon entropy is equally fundamental to computer science and information theory.

Fig. 2: The Entropy Universe.17 Graphic from Ribeiro, M. et al.
figure 2

The Entropy Universe. Entropy 2021, 23, 222. Creative Commons (CC BY 4.0).

Full size image

However, Gibbs and Shannon entropy share more than their essential role in the respective fields. Even though they describe different phenomena, we can look at many systems under the lens of both of them.

Thermodynamic entropy and the Gibbs equation

The term entropy was first introduced by Rudolf Clausius as an extensive thermodynamic variable when characterizing the Carnot cycle18, and is thus central to the second law of thermodynamics. Entropy represents a measure of energy that cannot be converted into work by a closed system19. Since entropy is a non-conserved property in irreversible processes and all natural processes are irreversible, the thermodynamic entropy of the universe always increases20. Entropy is therefore often described as the property that gives the universe an arrow of time21. It is, for example, both necessary and useful for the understanding of the possibility and directionality of chemical reactions and in the calculation of the efficiency of heat engines22,23. In the context of work done in a system during a non-equilibrium transformation, the more recent developments of the Crooks theorem24 and the related Jarzynski equality25 are relevant generalizations of the second law. However, in the following discussion, we focus on the equilibrium state.

There are several approaches to mathematically formulizing entropy. The most useful one for understanding the connection between entropy and information is the statistical description. This equation describes thermodynamic entropy based on the behavior of a system’s constituent particles. Since it is impossible to know all the coordinates of moving particles, this is done by using a statistical description of microstates and their probabilities. Such averaged, probability-weighed microstates can describe the macroscopic properties of a system26.

We can then calculate a system’s entropy using the Gibbs entropy equation:

$$S=-{k}_{B}{\sum}_{i}{p}_{i}\, {{\mathrm{ln}}}({p}_{i}).$$
(1)

In this equation, kB is the Boltzmann constant, and pi refers to the probability that the system is in a given microstate. Assuming an isolated system in thermal equilibrium, all microstates are equally probable. This, together with the fact that their probabilities must sum up to 1, simplifies the equation to the so-called Boltzmann’s entropy formula:

$$S={k}_{B}\, {{\mathrm{ln}}}(W),$$
(2)

Where W is the number of microstates that the system can occupy27.

Most of the possible microstates are “disordered”, meaning the system is far more likely to be in a “disordered” than an “ordered” state, which is where the popular description of entropy as a measure of disorder comes from. Boltzmann himself stated that entropy arises from the fact that disordered states are the most likely ones in a system of mechanically colliding particles28.

Shannon entropy

While Gibbs entropy describes microstates in a thermodynamic system, Shannon entropy deals with a system’s information. In his famous publication “A mathematical theory of communication”, Claude Shannon formulated two main information theoretical properties5:

First, the self-information content I of a random event is a function of the probability (P) of the event, with highly probable events carrying little information (little surprise).

$$I=\,-\log \left(P\right)$$
(3)

Secondly, for a discrete random variable with symbol probabilities p1…pn the entropy (i.e., Shannon entropy H) is defined as:

$$H=\,-{\sum }_{i=1}^{n}{p}_{i}\, {{\mathrm{log}}}({p}_{i})$$
(4)

Here, pi is the probability of symbol i, n the number of possible symbols, and the logarithm is with respect of base 2 for an expression of the entropy in bits.

Shannon developed this theory in the context of what he called the “fundamental problem of communication”—the issue for a receiver of a message to be able to identify what data the signal transmitted through a channel contains. He concluded that information entropy marks an absolute theoretical limit on how well data can be losslessly compressed in a channel, which became famous as the source coding theorem. This work still has important implications for data storage and compression, as well as cryptography and cryptanalysis today.

Entropy as a concept to bridge natural sciences and information theory

Relationship between thermodynamic and information entropy

The relationship between thermodynamic entropy and Shannon’s entropy of information has been widely discussed29. The two entropy terms were connected by Landauer30, who related logical operations to thermodynamic effects. The resulting Landauer principle states that irreversible logical operations, e.g., erasing data, also lead to physical irreversibility, under generation of heat equal to at least kBT, with kB being the Boltzmann constant and T the temperature at which the operation is performed. More recently, fluctuation theorems and stochastic thermodynamics have been applied to further understand the physical connections between thermodynamics and information, taking the gedanken experiment of Maxwell’s demon31,32 as a basis. However, some fundamental questions concerning the physical relationship between information and thermodynamics are not yet fully solved33.

Jaynes34, on another note, found that information I and thermodynamic entropy S can both be expressed in bits. Layzer35, along similar lines, found a quantitative relationship between information and entropy. He thought about systems in terms of their finite information content, meaning there is a maximum of information, Imax, that can be known about a given system. This information is divided into known (I), and unknown (H) information, whereby H is equal to thermodynamic entropy expressed in bits. This leads to a conservation law, stating that the sum of known information and entropy is constant:

$${I}_{\max }={H}_{\max }=I+H={const}$$
(5)

This means no gain of information can be attained without losing an equal amount of entropy and vice versa35.

To summarize, the expressions of both thermodynamic and information entropy have similar forms and can be expressed in bits. They are both formulated probabilistically, reflecting the fact that both are descriptions of microstates within the space of possibilities. However, their meaning is different: While thermodynamic entropy can be considered a measure of thermal “disorder” or randomness of a macroscopic system, information entropy refers to the arrangement uncertainty of carriers of information. This bridge between thermodynamics and information theory becomes practically relevant when, for example, characterizing and exploiting physical systems for generating randomness that can be used for e.g., cryptography.

Applications of randomness

Entropy and randomness in the form of stochastic processes are omnipresent in nature and therefore touch many scientific disciplines. Nevertheless, most experimental scientists often experience these processes as mere noise in a measurement channel. Therefore, in many fields, random effects are usually considered uninteresting at best, while in the worst case, they become a major obstacle for data measurement and analysis. It is relatively rare that a random process is at the center of attention rather than a side effect to be dealt with.

This is at odds with the significance of randomness in computer science. Randomness or pseudorandomness is a critical resource that can make algorithms faster or simpler, useful across a wide range of applications. A key benefit of randomness in algorithms is to avoid worst-case situations in favor of manageable average-case scenarios. This is, for example, leveraged in the randomization of sorting algorithms36. Further applications include randomized testing, for example, to quickly determine whether a number is prime or not37, and Monte Carlo methods to solve numerical problems by simulating random samples and using statistical analysis to estimate quantities38. For efficient data structures, randomized hash functions are leveraged, and in networks, randomization is used to avoid synchronization problems39. Another application closely related to randomness is cryptography. In this context, randomness and entropy are informally understood as unpredictability40: The more unpredictable a sequence of bits, the higher the Shannon entropy, and the stronger the cryptographic security. Pattern-devoid cryptography is therefore considered the most secure and is proposed as the future of cryptography in a world where artificial intelligence and quantum computing threaten current systems41,42.

Access to truly random numbers is therefore vital for modern cryptography, and their quality is crucial for the system’s security. Since the advent of personal computers, cryptographic algorithms are more present than ever, with passwords, online banking, secure internet communication, and many other services relying on encryption protocols43. Within these applications, random numbers are, for example, used for secret- and public-key cryptography, to seed pseudo-random number generators, and as padding bits44. The availability of high-quality random numbers is therefore essential for cryptography and the security race between attackers and defenders.

Using physical sources of randomness and entropy

For the abovementioned reasons, random numbers are in high demand. Kerckhoffs’ principle of cryptography states that a cryptosystem should be secure even if everything about the system is known (except, of course, the key)45, by definition ruling out security by obscurity (such as steganography). Shannon reformulated this principle as the assumption that “the enemy knows the system”, nowadays known as Shannon’s maxim46. From that, it follows that a random number generator suitable for cryptography must produce entirely unpredictable bits even if every detail about it is known, which may limit pseudorandom (i.e., algorithmic) number generators (PRNGs) for that purpose. True random number generators (TRNGs), on the other hand, exclusively source randomness from fundamentally nondeterministic physical processes43, highlighting the importance of entropy in natural systems.

For typical applications in computation, separate hardware TRNGs can be grouped into different sub-categories, as shown in Fig. 3, depending on the source type. However, independent of the category, a TRNG extracts some form of entropy from a system and expresses it in bits.

Fig. 3: Classification of random number generators (RNGs).
figure 3

Physical RNGs are sub-categorized into noise-based, chaos-based, free-running oscillators and quantum-based sources. Graphic based on Stipčević and Koç43, with added examples for each subcategory108,121,122,123,124,125,126.

Full size image

Different TRNGs have distinct advantages and drawbacks. For example, they have different bit streams and (random) information densities, are more or less cross-operable with computational systems, and can have a bias towards 0 or 1, meaning debiasing and post-processing are needed.

A typical and easily accessible source of randomness is electrical noise, which has been implemented in many variants47. Notably, laser phase noise48, and noise extracted from super-luminescent LEDs49 have also been reported as TRNGs. An interesting non-electronic TRNG based on noise uses astronomical imaging, drawing entropy from the randomness of cosmic rays50. Examples of quantum random number generators include radioactive decay51 and photon beam splitters52. A notable representation of a chaos-based random number generator is lava lamp imaging, which has been reported by cyber security provider Cloudflare53. However, the examples do not end there, and many other sources of entropy have been explored for random number generation, including several biological systems54,55,56. On the one hand, this diversity of RNGs makes for a versatile toolbox to e.g., generate seeds for cryptosystems. At the same time, it also showcases the usefulness of random processes across scientific disciplines.

Physical unclonable functions

An example that combines physical entropy and cryptography more directly than mere random number generation are PUFs. In this case, physically sourced randomness is used to implement cryptographic one-way functions within objects. The term one-way function refers to a type of mathematical algorithm that is easy to compute in one direction, but computationally hard, i.e., in practice infeasible, to invert57. Due to their mathematical complexity, such functions are widely used in cryptography, and vital in many applications such as password protection, online banking, or blockchain technologies.

In 2002, Pappu et al.58 introduced the idea of using an object with random components as a physical version of a one-way function. It is based on a token consisting of a hardened epoxy with encased glass spheres, which are randomly arranged due to random elements in the manufacturing process. Shining a laser on the token generates a 2D speckle pattern that is specific to the incident angle and that can be mapped to a 1D bitstring, generating a key. Due to the token’s random microstructure, the speckle cannot be predicted, and neither can the laser orientation be inferred from it (see Fig. 4). Still, the diffraction pattern is reproducible, its generation corresponding to a “computation” performed by the token as a response to the laser beam. This mimics the working principle of mathematical one-way algorithms or hash functions, but in this case directly uses the entropy of a physical process for a cryptographic system, which can be analyzed in terms of information entropy.

Fig. 4: Physical unclonable functions.
figure 4

a For the same challenge (input), the response (output) depends on the physical properties of the PUF. b for the same PUF, the response depends on the challenge. c for the same challenge and PUF, the response has to identical, independent of the timepoint of the operation. d Example of an optical PUF similar to the one reported by Pappu et al.58: a laser source is shone at an optical diffuser that generates a speckle response based on the input (challenge) and diffuser (PUF) properties. Graphic from Mesaritakis et al.127, Creative Commons (CC BY 4.0).

Full size image

This marks a form of object-bound cryptography. Re-generating an equivalent object is exceedingly improbable, and the random complexity is too high to sufficiently analyze and/or purposefully reproduce it. This gives PUFs a layer of security tied to their physicality —not only is the randomness inseparably connected to the object, but it cannot be accessed by any means other than physical examination. PUFs are therefore cited as an alternative to mathematical one-way algorithms and cryptographic hash functions, some of which are known to be vulnerable to attacks by quantum computers58, e.g., through the realization of Shor’s algorithm for prime factorization59.

Many different implementations of PUFs have been reported since the realization of the above-described optical PUF. The increasing amount of literature on the subject has led to an emerging research field, with PUFs being theoretically and experimentally analyzed and classified based on their properties, applications, and security60,61,62,63. One common problem that plays into such evaluations and that must be tackled when practically implementing a PUF is the matter of error correction64. In contrast to mathematical functions implemented in a computer, which are essentially error-free, physical processes are inherently noisy, which necessitates error-correction to extract a reproducible key from the measurements of a physical process. While PUFs leverage random processes for means of cryptography and authentication, the measurements from which a signal has to be extracted are corrupted by random noise. This is typically achieved through so-called fuzzy extraction algorithms65,66, an early implementation of which was published by Guajardo et al.67 Such algorithms use a part of the information of the PUF readout to generate helper data that can be used to retrieve the same key from a future readout, despite that readout differing slightly from the first one due to noise.

Beyond the optical PUF described above, there exists a variety of practical implementations using different substrates. A large body of research focuses on silicon-based PUFs. For example, an arbiter PUF was proposed that uses random interconnect and transistor gate time delays caused by manufacturing variabilities68. SRAM PUFs, on the other hand, use the favored SRAM cell power-up state as the response and the cell’s address as the challenge69.

Applications such as anti-counterfeiting allow for a broader selection of substrates. Many of them are based on nanostructures, for example, nanoseeds based on PbS quantum dots and Ag nanocrystals70, multilayer superpositions of metallic nanopatterns replicated from self-assembled block copolymer nanotemplates71, and semiconducting polymer nanoparticles as fluorescent taggants72. Edible unclonable functions in the form of spray-tagged fluorescent silk proteins mark an interesting example using biomolecules73.

Despite their differences in substrate, methodology, complexity, and applicability, what these implementations have in common is their use of a random physical manufacturing process with an analytical method that is able to generate reproducible challenge-response pairs in the respective system—be this optical, electronic, chemical, or spectroscopic. Any system involving randomness that can be read out in such a manner can be considered the starting point of a potential PUF, which applies to a plethora of processes that have yet to be explored.

However, this research field is not merely an abstract study of physical systems, but PUFs have relevant applications. They have gained importance in the electronics industry, which is faced with numerous challenges regarding the authenticity and safety of information, products, and identities. For example, memory-based intrinsic PUFs are being used to authenticate a memory chip’s unique identity through random variations in semiconductor production. Such secure device fingerprints are considered as a trust anchor for internet of things applications74. It is therefore to be expected that PUFs will increase in relevance with the arrival of Web 3.0 and the continuing implementation of blockchain technologies, bridging the physical and the digital world.

PUFs are therefore a great example of how entropy sourced from random processes can be made accessible and put to use for real-world applications. Their physical randomness enables cryptographic applications, with the system’s Shannon entropy determining its security. Hence, PUFs represent one of many instances where an experimental procedure can be understood and characterized as an information processing step, with binary numbers as input and output.

Molecular information technology

While not all PUFs leverage a molecular form of entropy, the underlying concept overlaps with the broader field of molecular information technology. This research area considers information processing by molecular means, which is a common feature in biological and chemical systems75.

Understanding DNA’s biological function as the information medium of life according to the central dogma of molecular biology has led to a profound transformation of the view of biology, which is now considered an information science76,77. Today, we understand that DNA is by no means a static data storage medium, but it can be copied, edited, deleted, and translated by molecular machines. Throughout these processes, (thermodynamic) entropy and randomness in the form of stochastic effects play a significant role in evolution. Living systems are dynamically unstable, and different forms of randomness are key components of the ongoing development of life. This applies to both ontogenesis and phylogenesis, with random events having an impact on multiple levels. More specifically, genetic drift78, crossing-over during meiosis79, and horizontal gene transfer80 are some examples of processes contributing to genetic changes that are at least partially governed by randomness (i.e., probabilistic, unpredictable effects) and that enable evolutionary adaptation.

The understanding of these processes and the perception of DNA as a dynamic information carrier can be considered the door opener for digital applications within a chemical substrate. This transferability between a molecular understanding of information (such as the chemistry of DNA) and digital data was, for example, suggested by physicist Richard Feynman in a 1959 lecture, where he mentioned the idea of storing information in arrangements of atoms81,82. In the 1960s, the concept of using a DNA sequence consisting of the nucleobases A, C, G, and T for digital information storage was formulated by Norbert Wiener83. Remarkably, decades later, the first implementation of DNA-based data storage was not primarily a scientific endeavor, but an art project by Joe Davis. In 1996, he stored 35 bits of digital information encoding an icon called Microvenus in an 18-nucleotide sequence84. In parallel, it was computer scientist Leonard Adleman who first implemented DNA-based molecular computation by solving complex combinatorial problems through biochemical operations85.

Since this pioneering work, applications of synthetic DNA in information technology have gained versatility86. Leveraging the extremely high information density of >107 GB/g87,88, digital data storage in DNA has advanced significantly, highlighting the intersection between biotechnology and computer systems89. Notable innovations include refined encoding and storage, for example, by enabling random access90 and employing error-correcting schemes91,92. This overall progress has enabled the implementation of both in vitro and in vivo rewritable databases93,94. Step-by-step guides95 now enable anyone with basic programming knowledge and access to publicly available lab services to write and read their data in DNA, which can be used as a starting point for transferring the concept to adjacent technologies.

On the computational side, matrix multiplication96 and addition97 have been achieved, and the NP-complete Boolean satisfiability problem was solved using DNA98. With the implementation of DNA logic circuits and programmable gate arrays99,100,101,102, the field is continually moving closer to general-purpose computation.

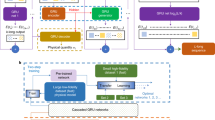
Another interesting milestone, reported in the 1990s, was the development of DNA programs able to break the U.S. government’s Data Encryption Standard (DES) in an estimated 4 months of laboratory work as opposed to 10,000 years on a computer at the time103,104,105. This lay the groundwork for the emerging field of DNA cryptography, including steganography106,107. Notably, DNA has also been shown to work as a random number generator108: A mix of all four nucleobases for chemical synthesis of DNA produces random strands, which can then be read using next-generation sequencing. In this system, the entropy of the intermixed fluids translates into DNA sequences, which store the randomness in a linear form that can easily be read in a binary format with a density of up to 2 bit/position (the four bases representing 00, 01, 10, and 11, respectively). This is an example of random digits stemming from a mix, which is guided by thermodynamic principles109. The synthesis (and, by extension, sequencing) brings what we understand as Gibbs entropy into a quasi-digital format that can be analyzed in terms of Shannon entropy (Fig. 5). This also gave rise to the recent implementation of DNA-based chemical unclonable functions, which work in analogy to PUFs, but enable decentralized authentication and product tagging110,111. However, aside from random DNA synthesis, mixing of bases can also be leveraged for DNA data storage using a composite letter code based on mixing ratios, as implemented by Anavy et al.112. This method increases the Shannon entropy per DNA synthesis cycle, allowing for more efficient data writing.

Fig. 5: Schematic illustration of thermodynamic and information entropy.
figure 5

Examples of low and high entropy states (left). Random DNA synthesis is a tool that can convert the thermodynamic entropy of a mixture of nucleoside phosphoramidites to DNA sequences of high information entropy (right).

Full size image

Molecular data storage and unclonable functions using DNA as a substrate are thus illustrative examples of the link between Gibbs and Shannon entropy. Looking at Eq. (5) and the conservation law between known and unknown information—or “useful” and “random” information, unclonable functions maximize the latter, while data storage aims at minimizing it. This is achieved by error-correcting codes, which can be considered as compensating for the noise introduced by Gibbs entropy in the read-and-write process. Fountain codes used for error-correction are a notable example for this, because they themselves rely on random numbers to recover data based on randomly selected subsets92.

What unifies the research described above is the view of DNA’s chemical properties from an information perspective. Its highly direct physical representation of digital information as we read and understand it makes DNA an ideal medium to bridge the physical with the digital world. With these advantages in mind, several other molecular substrates are now under investigation as data carriers and computers. This includes biomolecules such as peptides and proteins113,114,115, but also various synthetic polymers116.

Molecular data storage and computation are expanding fields with large research communities and broad funding schemes, as well as ongoing commercial efforts via venture-funded university spin-off companies. Moreover, the innovations made within DNA information technology feed back into biology, for example by advancing synthesis and reading technologies. This example of mutual benefit demonstrates how viewing a principle previously assigned to one discipline from an information perspective can spur new inter- and transdisciplinary research.

Conclusion and outlook

In this work, we have given an overview of different understandings of entropy and their intersection within experimental disciplines. This perspective was motivated by our own fascination with randomness and entropy in experimental systems, and how these concepts connect to information theory. We have provided examples where this connection has been applied, highlighting the importance of random numbers and physical sources of entropy, and finding synergies by looking at physical systems from an information perspective. Presenting the use cases of PUFs and molecular data science, we showed that valuable contributions to information technology, computation, and cryptography were made through highly inter- and even transdisciplinary collaborations. We therefore conclude that it is worth looking at experimental systems through an information lens and vice versa. We believe that knowing the different entropy terms, as well as understanding the relationship between randomness and information, can facilitate this change in perspective.

In addition to using established terms of entropy of equilibrium systems - as done in this perspective - randomness, entropy, and information also intersect in the research field of stochastic thermodynamics and fluctuation theorems in non-equilibrium nanoscale systems24,25,117. This is relevant for molecular and colloidal systems often investigated in the experimental sciences. While the effects of the main fluctuation theories can be experimentally observed118, and these theories have been used to connect entropy and information119,120, further research on technical use cases is required.

More generally, we hope that this high-level overview of the subject will facilitate collaborations by presenting the theoretical basics as well as some applications of physical information systems. We believe this connection to be helpful in finding common ground between experimental scientists and theorists. As specialists, we are sometimes ignorant of disciplinary bias that shapes how we look at systems and data, perhaps even assuming all scientists think in the same basic concepts and use similar mental models. Based on our personal experience of working within interdisciplinary consortia, we have found, however, that this is not always the case. Collaborating with chemists, biologists, physicists, material scientists, engineers, mathematicians, computer scientists, and multidisciplinary artists has sensitized us to the difficulties of communicating across disciplines and of publishing to broader audiences. Successful inter- or even transdisciplinary collaboration, therefore, often requires overcoming these gaps by reflecting and communicating what we take for granted in order to find a common language and understanding.

Ultimately, we therefore hope this work will spur the fascination for randomness, entropy, and information in physical systems, thus inspiring new cutting-edge research by encouraging and facilitating the exchange between experimental researchers and information scientists.