Introduction

The fields of non-linear dynamics and chaos theory deal with deterministic systems that exhibit complex behaviour and are characterised by their strong dependence on initial conditions1,2,3. The discovery of chaotic behaviour in dynamic deterministic models broke the assumption that deterministic systems were fully predictable1,4. Since then, fractals (i.e., Rényi dimensions5) have played an important role describing the complexity of dynamic systems2. Biological systems are ideal to study non-linear dynamics because of their vast complexity, their obvious dependence on initial conditions and their lack of predictability in the long term (e.g., population dynamics, infection or growth rates6,7). Non-linear dynamics and fractals have found multiple applications in the field of biology, from investigating the chaotic nature of population dynamics8,9 to relating the structural and functional temporal complexity of the human brain10,11. Even though chaos was thought to be rare in nature for decades, recent analyses using improved methodologies and long time series suggest that chaos, nonlinear and complex dynamics are more common across nature than previously thought3,7,9,12.

The correlation dimension4,5 is an entropy-based metric that provides an estimate of the degrees of freedom of the system (e.g., the number of different drivers controlling its temporal behaviour). Hence, the correlation dimension can be used as a metric of temporal complexity. Systems that behave more periodically are characterised by an attractor (i.e., the hypervolume in phase-space where the system is preferentially found) with very few degrees of freedom (Supplementary Fig. S1a). These systems present low values of correlation dimension, low temporal complexity, and thus, high predictability. Instead, chaotic systems are characterised by a larger number of degrees of freedom, so they have higher correlation dimension values, and are only predictable in the short term (Supplementary Fig. S1b). Finally, completely random systems, or systems without any kind of underlying pattern, have infinite degrees of freedom (i.e., non-saturating or infinite correlation dimension), and are thus unpredictable at all timescales (Supplementary Fig. S1c). Nonetheless, other methods used to quantify the temporal complexity of time series, such as ordinal pattern statistics, permutation entropy or Fisher information, typically estimate very low complexity in completely random time series. This is because random time series lack the meaningful structure or patterns that these complexity measures are designed to capture13,14,15.

Changes in the attractor of a system (i.e., changes in the temporal dynamics of a biological system) result in alterations in its temporal complexity; significant drops or increases in the degrees of freedom of the attractor are indicative of regime shifts within the system4. This is why the correlation dimension has been employed to investigate the nonlinear dynamics of environmental and biological time series16,17. For example, hydrological studies have provided strong evidence for low-dimensional chaos in precipitation and stream runoff time series, suggesting variations in the dimensionality of their attractors amongst catchments18,19. Other studies have pointed out that the temporal complexity of climate subsystems (e.g., temperature and precipitation) may differ between dry and humid climates20. In biological systems, low-dimensional chaos has been detected in fruit production time series17 and several studies have demonstrated that changes in the short-term temporal complexity of organismal functions (e.g., heart rate) correlate with fluctuations in the health status and the activities performed by that organism21,22. Changes in temporal complexity of organismal and ecosystem level properties could also happen due to changes in limiting factors, such as constrained photosynthesis and respiration due to droughts or weather extremes. At larger timescales, temporal complexity of ecosystem functioning could change due to ecosystem shifts, for instance, from a forest to a savannah, losing or gaining different species with distinct phenology and functioning.

At the individual level, the temporal dynamics of electroencephalograms (a medical test that records electrical activity in the brain) have been found to become random when individuals are awake, present low-dimensional chaos when sleeping (4–5 degrees of freedom) and, most interestingly, drop down to around 2 degrees of freedom during epileptic crises22. More recently, a decrease with age was detected in the structural complexity of the human brain10. Other studies have found that the attractor of the heart rate of a healthy person is more complex than that of a person that died of a cardiac arrest a few days later, which became much more periodic21. These results seem to indicate that reduced complexity, either temporal or structural, is related to detrimental effects for the functioning of key organismal functions, because it indicates a reduced capacity of the system to react to environmental stimuli (e.g. climate or hydrological changes in ecosystems). The temporal complexity in the behaviour of a system should reflect the capacity of the system to exist in a wide range of states, in response to a wide range of drivers and to withstand large environmental variability. Hence, temporal complexity of a biological system should represent endogenous (i.e., internal functioning) and exogenous (i.e., environmental variability) sources of complexity. Whether high or low short-term (from minutes to days) temporal complexity in the functioning of entire ecosystems relates to other ecosystem properties that drive or indicate their status (e.g., annual production, interannual variability, biomass accumulation or species richness) is so far unknown. To date, no study has focused on the temporal complexity of the functioning of ecosystems and its drivers beyond assessing the non-linearity of population dynamics9,12. While there is a long history of examining ecological stability23,24,25 the metrics tend to focus on simple variability and response rates. Here we propose that the more complex temporal dynamics captured by the correlation dimension may provide additional insights into the dynamics of ecosystems, e.g. their capacity to respond to stimuli or their predictability, rather than just variability.

The carbon (C) cycle of an ecosystem integrates the C uptake and release processes of all organisms within the ecosystem and can be approximated by estimating the gross primary production (sum of all CO2 entering the system through photosynthesis) and the ecosystem respiration (sum of all respiratory CO2 production). Studying nonlinear dynamics of the C cycle is a promising line of research because assessing these dynamics can help identify the conditions under which ecosystems experience changes in their short-term functioning (e.g. half-hourly). This understanding could elucidate the implications of short-term changes in functioning for the resistance and resilience of ecosystems to disturbances26, which co-determine ecosystem functioning at longer time-scales, such as annual C uptake or the interannual variability in C uptake. Identifying the drivers of the temporal complexity of the C balance in ecosystems is essential for improving predictions of the coupled C-climate system in the future. This is because we have reasonably good projections for future climate change, but the future trajectories of C sinks, on which climate change projections and mitigation policies critically depend, remain highly uncertain27.

Hence, we here use data from 57 ecosystems monitored with eddy-covariance towers, including 36 forests, 11 shrublands and savannahs, and 10 grasslands, to calculate the correlation dimension of half-hourly time series of gross primary production (GPP, representing ecosystem photosynthesis), ecosystem respiration (Re; integrating respiration from both the autotrophic and heterotrophic components) and net ecosystem production (NEP, as the difference between GPP and Re) as a proxy for the temporal complexity of ecosystem functioning. We investigate the effects of annual mean C fluxes and their interannual variability and seasonality, as well as climate, species diversity, leaf nitrogen (N) and phosphorus (P) concentrations, atmospheric N deposition, standing biomass and stand age on the temporal complexity of ecosystem functioning. These are all factors that have been repeatedly reported to be important drivers of ecosystem C fluxes28,29,30. We also study temporal trends in short-term temporal complexity of ecosystem functioning and investigate the drivers of these trends.

We hypothesise that: i) ecosystems with greater short-term temporal complexity in weather patterns will generally exhibit higher temporal complexity in ecosystem functioning due to the dependence of C fluxes on climate and environmental fluctuations31,32,33 (H1,), ii) ecosystems with greater temporal complexity are expected to have larger annual C fluxes for two reasons 1) reduced temporal complexity has been shown to be detrimental to the functioning of organisms16, and 2) more productive ecosystems can support a larger number of interacting organisms, resulting in greater exchanges of energy and matter. This capacity allows for the temporal superposition of the functioning of more organisms and processes, leading to a more complex temporal behaviour at the ecosystem level (H234,35,), and iii) old forests, or ecosystems with large standing biomass, are expected to exhibit lower temporal complexity in GPP compared to young forests or ecosystems with minimal biomass. This phenomenon is attributed to their reduced sensitivity to short-term environmental fluctuations and the theoretical decrease of productivity36 (GPP to biomass ratio) of the autotrophic compartment over time. We conjecture the opposite for Re due to a more developed and species-rich heterotrophic compartment leading to increased heterotrophic respiration per unit of biomass production37,38 (H3). We further explore the causal relationships between annual C fluxes, their short-term temporal complexity and their interannual variability using directed acyclic graphs to investigate how short-term ecosystem responses relate to annual and multiannual temporal behaviour.

Results

Temporal complexity in C fluxes and weather variables

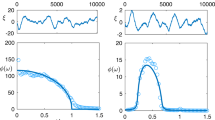
We found cone-like attractors for GPP and NEP, mostly presenting daily cycles (typically showing lags around 6 h per dimension), while for Re they were generally long and relatively thin (Fig. 1). We speculate that long-thin attractors could indicate that there is no differential seasonal response in the system, while cone-like attractors could indicate that the system behave differently depending on the season. Interestingly, clearer trajectories seemed more likely to occur in C flux variables with greater short-term temporal complexity (hereafter, temporal complexity), hence showing that more complex attractors are related to higher dimensional chaotic dynamics. However, further research is needed to confirm whether the interpretation of the shapes of these attractors would hold for other systems. Regarding weather, temperature and VPD showed tunnel-like attractors (Supplementary Fig. S2) indicating diurnal cycles over seasons, and precipitation presented mussel-shaped attractors mostly due to the smoothing performed for visualisation purposes. Wind speed generally presented irregular attractors with no clear shape, coinciding with the highest temporal complexity. Carbon fluxes were generally less temporally complex than weather variables, both when analysing multiannual time series and individual years (Supplementary Fig. S3).

Fig. 1: Examples of the three-dimensional attractors of gross primary production (GPP), ecosystem respiration (Re) and net ecosystem production (NEP).
figure 1

Attractors displayed are from the two sites showing the lowest (top row) and highest (bottom row) correlation dimension in their fluxes within our dataset (trajectories were smoothed using local regressions spanning 48 observations to improve visualisation). Panels a–c show fluxes for site FI-Sod (Sodankyla, Finland) for the year 2001. Panels d–f show fluxes for site FR-LBr (Le Bray, France) for the year 1997. See Supplementary Fig. S1 for idealised cycles and their interpretation. Blue lines of the attractor indicate winter, red indicates spring, yellow indicates summer and grey indicates autumn.

Full size image

When analysing the entire time series per site (Supplementary Fig. S3a), GPP typically presented less than 4.5 degrees of freedom, being the least temporally complex variable amongst C fluxes (Tukey test for multiple comparisons, N = 171, p < 0.001, against Re and NEP). Degrees of freedom of Re ranged from 1.7 to almost 7.8 and presented, on average, significantly fewer degrees of freedom than NEP (p < 0.001), which ranged from 3.5 to 8.5. Regarding weather variables, precipitation presented the lowest average complexity ranging from 0.2 to 6.3 degrees of freedom (p < 0.001, against all other weather variables), most likely because zero is by far the most likely value of precipitation at the half-hourly scale. Degrees of freedom ranged from 0.8 to 10.2 for VPD, from 4.5 to 11.5 for temperature, and from 8.0 to 14.2 for wind speed, with VPD and wind speed being, respectively and on average, the least and the most complex weather variables amongst these three (p < 0.001, for all three pairwise comparisons).

Temporal complexity of GPP presented a clear seasonal pattern, being higher in spring and especially summer compared to winter and autumn when they presented a more periodic behaviour (Supplementary Fig. S4, p < 0.001). In contrast, Re and NEP showed higher complexity during winter and summer compared to spring and autumn. Seasonal differences in the temporal complexity of C flux variables were generally larger than those of weather variables (Supplementary Fig. S5), indicating a clear biological signature.

Drivers of temporal complexity in ecosystem functioning

Our analyses, combining the best performing models (ΔBIC < 2) and using all forest, shrubland and grassland ecosystems (N = 57 sites) indicated that the temporal complexities of GPP and Re were negatively related to their interannual variability, one of their most important predictors (see Supplementary Materials: Model summaries, Section 1, Supplementary Tables S1–S3). Additionally, ecosystems with stronger seasonality presented lower temporal complexity in GPP. Temporal complexity in NEP was positively related to temporal complexity in Re. Ecosystem type, however, did not emerge as a relevant predictor of temporal complexity for any C flux. This finding suggests that the dominant vegetation type of an ecosystem may not be an important factor controlling the temporal complexity of C fluxes. Generally, ecosystems located under more temporally complex weather also showed more complex functioning (e.g., wind speed and Re, temperature and NEP; Fig. 2h), thus supporting hypothesis H1. Climate differences amongst sites, however, did not arise as a very important predictor of temporal complexity in C fluxes. Ecosystems with higher standing biomass were found to have lower temporal complexity in GPP (supporting H3), but ecosystems with higher green biomass (i.e., EVI) generally showed higher temporal complexity in Re (also supporting H3, Fig. 2). More diverse ecosystems, presenting higher plant species diversity, were also more likely to present higher temporal complexity in NEP (Fig. 2g). Ecosystems receiving larger atmospheric nitrogen deposition rates presented higher temporal complexity in GPP but lower temporal complexity in Re.

Fig. 2: Partial residuals plots showing the relationship between temporal complexity of carbon fluxes across ecosystems and biotic and abiotic predictors.
figure 2

Data and relationships were extracted from the subset of models with ΔBIC < 2. Panels a, b, d, e, g and h correspond to analyses performed with all ecosystem types (N = 57). Panels c, f and i correspond to analyses performed using only forest sites (36 out of 57 sites in total). Parameter estimates shown (β ± standard error of the mean) are standardised parameter estimates; significance is based on to two-sided t-tests based on N = 57. The shaded area represents the 95% confidence interval of the slopes. Significance levels: * indicates p < 0.05, ** indicates p < 0.01 and *** indicates p < 0.001. GPP gross primary production, Re ecosystem respiration, NEP net ecosystem production, CD correlation dimension, EVI enhanced vegetation index, df degrees of freedom (df).

Full size image

Leaf nutrient concentrations played a minor role in controlling the temporal complexity of C fluxes, even though foliar N and P concentrations were included in some of the best models explaining spatial variability in temporal complexity across ecosystems (Supplementary Tables S1 and S3). Overall, foliar N and P concentrations were positively related to GPP temporal complexity, and foliar P concentration was negatively related to NEP temporal complexity. Our analyses using only forests (N = 36 sites) mostly replicated the findings described above when including all ecosystem types. However, in forests we found a contrasting effect of stand age on Re and NEP temporal complexity (positive relationship) compared to that on GPP (negative relationship, Fig. 2c, f, i, and Supplementary Materials: Model summaries, Section 2, Supplementary Tables S4–S6). Again, these results support H3 for GPP and Re, suggesting a contrasting behaviour between autotrophic and heterotrophic processes (affecting only Re and NEP) in forest ecosystems.

Regarding the causal relationships amongst mean annual C fluxes, interannual variability, and temporal complexity, our analyses found that the model with the strongest statistical support (Supplementary materials: Model Summaries, Section 3) included negative causal effects from mean annual sums to interannual variability (Fig. 3a–d; Supplementary Table S7), positive causal effects from mean annual sums to temporal complexity (Fig. 3a, e–g), supporting the hypothesis that higher temporal complexity is associated with larger C fluxes (H2), and negative causal effects from temporal complexity to interannual variability (Fig. 3a).

Fig. 3: Causal effects amongst mean annual sums, interannual variability and temporal complexity of C fluxes.
figure 3

Panel a shows the directed acyclic graph indicating the direct standardised effects (±standard error of the mean) amongst variables. The direction of the arrows was decided based on the best fit of the different candidate models (see Methods). Panels b–g show the total effects of predictors (Y axes) on response variables (X axes). Effects shown as standardised parameter estimates indicating mean ± standard error of the mean as confidence intervals (β, N = 57, Supplementary Table S7). Dashed lines indicate non-significant paths, and the transparency indicates the strength of the relationship. GPP gross primary production, Re ecosystem respiration, NEP net ecosystem production, CD correlation dimension and IAV interannual variability.

Full size image

Trends in temporal complexity of ecosystem functioning

There was a statistically significant annual increase in the temporal complexity of GPP across all ecosystems, primarily driven by increases in temporal complexity during spring and autumn (Table 1). The temporal complexity of Re and NEP did not present any significant trend at the annual scale; however, Re showed a decrease in temporal complexity during winter. Our analyses did not reveal statistically significant trends in the temporal complexity of annual weather variables, except for a declining trend in precipitation, which was also observed during spring and autumn. Overall, the detected trends in temporal complexity, both in C fluxes and weather variables, were relatively low, mostly below 0.05 degrees of freedom per year. Conversely, we found significant and substantial increases in annual C fluxes, particularly during summer and autumn (Table 1). Additionally, annual average wind speed exhibited a statistically significant decreasing trend over time, but no other weather variable showed statistically significant changes at the annual scale, despite identifying several significant seasonal trends for all of them (Table 1).

Table 1 Trends in temporal complexity and seasonal means in carbon flux and weather variables
Full size table

Additional analyses showed that ecosystems with increasing annual GPP and Re were more likely to show positive trends in the temporal complexity of, respectively, GPP and Re (Supplementary Fig. S6). Besides the positive relationship between productivity and temporal complexity, our results indicated that ecosystems with larger standing biomass also experienced higher increases in temporal complexity of GPP and Re over time, while ecosystems with larger green biomass (EVI) showed stronger increases in temporal complexity of NEP (Fig. 4, Supplementary Materials: Model Summaries, Section 4, Supplementary Tables S8–S10). Instead, ecosystems with high N deposition generally showed negative trends for NEP temporal complexity. For GPP, we also found that ecosystems with higher temporal complexity experienced higher increases in complexity over time, the exact opposite of what we found for trends in NEP temporal complexity (Fig. 4e, f).

Fig. 4: Partial residuals plots showing the effect of the main drivers explaining trends in temporal complexity of carbon fluxes (correlation dimension).
figure 4

Data and relationships were extracted from the subset of models with ΔBIC < 2 (panels a–f). Parameter estimates shown (β ± standard error of the mean) are standardised parameter estimates; significance is based on two-sided t-tests performed on N = 57. The shaded area represents the 95% confidence interval of the slopes. GPP gross primary production, Re ecosystem respiration, NEP net ecosystem production, CD correlation dimension, EVI enhanced vegetation index, and df degrees of freedom.

Full size image

Discussion

Temporal complexity of ecosystem functioning

Our results indicate that the temporal complexity of ecosystem functioning is generally lower than that of environmental conditions (Supplementary Fig. S3). This implies that the dynamics of ecosystem functioning are more predictable than the environmental conditions they are subjected to. Hence, our analyses provide evidence for internal regulatory mechanisms within ecosystems that impose a higher degree of order upon underlying environmental stochasticity16,39. Alternatively, these results might also suggest that biological systems exhibit delayed responses to environmental variation due to lags in internal sensing and physiological changes. These observations imply that ecosystems function as filters of more complex inputs, involving lagged responses to stimuli, buffers, pools, and memory, akin to what has been described for catchments40. Further, we found that sites with more complex environmental conditions also exhibit higher temporal complexity in their functioning (Fig. 2h). These findings support our initial hypothesis (H1) and imply that ecosystems, and individual organisms alike, modulate their functioning depending on environmental conditions by which their functioning is constrained.

Across seasons, temporal complexity of carbon fluxes changes proportionally more than temporal complexity of weather variables, which mostly show the same patterns throughout the year (Supplementary Figs. S4 and S5). These findings denote changes in the functioning of individual organisms and species that propagate to the ecosystem scale. The observed changes may mostly arise because of phenological differences, that impose different responses to environmental stimuli, limited by temperature, light or water availability. The seasonal on-off switch of different organisms performing different functions in the ecosystem, involved in autotrophic and heterotrophic processes, may be the primary driving force of the differences in the seasonal changes in temporal complexity between GPP, Re and NEP. While GPP temporal complexity peaks during spring and summer (active periods) Re and NEP temporal complexity vary much less across seasons and peak at winter and summer. The lower seasonal variability of Re and NEP temporal complexity suggest a stronger inertia of the functioning of heterotrophic than autotrophic processes. One explanation for this could be the buffering effect of the soil or big organic structures like deadwood, whose functioning changes steadily across seasons (e.g., due to smaller temperature changes than in the atmosphere). An alternative explanation would involve the different degree of functional diversity affecting autotrophic and heterotrophic processes, with the latter presumably being much higher than the first41. This could stabilise heterotrophic functioning across time42,43 and overall lead to higher temporal complexity than that of the autotrophic compartment, as observed here (Supplementary Figs. S3 and S4). Further research is needed to confirm whether higher temporal complexity in ecosystem functioning is found in ecosystems with higher diversity (as found here for NEP, Fig. 2g), niche complementarity or species temporal asynchrony44,45,46, as suggested above. It is also needed to further assess the relationship between temporal complexity and ecosystem stability metrics such as resistance, resilience and invariability, all of which are known to be driven by these abovementioned ecological properties24,25,26,47.

On the other hand, different lines of evidence provided by our results indicate that more productive ecosystems tend to be more temporally complex, both across ecosystems (Fig. 3) and across seasons or years (Supplementary Figs S4 and S6), supporting our second hypothesis (H2). Our results suggest that higher productivity causes the ecosystem to be more temporally complex (Fig. 3, Supplementary Table S7, Supplementary Materials: Section 3) and that higher productivity and complexity reduce interannual variability together, thus increasing the resistance of the ecosystems to environmental stochasticity on a multiannual scale. This negative causal effect of temporal complexity on interannual variability also supports the above-mentioned conjecture that short-term temporal complexity may reflect niche complementarity or temporal asynchrony of different species within a community (see also Fig. 2g), given the often-found negative relationship between diversity and interannual variability47,48. In any case, our results neatly show how the short-term behaviour of an ecosystem can influence and be indicative of its status at larger timescales. Substantial drops in the short-term temporal complexity of the carbon cycle could be used as a warning signal for potential changes in ecosystem functioning at larger temporal scales, such as reduced decadal resistance and resilience26.

Mechanisms behind the drivers of ecosystem temporal complexity across space and time

Consistent with our third hypothesis (H3), we found that older forests and ecosystems with larger standing biomass tend to exhibit lower temporal complexity in GPP, regardless of ecosystem type (Fig. 2a, c). This result may emerge because ecosystems with greater standing biomass present lower sensitivity to environmental fluctuations due to a lower fraction of responsive biomass. Also, larger biological structures can store larger reserves (e.g., non-structural carbohydrates and nutrients in woody tissues49) and provide comparatively more resources for photosynthesis, making it less variable over time. Ecosystems with larger biomass generally show larger C fluxes (log-log relationships [N = 57], GPP ~ biomass: 0.23 ± 0.03; r2 = 0.45; p < 0.001; Re ~ biomass: 0.17 ± 0.03; r2 = 0.35; p < 0.001) and larger energy inputs in the system could support stronger species interactions like symbiotic associations within the rhizosphere, providing additional nutrients50 and enhancing ecosystem resistance and resilience. The relaxation of limiting factors (i.e., water, nutrients) could make photosynthesis to be mostly driven by light availability resulting in a more periodic behaviour (Supplementary Fig. S1). Following our expectations, opposite results were found for Re (and also NEP) temporal complexity compared to those of GPP. For both Re and NEP, temporal complexity was generally higher in older forests (Fig. 2f, i) and stands with higher green biomass (Fig. 2d). We conjecture that a more developed heterotrophic compartment, with increased species and functional diversity, could foster the short-term response of the ecosystem (on-off switching of organisms) to environmental fluctuations and provide a more complex temporal behaviour. Higher plant diversity should relate to higher diversity in phenological rhythms amongst the species within the community, stabilising seasonality across years51,52, even though exceptions may occur53. The on-off switch of the different species should also promote short-term temporal complexity of NEP as shown in Fig. 2g. Hence, our results seem to suggest divergent temporal behaviours of GPP and Re (and consequently NEP) depending on the successional stage of the ecosystem. While productivity becomes more periodic over successional stages due to a less environmentally-constrained autotrophic compartment, the opposite would occur for Re (and NEP) due to the increased complexity of the functioning of the heterotrophic compartment, potentially increasing in species and functional diversity as necromass and microhabitats increase through the ecological succession39.

Across years, however, we found that ecosystems with greater biomass were more likely to experience an increase in temporal complexity of ecosystem functioning than those with less biomass, which were more likely to decrease their temporal complexity (Fig. 4a–c; Supplementary Materials: Section 4). The decrease in temporal complexity over time experienced by ecosystems with low biomass agrees with the results discussed above, showing lower temporal complexity in old forests or large biomass ecosystems. However, the finding that ecosystems with large standing biomass increase in complexity seem, at least, partially counterintuitive. These results could emerge because i) in our dataset, ecosystems with more biomass exhibit stronger increases in productivity over time than those with less biomass (GPP: β = 0.62 ± 0.11, p < 0.001; Re: β = 0.50 ± 0.12, p < 0.001; NEP: β = 0.48 ± 0.12, p = 0.001), thus driving an increase in temporal complexity, or because ii) ecosystems with large biomass accumulation experience a rebound in temporal complexity after a certain threshold (i.e., keystone species have settled but a few more specialised species arrive). On the other hand, while increases in GPP temporal complexity were found in ecosystems with more complex GPP (i.e., the more complex they are, the more complex they become), the opposite was found for NEP (Fig. 4e, f), pointing towards some sort of stabilisation mechanism between GPP and Re that pushes NEP temporal complexity towards intermediate values. Additionally, ecosystems receiving high rates of N deposition generally experienced a decrease in NEP temporal complexity (Fig. 4d). The mechanisms by which N deposition could affect NEP temporal complexity are unclear. On the one hand, N deposition reduces soil respiration54,55, potentially reducing respiration temporal complexity. On the other hand, however, N deposition increases GPP29 and that should increase GPP temporal complexity (Fig. 3).

Our results also showed a generally positive trend in complexity of GPP over time (Table 1), which additionally correlates with increasing annual GPP (Supplementary Fig. S6). Although the increase in GPP temporal complexity is small on average (<0.5 degrees of freedom over 20 years), this result indicates that ecosystem functioning is becoming more complex, indicating higher responsiveness to endogenous (e.g., species interactions) or exogenous (i.e., environmental) stimuli, mainly driven by an increase in productivity of the ecosystem. Large drops in the short-term temporal complexity of ecosystem functioning could be indicative of loss of productivity in the mid- to long-term (from years to decades) and potential regime shifts in the state of the ecosystem26.

By conducting an initial investigation of how the temporal complexity of C fluxes varies across ecosystems and an exploration of the factors driving this, we showed that the short-term temporal complexity of ecosystems is indicative of other ecosystem features at longer timescales, such as annual sums and their variability across years. This fact reflects the need to investigate how the temporal complexity of ecosystem functioning relates to ecosystem resistance and resilience to perturbations. Clearly, further research and theoretical development are required to fully understand these patterns, the biology underlying them, and to integrate these new insights with the existing knowledge of the drivers of ecosystem functioning and stability56. Further observations and experiments manipulating limiting factors for growth, community features such as species diversity or biomass, and the temporal complexity of the environment will also help us distinguish between the endogenous and exogenous components of the temporal complexity in the functioning of organisms and ecosystems. Nevertheless, our results make it clear that the temporal complexity of ecosystems could be used as an indicator of underlying ecosystem condition, with potential applications for monitoring ecosystem changes under increasing environmental pressures.

Methods

Datasets

We used gap-filled half-hourly C flux (GPP, Re and NEP) and weather (temperature, precipitation, VPD and wind speed) data derived from eddy-covariance towers from FLUXNET 2015 (Tier 2) (data available here: http://fluxnet.fluxdata.org/data/download-data). In this study we used a subset of 57 sites used in a previous study28 for which we had information about community composition, species abundance (from which we calculated Shannon’s diversity, H, for plant species that accounted for up to 95% of the abundance of the site) of the site footprint, stand age, leaf N and P concentrations, and time series of C fluxes of at least 60 months long (https://doi.org/10.6084/m9.figshare.13047956.v1). The selected sites (Supplementary Table S12) included boreal, temperate, and Mediterranean ecosystems, and consisted of forests (36), shrublands-savannahs (11) and grasslands (10). We used half-hourly values of NEP, GPP and Re (the last two, following the daytime partitioning method57) as well as weather variables (temperature, precipitation, VPD and wind speed) to calculate short-term temporal complexity measures of C fluxes and weather (see section below for further details). We then aggregated half-hourly C fluxes and weather variables into daily, monthly, and annual sums or means (depending on the variable) for further analyses at seasonal to annual time scales. With these data, we also calculated interannual variability (IAV) of C fluxes and weather variables using the proportional variability index58,59,60, hereafter PV, as the mean of the interannual PV for each month (e.g., \({{NEP}}_{{IAV}}=\,\frac{{{NEP}}_{{IAV},{January}}+\,\left[...\right]+\,{{NEP}}_{{IAV},{December}}}{12}\)). Further details about the dataset can be found in ref. 28. We also estimated the seasonality of C fluxes by calculating the PV index across the mean values for the twelve months of the year.

To further test the effect of nutrient availability, biomass and green biomass on short-term temporal complexity of ecosystem functioning, we downloaded, for each site, data for total N deposition, total standing biomass, and the enhanced vegetation index (EVI). Atmospheric N deposition consisted of dry and wet, oxidised and reduced N deposition, extracted from global gridded maps (2° × 2.5° resolution) for the study period61. We extracted aboveground standing biomass, for 1 km radius around the central coordinate of each site, from a global gridded dataset derived from a combination of data coming from Copernicus Sentinel-1 mission, Envisat’s ASAR instrument and JAXA’s Advanced Land Observing Satellite (ALOS-1 and ALOS-2), and other information from Earth observation sources (data for year 2010, accessed on 05/05/2022)62. We extracted EVI, as a proxy for green biomass, for 1 km radius around the central coordinate of the site and calculated the annual average values of terra and aqua products (MOD13Q1 and MYD13Q1) for the measurement period of C fluxes at each site.

Estimating short-term temporal complexity: calculating the correlation dimension

We calculated the correlation dimension4,5,10,16 of C fluxes as a measure of short-term temporal complexity of ecosystem functioning. The units of the correlation dimension are degrees of freedom. We performed these calculations for all three C fluxes (GPP, Re and NEP) and for weather variables (temperature, precipitation, VPD, and wind speed) for the whole time series (multiannual), annual (i.e., 17,520 or 17,568 data points) and seasonal (i.e., three-months, ~4320 data points) time series. Even though we used very long time series (including more than 5 years depending on the analyses, representing more than 87,600 records), we considered our estimations to reflect the short-time temporal complexity of the time series because we used half-hourly data and thus, the reconstructed attractor represents the behaviour of the system at a short time scale. To calculate the correlation dimension, we followed the procedure described in Huffaker et al. 20187 (see Supplementary Materials: Section 1: Calculating the correlation dimension, for a detailed description of the method). The code we used to calculate the correlation dimension and analyse our dataset is openly available at: https://doi.org/10.6084/m9.figshare.27374547.

Statistical analyses

We first explored the relationship between the temporal complexity of C fluxes (GPPCD, ReCD and NEPCD) and weather variables (TemperatureCD, PrecipitationCD, Wind speedCD and VPDCD) using linear mixed effects models (lme function in nlme v.3.1-162 R package) where the response variable was the correlation dimension (CD), the independent variable was the variable identity (e.g., GPP, Re…) and the random factor was the site. We used the Tukey tests for multiple pairwise comparisons (emmeans function in emmeans v.1.8.5 R package) to further investigate the differences between pairwise variables. We performed these analyses for multiannual and annual estimations of temporal complexity. We further compared seasonal temporal complexity of C fluxes and weather using mixed effects models in which the response variable was the CD of a given variable, the independent variable was the season, and the random factor was the site. Tukey tests were also used for multiple pairwise comparisons.

Drivers

The complete list of drivers used in this study and their ecological relevance can be found in Supplementary Table S13. We investigated the drivers of short-term temporal complexity of C fluxes (using multiannual estimates, see above) and tested whether sites in more temporally complex environments (H1), presenting larger fluxes (H2) and younger or with less standing biomass (H3) present higher temporal complexity while controlling for other potentially important factors (see below). To achieve this, we fitted linear models with the log-transformed correlation dimension of C fluxes as the response variables. As predictors, we included climate (i.e., the first three axes from a factor analysis used to reduce the dimensionality of the dataset, performed using the function fa.parallel from the psych v.2.3.363 R package; see Supplementary Table S11), weather temporal complexity (i.e., the correlation dimension of temperature, precipitation, VPD and wind speed), and standing biomass interacting with EVI (i.e., biomass × EVI) as a measure of green biomass. Additionally, as predictors, we included ecosystem type (i.e., forest, savannah or grassland), community-weighted leaf N and P concentrations, Shannon’s diversity index, total atmospheric N deposition, and the annual average, seasonality, and interannual variability of the C flux matching the response variable. For NEPCD we also included GPPCD and ReCD as predictors, and for ReCD we also included GPPCD as a predictor. From the saturated models we performed a multimodel average64 using the dredge function in MuMIn v.1.47.5 R package65. The average model was calculated using the N models with values of the Bayesian Information Criterion (BIC) < 2 (standard threshold) out of the total set of potential models. We also kept the model with the lowest BIC to visualise relationships using partial residuals plots (Figs. 2 and 4) using the visreg function in visreg v.2.7.0 R package66. To assess the importance of the predictors, we also calculated the explained variance of each predictor in the best models using the calc.relimp function (lmg metric) within the relaimpo v.2.2-6 R package67. These analyses were repeated using only forests (N = 36) and including also stand age as a predictor to further test H3.

Additionally, we used directed acyclic graphs (DAG), a form of structural equation modelling, to test the causal relationships between mean annual sums, interannual variability and short-term temporal complexity of C fluxes to further test whether more productive ecosystems also have a more complex short-term behaviour (H2). We tested six different DAG models representing different causal relationships (notice that cyclic setups are not possible, Supplementary Fig. S7): setup 1) mean annual sums (AS) affect (→) short-term complexity (CD), AS → interannual variability (IAV) and IAV → CD, setup 2) AS → CD, IAV → AS and IAV → CD, setup 3) AS → CD, AS → IAV and CD → IAV, setup 4) CD → AS, IAV → AS and IAV → CD, setup 5) CD → AS, AS → IAV and CD → IAV, and setup 6) CD → AS, IAV → AS and CD → IAV. In all setups tested, we included direct relationships from GPP to Re, from GPP to NEP and from Re to NEP for annual sums, short-term complexity and interannual variability. We fitted these models using the psem function in piecewiseSEM R package (version 2.3.0)68. The model setup with the strongest statistical support (lowest AIC) after removing non-significant paths was assumed to better capture the causal relationships between annual sums, interannual variability, and temporal complexity (setup 3).

Trends

To investigate whether short-term temporal complexity of ecosystem functioning changed over time, we used the seasonal estimations of the correlation dimension of C fluxes and fitted mixed effects models to estimate their temporal trends. Models included the correlation dimension of the C flux as the response variable, a first order interaction between the season and the year as fixed factors, a random slope for year depending on site, and a temporal autocorrelation structure of lag −1 (AR1) to account for temporal autocorrelation in the data. We then extracted the mean seasonal trend at each site to investigate whether all seasons experienced the same temporal patterns. We further fitted a similar model as described above, but removing the first order interaction between year and season to calculate the overall annual trend. We then extracted the site-specific annual slopes (i.e., individual trends per site: ΔGPPCD, ΔReCD and ΔNEPCD) and the general annual trend over all sites derived from the mixed effects models. The same analyses were also used to investigate the trends in the correlation dimension of weather variables (ΔTemperatureCD, ΔPrecipitationCD, ΔWind speedCD and ΔVPDCD), as well as the seasonal sums (or averages) of C fluxes (ΔGPP, ΔRe and ΔNEP) and weather (ΔTemperature, ΔPrecipitation, ΔWind speed and ΔVPD). Results from these analyses did not change when using only sites having records for ten years or more (N = 30 sites). We additionally calculated the trends in flux data quality (variable “NEE_VUT_REF_QC”) over time to control for potential changes in the temporal complexity of C fluxes due to changes in the quality of the data (decreasing trends would be indicative of better data quality over time). Trends in data quality were tested in our statistical models and did not show any significant effect on the trends in response variables.

We investigated the drivers of trends in short-term temporal complexity of C fluxes (ΔGPPCD, ΔReCD and ΔNEPCD) performing similar analyses as the ones described in the section “drivers” above. In these models we included ΔGPPCD, ΔReCD or ΔNEPCD as response variables, and the most important variables found in the previous analyses of drivers of short-term temporal complexity as predictors. We also included climate variables to control for potential confounding effects (i.e., the first three axes of a factor analysis with climate variables, see Supplementary Table S11), and predictors referring to trends: we included ΔGPP, ΔRe or ΔNEP (matching the response variable), the mean annual sums of the C flux (GPP, Re or NEP, again matching the response variable), trends in weather variables (ΔTemperature, ΔPrecipitation, ΔWind speed and ΔVPD), an overall trend of weather temporal complexity (an average of ΔTemperatureCD, ΔPrecipitationCD, ΔWind speedCD and ΔVPDCD), Shannon’s diversity, stand biomass, green biomass (EVI), total N deposition, and the site-specific trend in flux data quality. To further test H2, we also investigated whether ecosystems with increasing functional temporal complexity also tended to show increased annual sums in C fluxes. To do so, we used multiple linear regressions for each C flux in which the response variables were the trend mean in annual C fluxes (i.e., ΔGPP, ΔRe and ΔNEP) and the independent variables were ΔGPPCD, ΔReCD and ΔNEPCD. All analyses were performed in R statistical software v.4.3.269.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.