Integrating cross-sample and cross-modal data for spatial transcriptomics and metabolomics with SpatialMETA

Abstract

Simultaneous profiling of spatial transcriptomics (ST) and spatial metabolomics (SM) on the same or adjacent tissue sections offers a revolutionary approach to decode tissue microenvironment and identify potential therapeutic targets for cancer immunotherapy. Unlike other spatial omics, cross-modal integration of ST and SM data is challenging due to differences in feature distributions of transcript counts and metabolite intensities, and inherent disparities in spatial morphology and resolution. Furthermore, cross-sample integration is essential for capturing spatial consensus and heterogeneous patterns but is often complicated by batch effects. Here, we introduce SpatialMETA, a conditional variational autoencoder (CVAE)-based framework for cross-modal and cross-sample integration of ST and SM data. SpatialMETA employs tailored decoders and loss functions to enhance modality fusion, batch effect correction and biological conservation, enabling interpretable integration of spatially correlated ST-SM patterns and downstream analysis. SpatialMETA identifies immune spatial clusters with distinct metabolic features in cancer, revealing insights that extend beyond the original study. Compared to existing tools, SpatialMETA demonstrates superior reconstruction capability and fused modality representation, accurately capturing ST and SM feature distributions. In summary, SpatialMETA offers a powerful platform for advancing spatial multi-omics research and refining the understanding of metabolic heterogeneity within the tissue microenvironment.

Introduction

In recent years, spatial omics technologies have advanced rapidly, particularly spatial transcriptomics (ST), which systematically measures gene expression levels within the spatial context of tissues. ST technologies are categorized into imaging-based ST (iST) and sequencing-based ST (sST)^1,2,3. iST technologies include MERFISH⁴, seqFISH⁵, CosMx⁶, Xenium⁷, and STARMap⁸, while sST technologies encompass 10X Visium, Visium HD⁹, Slide-seq¹⁰, and Stereo-seq¹¹. ST facilitates the study of cell-cell interactions^12,13,14 and spatial pattern identification^15,16,17, offering profound insights into fields such as cancer research, neuroscience, developmental biology, and plant biology^1,2,3. Spatial metabolomics (SM) employs mass spectrometry imaging to measure metabolite intensities and their spatial position^18,19. Representative SM technologies include Desorption Electrospray Ionization (DESI)²⁰ and Matrix-Assisted Laser Desorption/Ionization (MALDI)²¹. These techniques are primarily applied to investigate cancer-associated metabolic reprogramming, enabling the identification of crucial biomarkers with potential diagnostic or therapeutic applications^19,22.

Combining ST and SM allows for a comprehensive characterization of tissue microenvironment across spatial, transcriptomic, and metabolomic modalities. Particularly in cancer research, the tumor microenvironment (TME) presents unique properties including hypoxia, acidity, and nutrient deprivation, which suppress anticancer immune responses and diminish the effectiveness of immunotherapy in solid tumors^23,24. Therefore, integrating transcriptomic and metabolomic modalities is crucial for studying immune cell functional plasticity and metabolic state heterogeneity. Spatially resolved data can unveil intricate heterogeneities of tissue morphology, cell type composition, and cellular interactions, offering critical insights into tumor progression and therapeutic responses²⁵. Simultaneous ST and SM profiling has been widely applied in studies of prostate cancer (PC)²⁶, gastric cancer²⁷, clear cell renal cell carcinoma (ccRCC)²⁸, glioblastoma (GBM)²⁹, as well as human and mouse brains^30,31, providing valuable insights into metabolic reprogramming and metabolic heterogeneity under these contexts. Even though measurement of ST and SM on the same tissue section has been demonstrated³¹, most current spatial multi-omics practices typically use adjacent or serial sections from the same tissue sample^{27,28,29,30,31,32}.

The cross-modal (vertical) and cross-sample (horizontal) integration of non-spatial single-cell multi-omics data has been advanced through the application of machine learning and deep learning frameworks. Notable approaches for vertical integration include Seurat^33,34, totalVI³⁵, and Stabmap³⁶, methods such as Seurat CCA/RPCA³⁴, scVI³⁷, scANVI³⁸, SCALEX³⁹, scPoli⁴⁰, and scAtlasVAE⁴¹ are designed for horizontal integration. Recent advances in multi-omics integration have extended into spatial omics, with methods such as spaVAE⁴², spaMultiVAE⁴², SpatialGLUE⁴³, and MISO⁴⁴. Among them, spaVAE, spaMultiVAE, and SpatialGLUE are primarily designed for integrating ST with spatial proteomics (SP) or spatial epigenomics (SE), where both modalities are derived from the same tissue section. Recently, MISO was developed to integrate ST, SP, SE, and SM data derived from the same tissue sections, utilizing an algorithm specifically designed to incorporate histological images. However, most ST and SM data are obtained from adjacent tissue sections, which can create discrepancies in spatial morphology and resolution. This necessitates additional preprocessing steps to unify spatial coordinates and resolution. Moreover, SM data is represented as continuous mass spectrometry intensity, rather than sequencing counts as in ST, SP, or SE. This difference results in distinct feature distributions and necessitates specialized model design. In addition, capturing spatial consensus and heterogeneous patterns in ST and SM data across samples is crucial. Hence, it is essential to develop methods for the simultaneous vertical and horizontal integration of ST and SM data that effectively balance modality fusion, batch effect correction, and biological conservation, to accurately characterize the complexities of tissue microenvironments.

Here, we present SpatialMETA (Spatial Metabolomics and Transcriptomics Analysis), a method designed for the vertical and horizontal integration of ST and SM data. First, SpatialMETA aligns and reassigns ST and SM data to achieve a unified spatial resolution. It then employs a Conditional Variational Autoencoder (CVAE) framework to learn the joint latent embedding for vertical and horizontal integration. To correct batch effects in the latent space, conditioning is incorporated into the decoder. To account for modality-specific features, the reconstruction loss of ST data is modeled using a zero-inflated negative binomial (ZINB) distribution, while SM data is modeled with a Gaussian distribution. Additionally, shared decoders are applied simultaneously to both single-modality and joint embeddings, facilitating modality fusion and model interpretability. We also demonstrated the efficacy of SpatialMETA using previously published human ccRCC ST and SM data, revealing a spatial immune cluster enriched with lipid metabolism-associated features. SpatialMETA outperforms existing methods in both vertical and horizontal integration on human ccRCC²⁸, GBM²⁹, and mouse brain³¹ datasets, assessed by a series of designed metrics^45,46. SpatialMETA provides a comprehensive suite of analytical and visualization capabilities to facilitate in-depth data interpretation.

Results

SpatialMETA model architecture

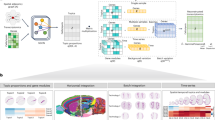
SpatialMETA comprises four key modules: alignment, reassignment, integration, and analysis (Fig. 1). To align the morphology of ST and SM data obtained from adjacent tissue sections, SpatialMETA incorporates rotation, translation, and non-linear distortion (Fig. 1a). Publicly available ST datasets employed in this study generally exhibit lower resolution compared to SM data. To address this discrepancy, SpatialMETA employs a K-nearest neighbor (KNN) approach, reassigning SM data to ensure consistency with the spots and resolution of ST data (Fig. 1b).

Fig. 1: Schematic representation of the integrated analysis of ST and SM with SpatialMETA.

a Schematic illustration for the alignment process between ST and SM data. SM spots align with ST spots or histology image derived from ST through rotation, translation, and non-linear distortion. b Schematic illustration for the reassignment process, in which SM data is adjusted to a unified resolution with ST data by k-nearest neighbors (KNN) computation. c Schematic illustration for spatially variable features (SVFs) identification before vertical or horizontal integration. d Schematic illustration for vertical and horizontal integration of ST-SM data using a conditional variational autoencoder (CVAE). e Schematic overview for downstream analysis and visualization capabilities of SpatialMETA. f Schematic illustration for different scenarios supported by SpatialMETA. SVGs spatially variable genes, SVMs spatially variable metabolites, TOI trajectories of interest, ROI spatial regions of interest.

SpatialMETA calculates the spatially variable features (SVFs) and adopts a CVAE framework to vertically and horizontally integrate the aligned ST and SM data (Fig. 1c, d). For vertical integration, separate encoders extract feature representations (ST-only and SM-only embeddings) from the original gene expression matrix (GEM) and normalized metabolite intensity matrix (MIM), respectively. These representations are concatenated and fed into a linear projection layer to generate a joint embedding, which is then utilized to reconstruct GEM and MIM data via ST or SM decoder. Additionally, the same ST or SM decoders are applied to the ST-only or SM-only embedding. This unique model design incorporates corresponding reconstruction losses that constrain the ST- and SM-only embedding to closely resemble the joint embedding within the latent space. Furthermore, angular similarity between the single-modality embedding and joint embedding quantifies the contribution of each modality, enhancing model interpretability.

For simultaneous vertical and horizontal integration, SpatialMETA employs a batch-invariant encoder and a batch-variant decoder. While batch labels are not utilized during encoding, they are incorporated into the joint, ST-only, or SM-only embeddings during decoding, facilitating effective batch effects correction across multiple samples. Additionally, Maximum Mean Discrepancy (MMD) losses are applied to ensure the comparability of joint embeddings across different samples⁴⁷. To model the feature distributions, SpatialMETA adopts a ZINB distribution for GEM, which is widely used in single-cell transcriptomics computational methods^37,48. MIM is modeled using a Gaussian negative log-likelihood loss (hereafter referred to as Gaussian loss), which reflects the typical intensity distribution of most spatially variable metabolites (SVMs) (Supplementary Fig. 1a).

SpatialMETA also offers a suite of analysis and visualization functionalities (Fig. 1e), including spatial clustering, identification of marker genes and metabolites, metabolite annotation and enrichment analysis, gene-metabolite correlation analysis, user-defined spatial trajectories of interest (TOI) for gene expression and metabolite intensity, interactive analysis for user-defined spatial regions of interest (ROI), quantification of modality contribution and network analysis for spatial clusters. SpatialMETA supports various scenarios, including vertical integration for ST and SM data from single sample, simultaneous vertical and horizontal integration of ST and SM data, as well as horizontal integration for SM data only (Fig. 1f).

Alignment and reassignment of ST and SM data

To demonstrate the performance of SpatialMETA in aligning and reassigning ST and SM data, we applied the method to publicly available datasets from ccRCC (Y7_T), ccRCC (R29_T), mouse brain (m3_FMP), and GBM (248_T)^28,29,31. Since these ST and SM datasets are obtained from adjacent tissue sections, they share overall morphological similarities but also exhibit variations in tissue morphology and misalignment in orientation. Additionally, differences in spatial resolution arise due to the use of different platforms and technologies. The raw ST and SM data, as initially presented, reflect these discrepancies in morphology and resolution (Supplementary Fig. 1b–e). While SM data exhibit morphological similarities to ST data and their corresponding ST histology images, positional discrepancies between SM and ST spots are evident.

SpatialMETA’s alignment module addresses these discrepancies by applying a series of transformations to the SM spot coordinates, including rotation, translation, non-linear distortion, and, optionally, diffeomorphic metric mapping. These transformations are optimized using gradient descent, adapted from the STalign method⁴⁹. Additionally, SpatialMETA provides an option to align the latent features of the SM data with either latent features derived from ST data or features from ST histology, utilizing rasterization to convert the spots into an image with a specified resolution⁴⁹. In most instances, the transformation is optimized by aligning the outline of SM spots with that of the ST histology image, given their high degree of morphological similarity. However, it is also feasible to align the outline of SM spots with the ST spots. This process enables the projection of the SM data, which lacks histology images, onto histology images derived from ST data in various datasets, including ccRCC (R29_T), mouse brain (m3_FMP), and GBM (248_T) (Supplementary Fig. 1f–m).

After the alignment of spatial coordinates for ST and SM data, SpatialMETA performs a reassignment step. In most datasets employed in this study, ST data generally exhibit lower resolution than SM data, except for the mouse brain (m3_FMP) sample, where their resolutions are comparable. By default, SpatialMETA reassigns SM data to ST coordinates to achieve a consistent spatial resolution (Supplementary Fig. 1n–q). For instance, in the ccRCC Y7_T sample, the raw ST data contain 2,018 spots, whereas the SM data have 10,145 spots (Supplementary Fig. 1b). SpatialMETA utilizes ST coordinates, identifies KNN spots in the SM data, and averages their MIM values to generate an aggregated SM dataset with 2,018 spots (Supplementary Fig. 1n). Furthermore, SpatialMETA offers the flexibility to reassign ST data to SM coordinates when ST data have higher spatial resolution, ensuring adaptability to emerging high-resolution ST technologies.

Vertical integration of ST and SM data and benchmark analysis

To evaluate the vertical and horizontal integration performance of SpatialMETA, we compared it with other state-of-the-art methods for non-spatial single-cell and spatial multi-omics data integration. The methods include deep learning-based approaches such as scVI³⁷, scANVI³⁸, totalVI³⁵, scPoli⁴⁰, spaVAE⁴², spaMultiVAE⁴², SpatialGLUE⁴³, and MISO⁴⁴ as well as traditional machine learning techniques, including Seurat RPCA/CCA/BNN^33,34, Stabmap³⁶,and principal component analysis (PCA) (Supplementary Fig. 2a, Supplementary Data 1). Among these methods, only MISO supports the incorporation of histological image data. We evaluated MISO under two configurations: MISO_2m, which integrates the ST and SM modalities; MISO_3m, which integrates ST, SM, and histological image embeddings. Additionally, we performed PCA on raw ST data, raw SM data, reassigned SM data, and reassigned SM combined with raw ST data, revealing a high degree of similarity in spatial patterns before and after the alignment and reassignment preprocessing (Supplementary Fig. 2b–d).

SpatialMETA facilitates the vertical integration of ST and SM data and provides interpretable quantification of modality contribution for each spatial spot (Fig. 2a). To evaluate its performance for vertical integration, we introduced four key metrics for benchmark analysis: reconstruction accuracy, continuity score, marker score, and biological conservation score (Fig. 2b, Supplementary Fig. 2e–i). Reconstruction accuracy is assessed using the Pearson Correlation Coefficient (PCC) and Cosine Similarity (CS), with higher values indicating better feature representation (Supplementary Fig. 2e). Continuity score, evaluating smoothness and consistency, is measured using CHAOS, and the percentage of abnormal spots (PAS), as proposed in SDMBench⁴⁶ (Supplementary Fig. 2f). Marker score, assessing the efficiency of modality fusion and the preservation of biologically meaningful spatial patterns, are quantified using Moran’s I and Geary’s C from SDMBench⁴⁶, along with specificity, logistic, and Mutual Information (MI) scores proposed in this study (Supplementary Fig. 2g, and see “Methods” for details). Biological conservation score was evaluated by measuring the preservation of cell-type level variation, using Adjusted Rand Index (ARI), Normalized Mutual Information (NMI), the Average Silhouette Width (ASW) of cell types, the cell-type separation Local Inverse Simpson’s Index (cLISI), and the Isolated label ASW, as introduced by scIB⁴⁵ (Supplementary Fig. 2h). These metrics were averaged as overall score, allowing a comprehensive benchmark against other vertical integration methods across eleven samples from ccRCC, mouse brain, and GBM. Overall, our benchmark results suggested that SpatialMETA outperformed existing methods, demonstrating superior performance in reconstruction and modality fusion (Fig. 2b). Additionally, we quantified the computational efficiency in terms of time and memory consumption, with SpatialMETA exhibiting reasonable memory usage and efficient processing time (generally less than 2 gigabytes (GB) and 100 s for memory and time consumption) (Supplementary Fig. 2j). To further evaluate the scalability of SpatialMETA, we simulated ST and SM datasets with varying degrees of spot numbers ranging from 10,000 to 100,000. The results showed approximately linear increases in both time and memory usage, with memory consumption primarily driven by data scale rather than model complexity (Supplementary Fig. 2k).

Fig. 2: Benchmarking and application of vertical integration using SpatialMETA.

a Schematic diagram illustrating the vertical integration process of SpatialMETA. b Summary of benchmarking metrics assessing the vertical integration performance of different tools on ST and SM data. The tools are arranged in descending order based on their overall scores. Source data are provided as a Source Data file. c–e Spatial plots comparing the original (upper left and middle panels) and denoised (lower left and middle panels) gene expression (left panels) and metabolite intensity (middle panels) data processed by SpatialMETA. Bar plots display the Pearson correlation coefficient (PCC) and cosine similarity between the original and denoised data for each method (right panels). Spatial plots visualizing Leiden clustering results derived from different tools for ccRCC (f), GBM (g), and mouse brain (h) datasets. Bar plots depicting spatial continuity scores for ccRCC (i), GBM (j), and mouse brain (k) datasets across tools, bars are color-coded by method. Stacked bar plots showing marker scores for ST (green) and SM (yellow) data across different tools for RCC (l), GBM (m), and mouse brain (n) samples. Imm immune clusters, Endo endothelial clusters, Stro stromal clusters, Mal malignant clusters. Note that the color legend is placed at the bottom of the figure, and the colors of clusters do not directly correspond to the same captured structures across different methods.

Compared to totalVI and spaMultiVAE, SpatialMETA generally achieves the highest PCC and CS scores, demonstrating superior reconstruction accuracy (Supplementary Fig. 2e). Furthermore, SpatialMETA effectively denoises both modalities in the reconstructed GEM and MIM, as represented by the selected spatially variable genes (SVGs) or SVMs (Fig. 2c–e). Given that the spot size of ST data employed in this study are larger than cell size, spot annotation could be performed by cell type deconvolution using scRNA-seq data as reference. For example, in the case of ccRCC (Y7_T), we conducted deconvolution and automatic cell type annotations via DestVI⁵⁰ using the original and reconstructed GEM along with the ccRCC scRNA-seq reference²⁸ (Supplementary Fig. 3a). The reconstructed GEM visually presents a more spatially homogeneous distribution in cell type deconvolution (Supplementary Fig. 3b–e).

To evaluate SpatialMETA’s ability to generate coherent spatial patterns through vertical integration, we benchmarked it against SeuratV5_BNN^33,34, totalVI¹, Stabmap³⁶, spaMultiVAE⁴², SpatialGLUE⁴³, and MISO⁴⁴. Leiden clustering was then performed using default parameters, and the continuity score was evaluated. For ccRCC Y7_T sample, the Leiden clustering results obtained from SpatialMETA were manually annotated (referred to as cluster annotation) into four main spatial clusters: immune clusters (Imm), endothelial clusters (Endo), stromal clusters (Stro), and malignant clusters (Mal), which were subsequently used for downstream analyses (Supplementary Fig. 4a–e). The results indicated that SpatialMETA, MISO, and SeuratV5_BNN consistently generated visually coherent spatial clusters evaluated with CHAOS and PAS scores (Fig. 2f–k, and Supplementary Fig. 2f). TotalVI exhibited variable performance across datasets. For example, it performed well on the mouse brain and GBM samples but was less effective on the ccRCC datasets (Fig. 2f–k). Moreover, the Geary’s C and Moran’s I scores demonstrated that SpatialMETA effectively integrates ST and SM features compared to other methods (Fig. 2l–n, and Supplementary Fig. 2g). Notably, MISO_3m achieved the best performance in terms of biological conservation. This enhancement compared to MISO_2m may be attributed to the incorporation of histological image information in MISO_3m (Fig. 2b, and Supplementary Fig. 2h).

To evaluate the effectiveness of the SpatialMETA model design, we systematically analyzed the impact of key model components on the performance of vertical integration (Supplementary Fig. 4f, g). Specifically, we compared different configurations of SM loss functions, including Mean Squared Error (MSE) and Gaussian, as well as the effect of SM data normalization, with or without normalization. Additionally, we evaluated decoder architectures under two scenarios: one utilizing the designed shared decoders and the other employing independent decoders, which directly input concatenated joint embeddings into separate ST and SM decoders (Supplementary Fig. 4f). Their performance was assessed using metrics such as reconstruction accuracy, continuity score, marker score, and biological conservation score. The benchmarking results highlighted the critical importance of Gaussian loss function and normalization for SM data in achieving effective vertical integration. Furthermore, the shared decoder architecture led to improved performance in modality fusion, outperforming the independent decoder model (Supplementary Fig. 4g).

Comprehensive downstream analyses for ST and SM data with SpatialMETA

SpatialMETA’s quantification of ST and SM contributions allows the identification of spatial clusters driven by either or both modalities. In the ccRCC Y7 sample, all five immune clusters (Imm_1 to 5) and stromal type 1 cluster (Stro_1) exhibit a balanced contribution from both ST and SM (Fig. 3a). Notably, among the immune subclusters, Imm_3 and Imm_5 showed a stronger reliance on ST compared to the other immune subtypes (Fig. 3b). In contrast, other spatial clusters, particularly the endothelial (Endo) and malignant (Mal) clusters, are predominantly driven by metabolomics (Fig. 3a, b). This pattern could be attributed to the unique metabolic characteristics of cancer cells, which adapt to survive in the hypoxic and nutrient-deprived TME^51,52. Additionally, endothelial cells undergo metabolic reprogramming to promote angiogenesis, supporting tumor growth within the TME by supplying oxygen and nutrients^53,54,55. In the mouse brain (m3_FMP) sample, most spatial clusters are primarily represented by ST, while SM plays a more prominent role in the cerebral cortex⁵⁶ (Fig. 3c, d). Most spatial clusters in the GBM (248_T) sample displayed a balanced contribution from both ST and SM, highlighting the importance of both modalities (Supplementary Fig. 5a, b). While SpatialGLUE’s model design incorporates the calculation of modality weights, it may not be ideally suited for integrating ST and SM data. This is evidenced in the integration results for the three samples, which are all dominated by SM (Supplementary Fig. 5c–e). Originally, SpatialGLUE was designed for integrating ST with SP or ST with SE, where these modalities differ from SM in terms of feature distribution, which may explain the suboptimal performance of SpatialGLUE in ST and SM integration.

Fig. 3: Downstream analysis of ST and SM contributions and immune-enriched spatial clusters using SpatialMETA.

a Violin plots showing the ST and SM contributions across different Leiden clusters identified by SpatialMETA for ccRCC (Y7_T). b Spatial plots visualizing the ST and SM contributions generated by SpatialMETA for ccRCC (Y7_T). Colored dashed outlines correspond to the clusters identified by SpatialMETA in Fig. 2f. c Violin plots showing the ST and SM contributions across different Leiden clusters derived by SpatialMETA for mouse brain (m3_FMP). d Spatial plots visualizing the ST and SM contributions generated by SpatialMETA for mouse brain (m3_FMP), with the black dashed line outlining the cerebral cortex region. e Spatial plot depicting immune-cell-enriched subclusters. Spots are colored by Leiden clusters as defined by SpatialMETA, consistent with those in Fig. 2f. f Scatter plot illustrating the upregulated differentially expressed genes/metabolites in each immune-cell-enriched spatial subcluster. Genes/metabolites with a log2FoldChange > 0.25 and false discovery rate (FDR) < 0.05 in each cluster are highlighted, with the top 5 genes and top 3 metabolites labeled. Dot size indicates the proportion of spots expressing the respective gene or metabolite in each subcluster. g Spatial plot depicting the expression of marker genes CYP2J2 and ACSM2A, as well as marker metabolites with m/z values of 267.1356 and 872.7177 in the Imm_4 subcluster (Wilcoxon test with adjusted p values). Spots are colored based on scaled gene expression or scaled metabolite intensity. h Dot plot displaying gene ontology (GO) term enrichment specific to the Imm_4 subcluster (hypergeometric test with adjusted p values). i Bar plot displaying enrichment of metabolite groups specific to the Imm_4 subcluster, assessed by hypergeometric test without multiple comparison adjustment. As detailed in the “Methods” section. Source data for (h, i) are provided as a Source Data file.

The transcriptional and metabolic characteristics identified by SpatialMETA can provide further insights into metabolic reprogramming with therapeutic potential. To demonstrate this, we focused on immune clusters for further analysis using SpatialMETA (Fig. 3e, f). The original ccRCC study divided tumor samples into four groups, with Y7_T sample defined as IM2 (immune subtypes 2) group, showing enriched fatty acid and amino acid metabolism²⁸. Here, we further analyzed sub-spatial clusters. Notably, the Imm_4 sub-cluster prominently expresses lipid synthesis-related genes (CYP2J2 and ACSM2A) and metabolites (Phosphatidylglycerol and PA (24:0/24:1(15Z))) (Fig. 3g). Pathway enrichment analysis in SpatialMETA revealed the upregulated lipid metabolism at both transcriptional and metabolic levels in Imm_4 (Fig. 3h, i). Notably, CYP2J2 has been reported as a diagnostic and prognostic biomarker associated with immune cell infiltration in RCC^57,58. Moreover, previous studies have highlighted lipid metabolic reprogramming as a key metabolic marker of RCC^59,60,61.

SpatialMETA also integrates several user-friendly analysis modules, including automatic annotation of metabolites based on the m/z values (Supplementary Fig. 5f), characterization of marker genes and metabolites for each spatial cluster (Supplementary Fig. 5g), and correlation analysis for user-defined genes and metabolites (Supplementary Fig. 5h, i). For metabolites of interest, users are recommended to perform additional experimental validation, such as liquid chromatography-mass spectrometry (LC-MS), to confirm their identities. In addition, SpatialMETA provides a user-interactive interface, as exemplified by its application to the Y7_T sample (Supplementary Fig. 6a). Users can draw a TOI from the malignant clusters to the immune clusters (Supplementary Fig. 6b), enabling the calculation and visualization of gene expression and metabolite intensity gradients along the trajectory (Supplementary Fig. 6c, d). Additionally, users can draw ROI, such as tumor core and immune infiltrated regions (Supplementary Fig. 6e), to calculate marker genes and metabolites within the ROIs (Supplementary Fig. 6f).

Simultaneous vertical and horizontal integration of ST and SM data and benchmark analysis

During vertical integration, SpatialMETA also supports horizontal integration to perform batch effect correction across samples (Fig. 4a). We utilized five publicly available ccRCC samples classified as the IM2 group in the original study to demonstrate this feature. The process begins by aligning and reassigning the ST and SM data from adjacent tissue sections derived from the same sample. Subsequently, batch-biased SVGs and SVMs were excluded from the list of SVFs and used as the input for the SpatialMETA model. This preprocessing step, compared to relying solely on highly variable genes and metabolites, alleviates batch effects (Supplementary Fig. 7a, b). Following this, the CVAE model within SpatialMETA further corrected the batch effect across samples, enabling the identification of unified spatial clusters characterized by unique transcriptional and metabolic states (Fig. 4b, and Supplementary Fig. 7c, d).

Fig. 4: Application of SpatialMETA to multiple ccRCC samples for vertical and horizontal integration of ST and SM data.

a Schematic representation for the vertical and horizontal integration of ST and SM data from multiple samples using SpatialMETA. b UMAP visualization of integrated ST-SM data from five ccRCC samples using SpatialMETA for dimensionality reduction, colored by samples (left panel), annotated Leiden clusters identified by SpatialMETA (right panel). c Network plot illustrating spatial distances between different spatial clusters. Node size represents the number of spots scaled using min-max normalization, and node color indicates Leiden clusters identified by SpatialMETA. Edge weights indicate reciprocal spatial distances between nodes, calculated as average distances among all spots within each spatial cluster and scaled using min-max normalization. Only the top 4 weighted edges for each node are retained. d Summary of benchmarking metrics evaluating the performance of vertical and horizontal integration of ST and SM data by different tools. The tools are arranged in descending order based on their overall scores. Source data of the benchmark are provided as a Source Data file. e Spatial plots for individual ccRCC samples, with spots colored by annotated Leiden clusters derived from SpatialMETA. The color legend is consistent with (b) (right). Imm immune clusters, Endo endothelial clusters, Stro stromal clusters, Mal malignant clusters.

Spatial network analysis for clusters in integrated ccRCC IM2 samples showed that endothelial clusters consistently exhibited closer spatial proximity to malignant clusters, indicating frequent co-localization (Fig. 4c, and Supplementary Fig. 7e)^62,63,64. This finding aligns with the original study, in which they reported enriched endothelial signatures in IM2 tumors²⁸. Notably, heterogeneity was also observed across samples. In sample R114_T, S15_T and Y27_T, the Imm_2 and malignant clusters co-localized, whereas in sample X49_T, no immune clusters co-localized with malignant clusters (Supplementary Fig. 7e).

We next conducted a benchmark analysis to evaluate the vertical and horizontal integration performance of SpatialMETA compared to existing methods, including Seurat RPCA/CCA^33,34, scVI³⁷, scANVI³⁸, totalVI³⁵, scPoli⁴⁰, spaVAE⁴², and PCA (Fig. 4d, and Supplementary Fig. 7f–k). The performance for vertical integration was assessed using metrics such as reconstruction accuracy, continuity score, marker score, as described previously. To assess the performance of horizontal integration, we employed batch ASW, Graph Integration LISI (iLISI), and Principal component regression (PCR) batch for batch correction, and ARI, NMI, cell type ASW, Isolated label ASW, and cLISI for biological conservation, as introduced by scIB⁴⁵. The overall integration score, which reflects both vertical and horizontal integration, was calculated as the mean of the cross-modality and cross-sample scores. Achieving a proper balance between modality fusion, batch correction, and biological conservation is crucial for effective vertical and horizontal integration of SM and ST data. For all five ccRCC samples, we performed both vertical and horizontal integration using the aforementioned methods. SpatialMETA achieved the highest overall scores, demonstrating superior performance in vertical integration, while maintaining a reasonable balance between batch correction and biological conservation (Fig. 4d). We visualized the unified spatial clusters in each sample, noting that other methods often exhibit biases toward vertical or horizontal integration (Fig. 4e, and Supplementary Fig. 8). For instance, while scPoli excelled at vertical integration, achieving high cross-modal overall score and providing smoother results, it failed to effectively remove batch effects, as evidenced by its lower cross-sample overall score and visual representation (Fig. 4d, Supplementary Fig. 8). In contrast, Seurat CCA/RPCA and spaVAE performed well in horizontal integration, but their vertical integration results were suboptimal (Fig. 4d, Supplementary Fig. 8). SpatialMETA outperformed other methods in both vertical and horizontal integration of the mouse brain samples, achieving the highest overall score and further demonstrating its robustness (Supplementary Fig. 9, 10).

Additionally, when only SM data are available, SpatialMETA supports horizontal integration and analysis of SM modality independently. Using the SM data of ccRCC samples as examples, we further benchmarked SpatialMETA against other horizontal integration methods, including Seurat CCA/RPCA, scVI, scANVI, scPoli, spaVAE, and PCA (Supplementary Fig. 11a). Overall, scPoli, SpatialMETA, and Seurat CCA/RPCA demonstrated superior performance compared to the other methods across continuity score, marker score, and batch correction metrics (Supplementary Fig. 11). The result indicated that while some horizontal integration tools not specifically designed for SM data, such as scPoli and Seurat CCA/RPCA, can still effectively applied for SM-only integration.

Discussion

In this study, we introduced SpatialMETA, a robust deep learning-based framework for the vertical and horizontal integration of ST and SM data. With the specialized model design for decoders and loss functions, SpatialMETA achieves a balanced performance across modality fusion, batch effect correction and biological conservation. This approach offers the potential to study the microenvironmental spatial organization and metabolic heterogeneity of tissues. When applied to the vertical integration of ccRCC ST and SM data, SpatialMETA characterizes a sub-spatial cluster of tumor-infiltrating immune cells with upregulated lipid metabolic pathways. Additionally, the horizontal integration of ST and SM data across samples enables the identification of unified spatial clusters and their consistent interactions. Benchmark analyses demonstrate that, compared to previously published non-spatial single-cell or spatial multi-omics tools, SpatialMETA achieved superior overall performance in vertical and horizontal integration of ST and SM data.

Current spatial multi-omics strategies can be generally categorized into two main approaches. The first approach involves multimodal profiling on the same tissue section, generating spatial multi-omics data that retain identical spatial morphology. Techniques following this approach either utilize the same spatial spots, such as Stereo-CITE-seq⁶⁵, spatial ATAC-RNA-seq⁶⁶, and CUT&Tag-RNA-seq⁶⁶, or employ different spatial spots with varying resolutions, as demonstrated in a recent method by Vicari et al.²⁷. However, these methods face experimental challenges, including conflicting tissue embedding requirements for different modalities, and technical limitations that may compromise the quality of one modality during the acquisition of another³². The second approach utilizes adjacent tissue sections for multimodal profiling, enabling the independent acquisition of each modality, as observed in the majority of ST and SM joint profiling studies^27,28,29,30. While this method bypasses the experimental constraints of the first approach, it introduces computational challenges due to morphological and resolution discrepancies between adjacent multi-modal sections, which necessitate alignment and reassignment during preprocessing.

Several single-modality spatial alignment algorithms for ST have been rapidly developed, such as STalign⁴⁹, PASTE⁶⁷, GPSA⁶⁸, and Spateo⁶⁹, which consider both spot coordinates and transcriptomic similarity to align series of sections from the same sample. Nevertheless, multi-modal integration methods like spaVAE, spaMultiVAE, and SpatialGLUE do not incorporate alignment, as they are designed for spatial multi-modal integration within the same tissue section and spot coordinates. Currently, most ST and SM techniques rely on adjacent tissue sections, resulting in different spatial morphology and resolution, thereby necessitating alignment and reassignment. In SpatialMETA, we align the SM to the ST using rotation, translation, and non-linear distortion, and perform reassignment using KNN. This process alters only the spatial coordinates and resolution of the SM data with minor influence on biological conclusions, such as the identification of marker metabolites within specific spatial clusters. Recently, MISO has incorporated the iStar⁷⁰ method that utilizes histological images to enhance resolution alignment when ST and SM data are generated from the same tissue section. Such approaches may become increasingly important as emerging technologies enable multi-modal data acquisition from the same tissue section, preserving spatial morphology during resolution unification. Notably, the alignment and reassignment are currently applied only between two adjacent sections within a single sample. However, for future applications in 3D spatial omics, alignment across multiple sections may be necessary to capture the full spatial features. Looking ahead, we propose that, beyond morphological similarity, shared spatial patterns across modalities could further enhance alignment accuracy.

Furthermore, recent advancements in high-resolution spatial transcriptomics and proteomics technologies, such as CosMx⁶, Xenium⁷, Visium HD⁹, Stereo-seq¹¹, Slide-seq¹⁰, and CODEX⁷¹, when combined with SM modalities, present new opportunities and challenges for spatial multi-omics integration. High-resolution spatial omics data, which can profile millions of individual spots or cells within each tissue section, poses significant challenges for the computational scalability of analysis. SpatialMETA demonstrates efficient memory usage, exhibiting approximately linear growth with an increasing of spots number. This scalability highlights SpatialMETA’s potential applicability for high-resolution multi-omics data integration. Additionally, high-resolution ST datasets often exhibit low sequencing depth per spot, which underscores the importance of incorporating histological image data. In this context, methods like MISO, which integrate image-derived features, provide valuable enhancements for modality fusion⁴⁴. High-resolution spatial omics facilitates the spatial profiling at the single-cell level. Therefore, incorporating single-cell segmentation algorithms such as Cellpose3⁷², and Proseg⁷³ would enable the reassignment of ST and SM data based on individual cells, which may further enhance the multi-modality integration.

Multi-omics captures cellular identity from different molecular layers, and the integration of these datasets provides a more comprehensive understanding of cell types and states. An optimal vertical integration approach entails deriving a joint embedding that simultaneously extracts features from multi-modal data. Similar to existing methods for vertical integration of non-spatial single-cell multi-omics data, such as MultiVI⁷⁴, totalVI³⁵, Cobolt⁷⁵, GLUE⁷⁶ and scMVP⁷⁷, SpatialMETA employs an encoder-decoder framework to obtain a joint embedding and reconstruct input matrices. SpatialMETA further utilizes shared decoders for both the joint embedding and the ST- or SM-only embeddings, ensuring consistency between the joint embedding and individual modality embeddings. This approach facilitates effective modality fusion and enhances the accuracy of ST and SM data reconstruction. Additionally, the model design enables the calculation of the angular similarity between embeddings, improving the interpretability of modality contributions. Additional ablation studies on model components further emphasizes the importance of shared decoders, the selection of appropriate SM loss function, and SM-specific normalization to achieve optimal integration performance. For vertical integration of spatial multi-omics, Tian et al. developed spaVAE, which uses a joint embedding for vertical integration, while horizontal integration is achieved by incorporating the batch information using another VAE framework, spaMultiVAE⁴². In contrast, SpatialMETA simultaneously integrates both batch information and the joint embedding, enabling vertical and horizontal integration within a single VAE framework. SpatialGLUE incorporates spatial position information through graph neural network (GNN) framework⁴³, while MISO adopts Vision Transformers for histological image representation learning⁴⁴. In summary, future computational methods for spatial multi-omics integration should consider the incorporation of spatial or image features to enhance the vertical integration performance.

In both single-cell and spatial omics horizontal integration, batch variations arise from both technological and biological factors³². It is crucial to avoid overcorrecting true biological variation while effectively removing technological variation during horizontal integration across different samples. Similar to SCALEX³⁹ and scAtlasVAE⁷⁸, we introduce a batch-variant decoder to ensure biological conservation, where the latent embeddings are derived solely from the original matrix and remains independent of batch information. To facilitate batch correction and inspired by scArches⁴⁷, we incorporated the MMD loss function to ensure that the latent embeddings from different batches are similar. Additionally, achieving an optimal balance between batch correction and biological conservation is critical when evaluating horizontal integration. Therefore, we adopted previously established metrics to comprehensively assess the effectiveness of SpatialMETA’s horizontal integration^45,46. Notably, for the SM-only horizontal integration, some existing methods not specifically designed for SM data may still be applicable, offering additional options for integrating SM data across batches.

SpatialMETA demonstrates robust performance in vertical and horizontal integration of ST and SM data, however, several limitations remain. Firstly, SpatialMETA is designed for low-resolution ST and SM data. With the rapid development of single-cell resolution spatial omics technologies, alignment and reassignment could be achieved on cellular or subcellular levels, necessitating computational advancements for precise cell segmentation. Secondly, SpatialMETA primarily focuses on the integration of ST and SM data. As spatial multi-omics technologies continue to evolve, future iterations of SpatialMETA will need to accommodate vertical integration involving more than two modalities. Thirdly, the horizontal integration capabilities of SpatialMETA have been demonstrated on a limited number of samples from a single study. With the exponential growth of spatial omics datasets, we foresee that the horizontal integration of SpatialMETA will be instrumental in constructing comprehensive spatial multi-omics atlases. Lastly, collaborative efforts between experimental and computational biologists are crucial for validating the practical applications and biological significance of spatial multi-omics data integration.

Methods

Datasets and preprocessing

The ST and SM datasets used in this study were preprocessed into GEM and MIM formats, respectively. These datasets were derived from human ccRCC, GBM, and mouse brain samples, obtained from previously published studies. Detailed information of the datasets and their respective sources are provided in Supplementary Data 2. The ST datasets were generated using the 10x Genomics Visium platform, while the SM datasets were produced using both the MALDI and DESI platforms. The raw GEM and MIM data, as originally provided in the respective publications, were processed according to the SpatialMETA tutorial for subsequent integration and analysis. Additionally, all Leiden clusters in this study were performed using the default parameters of the ‘scanpy.tl.leiden’ function.

Overview of SpatialMETA

SpatialMETA consists of four key components: alignment between ST and SM with different morphologies, reassignment between ST and SM with different resolutions, vertical and horizontal integration between ST and SM from different samples, extensive analysis and visualization capabilities.

Alignment between ST and SM

We implement an alignment module (${\boldsymbol{\phi }}$) to perform biological meaningful alignment between ST and SM, which requires considerations on registration of two modalities: spot coordinate from ST (${{\rm{Coord}}}_{{\rm{ST}}}\in {{\mathbb{R}}}^{2}$) and SM (${{\rm{Coord}}}_{{\rm{SM}}}\in {{\mathbb{R}}}^{2}$), histological image from ST (${{\rm{Image}}}_{{\rm{ST}}}\in {{\mathbb{R}}}^{3}$) and SM (${{\rm{Image}}}_{{\rm{SM}}}\in {{\mathbb{R}}}^{3}$), and transcriptomic features from ST and metabolomic features from SM. An alignment between ST and SM requires a transformation $\phi :{{\mathbb{R}}}^{2}\to {{\mathbb{R}}}^{2}$, which can be represented by an affine transformation matrix ${\bf{A}}$ which include a rotation matrix ${\bf{R}}\in {{\mathbb{R}}}^{2\times 2}$, a translation matrix ${\bf{t}}\in {{\mathbb{R}}}^{2\times 1}$, a scaling matrix ${\bf{S}}\in {{\mathbb{R}}}^{2\times 2}$ for non-linear distortion, and a diffeomorphism term ${\boldsymbol{\varphi }}$, to transform ${{\rm{Coord}}}_{{\rm{SM}}}$ to the ${{\rm{Coord}}}_{{\rm{SM}}}^{{\prime} }$ within same coordinate system with ${{\rm{Coord}}}_{{\rm{ST}}}$:

$$\phi \left({{\rm{Coord}}}_{{\rm{SM}}}^{{\prime} }\right)={\rm{R\cdot S\cdot }}{\rm{\varphi }}\left({{\rm{Coord}}}_{{\rm{SM}}}\right)+{\rm{t}}$$

(1)

where ${\bf{S}}$ is a diagonal matrix constructed from two scaling factor ${s}_{1}$ and ${s}_{2}$:

$${\rm{S}}=\left[\begin{array}{cc}{s}_{1} & 0\\ 0 & {s}_{2}\end{array}\right]$$

(2)

As ST and SM are often measured on adjacent or serial sections from the same tissue sample, and the outlines from each slide are similar. We transform ${{\rm{Image}}}_{{\rm{ST}}}$ into 2-dimensional point set with the same coordinate system as ${{\rm{Coord}}}_{{\rm{ST}}}$, as registration between ${{\rm{Image}}}_{{\rm{ST}}}$ and ${{\rm{Coord}}}_{{\rm{ST}}}$ is provided by common ST sequencing platforms. As ${{\rm{Image}}}_{{\rm{SM}}}$ is often unavailable, we use the outline from the SM spot coordinates ${{\rm{Coord}}}_{{\rm{SM}}}$ using the concave hull algorithm to represent the shapes of the SM tissue sections. To model the transcriptomic features and metabolomic features, we use two independent variational autoencoders to learn the latent representations ST (${{\rm{Latent}}}_{{\rm{ST}}}\in {{\mathbb{R}}}^{L}$) and SM (${{\rm{Latent}}}_{{\rm{SM}}}\in {{\mathbb{R}}}^{L}$) at spot level, and then rasterized into the image space as described in STalign⁴⁹.

Optionally, a linear projection layer ${{\mathcal{F}}}_{{\rm{SM}}\to {\rm{Image}}}:{{\mathbb{R}}}^{L}\to {{\mathbb{R}}}^{3}$ was trained to learn the relationship between histological features and metabolomic features. A linear projection layer ${{\mathcal{F}}}_{{\rm{SM}}\to {\rm{ST}}}:{{\mathbb{R}}}^{L}\to {{\mathbb{R}}}^{L}$ was trained to learn the relationship between transcriptomic features and metabolomic features.

Our alignment module computes ${\bf{A}}$, ${\boldsymbol{\varphi }}$, and ${\bf{S}}$ by adopting the stochastic gradient descent of Large Deformation Diffeomorphic Metric Mapping adapted from STalign⁴⁹, with modifications on the default weight parameters and optimization objective functions:

$${{\mathcal{L}}}_{{\rm{alignment}}}={\lambda }_{1}\times {{\mathcal{L}}}_{{\rm{point}}}+{{\lambda }_{2}\times {\mathcal{L}}}_{{\rm{histo}}}+{\lambda }_{3}\times {{\mathcal{L}}}_{{\rm{features}}}$$

(3)

Where ${\lambda }_{1}({\rm{default}}=1)$, ${\lambda }_{2}$ (default = 0), and ${\lambda }_{3}$ (default = 0) are weight parameters, and

$${{\mathcal{L}}}_{{\rm{point}}}={\rm{PointDistance}}\left({\rm{AlphaShape}}\left({{\rm{Coord}}}_{{\rm{ST}}}\right),{\rm{AlphaShape}}\left({{\rm{Image}}}_{{\rm{ST}}}\right)\right)$$

(4)

$${{\mathcal{L}}}_{{\rm{histo}}}={\rm{MSE}}\left({{\rm{Image}}}_{{\rm{ST}}},{{\mathcal{F}}}_{{\rm{SM}}\to {\rm{Image}}}({\rm{Latent}}_{{\rm{SM}}})\right)$$

(5)

$${{\mathcal{L}}}_{{features}}={\rm{MSE}}\left({{\rm{Latent}}}_{{\rm{ST}}},{{\mathcal{F}}}_{{\rm{SM}}\to {\rm{ST}}}({\rm{Latent}}_{{\rm{SM}}})\right)$$

(6)

are objective functions for different measurement. ${\rm{MSE}}$ calculates the mean squared error between two sets of latent representation.

${\rm{PointDistance}}(P,Q)$ calculates the pairwise Euclidean distance between two sets of points $P=\{{{\bf{p}}}_{1},{{\bf{p}}}_{2},{\boldsymbol{\cdots }},{{\bf{p}}}_{{\rm{n}}}\}$ and $Q=\{{{\bf{q}}}_{1},{{\bf{q}}}_{2},{\boldsymbol{\cdots }},{{\bf{q}}}_{{\rm{m}}}\}$. First, for each point ${{\boldsymbol{p}}}_{i}\in {\rm{P}}$, we find the closest point ${{\boldsymbol{q}}}_{j}\in Q$, and vise versa. Let ${NN}(i)=j$ denote the index of closest point in $Q$ to $P$, and ${NN}(j)=i$ denote the index of closest point in $P$ to $Q$. Then,

$$ {\rm{PointDistance}}\left(P,Q\right) \\ =\frac{1}{N}\left[\mathop{\sum }\limits_{i=1}^{N}{\rm{dist}}\left({{\boldsymbol{p}}}_{i},{{\boldsymbol{q}}}_{{\text{NN}}\left(i\right)}\right)\cdot {w}_{I}+\mathop{\sum }\limits_{j=1}^{M}{\rm{dist}}\left({{\boldsymbol{q}}}_{j},{{\boldsymbol{p}}}_{{\text{NN}}\left(j\right)}\right)\cdot {w}_{J}\right]$$

(7)

where ${w}_{I}$ and ${w}_{J}$ are the weights for the two sets of points, and ${dist}$ calculates the Euclidean distance between two points.

${\rm{AlphaShape}}(P)$ finds the edge of a set of points $P=\{{{\boldsymbol{p}}}_{1},{{\boldsymbol{p}}}_{2},\cdots,{{\boldsymbol{p}}}_{n}\}$, where each point ${{\boldsymbol{p}}}_{i}={x}_{i},{y}_{i}$ is a point in a 2D plane, the goal is to find the concave hull of the points using Delaunay triangulation and edge detection based on the circumradius of the triangles. The Delaunay triangulation divides $P$ into a set of triangles $T=\{{t}_{1},{t}_{2},\cdots,{t}_{k}\}$, and each triangle ${t}_{k}$ has three vertices ${t}_{k}=({v}_{a},{v}_{b},{v}_{c})$. The circumradius ${R}_{k}=\frac{{abc}}{4A}$, where $a,b,c$ are side lengths and $A$ is the area of the triangle. The triangle edges would be considered as bounardy edges if ${R}_{k} > \alpha$, where $\alpha$ (default = 1) is a user-defined parameter. Vertices from boundry edges are used as outline spots.

In addition, if there is a significant difference between the SM and ST data positions, the SM image needs to be manually flipped and rotated by a large angle to ensure more effective alignment before using the automatic SpatialMETA Alignment Module.

Reassignment between ST and SM

After aligning the ST and SM data, the spatial positions of the ST spots are extracted and used as the new reassigned SM coordinates. Then, we perform the KNN calculation on the raw SM data to establish a correspondence between the new SM spots and the raw SM data. The process is detailed as follows:

• 1) KNN Calculation: For each new SM spatial position (aligned with the ST spots), the $K$ nearest raw SM spots are identified based on their Euclidean distance, with a default setting of $K=5$. Users can adjust this value as needed for their specific analysis. An increased $K$ value results in each new SM spot being derived from a larger number of neighboring raw SM spots, which in turn produces a smoother distribution of the MIM in the newly generated SM data.

• 2) Distance Threshold: To ensure that only nearby SM spots are included in the KNN calculation, a distance threshold is applied, filtering out those too far from the reassigned SM spot. This threshold is determined as the product of ${d}_{\min }$ and ${f}_{\mathrm{dist}}$, where ${d}_{\min }$ represents the minimum inter-spot distance in the ST data, computed via the “calculate_min_dist” function (recommended) or manually defined by the user. ${f}_{\mathrm{dist}}$ is a scaling factor with a default value of 1.5, which can also be user-defined.

• 3) Average Calculation: After identifying the $K$ nearest raw SM spots, the MIM for the new SM spot is computed by averaging the values of the $K$ nearest raw SM spots.

Vertical and horizontal integration among ST and SM

The vertical and horizontal integration of ST and SM in SpatialMETA is based on a CVAE. We denote the gene expression counts of each spot as ${{\bf{X}}}_{{\rm{st}}}=\{{{\bf{X}}}_{1}^{{\rm{st}}},\ldots,{{\bf{X}}}_{n}^{{\rm{st}}}\}\in {{\mathbb{R}}}^{G}$, where $G$ is the number of selected SVGs and n is the number of spots. Similarly, the metabolite intensity values of each spot are denoted as ${{\boldsymbol{X}}}_{{\rm{sm}}}=\{{{\bf{X}}}_{1}^{{\rm{sm}}},\ldots,{{\bf{X}}}_{n}^{{\rm{sm}}}\}\in {{\mathbb{R}}}^{M}$, with $M$ indicating the number of selected SVMs and n is the number of spots.

Encoding

SpatialMETA utilizes two batch-invariant encoders, ${{\mathcal{F}}}_{e{\rm{ncoder}}}^{{\rm{st}}}$ for ST data and ${{\mathcal{F}}}_{e{\rm{ncoder}}}^{{\rm{s}}{\rm{m}}}$ for SM data, to obtain their respective embeddings:

$${{\boldsymbol{q}}}_{{\rm{st}}}={{\mathcal{F}}}_{{\rm{encoder}}}^{{\rm{st}}}\left({{\bf{X}}}_{{\rm{st}}}\right)$$

(8)

$${{\bf{q}}}_{{\rm{sm}}}={{\mathcal{F}}}_{{\rm{encoder}}}^{{\rm{sm}}}\left({{\bf{X}}}_{{\rm{sm}}}\right)$$

(9)

Vertical integration

In the vertical integration process, the ST and SM representation ${{\bf{q}}}_{{\rm{st}}}$ and ${{\bf{q}}}_{{\rm{sm}}}$ are concatenated to form the joint representation ${{\bf{q}}}_{{\rm{joint}}}$. The joint representation is passed through a Multivariate Normal distribution ${\mathscr{N}}$, where the mean (${{\boldsymbol{\mu }}}_{{\rm{joint}}}$) and variance (${{{\boldsymbol{\sigma }}}_{{\rm{joint}}}}^{2}$) are computed as follows:

$${{\boldsymbol{\mu }}}_{{\rm{joint}}}={{\mathcal{F}}}_{{\rm{mean}}}\left({{\bf{q}}}_{{\rm{joint}}}\right)$$

(10)

$${{\boldsymbol{\sigma }}}_{{\rm{joint}}}={{\mathcal{F}}}_{\exp }\left({{\bf{q}}}_{{\rm{joint}}}\right)+\epsilon$$

(11)

$${{\bf{z}}}_{{\rm{joint}}}={\mathscr{N}}\left({{\boldsymbol{\mu }}}_{{\rm{joint}}},{{{\boldsymbol{\sigma }}}_{{\rm{joint}}}}^{2}I\right)$$

(12)

where $\epsilon$ is typically a small number (default is 1e-4) added to prevent ${\boldsymbol{\sigma }}$ from being zero.

Latent embeddings for each modality

Additionally, the means of the individual ST and SM embeddings are computed as:

$${{\boldsymbol{\mu }}}_{{\rm{st}}}={{\mathcal{F}}}_{{\rm{mean}}}\left({{\bf{q}}}_{{\rm{st}}}\right)$$

(13)

$${{\boldsymbol{\mu }}}_{{\rm{sm}}}={{\mathcal{F}}}_{{\rm{mean}}}\left({{\bf{q}}}_{{\rm{sm}}}\right)$$

(14)

Decoding for joint embedding

To decode the joint embedding ${{\bf{z}}}_{{\rm{joint}}}$, SpatialMETA employs two batch-variant neural networks: ${{\mathcal{F}}}_{{\rm{decoder}}}^{{\rm{st}}}$ serves as the ST decoder, and ${{\mathcal{F}}}_{{\rm{decoder}}}^{{\rm{sm}}}$ serves as the SM decoder. These decoders reconstruct the respective data for ST and SM as follows:

$$\left({{\bf{r}}}_{{\rm{mean}}}^{{\rm{st}}},{{\bf{r}}}_{\mathrm{var}}^{{\rm{st}}},{{\bf{r}}}_{{\rm{gate}}}^{{\rm{st}}}\right)={{\mathcal{F}}}_{{\rm{decoder}}}^{{\rm{st}}}\left({{\bf{z}}}_{{\rm{joint}}},{\bf{B}}\right)$$

(15)

$${\left({{\boldsymbol{r}}}_{m{\rm{ean}}}^{{\rm{sm}}},{{\boldsymbol{r}}}_{v{\rm{ar}}}^{{\rm{sm}}}\right)={\mathcal{F}}}_{{\rm{decoder}}}^{{\rm{sm}}}\left({{\bf{z}}}_{{\rm{joint}}},{\bf{B}}\right)$$

(16)

where ${\bf{B}}$ represents the batch information, which could be samples, studies and sequencing platforms. When SpatialMETA is applied to a single sample for vertical integration only, ${\bf{B}}$ is set to None. When SpatialMETA is applied to multiple samples for both vertical and horizontal integration, ${\bf{B}}$ is included to account for batch effects.

Batch embeddings

The batch embeddings are computed as:

$${{\mathcal{F}}}_{{\rm{emb}}}\left({\bf{B}}\right)=\left\{{{\bf{f}}}_{{{\rm{emb}}}_{1}},\ldots,{{\bf{f}}}_{{{\rm{emb}}}_{H}}\right\}$$

(17)

where the batch index for each spot is denoted as ${\bf{B}}=\{{\bf{B}}_{1},\ldots,{{\bf{B}}}_{{\rm{n}}}\}\in {{\mathbb{R}}}^{H}$, with $H$ representing the number of batch levels and $n$ representing the number of spots. Each batch index ${{\bf{B}}}_{{\rm{n}}}$ is defined as ${{\bf{B}}}_{{\rm{n}}}=\{{b}_{n,1},\ldots,{b}_{n,H}\}$. These batch embeddings are trainable parameters optimized through the reconstruction loss to capture batch-specific gene expression and metabolite intensity patterns, thereby enabling batch correction. In this study, only a single batch level, “sample” was used due to the limited number of samples. However, for datasets integrating samples from different projects, multiple batch levels (e.g., [“sample”, “project”]) can be incorporated to achieve more comprehensive batch correction.

Decoding for ST and SM embedding

For the corresponding ST and SM reconstruction, the shared decoder ${{\mathcal{F}}}_{{\rm{decoder}}}^{{\rm{st}}}$ and ${{\mathcal{F}}}_{{\rm{decoder}}}^{{\rm{sm}}}$ are used as follows:

$$\left({{\bf{r}}}_{{\rm{mean}}}^{{\rm{s}}{{\rm{t}}}_{{\rm{cor}}}},{{\bf{r}}}_{\mathrm{var}}^{{\rm{s}}{{\rm{t}}}_{{\rm{cor}}}},{{\bf{r}}}_{{\rm{gate}}}^{{\rm{s}}{{\rm{t}}}_{{\rm{cor}}}}\right)={{\mathcal{F}}}_{{\rm{decoder}}}^{{\rm{st}}}\left({{\boldsymbol{\mu }}}_{{\rm{st}}},{\bf{B}}\right)$$

(18)

$${\left({{\bf{r}}}_{{\rm{mean}}}^{{\rm{s}}{{\rm{m}}}_{{\rm{cor}}}},{{\bf{r}}}_{\mathrm{var}}^{{\rm{s}}{{\rm{m}}}_{{\rm{cor}}}}\right)={\mathcal{F}}}_{{\rm{decoder}}}^{{\rm{sm}}}\left({{\boldsymbol{\mu }}}_{{\rm{sm}}},{\bf{B}}\right)$$

(19)

ST and SM contribution calculation

To assess the influence of each modality on the joint embedding for each spot, the contribution of input ${{\bf{X}}}_{{\rm{st}}}$ and ${{\bf{X}}}_{{\rm{sm}}}$ to joint embedding ${{\bf{z}}}_{{\rm{joint}}}$ was determined by calculating the the angular distances as the following:

$${\theta }_{{\rm{st}}}^{{\rm{i}}}=\frac{{{\boldsymbol{\mu }}}_{{\rm{st}}}^{{\rm{i}}}\cdot {{\bf{z}}}_{{\rm{joint}}}^{{\rm{i}}}}{{|{\boldsymbol{\mu }}}_{{\rm{st}}}^{{\rm{i}}}\left|{\boldsymbol{*}}{|{\bf{z}}}_{{\rm{joint}}}^{{\rm{i}}}\right|}$$

(20)

$${\theta }_{{\rm{s}}{\rm{m}}}^{{\rm{i}}}=\frac{{{\boldsymbol{\mu }}}_{{\rm{s}}{\rm{m}}}^{{\rm{i}}}\cdot {{\bf{z}}}_{{\rm{joint}}}^{{\rm{i}}}}{{|{\boldsymbol{\mu }}}_{{\rm{s}}{\rm{m}}}^{{\rm{i}}}\left|{\boldsymbol{*}}{|{\bf{z}}}_{{\rm{joint}}}^{{\rm{i}}}\right|}$$

(21)

where $i=1,\ldots,n$, $n$ is the number of spots. The final modality contribution is defined as the difference between ${\theta }_{{\rm{st}}}^{i}$ and ${\theta }_{{\rm{s}}{\rm{m}}}^{i}$ shifted by the factor 0.5 to scale the values between 0 and 1.

ST and SM decoder outputs

The ST decoder outputs the mean (${{\bf{r}}}_{m{\rm{ean}}}^{{\rm{st}}}$ and ${{\bf{r}}}_{m{\rm{ean}}}^{{\rm{st}}\_{\rm{cor}}}$), variance (${{\bf{r}}}_{\mathrm{var}}^{{\rm{st}}}$ and ${{\bf{r}}}_{\mathrm{var}}^{{\rm{st}}\_{\rm{cor}}}$), and dropout probability (${{\bf{r}}}_{g{\rm{ate}}}^{{\rm{st}}}$ and ${{\bf{r}}}_{g{\rm{ate}}}^{{\rm{st}}\_{\rm{cor}}}$) of the gene expression counts to parameterize the zero-inflated negative-binomial distribution (ZINB) and model the raw GEM. Meanwhile, the SM decoder outputs the mean (${{\bf{r}}}_{m{\rm{ean}}}^{{\rm{sm}}}$ and ${{\bf{r}}}_{m{\rm{ean}}}^{{\rm{sm}}\_{\rm{cor}}}$), and variance (${{\bf{r}}}_{\mathrm{var}}^{{\rm{sm}}}$ and ${{\bf{r}}}_{\mathrm{var}}^{{\rm{sm}}\_{\rm{cor}}}$) of the metabolite intensity values to parameterize the Gaussian distribution and model the raw MIM.

Total loss function in SpatialMETA

Let ${{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{sm}}}\left({X}_{i}^{{\rm{sm}}}\right)$ denote the reconstruction loss for SM from ${{\bf{z}}}_{{\rm{joint}}}$ and ${{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{st}}}\left({X}_{i}^{{\rm{st}}}\right)$ denote the reconstruction loss for ST from ${{\boldsymbol{z}}}_{{\bf{joint}}}$. Similarly, ${{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{s}}{{\rm{m}}}_{{\rm{cor}}}}\left({X}_{i}^{{\rm{sm}}}\right)$ represents the reconstruction loss for SM from ${{\boldsymbol{\mu }}}_{{\rm{sm}}}$, and ${{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{s}}{{\rm{t}}}_{{\rm{cor}}}}({X}_{i}^{{\rm{st}}})$ represents the reconstruction loss for ST from ${{\boldsymbol{\mu }}}_{{\rm{st}}}$. Additionally, ${{\mathcal{L}}}_{{\rm{MMD}}}({q}_{{\rm{i}}})$ denotes the MMD to ensure comparable joint embeddings across samples, as defined in scArches⁴⁷. ${{\mathcal{L}}}_{{\rm{KL}}}({q}_{{\rm{i}}})$ represents the KL-divergence loss for the variational distribution. The total loss function for SpatialMETA combines the total reconstruction losses for ST and SM, the MMD loss, and the KL-divergence loss. It is expressed as:

$${{\mathcal{L}}}_{{\rm{total}}}=\frac{1}{N}{\sum }_{i=1}^{N}\left(\begin{array}{c}{{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{sm}}}\left({X}_{i}^{{\rm{sm}}}\right)+{{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{s}}{{\rm{m}}}_{{\rm{cor}}}}\left({X}_{i}^{{\rm{sm}}}\right)+\\ {{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{st}}}\left({X}_{i}^{{\rm{st}}}\right)+{{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{s}}{{\rm{t}}}_{{\rm{cor}}}}\left({X}_{i}^{{st}}\right)+{{{\mathcal{L}}}_{{\rm{MMD}}}\left({q}_{i}\right){\mathscr{+}}{\mathcal{L}}}_{{\rm{KL}}}\left({q}_{i}\right)\end{array}\right)$$

(22)

where $i=1,\ldots,N$, $N$ is the number of spots. The weights for each loss component can be defined by the user to emphasize specific objectives.

Horizontal integration for SM data

Similar to the horizontal integration among ST and SM, we denote the metabolite intensity values of each spot as ${{\bf{X}}}_{{\rm{sm}}}=\{{X}_{1}^{{\rm{sm}}},\ldots,{X}_{n}^{{\rm{sm}}}\}\in {{\mathbb{R}}}^{M}$, where $M$ represents the selected SVMs and $n$ representing the number of spots. If batch information is available, the batch index of each spot is annotated as ${\bf{B}}=\{{\bf{B}}_{1},\ldots,{{\bf{B}}}_{n}\}\in {{\mathbb{R}}}^{H}$, where $H$ denotes the number of batch levels, and ${{\bf{B}}}_{n}={b}_{n,1},\ldots,{b}_{n,H}$} with $H$ being the number of batch levels.

Then, a batch-invariant neural network ${{\mathcal{F}}}_{e{\rm{ncoder}}}^{{\rm{sm}}}\left({{\bf{X}}}_{{\rm{sm}}}\right)\to ({{\bf{q}}}_{{\rm{sm}}})$ serving as the encoder for SM. Additionally, a batch-variant neural network ${{\mathcal{F}}}_{d{\rm{ecoder}}}^{{\rm{sm}}}\left({\bf{z}},{\bf{B}}\right)\to ({{\bf{r}}}_{m{\rm{ean}}}^{{\rm{sm}}},{{\bf{r}}}_{v{\rm{ar}}}^{{\rm{sm}}})$ acts as the SM decoder. The horizontal integration process mirrors the aforementioned approach, with the SM decoder outputting the mean (${{\bf{r}}}_{m{\rm{ean}}}^{{\rm{sm}}}$), and variance (${{\bf{r}}}_{\mathrm{var}}^{{\rm{sm}}}$) of the metabolite intensity values to parameterize the Gaussian distribution and model the raw MIM.

Moreover, the total loss function, which incorporates the average reconstruction loss for SM, the MMD loss, and the average KL-divergence loss, is expressed as:

$${{\mathcal{L}}}_{{\rm{total}}}^{{\rm{sm}}}=\frac{1}{N}{\sum }_{i=1}^{N}\left({{\mathcal{L}}}_{{\rm{recon}}}^{{\rm{sm}}}\left({X}_{i}^{{\rm{sm}}}\right)+{{{\mathcal{L}}}_{{\rm{MMD}}}\left({q}_{i}\right){\mathscr{+}}{\mathcal{L}}}_{{\rm{KL}}}\left({q}_{i}\right)\right)$$

(23)

where $i=1,\ldots,N$, $N$ is the number of spots. The weights for each loss component can be defined by the user to emphasize specific objectives.

Benchmark metrics calculation

For the benchmarking of vertical integration on individual samples, we categorized the metrics into four components: (1) Reconstruction accuracy, (2) Continuity scores, and (3) Marker scores, (4) Biology conservation.

The overall score for vertical integration was calculated as the mean of the four component scores:

$${\mathrm{Overall}}\,{\mathrm{score}}=\frac{\begin{array}{c}{\mathrm{Reconstruction}}\,{\mathrm{accuracy}}\,+\,{\mathrm{Continuity}}\,{\mathrm{score}}\,+\\ {\mathrm{Marker}}\,{\mathrm{score}}\,+\,{\mathrm{Biology}}\,{\mathrm{conservation}}\end{array}}{4}$$

(24)

• (1). Reconstruction accuracy: To evaluate the reconstruction accuracy of SpatialMETA, two quantitative metrics were utilized: Pearson Correlation Coefficient (PCC) and Cosine Similarity (CS). These metrics were computed between the original data matrix ${{\bf{X}}}_{{\rm{original}}}$ and ${{\bf{X}}}_{{\rm{reconstructed}}}$ for each variable (e.g., gene expression or metabolite intensity) independently. The Reconstruction Accuracy score was defined as the mean of PCC and CS.

$${\mathrm{Reconstruction}}\,{\mathrm{accuracy}}=\frac{{\mathrm{PCC}}+{\mathrm{CS}}}{2}$$

(25)

Pearson Correlation Coefficient (PCC)

The PCC was calculated for each feature $i$ as follows:

$${{\rm{PCC}}}_{i}=\frac{{\rm{Cov}}\left({{\rm{x}}}_{i}^{{\rm{original}}},{{\rm{x}}}_{i}^{{\rm{reconstructed}}}\right)}{\sigma \left({{\rm{x}}}_{i}^{{\rm{original}}}\right)\cdot \sigma \left({{\rm{x}}}_{i}^{{\rm{reconstructed}}}\right)}$$

(26)

$${\rm{MeanPCC}}=\frac{1}{N}{\sum }_{i=1}^{N}{{\rm{PCC}}}_{i}$$

(27)

Where ${{\rm{x}}}_{i}^{{\rm{original}}}$ and ${{\rm{x}}}_{i}^{{\rm{reconstructed}}}$ represent the $i$-th feature of ${X}_{{\rm{original}}}$ and ${X}_{\mathrm{reconstructed}}$, repectively. ${\rm{Cov}}$ denotes covariance, and $\sigma$ denotes the standard deviation, and $i=1,\ldots,N$, where $N$ is the number of features.

Cosine similarity (CS)

The cosine similarity for each feature $i$ was calculated as:

$${{\rm{CS}}}_{i}=\frac{{{\rm{x}}}_{i}^{{\rm{original}}}{\cdot {\rm{x}}}_{i}^{{\rm{reconstructed}}}}{{{\rm{|x}}}_{i}^{{\rm{original}}}|*|{{\rm{x}}}_{i}^{{\rm{reconstructed}}}|}$$

(28)

$${\rm{MeanCS}}=\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{{CS}}_{i}$$

(29)

Where ${{\rm{x}}}_{i}^{{\rm{original}}}$ and ${{\rm{x}}}_{i}^{{\rm{reconstructed}}}$ represent the $i$-th feature of ${X}_{{\rm{original}}}$ and ${X}_{{\rm{reconstructed}}}$, repectively. $i=1,\ldots,N$, where $N$ is the number of features.

• (2). Continuity scores: These metrics assess the smoothness and consistency of the data embedding. This is evaluated using CHAOS and PAS, as defined in SDMBench⁴⁶. Since lower CHAOS and PAS scores indicate better performance, they were transformed as $1-{\rm{CHAOS}}$ or $1-{\rm{PAS}}$ before aggregation. The overall continuity score was then calculated as the mean of the transformed scores:

  $$\mathrm{Continuity}\,\mathrm{score}=\frac{\left(1-\mathrm{CHAOS}\right)+\left(1-\mathrm{PAS}\right)}{2}$$

  (30)

• (3). Marker scores: Marker scores evaluate the accuracy of modality fusion and the preservation of biological spatial patterns. This is evaluated using Moran’s I and Geary’s C, as defined in SDMBench⁴⁶, along with Specificity, Logistic, and Mutual Information(MI) scores. Similarly, Geary’s C was transformed as $1-{\mathrm{Geary}}^{{\prime} }\mathrm{sC}$. The marker score was calculated as:

$$\mathrm{Marker}\,\mathrm{score}=\frac{\begin{array}{c}{\mathrm{Moran}}^{{\prime} }{\rm{s}}\,{\rm{I}}\,+\,\left(1-{\mathrm{Geary}}^{{\prime} }{\rm{s}}\,{\rm{C}}\right)\,+\\ \mathrm{Specificity}\,+\,\mathrm{Logistic}\,+\,\mathrm{MI}\end{array}}{5}$$

(31)

Specificity score

The specificity score quantifies how specific the expression of a gene, or the intensity of a metabolite is specific to particular spatial clusters within a dataset. The calculation involves the following steps:

• 1) Feature filtering: To mitigate the influence of lowly expressed or sparse features, an initial filtering step was applied. Features with an excessively high proportion of zero expression across all spatial spots were excluded. Specifically, features were excluded if their proportion of zero values exceeded a predefined threshold (default: 99%, i.e., features with zero expression in ≥99% of spots). To ensure robustness, filtering was performed at multiple zero-percentage thresholds (100%, 99%, 98%, 95%), and the final specificity score was computed as the mean across these thresholds. ST and SM datasets were processed independently.

• 2) Specificity score calculation: For each feature $i$, its specificity to a spatial cluster $c$ is calculated as:

$${\mathrm{Specificity}}_{i}=\frac{\mathrm{Mean}\,{\mathrm{Expression}}_{i,c}}{\mathrm{Mean}\,{\mathrm{Expression}}_{i}}$$

(32)

$${\rm{Specificity\; Score}}=\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}\mathop{\max }\limits_{c}\left({{\rm{Specificity}}}_{{\rm{g}},{\rm{c}}}\right)$$

(33)

where ${{\rm{Mean\; Expression}}}_{i,c}$ is the average expression of feature $i$ in spatial cluster $c$, and ${{\rm{Mean\; Expression}}}_{i}$ is the overall average expression of feature $i$ across all spatial clusters and $N$ is the number of features.

Logistic score

An effective spatial clustering method should consider feature characteristics, enabling accurate prediction of spatial clusters based on feature expression. The logistic score evaluates this predictive capability as follows:

• 1) The dataset is divided into training and testing sets.

• 2) A logistic regression model is trained on the training data using feature expression values as input and spatial cluster labels as the target.

• 3) The trained model is then used to predict cluster labels on the testing set (${X}_{{test}}$).

• 4) The accuracy of the predictions is calculated as:

$${\rm{Accuracy}}=\frac{{\rm{Number}}\; {\rm{of}}\; {\rm{correctly}}\; {\rm{predicted}}\; {\rm{clusters}}}{{\rm{Total}}\; {\rm{number}}\; {\rm{of}}\; {\rm{clusters}}\; {\rm{in}}\; {\rm{the}}\; {\rm{test}}\; {\rm{set}}}$$

(33)

Mutual information score

The Mutual Information Score measures the dependency between feature expression levels and spatial cluster labels. The mutual information (MI) for each feature $i$ is computed as:

$${\rm{MI}}\left({\rm{i}},{\rm{c}}\right)=\sum_{x,y}P\left(x,y\right)\log \left(\frac{P\left(x,y\right)}{P\left(x\right)P\left(y\right)}\right)$$

(34)

$${\rm{Mean}}\; {\rm{MI}}=\frac{1}{N}{\sum }_{i=1}^{N}{\rm{MI}}\left(i,c\right)$$

(35)

Where $P(x,y)$ is joint probability distribution of the feature values and cluster labels, and $P\left(x\right),{P}(y)$ are their marginal probabilities, and $i=1,\ldots,N$, $N$ is the number of features.

• (4). Biology conservation: To assess the conservation of biological information, metrics such as ARI, NMI, Cell type ASW, Isolated label silhouette, and Graph cLISI score, as defined in scIB⁴⁵, were utilized. The ground-truth labels used for evaluation (specified via the “label key” parameter in scIB) were manually annotated based on histological features identified through H&E staining (Supplementary Fig. 2i). The biology conservation score was computed as:

$$ {\mathrm{Biology}}\,{\mathrm{conservation}}\,{\mathrm{score}} \\ =\frac{\begin{array}{c}{\mathrm{ARI}}\,+\,{\mathrm{NMI}}\,+\,{\mathrm{Cell}}\,{\mathrm{type}}\,{\mathrm{ASW}}\,+\\ {\mathrm{Isolated}}\,{\mathrm{lable}}\,{\mathrm{silhouette}}\,+\,{\mathrm{Graph}}\,{\mathrm{cLISI}}\end{array}}{5}$$

(36)

For benchmarking simultaneous vertical and horizontal integration across samples, we categorized the evaluation metrics into five broad groups: (1) Reconstruction accuracy, (2) Continuity scores, and (3) Marker scores, (4) Biology conservation, (5) Batch correction.

The definitions for Reconstruction Accuracy, Continuity Scores, Marker Scores, and Biological Conservation were identical to those described in the vertical integration benchmarking (see above). Additional metrics were introduced to assess Batch Correction performance in the horizontal integration context.

Batch correction

Batch correction performance was evaluated using metrics including Batch ASW, Graph iLISI score, and PCR batch score, as defined in scIB⁴⁵. The batch correction was computed as:

$${\mathrm{Batch}}\,{\mathrm{correction}}\,{\mathrm{score}}=\frac{{\mathrm{Batch}}\,{\mathrm{ASW}}+{\mathrm{Graph}}\,{\mathrm{iLISI}}+{\mathrm{PCR}}\,{\mathrm{batch}}}{3}$$

(37)

In addition, the cross modality overall scores are calculated:

$$ {\mathrm{cross}}\,{\mathrm{modality}}\,{\mathrm{score}} \\ =\frac{{\mathrm{Continuity}}\,{\mathrm{score}}\,+\,{\mathrm{Marker}}\,{\mathrm{score}}\,+\,{\mathrm{Reconstruction}}}{3}$$

(38)

The cross sample overall scores are calculated:

$$\mathrm{cross}\,\mathrm{sample}\,\mathrm{score}=\frac{\mathrm{Biology}\,\mathrm{conservation}\,+\,\mathrm{Batch}\,\mathrm{correction}}{2}$$

(39)

The overall scores are calculated:

$$\mathrm{overall}\,\mathrm{score}=\frac{\mathrm{cross}\,\mathrm{modality}\,\mathrm{score}\,+\,\mathrm{cross}\,\mathrm{sample}\,\mathrm{score}}{2}$$

(40)

Metrics from SDMBench and scIB were used with their default scaling (normalized to [0,1]). The additional metrics defined in this study (PCC, CS, Specificity, Logistic, and MI) were also scaled to the [0,1] range across all metrics.

The full Python code of the benchmark metrics and the visualization Jupyter notebook are available at: https://github.com/WanluLiuLab/SpatialMETA/tree/master/benchmark. Detailed benchmark metric values are provided in source data files.

Extensive analysis and visualization

The joint data of ST and SM in the AnnData format⁷⁹. In this structure, the spots information and annotation are contained with DataFrames “obs”. Similarly, the genes and metabolites information and annotation are stored within DataFrames “var”, and the distinction between genes and metabolites is made using the “var.type” attribute, which categorizes entries as either ST or SM.

To annotate metabolites, we first reference the Human Metabolome Database (HMDB)⁸⁰. All metabolites from HMDB undergo user-defined adduct addition to generate new m/z values. A user-defined tolerance (ppm) is then applied to calculate the m/z range for each metabolite. Each metabolite is individually searched within its respective m/z range to identify matching annotations (Supplementary Fig. 5f).

To determine the enrichment of the annotated metabolites, we perform a hypergeometric distribution test. This statistical test assesses whether the number of annotated metabolites associated with a specific pathway is greater than expected by chance. The hypergeometric test is defined by the following formula: $P\left(k;n,K,N\right)=\frac{(\begin{array}{c}K\\ k\end{array})(\begin{array}{c}N-K\\ n-k\end{array})}{(\begin{array}{c}N\\ n\end{array})}$, where $N$ is the total number of metabolites, $K$ is the number of metabolites annotated to the pathway of interest, $n$ is the number of annotated metabolites in the study, and $k$ is the number of annotated metabolites in the study that are associated with the pathway.

The interactive analysis and visualization of SpatialMETA is built by Python Graphing Library, Plotly Dash. SpatialMETA loads spatial data in AnnData format along with histology images. Users can interact with the spatial data through various functionality such as box select, lasso select, draw trajectory, and draw closed freeform. These interactive operations are recorded in AnnData object.

Calculation of spatially variable genes and metabolites

The SVGs and SVMs for each sample were calculated using Moran’s I method, as provided by Squidpy⁸¹. To remove batch-biased SVGs and SVMs, we first calculated the shared sample numbers for each gene and metabolite, setting a threshold to ensure they are shared among multiple samples (“min_samples”, default is 2). For each sample, we identified batch-biased SVGs and SVMs by calculating the fold change of each gene or metabolite between one sample and the others. Genes or metabolites with a fold change greater than the threshold (“min_logfc”, default is 3) were defined as batch-biased SVGs and SVMs. Additionally, these genes or metabolites had to be expressed in a certain proportion of spots within the sample (“min_frac”, default is 0.8). The batch-biased SVGs and SVMs were removed to facilitate better vertical integration.

Annotation of spatial clusters

We employed the ccRCC scRNA-seq reference (Supplementary Fig. 3a) for spatial transcriptomic deconvolution using DestVI⁵⁰. For the ST data, we calculated the top 2000 SVGs, and for the scRNA-seq data, we identified the top 2000 highly variable genes. We then intersected these gene sets, retaining only the overlapping genes. For the scRNA-seq data, we used the “CondSCVI” model, while for the ST data, we utilized the “DestVI.from_rna_model”. Referring to the deconvolution prediction results, we manually annotated the spatial clusters according to marker gene expression: Imm (immune clusters; CD8A, CD3D, CD74), Endo (endothelial clusters; CD34, PECAM1, APLN), Stro (stromal clusters; COL3A1, ACTA2, COL1A1), and Mal (malignant clusters; NDUFA4L2, CNDP2, EGFR).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.