Introduction

In recent years, the integration of machine learning (ML) and robotics into continuous flow chemistry has driven the development of automated and self-optimizing platforms to enhance chemical processes1,2,3. These platforms, known as self-driving laboratories (SDL), enable the optimization of process descriptors such as temperature, gas and liquid flow rates, and concentration, while minimizing experimental resources and maximizing useful data generation4,5,6,7. Recent developments in self-driving laboratory (SDL) frameworks have moved beyond basic reaction-condition optimization to include hardware reconfiguration4,8, the use of advanced additive manufacturing to dynamically create and adapt reactor architectures9, and the integration of catalyst design with automated process optimization10,11. Despite these advances, a systematic and targeted exploration of reactor geometry itself remains underdeveloped.

This is particularly critical in multiphasic systems, where variables such as surface-to-volume ratio, flow patterns, and thermal management strongly influence heat and mass transfer, ultimately affecting both yield and selectivity12,13,14,15. Consequently, advanced SDLs now offer robust capabilities for high-throughput experimentation and process optimization. However, a truly comprehensive approach that addresses both the reactor’s internal geometry and its operational parameters remains underexplored, especially in the context of more complex chemical transformations.

In parallel, recent advances in 3D printing technology have opened new possibilities for the fabrication of flow reactors with complex and customized geometries16,17,18,19. Periodic open-cell structures (POCS) fabricated via 3D printing are highly engineered architectures characterized by repeating unit cells with interconnected pores20,21. These geometries enable superior heat and mass transfer compared to conventional packed-bed reactors12,22,23,24,25,26. Additionally, several studies have explored the impact of advanced geometric designs on mixing efficiency and reaction performance in continuous flow systems, underscoring their relevance for catalytic applications13,27,28,29,30. However, the design of advanced structured reactors requires specialized software and is done on a case-by-case basis, lacking generality in the approach. In this sense, the design of heterogeneous or immobilized catalytic reactors presents unique challenges, as it requires the simultaneous optimization of multi-scale parameters related to reactor geometry (free-volume, surface area, tortuosity, etc.) and catalyst features (active sites, open porosity, etc.). Both aspects are critical for promoting efficient catalytic interactions31.

Traditional optimization approaches, such as one-factor-at-a-time (OFAT) or factorial experimental designs, prove insufficient due to the high dimensionality of the parameter space and the limited ability to handle such complexity32,33,34. The use of computational flow dynamics (CFD) simulation can be a useful technique for the determination of optimal geometries, but they are generally computationally expensive and slow. On the other hand, the use of artificial intelligence (AI) to develop innovative structured devices for advanced reaction and separation technologies is still in its early stages. Although recent studies have shown that AI can effectively optimize flow dynamics in continuous-flow reactors9, its application to the systematic design and fabrication of advanced and complex geometries remains limited.

To address these challenges, we have developed Reac-Discovery, a semi-autonomous digital platform that integrates the design, fabrication, and optimization of catalytic reactors. This methodology enables simultaneous process and topology optimization, allowing for the rapid optimization of complex multiphasic chemical transformations. This is achieved with tailored reactor designs that enhance performance, reduce material usage, and improve reaction efficiency. This closed-loop integration of design, fabrication, and evaluation positions Reac-Discovery as a comprehensive solution for the creation of advanced catalytic reactors, overcoming the limitations of conventional approaches by seamlessly combining process and topological descriptors into a unified digital framework.

The efficiency of the platform has been demonstrated at the outset by the low-pressure heterogeneous hydrogenation of acetophenone to 1-phenylethanol—a benchmark transformation that yields a valuable intermediate for fine-chemical synthesis35—and subsequently by the low-pressure CO₂ cycloaddition to epoxides, a more challenging, exergonic yet thermodynamically demanding reaction prized for its high atom economy. The CO2 cycloaddition to epoxides is an important transformation for the synthesis of electrolytes in lithium-ion batteries, green solvents for industrial processes, monomers for producing polycarbonates, a class of biodegradable and recyclable plastics, and as precursors in pharmaceuticals and fine chemicals36.

Both the low-pressure hydrogenation of acetophenone and the CO₂ cycloaddition to epoxides, despite their distinct thermodynamic profiles and mechanistic intricacies, share a common operational framework that critically shapes their performance: they are intrinsically gas–liquid–solid, multiphase transformations in which the active catalyst resides at the surface of a heterogeneous support. In both cases, the overall reaction rate is governed not only by the intrinsic activity of the catalytic sites but also by the efficiency with which the gaseous reactant permeates the liquid phase and reaches those surface sites.

The mass transfer of the gas (H2 or CO2) into the liquid phase and subsequently to the catalyst surface dictates the local concentration of reactant available for adsorption and activation. Any limitation in gas dissolution or diffusion through boundary layers immediately translates into lowered turnover frequencies, irrespective of how active the catalyst itself might be. Second, the design of the reactor profoundly influences hydrodynamics, interfacial area, and mixing regimes, thereby determining whether the process is reaction-limited (chemical kinetics) or diffusion-limited (mass transfer).

Finally, because the catalytic function is localized at the solid surface, any engineering strategy must be evaluated in light of its impact on both the microenvironment of the active sites and the macroscopic transport phenomena. In this way, the “apparent” activity of these two benchmark reactions becomes inseparable from the interplay between heterogeneous catalysis and multiphase mass transfer, underscoring the necessity of a holistic catalytic, material, and structure optimization for advanced structured reactor discovery. This can only be achieved through the comprehensive Reac-Discovery framework, which unifies the discovery, design, fabrication, and optimization of complex catalytic reactors.

Results and discussion

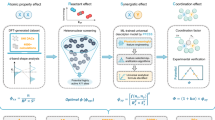
Reac-Discovery is organized into three modules, defined as Reac-Gen, Reac-Fab, and Reac-Discovery, which operate in an interconnected fashion (Fig. 1). Reac-Gen facilitates the digital construction of POCS employing their fundamental mathematical equations with a variation of three parameters that define the topology for each structure, namely size, level, and resolution (ESI, section 1.1). In this context, the size (S) parameter in Reac-Gen defines the spatial boundary of the scalar field along each axis (x, y, z), directly determining the bounding box dimensions in millimeters (mm) and influencing the overall scale of the reactor geometry. Larger size values increase the number of periodic units defined within the scalar field, resulting in more structured and complex geometries, while preserving the overall bounding box and geometric periodicity. The level threshold (L) sets the isosurface cutoff, defining the boundary between solid and void regions within the scalar field. This parameter directly impacts the porosity and wall thickness of the structure, allowing fine control over mechanical and catalytic properties. The resolution (R) specifies the number of sample points along each axis within the size boundary, controlling voxel density. Higher resolution values result in smoother and more refined geometries, enhancing mesh fidelity and capturing intricate structural details critical for catalytic applications. Furthermore, Reac-Gen incorporates a slicing routine capable of computing axially distributed geometric descriptors such as void area, hydraulic diameter, local porosity, specific surface area, and wetted perimeter. These are combined with macroscopic parameters including total surface area, free volume, and tortuosity, providing a detailed multiscale characterization of the structures. This comprehensive geometric information enables accurate machine learning correlations between reactor topology and catalytic performance, as experimentally evaluated through Reac-Eval.

Fig. 1: Integration of Reac-Discovery and its essential components for the digital design of catalytic reactors.
figure 1

A Reac-Gen: parametric generation of periodic open-cell (POC) structures and geometrical analysis, with feedback through machine learning (ML). B Reac-Fab: algorithmic validation of printability and fabrication of reactors via 3D printing (3DP), followed by catalytic functionalization. C Reac-Eval: self-driving laboratory with real-time nuclear magnetic resonance (NMR) monitoring and simultaneous optimization of processes and geometries using artificial neural networks (ANNs).

Full size image

The next module, Reac-Fab, employs stereolithography to fabricate validated structures with high-resolution 3D printing (see ESI, section 1.2 for more details). Printability is validated through a predictive ML model, which assesses structural viability before fabrication. This modular and automated approach allows for high-throughput workflows, maximizing efficiency and reducing experimental costs.

Finally, Reac-Eval is a self-driving laboratory designed to simultaneously evaluate multiple structured catalytic reactors previously designed (Reac-Gen) and 3D printed (Reac-Fab) (see ESI, section 1.3). Through real-time monitoring using benchtop NMR analysis, this module tracks the progress of randomly generated reactions, varying process descriptors such as flow rates, concentration, and temperature. The data collected from monitoring with a benchtop NMR spectrometer is used to train two ML models: one for process optimization and the other for reactor geometry refinement.

Reac-Discovery: understanding its core components

Reac-Gen includes a predefined library of 20 surface equations, including triply periodic minimal structures, such as Gyroid, Schwarz, and Schoen-G, known for their optimal properties in catalytic applications37,38,39. For example, the implicit equation for the Gyroid surface is defined as (Eq. (1)):

$$\sin \left(x\right)\cdot \cos \left(y\right)+\sin \left(y\right)\cdot \cos \left(z\right)+\sin \left(z\right)\cdot \cos \left(x\right)={{{\rm{L}}}}$$
(1)

Where L is the level threshold that controls the transition between solid and void regions. This library is expandable, allowing the incorporation of additional equations to explore a broader diversity of periodic structures in the future.

Reac-Gen (Fig. 2A) has coded the surface equations necessary to generate up to 20 POCS families, with tailored geometries to fit into macroscopic reactor configurations (see Fig. S1). The input parameters for the overall algorithm are the size (Figs. S2 and S3), resolution (Figs. S4–S6) and level (Figs. S7 and S8), specific POCS families, and the macroscopic geometry to be developed (Figs. S9 and S10). The resolution was found to have a limited influence on the macroscopic properties of the POCS later fabricated and therefore was kept constant. Once the configurations are defined, the mathematical equations are applied to the parametrically defined grid, and the geometries are scaled and adapted to the macroscopic reactor configuration (Fig. S1). Furthermore, Reac-Gen calculates reactor descriptors, including packing percentage, free volume, surface area, and tortuosity, which are fundamental outputs of this process (Fig. S11). This analysis provides a robust foundation for evaluating the potential performance of each design in specific reactions. This data will be used for subsequent ML-based structure-activity correlations. Reac-Gen generates the .stl files ready to be fabricated in the second module, named Reac-Fab.

Fig. 2: Functional workflow of the Reac-Gen and Reac-Fab modules.
figure 2

A Reac-Gen: generation and structural assessment of catalytic reactors through mathematical surface equations and structural metric analysis. XLSX (Excel) files are generated with structural metrics, and STL (Standard Tessellation Language) files are produced for subsequent 3D printing (3DP) in the Reac-Fab module. B Reac-Fab: machine learning (ML)-based printability validation, 3DP of the reactor, surface functionalization, and post-processing for catalytic applications.

Full size image

In Reac-Fab (Fig. 2B), the designs generated by Reac-Gen are first validated with a tailored printability algorithm, which relies on a neural network classifier trained with experimental data from 236 initial tests of different structures (Fig. S12). The ML model is trained using a set of critical geometric attributes generated by Reac-Gen. These include free volume, surface area, tortuosity, size, level threshold, minimum hydraulic diameter, neck diameter, and topological connectivity (Euler characteristic). Together, they capture essential aspects influencing the success of fabrication, such as the presence of thin regions, porous domains, and complex flow pathways. Experimental validation was performed by comparing theoretical and experimental weights, calculated using the resin density and digital volume data (see ESI, section 1.2), applying a 5% tolerance margin to categorize structures as printable (“Yes”) or non-printable (“No”). This combination of predictive topological descriptors and experimental categorization enables a robust, practical classification framework without requiring specialized fabrication equipment. The resulting model achieved a prediction accuracy of 91% on unseen data.

In this work, the printing parameters had been previously optimized24, but in a more general context, printing parameters and techniques could be part of the modeling. This methodology ensures that the digital structures autonomously generated by Reac-Gen can be fabricated employing specific materials’ formulations and 3D printing techniques. This automated process enhances efficiency by eliminating the need for extensive preliminary testing and guarantees that the fabricated structures are mechanically robust and suitable for subsequent functionalization and use in flow chemistry applications. The printability algorithm developed, and more generally, Reac-Fab can, in principle, be extended to other materials and printing technologies. To demonstrate this, we applied the same methodology to FDM printing of POCS employing PLA (see SI, Fig. S13).

The catalytic reactors used in this work are based on an acrylate-based formulation developed by our group24, with surfaces chemically modified depending on the case study. The functionalization protocols are tailored to each specific application, in this case, the covalent immobilization of ionic liquids (ILs) and Pd nanoparticles (PdNPs) (Figs. S14 and S15). Employing this formulation and with the optimized printing parameters, resolutions of ca. 50 μm can be achieved by employing low-cost 3D printers (Elegoo Mars 3 and 4). This implies a feature factor of up to 200 compared to the reactor diameter employed in this work (Figs. S16–S20). Subsequently, the catalytic reactors are packed in Omnifit columns that are readily available to be integrated into the next module (Fig. S21), Reac-Eval, thus closing the iterative cycle of design, fabrication, and evaluation that characterizes the Reac-Discovery platform.

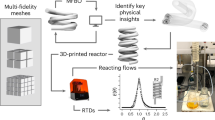
Reac-Eval is dedicated to the iterative optimization of process and topological descriptors. This module combines ML algorithms with real-time monitoring to refine both reactor performance and reaction conditions (see ESI, section 1.3 for details). Figure 3A provides a detailed representation of the Reac-Eval workflow, illustrating the sequence from experimental data generation to machine-learning-driven optimization. It highlights the module’s ability to iteratively evaluate and optimize catalytic reactors in an integrated and efficient manner.

Fig. 3: Workflow and platform of the Reac-Eval module for reactor optimization.
figure 3

A Workflow of the Reac-Eval module. The process starts with defining boundary conditions and generating a random set of reaction conditions, which are automatically executed by the self-driven laboratory with real-time monitoring via nuclear magnetic resonance (NMR). Performance and productivity metrics are used to train two machine learning (ML) models: M1, responsible for optimizing process parameters, and M2, focused on geometry parameter optimization. B Schematic of the self-driven platform that employs Reac-Eval to evaluate 3D-printed reactors concurrently with real-time benchtop NMR monitoring. C Experimental setup corresponding to (B). Left: automated flow chemistry platform integrated with an automatic sample collector. Right: benchtop NMR spectrometer set up for real-time monitoring.

Full size image

Reac-Eval combines a commercial Vapourtec RS-400 platform and a low-field NMR with high resolution (Magritek Spinsolve 80 Ultra) (Figs. 3B and 5C). A Python-based interface has been developed to fully control the different hardware involved in an integrated fashion with the rest of the Reac-Discovery modules. This integration facilitates the collection of critical data, such as reaction performance and selectivity, ensuring precise automated control and seamless connectivity between experimental data and predictive models.

The optimization process begins with the generation of a diverse set of reaction conditions. To systematically explore this design space while ensuring both diversity and efficiency, a structured randomization protocol was implemented (see ESI, section 1.3.1). Upper and lower boundaries were explicitly defined for each experimental parameter, including gas and liquid flow rates, temperature, concentration, and reactor topological descriptors such as size and level. Within these limits, a grid of discrete values was generated using equidistant sampling, resulting in a high-dimensional factorial design. From this full space, a representative subset (typically 3% of all possible combinations) was selected using stratified random sampling. This provided the foundation for reaction execution and analysis, supporting robust machine-learning-driven optimization.

The optimization capabilities are based on two neural network models: one (M1) focused on optimizing process descriptors such as temperature, flow rates, and concentration (see ESI, section 1.3.2), and the other (M2) aimed at refining topological descriptors provided by Reac-Gen: Size, Level, Resolution, and geometry type (see ESI, section 1.3.3). These models utilize a multilayer perceptron architecture40, trained with advanced strategies to prevent overfitting and enhance generalizability. These strategies included early stopping41 to halt training after 10 epochs without validation loss improvement, K-Fold cross-validation42 for robust evaluation, and feature scaling using z-score normalization43. The architecture itself was compact, consisting of two hidden layers, and employed Rectified Linear Unit (ReLU) activation functions44. The Adaptive Moment Estimation (Adam)45 optimizer with a learning rate of 0.001 was used, while batch training with randomized data splits further improved model generalization, ensuring accurate predictions of performance and productivity metrics, including Space-Time Yield (STY). The trained models can be employed to feed back into Reac-Gen to generate optimized POCS-based reactors for the transformation studied.

Case study 1: hydrogenation of acetophenone

The heterogeneous hydrogenation of acetophenone to 1-phenylethanol (Fig. 4A) was selected as a benchmark reaction because it is a well-known reaction and hydrogenations are industrially relevant transformations for the fine chemical and pharmaceutical synthesis46. Besides, it is a multiphasic reaction with all the associated challenges of efficient gas–liquid–solid mass transfer47,48.

Fig. 4: G1 optimization campaign for the hydrogenation of acetophenone.
figure 4

A Hydrogenation of acetophenone to 1-phenylethanol, catalyzed by palladium nanoparticles (Pd NPs) supported on 3D-printed polymeric structures functionalized with ionic liquids. High-resolution transmission electron microscopy (HRTEM) of the Pd NPs demonstrating a small size and uniform distribution (right). B Representation of the nine initial gyroid catalytic structures defined by the parameters Level and Size, emphasizing the resulting variations in gyroid topology. C Architecture of the artificial neural network (ANN) model M1. The input layer includes process descriptors (red: reaction temperature, T; volumetric liquid flow rate, QL; volumetric gas flow rate, QG; and reagent initial concentration in the liquid phase, C) and topological descriptors (blue: reactor size and level). The output layer corresponds to performance descriptors (yield and space-time yield, STY). D Correlation between predicted and experimental yield (%) for model M1, including linear fit, coefficient of determination (R²), and mean absolute percentage error (MAPE). Source data are provided as a Source Data file.

Full size image

Before starting the experimental campaign, the functionalization of the 3D-printed structures with RMI.Cl (R-methylimidazolium chloride, where R represents the polymer anchoring group) and the generation of PdNPs employing NaBH4 as a reducing agent were studied to determine the presence of small nanoparticles (Figs. 4A and S22). Two optimization campaigns were sequentially planned: the first generation (G1), which focused on initial correlations between reactor design, process parameters, and catalytic activity, and the second generation (G2), which refined these insights to optimize reactor geometries and process conditions for enhanced performance (Fig. S23). Initially, in the G1 campaign, 9 digital reactors with gyroid geometry were generated by Reac-Gen, varying the size and level of the topologic descriptor (Fig. 4B and Table S1). As can be observed, higher values of size correspond to smaller unit cells, which in turn generate smaller pores and higher surface area values. The level parameter determines the wall thickness, which affects parameters like packing percentage and free volume. Lower-level values result in thicker walls, which enhance mechanical strength and simplify the printing process; however, they also reduce the structural pore size, surface area, and internal volume. Striking this balance is critical: while thinner walls increase catalytic activity by offering greater surface area, they may compromise the structural robustness required for reliable reactor fabrication.

The platform was capable of executing and monitoring four parallel hydrogenation reactions, each catalyzed by columns with distinct topological features. Initially, 60 training experiments were executed sequentially by Reac-Eval, coordinating the temperature of each reactor, flows of gas and liquid, as well as selecting the appropriate channel for the reactors, enabling the catalytic reactors to be swapped without interrupting the reaction sequence. The samples were collected, and NMR spectra were acquired in an automated fashion. 1H NMR was employed to characterize the reaction mixture (Fig. S24).

The initial dataset generated a pool of yield and STY values (Fig. S25), which allowed the modeling of the system employing a multilayer perceptron neural network with 2 hidden layers and 12 neurons per layer (Fig. 4C). The output layer was the STY and yield. A coefficient of determination (R²) of 0.976 was achieved against the predicted values by the model (Fig. 4D, black dots) and was validated by testing a range of experimental conditions and comparing them to the predictions (Fig. 4D, red dots). Additionally, the Mean Absolute Percentage Error (MAPE), a statistical measure used to evaluate the accuracy of a prediction model, was calculated to be 1.12%, demonstrating the model’s accuracy in predicting experimental outcomes with minimal deviation. The algorithm then generated over one million possible combinations of process and topologic descriptors, constrained by the predefined process and topology limits. These combinations were passed through the trained model (M1), which predicted and sorted the results to identify the optimal process conditions and initial topological parameter (Fig. S26). The results of G1 confirm that Reac-Discovery is capable of successfully modeling the experimental performance of the reaction studied.

In the second optimization campaign (G2), the neural network model (M2) was trained using the initial dataset from G1 (Fig. S25). The input features and targets used during M2 training (Fig. 5A) were expanded to include geometric reactor descriptors. In this way, different POCS geometries can be included in the discovery and optimization campaign. The model achieved an R² of 0.999 and a MAPE of 3.33, indicating a very strong correlation between predicted and experimental values with an average deviation of only 3.33% across all tested conditions.

Fig. 5: G2 optimization campaign for the hydrogenation of acetophenone.
figure 5

A Architecture of the artificial neural network (ANN) model M2. The input layer includes process descriptors (red: reaction temperature, T; volumetric liquid flow rate, QL; volumetric gas flow rate, QG and reagent initial concentration in the liquid phase, C), topological descriptors (blue: reactor size and level) and reactor descriptors (gray: tortuosity, τ; surface area, SA; free volume, FV and packing percentage, PP). The output layer corresponds to performance descriptors (yield and space-time yield, STY). B Parallel-coordinates plot showing the optimized topological and process parameters for STY and yield across the explored parameter ranges. C SHAP (SHapley Additive exPlanations) feature-importance analysis for model M2. D Predicted STY values for different reactor configurations generated with Reac-Gen and evaluated with model M2. The area of each circle scales with the predicted STY, and colors denote different reactor topologies (see legend). The highlighted point corresponds to the Lidinoid S15L0 geometry selected for experimental validation (predicted STY = 352 g L⁻¹ h⁻¹). Source data are provided as a Source Data file.

Full size image

Subsequently, multiple 3D printable POCS (480 in total) were calculated with different reactors, topological descriptors, geometry types, and previously optimized process parameters. M2 results were compared against this POCS database to identify the best-performing structures and process conditions in terms of yield and STY (Fig. 5B). This enabled a comprehensive optimization, achieving a global system refinement as the primary outcome of the G2 campaign.

The SHAP analysis (SHapley Additive exPlanations, an interpretability method for ML models)49 of model M2 (Fig. 5C) revealed that temperature (T), packing percentage (PP) (solid volume/total volume), concentration of acetophenone (C) and hydrogen volumetric flow rate (QG) were the variables with the greatest impact on STY predictions. Specifically, temperature directly affects reaction kinetics, concentration determines the amount of reactant available in the flow, and PP is related to the reactor’s volume. Accordingly, the model selected conditions with temperature and gas flow at their maximum tested values, combined with a reactor geometry that exhibited intermediate surface area and tortuosity values. The optimal values (Fig. 5B) and their influence on the model (Fig. 5C) suggest that the STY values are dominated by the kinetics of the reaction and the reactor volume. Higher temperatures and concentrations lead to improved productivity (gprod h−1), and higher PP represents smaller reactor volumes. Therefore, parameters such as surface area or tortuosity have limited influence on the STY observed. In this way, Fig. 5D suggests a clustering of high-performing geometries with high values of PP. At around values of PP 50%, the STY values are the largest observed, represented by the area of the circles. On the other hand, specific surface area (surface area/solid volume) has no significant influence on the STY. This result indicates that for this reaction, the specific reactor geometry has a limited influence on performance.

Once validated, the optimal structure was digitally designed using Reac-Gen and subsequently fabricated and functionalized in Reac-Fab. From this set, the best reactor was tested in the self-driven lab of Reac-Eval to validate the M2 model and to assess the optimization efficiency of the G2 campaign. The best result for STY predicted and experimentally validated corresponded to the Lidinoid geometry (Fig. S27). In this case, the predicted STY was 352 g L−¹ h−¹, while experimental values observed were 337 g L⁻¹ h⁻¹ (Fig. 5D), confirming the close agreement and therefore the high predictive accuracy of the optimization approach.

Case study 2: CO2 cycloaddition

Following the implementation of Reac-Discovery in the hydrogenation, the triphasic CO₂ cycloaddition to epichlorohydrin (Fig. 6A) was addressed employing covalently supported ionic liquids (SILP) as catalyst24,27. This exergonic yet thermodynamically demanding reaction is highly valued for its industrial relevance, high atom economy, and environmental importance as a CO₂ valorization strategy, and it also presents significant gas–liquid–solid mass transfer challenges50,51,52. In this case, covalently supported butylimidazolium with chloride as counterion was employed as a catalyst. The reactors were functionalized and characterized according to previously reported methods (Fig. S28)24.

Fig. 6: Optimization campaigns G1–G2 employing Reac-Discovery for the CO₂ cycloaddition to epichlorohydrin.
figure 6

A CO₂ cycloaddition to epichlorohydrin, catalyzed by ionic liquid (IL) functional groups immobilized on 3D-printed polymeric reactors. B Architecture of the artificial neural network (ANN) model M2. The input layer includes process descriptors (red: reaction temperature, T; volumetric liquid flow rate, QL; volumetric gas flow rate, QG and reagent initial concentration in the liquid phase, C), topological descriptors (blue: reactor size and level) and reactor descriptors (gray: tortuosity, τ; surface area, SA; free volume, FV and packing percentage, PP). Output layer corresponds to performance descriptors (yield and space-time yield, STY). C Parallel-coordinates plot showing the optimized topological and process parameters for STY and yield across the explored parameter ranges. D SHAP (SHapley Additive exPlanations) feature-importance analysis for model M2. E Predicted STY for different reactor configurations generated with Reac-Gen and evaluated with model M2. The area of each circle scales with the predicted STY, and colors denote reactor topology (see legend). The highlighted data point corresponds to the Schoen G geometry selected for experimental validation (Size = 35, Level = 0; predicted STY = 803 g L⁻¹ h⁻¹). F Comparison of experimental and ML-predicted STY for the G2’s top four reactor geometries. Source data are provided as a Source Data file.

Full size image

Similar to Case Study 1, Reac-Discovery began with the evaluation by 1H NMR (Fig. S29) of an initial dataset of 60 reaction conditions (Fig. S30), achieving a maximum yield of 70% and a STY of 412 g L⁻¹ h⁻¹. M1 achieved an R² of 0.943 (Fig. S31). Additionally, the Mean Absolute Percentage Error (MAPE) was calculated to be 3.27%, demonstrating the model’s accuracy in predicting experimental outcomes with minimal deviation. In this way, the G1 optimization campaign predicted a maximum yield of 90% and a theoretical STY of 563 g L−1 h−1, which were experimentally validated.

The second optimization campaign (G2) was performed in an analogous fashion to case study 1 (Fig. 6B), determining the optimal geometrical and process parameters (Fig. 6C). In this case, a higher tortuosity and surface area favor mixing and catalyst-to-substrate ratios within the reactor. The employment of high temperatures and medium liquid flow rate enhances reaction kinetics and therefore leads to higher STYs. The SHAP analysis of model M2 for this reaction (Fig. 6D) revealed that temperature (T), liquid flow rate (QL), and surface area (SA) were the variables with the greatest influence on the model predictions. In this system, high values of temperature directly influence reaction kinetics and transport coefficients. As the liquid flow rate increases, so does productivity if the catalytic reaction is not limiting the overall performance of the reactor. The surface area is related to the available catalytic sites and, therefore, the higher it is, the more activity and productivity are observed. In a multiphasic system, tortuosity influences mixing by forcing enhanced contact between the different phases53. This behavior indicates that in the CO₂ cycloaddition reaction, the mechanism has a strong dependence on gas–liquid mass transfer and on the contact with the catalytic surfaces. In this context, a higher surface area provides a greater number of accessible catalytic sites, increasing overall conversion. Higher tortuosity favors a more uniform flow distribution and increases the contact time of reactants with the catalytic surface, thereby enhancing reaction efficiency.

The model suggests that high specific surface area and tortuosity will lead to enhanced STY values. The mapping of the performance of all calculated structures against these parameters confirmed this trend (Fig. 6E). In a second iteration of the Reac-Discovery platform, the best four structures identified were fully generated, fabricated, functionalized, and evaluated to confirm the predictive ability of the platform. The experimental results demonstrated a high level of accuracy in the predictions, achieving an R² of 0.999 (Fig. 6F) and a MAPE of 1.75%, confirming that all four geometries performed efficiently under the optimized conditions. The best results predicted and experimentally validated correspond to the Schoen_G geometry with a surface area of 4.356 mm² per cm of length, a tortuosity of 11, a free volume of 5.5 mL, and a packing percentage of ca. 37% (Fig. 7). Under these optimized conditions, the highest values of STY of 803 g L⁻¹ h⁻¹, were obtained (Fig. S32), surpassing previously reported values for this reaction under triphasic conditions using immobilized catalytic reactors (see Table S2)54,55. Furthermore, the versatility of the reactors was demonstrated for 4 additional epoxides, which showed conversions ranging from 40–90% (Fig. S33).

Fig. 7: Comparison of optimal structured reactors for the different reactions studied.
figure 7

A Pd NP (palladium nanoparticles) reactor based on Lidinoid S15L0 geometry predicted for the hydrogenation of acetophenone. B SILP (supported ionic liquid phase) reactor based on Schoen_G S35L0 geometry predicted for the cycloaddition of CO₂ to epichlorohydrin. Gray boxes denote reactor descriptors (specific surface area, SA; free volume, FV; packing percentage, PP; and tortuosity, τ; while green highlights the targeted performance descriptor, the space-time yield (STY, g L⁻¹ h⁻¹). IDS denotes the Initial Data Set prior to optimization campaigns G1 and G2. Source data are provided as a Source Data file.

Full size image

For comparison, we printed a classical honeycomb reactor structure, printed at the highest possible resolution and functionalized following the same protocol (Fig. S34). Under the G2 optimized conditions, it achieved an STY of 167 g L−¹ h−¹, highlighting the superior performance of structures developed through Reac-Discovery and demonstrating the potential of this methodology to deliver a fully optimized catalytic framework for continuous flow reactors.

This integrated approach ensures precision in design and fabrication but also represents a significant advancement in resource efficiency. By minimizing experimental redundancies, reducing human intervention, and accelerating research timelines, Reac-Discovery establishes a robust framework for modern chemical reactor development.

Very interestingly, both case studies showcased by Reac-Discovery reached very different structured reactors (Fig. 7). The increased values of STY optimized in the training dataset, G1 and G2, indicate how the platform can perfect the reactor performance by the application of the ML algorithms. All these indicate that Reac-Discovery is a data-driven intelligent platform capable of rapidly offering tailored solutions to the different chemistries evaluated. The database of calculated structures can be expanded to be able to predict even higher values of STY.

To conclude, this work demonstrates the potential of the Reac-Discovery platform for designing, fabricating, and optimizing catalytic reactors with POCs. The platform integrates three key components: parametric generation algorithms (Reac-Gen), micrometric-resolution reactor validation and fabrication (Reac-Fab), and ML-guided optimization of process and topological parameters (Reac-Eval).

The platform was applied for the development of optimized reactors for multiphase gas-liquid reactions catalyzed by immobilized catalysts. Two case studies have been considered. The initial interaction with the heterogeneous hydrogenation of acetophenone validated the platform’s ability to accurately predict and optimize reactor geometry and operating conditions.

In a second campaign, the platform achieved STYs of up to 803 g L−¹ h−¹ for the cycloaddition of CO2 to epoxides. This represents the best-performing reactor reported in the literature for the heterogeneously catalyzed CO₂ cycloaddition reaction under mild triphasic conditions. This demonstrates the effectiveness of combining advanced geometric design (based on key descriptors such as surface area, porosity, and tortuosity) with precise control of reaction conditions (liquid and gas flow, temperature, and concentration). The iterative and modular approach of Reac-Discovery enabled the systematic exploration of multiple configurations, facilitating rapid convergence toward optimal geometries and operating conditions.

In addition to enhancing catalytic performance, the described methodology reduces resource consumption, human intervention, and development time by integrating real-time data capture with ML algorithms for informed decision-making. These results underscore the potential of the Reac-Discovery methodology to explore more complex catalytic reactions and to develop reactors optimized for the performance of multiphase systems.

Methods

Reac Gen platform

Structure generation

All calculations and structure generations were performed through Python (version 3.13.0), utilizing libraries such as NumPy (version 2.1.0), Trimesh (version 4.5.1), and Pandas (version 2.2.3). Reac-Gen generates 3D structures based on implicit mathematical surface functions to obtain Gyroids, Schwarzs, and other minimal surface geometries. Each geometry was defined by three parameters: size (S), resolution (R), and level threshold (L). These parameters determine the bounding dimensions, voxel density, and isosurface cutoff for the generated structure. Further details are provided in Supplementary Section 1.1.

Parameter definitions

Size (S)

Defines the spatial boundary of the scalar field on each axis (x, y, z), which determines the bounding box dimensions in millimeters (mm).

Resolution (R)

Specifies the number of sample points along each axis within the size boundary, controlling voxel density. Higher resolution values improve geometric fidelity.

Level threshold (L)

Determines the isosurface cutoff, dictating the boundary between solid and void regions within the scalar field. This parameter directly influences the structure’s porosity and wall thickness.

Implicit surface function and voxel mesh generation

Each geometry was generated by evaluating the chosen surface function over a 3D grid created using np.meshgrid. For example, the gyroid surface function was defined as:

def generate_gyroid(size, resolution, level):

x = np.linspace(-size, size, resolution)

y = np.linspace(-size, size, resolution)

z = np.linspace(-size, size, resolution)

X, Y, Z = np.meshgrid(x, y, z)

gyroid = np.sin(X) * np.cos(Y) + np.sin(Y) * np.cos(Z) + np.sin(Z) * np.cos(X)

This generates a scalar field that is thresholded at level (L) to create a binary volume matrix:

gyroid_volume = gyroid > level

The binary matrix is then converted to a triangular mesh using marching cubes via the trimesh library:

gyroid_mesh=trimesh.voxel.ops.matrix_to_marching_cubes(gyroid_volume, pitch=2*size/resolution)

Continuous structure generation for extended height

To generate reactors with defined heights, the scalar field of the implicit equation is extended directly along the z-axis by adjusting the evaluation domain to span the desired length. This procedure enables the creation of vertically continuous structures without internal interfaces or discontinuities. The resolution along z is scaled proportionally to the domain extension to maintain uniform voxel density. The resulting binary volume is then processed using the marching cubes algorithm to reconstruct a three-dimensional mesh suitable for additive manufacturing.

Scaling and clipping to cylindrical dimensions

The generated mesh was scaled to match specific cylindrical reactor dimensions (width, depth, and height in mm). Scaling factors were calculated based on the target dimensions, and the mesh is scaled using the following script:

scaled_mesh = scale_mesh_to_dimensions(gyroid_mesh, desired_dimensions_mm)

To fit the mesh within a cylindrical boundary, the scaled mesh was intersected with a cylinder of the same radius and height:

cylindrical_mesh,_ = cut_with_cylinder(scaled_mesh, desired_dimensions_mm)

Data export and logging

Each generated structure is exported as an STL file, named according to the geometry parameters. Metrics are logged in an Excel file for further analysis:

save_to_stl(stacked_mesh, geometry_name, size, resolution, level, dimensions_mm)

save_metrics_to_excel(metrics)

The recorded parameters—geometry type, size, and level threshold—along with the STL files, ensure reproducibility and simplify data management without overcomplicating the experimental workflow.

Reac-Fab platform

Materials

All reagents and solvents used in this work were commercially available and were used without further purification. In general, the following materials were employed: Pentaerythritol Tetraacrylate (>99%, Aldrich), PETA, Glycidyl methacrylate (97%, Aldrich), GMA; Phenylbis(2,4,6-trimethylbenzoyl) phosphine oxide (97%, Aldrich), BAPO; Methyl Red (ACS reagent, crystalline, Aldrich), MR; Pentaerythritol tetrakis (3,5-di-tert-butyl-4-hydroxyhydrocinnamate) (98%, Aldrich); hydrochloric acid (37%, Scharlab); 2-Propanol (for analysis, Supelco); Ethanol absolute (for analysis, Supelco).

Specific reagents used in each case study are described individually below:

Case Study 1. 1-methylimidazole (99%, Aldrich); hydrochloric acid (37%, Scharlab); acetophenone (99%, Aldrich); Sodium borohydride (98%, Aldrich); Palladium(II) chloride (99.9%, Aldrich), PdCl₂; Milli-Q water; Hydrogen gas (99.999 % purity) was supplied by Nippon Gases (Madrid, Spain).

Case Study 2. 1-butylimidazole (98%, Aldrich); Epichlorohydrin (98%, Aldrich); Carbon dioxide (99.998 % purity) was supplied by Nippon Gases (Madrid, Spain).

3D printing procedure

The structures generated by Reac-Gen were printed in Reac-Fab using an Elegoo Mars 3 LCD UV-curing 3D printer. The STL files created in ReacGen were loaded into the slicing software Chitubox, allowing for fine-tuning of printing conditions. The following previously optimized parameters were used during 3D printing:

  • Layer thickness: 0.05 mm.

  • Burn-in layers: 10 layers with an exposure time of 22 s per layer.

  • Normal exposure time: 18 s per layer.

  • Waiting time (after exposure): 2.5 s.

After printing, each structure was carefully removed from the build platform and washed in isopropanol (IPA) in three consecutive 25 mL washes to remove any uncured resin.

Printability validation algorithm

A neural network (NN) model was implemented in Python to validate the printability of Reac-Gen structures. Input features included design parameters (size, level threshold) and geometric descriptors (free volume, surface area, tortuosity, minimum hydraulic and neck diameters, Euler characteristic).

Test structures (1 cm) were printed and weighed to generate the training dataset, comparing experimental weights with theoretical values from resin density; deviations ≤5% were labeled printable. The NN, implemented in TensorFlow with preprocessing in scikit-learn, consisted of two hidden layers and a sigmoid output, trained with binary cross-entropy loss and the Adam optimizer. After hyperparameter tuning, the final model was integrated into Reac-Fab, enabling automated real-time validation of Reac-Gen designs. Further details are provided in Supplementary Section 1.2.3.

Functionalization of 3D-printed structures

In the first case study (acetophenone hydrogenation), PdNP immobilization was performed in two steps. For a functionalization volume of 16 mL, 4.184 mL HCl (37 wt%, 47.4 mmol), 7.792 mL absolute ethanol (133.9 mmol), and 4.024 mL 1-methylimidazole (50.7 mmol) were added under ice-bath conditions (0–4 °C). The mixture was then heated to 40 °C and stirred at 250 rpm for 6 h, promoting epoxide ring opening and covalent attachment of a methylimidazolium layer. Reactors were rinsed with ethanol and dried under ambient conditions.

In the second step, a 0.12 M PdCl₂ solution (prepared in Milli-Q water with five drops of concentrated HCl) was pumped at 150 µL min⁻¹ for 2 h under continuous flow, followed by a 1 h wash with Milli-Q water at 500 µL min⁻¹. Pd(II) reduction was achieved by passing a freshly prepared 0.12 M NaBH₄ solution at 150 µL min⁻¹ for 1 h under ice-bath conditions, yielding 2–5 nm Pd(0) nanoparticles. The process was confirmed by color change (orange → brown → black), and reactors were finally rinsed with water and ethanol.

In the second case study (CO₂ cycloaddition), functionalization was performed in a single step using 1-butylimidazole. The same functionalization procedure as described for the initial palladium immobilization was followed. For a 16 mL functionalization volume, 3.580 mL HCl (37 wt%, 40.6 mmol), 6.649 mL absolute ethanol (114.2 mmol), and 5.768 mL 1-butylimidazole (56.7 mmol) were used. After rinsing with ethanol until clear and drying under air flow, the reactors were packed into Omnifit columns and integrated into the Reac-Eval platform. Further details are provided in Supplementary Section 1.2.4.

Reac-Eval

Generation of the random reaction set

A structured randomization protocol was implemented in Python (v3.13.0) to efficiently explore the experimental design space while maintaining diversity. The algorithm employed NumPy (v2.1.0) for numerical operations, Pandas for data handling, and the random module for stochastic sampling.

Upper and lower limits were set for all parameters, including gas and liquid flow rates, temperature, concentration, and reactor topological descriptors (size and level). Within these boundaries, a discrete grid of values was generated using equidistant sampling, resulting in a high-dimensional factorial design. From the complete design space (1975 possible combinations), a representative subset of 3% (i.e., 60 experiments) was selected using stratified random sampling.

The 3% subset balanced diversity and experimental efficiency, providing sufficient coverage of the six key parameters while remaining compatible with the throughput of the Reac-Eval platform. Although Reac-Discovery can operate iteratively (G1 and G2 campaigns), in the reported case studies the initial dataset already enabled high-accuracy predictions without retraining, as confirmed by low MAPE values and strong agreement between predicted and validated optimal conditions. Further details are provided in Supplementary Section 1.3.1.

Defined parameter

Case Study 1. Gas and liquid flow rates were set in units of µL/min, within the following ranges: 2000–6000 µL/min for gas flow and 100–400 µL/min for liquid flow. The reactor structure was adjusted according to the following parameters: Size (2–8) and Level (0.25–0.75), optimizing tortuosity and contact area. Temperature limits were established between 30 and 70 °C, and the acetonitrile concentration ranged from 0.5 to 3 M, allowing evaluation across a wide scope of reactive conditions.

Case Study 2. Gas and liquid flow rates were set in units of µL/min, within the following ranges: 100–500 µL/min for gas flow and 50–300 µL/min for liquid flow. The reactor structure was adjusted according to the following parameters: Size (2–8) and Level (0.25–0.75), optimizing tortuosity and contact area. Temperature limits were established between 30 and 120 °C, and the epoxide (substrate) concentration ranged from 1 to 4 M, allowing evaluation across a wide scope of reactive conditions.

The parameter limits were defined based on the operational capabilities of the Vapourtec R-Series flow system and the physical constraints of the 3D-printed catalytic reactors. These limits ensure compatibility between experimental setups and computational predictions.

Execution and analysis of reactions

The self-driven Reac-Eval laboratory integrated an 80 MHz SpinSolve Ultra benchtop NMR spectrometer (Magritek) for continuous-flow, in situ monitoring, together with a Vapourtec R-4 Flow Reactor Heater, R2S and R2C peristaltic and HPLC pumps, and an autosampler. Control of both Vapourtec R-Series and SpinSolve software was coordinated via UA-OPC (OPC Unified Architecture) communication, ensuring synchronized management of reaction parameters.

Automation was handled by MASP_LIBRARY, a Python-based tool developed in-house, which provides centralized control of the SpinSolve NMR and Vapourtec R-Series flow system. The library regulates flow rates, temperature, pressure, and peripheral hardware (pumps, heaters, autosamplers, valves), enabling fully automated execution of reactions.

MASP_LIBRARY executes protocols defined by the Random Reaction Set algorithm, automating heating, residence time, and flow adjustments while continuously monitoring pressure and other parameters. Direct interfacing with the NMR spectrometer enables real-time quantification of yield and selectivity, supplying training data for machine learning models. Further details are provided in Supplementary Section 1.3.2.

Optimization of process descriptors (G1)

The neural network model (M1) was developed in Python using TensorFlow (v2.12.0) and Keras (v2.12.0) for architecture, training, and optimization. Input variables included gas and liquid flow rates, temperature, concentration, and reactor geometry (size and level), mapped to corresponding input nodes.

The network was implemented as a multilayer perceptron (MLP) with hidden layers tuned to balance complexity and efficiency. ReLU activations were applied to hidden layers, with a linear activation in the output layer for regression of performance and conversion. Training employed a Mean Squared Error (MSE) loss function and the Adam optimizer (learning rate = 0.001).

To prevent overfitting with limited data, early stopping was implemented (patience = 10) based on validation loss. Predictions were considered valid within a 5% tolerance for performance and conversion; if this threshold was exceeded, the model was retrained using an expanded dataset incorporating new experimental results. Further details are provided in Supplementary Section 1.3.3.

Optimization of geometry descriptors (G2)

Neural network training (M2) was carried out in Python (v3.13.0) using TensorFlow (v2.12.0) for model construction and training, Pandas (v2.2.3) for data manipulation, and NumPy (v2.1.0) for numerical operations. The initial dataset was expanded by incorporating reactor metrics generated by Reac-Gen, including tortuosity, surface area, structure volume, packing percentage, and reactor construction parameters (size and level). This dataset formed the basis for reactor geometry optimization.

The neural network was implemented as a MLP with two hidden layers and ReLU activations. Training employed the Adam optimizer (learning rate = 0.001) with MSE as the loss function. To avoid overfitting, the same early stopping strategy as in M1 was applied. Further details are provided in Supplementary Section 1.3.4.