Introduction

In recent years, the unique properties of Deoxyribonucleic acid (DNA), including its environmental friendliness1, long-term stability2,3,4, and ability to store vast amounts of information in a compact form5,6, have made it an attractive medium for data preservation. This has provided a promising solution to the growing demand for large-scale data storage, i.e., the zettabyte era in DNA7. Alongside the progress in synthetic biology, DNA synthesis technologies have also seen significant advancements. Several array-based synthesis technologies have been developed and commercialized, including inkjet printing, thermal, photochemical, and electrochemical synthesis. These methods have their own advantages and disadvantages in terms of synthesis density, coupling efficiency, length, fidelity, time, and cost8. Among these, inkjet printing synthesis is widely used for its high fidelity, and the majority of current DNA data storage systems employ this method. Some studies have also utilized photochemical synthesis and electrochemical synthesis technologies for data writing. Their findings indicate that these methods often result in a high probability of nucleotide errors and synthesis non-uniformity, yet they also offer advantages such as higher throughput and lower costs9,10. Nonetheless, these studies can recover data by using error correction codes and increasing the mean coverage rate (i.e., the average number of received readings of the encoded DNA sequences). This suggests that these synthesis methods are promising for application to DNA data storage systems. However, the increase in mean coverage rate also introduces more inhomogeneity and instability, increasing the cost, time, and difficulty of sequencing and data processing. A high coverage rate also does not guarantee 100% data recovery when synthetic folding is unstable9.

Recent advancements in DNA-based data storage have highlighted the need for robust error correction codes capable of correcting errors inherent in DNA synthesis, including nucleotide insertions, deletions, and substitutions. Traditional codes such as Reed-Solomon (RS) codes9,11,12,13, Low-density Parity-check (LDPC) codes14, and cyclic redundancy check (CRC) codes15,16, have been employed to detect errors. Moreover, several IDS-specific error correction codes have been designed to correct IDS errors effectively. Notable examples include the Varshamov-Tenengolts (VT) code17, the watermarker code18, the HEDGES code19, the DNA-Aeon code15, the Spider-web code20, and CHN code21. The robustness of these codes has been validated in in-vitro experiments. Additionally, although some codes have not yet been tested in wet experiments, simulations indicate that IDS-specific error correction codes, such as the single IDS error correction code22, the multiple IDS error correction code based on number theory23, and the time-varying code24, possess strong error correction capabilities. Many coding schemes targeting specific information formats and special requirements, such as the data random access schemes13,25, the PELMI storage scheme for images26, the k-WMU code for the design of address sequences27, the DNA Palette code for the time-series archival data28, and the HELIX storage system for spatial-temporal omics images have also been proposed29. These methods offer reliable solutions for storage optimized for particular domains. However, the error-correction capabilities of the aforementioned codes are limited, as none can correct more than 8% of IDS errors, which aligns with the IDS error rates observed in our electrochemical synthesis experiments. An alternative approach to data recovery involves multiple synthesis attempts and increasing sequencing coverage to select the correct sequence from numerous sequencing reads9,30,31. Nevertheless, achieving correct sequence synthesis remains challenging for methods with high error rates. For example, in experiments conducted by Antkowiak et al.9, only one out of three files was successfully recovered, even with high coverage rates.

Besides, the majority of the aforementioned coding schemes utilize concatenated codes in the form of block interleavers, with the outer code correcting dropout errors and the inner code correcting or detecting IDS errors. However, block interleavers inherently lack support for parallel decoding, which constrains improvements in data retrieval speed. To facilitate parallel decoding, the data block must be subdivided into smaller, independent blocks, allowing concurrent decoding of each block. In this approach, however, the encoding and decoding processes of individual sub-blocks are independent, precluding the exchange of information between them that could otherwise enhance correction capabilities. Furthermore, studies have shown that the accuracy of DNA synthesis and sequencing is closely linked to the biochemical properties of oligos, such as high GC content, long homopolymers, and the presence of undesired motifs32,33,34.

There is a pressing need for a coding scheme that can satisfy biochemical constraints, enable parallel decoding, and provide strong IDS error correction capability at low coverage rates. In this study, we propose DNA StairLoop, a coding scheme for DNA-based data storage that meets these requirements. Specifically, the scheme has the following characteristics: (i) The encoding structure utilizes a staircase interleaver35, enabling information exchange between data blocks to enhance overall error resilience. The row and column component codes can differ, allowing the flexible use of various error correction codes such as convolutional codes and LDPC codes. (ii) A soft-input soft-output (SISO) row decoder is employed to correct IDS errors in both convolutional and LDPC codes, supporting iterative decoding to improve error correction performance. (iii) The staircase interleaver enables highly parallel decoding. In our experiments, this parallel decoding capability, based on the interleaver’s structure, resulted in significant time reduction, even when tested across thousands of nodes, demonstrating its potential to effectively reduce decoding time. Additionally, we propose an extended encoding scheme using the convolutional code with a code rate of 1/3, which maintains a GC content between 33.3% and 66.6% within a sliding window and prevents the formation of homopolymers exceeding three consecutive nucleotides. In our experiments, we adopted it as the row code and the LDPC code as the column code. The effectiveness and robustness of our coding scheme have been verified by in-silico and in-vitro storage experiments. The simulation results show that our scheme can achieve higher IDS error correction capability. When the mean coverage rate is 15x and the IDS error rate is 10%, we can achieve 100% data recovery, which is better than other coding methods. In the two in-vitro storage experiments, we found that the raw information was recovered without any errors, although the sequencing reads showed a relatively high number of base errors (more than 6% in some blocks) and sequence dropout errors (more than 30% in some blocks). These results demonstrate the effectiveness of StairLoop under high error rate conditions.

Results

Coding structure overview

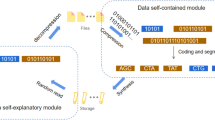
DNA StairLoop is an error correction coding scheme designed for synthesis techniques with high and unstable error rates, such as photochemical and electrochemical synthesis (Fig. 1a). It has the following features:

Fig. 1: Overview of the DNA StairLoop coding scheme.
figure 1

a The error distribution of Yan et al.28, Antkowiak et al.9, and Nguyen et al.10. b Illustration of the encoding structure. The raw binary data are first divided into short sequences and then sequentially input into the blocks (in the positions of the raw information bits), forming a staircase layout. The raw information blocks subsequently undergo row encoding and column encoding to generate codewords, i.e., oligos. c Diagram of the decoding structure. The sequencing data first undergo raw decoding and are subsequently restored to the staircase blocks according to their indices. The row decoder is soft-input and soft-output, producing extrinsic information in the form of the log-likelihood ratio (LLR) of the raw information bits. The column decoder receives this extrinsic information and performs soft-decision column decoding, which outputs extrinsic information in the form of the LLR of the raw information bits as well. This extrinsic information is iteratively input back into the row decoder. The message passing path follows the red arrows shown in the diagram. The iteration between the row and column decoders continues until the stopping criterion is met, ultimately producing the decoded bits. d Trellis diagram of the row decoding scheme. The forward message, backward message, and current message are obtained from the trellis by tracing all possible trellis paths in the joint encoding state (ES) - drift state (DS) graph. The LLR of the i-th information bit is subsequently calculated based on the forward message, backward message, and current message in the i-th decoding moment. e Flowchart for parallel decoding. The stepped matrix is equally distributed among different nodes. Row and column decoding is performed within each node, and the first and last outer information matrix that is decoded is passed to the previous and next nodes. Source data are provided as a Source Data file.

Full size image
  1. 1.

    The original message is written in a staircase interleaver, in which the connections between successive data bit matrices are of the staircase type (Fig. 1b).

  2. 2.

    The encoding structure is a serial-concatenated code with independent row codes and column codes. The component codes can be convolutional codes or block codes. For different combinations of component codes, the encoding and decoding schedules are distinct, as shown in Supplementary Fig. 1.

  3. 3.

    The decoder is iterative and follows the turbo principle. Specifically, the row decoder and column decoder are both soft-in and soft-out, which iteratively feed the probabilities of the information bits back and forth to each other (Fig. 1c).

  4. 4.

    The row decoder is specifically designed for DNA-based data storage. It can work in conjunction with the BCJR algorithm for convolutional codes and the sum-product algorithm for LDPC codes, enabling the traditional decoding algorithms to correct insertion and deletion (indel) errors (Fig. 1d).

  5. 5.

    The staircase matrix divides the parity nodes into parallel nodes. The nodes decode and pass information from the outer matrices; the first and last nodes communicate with the upper and lower nodes. The DNA StairLoop scales well in parallel because the information transfer involves only a single matrix and uses nonblocking communication (Fig. 1e).

Encoding Strategy and Staircase Interleaver Design

The staircase interleaver can be seen as a generalized block-type interleaver. Raw binary data are written into information matrices in a predefined order B1, B2, …, BF−1, and arranged in a staircase pattern, as shown in Fig. 1b. Specifically, the original information sequences consist of B2i−1 matrices of size \({k}_{r}^{o}\times {k}_{c}^{o}\) and B2i matrices of size \({k}_{r}^{e}\times {k}_{c}^{e}\), where i = 1, 2, …, ⌈(F − 1)/2⌉. The parameters \({k}_{r}^{o}\), \({k}_{c}^{o}\), \({k}_{r}^{e}\) and \({k}_{c}^{e}\) can vary depending on the specific encoding scheme. According to the structure of the staircase interleaver, the encoding process is performed in two phases, i.e., row encoding and column encoding. For simplicity, we refer to the column encoder as “Ec” and the row encoder as “Er”. Both Er and Ec can be selected from convolutional codes or block codes (particularly LDPC codes) and may differ from each other. We provide four interleaver configurations with distinct component codes, as detailed in Supplementary Section 1. The arrangement of information bits varies significantly among these configurations due to differences in interleaver design. This variation arises because block codes require extrinsic information for all codeword bits during iterative decoding, whereas convolutional codes require only systematic information bits. Consequently, the encoding schedules also differ. The transmitted codewords are consistently structured as row sequences.

Encoding proceeds recursively on each matrix pair. First, matrices B0 and BF are initialized to reference states known to the encoder and decoder, e.g., matrices of all zero symbols. Two error-correction codes in the systematic form are given: the row code and the column code. For i = 1, …, ⌈(F − 1)/2⌉, row encoding proceeds on the matrix pair [B2i−2B2i−1], generating the row codeword matrix pair \([{B}_{2i-2}\,{B}_{2i-1}\,{B}_{i,r}^{P}]\). The additional elements in the j-th row of \({B}_{i,r}^{P}\) are the parity symbols that result from encoding the information symbols in the j-th row of [B2i−2B2i−1]. Column encoding proceeds on the matrix pair \({\left[{B}_{2i-1}{B}_{2i}\right]}^{T}\), generating the column codeword matrix pair\({\left[{B}_{2i-1}{B}_{2i}{B}_{i,c}^{P}\right]}^{T}\). The additional elements in the j-th column of \({B}_{i,c}^{P}\) are the parity symbols that result from encoding the information symbols in the j-th column of \({\left[{B}_{2i-1}{B}_{2i}\right]}^{T}\). Herein, the relationship between successive matrices satisfies the following relation: each of the rows is a valid codeword of the row encoder, and each of the columns is a valid codeword of the column encoder.

According to the relationships of the codewords, the connections within the staircase interleaver are clearly defined. We call two consecutive matrices of the same layer as a block, such as [B0B1]. On the one hand, the parity-check information is transmitted between the staircase blocks, allowing the encoder to emulate the performance of long codes. On the other hand, the independence of nonadjacent blocks within the staircase interleaver enhances the parallelism of the decoding process.

Iterative Decoding Strategy

A key feature of DNA StairLoop is the use of soft-decision decoders, which enhance error correction through iterative decoding (Fig. 1c). Like the encoders, we call the column decoder “Dc” and the row decoder “Dr”. Since DNA strands suffer IDS errors in transmission, the row decoder Dr aims to regain synchronization or to correct IDS errors. The column decoder Dc uses the soft output of the row decoder to compute likelihood information without suffering from IDS errors. In this case, we propose an IDS error correction strategy to improve the row decoder, which is presented in detail below. However, the BCJR algorithm for the convolutional code and the sum-product algorithm for the LDPC code can be applied to the column decoder with a few minor adaptations. Given that our coding scheme is a generalized serial connection and that Dc does not directly observe the transmission information of the channel, it relies on the information received from Dr to output the log-likelihood ratio (LLR) on the Ec output bits. Dr receives the channel LLRs on the received bits and the extrinsic information from Dc to calculate the corresponding LLR values.

Consider the row decoder Dr as an example. Let v = {v1, v2, …, vn} ∈ {0, 1}n and r = {r1, r2, …, rN} ∈ {0, 1}N denote the channel inputs of length n and outputs of length N, respectively. Let S denote the encoding syndrome constraint. Then the posterior L-value of vt can be written as

$$L({v}_{t})= \log \frac{Pr\left[{v}_{t}=0| {{{\boldsymbol{r}}}},{S}\right]}{Pr\left[{v}_{t}=1| {{{\boldsymbol{r}}}},{S}\right]} \\= \log \frac{Pr\left[{{{\boldsymbol{r}}}},{S}| {v}_{t}=0\right]}{Pr\left[{{{\boldsymbol{r}}}},{S}| {v}_{t}=1\right]}+\log \frac{Pr\left[{v}_{t}=0\right]}{Pr\left[{v}_{t}=1\right]}\\= {L}_{e}^{(r)}({v}_{t})+{L}_{e}^{(c)}({v}_{t}),$$
(1)

of which only \({L}_{e}^{(r)}({v}_{t})\) is passed to Dc, and \({L}_{e}^{(c)}({v}_{t})\) is the interleaved extrinsic information from the previous Dc iteration.

The outline of the iterative decoding scheme is as follows:

  1. 1.

    All the metrics are initialized appropriately, and the extrinsic information is set to zero.

  2. 2.

    Row decoder: The row decoding algorithm is run with received bits and the extrinsic information from Dc to obtain the soft decision of the information symbols of Er, and the extrinsic information is sent to Dc.

  3. 3.

    Column decoder: The column decoding algorithm is run with the extrinsic information from Dr to obtain the soft decision of the output symbols of Ec, and the extrinsic information is sent to Dr.

  4. 4.

    Steps 2 and 3 are repeated until the preset maximum number of iterations is reached (or the stopping criterion is satisfied). According to the final soft decision computed by Dc, decisions are made on information bits.

Row Decoding Strategy

The processes of DNA synthesis and sequencing introduce nucleotide IDS errors within a single DNA strand, which are typically modeled as an IDS channel (Supplementary Fig. 2)36,37. The input to the row decoder is a DNA sequencing read containing IDS errors. Consequently, the row decoder must be capable of correcting IDS errors and re-establishing sequence synchronization.

In this work, we provide an IDS error-correction strategy to modify the conventional decoding algorithms of the convolutional code and the LDPC code to correct IDS errors (Fig. 1d). The IDS channel model can be conveniently represented by a trellis, where each input vi corresponds to a trellis node (Supplementary Fig. 3). However, unlike the discrete-time intersymbol interference channel38, each trellis node of the IDS channel model cannot correspond to a single output because of indel errors. To cope with indel errors, we introduce a hidden state variable into the trellis graph, called the synchronization drift. For t = 1, 2, …, n, the drift state is defined as \({{{{\mathcal{D}}}}}_{t}\) at time t, and its realization dt is defined as the number of insertions minus the number of deletions that occurred until symbol vt is transmitted. In addition, we define the encoding state at time t as \({{{{\mathcal{S}}}}}_{t}\), of which the realization st is determined by the encoding scheme.

The key innovation behind the row decoding strategy is the transmission of the encoding state (ES) and the drift state (DS), which facilitates the maximum a posteriori (MAP) decoding. According to the Bayesian formula, we can obtain

$$Pr\left[{{{{\boldsymbol{v}}}}}_{1}^{n}| {{{{\boldsymbol{r}}}}}_{1}^{N},{S}\right]={\left(Pr\left[{{{{\boldsymbol{r}}}}}_{1}^{N},{S}\right]\right)}^{-n}{\prod }_{t=1}^{n}{{{\mathcal{F}}}}\left[{v}_{t},{{{{\boldsymbol{r}}}}}_{1}^{N}\right],$$
(2)

where each factor is

$$ {{{\mathcal{F}}}}\left[{v}_{t},{{{{\boldsymbol{r}}}}}_{1}^{N}\right] \\= Pr\left[{v}_{t},{{{{\boldsymbol{r}}}}}_{1}^{N},{S}| {{{{\boldsymbol{v}}}}}_{1}^{t-1}\right]\\= Pr[{v}_{t}]Pr\left[{{{{\boldsymbol{r}}}}}_{1}^{{d}_{t-1}+t-1},{S}| {{{{\boldsymbol{v}}}}}_{1}^{t}\right]Pr\left[{{{{\boldsymbol{r}}}}}_{{d}_{t-1}+t}^{{d}_{t}+t},{S}| {{{{\boldsymbol{r}}}}}_{1}^{{d}_{t-1}+t-1},{{{{\boldsymbol{v}}}}}_{1}^{t}\right] \\ Pr\left[{{{{\boldsymbol{r}}}}}_{{d}_{t}+t+1}^{N},{S}| {{{{\boldsymbol{r}}}}}_{1}^{{d}_{t}+t},{{{{\boldsymbol{v}}}}}_{1}^{t}\right] \\= {\sum}_{{s}_{t-1},{s}_{t},{d}_{t-1},{d}_{t}}Pr[{v}_{t}]Pr\left[{{{{\boldsymbol{r}}}}}_{{d}_{t-1}+t}^{{d}_{t}+t},{s}_{t},{d}_{t}| {v}_{t},{s}_{t-1},{d}_{t-1}\right] \\ Pr\left[{{{{\boldsymbol{r}}}}}_{1}^{{d}_{t-1}+t-1}| {s}_{t-1},{d}_{t-1}\right]Pr\left[{{{{\boldsymbol{r}}}}}_{{d}_{t}+t+1}^{N}| {s}_{t},{d}_{t}\right].$$
(3)

Each factorization can be illustrated in the factor graph (Supplementary Fig. 3), where for each factor of Eq. (3), there is a single trellis node, and for each variable on which the factor depends, there is a single connected edge. Armed with the above graph representation of the trellis, the message-passing algorithms can be used on IDS channel models. Then, the maximum posterior probability of each input symbol can be calculated. The details of the decoding strategy are presented in Supplementary Section 2.

In addition, by jointly calculating the MAP of each input symbol on multiple copies, the decoder can obtain higher performance gains from the sequencing redundancy and skip the complex multiple sequence alignment (MSA) process. In contrast to MSA technology, which makes hard decisions on the basis of majority voting39,40, this decoding strategy outputs soft information, which is more applicable to the iterative decoding scheme.

Parallel Decoding Strategy

The DNA StairLoop adopts a parallel decoding method that acts on the staircase interleaver, which enables the parallel decoding of thousands of nodes to increase the decoding speed. Figure 1e illustrates the decoding process of DNA StairLoop, which is divided into two parts: local decoding and communication. When decoding, the staircase blocks are evenly divided and distributed to parallel nodes, and each parallel node performs inverse-order row decoding and sequential column decoding in its local decoding. When a node finishes decoding the last set of blocks in the inwards row, it passes the outer information to the next node and continues to decode the previous blocks in the inwards row, which does not hinder the decoding process because the nonblocking time passes. Column decoding also passes the outer information to the previous node after decoding the first block and continues with column decoding. We experimentally verified that parallelism can be maintained, even with thousands of nodes. This helps reduce the time-consuming decoding problem in large-scale storage.

Performance Evaluation of In-Vitro Experiments

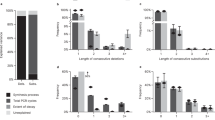
We performed three in-vitro storage experiments under different emerging DNA synthesis techniques to validate the robustness of DNA StairLoop (Fig. 2a and b). In the first and second experiments, we encoded a photo of the Oracle experiment into 45,360 sequences with a length of 130 nt (Fig. 2a). The encoding process utilized our extended convolutional code as the row code and the IEEE 802.11 (WiFi) LDPC codes as the column code. Both experiments showed high nucleotide error rates. In addition, the sequencing depth was markedly uneven, with substantial variability, which we quantify using the sequence dropout rate (Fig. 2c). In the first experiment, nucleotide IDS error rates were generally high, exceeding 6% in some blocks. Sequence dropout rates were also high, exceeding 10% in several consecutive blocks. In the second experiment, sequence dropout error rates were even higher, exceeding 30% in some blocks. Both experiments recovered 100% of all original data. In the third experiment, three images and a text file were compressed to 740 KB and encoded into 148,100 sequences, each of which was 127 nt in length (Fig. 2a). The DNA synthesis parameters used in Experiment 3 were consistent with Experiment 1. The details of Experiment 3 are shown in Supplementary Section 5.3.

Fig. 2: Results of the in-vitro storage experiments.
figure 2

a The coding scheme of the three experiments. b Input file size, type, and the number and length of encoding oligos (without primers). The total stored file size was 1.04 MB. c Error distribution of Experiment 1 and Experiment 2, respectively. d The byte error rate after decoding under different experiments, sequencing depths, and block indices. It can be seen that iterative decoding helps to improve the error correction capability. e In Experiment 2, the data recovery result without iteration at a sequencing depth of 3.5x. There are many mosaic points, as shown in the zoomed-in image. f The data recovery results at different sequencing depths. Because our interleaver is staircase-type and the blocks are relatively independent, the residual errors after decoding tend to cluster. Source data are provided as a Source Data file.

Full size image

Since the coding blocks are relatively independent, the error correction capability of a single block can be used to estimate the maximum correctable error rate for DNA StairLoop. In Block 63 of Experiment 1 (sequencing depth: 2.69 × ), StairLoop demonstrated error-free data recovery under error conditions comprising the dropout rate of 18.98% and the IDS error rate of 6.48%, confirming exceptional specificity in IDS error correction. Simultaneously, Block 47 of Experiment 2 (sequencing depth: 1.28 × ) revealed system robustness through maintained 100% recovery despite intensified dropout errors (32.87% dropout with 0.87% IDS errors). These complementary scenarios collectively validate StairLoop’s twofold competencies: 1) error-free data recovery at very low sequencing depths with  > 30% dropout error and  > 6% IDS error, and 2) universal adaptability to different DNA synthesis technologies. The systematic experimental verification establishes StairLoop’s capacity to address predominant error regimes in DNA data storage systems.

The error correction performance of DNA StairLoop is mainly attributed to two mechanisms: (1) The iterative decoding strategy gradually improves the decoding accuracy through cyclic error correction (Fig. 2d). As shown in Fig. 2e, without iterative decoding, there are many residual errors in the decoded data, which leads to some mosaic spots in the image. However, after iteration, the data can be recovered error-free. (2) The interleaver architecturally enhances the error correction capability by implementing a staircase matrix structure to prevent error aggregation. This makes DNA StairLoop outperform existing DNA coding schemes in terms of error resistance. Thus, data can be recovered losslessly at lower sequencing depths and higher dropout rates (Fig. 2f).

Performance evaluation of in-silico experiments

We performed simulations to evaluate the effectiveness of the DNA StairLoop and compared its error correction performance with that of state-of-the-art algorithms (Table 1). We evaluated the error correction capabilities of DNA Fountain code12, DNA-Aeon code15, DNA CHN code21, the coding scheme of Antkowiak et al.9, and our own code at an mean coverage of 15x, under different IDS error rates (Fig. 3a). To ensure a fair comparison, we adjusted the encoding parameters so that all codes operated at nearly identical code rates. The details of the experimental setup are shown in Supplementary Section 4.1. The IDS error rates used in the simulations are consistent with those observed in our electrochemical synthesis experiment. The DNA StairLoop can successfully decode information with an error rate as high as 10%, and its maximum error resilience exceeds that of DNA-Aeon and DNA Fountain. Fig. 3b shows that StairLoop’s error correction capability is virtually independent of the type of error, with full recovery at 10% error rate achieved for any error type. These findings demonstrate that our code is a viable solution for error-prone synthesis methods. In addition, we verified in Supplementary Section 4.3 that the error-correction capability of the DNA StairLoop degrades when the staircase interleaver is not used, which proves that the staircase interleaver can improve the error-correction capability. Iterative decoding is a key factor in the high error-correction capability. We show the flow of iterative decoding in Fig. 3c and its impact as the error rate increases in Fig. 3d. As the number of iterations increases, the decoding recovery rate continues to improve. Even for an unpredictable high error rate, the decoded recovery rate can still be improved through iteration. For instance, when the IDS error rate is 11%, the decoding effect is significantly improved as the number of iterations increases. In addition, the direct input of DNA StairLoop can duplicate sequencing reads rather than the central sequence obtained by clustering methods. The staircase interleavers have faster iterative decoding compared to independent chunking, as shown in Supplementary Table 6.

Table 1 Comparison among popular DNA coding schemes and key achievements
Full size table
Fig. 3: Simulation experiment results. The experiment was repeated three times.Data are presented as mean values +/− SD.
figure 3

a Percentage of Successful Decoding Attempts at a Given IDS Error Ratio. We simulated the recovery when storing 5 KB of data, where the mean coverage rate was 15x, and the proportion of substitution, deletion, and insertion error rates was 13: 31: 6. For a fair comparison, the DNA Fountain code and DNA-Aeon code were configured to have similar code rates and GC content constraints as the DNA StairLoop. b Impact of Decoded bit recovery rate at Single Error Rate. This parallel simulation was conducted on a supercomputer, with the number of blocks for DNA StairLoop set to 4000. c Iterative Decoding Process. d Impact of Iterative Decoding on Recovery Rate. e Parallel Decoding Process. f Impact of Increasing Parallel Nodes on Decoding Time and Accuracy. Source data are provided as a Source Data file.

Full size image

Figure 3e illustrates the message-passing process between different nodes when parallel decoding. Figure 3f illustrates the trend in decoding time and accuracy as the number of nodes increases from 2 to 1000. The results indicate a linear decrease in decoding time with the addition of nodes, demonstrating that DNA StairLoop maintains strong parallel efficiency, even at the scale of thousands of nodes. This scalability significantly reduces the overall decoding time. In addition, the bit recovery rate is not affected by parallel decoding. StairLoop under parallel decoding has a decoding speed advantage over other high error correction algorithms, as detailed in Supplementary Table 5.

Simulation experiments demonstrated that DNA StairLoop, which uses both iterative and multiple sequence decoding algorithms, exhibits exceptionally high error-correction capability, effectively addressing the challenges posed by high-error-rate synthesis methods. Moreover, its highly parallel decoding architecture substantially increases decoding speed, thereby minimizing the additional time costs typically associated with time-consuming decoding processes.

Discussion

DNA-based data storage systems record information by writing it into a sequence of nucleic acid strands. Unlike traditional storage media, the synthesis and sequencing of nucleotide sequences will lead to challenges in writing and reading information, resulting in complex burst errors, particularly when using electrochemical synthesis technologies. This leads to challenges in the recovery of DNA data.

To achieve reliable information storage at such a high IDS error rate and poor synthesis uniformity, we propose a staircase interleaver-based information encoding scheme and its soft-decision iterative decoding scheme. The use of the staircase interleaver ensures that the data matrices are both independent and transitive, making parallel computations with a low-error floor possible. On the decoding side, our proposed error correction strategy for the row component code can correct IDS errors. The iterative exchange of LLRs between row and column component codes can further enhance the error correction performance.

Notably, our proposed row decoding scheme can cooperate with traditional decoding algorithms for convolutional codes and block codes, enabling these codes, which can correct only substitution errors and erasure errors, to correct IDS errors. This makes it feasible to use convolutional codes or block codes as row codes. We propose four types of encoding structures for different row and column component codes. In the experiments, we employed an encoder using convolutional codes as row codes and LDPC codes as column codes. This is because encoders with convolutional codes acting as row codes can effectively implement artificially defined biochemical constraints, which is more challenging for LDPC codes. Furthermore, preliminary tests of the four encoding structures revealed that the combination of convolutional codes and LDPC codes has a greater error correction potential.

We performed in-silico and in-vitro experiments to test the reliability and robustness of our coding scheme. Compared to existing state-of-the-art encodings, DNA StairLoop has an advantage in terms of reliable data recovery under high IDS error rates and low coverage rates. If an unexpectedly large number of IDS errors are found in received reads, StairLoop can improve the accuracy of data recovery by adjusting the number of iterative decoding executions. Multiple parameters of the codec, such as the number of blocks of the information matrix, the encoding structure of the row codes, the code rate of the column codes, and the number of iterative decodes, can be adjusted to further customize the base sequence constraints and improve the error correction capability, in accordance with the synthesis, storage, and sequencing methodology in use, as well as the expected decoding byte error rate requirements. In addition, if high IDS error rates are not taken into account during encoding, the number of iterative decoding executions can be adjusted to improve decoding performance.

However, DNA StairLoop still has limitations, including decoding speed and code rate. The need for multiple iterations during decoding reduces its speed. Moreover, the use of convolutional codes results in a lower code rate compared to many LDPC and RS codes. In future work, we will focus on further optimizing the algorithm code to enhance computational speed. Additionally, we will explore the application of punctured convolutional codes in the DNA StairLoop encoding scheme to improve the code rate.

Overall, DNA StairLoop is suitable for emerging DNA synthesis technologies with high or unstable error rates. For high-fidelity DNA synthesis methods, this coding approach may cause some redundancy. However, improving the uniformity and synthesis accuracy of emerging technologies via hardware can be quite challenging. If we can compensate for hardware shortcomings from a software perspective, we believe it is valuable and promising.

Methods

In all experiments, the primers used were GTAAAACGACGGCCAG and GTCATAGCTGTTTCCTG. In the first and third in-vitro storage experiments, the DNA sequences were synthesized by GenScript using two 8M chips. For the second experiment, a DNA synthesis device under testing by GenScript was employed for the process. Sequencing reads were obtained from the oligo pool via Illumina double-ended PE150 sequencing, following PCR amplification.

The amplification procedure was as follows: The amplification system was prepared by adding 25 μL of amplification MasterMix enzyme, 0.5 μL of forward primer (F, 50 μM), 0.5 μL of reverse primer (R, 50 μM), 2 μL of template DNA (8 ng), and nuclease - free water to a final volume of 50 μL in a PCR tube. The mixture was gently vortexed and briefly centrifuged. The prepared amplification system was then placed into a PCR machine with the following program: an initial denaturation at 98 °C for 30 sec; 20 cycles of denaturation (98 °C, 10 sec), annealing (60 °C, 10 sec), and extension (72 °C, 15 sec); a final extension at 72 °C for 5 min; and a hold at 4 °C. The PCR machine was started to perform DNA amplification. After amplification, the product was stored at 4 °C or −20 °C for subsequent analysis. All reagents and samples were kept on ice until use, and after each step, gentle vortexing and brief centrifugation were performed to ensure thorough mixing.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.