Dimensionless learning based on information

Abstract

Dimensional analysis is one of the most fundamental tools for understanding physical systems. However, the construction of dimensionless variables, as guided by the Buckingham-π theorem, is not uniquely determined. Here, we introduce IT-π, a model-free method that combines dimensionless learning with the principles of information theory. Grounded in the irreducible error theorem, IT-π identifies dimensionless variables with the highest predictive power by measuring their shared information content. The approach is able to rank variables by predictability, identify distinct physical regimes, uncover self-similar variables, determine the characteristic scales of the problem, and extract its dimensionless parameters. IT-π also provides a bound of the minimum predictive error achievable across all possible models, from simple linear regression to advanced deep learning techniques, naturally enabling a definition of model efficiency. We benchmark IT-π across different cases and demonstrate that it offers superior performance and capabilities compared to existing tools. The method is also applied to conduct dimensionless learning for supersonic turbulence, aerodynamic drag on both smooth and irregular surfaces, magnetohydrodynamic power generation, and laser-metal interaction.

Introduction

Physical laws and models must adhere to the principle of dimensional homogeneity^1,2, i.e., they must be independent of the units used to express their variables. A similar idea was first introduced by Newton in his Principia, under the term “dynamically similar systems”³, although Galileo had already employed the notion of similar systems when discussing pendulum motions. Over the following centuries, the concept of similar systems was loosely applied in a variety of fields, including engineering (Froude, Bertrand, Reech), theoretical physics (van der Waals, Onnes, Lorentz, Maxwell, Boltzmann), and theoretical and experimental hydrodynamics (Stokes, Helmholtz, Reynolds, Prandtl, Rayleigh)³. The approach was formally articulated in the early 20th century, laying the foundation for what is known today as dimensional analysis^1,4,5.

The applications of dimensional analysis extend beyond the construction of dimensionally consistent physical laws. It provides the conditions under which two systems share identical behavior (dynamic similarity), allowing predictions from laboratory experiments to be extended to real-world applications^3,6. Dimensional analysis also facilitates dimensionality reduction, i.e., simplifying physical problems to their most fundamental forms, thus decreasing the amount of data required for analysis^7,8. Another application is the discovery of self-similar variables, for which systems exhibit invariant solutions under appropriate scaling⁹. Finally, dimensional analysis can reveal the physical regimes in which different phenomena dominate (e.g., incompressible versus compressible flow), enabling researchers to identify the most influential physical mechanisms in a given context¹⁰.

A key landmark of dimensional analysis is the Buckingham-π theorem¹, which offers a systematic framework for deriving dimensionless variables. However, the solution is not unique, as there are infinitely many possible ways to construct these variables. To address this limitation, recent studies have developed data-driven tools to identify unique dimensionless variables that minimize the error for a given model structure, particularly in the data-rich context enabled by modern simulations and experiments. These methods combine dimensional analysis with machine learning techniques to identify dimensionless variables using multivariate linear regression¹¹, polynomial regression^12,13,14, ridge regression¹⁵, hypothesis testing¹⁶, Gaussian process regression¹⁷, neural networks^13,15,18,19, sparse identification of nonlinear dynamics^12,15, clustering²⁰, symbolic regression^13,21,22 and entropic principles^23,24. Table 1 offers a non-exhaustive comparative overview of data-driven methods for discovering dimensionless variables, highlighting their respective capabilities. These include applicability to ordinary and partial differential equations (ODEs/PDEs), the ability to rank dimensionless variables by predictability (and thus relative importance), identification of distinct physical regimes, detection of self-similar behavior, and extraction of characteristic scales (e.g., length and time scales of the system). Another key capability is whether the method can determine a bound on the minimum possible error across all models–which in turn enables the definition of a model efficiency. The comparison in Table 1 indicates that, although many approaches incorporate several of these properties, no single method currently supports all of these capabilities simultaneously. One notable shortcoming of previous data-driven methods is that they are not model-free; i.e., the discovery of dimensionless variables relies on a predefined model structure (e.g., linear regressions, neural networks,...). This can lead to potentially biased results, as the dimensionless variables identified may not be optimal for other models. A detailed account of the challenges in dimensionless learning can be found in the Supplementary Materials.

Table 1 Overview of some data-driven dimensionless learning methods and their capabilities

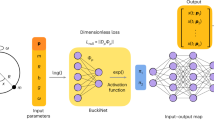
In this work, we present IT-π, an information-theoretic, model-free method for dimensionless learning. An overview of the method is shown in Fig. 1. Our approach is motivated by a fundamental question: Which dimensionless variables are best suited for predicting a quantity of interest, independent of the modeling approach? IT-π addresses this question by unifying the Buckingham-π theorem with the irreducible error theorem. The central idea is that the predictive capability of a model is bounded by the amount of information shared between the input (dimensionless variables) and the output (dimensionless quantity of interest)^25,26.

Fig. 1: Illustration of the dimensionless learning capabilities enabled by IT-π.

a Ranking of candidate dimensionless variables based on their predictability. b Example of regime detection for the skin friction coefficient C_f in a wall-bounded turbulent flow, with Reynolds number (Re) and Mach number (Ma) as dimensionless inputs. The score R_Re quantifies the relative importance of Re in predicting C_f. (c) Degree of dynamic similarity (DoS) between the lift coefficient of a wind tunnel-scaled aircraft model and that of the corresponding full-scale vehicle. d Characteristic length scale (S_l) and time scale (S_t) identified for a simple pendulum. e Model efficiency in predicting a target quantity Π_o using a neural network with inputs Π and prediction error ϵ_f. Additional details and discussion of the examples are provided in the text.

This manuscript is organized as follows. We begin by introducing the information-theoretic irreducible error theorem, which establishes the minimum achievable error across all possible models. This theorem serves as the foundation for a generalized formulation of the Buckingham-π theorem, while enabling all capabilities outlined in Table 1. We then apply IT-π to a broad set of validation and application cases. The validation cases, which have known analytical solutions, are used to benchmark the performance of IT-π. In contrast, the application cases—where no optimal solution is known—are used to discover new dimensionless variables governing the underlying physics. Finally, we compare the performance of IT-π with other dimensionless learning methods across all studied cases.

Results

Dimensionless learning based on information

A physical model (or law) aims to predict a dimensional quantity q_o using a set of n dimensional input variables, ${{{\bf{q}}}}=\left[{q}_{1},{q}_{2},\ldots,{q}_{n}\right]$, through the relation ${\hat{q}}_{o}={{{\mathcal{F}}}}({{{\bf{q}}}})$, where ${\hat{q}}_{o}$ is an estimate of q_o. As an example, consider the prediction of the gravitational force between two objects, q_o = F_g, which depends on ${{{\bf{q}}}}=\left[{m}_{1},{m}_{2},r,G\right]$, where m₁ and m₂ are the masses of the objects, r is the distance between their centers of mass, and G is the gravitational constant. According to the Buckingham-π theorem¹, physical models can be reformulated in a dimensionless form as ${\hat{\Pi }}_{o}=f({{{\mathbf{\Pi }}}})$, where ${\hat{\Pi }}_{o}$ denotes the predicted dimensionless output, and ${{{\mathbf{\Pi }}}}=\left[{\Pi }_{1},{\Pi }_{2},\ldots,{\Pi }_{l}\right]$ is the set of dimensionless input variables. Each dimensionless variable has the form ${\Pi }_{i}={q}_{1}^{{a}_{i1}}\,{q}_{2}^{{a}_{i2}}\,\cdots \,{q}_{n}^{{a}_{in}}$ and the number of required dimensionless inputs is upper bounded by l = n − n_u, where n_u is the number of fundamental units involved in the problem (e.g., length, time, mass, electric current, temperature, amount of substance, and luminous intensity). For a given L_p-norm, the success of the model is measured by the error ${\epsilon }_{f} \,=\parallel \!\!{\Pi }_{o}-{\hat{\Pi }}_{o}{\parallel }_{p}$.

Irreducible error as lack of information

Our approach is grounded in the information-theoretic irreducible error theorem [see proof in the Supplementary Materials]^27,28. The key insight is that prediction accuracy of any model is fundamentally limited by the amount of information the input contains about the output, where information here is defined within the framework of information theory²⁹. More precisely, the error across all possible models f is lower-bounded by

$${\epsilon }_{f}\, \ge \, {e}^{-{I}_{\alpha }({\Pi }_{o};{{{\mathbf{\Pi }}}})}\cdot c(\alpha,p,{h}_{\alpha,o})\, \equiv \, {\epsilon }_{LB},$$

(1)

where ${I}_{\alpha}({\Pi }_{o}; {{\mathbf{\Pi}}})$ is the Rényi mutual information of order α³⁰, which measures the shared information between Π_o and Π. The value of $c\, ({\alpha}, p, h_{{\alpha},o})$ depends on the L_p-norm, α and the information content of Π_o, denoted by h_α,o [see Methods]. The irreducible (lower bound) error is denoted as ϵ_LB. The inequality in Eq. (1) represents a fundamental mathematical constraint that holds regardless of the complexity of the statistical relationship between input and output, and must therefore be satisfied by any predictive model, irrespective of its form. When an exact functional relationship exists between the input and the output, the information measure ${I}_{\alpha} ({\Pi }_{o}; {{\mathbf{\Pi}}})$ converges to infinity, indicating that an exact model is possible (ϵ_LB = 0). In contrast, if some of the variables influencing Π_o are inaccessible or unmeasurable, ${I}_{\alpha} ({\Pi }_{o}; {{\mathbf{\Pi}}})$ remains finite, leading to an irreducible error (ϵ_LB > 0) that cannot be eliminated. It is interesting to note that the inequality in Eq. (1) holds for a range of values of α. However, the most useful case occurs when ϵ_LB is maximized, yielding the tightest bound. A detailed analysis of the role of α in Eq. (1) is provided in the Supplementary Material.

The irreducible error ϵ_LB has several useful properties. First, it is independent of any particular model f. Second, it is invariant under bijective transformations of inputs when the output is fixed, reflecting the principle that such transformations produce alternative yet equivalent model formulations. Third, it is sensitive to the choice of the L_p-norm for the error. For example, predicting extreme events (captured by high L_p-norms) may be more challenging and require different variables than predicting weaker, common events (captured by low L_p-norms) [see example in the Supplementary Materials]. Finally, Eq. (1) naturally leads to the definition of the normalized irreducible error ${\tilde{\epsilon }}_{LB}={e}^{-{I}_{\alpha }({\Pi }_{o};{{{\mathbf{\Pi }}}})},$ which ranges from 0—when exact predictions are possible—to 1—when predictions are essentially random guesses. Occasionally, we will refer to the percentage form of ${\tilde{\epsilon }}_{LB}$, defined as $\%{\tilde{\epsilon }}_{LB}={\tilde{\epsilon }}_{LB}\times 100$.

Information-theoretic Buckingham-π theorem (IT-π)

Following Eq. (1), we define the optimal dimensionless inputs ${{{{\mathbf{\Pi }}}}}^{ * }=\,[{\Pi }_{1}^{ * },{\Pi }_{2}^{ * },\ldots,{\Pi }_{{l}^{ * }}^{ * }]$ and dimensionless output ${\Pi }_{o}^{ * }$ for a given L_p-norm as those satisfying

$${{{{\mathbf{\Pi }}}}}^{ * },\ {\Pi }_{o}^{ * }=\arg {\min }_{{{{\mathbf{\Pi }}}},{\Pi }_{o}}{\max }_{\alpha }[{\epsilon }_{LB}].$$

(2)

Figure 2 illustrates the optimization process from Eq. (2). This model-free formulation ensures that the identified dimensionless variables yield the highest predictive capabilities irrespective of the modeling approach. If desired, the output can be fixed in dimensionless form, requiring only Π* to be discovered. The irreducible error using the optimal dimensionless inputs Π* is denoted by ${\epsilon }_{LB}^{ * }={\epsilon }_{LB}({{{{\mathbf{\Pi }}}}}^{ * })$. It is satisfied that ${\epsilon }_{f}\ge {\epsilon }_{LB}\ge {\epsilon }_{LB}^{ * }$. The optimization problem from Eq. (2) can be efficiently solved by employing the covariance matrix adaptation evolution strategy (CMA-ES)³¹ constrained to the dimensionless candidates for Π and Π_o from the (classical) Buckingham-π theorem [see Methods]. Next, we discuss the different capabilities enabled by IT-π, with illustrative examples provided in Fig. 1.

Fig. 2: Schematic of the optimization process in IT-π.

Circles represent the information content of the dimensionless input (Π) and output (Π_o). The overlapping region denotes their mutual information of order α, I_α(Π_o; Π). The area enclosed by the dashed line corresponds to the amount of information in Π_o that cannot be inferred from Π, which is related to the irreducible error ϵ_LB. The optimization is conducted with CMA-ES and proceeds from left to right, evaluating candidate pairs of Π and Π_o to minimize ϵ_LB until the optimal value ${\epsilon }_{LB}^{ * }$ is reached. The candidates are constrained to be dimensionless by the Buckingham-π theorem. The value of α determines the sensitivity of IT-π to different L_p-norms and is learned as part of the optimization process.

Ranking of dimensionless variables by predictability

The variables in Π* can be ranked by predictability according to ${\epsilon }_{LB}({\Pi }_{1}^{ * })\ge {\epsilon }_{LB}({\Pi }_{2}^{ * })\ge \cdots \ge {\epsilon }_{LB}({\Pi }_{{l}^{ * }}^{ * })$. This ranking applies not only to individual variables but also to pairs of variables, such as ${\epsilon }_{LB}([{\Pi }_{1}^{ * },{\Pi }_{2}^{ * }])\ge {\epsilon }_{LB}([{\Pi }_{1}^{ * },{\Pi }_{3}^{ * }])$, triplets, and so on. If considering additional variables no longer provides new information about the output, then the error does not decrease further, i.e., ${\epsilon }_{LB}([{\Pi }_{1}^{ * },{\Pi }_{2}^{ * },\ldots,{\Pi }_{{l}^{ * }}^{ * }])={\epsilon }_{LB}([{\Pi }_{1}^{ * },{\Pi }_{2}^{ * },\ldots,{\Pi }_{{l}^{ * }+1}^{ * }])={\epsilon }_{LB}^{ * }$, where l* is the minimum number of dimensionless variables to maximize predictability of the output. Note that the number of dimensionless variables provided by the original Buckingham-π theorem, l = n − n_u¹, represents an upper bound—i.e., the actual number of dimensionless variables required for a predictive model may be smaller. In contrast, the value of l* is tight, improving upon both Buckingham’s original bound, l≥l*, and the subsequent refinement proposed by Sonin⁷. Identifying the exact number of required inputs has several advantages. For instance, it provides a clear guideline for selecting the optimal set of inputs to balance model complexity with prediction accuracy. In the Applications section, we present a case in which Buckingham-π yields l = 7 dimensionless variables, whereas IT-π identifies a significantly smaller set with l* = 2.

Detection of physical regimes

Physical regimes are distinct operating conditions of a system, each governed by a particular set of dimensionless variables. As these variables vary and fall within specific intervals, the system transitions to a different regime, where new effects become dominant. For instance, in fluid mechanics, incompressible and compressible flow represent two distinct physical regimes, each governed by unique flow characteristics. In the incompressible regime, the flow physics are governed solely by the dimensionless Reynolds number. In contrast, compressible flows require both the Reynolds and Mach numbers to accurately characterize the dynamics.

IT-π identifies physical regimes by evaluating the predictive significance of each dimensionless input, ${\Pi }_{i}^{ * }$, within specific regions of the dimensionless space. First, Π* is divided into M regions, labeled as r₁, r₂, …, r_M. In each region r_k, a prediction score for ${\Pi }_{i}^{ * }$ is computed as ${R}_{i}({r}_{k})={I}_{\alpha }({\Pi }_{o}^{ * };{\Pi }_{i}^{ * }\in {r}_{k})/{I}_{\alpha }({\Pi }_{o}^{ * };{{{{\mathbf{\Pi }}}}}^{ * }\in {r}_{k})\in [0,1]$. The score R_i(r_k) represents the relative importance of ${\Pi }_{i}^{ * }$ in predicting the output ${\Pi }_{o}^{ * }$ within the region r_k. By comparing these scores across regions, one can categorize dimensionless inputs into distinct physical regimes. Consider the example of predicting the skin friction of a turbulent flow in a pipe, the Reynolds number (Re) dominates in the incompressible flow regime without the influence of additional physical effects (e.g., buoyancy, magnetic forces, etc), as it would be indicated by a prediction score ${R}_{{{{\rm{Re}}}}}({r}_{{{{\rm{incompressible}}}}})\approx 1$. However, in the compressible flow regime, ${R}_{{{{\rm{Re}}}}}({r}_{{{{\rm{compressible}}}}}) < 1$, indicating the need for an additional dimensionless number to fully determined the skin friction—in this case, the Mach number.

Degree of dynamic similarity

According to classical dimensional analysis, dynamic similarity is achieved when all dimensionless inputs governing a physical system are exactly matched between the scaled model and full-scale system. IT-π generalizes this concept by requiring similarity only for the optimal subset of l* dimensionless variables, relaxing the conservative requirement of matching all l variables prescribed by classical theory. Furthermore, the quantity ${{{\rm{DoS}}}}=1-{\tilde{\epsilon }}_{LB}\in [0,1]$ measures the degree of dynamic similarity that can be achieved. Consider, for example, a wind tunnel experiment of a scaled model of an aircraft where technical limitations restrict the control to only a few dimensionless variables ${{{\mathbf{\Pi }}}}^{\prime}$. In this scenario, the value of ${{{\rm{DoS}}}}=1-{\tilde{\epsilon }}_{LB}({{{\mathbf{\Pi }}}}^{\prime} )$ quantifies the degree of dynamic similarity attainable matching only those variables. This contrasts with traditional theory, which merely indicates whether dynamic similarity is or is not attained without offering insight into the extent of similarity when it is not perfectly achieved.

Characteristic scales

The characteristic scales of a physical problem refer to the length, time, mass, and other fundamental quantities that can be constructed from the parameters involved in the system under study. These are essential not only for non-dimensionalization, but also for understanding the order of magnitude of the variables controlling the system. To define these scales, we can divide the dimensional inputs into two sets ${{{\bf{q}}}}=[{{{{\bf{q}}}}}_{v},{{{{\bf{q}}}}}_{p}]$, where q_v consists of variables that vary in each simulation/experiment (i.e., dependent and independent variables), and q_p consists of variables that remain fixed for a given simulation/experiment but change across problem configurations (i.e., parameters). The characteristic scales are constructed from q_p. For example, for a pendulum with the governing equation ${{{\rm{d}}}}/{{{\rm{d}}}}t[\theta,\dot{\theta }]=[\dot{\theta },-g/l\sin \theta ]$, the variables are time (t), angular displacement (θ), and angular velocity ($\dot{\theta }$), yielding ${{{{\bf{q}}}}}_{v}=[t,\theta,\dot{\theta }]$, whereas the parameters include the pendulum length (l) and gravitational acceleration (g), giving q_p = [l, g]. As such, the characteristic length and time scales of the pendulum are obtained from q_p as $[{S}_{l},{S}_{t}]=[l,\sqrt{l/g}]$.

IT-π extracts the characteristic scales, ${{{\bf{S}}}}=[{S}_{1},{S}_{2},\ldots,{S}_{{n}_{u}}]$, from Π* by identifying the combination of quantities in q_p required to non-dimensionalize the variables in q_v [see the Supplementary Materials for the theory and algorithm]. In the previous example of the pendulum, IT-π will identify the optimal variable ${\Pi }^{ * }=\dot{\theta }{S}_{t}$ with characteristic time scale ${S}_{t}=\sqrt{l/g}$. If the dimensional group Π_i depends solely on quantities from q_p, then it represents a dimensionless parameter (rather than a dimensionless variable), as it encapsulates a relationship only between characteristic scales. One example of dimensionless parameter is the Reynolds number, that can be expressed as a ratio of two length scales and does not change for a given flow setup.

Self-similarity

Another capability of IT-π is the detection of self-similar variables—those that cannot be made dimensionless using only the parameters in q_p. In such instances, IT-π identifies the need to incorporate additional variables from q_v to non-dimensionalize Π*. The latter variable is then classified as self-similar, as it reveals an invariance between the ratios of the dependent and/or independent variables that govern the system.

Model efficiency

A foundational property of IT-π is its model-free formulation. This naturally leads to a definition of model performance relative to the theoretical optimum. Specifically, we introduce the model efficiency $\eta (f)={\epsilon }_{LB}^{ * }/{\epsilon }_{f}\in [0,1]$, which quantifies how closely the predictions of the model, ${\hat{\Pi }}_{o}=f({{{\mathbf{\Pi }}}})$, approach the theoretical limit. A low value of η indicates that the model underperforms relative to the optimal model. This underperformance may stem from inadequate inputs or insufficient model complexity (e.g., too few layers or neurons in an artificial neural network). Conversely, a value of η close to 1 implies that the model is extracting all the useful information from the inputs, and further improvements are not possible. An interesting interpretation of this efficiency is its analogy to the Carnot cycle in thermodynamics³²; in this context, it serves as the Carnot cycle of physical laws, setting a theoretical benchmark for the limits of predictive model performance. A diagnostic tool for assessing whether a model is suboptimal, optimal, or overfitting under finite-sample conditions is provided in the Supplementary Materials.

Validation

We validate IT-π on physical systems with known optimal dimensionless inputs and physical properties. Our test cases include the Rayleigh problem, the Colebrook equation, and the Malkus-Howard-Lorenz water wheel. Figure 3 summarizes these cases by presenting the system equations alongside the physical properties identified by IT-π, such as the optimal dimensionless inputs and outputs, self-similarity, physical regimes, characteristic scales, input ranking, and the information-theoretic irreducible error. Although IT-π infers a complete set of properties for each case, the figure highlights only the most relevant ones for clarity. Additional validation cases—including turbulent Rayleigh-Bénard convection and the Blasius laminar boundary layer—are discussed in the Methods.

Fig. 3: Summary of validation cases.

Schematic representations of the physical systems (a–c), the corresponding systems of equations, and the optimal dimensionless inputs and outputs discovered by IT-π, are shown alongside the inferred physical properties, including self-similarity, distinct physical regimes, characteristic scales, relevant dimensionless parameters (where applicable), and the irreducible model error. d Rayleigh problem: Optimal dimensionless velocity profiles ${\Pi }_{o}^{ * }$ as a function of Π*, with colors indicating different times t. e Colebrook equation: Contour plot of the prediction score R₁ (i.e., the relative importance of ${\Pi }_{1}^{ * }$) as a function of the dimensionless inputs. The result is obtained by dividing the dimensionless inputs Π* into 10 clusters using the KNN method. f, g, i Normalized irreducible error (${\tilde{\epsilon }}_{LB}$) for individual components of Π* and for all components combined, for (f) the Rayleigh problem, (g) the Colebrook equation, and (i) the Malkus waterwheel. Error bars indicate the uncertainty in the normalized irreducible error, computed as the difference between the error bound estimated using the full dataset and that estimated using half the data. Additional details regarding the symbols and definitions of all variables are provided in the main text.

The Rayleigh problem

³³ (see Fig. 3, Column 2) involves an infinitely long wall that suddenly starts moving with a constant velocity U in the wall-parallel direction within an initially still, infinite fluid. In the absence of a pressure gradient, the analytical solution for the flow velocity is $u=U{{\mathrm{erfc}}}\,\left(\xi /2\right)$, where $\xi=y/\sqrt{\mu t/\rho }$ is a self-similar variable that combines the distance from the wall (y), viscosity (μ), density (ρ), and time (t) such that the flow profile remains identical when scaled by U.

We generated samples of the velocity over time, q_o = u, with input variables q = [q_v, q_p], where q_v = [y, t] and q_p = [U, μ, ρ], and performed dimensionless learning using IT-π. The optimal dimensionless input and output discovered are Π* = yρ^0.5/(t^0.5μ^0.5) and ${\Pi }_{o}^{ * }=u/U$, respectively. These dimensionless variables coincide with the analytical solution and successfully collapse the velocity profiles across different times, as shown in Fig. 3(d). IT-π further identifies Π* as a self-similar variable because the characteristic length and time scales cannot be constructed using only U, μ and ρ. Finally, the near-zero irreducible error reported in Fig. 3(f) indicates that there exists a model capable of exactly predicting the output. Consequently, no additional dimensionless inputs are required. Note that IT-π identifies the need of only one dimensionless input (l* = 1), which is less than the number of two inputs (l = 2) inferred from the Buckingham-π theorem.

The Colebrook equation

³⁴ (see Fig. 3, Column 3) is a widely used formula in fluid mechanics for calculating the friction coefficient, C_f, which measures the resistance encountered by turbulent flow inside a pipe. Accurately determining C_f is crucial for designing efficient piping systems and predicting energy losses due to friction in various engineering applications³⁵. This coefficient depends on several factors, including the average roughness in the interior surface of the pipe (k), its diameter (D), the flow velocity (U), density (ρ), and viscosity (μ).

After generating samples for q_o = C_f and q = [U, ρ, D, k, μ], IT-π discovered the optimal dimensionless inputs ${\Pi }_{1}^{ * }=k/D$, and ${\Pi }_{2}^{ * }=\mu /(U\rho D)$, both of which are consistent with the equation. The former represents the relative roughness height, whereas the latter is related to the Reynolds number $R{e}_{D}\equiv 1/{\Pi }_{2}^{ * }$. The ranking in Fig. 3(g) shows that ${\Pi }_{1}^{ * }$ and ${\Pi }_{2}^{ * }$ individually yield normalized irreducible errors (${\tilde{\epsilon }}_{LB}$) in the output prediction of 40% and 20%, respectively. When both inputs are considered, they reduce the normalized irreducible error to nearly 0%. The physical regimes identified by IT-π are illustrated in panel (e) of Fig. 3. The figure depicts the prediction score R₁ for ${\Pi }_{1}^{ * }$ across the dimensionless input space, that quantifies the importance of the roughness height in predicting the friction coefficient C_f. The results reveal two flow regimes: one where the relative roughness height, ${\Pi }_{1}^{ * }$, predominantly determines the friction factor (R₁ ≈ 1), and a second regime where both the relative roughness height, ${\Pi }_{1}^{ * }$, and the Reynolds number, ${\Pi }_{2}^{ * }$, are needed to explain C_f. A similar conclusion can be drawn from R₂, which is omitted here for brevity. The regimes identified by IT-π are consistent with those from classical rough-wall turbulence analysis: the fully rough regime, where pressure drag dominates over viscous drag, and the transitionally rough regime, where both pressure and viscous drag influence the total drag^36,37.

The Malkus-Howard-Lorenz water wheel

³⁸ (see Fig. 3, Column 4) is a mechanical system that exhibits chaotic dynamics. Water flows into compartments on a rotating wheel, creating complex, unpredictable motion similar to that observed in the Lorenz system³⁹. The dynamics of the system depend on the angular velocity (ω) and mass distributions (m₁ and m₂). The key system parameters include the wheel’s radius (r), gravitational acceleration (g), moment of inertia (I), rotational damping (ν), leakage rate (K), and the water influx (ϕ).

Without loss of generality, we focus on the output $\dot{\omega }$, although the same approach extends to the other outputs, $\dot{{m}_{1}}$ and $\dot{{m}_{2}}$. The optimal dimensionless inputs discovered by IT-π are ${\Pi }_{1}^{ * }=rg{m}_{1}/(I{K}^{2})$ and ${\Pi }_{2}^{ * }=\nu \omega /(I{K}^{2})$ with the dimensionless output ${\Pi }_{o}^{ * }=\dot{\omega }/{K}^{2}$, which recover the analytically derived dimensionless variables. The ranking in Fig. 3(i) reports the predictive capabilities of the discovered Π* groups. Using ${\Pi }_{1}^{ * }$ or ${\Pi }_{2}^{ * }$ alone as inputs results in $\%{\tilde{\epsilon }}_{LB}$ of 50% and 30%, respectively, while considering both of them reduces considerably the normalized irreducible error. Finally, IT-π uncovers the characteristic time and mass scales as S_t = 1/K and S_m = IK²/(rg), along with the dimensionless parameter Π_p = ν/(IK). Hence, the dimensionless input and output can be rewritten as ${\Pi }_{o}^{ * }=\dot{\omega }{S}_{t}^{2}$, ${\Pi }_{1}^{ * }={m}_{1}/{S}_{m}$, and ${\Pi }_{2}^{ * }=\omega {S}_{t}{\Pi }_{p}$.

Applications

We have applied IT-π to dimensionless learning across several challenging problems, including supersonic turbulence, aerodynamic drag on both smooth and irregular surfaces, magnetohydrodynamic power generation, and laser-metal interaction. Here, we focus on the discovery of previously unknown scaling laws for supersonic flows over smooth and rough surfaces. The other applications can be found in the Methods section.

Accurate prediction of high-speed turbulence near solid boundaries is essential for advancing both commercial aviation and space exploration⁴⁰. However, significant challenges arise due to the complex interplay of the variables within these systems. The challenges are twofold. From a fundamental physics perspective, it is necessary to determine the scaling laws that govern key quantities of interest, such as mean velocity and wall fluxes. From a computational modeling standpoint, developing parsimonious models is needed for achieving accurate predictions. We leverage IT-π to tackle both challenges. We also demonstrate the use of the model efficiency in guiding the complexity of artificial neural network (ANN) to predict wall heat flux.

Dimensionless learning for mean velocity

Firstly, we discover a local scaling for the mean velocity profile in compressible turbulent channels using high-fidelity simulation data from existing literature^41,42. The dataset, which spans different Reynolds and Mach numbers, includes the mean velocity q_o = u and the flow state ${{{\bf{q}}}}=\left[y,\rho,\mu,{\rho }_{w},{\mu }_{w},{\tau }_{w}\right]$, where y is the wall-normal distance, ρ and μ are the local density and viscosity, ρ_w and μ_w are the density and viscosity at the wall, and τ_w is the wall shear stress. By limiting the number of inputs to one, IT-π identifies the optimal dimensionless variable with the highest predictive capabilities. The dimensionless inputs and outputs discovered by IT-π are summarized in Fig. 4 (Column 2, Row 2). Panels (c) and (d) demonstrate that the scaling identified by IT-π improves the collapse of the compressible velocity profiles across the range of Mach and Reynolds numbers considered compared to the classic viscous scaling⁴³. A closer inspection of the dimensionless input and output variables reveals that this improvement is accomplished by accounting for local variations in density and viscosity.

Fig. 4: Summary of compressible wall-bounded turbulence applications.

Left column: Velocity scaling for compressible turbulence. Right column: Wall shear stress and heat flux in supersonic turbulence over rough walls. a, b Schematic representations of the physical systems. c, d Solid lines of different colors represent velocity profiles at various Mach and Reynolds numbers; the dashed line corresponds to the incompressible turbulence velocity profile. c Viscous velocity profile u⁺ versus y⁺, where ${u}^{+}=u/\sqrt{{\tau }_{w}/{\rho }_{w}}$ and ${y}^{+}=y\rho \sqrt{{\tau }_{w}/{\rho }_{w}}/\mu$. d Dimensionless velocity profile obtained using IT-π scaling. e, f Dimensionless (e) wall shear stress and (f) wall heat flux plotted against the optimal dimensionless inputs. For compactness, the optimal dimensionless variables are expressed in terms of the Mach number (M), Prandtl number (Pr), and Reynolds number (Re), with definitions provided in the figure panels. The continuous lines represent data from the same simulation, colored by their mean ${\Pi }_{1}^{ * }$ to aid visualization. g–i Normalized irreducible error, with uncertainty shown as error bars reported in Fig. 3, for (g) dimensionless velocity profile, (h) wall shear stress, and (i) wall heat flux. Additional details regarding the symbols and definitions of all variables are provided in the main text.

Dimensionless learning for wall fluxes

Next, we identify the optimal dimensionless variables for predicting wall fluxes in compressible turbulence over rough walls²³. The output variables are the wall stress and heat flux, q_o = [τ_w, q_w], while the input variables are q = [y, u, ρ, T, T_w, μ, κ, c_p, k_rms, R_a, ES]. Here, y is the wall-normal distance; u, ρ, T, and μ represent the velocity, density, temperature, and viscosity, respectively; T_w is the wall temperature; κ is the thermal conductivity; and c_p is the specific heat capacity. The last three inputs (k_rms, R_a, ES) characterize the geometric properties of the surface roughness. These include the root-mean-square roughness height (k_rms), the first-order roughness height fluctuations (R_a), and the effective slope (ES)²³.

Figure 4 (Column 3, Row 2) summarizes the dimensionless forms of the optimal inputs and outputs discovered by IT-π. These forms combine the local Reynolds, Mach, Prandtl, and roughness numbers. The dimensionless wall shear stress and heat flux are presented in Fig. 4(e,f) as functions of the identified dimensionless inputs. For both wall shear stress and heat flux, two dimensionless inputs were sufficient to achieve ${\tilde{\epsilon }}_{LB}^{ * }\approx 0.1$, while the addition of further variables resulted in only marginal improvements in the irreducible error. Note that this number of variables is considerably smaller than the seven dimensionless variables anticipated by the Buckingham-π theorem.

Artificial neural network model for wall heat flux

To illustrate the application of the model efficiency η in guiding model complexity, we train three separate ANNs to predict the wall heat flux using the optimal dimensionless inputs from IT-π. The models are denoted by ANN₁, ANN₂ and ANN₃. Each model exhibits a different degree of complexity: ANN₁ has 9 tunable parameters (i.e., weights and biases), ANN₂ has 120, while ANN₂ has 781. The simplest model, ANN₁, achieves an efficiency of η₁ = 30%, indicating the need for additional layers and neurons to better capture the underlying input-output relationships. The second model, ANN₂, improves upon this with an efficiency of η₂ = 65%. The third model, ANN₃, attains an efficiency of η₃ = 98%, essentially matching the information-theoretic limit in predictability. As a result, we can conclude that no additional model complexity is needed beyond ANN₃. We show in the Supplementary Materials that training an ANN of similar complexity to ANN₃ using four suboptimal inputs from the Buckingham-π theorem results in a reduced efficiency of 82% despite using four inputs instead of two.

Comparison of IT-π with previous dimensionless learning methods

We compare IT-π against four dimensionless learning methods: Active Subspaces¹⁷, PyDimension¹², BuckiNet¹⁵, and BSM²¹. BuckiNet specifically refers to the constrained optimization approach via kernel ridge regression, which is one of the three approaches proposed by Bakarji et al. (2022). The comparison spans all validation and application cases discussed above. A summary of each method’s capabilities was provided in Table 1, and further details on their formulations are available in the Supplementary Materials.

The results are summarized in Table 2. The specific dimensionless variables identified by each method, along with implementation details and model parameters, are provided in the Methods section. Here, we offer an overview of the performance. In the validation cases, success is measured by the ability to recover the analytical optimal dimensionless variables. For the application cases—where ground-truth solutions are unknown—performance is quantified by the normalized irreducible error ${\tilde{\epsilon }}_{LB}$ associated with the input and output variables identified by each method, with lower values indicating better performance. The results clearly demonstrate that IT-π consistently outperforms or matches the other methods across both validation and application cases, particularly in the latter. It is worth noting that even in scenarios where existing methods successfully identify the optimal dimensionless variables, only IT-π is capable of simultaneously inferring key physical properties such as self-similar variables, distinct physical regimes, characteristic scales, and governing dimensionless parameters. Moreover, none of the other methods can provide a lower error bound that is independent of specific modeling assumptions.

Table 2 Comparison of Active Subspaces, PyDimension, BuckiNet, and BSM across validation and application cases: Rayleigh problem, Colebrook equation, Malkus waterwheel, Rayleight-Bénard convection, Blasius boundary layer, Velocity scaling, Wall flux, Skin friction, MHD generator, Laser-metal interaction

In terms of computational cost, all methods generate solutions within seconds to minutes for the cases considered [see Table 3]. Therefore, the predictability of the discovered dimensionless inputs and outputs is more important than the sheer computational cost of the method. This situation may change when dealing with a large number of samples. In such scenarios, IT-π offers efficient linear scaling with respect to the number of samples, performing similarly to or better than other methods. Beyond scaling, computational efficiency also depends on the structural design of the algorithm itself. Some of the previous approaches rely on a two-level optimization process, involving an outer loop that searches over candidate input combinations (e.g., powers of dimensionless groups), and an inner loop that fits model parameters (e.g., regression coefficients) to evaluate the performance of each candidate. In contrast, IT-π eliminates this overhead by directly evaluating the irreducible model error, bypassing the need to fit any model.

Table 3 Comparison of running times (in seconds) to compute the dimensionless variables for Active Subspaces, PyDimension, BuckiNet, BSM, and IT-π across different validation and application cases

Discussion

The concept of dimensional homogeneity—i.e., the invariance of physical laws under transformation of units—is arguably one of the most fundamental principles in physics. This simple yet powerful idea gave rise to the field of dimensional analysis, which is widely used across multiple disciplines. In this work, we have introduced IT-π, a formulation of dimensional analysis based on information. Our approach is rooted in the information-theoretic irreducible error, which allows us to identify the most predictive dimensionless numbers with respect to a quantity of interest. The idea goes beyond merely identifying a unique set of variables; it is the realization that the information content in the variables of a system is fundamental to understanding the governing physical laws and their inherent limitations^25,44,45. One can view IT-π as the Carnot cycle of physical laws: just as the thermodynamic Carnot cycle sets an upper limit on the work extractable from two thermal reservoirs—irrespective of the engine’s technology—IT-π extends this principle to predictive models irrespective of the modeling approach. In this interpretation, the predictive power of a set of variables is fundamentally constrained by the amount of information they share with the quantity to be predicted, regardless of whether the relationships are modeled through linear regression, sophisticated neural networks, or analytical equations.

We have shown that IT-π offers a complete set of dimensionless learning tools, including ranking inputs by predictability, identifying distinct physical regimes, uncovering self-similar variables, and extracting characteristic scales and dimensionless parameters. IT-π is also sensitive to the norm used to quantify errors and the optimal set of dimensionless variables may vary depending on the error metric of interest (e.g., prediction of ordinary versus rare events). Although some of these features are available through other methods, none encompass them all. Even in cases where alternative methods apply, IT-π distinguishes itself by being grounded in a theorem rather than relying on heuristic reasoning. This makes IT-π independent of specific modeling assumptions.

In additional to its model-free nature, IT-π offers unique capabilities that other methods do not, such as establishing bounds on the irreducible error and evaluating model efficiency. The former allows us to precisely determine the actual number of relevant dimensionless variables, l*, which is typically overestimated by the Buckingham-π theorem. Moreover, IT-π quantifies the degree of dynamic similarity achievable with the optimal variables, rather than providing merely a binary yes-or-no answer as classical dimensional analysis does. This feature can be decisive in designing laboratory experiments for extrapolation to real-world applications. For example, consider predicting the heat flux over a rough surface as discussed in the application above. According to Buckingham-π, seven dimensionless variables would be required. If three different values must be measured to capture the scaling behavior of each variable, that would entail ~3⁷ = 2187 experiments. In contrast, IT-π determined that only two dimensionless variables are necessary to achieve a dynamic similarity of 92% (i.e., an 8% normalized irreducible error). This entails a significantly reduced effort of only 3² = 9 experiments. The same reasoning applies to the construction of predictive modeling: models with fewer inputs require orders of magnitude less training data compared to those with high-dimensional inputs. In the previous example, this factor would be of the order of 1000.

Model efficiency is another distinctive feature of IT-π that can guide the structural complexity in model design. For instance, machine-learning models are typically built with various architectures and tunable parameters (e.g., weights and biases). In this context, the model efficiency can determine whether a model operates near its theoretical optimum—eliminating the need to explore alternative architectures—or if there is potential for further improvement. We have applied this concept to determine the optimal number of tunable parameters for developing an ANN model for wall heat prediction. Our results have shown that ANNs with only a few tens of parameters fail to fully leverage the available input information, whereas nearly 1000 parameters are necessary to extract that information efficiently.

We have successfully validated IT-π using cases with established optimal dimensionless variables. These include classic problems in fluid dynamics and dynamical systems, such as the Rayleigh problem, the Colebrook equation, the Malkus-Howard-Lorenz water wheel, the Rayleigh-Bénard convection, and the Blasius laminar boundary layer. Moreover, IT-π was applied to conduct dimensionless learning for supersonic turbulence, aerodynamic drag on both smooth and irregular surfaces, MHD power generation, and high-energy material processing. In all cases, IT-π has been shown to outperform or match existing methods for dimensionless learning.

It is also important to acknowledge some shortcomings of the approach. The first relates to its model-free nature. As mentioned above, one of the key strengths of IT-π is that its results do not depend on any underlying model. However, some may view this as a weakness, as it leaves the task of identifying the optimal model to the practitioner. A more evident challenge is the amount of data required. When many variables are involved, IT-π necessitates the estimation of mutual information in high dimensions. Although advanced tools exist for high-dimensional estimation^{46,47,48,49,50}, the curse of dimensionality can render results inconclusive in certain scenarios. Therefore, estimating the uncertainty in the normalized irreducible error is crucial to determine whether the conclusions drawn from IT-π are statistically significant or merely reflect insufficient data. In all the results presented above, we have quantified the statistical uncertainty in the irreducible error, Δϵ_LB, which is represented by the error bars in the plots. The methodology used to estimate uncertainty in IT-π under a finite sample regime is detailed in the Supplementary Materials, along with a further evaluation of the sensitivity of IT-π to the amount of available data.

In conclusion, IT-π offers a new perspective to dimensional analysis rooted in information. Its broad applicability makes it a useful tool across diverse disciplines—from fluid dynamics and thermodynamics to electromagnetism, astrophysics, materials science, and plasma physics. By effectively addressing challenges in scaling laws, similarity solutions, and the identification of governing dimensionless parameters, IT-π provides a powerful tool for dimensionless learning of complex physical systems.

Methods

Constructing dimensionless variables using the Buckingham-π theorem

The Buckingham-π theorem is used to construct dimensionless candidates Π and Π_o. The i-th dimensionless variable has the form

$${\Pi }_{i}={q}_{1}^{{a}_{i1}}\cdot {q}_{2}^{{a}_{i2}}\cdots {q}_{n}^{{a}_{in}}\equiv {{{{\bf{q}}}}}^{{{{{\bf{a}}}}}_{i}},$$

where ${{{{\bf{a}}}}}_{i}={[{a}_{i1},{a}_{i2},\ldots,{a}_{in}]}^{T}$ is the vector of exponents for Π_i. The input candidate Π is then obtained from the solution to Da_i = 0, where D is the dimension matrix containing the powers of the fundamental units for q, ${{{\bf{D}}}}=[{{{{\bf{d}}}}}_{1},{{{{\bf{d}}}}}_{2},\ldots,{{{{\bf{d}}}}}_{n}],$ and d_i is the dimensional vector for the physical quantity q_i. For example, the velocity q₁ = u = [length]¹[time]⁻¹ has d₁ = [1, −1, 0, 0, 0, 0, 0]^T and so on. The solution a_i can be expressed as ${{{{\bf{a}}}}}_{i}={\sum }_{j=1}^{n-{n}_{u}}{c}_{ij}{{{{\bf{w}}}}}_{j}={{{\bf{W}}}}{{{{\bf{c}}}}}_{i},$ where ${{{\bf{W}}}}=[{{{{\bf{w}}}}}_{1},{{{{\bf{w}}}}}_{2},\ldots,{{{{\bf{w}}}}}_{n-{n}_{u}}]$ is the matrix of basis vectors of the null space of D, and ${{{{\bf{c}}}}}_{i}={[{c}_{i1},{c}_{i2},\ldots,{c}_{i(n-{n}_{u})}]}^{T}$ is the coefficient vector corresponding to a_i. In conclusion, non-dimensional variables are obtained by ${{{\mathbf{\Pi }}}}={{{{\bf{q}}}}}^{{{{\bf{WC}}}}}=[{{{{\bf{q}}}}}^{{{{\bf{W}}}}{{{{\bf{c}}}}}_{1}},{{{{\bf{q}}}}}^{{{{\bf{W}}}}{{{{\bf{c}}}}}_{2}},\ldots,{{{{\bf{q}}}}}^{{{{\bf{W}}}}{{{{\bf{c}}}}}_{l}}],$ where ${{{\bf{C}}}}=\left[{{{{\bf{c}}}}}_{1},{{{{\bf{c}}}}}_{2},\ldots,{{{{\bf{c}}}}}_{l}\right]$. The dimensionless output Π_o is constructed similarly with the matrix of basis vectors W_o and coefficients c_o. An important consideration when some variables q_i may be negative is to generalize the formulation to avoid imaginary numbers. Specifically, we define ${\Pi }_{i}={{{\rm{sgn}}}}({q}_{1})\,| {q}_{1}{| }^{{a}_{i1}}\,{{{\rm{sgn}}}}({q}_{2})\,| {q}_{2}{| }^{{a}_{i2}}\,\cdots \,{{{\rm{sgn}}}}({q}_{n})\,| {q}_{n}{| }^{{a}_{in}},$ where ∣ ⋅ ∣ denotes the absolute value and ${{{\rm{sgn}}}}(\cdot )$ is the sign function. This approach preserves the sign information of each q_i while ensuring that the resulting dimensionless variables remain real-valued.

Information content of variables

Consider the random variables Π_o and Π, whose realizations are denoted by π_o and π, respectively. They are characterized by the joint probability distribution ${\rho }_{{\Pi }_{o},{{{\mathbf{\Pi }}}}}({\pi }_{o},{{{\mathbf{\pi }}}})$ with corresponding marginal distributions ${\rho }_{{\Pi }_{o}}({\pi }_{o})$ and ρ_Π(π). The Rényi mutual information of order α > 0³⁰ between Π_o and Π is

$${I}_{\alpha }({\Pi }_{o};{{{\mathbf{\Pi }}}})={h}_{\alpha }({\Pi }_{o})-{h}_{\alpha }({\Pi }_{o}| {{{\mathbf{\Pi }}}}),$$

where h_α(Π_o) and h_α(Π_o∣Π) are the Rényi entropy and conditional Rényi entropy, respectively, which are given by

$${h}_{\alpha,o}\equiv {h}_{\alpha }({\Pi }_{o})=\mathop{\lim }_{\alpha ^{\prime} \to \alpha }\frac{1}{1-\alpha ^{\prime} }\log \left(\int{\rho }_{{\Pi }_{o}}^{\alpha ^{\prime} }({\pi }_{o})\,{{{\rm{d}}}}{\pi }_{o}\right),$$

$${h}_{\alpha }\left({\Pi }_{o}| {{{\mathbf{\Pi }}}}\right)=\mathop{\lim }_{{\alpha }^{\prime}\to \alpha }\frac{1}{1-{\alpha }^{{\prime} }}\int{\rho }_{{{{\mathbf{\Pi }}}}}({{{\mathbf{\pi }}}})\log \left(\int{\rho }_{{\Pi }_{o}| {{{\mathbf{\Pi }}}}}^{{\alpha }^{{\prime} }}\left({\pi }_{o}| {{{\mathbf{\pi }}}}\right)d{\pi }_{o}\right)d{{{\mathbf{\pi }}}}.$$

The Rényi mutual information between Π_o and Π quantifies the amount of information about Π_o that can be extracted from Π. It generalizes the Shannon mutual information²⁹ by introducing the order parameter α, which is particularly valuable in situations where emphasis on tail distributions is critical. IT-π leverages the parameter α to adjust sensitivity with respect to the L_p-norm, balancing the influence of high-probability events against that of low-probability events. When the value of α is equal to one, the Rényi entropy corresponds to the Shannon entropy²⁹.

Optimization with CMA-ES

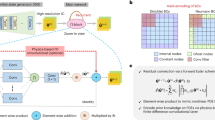
The optimal dimensionless input and output variables are identified by solving Eq. (2), where the candidate sets Π and Π_o are constructed using the previously defined coefficient matrix C. The optimization is carried out over the entries of C. Specifically, the problem $\arg {\min }_{{{{\mathbf{\Pi }}}},{\Pi }_{o}}{\max }_{\alpha }[{\epsilon }_{LB}]$ is solved using the Covariance Matrix Adaptation Evolution Strategy (CMA-ES)³¹, a stochastic, derivative-free algorithm designed for non-linear and non-convex continuous optimization problems. CMA-ES generates candidate solutions by sampling from a multivariate Gaussian distribution and iteratively updates its mean and covariance matrix to efficiently explore the search space and converge toward an optimal solution that maximizes the mutual information. To determine the value of α that yields the tightest possible bound, ${\max }_{\alpha }[{\epsilon }_{LB}]$, we perform a golden-section search over the interval $\alpha \in \left(1/(1+p),10\right]$⁵¹. A schematic overview of the IT-π workflow for discovering optimal dimensionless variables is shown in Fig. 5, and the corresponding pseudocode is provided in the Supplementary Materials.

Fig. 5: Workflow of IT-π for discovering optimal dimensionless variables.

This schematic illustrates a specific example in which the input dimensionless variables Π = [Π₁, Π₂] are optimized. Each generation of the CMA-ES algorithm maintains a population of candidate solutions (represented by blue dots), where each individual encodes a set of exponents (c₁, c₂) that define the candidate dimensionless variables. For each individual, the variables are constructed as ${\Pi }_{1}={{{{\bf{q}}}}}^{{{{\bf{W}}}}{{{{\bf{c}}}}}_{1}}$ and ${\Pi }_{2}={{{{\bf{q}}}}}^{{{{\bf{W}}}}{{{{\bf{c}}}}}_{2}}$, where q represents the set of dimensional quantities and W is the matrix of basis vectors. The fitness of each candidate is evaluated using the irreducible error across Rényi orders, $J={\max }_{\alpha }[{\epsilon }_{LB}]={\max }_{\alpha }\left[{e}^{-{I}_{\alpha }({\Pi }_{o};{{{\mathbf{\Pi }}}})}\cdot c(\alpha,p,{h}_{\alpha,o})\right],$ where I_α denotes the Rényi mutual information. The optimal α is found through golden-section search in the range (1/(1 + p), 10]. The algorithm evolves the population across generations by updating the mean and covariance of the sampling distribution, navigating the fitness landscape (whose constant-value contours are shown as dark purple dashed lines) to minimize the irreducible error. The final generation yields the maximally predictive dimensionless variables ${{{{\mathbf{\Pi }}}}}^{ * }=[{\Pi }_{1}^{ * },{\Pi }_{2}^{ * }]=[{{{{\bf{q}}}}}^{{{{\bf{W}}}}{{{{\bf{c}}}}}_{1}^{ * }},{{{{\bf{q}}}}}^{{{{\bf{W}}}}{{{{\bf{c}}}}}_{2}^{ * }}]$. The dimensionless output Π_o can either be included in the optimization or treated as fixed. For clarity, this schematic illustrates only the optimization of c₁ and c₂ associated with the input variables.

In the main text, the error norm is set to p = 2, which is the standard choice for measuring prediction errors. An illustrative example demonstrating the use of alternative L_p norms is provided in the Supplementary Materials. The CMA-ES algorithm is executed with a population size of 300, coefficient bounds c_ij ∈ [−2, 2], a maximum of 50,000 iterations, and an initial standard deviation of 0.5. For all cases presented above, the exponents c_ij are rounded to a finite number of significant digits without compromising the value of ϵ_LB. When ${\Pi }_{o}^{ * }$, p, and α are fixed, the function c(α, p, h_α,o) becomes constant, and the task of identifying the most predictive non-dimensional input simplifies to maximizing mutual information: ${{{{\mathbf{\Pi }}}}}^{ * }=\arg {\max }_{{{{\mathbf{\Pi }}}}}{I}_{\alpha }\left({\Pi }_{o}^{ * };{{{\mathbf{\Pi }}}}\right).$

Details about validations cases

The Rayleigh problem dataset consists of samples uniformly generated over y ∈ [0, 1] m, t ∈ [0.01, 5] s, U ∈ [0.5, 1.0] m/s, $\mu \in [1{0}^{-3},1{0}^{-2}]\;{{{\rm{kg/m/s}}}}$ and ρ = 1 kg/m³. For the Colebrook dataset, ${\log }_{10}R{e}_{D}$ is uniformly sampled in [3,5], yielding Reynolds numbers in $[1{0}^{3},1{0}^{5}]$, and ${\log }_{10}(k/D)$ is uniformly sampled in [−5, −0.7]. The discovered dimensionless inputs $[{\Pi }_{1}^{ * },{\Pi }_{2}^{ * }]$ are divided into 10 clusters using the K-Nearest Neighbors (KNN) clustering algorithm⁵². For the Malkus waterwheel dataset, the physical variables are uniformly sampled within the following ranges: radius r ∈ [0.3, 0.7] m, water influx rate q ∈ [0.0001, 0.0005] kg/s, moment of inertia I ∈ [0.05, 0.2] kg ⋅ m², rotational damping ν ∈ [0.01, 0.1] kg ⋅ m²/s, and water leakage rate K ∈ [0.01, 0.1] s⁻¹, gravitational acceleration g = 9.8 m/s². The system is simulated over a time span of t ∈ [0, 50] s with 500 evaluation points.

Details about application cases

Data for compressible wall-bounded turbulence application

The dataset for mean-velocty transformation comprises mean flow profiles from direct numerical simulation (DNS) of four compressible channel flows and two compressible pipe flows^41,42, characterized by bulk Mach numbers $\left({M}_{b}={U}_{b}/\sqrt{\gamma R{T}_{w}}\right)$ between 1.5 and 4.0, and bulk Reynolds numbers $\left(R{e}_{b}={\rho }_{b}{U}_{b}\delta /{\mu }_{w}\right)$ from 8430.2 to 23977.6, where ${\rho }_{b}=1/\delta \int_{0}^{\delta }\rho dy$ and ${U}_{b}=1/\delta \int_{0}^{\delta }udy$ are the bulk density and velocity, respectively; T_w and μ_w are the mean temperature and dynamic viscosity at the wall; and δ is the channel half-height. The dataset for wall shear stress and heat flux in supersonic turbulence over rough wall includes DNS of turbulent channel flows over and rough surfaces²³. Ten irregular, multiscale rough surfaces were generated using Gaussian probability density functions. Simulations were driven with uniform momentum and energy sources to achieve ${M}_{c}={U}_{c}/\sqrt{\gamma R{T}_{w}}=0.5,1,2,4$ and Re_c = ρ_cU_cδ/μ_w = 4000, 8000, 16000, where ρ_c and U_c are the mean density and velocity at the channel centerline, respectively; T_w and μ_w are the mean temperature and dynamic viscosity at the wall; and δ is the channel half-height.

Neural networks for predicting the wall flux

The data is split into training (70%), validation (15%), and testing (15%) sets, with L₂ regularization (factor 0.9) used to control overfitting. Each network follows a feedforward architecture. The simplest network ANN₁ consists of 1 hidden layers with 2 neurons, ANN₂ have 2 hidden layers with 10 neurons per layer, while ANN₃ have 4 hidden layers with 15 neurons per layer. All are trained using gradient descent with momentum and an adaptive learning rate. The training process employs a learning rate of 10⁻⁵, with a maximum of 50000 iterations and a validation tolerance of 40,000 epochs without improvement before stopping.

Additional validation cases

We validate IT-π using datasets from previous studies^12,15,21 with known optimal dimensionless inputs: the turbulent Rayleigh-Bénard convection and the Blasius laminar boundary layer. Figure 6 summarizes each case, detailing the system equations, optimal dimensionless inputs and outputs discovered from IT-π. The figure also shows a visualization of ${\Pi }_{o}^{ * }$ as a function of Π*.

Fig. 6: Summary of additional validation cases.

System schematics (a, b), system equations (c, d), optimal dimensionless inputs and outputs discovered from IT-π (e, f), visualization of ${\Pi }_{o}^{ * }$ as a function of Π* (g, h). Left column: Rayleigh-Bénard convection system; right column: Blasius laminar boundary layer. Additional details regarding the symbols and definitions are provided in the main text.

The Rayleigh-Bénard convection system

(Fig. 6, Column 2) describes convection occurring in a planar horizontal layer of fluid heated from below in a container with height h. The system is governed by the equations in Fig. 6 (Column 2, Row 2), with parameters include viscosity (μ), density (ρ), temperature differences between the top and the bottom plane (ΔT), thermal expansion coefficient (α), and thermal diffusivity (κ). The dimensionless output is set to the Nusselt number ${\Pi }_{o}^{ * }={q}_{w}h/\left(\lambda \Delta T\right)$, where q_w is the heat flux, λ is the thermal conductivity. The data¹² include samples of the output q_o = q_w, inputs q = [h, ΔT, λ, g, α, μ, ρ, κ]. IT-π discovered the optimal dimensionless input ${\Pi }^{ * }=\rho {h}^{3}\Delta Tg\alpha /\left(\mu \kappa \right)$, which is consistent with the Rayleigh number⁵³.

The Blasius laminar boundary layer

(Fig. 6, Column 3) describes the two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. The system is governed by the equations in Fig. 6 (Column 3, Row 2), with variables including the streamwise velocity (u), wall-normal velocity (v), free-stream velocity (U), pressure (p), viscosity (μ), density (ρ), streamwise distance (x) and wall normal distance (y). We focus on the output u. The data¹⁵ include samples of the output q_o = u, and inputs ${{{\bf{q}}}}=\left[U,\mu,\rho,x,y\right]$. IT-π discovers the optimal, self-similar, dimensionless input ${\Pi }^{ * }={U}^{0.5}{y}^{1.0}{\rho }^{0.5}/\left({\mu }^{0.5}{x}^{0.5}\right)$, which is equivalent to the analytical Blasius similarity variable⁵⁴.

Additional application cases

Skin friction under pressure gradient effects

We apply IT-π to identify the most predictive model for wall friction in turbulent flow over smooth surfaces under different mean pressure gradients (see Fig. 7, Column 2). Friction scaling and predictive modeling in smooth-wall turbulence have been extensively studied for over a century, owing to their crucial role in reducing operational costs in engineering applications such as pipeline transport and aviation. We use the data compiled by Dixit et al.⁵⁵, which includes experimental measurements and simulation results for various flow conditions: mean zero-pressure-gradient (ZPG) flows in channels, pipes, and turbulent boundary layers; mean adverse-pressure-gradient (APG) turbulent boundary layers; mean favorable-pressure-gradient (FPG) turbulent boundary layers; and turbulent boundary layers on the pressure side of an airfoil. For a detailed description of the data, please refer to Dixit et al.⁵⁵ and the references therein.

Fig. 7: Summary of additional application cases.

System schematics (a–c), optimal dimensionless inputs and outputs discovered from IT-π (d–f), visualization of ${\Pi }_{o}^{ * }$ as a function of Π* (g–j). Second column: skin friction under pressure gradient effects; third column: magnetohydrodynamics power generator; fourth column: laser-metal interaction. Additional details regarding the symbols and definitions are provided in the main text.

The dimensional input variables include ${{\bf{q}}}=[{U}_{\infty }, \mu,\rho,M,\delta,{\delta }^{ * },{\theta }_{m}]$, where U_∞ is the free-stream velocity, μ is the viscosity, ρ is the density, $M=\! \int_{0}^{\delta }{u}^{2}dy$ is the total mean-flow kinetic energy, δ is the boundary layer thickness at 99% of the free-stream, ${\delta }^{ * }=\int_{0}^{\delta }\left(1-u/{U}_{\infty }\right)dy$ is the boundary layer displacement thickness, and ${\theta }_{m}=\int_{0}^{\delta }u/{U}_{\infty }\left(1-u/{U}_{\infty }\right)dy$ is the boundary layer momentum thickness, where y is the wall-normal distance. The output variable ${q}_{o}={u}_{\tau }=\sqrt{{\tau }_{w}/{\rho }_{w}}$ is the friction velocity, with τ_w the wall shear stress and ρ_w the flow density at the wall. We define the dimensionless output as ${\Pi }_{o}^{ * }={u}_{\tau }/{U}_{\infty }$, where u_τ is the friction velocity, as this is a common form for modeling skin friction. For simplicity, we restrict the number of input variables to one. Under these conditions, IT-π identifies the most predictive single variable as

$${\Pi }^{ * }={\left(\frac{\rho {U}_{\infty }\delta }{\mu }\right)}^{\frac{4}{7}}{\left(\frac{{\delta }^{ * }}{{\theta }_{m}}\right)}^{\frac{9}{10}}{\left(\frac{{U}_{\infty }\mu }{\rho M}\right)}^{\frac{4}{9}},$$

with the exponents constrained to be rational numbers. Figure 7(g),(h) demonstrates that the scaling identified by IT-π significantly improves the collapse of the friction velocity data compared to the classic approach⁴³. Π* is the product of three dimensionless groups: the first two correspond to the classic free-stream Reynolds number and the shape factor. The third term is more interesting: it represents the transfer of kinetic energy from mean flow to large eddies of turbulence, which is derived from the momentum integral equation by Dixit et al.⁵⁶.

Magnetohydrodynamics power generator

Magnetohydrodynamic (MHD) generators represent an innovative solution for sustainable and clean energy production^57,58. Unlike conventional generators that rely on moving mechanical components—such as turbines—MHD generators convert thermal energy directly into electrical power. This direct conversion not only minimizes mechanical losses but also allows these systems to operate efficiently at extremely high temperatures⁵⁸. Moreover, owing to their unique operational characteristics, MHD generators offer the highest theoretical thermodynamic efficiency among all established methods of electricity generation. In this section, we employ IT-π to identify the critical dimensionless input variables governing the flow velocity within the generator (see Fig. 7, Column 3).

The dataset used is obtained from numerical simulations of steady-state MHD duct flow reported by Glaws et al.⁵⁹. In this MHD generator configuration, an electric current is induced by propelling a conducting fluid through a square cross-sectional duct at a specified flow rate while subjecting it to an externally applied vertical magnetic field. The interaction between the moving fluid and the magnetic field causes the field lines to bend, thereby producing a horizontal electric current. The set of dimensional input variables is defined as ${{{\bf{q}}}}=[h,\mu,\rho,\frac{dp}{dx},\eta,{B}_{0}],$ where h denotes the side length of the square duct, μ and ρ represent the viscosity and density of the conducting fluid, respectively, $\frac{dp}{dx}$ is the applied pressure gradient, η is the magnetic resistivity of the fluid, and B₀ is the magnitude of the applied magnetic field.

The quantity to predict is the average flow velocity, u, and we are interested in identifying the single dimensionless input with the highest predictive capability. Using the dimensionless output ${\Pi }_{o}^{ * }=u\,\rho \,h/\mu$, IT-π identifies the most predictive dimensionless input as ${\Pi }^{ * }={h}^{3}\,\rho \,\frac{dp}{dx}/{\mu }^{2}$. This result is consistent with physical intuition: the average flow velocity is fundamentally governed by the balance between the driving force (represented by the pressure gradient) and the resisting force (arising from viscosity). Hence, the dimensionless group Π* encapsulates the interplay between these competing effects.

Laser-metal interaction

Quantifying laser-metal interactions is critical for improving precision in advanced manufacturing processes such as additive manufacturing, laser cutting, and welding in aerospace applications⁶⁰. We employ IT-π to identify the single most predictive dimensionless input governing the formation of a keyhole in a puddle of liquid metal melted by the laser (see Fig. 7, Column 4).

The dataset used comes from high-speed X-ray imaging experiments of keyhole dynamics reported by Xie et al.¹². The set of dimensional input variables is defined as

$${{{\bf{q}}}}=\left[\eta P,{V}_{s},{r}_{0},\alpha,\rho,{C}_{p},{T}_{1}-{T}_{0}\right],$$

where ηP denotes the effective laser power, V_s represents the laser scan speed, r₀ is the laser beam radius, and α, ρ, and C_p are the thermal diffusivity, density, and heat capacity of the material, respectively. T₁ − T₀ is the temperature difference between melting and ambient conditions. The quantity of interest is the normalized keyhole depth, defined as ${\Pi }_{o}^{ * }=e/{r}_{0}$. IT-π identifies the most predictive dimensionless input as ${\Pi }^{ * }=\frac{{\eta P}^{0.7}}{{{V}_{s}}^{0.3}{\rho }^{0.7}{{C}_{p}}^{0.7}{({T}_{1}-{T}_{0})}^{0.7}{r}_{0}{\alpha }^{0.4}}.$

Details about comparison with other dimensionless learning methods

The dimensionless input discovered by other methods using the same output ${\Pi }_{o}^{ * }$, is summarized in the Supplementary Material. Active Subspaces employs Gaussian Process Regression with a radial basis function (RBF) kernel, which is initialized with a width of 1 and optimized using 5 restarts. The gradients of the response surface are estimated using finite differences. PyDimension uses a 10th-order polynomial regression model, optimizing the basis coefficients with a pattern search method that is initialized on a grid ranging from  −1 to 1 in intervals of 0.1. BuckiNet utilizes Kernel Ridge Regression with an RBF kernel (width = 1) and a regularization parameter of 1 × 10⁻⁴. Its optimization includes an L₁ regularization term of 1 × 10⁻³. For BSM, the optimization minimizes a distance-based loss over 40 iterations, balancing prediction accuracy and dimensional consistency with a weight of 1 × 10⁻³. It is also worth noting that the results were found to be sensitive to the model parameters for each method. For all validation cases where the optimal solution is known, we tune the hyperparameters of all baseline methods to best match the known results. In application cases (where the true solution is not known), we evaluate the performance of existing methods using the standard or recommended hyperparameter settings provided by their original implementations. This approach reflects practical usage scenarios, where domain users often rely on default or minimally tuned settings. A discussion on the influence of hyperparameters and the sensitivity of each method is provided in the Supplementary Material.

The corresponding running times for methods across various cases are summarized in Table 3. Assuming identical optimization methods and candidate solutions across all approaches, the primary cost differences arise from the function evaluation of a single solution. Active Subspaces and BuckiNet require kernel matrix inversions with a computational cost of $O({N}_{{{{\rm{samples}}}}}^{3})$, where N_samples is the number of data samples. For PyDimension, fitting an m-th order polynomial model incurs a cost of $O({N}_{{{{\rm{samples}}}}}^{2}{m}^{2})$. In the case of BSM, the cost is $O\left({N}_{{{{\rm{samples}}}}}\cdot {n}_{t}^{2}\right)$, where n_t is the number of independent variables. For IT-π, when using the histogram method with N_bins bins to estimate the probability distribution, the computational cost is $O\left({N}_{{{{\rm{samples}}}}}+{N}_{{{{\rm{bins}}}}}^{l+1}\right)$.